Abstract
Precision measurements of the pendulum period as a function of the amplitude can now be made with a variety of instruments including MEMs gyro/accelerometers, and thus theoretical expressions are required for comparison. Unfortunately exact solution of the pendulum equation involves elliptic integrals, which cannot be expressed in terms of elementary functions, and therefore a wide variety of approximations have been published. These range from simple single-term formulae to more sophisticated equations, which apply to a wider range of amplitudes, to an iterative procedure for calculating the precise period. The published approximations are compared as Taylor series expansions, and graphically to indicate their accuracy and their regions of applicability.
Export citation and abstract BibTeX RIS
1. Introduction
The small angle oscillations of simple and compound pendulums are widely used in introductory physic courses [1] as examples of simple harmonic motion (SHM) and a wide array of instrumentation is now available for laboratory measurements. Period measurements are typically made with photogates [2] while the angular motion can be recorded on video [3], by rotary motion sensors [4], or symmetric differential capacitive sensors [5]. However, the advent of micro electro mechanical, MEMs, gyros/accelerometers, such as those in smartphones, has made detailed measurement of pendulum motion, with amplitude up to 180°, easy to implement in the undergraduate laboratory. Photogate measurements of the pendulum period can have an intrinsic precision of ±2 µs. With random perturbations generally increasing the scatter to ±20 µs, however, commercial IR LED photogates have an uncertainty ±100 µs [2], i.e. typically ±0.01% of the period. Even with rudimentary analysis of MEMs gyro data a precision of 0.2% can easily be achieved provided the parameters of the pendulum are carefully controlled, a precision bearing is used and damping minimized. When such data is compared with an approximate expression for the period, the latter should therefore be of comparable or greater accuracy, i.e. at least 0.1% and preferably 0.01%.
Galileo observed the oscillation of pendulums in the cathedral at Pisa in 1581 and, within the precision of his pulse, concluded that the period was independent of the amplitude [6]. In 1673 Huygens derived the expression  for the period of small oscillations, where l is the length of the simple pendulum and g is the acceleration due to gravity, and that the tautochrone is a cycloid [7], i.e. that pendulums are not isochronous. The theory for finite amplitude oscillations of pendulums was first treated by Euler [8] in 1736, with Bernoulli developing the first approximation
for the period of small oscillations, where l is the length of the simple pendulum and g is the acceleration due to gravity, and that the tautochrone is a cycloid [7], i.e. that pendulums are not isochronous. The theory for finite amplitude oscillations of pendulums was first treated by Euler [8] in 1736, with Bernoulli developing the first approximation  in 1749, where φ0 is the amplitude in radians.
in 1749, where φ0 is the amplitude in radians.
The equation for the angular displacement  of a pendulum is [1]
of a pendulum is [1]  , see below, and for small amplitude this can be approximated as
, see below, and for small amplitude this can be approximated as  , leading to SHM with a period T0 = 2π/ω0 independent of the amplitude. However, for large angular displacements the full non-linear equation
, leading to SHM with a period T0 = 2π/ω0 independent of the amplitude. However, for large angular displacements the full non-linear equation  is required, the solution of which leads to a variation of the period of oscillation with amplitude [1].
is required, the solution of which leads to a variation of the period of oscillation with amplitude [1].
The standard treatment of the large angle period of a pendulum is based on integration of the velocity over a quarter oscillation, as derived from conservation of energy, and leads to an elliptic integral of the first kind [1], which can be approximated by a series expansion [1]. Carvalhaes and Suppes [9] have utilized the fact that the arithmetic-geometric mean, AGM, rapidly converges to the elliptic integral of the first kind and use the AGM to calculate precise values of the period. Qureshi, Rafat and Azad [10] give an exact equation, but in terms of hypergeometric functions. However, for some applications a simple approximate formula for the variation of the period with amplitude is useful and such formulae continue to be published. Some of the approximate formulae have previously been compared [11–14] and the present paper presents a more comprehensive review. The formulae, together with their Taylor series expansions, and their percentage deviations Δ(30°) and Δ(90°) from the exact period at amplitudes of 30° and 90° are listed in table 1. In order to illustrate the accuracy and range of applicability of the various approximate formulae their percentage deviations from the exact period are presented as a function of the amplitude in figures 3–5. An Excel spreadsheet of the percent deviations is available as supplementary material (http://stacks.iop.org/EJP/42/015005/mmedia).
2. Pendulum oscillations
Taking moments about the pivot P of a pendulum of mass m and radius of gyration k, suspended with its center of mass a distance a from the pivot, see figure 1, in the absence of dissipative forces, leads to


where Ip is the moment of inertia about the horizontal pivot, g is the acceleration due to gravity and φ is the angular displacement from the equilibrium position,  , i.e.
, i.e.  for a simple pendulum of length l. Then for small angles, approximating sin φ ≈ φ, and release from rest i.e.
for a simple pendulum of length l. Then for small angles, approximating sin φ ≈ φ, and release from rest i.e.  ,
,  leads to the oscillatory solution
leads to the oscillatory solution  with amplitude φ0, and small angle period [1]:
with amplitude φ0, and small angle period [1]:

Figure 1. A compound pendulum of mass m and radius of gyration k, suspended with its center of mass a distance 'a' from the fixed bearing at P.
Download figure:
Standard image High-resolution image3. Large amplitude period
The period of oscillation at finite amplitude φ0 can be derived by integrating the angular velocity  as derived from conservation of energy, i.e.
as derived from conservation of energy, i.e.  so
so
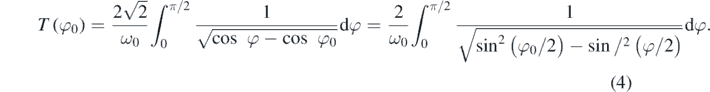
This is an elliptic integral of the first kind, which cannot be expressed in terms elementary functions. It can however be expanded in terms of the series [1, 15–19]:
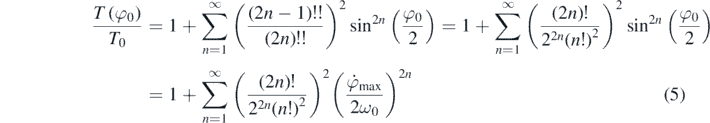
where  is the maximum angular velocity [2]. Then expanding
is the maximum angular velocity [2]. Then expanding  as
as
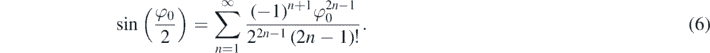
And collecting terms [20]:
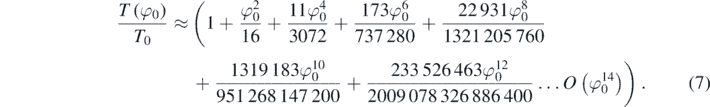
This truncated series, of which the first term was derived by Bernoulli, and only the first three terms are usually employed, provides a lower limit for the period [21].
The period  as a function of the amplitude φ0 can be rapidly evaluated to any degree of precision by the arithmetic-geometric mean (AGM) as described by Carvalhaes and Suppes [9, 22, 23]. It can be easily implemented in a spreadsheet, and is used here as the exact value for comparison with the approximate expressions. The paper by Villarino [22] establishes the rigorous upper and lower bounds for the errors in a truncated AGM calculation of the pendulum period.
as a function of the amplitude φ0 can be rapidly evaluated to any degree of precision by the arithmetic-geometric mean (AGM) as described by Carvalhaes and Suppes [9, 22, 23]. It can be easily implemented in a spreadsheet, and is used here as the exact value for comparison with the approximate expressions. The paper by Villarino [22] establishes the rigorous upper and lower bounds for the errors in a truncated AGM calculation of the pendulum period.
Many authors have however attempted to produce simple formulae for the variation of the period with the amplitude, see table 1. Such formulae are often either derived or justified by expanding them in a series, and comparing the coefficients with those of equation (7) [24]. Later authors have improved earlier formulae by parameterizing the deviations from the exact solution [25], but at the expense of simplicity. The various mathematical techniques employed in the published derivations have been: asymptotic series expansion, equations (9), (22)–(27) and (49); iteration of the AGM, equations (32)–(35); rational approximation methods, equations (44), (51)–(53); the equivalent oscillator approach, equation (54) and the averaging/residual minimizing method, equations (31), (37) and (55).
Salinas-Hernández et al [26] have proposed a procedure for calculating both the period and the trajectory of a non-linear pendulum by approximating the denominator of equation (4) by two integratable polynomials, but this involves multiple calculations, and does not lead to a simple equation.
Table 1. Period approximation equations with their Taylor series expansions. The percent deviations are  and
and 
| Authors |

| Δ(30°) | Δ(90°) |
|---|---|---|---|
| Bernoulli [30] (1749) |
 | −2.7 E−2 | −2.2 E 0 |
| Denman [31, 32] (1959) Gil and Gregorio [33] (2006) |
 | 2.4 E−3 | 1.7 E−1 |
| Pars [22] (1965) |
 | 5.8 E−1 | 6.2 E 0 |
| Thurston [34] (1972) Benacka [35] (2009) |
 | −5.8 E−1 | −5.9 E 0 |
| Average of Pars [22] (1965) & Thurston [34] (1972) |
 | −1.0 E−2 | 2.1 E−2 |
Table 1. (Continued).
| Ganley [36] (1985) Parwani [37] (2004) |
 | 7.4 E−3 | 3.2 E−3 |
| Cadwell and Boyko [38] (1991) Belendez et al [28] (2006) |
 | 1.8 E−2 | 1.9 E 0 |
| Cromer [17] (1995) |
 | −1.1 E 1 | −6.5 E 0 |
| Molina [39] (1997) |
 | 3.5 E−3 | 3.5 E−1 |
 | −3.4 E 0 | −2.9 E 1 | |
| Kidd and Fogg [40] (2002) Millet [41] (2003) |
 | 7.5 E−3 | 7.5 E−1 |
Table 1. (Continued).
| Hite [42] (2005) Belendez et al [43] (2009) |
 | 1.6 E−5 | 1.4 E−2 |
| Lima and Arun [44] (2006) |
 | 2.5 E−3 | 2.5 E−1 |
| Belendez et al [28] (2006) |
 | ||
 | −2.6 E−3 | −3.8 E−1 | |
 | −2.5 E−3 | −2.7 E−1 | |
 | −2.5 E−3 | −2.7 E−1 | |
 | 2.0 E−2 | 2.3 E 0 |
Table 1. (Continued).
| Belendez et al [45] (2006) |
 | −2.5 E−3 | −2.7 E−1 |
| Belendez et al [24] (2007) |
 | −8.9 E−1 | −8.3 E 0 |
| Gatland [21] (2007) |
 | 1.3 E−4 | −8.1 E−3 |
| Amore [46] (2007) |
 | 1.8 E 0 | 2.2 E 1 |
| Lima [47] (2008) |
 | −1.1 E−1 | −5.8 E−1 |
Table 1. (Continued).
| Carvalhaes and Suppes [9, 22] (2008) Belendez et al [29] (2011) |
 | −7.5 E−3 | −7.4 E−1 |
 | −1.4 E−7 | −1.4 E−3 | |
| Carvalhaes and Suppes [9] (2008), |
 | <1.0 E−15 | <1.0 E−15 |
| Carvalhaes and Suppes [9] (2008), Van Baak [18] (2013) |
 | 0.00 | 0.00 |
| Yuan Qing-Xin & Ding Pei [48] (2009) |
 | 7.6 E−6 | 2.7 E−3 |
| Yuan Qing-Xin & Ding Pei [49] (2010) |
 | 4.5 E−2 | −2.8 E−3 |
Table 1. (Continued).
| Turkyilmazoglu [50] (2010) |
 | −1.4 E 0 | −1.4 E 1 |
 | −2.9 E 3 | −3.2 E 2 | |
 | −1.4 E 0 | −1.4 E 1 | |
| Belendez et al [29] (2011) |
 | −2.4 E−9 | −2.1 E−4 |
| Johannessen [51] (2011) |
 | −4.9 E−4 | −4.0 E−2 |
 | |||
| Turkyilmazoglu [52] (2011) |
 | −3.4 E−6 | 9.7 E−4 |
| Douvropoulos [27] (2012) |
 | 1.2 E−2 | 2.2 E−1 |
| Xue De-Sheng [25] (2012) |
 | −5.3 E−3 | 1.6 E−2 |
Table 1. (Continued).
| Butikov [53] (2012) |
 | −3.0 E 1 | −1.2 E 1 |
| Hafez [14] (2015) |
 | −1.6 E−1 | −3.1 E−1 |
| Benacka [13] (2017) |
 | −1.2 E−8 | −1.0 E−2 |
| Fernandes et al [54] (2017) |
 | 3.2 E−3 | −5.2 E−3 |
| Salas [55] (2019) |
 | 6.1 E−6 | −5.4 E−3 |
 | −1.9 E−7 | −1.7 E−2 | |
 | −5.9 E−11 | −5.1 E−4 |
Douvropoulos [27] proposes the following approximation to the pendulum period:

with appropriate values of ν and μ, which in its simplest form is  , but can be enhanced as
, but can be enhanced as  where
where  is the zero order Struve function and leads to equation (45).
is the zero order Struve function and leads to equation (45).
Belendez et al [28] have developed a series of expressions using the harmonic balance method. The increase of order from N = 1 to N = 2 produces a significant increase in accuracy, but further terms have only a minor effect. Their subsequent equation (41) [29] is significantly more accurate than equations (23) to (28).
Benacka [19] (2009) developed the elliptic integral to calculate  , with upper and lower limits to the error if only a finite number n of terms are considered. He deduced that n = 12 was required for accuracy 0.1% up to 90°. The proposed spreadsheet calculations could then be used to calculate
, with upper and lower limits to the error if only a finite number n of terms are considered. He deduced that n = 12 was required for accuracy 0.1% up to 90°. The proposed spreadsheet calculations could then be used to calculate  .
.
4. Period approximations
The derivation of these expressions involve the application of perturbation theory and mathematical techniques which can be applied to other nonlinear oscillating systems, and as such have pedagogical value independent of the resulting equation. However, only those which are elegantly simple or are significantly accurate should be considered for analysis of experimental data, as precise values can be simply calculated using the AGM [9]. When fitting experimental angular velocity data, such as is supplied by MEMs gyros, it is necessary to include an easily differentiable expression for the angular frequency  into the angular displacement
into the angular displacement  , i.e. a simple equation for
, i.e. a simple equation for  . A further use of these approximations is in developing formulations of the temporal variation of the pivot forces on the pendulum [58], or other variables such as the angular displacement, velocity, and acceleration.
. A further use of these approximations is in developing formulations of the temporal variation of the pivot forces on the pendulum [58], or other variables such as the angular displacement, velocity, and acceleration.
The equations can be arbitrarily divided into three regions, namely (a) simple equations for amplitudes φ0 < 5 deg, as used for Pendulum clocks and measurements [16] of the acceleration due to gravity, (b) intermediate equations for amplitudes φ0 < 90 deg, i.e. for undergraduate measurements with simple pendulums consisting of a string and bob, and (c) complex equations for amplitudes 90 < φ0 < 180 deg, i.e. for experimental investigations of large amplitude nonlinear oscillations of compound pendulums.
5. Concise small amplitude approximations
Pendulum measurements [16] of g should not be made at very small amplitudes, as the bearing friction can significantly affect the period. Such undergraduate measurements can be made with pendulums of period 1 to 3 s with a precision [16] of ±170 µs, i.e. ∼0.005%. The correction for circular error should therefore be of similar precision and is generally made using the first, or first two terms, of the series expansion [16], equation (7), but equation (10) is to be preferred. Millet [41] has suggested that college level physics texts should introduce at least a first approximation to the period variation with amplitude, and suggested equation(19) due to Kidd and Fogg [40]. These equations are compared with other concise approximations in table 1 and figure 2, which shows  as a function of the square of the amplitude. Figure 3 shows the absolute value of the percentage deviation
as a function of the square of the amplitude. Figure 3 shows the absolute value of the percentage deviation  , on a log scale, as a function of the amplitude φ0, with positive values shown as red dots. Equation (41) is included in all plots as a reference.
, on a log scale, as a function of the amplitude φ0, with positive values shown as red dots. Equation (41) is included in all plots as a reference.
Figure 2. The ratio  of the period at amplitude φ0, versus
of the period at amplitude φ0, versus  in radians squared. The numbers in brackets are the equation labels, see table 1.
in radians squared. The numbers in brackets are the equation labels, see table 1.
Download figure:
Standard image High-resolution imageIf one considers only approximations containing a single term in the amplitude φ0, then figure 3 shows that equation (10)  proposed by Denman [31] is significantly more accurate than the two term series expansion
proposed by Denman [31] is significantly more accurate than the two term series expansion  , and is accurate to within <0.01% up to amplitude 40°, <0.2% up to amplitude 90° and <0.5% up to 146°, see figure 3. It is simple, can be incorporated in the angular displacement as
, and is accurate to within <0.01% up to amplitude 40°, <0.2% up to amplitude 90° and <0.5% up to 146°, see figure 3. It is simple, can be incorporated in the angular displacement as  , and is more than adequate for most undergraduate experiments. If a slightly more complex equation is considered then equation (33),
, and is more than adequate for most undergraduate experiments. If a slightly more complex equation is considered then equation (33),  due to Carvalhaes and Suppes [9, 22] is accurate to <0.001% up to amplitude π/2, see figure 3.
due to Carvalhaes and Suppes [9, 22] is accurate to <0.001% up to amplitude π/2, see figure 3.
Figure 3. The absolute value of the percentage deviation  of the concise period approximations from the exact period, as a function of the amplitude. The red dotted data are positive deviations. The numbers in brackets are the equation labels, see table 1.
of the concise period approximations from the exact period, as a function of the amplitude. The red dotted data are positive deviations. The numbers in brackets are the equation labels, see table 1.
Download figure:
Standard image High-resolution imageThe upper limit of  established by Pars [22] is almost at much too large as the lower limit of
established by Pars [22] is almost at much too large as the lower limit of  due to Thurston [34] and the weighted average is accurate to within <0.03% up to 90°. It is also interesting to note that the absolute values of
due to Thurston [34] and the weighted average is accurate to within <0.03% up to 90°. It is also interesting to note that the absolute values of  for the Kidd and Fogg [40] equation (19) and the Carvalhaes and Suppes [9] CS1 equation (32) are almost identical, see figure 3, but are of opposite sign, thus their average is significantly more accurate than either.
for the Kidd and Fogg [40] equation (19) and the Carvalhaes and Suppes [9] CS1 equation (32) are almost identical, see figure 3, but are of opposite sign, thus their average is significantly more accurate than either.
6. Medium amplitude approximations
The absolute values of the percentage deviations  of the period approximations from the exact period are shown for some intermediate equations in figures 4(a) and (b)). The two extra terms in the polynomial expansion due to Fernandes [54] clearly improve the accuracy over the Hafez approximation [14]. Equation (41),
of the period approximations from the exact period are shown for some intermediate equations in figures 4(a) and (b)). The two extra terms in the polynomial expansion due to Fernandes [54] clearly improve the accuracy over the Hafez approximation [14]. Equation (41), ![${T}_{\mathrm{B}\mathrm{e}\mathrm{8}}\left({\varphi }_{0}\right)=4{T}_{0}/\left[{\left(1+\sqrt{\mathrm{cos}\left({\varphi }_{0}/2\right)}\right)}^{2}-{\left\{\left(1-\sqrt{\mathrm{cos}\left({\varphi }_{0}/2\right)}\right)/2\right\}}^{4}\right]$](https://content.cld.iop.org/journals/0143-0807/42/1/015005/revision5/ejpabad10ieqn41.gif) due to Belendez [29], which is an augmentation of equation (33), is accurate to < 0.001% up to amplitudes of 105°, so is the preferred equation for medium amplitudes and more than adequate for comparison with experimental data up to φ0 < π/2.
due to Belendez [29], which is an augmentation of equation (33), is accurate to < 0.001% up to amplitudes of 105°, so is the preferred equation for medium amplitudes and more than adequate for comparison with experimental data up to φ0 < π/2.
Figure 4. The absolute value of the percentage deviation  from the exact period, as a function of the amplitude, for some of the intermediate period approximations. The numbers in brackets are the equation labels, see table 1.
from the exact period, as a function of the amplitude, for some of the intermediate period approximations. The numbers in brackets are the equation labels, see table 1.
Download figure:
Standard image High-resolution image7. Large amplitude approximations
The concise equations do not reproduce the elliptic integral at large amplitudes, so more complex equations are required. The equation (31) due to Lima [47], equation (37) due to Yuan Qing-Xin and Ding Pei [48], equation (54) due to Big Alabo, equation (40) due to Turkilmazoglu and equation (46) due to Xue De-Sheng [25] are shown in figure 5, which indicates that the latter has an accuracy of <0.017% throughout the amplitude range and better than 0.010% above φ0 = 2 radians. Below this amplitude equation (41) is the most accurate of these equations.
Figure 5. The absolute value of the percentage deviation  of the period approximations from the exact period for large amplitudes. The red dotted data are positive deviations. The numbers in brackets are the equation labels, see table 1.
of the period approximations from the exact period for large amplitudes. The red dotted data are positive deviations. The numbers in brackets are the equation labels, see table 1.
Download figure:
Standard image High-resolution imageThe equation:
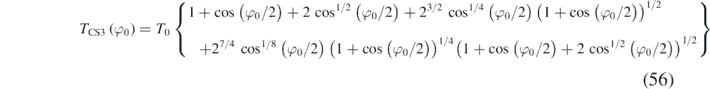
due to Carvalhaes and Suppes [9] is a series expansion of the AGM and is not shown in figure 5 as it is accurate to <10−10% up to amplitudes of 150°, and to <0.001% up to amplitudes of 179°. Thus this somewhat complex equation is the most accurate algebraic representation of the period variation with amplitude, except at extremely large amplitudes.
Cromer [17], Turkyilmazoglu [50] and Butikov [53] developed equations (16), (44) and (47) for the variation of the period at amplitudes close to 180 degrees, see figure 5, but they are only applicable at extremely large amplitudes. However, as suggested in Wikipedia [57], a weighting function such as  , with adjustable parameter r, can be used to combine them with an expression such as (21) or (41), which is accurate at low and medium amplitudes, but not at high amplitudes, see figure 5.
, with adjustable parameter r, can be used to combine them with an expression such as (21) or (41), which is accurate at low and medium amplitudes, but not at high amplitudes, see figure 5.
8. Damping
It should be pointed out that all the expressions in table 1 assume there are no dissipative torques, i.e. no damping. Real pendulums are, however, damped by air resistance and friction, and these can affect the period of oscillation. The effect of damping can be modelled as a combination of effects which are independent of the angular velocity, i.e. friction, proportional to the angular velocity, i.e. viscous, and proportional to the square of the angular velocity, i.e. turbulent drag. For a typical laboratory pendulum the effects of damping on the period, for amplitudes less than 1.5 radians, are generally negligible, the primary effect being the constant small shift due to viscous damping, as in SHM. However, at low amplitudes the pendulum bearing can significantly affect the oscillation period [59, 60]. For amplitudes above 2.5 radians the effect of damping on the oscillation period can become significant, thus limiting the applicability of the formulae in table 1. The effects of viscous damping on the period of the nonlinear pendulum have been calculated by Johannessen [61] and Braza [62], while Hinrichsen [63] has investigated the effects of frictional and turbulent drag on the period at amplitudes up to 179°.
9. Conclusion
The development of approximate expressions for the period of a pendulum in terms of simple geometrical functions serves the pedagogical purpose of validating the mathematical techniques required, which can therefore be used for other nonlinear oscillators. However, for the evaluation of experimental measurements of pendulum periods the exact period can be simply calculated to any required precision using the AGM [9], and this is generally as easy as implementing some of the more complex equations listed in table 1. The concise expressions do, however, serve the purpose of clarifying the nature of the variation, and for inclusion in expressions of the angular displacement  when fitting experimental data.
when fitting experimental data.
Millet [41] suggested one of the concise expressions should be included in modern text books, as the period variation can now be easily observed in undergraduate laboratories. For this purpose the almost forgotten equation (10)  due to Denman [31] is suggested, as it can be derived using perturbation theory [32], is elegantly concise with only the simple term
due to Denman [31] is suggested, as it can be derived using perturbation theory [32], is elegantly concise with only the simple term  , and as shown in figure 3, is more accurate than even the first two terms of the series expansion equation (7). For precision simple pendulum experiments equation (33)
, and as shown in figure 3, is more accurate than even the first two terms of the series expansion equation (7). For precision simple pendulum experiments equation (33)  is slightly more complex but significantly more accurate, see figure 3.
is slightly more complex but significantly more accurate, see figure 3.
If an even more accurate equation is required for medium amplitude experiments, then equation (41) ![${T}_{\mathrm{B}\mathrm{e}\mathrm{8}}\left({\varphi }_{0}\right)=4{T}_{0}/\left[{\left(1+\sqrt{\mathrm{cos}\left({\varphi }_{0}/2\right)}\right)}^{2}-{\left\{\left(1-\sqrt{\mathrm{cos}\left({\varphi }_{0}/2\right)}\right)/2\right\}}^{4}\right]$](https://content.cld.iop.org/journals/0143-0807/42/1/015005/revision5/ejpabad10ieqn49.gif) is recommended. For large amplitudes, i.e. between 90° and 179° equation (34) is by far the most accurate, but at this point it is probably easier to use the AGM [9]. At extremely large amplitudes, >178° the elegantly simple equation (16)
is recommended. For large amplitudes, i.e. between 90° and 179° equation (34) is by far the most accurate, but at this point it is probably easier to use the AGM [9]. At extremely large amplitudes, >178° the elegantly simple equation (16) ![${T}_{\mathrm{C}\mathrm{r}}\left({\varphi }_{0}\right)=4{T}_{0}/\mathrm{ln}\left[4/\mathrm{cos}\left({\varphi }_{0}/2\right)\right]$](https://content.cld.iop.org/journals/0143-0807/42/1/015005/revision5/ejpabad10ieqn50.gif) , and equation (47)
, and equation (47) ![${T}_{\mathrm{B}\mathrm{u}}\left({\varphi }_{0}\right)=2{T}_{0}/\pi \enspace \mathrm{ln}\left[8/\left(\pi -{\varphi }_{0}\right)\right]$](https://content.cld.iop.org/journals/0143-0807/42/1/015005/revision5/ejpabad10ieqn51.gif) are appropriate, but it should be born in mind that damping can have a significant effect on the period at these amplitudes [63].
are appropriate, but it should be born in mind that damping can have a significant effect on the period at these amplitudes [63].
Acknowledgments
The author would like to acknowledge the contributions of the referees which materially enhanced the quality of this review.
Supplementary data 2020 percent pendulum period approximations.









