Breather Structures and Peregrine Solitons in a Polarized Space Dusty Plasma

1 Introduction

The plasma physicists have rejuvenated the research in the dusty plasma after the confirmation of presence of dust grains in Saturnian rings by Cassini and Voyager space missions [1]. It has been remarkably reported that such kind of dusty plasma is extremely abundant in various space/astrophysical environments (e.g., solar nebulae and comet tails) [2–6] and laboratory (e.g., manufacturing and processing of semiconductor devices) [7, 8]. The characteristic features of different nonlinear wave excitations in various space dusty plasma environments have been explored by numerous researchers. Prolific literature has confirmed the existence of extremely massive (i.e., nearly ${10}^6$ to ${10}^{12}{m}_i$) and excessively charged dust due to its momentous role for generation of DA nonlinear waves in space dusty plasma environments. Numerous theoretical and experimental investigations [9–11] have reported that charged dust reacts with electromagnetic as well as gravitational fields and gives rise to new low frequency modes like dust ion acoustic (DIA) waves [12], dust acoustic waves [13], and other modes. In low frequency dust acoustic waves, dust mass provides the inertia and pressure of electrons/ions provides the restoring force. Over the last few decades, many researchers have studied the variety of DA nonlinear structures such as solitons, shocks, double layers, and rogue waves, in magnetized/unmagnetized dusty plasmas in the framework of non-Maxwellian distributions [14–18]. Amin et al. [14] studied the MI of dust acoustic and dust ion acoustic waves and found that both DA and DIA waves are modulationally unstable. Shukla et al. [16] derived the dispersion relation for DAWs in a nonuniform dusty magnetoplasma. Labany et al. [17] studied the combined effects of adiabatic dust charge fluctuations and inhomogeneity on the salient features of DA solitons in a magnetized dusty plasma consisting of negatively charged dust, Boltzmann ions, and nonextensive electrons. They noticed the significant variation in the characteristics of DA solitary waves under the influence of dust charge fluctuations. El-Taibany and Sabry [18] illustrated the 3D DA solitary waves and double layers in the presence of magnetic field and nonthermal ions. It is believed that dust grains embedded in a dusty plasma are responsible for various kind of forces. Hamaguchi and Farouki [19] explored one of such forces as polarization force which occurs due to the deformation of the Debye sphere around the dust in nonuniform plasma. They found that difference in positive ion density on either side of negative dust leads to occurrence of the polarization force. The direction of polarization force is opposite to the electrostatic force and independent of sign of charge on dust [20]. Further, the polarization force has a great impact on the characteristics of DA waves. Numerous investigations have also been reported to demonstrate the variety of nonlinear structures by varying the polarization force in the framework of Maxwellian and non-Maxwellian distributions in various space plasma environments [21–27]. Singh et al. [26] illustrated that the superthermality of ions and polarization force have intense influence on the characteristics of DA periodic (cnoidal) waves in a superthermal polarized dusty plasma. In the recent past, Singh et al. [27] investigated the head-on collision among DA multisolitons in a dusty plasma having ions following the hybrid distribution in the presence of polarization force. It was found that rarefactive DA multisolitons are formed and phase shifts are strongly influenced by the polarization force.

Over the last few decades, the study of modulational instability and evolution of nonlinear envelope solitons in the context of nonlinear Schrödinger equation (NLSE) becomes an intriguing area of research in different plasma systems. The rational solutions of NLSE describe broad range of spatially and temporally localized sets of soliton solutions. One of such rational solutions is called Peregrine soliton [28] or prototype of the rogue waves resulting from counterbalance between nonlinearity and group velocity dispersion. The investigation of rogue waves has enhanced comprehensive understanding of evolution and formation of these mysterious waves in the ocean [29, 30]. It is demonstrated that the Peregrine breather plays a pivotal role for exclusive study of rogue waves [31]. It is reported that rogue waves are usually singular and large amplitude waves with draconian effects on living creatures. The rogue waves are known for their sudden appearance as a deep hole and huge crest in a serial pattern. Rogue waves have extremely large amplitude waves that evolve suddenly and then collapse without clue. Such kinds of waves are also observed in nonlinear optics, superfluids, and Bose–Einstein condensates [32, 33]. Further, it is also illustrated that the breather solutions of NLSE can be categorized as Kuznetsov–Ma breathers (space localized patterns and periodic in time) [34, 35] and the second class of breathers is the Akhmediev breather (which is periodic in space and localized in time) [36]. An experimental investigation of the formation of Peregrine solitons was reported by Bailung et al. [37] in a multicomponent plasma composed of negative ions. They illustrated that wave becomes modulationally unstable for critical value of negative ions density. Pathak et al. [38] have experimentally illustrated the occurrence of higher-order Peregrine breathers with amplitude five times the background carrier wave in multispecies plasma and verified their findings with second-order rational solution of breathers obtained from NLSE. Numerous researchers [39, 40] have also studied the evolutionary dynamics of such kind of nonlinear coherent solutions in different plasma environments. The nonlinear superposition of first-order rogue waves yields a complex and localized nonlinear structure with excessively large amplitude known as higher-order rogue waves and becomes a fascinating area of research. Such kind of pecking-order of higher-order breather solutions with a huge amplitude is called SRWs. Moreover, the rogue waves are first-order rational solution while SRWs are higher-order solution of NLSE. The nonlinear superposition of these TRWs forms the SRWs. The amplitude of SRWs goes on rising as triplets are replaced by sextets and so on [41, 42]. The observation of these higher- (second-) order rogue waves (RWs) has been verified in laboratory experiment including theoretical investigation [37, 38]. Numerous investigations of dust acoustic rogue waves have been reported in different plasma environments [43–50]. Singh and Saini [49] have observed that polarization force controls the MI domain of DA waves in a superthermal dusty plasma. They have also illustrated the evolutionary transition of DARW triplets to SRWs in a space dusty plasma. Recently, Jahan et al. [50] have studied the MI and DA rogue waves in a four-component dusty plasma having inertial two fluids of heavy as well as light negatively charged dust grains, superthermal electrons, and nonthermal ions. It is remarked that the conditions for the existence of DARWs are strongly altered under the influence of nonthermality of ions and superthermality of electrons.

Various satellite observations have disseminated the prevalence and abundance of energetic charged particles that exhibit nonthermal tails in the planetary magnetospheres and solar wind [51, 52]. Cairns et al. [53] introduced a new kind of distribution referred to as Cairns distribution in order to explore the concept of negative potential electrostatic wave structures observed by the Freja satellite [54]. They illustrated that the occurrence of charged particles obeying nonthermal distribution can appreciably change the propagation properties of ion acoustic waves in conformity with observations of Freja [54] and Viking [55] satellites. Nonthermal charged particles have been found in the Earth’s bow-shock [56], Mar’s ionosphere [57], lunar vicinity [58], and the Jupiter and Saturn environments [59]. A large number of studies have focused on the characteristics of different nonlinear waves in the framework of nonthermal Cairns distribution in various plasma systems [27, 60–62]. Singh [60] studied the propagation of ion acoustic waves (IAWs) in an inhomogeneous electron-ion plasma having nonthermal electrons obeying Cairns distribution. The characteristics of nonlinear IAWs are strongly affected by the density inhomogeneities as well as nonthermality of electrons. Kalita and Kalita [61] studied the dust acoustic waves in a dusty plasma composed of weakly relativistic electrons, nonthermal ions (obeying Cairns distribution), and negatively charged dust. They found that the variation in nonthermal parameter of ions significantly modifies the amplitude of both compressive and rarefactive solitons. Shan et al. [62] studied the influence of nonthermality of electrons as well as protons on the formation of electrostatic ion acoustic waves in an ionospheric plasma.

In our present investigation, we have explored the MI of DAWs and hierarchy of DA breathers, Peregrine solitons, TRWs, and SRWs in a nonthermally polarized space dusty plasma having Cairns distributed nonthermal ions, Maxwellian electrons, and negatively charged dust fluid. Our present optimum knowledge authenticates that no such type of investigation has been carried out yet. We have used multiple-scale perturbation technique to obtain NLSE to study the MI and from its solution, the full class of $DA$ breathers and TRWs as well as SRWs are illustrated. The basic fluid model of $DAWs$ is given in Section 2. In Section 3, we have presented the derivation of NLSE. In Section 4, modulational instability, analytical solutions of NLSE for study of DA breathers (Akhmediev breather, Kuznetsov–Ma breather, and Peregrine solitons), TRWs, and SRWs are discussed. In Section 5, conclusions are presented.

2 Fluid Model

In this present investigation, we have examined the influence of polarization force and nonthermality of ions, on the evolution of dust acoustic rogue waves, breathers, and Peregrine solitons in a polarized space dusty plasma having negative dust fluid, Boltzmann electrons, and ions obeying Cairns nonthermal distribution. The modified expression for polarization force under the effect of nonthermal ions can be written as [27]

 where $R=Z_d{e}^2/4k_B{T}_i{\lambda }_{Di0}$, ${\lambda }_{Di0}=\sqrt{{\mathit{ϵ}}_0{k}_B{T}_i/n_i{e}^2{C}_{\alpha 1}}$, $C_{\alpha 0}=\left(C_{\alpha 1}-2C_{\alpha 2}\varphi \right)$, $C_{\alpha 1}=1-\text{Λ}$, $C_{\alpha 2}=1/2$, and $\text{Λ}=\frac{4\alpha }{1+3\alpha }$. α measures the energy spectrum of nonthermal ions. Equation 1 illustrates that the polarization force is significantly revamped by nonthermality of ions (for more details, see Ref. 27). The expression for polarization force in Maxwellian limit ($\alpha \to 0$) agrees exactly with the expression in Asaduzzaman et al. [25]. Numerically, it is found that the polarization parameter R is decreased with rise in α (i.e., increase in nonthermality of ions) and temperature of ions.

The normalized expression for number density of nonthermally distributed ions by using Taylor’s expansion can be written as [27]

where α is the spectral index of nonthermally distributed ions. For low effect of nonthermality of ions, α is small. We have considered the normalized number density of electrons which is given as $n_e={\delta }_e\text{exp}\left(\sigma \varphi \right)$ [49].

The nonthermally modified polarization force term is used in the dust momentum equation to examine the role of polarization force and nonthermality of ions on $DARWs$, breathers, and Peregrine solitons. At equilibrium, the charge neutrality yields $n_{e0}+Z_{d0}{n}_{d0}=n_{i0}$, where $n_{j0}$ for ($j=e,i,d$) are unperturbed densities of different species (i.e., electrons, ions, and dust), respectively. The set of normalized fluid model equations governs the dynamics of DAWs is written in the following form [27]:

and

 where ${\chi }_p=\left[1-R\cdot \text{Ξ}\right]$ and $\text{Ξ}=\left(C_{\alpha 1}-2C_{\alpha 2}\varphi +1/2C_{\alpha 1}^2\varphi \right)$. The $n_d$ is normalized by $n_{d0}$ and $u_d$ is normalized by dust sound speed $C_d={\left(Z_{d0}{k}_B{T}_i/m_d\right)}^{1/2}$. The electrostatic potential ϕ is normalized by $k_B{T}_i/e$. The spatial and time coordinates are also normalized by dust Debye radius (i.e., ${\lambda }_{Dd}={\left(k_B{T}_i/4\pi e^2{Z}_{d0}{n}_{d0}\right)}^{1/2}$) and inverse of dust plasma frequency (i.e., ${\omega }_{pd}^{-1}={\left(m_d/4\pi Z_{d0}^2{\mathit{e}}^2{n}_{d0}\right)}^{1/2}$), respectively. Also, $\sigma =T_i/T_e$, ${\delta }_e=n_e/Z_{d0}{n}_{d0}=1/\left(\rho -1\right)$ and ${\delta }_i=n_i/Z_{d0}{n}_{d0}=\rho /\left(\rho -1\right)$, and $\rho =n_{i0}/n_{e0}$.

3 Derivation of the Nonlinear Schrödinger Equation

To analyze the characteristics of modulated DAWs in nonthermally polarized space dusty plasma, NLSE is derived from Eqs 3–5 by employing expansion of dependent state variables and following stretching coordinates:

where finite parameter $\mathit{ϵ}\ll 1$ and ${\text{Λ}}_g$ represents the group velocity of envelope. The dependent state variables can be expanded as

where ${\mathrm{\Upsilon }}_{\ell }^{\left(m\right)}={\left[n_d{u}_d\varphi \right]}^{\prime }$ and ${\Upsilon }_0={\left[100\right]}^{\prime }$. By adopting multiscale technique, we have taken the fast scale in the phase via $\left(kx-\omega t\right)$ with slow scaling via $\left(\zeta ,\tau \right)$ in terms of ${\ell }^{\text{th}}$ harmonics. Further, $n_{\ell }^{\left(m\right)}$, $u_{\ell }^{\left(m\right)}$, and ${\varphi }_{\ell }^{\left(m\right)}$ are real, such that ${\mathrm{\Upsilon }}_{-\ell }^{\left(m\right)}={\mathrm{\Upsilon }}_{\ell }^{\mathrm{\star }\left(m\right)}$, the star shows the complex conjugate.

By putting Eqs 6 and 7 into Eqs 3–5 and equating terms of first-order $\left(m,\ell \right)=\left(\mathrm{1,1}\right)$, the first-order quantities are obtained as.

Further, we obtain

where ${\chi }_1=1-R{C}_{\alpha 1}$ and ${\mathit{\varrho }}_1={\delta }_e\sigma +{\delta }_i{C}_{\alpha 1}$. Equation 9 represents the dispersion relation of DAWs. Now, equating terms for $\left(m,\ell \right)=\left(\mathrm{2,1}\right)$ and the analogy condition can be written as

Equation 10 represents the group velocity of the $DAWs$.

From the expressions corresponding to third harmonics $\left(m,\ell \right)=\left(\mathrm{3,1}\right)$ and with some algebraic manipulations, the final expression for NLSE is obtained as follows:

where P and Q are dispersion and nonlinear coefficients, respectively. Expressions for these coefficients and other steps involved in the derivation of NLSE are illustrated in Appendix.

4 Modulational Instability and Breathers Solutions

In this section, we have performed numerical analysis to examine the MI of DAWs and dynamics of DA breathers, Peregrine solitons, and evolution of DA-TRWs to SRWs in a nonthermal polarized dusty plasma. For numerical analysis, we have used MATHEMATICA-10 based program. We have discussed the combined influence of different plasma parameters (e.g., $\rho ,\sigma ,R$, and α) on the characteristics of different kinds of $DA$ breathers, RW triplets, and super rogue waves. We have used data for numerical analysis for physical parametric ranges associated with planetary rings [65] in dusty plasma: $n_{i0}=5\times {10}^7$, $n_{e0}=4\times {10}^7$, $Z_d=3\times {10}^3$, $n_d={10}^7{\text{cm}}^{-3}$, $T_i=0.05$, $T_e=50\text{eV}$, and $R=0-0.155$. The experimental parametric ranges are as follows [21]: $n_{i0}=7\times {10}^7$, $n_{e0}=4\times {10}^7{\text{cm}}^{-3}$, $Z_d=3\times {10}^3$, $n_d={10}^7{\text{cm}}^{-3}$, $T_i=0.3$, $T_e=8\text{eV}$, and $R=0-0.155$.

4.1 Modulational Instability

We ensure that Eq. 11 represents a plane wave solution $\Phi ={\text{Φ}}_0\text{exp}\left(\iota Q|{\text{Φ}}_0{|}^2\tau \right)$ which can be linearized by employing $\text{Φ}={\text{Φ}}_0+\epsilon {\text{Φ}}_{\left(\mathrm{1,0}\right)}\text{cos}\left(\tilde{k}\zeta -\tilde{\omega }\tau \right)$ (i.e., the perturbed wave number ($\tilde{k}$) associated with the frequency ($\tilde{\omega }$) is different from its homologue). The dispersion relation in this perturbed case can be written as [63]

It is noted that when the ratio of P to Q is positive (i.e., $P/Q>0$), unstable modulated envelope is observed for $\tilde{k}<\widetilde{k_c}={\left(2Q|\widetilde{{\text{Φ}}_0}{|}^2/P\right)}^{1/2}$. The growth rate (${\text{Γ}}_g$) of DAWs is determined as follows [63]:

It is observed that MI gets stabilized by developing a train of envelope in the form of bright solitons. When the ratio of P to Q is negative (i.e., $P/Q<0$), stable modulated envelope is formed in the given plasma system.

The stability profile of DAWs is examined in Figure 1A which illustrates the variation of critical wave number $k\left(=k_c\right)$ with polarization parameter (R). The shaded (white) region associates with modulationally unstable (stable) regime of modulated DA carrier wave. The boundary line which separates the shaded area ($P/Q>0$) and the white area ($P/Q<0$) gives $k_c$ at fixed value of R. An increase in R yields the deviation of $k_c$ for higher values (i.e., impact of polarization force is to contract the wave number region). Figure 1B shows the variation of $k\left(=k_c\right)$ with the nonthermality parameter of ions (α). An increase in α moves the $k_c$ in smaller value region. It is seen that the impact of nonthermality of ions is to broaden the wave number domain, where unstable region shows MI growth rate. Figure 3C highlights the influence of R and α on the growth rate of MI of DAWs. An increase in both R and α shrinks the maximum growth rate of DAWs. It is discerned that the polarization parameter and nonthermality of ions play pivotal role to change the growth rate of MI. It is stressed that the impact of nonthermality of ions and polarization force (via R) have strong influence on the MI of DAWs.

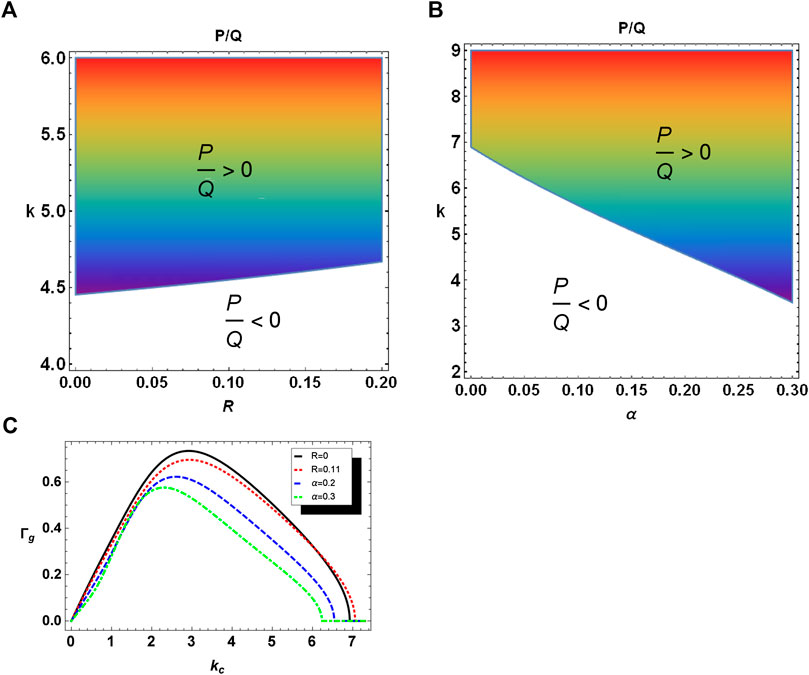
FIGURE 1. The contour plot of $P/Q$ in plane of (A)$k-R$ and (B)$k-\alpha$. (C) The variation of growth rate (${\text{Γ}}_g$) of MI vs. $k_c$ for different values of polarization parameter R and nonthermality parameter α.

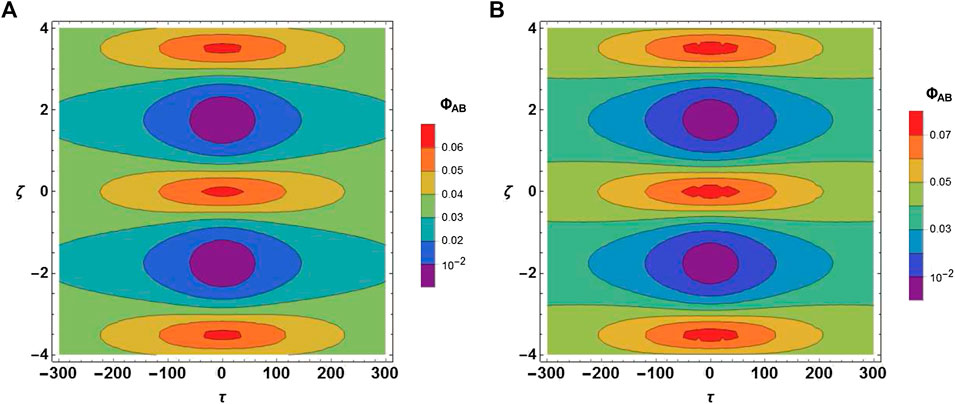
FIGURE 3. The variation of DA Akhmediev breathers profile in ζ-τ plane (A) for $R=0.1$ and (B)$R=0.11$ at fixed values of $\alpha =0.1$ and $\rho =1.11$.

Now, the main focus of our investigation is to analyze solutions for $PQ>0$ (i.e., for modulational unstable region). In this regime, nonlinear structures under study are rogue waves (localized in space as well as time), Akhmediev breather (localized in time but periodic in space), Kuznetsov–Ma breather (localized in space but periodic in time), TRWs, and SRWs. The detailed study of different kinds of breathers and other nonlinear structures is summarized as follows.

4.2 Peregrine Solitons

The Peregrine structure [28] as a prototype model for rogue waves has been adopted as a single rogue profile whose amplitude reduces in both time and space. The Peregrine solitons have been examined experimentally in water wave tank [40] and also in plasma [37] situations. The NLS Eq. 11 provides a first-order rational solution confined in both τ and ζ-plane given by

Here, we have presented the standard solution of Peregrine solitons (i.e., rogue waves). In the limiting case, when both $R=0$ and $\alpha =0$,t the findings of our study agree with results for Maxwellian case of Ref. 64. The RWs are characterized as several times larger in amplitude than their surrounding waves and are more unpredictable. The profile of RWs formation in many experiments can be illustrated as the train of solitons developed due to the modulational instability of monochromatic wave packets which superimpose and suck energy from neighboring waves which further yields extremely large amplitude rogue waves (Peregrine solitons).

Figure 2A depicts the absolute of amplitude profile of DARWs for distinct values of polarization parameter R. It is seen that rise in R leads to escalating the amplitude of DARWs, whereas Figure 2B shows that increase in α (i.e., nonthermality of ions) reduces the amplitude of DARWs. Consequently, the polarization parameter increases the nonlinearity which leads to enhancing the amplitude of DARWs whereas nonlinearity decreases with the increase in nonthermality of ions and hence amplitude enervates.

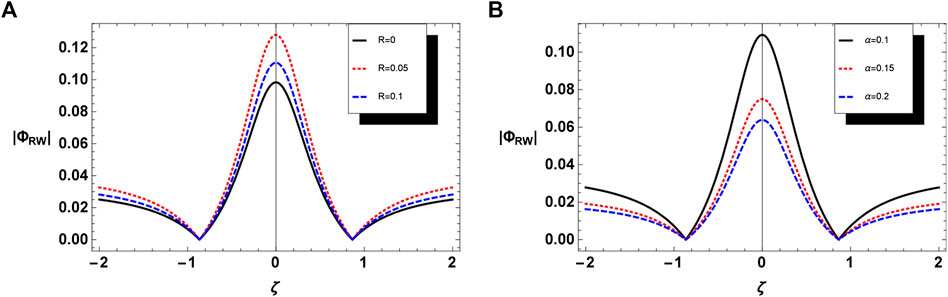
FIGURE 2. The variation of DARW portrait with respect to ζ (A) for different values of R and (B) for different values of α at fixed values of $\sigma =0.01$ and $\rho =1.11$.

4.3 Akhmediev Breather

The Akhmediev breather [36] is an exact solution of the NLSE Eq. 11 which illustrates the MI regime. The associated waveforms (periodic in space and confined in time) are given by

Here, free parameter “$\aleph$” measures the physical nature of the solution with relations ç $=\sqrt{4\left(1-2\aleph \right)}$ and $\wp =\sqrt{2\aleph }$ç. For $0<\aleph <0.5$ (i.e., the spatial frequency of wave modulation) “ç” and “$\wp$” must be real such that $0<\wp$, ç $<2$, and the solution demonstrates the AB which is confined in time and has a periodicity in space ζ with period $2\pi /$ç. This solution can be reduced to the confined solution (in space as well as time) with the rise in the converter parameter $\aleph$ up to the limit $\aleph \to 0.5$. Hence, the maximum amplitude of the AB is given by

Figures 3A,B illustrate the variation of DA-AB for distinct values of polarization parameter (via R). It is observed that amplitude of DA-AB escalates with rise in polarization parameter. Figures 4A,B show the variation of DA Akhmediev breather for distinct values of nonthermality parameter (via α). It is found that amplitude of DA-AB reduces with rise in nonthermality of ions.

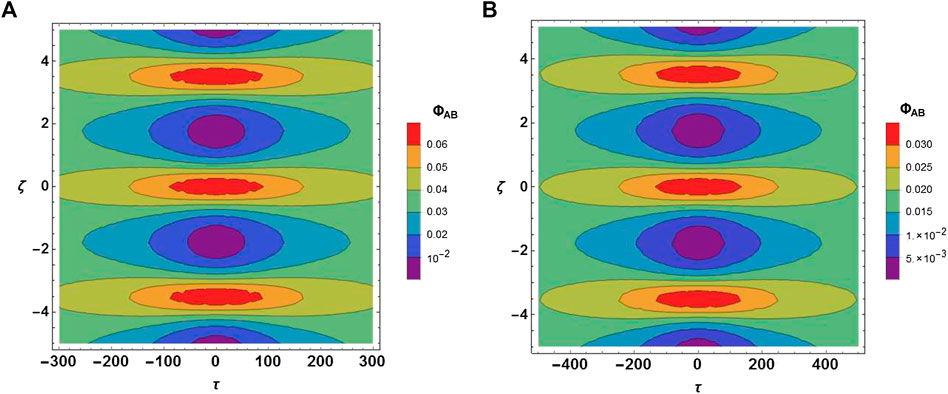
FIGURE 4. The variation of DA Akhmediev breathers profile in ζ-τ plane (A) for $\alpha =0.2$ and (B)$\alpha =0.3$ at fixed values of $R=0.11$ and $\rho =1.11$.

4.4 Kuznetsov–Ma Breather

Kuznetsov [34] and Ma [35] introduced one of the breather solutions which is named Kuznetsov–Ma (KM) breather. On the contrary to the AB, KM breather is periodic in time and confined in space and is given by [34, 35]

Here, $0.5<\aleph <\mathrm{\infty }$; the variables “ç “and “$\wp$ “ are imaginary. Moreover, the hyperbolic functions are changed into the circular trigonometric functions and vice versa. Such solutions are periodic in time domain with periodicity $2\pi /\left(\wp P\right)$. The maximum amplitude of the DA-KM breather is given by

Figures 5A,B depict the variation in DA-KM breather for distinct values of polarization parameter (via R). It is observed that amplitude of DA-KM breather increases with increase in polarization parameter. Figures 6A,B show the variation in DA-KM breather for distinct values of nonthermal parameter (via α). It is found that the absolute amplitude of DA-KM breather decreases with rise in nonthermality of ions.

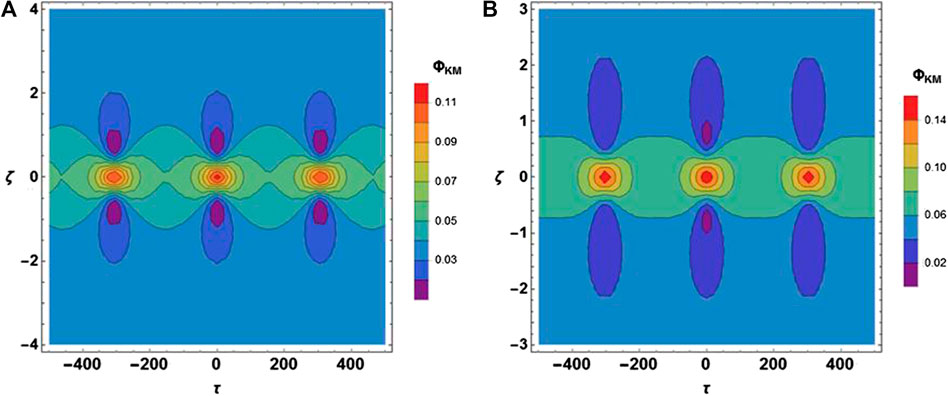
FIGURE 5. The variation of DA Kuznetsov–Ma breather profile in ζ - τ plane (A) for $R=0.1$ and (B)$R=0.11$ at fixed values of $\alpha =0.1$ and $\rho =1.11$.

FIGURE 6. The variation of DA Kuznetsov–Ma breather profile in ζ - τ plane (A) for $\alpha =0.2$ and (B)$\alpha =0.3$ at fixed values of $R=0.11$ and $\rho =1.11$.

The maximum amplitude of breathers can be recapitulated as

Figures 7A–C illustrate the evolution of DA-AB, DA-KM breather, and DARWS for different $\aleph$ values. It is important to note that the maximum amplitude of DARWs is higher than AB and lower than KM (i.e., $|\text{Φ}{|}_{KM\left(max\right)}>|\text{Φ}{|}_{RW\left(max\right)}>|\text{Φ}{|}_{AB\left(max\right)}$). It is also seen that, for AB, the spatial gap of neighboring peaks increases with the rise in $\aleph$ which leads to suppressing the wave frequency and consequently strongly localized structures in both space and time dimensions until $\aleph =0.5$ which evolves the DARWs. On the other hand, for the KM breather, the temporal gap of the neighboring peaks shrank with the increment in $\aleph$ (i.e., the wave frequency enhances).

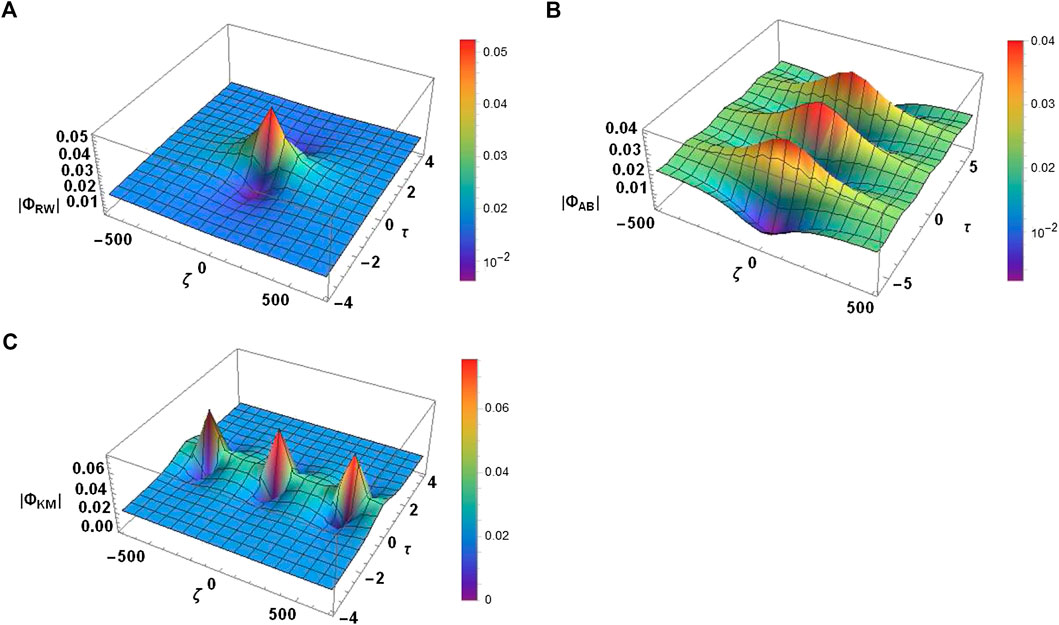
FIGURE 7. The 3D profile of (A) DA rogue waves at $\aleph =0.5$, (B) DA Akhmediev breather at $\aleph =0.2$, and (C) DA Kuznetsov–Ma breather at $\aleph =2$ with respect to ζ and τ whereas $R=0.11$, $\alpha =0.2$, and $\rho =1.11$ are fixed.

4.5 Rogue Wave Triplets and Super Rogue Waves

Over the last many years, the rogue wave triplets and super RWs solutions of NLSE have been studied theoretically as well as experimentally by numerous researchers [38, 41, 42]. It is found that rogue wave triplets are second-order RWs, and the nonlinear superposition of these DA-TRWs can give birth to higher amplitude SRWs that are also confined in both time and space domains. The higher-order rational solution of Eq. 11 recognizes the DA-TRWs solution for unstable regime [41]:

where

Here, ${\theta }_1$ and ${\theta }_2$ represent the changeover of DA-TRWs to SRWs and also site of these triplets. We consider ${\theta }_1=1000$ and ${\theta }_2=0$ to portrait a qualitative fashion. Here, $A=\left({\theta }_1^{1/3}/\sqrt{2},0\right)$, $B=\left(-\sqrt{2}{\theta }_1^{1/3}/4,\sqrt{3}{\theta }_1^{1/3}/4P\right)$, and $C=\left(-\sqrt{2}{\theta }_1^{1/3}/4,-\sqrt{3}{\theta }_1^{1/3}/4P\right)$ are the sites of DA-TRWs in ($\zeta -\tau$). If we choose ${\theta }_1={\theta }_2=0$, then DA-SRWs are evolved after the overlapping of first-order DA-TRWs.

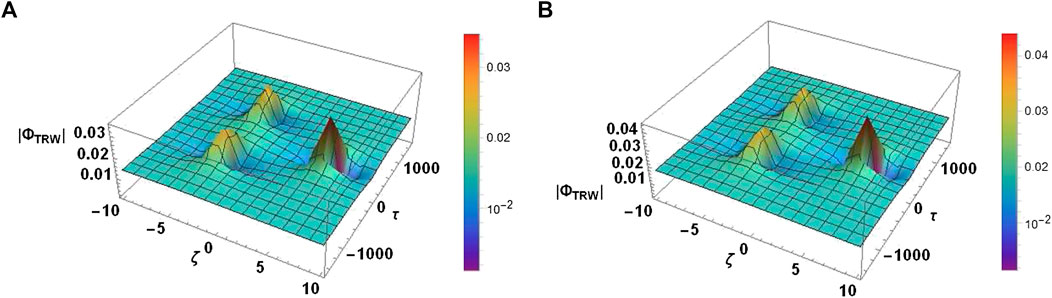
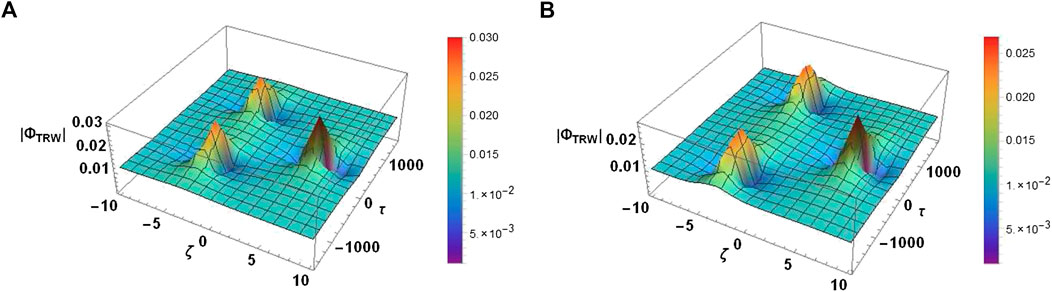
Figures 8A,B display the influence of absolute of the amplitude of DA-TRWs for distinct values of polarization force (R). An increase in R produces enhancement in the amplitude of DA-TRWs. Figures 9A,B demonstrate the absolute of the DA-TRWs profile for distinct values of α. It is remarked that with an increment in α (i.e., nonthermality of ions) the absolute amplitude DA-TRWs is enervated. The nonlinearity decreases as the nonthermality of ions increases and consequently, the amplitude of DA-TRWs gets reduced. To demonstrate the evolutionary of DA-SRWs in space dusty plasma, we choose ${\theta }_1={\theta }_2=0$. The DA super rogue waves are evolved in the given plasma model due to nonlinear superposition of second-order DA-TRWs. Figure 10A depicts the variation of DA-SRWs for distinct values of polarization parameter R. It is noticed that the rise in R escalates the amplitude of DA-SRWs. Figure 10B illustrates that an increase in α leads to reducing the amplitude of DA-SRWs. It is conspicuous that rise in the value of R (α) enhances (reduces) the nonlinearity and increases (suppresses) the amplitude of DA-SRWs. It is remarked that the polarization force and nonthermality of ions substantially revamp the evolution of DA breathers, Peregrine solitons, and different rogue wave structures.

FIGURE 8. The variation of DA-TRWs portrait in ζ-τ plane (A) for $R=0.1$ and (B)$R=0.13$ whereas $\alpha =0.2$ and $\rho =1.11$ are fixed.

FIGURE 9. The variation of DA-TRWs portrait in ζ-τ plane (A) for $\alpha =0.2$ and (B)$\alpha =0.3$, whereas $R=0.11$ and $\rho =1.11$ are fixed.

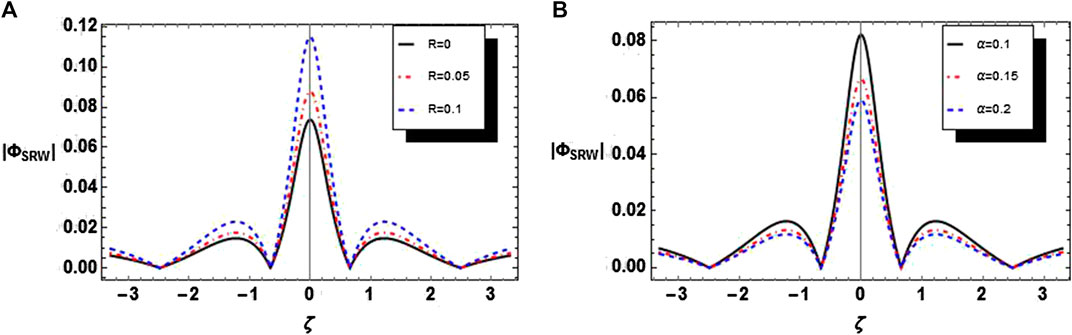
FIGURE 10. The variation of DA-SRWs portrait vs. ζ (A) for different values of R and (B) for different values of α whereas $\sigma =0.01$ and $\rho =1.11$ are fixed.

5 Conclusion

We have numerically studied the evolution of different kinds of DA breathers, Peregrine solitons, rogue wave triplets, and super rogue waves in a dusty plasma containing negatively charged dust fluid, Maxwellian electrons, and nonthermal ions (obeying Cairns distribution) in the presence of polarization force. First, the role of nonthermality of ions on the polarization force is discussed. By applying the multiple-scale perturbation technique, the NLSE is derived to analyze the MI of the DAWs. It is conspicuous that the polarization parameter controls the wave number domain whereas nonthermality of ions broadens the instability regime. The evolution of dust acoustic AB, KM breather, Peregrine solitons, DA-TRWs, and higher-order SRWs has been illustrated under the impact of nonthermal polarization force. Furthermore, an epoch-making role of all physical parameters like nonthermality of ions and polarization force on the characteristics of dust acoustic AB, KM breather, and first- as well as second-order RWs has been studied. The paramount findings of this study might provide the physical insight of nonlinear coherent structures in planetary rings where nonthermal ions are prevalent in different space environments. We propose to perform a dusty plasma experiment to validate our theoretical predications as formation of IA freak waves has already been examined experimentally by the researchers [37, 38].

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding authors.

Author Contributions

All authors have contributed equally.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Main Steps for the Derivation of Nonlinear Schrödinger Equation

From second harmonics $\left(m,\ell \right)=\left(\mathrm{2,1}\right)$, we obtain

Further, the second harmonics $\left(m,\ell \right)=\left(\mathrm{2,2}\right)$ are given due to the self nonlinear interactions of the carrier waves as

These self-interactions provide the zeroth-order harmonics which can be analytically obtained by collecting $\left(m,\ell \right)=\left(\mathrm{3,0}\right)$:

Equating the third harmonics $\left(m,\ell \right)=\left(\mathrm{3,1}\right)$, we get the following set of equations:

Now, substituting Eqs 8, A2, and A3 along with Eq. A1 in Eqs A4–A6, we get

Now, eliminating the $n_1^{\left(3\right)}$, $u_1^{\left(3\right)}$, and ${\text{Φ}}_1^{\left(3\right)}$ and after some algebraic manipulations, we obtain the known NLS equation given by Eq. 11.

The expressions for dispersion coefficient (P) and nonlinear coefficient (Q) are given as

Acknowledgments

The authors acknowledge the support by DRS-II (SAP) No. F 530/17/DRS-II/2015(SAP-I) UGC and DST-PURSE.

References