Variational upscaling for modeling state of strain-dependent behavior and stress-induced crystallization in rubber-like materials

Abstract

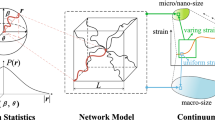
The purpose of this paper is to present a general upscaling strategy for deriving macroscopic constitutive laws for rubber-like materials from the knowledge of the network distribution and a mechanical description of the individual chains and of their free energy. The microscopic configuration is described by the position of the cross-links and is not obtained by an affine assumption but by minimizing the corresponding free energy on stochastic large representative volume elements with adequate boundary conditions. This general framework is then approximated by using a microsphere (directional) description of the network. It is presented in a global setting and is extended in order to handle situations with tube-like constraints and stress-induced crystallization.

Appendix: Time discretization and Newton algorithm

Let us introduce the chain traction $f_R$ as imposed by equilibration together with the constitutive expression $\displaystyle f(\lambda , \lambda _{\chi })= \frac{1}{Nb} \frac{\partial \psi _R}{\partial \lambda }$ for the chain traction and $\displaystyle f_\chi (\lambda , \lambda _{\chi })= - \frac{\partial \psi _R}{\partial \lambda _\chi }$ of the crystallization thermodynamic force. Moreover, the notations $\lambda _0(\lambda _{\chi })$ and $\lambda _Y(\lambda _\chi )$ denote the solutions of $f_\chi (\lambda _0(\lambda _\chi ),\lambda _\chi )=0$ and of $f_\chi (\lambda _0(\lambda _\chi ),\lambda _\chi )=Y(\lambda _\chi )$, respectively.

After time implicit discretization, the flow rule (41) writes

• 1. if $f_R< f(\lambda _E,0)$, there are no crystallites, $\lambda _{\chi }^{n+1} = 0$ and $\lambda$ is obtained by solving $f(\lambda ,0)=f_R$;

• 2. if $f(\lambda _E,0)< f_R \le f(\lambda _0(\lambda _{\chi }^n), \lambda _{\chi }^n)$, we are in a fusion phase, $\lambda$ and $\lambda _{\chi }^{n+1}$ being obtained by solving

  $$\begin{aligned}&f_\chi (\lambda , \lambda _{\chi }^{n+1}) =0,\\&f(\lambda , \lambda _{\chi }^{n+1})=f_R; \end{aligned}$$

• 3. if $f(\lambda _0( \lambda _{\chi }^n), \lambda _{\chi }^n)< f_R \le f(\lambda _Y( \lambda _{\chi }^n), \lambda _{\chi }^n)$, we are in a freezing situation, $\lambda _{\chi }^{n+1} =\lambda _{\chi }^{n}$, $\lambda$ being obtained by solving $f(\lambda ,\lambda _{\chi }^{n+1})=f_R$;

• 4. if $f(\lambda _Y( \lambda _{\chi }^n), \lambda _{\chi }^n)< f_R \le f(\lambda _0( \lambda _{\chi ,sat}), \lambda _{\chi ,sat})$, we are in a crystallization phase, $\lambda$ and $\lambda _{\chi }^{n+1}$ being obtained by solving

  $$\begin{aligned}&f_\chi (\lambda , \lambda _{\chi }^{n+1}) =Y ( \lambda _{\chi }^{n+1}),\\&f(\lambda , \lambda _{\chi }^{n+1})=f_R; \end{aligned}$$

• 5. if $f(\lambda _0( \lambda _{\chi ,sat}), \lambda _{\chi ,sat}) < f_R$, we are at saturation, $\lambda _{\chi }^{n+1}=\lambda _{\chi ,sat}$ and $\lambda$ is obtained by solving $f(\lambda ,\lambda _{\chi ,sat})=0$.

All above nonlinear systems reduce to a nonlinear scalar equation with respect to the unknown $f_a=\frac{\partial {\psi _\beta }}{\partial \lambda }(\lambda _a)$ with $\lambda _a=(\lambda -\lambda _\chi )/(1-\lambda _\chi )$. They explicitly define the total elongation $\lambda$ and the new crystallization ratio $\lambda _\chi$ of a given chain together with their derivatives in function of the chain traction $f_R$.

Applying the Newton algorithm to the nonlinear stress Eq. (28) leads then to the following algorithm where we have omitted the superscript ${n+1}$ for simplicity:

For a given stress tensor $\underline{\underline{S}}_{\mathrm{c}}$, and while the residual is not sufficiently small

• 1. Compute the orientation vector $\displaystyle \underline{f}= \underline{\underline{S}}_{\mathrm{c}}\cdot \underline{\underline{l}}_0^{-t} \cdot \underline{R}$ for every orientation $\underline{R}$;

• 2. Compute its norm after transport $f_R=| \underline{f}|_{\mathrm{C}} = \sqrt{\underline{f} \cdot \underline{\underline{C}} \cdot \underline{f}}$ and its derivative with respect to $\underline{\underline{S}}_{\mathrm{c}}$ defined by

  $$\begin{aligned} \underline{\underline{U}}_R : \underline{\underline{\mathrm{d}S}} = \frac{\partial f}{\partial \underline{\underline{S}}_{\mathrm{c}}} : \underline{\underline{\mathrm{d}S}} = \frac{1}{2 f_R}( \underline{\mathrm{d}f} \cdot \underline{\underline{C}} \cdot \underline{f} + \underline{f} \cdot \underline{\underline{C}} \cdot \underline{\mathrm{d}f}) \end{aligned}$$

  with $\displaystyle \underline{\mathrm{d}f} = \underline{\underline{\mathrm{d}S}} \cdot \underline{R}= \underline{R}\cdot \underline{\underline{\mathrm{d}S}}^t$.

• 3. For all N, compute the chain extension $\lambda _{R,N}(f_R)$ and its derivative $\frac{\mathrm{d} \lambda _{R,N} }{d f_R}$ as indicated in the above resolution of the time discretized flow rule.

• 4. Compute by directional integration

  $$\begin{aligned} \underline{\underline{S}}_{inv} = \underline{\underline{l}}_0^{-t} \cdot \int _{S^{2} \times N} Nb \frac{\lambda _{R,N}}{f_R} \underline{R}\otimes \underline{R}P(N, \underline{R}) \mathrm{d}N |\mathrm{d}\underline{R}| \, \cdot \underline{\underline{l}}_0^{-1}, \end{aligned}$$

  the equilibration residual

  $$\begin{aligned} \underline{\underline{\text{ Res }}} = \underline{\underline{S}}_{\mathrm{c}}\cdot \underline{\underline{S}}_{inv} - \frac{1}{9} \underline{\underline{\text {Id}}}, \end{aligned}$$

  and its derivative with respect to $\underline{\underline{S}}_{\mathrm{c}}$

  $$\begin{aligned}&\underline{\underline{\underline{\underline{M}}}}: \underline{\underline{\mathrm{d}S}} := \frac{\partial \underline{\underline{S}}_{inv}}{\partial \underline{\underline{S}}_{\mathrm{c}}}: \underline{\underline{\mathrm{d}S}}\\&\quad = \underline{\underline{l}}_0^{-t} \cdot \int _{S^{2} \times N} Nb \left( \frac{1}{f_R} \frac{\mathrm{d} \lambda _{R,N} }{\mathrm{d} f_R}- \frac{\lambda _{R,N}}{f_R^2}\right) \underline{R}\otimes \underline{R}\, \underline{\underline{U}}_R: \mathrm{d} \underline{\underline{S}} P(N, \underline{R}) \mathrm{d}N |\mathrm{d}\underline{R}| \cdot \underline{\underline{l}}_0^{-1}, \\&\frac{\mathrm{d} \underline{\underline{\text{ Res }}}}{\mathrm{d} \underline{\underline{S}}_{\mathrm{c}}}: \underline{\underline{\mathrm{d}S}}= \underline{\underline{\mathrm{d}S}}:\underline{\underline{S}}_{inv} + \underline{\underline{S}}_{\mathrm{c}}\cdot \underline{\underline{\underline{\underline{M}}}} : \underline{\underline{\mathrm{d}S}}. \end{aligned}$$

• 5. Solve the linear system

  $$\begin{aligned} \frac{\mathrm{d} \underline{\underline{\text{ Res }}}}{\mathrm{d} \underline{\underline{S}}_{\mathrm{c}}} : \mathrm{d}\underline{\underline{S}}_{\mathrm{c}}= - \underline{\underline{\text{ Res }}}, \end{aligned}$$

  set $\underline{\underline{S}}_{\mathrm{c}}= \underline{\underline{S}}_{\mathrm{c}}+\mathrm{d}\underline{\underline{S}}_{\mathrm{c}}$ and go back to step 1 of algorithm.