1 Introduction

Synthetic microcapsules consist of a viscous fluid covered by a thin polymeric membrane. They have been used in a broad range of applications such as protection and targeted release of active agents in cosmetic and pharmaceutical industries (Casanova and Santos 2016; Gombotz and Wee 1998), fermentation and flavor conservation in food processing units (Gharsallaoui et al. 2007), and anti-body production in biomedical applications (Murua et al. 2008). Thus, it is required to accurately determine mechanical properties of microcapsules to efficiently increase their performance.

For calculating mechanical properties of microcapsules, several experimental techniques are employed such as partial probing of membrane using (colloidal) Atomic Force Microscopy (AFM) (Fery and Weinkamer 2007; Dubreuil et al. 2003), suction of compliant microcapsules through micropipettes in Micropipette Aspiration (MA) (Hochmuth et al. 1982; Hochmuth 2000), and monitoring the deformation of microcapsules using optical tweezers (Helfer et al. 2001). However, these techniques are often cumbersome and time consuming especially for highly deformable microcapsules. An alternative approach is to investigate the deformation of compliant microcapsules in microfluidic devices (e.g. micro-constrictions) where they deform into a range of bullet, slug and parachute shapes depending on their membrane mechanical properties. Subsequently, mechanical properties of microcapsules can be measured by quantitative parameters based on capsule dynamics and deformation under different flow conditions.

In the literature, there are several experimental studies such as those by Leclerc et al. (2012), Risso et al. (2006), Dawson et al. (2015), Lee and Fung (1969) and Vitkova et al. (2004), addressing the deformation of synthetic microcapsules in constrictions. It was experimentally observed that capsules tend to increase their axial length and decrease their radial width as capillary number increases. In spite of presenting useful results; however, the main challenge is to find a proper correlation between mechanical properties with capsule deformation in micro-constrictions. Alternatively, numerical studies have been carried out to investigate the significance of different influential parameters including capillary number (Park and Dimitrakopoulos 2013; Kusters et al. 2014; Luo and Bai 2017), viscosity ratio (Park and Dimitrakopoulos 2013), and particle types (Kusters et al. 2014; Wang et al. 2014), on the deformation of microcapsules. These numerical studies have explained the behaviour of microcapsules in various simulation conditions complementing earlier experimental investigations. In practical circumstances, on the other hand, it is important to have quantitative metrics to correlate deformation of microcapsules to their mechanical properties which generally seems to be ignored in literature, to the best knowledge of the authors.

In this paper, we investigate the dynamics of microcapsules in constrictions using the Discrete Multi-Physics (DMP) (Alexiadis 2015), a hybrid particle-based model which combines the Smoothed Particle Hydrodynamics (SPH) method for simulating the fluid flow and the Mass-Spring Model (MSM) for modeling the elastic membrane. It has been shown that the proposed model is suitable for simulation of Fluid-Solid Interactions (FSI) (Alexiadis 2015, 2014; Ariane et al. 2018). The proposed model has several advantages over other techniques such as the Immersed Boundary Methods for simulating fluid-solid interactions. For instance, the fluid and solid phases are explicitly distinguished since they are assigned with phase identities i.e. particle types, and no further effort is required for capturing the interface due to its particle-based nature. In addition, since the fluid phases inside and outside of the microcapsule are represented by a constant number of particles, the mass will be automatically conserved. The proposed method is further extendable to more sophisticated phenomena such as membrane rupture, as it has been illustrated for particle under extreme shear rate as discussed in our previous paper (Rahmat et al. 2019), which are generally difficult to tackle in conventional techniques.

This study aims to elaborate the correlation between the deformation and dynamics of microcapsules and their mechanical properties utilizing a systematic approach by investigating the effect of important dimensionless parameters. Subsequently, several quantitative parameters are extracted as potential metrics and it is shown that how their trends vary by the effect of different influential parameter (e.g., capillary number and constriction size). The discussion is followed by a correlation and dependency analysis to evaluate the importance of each of these metrics in extracting the mechanical properties of microcapsules.

2 Governing equations

2.1 General equations

The governing equations for an incompressible Newtonian fluid in laminar flow can be written as

$$\begin{aligned}&\frac{\mathrm {D}\rho }{\mathrm {D}t} = - \rho \varvec{\nabla }\cdot \mathbf {u}, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\mathrm {D}\mathbf {u}}{\mathrm {D}t} = \frac{- \varvec{\nabla }p}{\rho } + \frac{1}{\rho } \left( \varvec{\nabla }\cdot \mu \varvec{\nabla }\mathbf {u}\right) + \mathbf {F}, \end{aligned}$$
(2)

where \(\mathbf {u}\) is the velocity vector, and \(\rho\), \(\mu\) and p are density, kinematic viscosity and pressure, respectively. t is time, \(\frac{\mathrm {D}}{\mathrm {D}t}\) is the material time derivative and \(\mathbf {F}\) is the volumetric body force.

As stated earlier, the present numerical approach is based on the Discrete Multi-Physics (DMP) model (Alexiadis 2015) which utilizes the SPH method for the simulation of fluid flow and the MSM model for assigning elasticity to membrane particle. In the following, the SPH method and MSM model are briefly introduced and their coupling is discussed.

2.2 The SPH method

The smoothed particle hydrodynamics method was initially developed for astrophysical modelling purposes (Gingold and Monaghan 1977). Subsequently, the method was successfully extended to fluid dynamics (Monaghan 1994; Monaghan and Lattanzio 1985), showing merits especially in applications with large deformations. Within the framework of the SPH method, the simulation domain is populated by freely moving particles, where the physical properties are averaged over computational particles using a smoothing kernel function, and the governing equations are discretized on these particles. Different fluid/solid phases will be assigned to a certain group of SPH particles keeping the material properties such as density, mass, viscosity etc. This is an advantage of particle-based methods which automatically resolve the conservation of mass as well as explicit capturing of the interface between different material phases. SPH has been applied to a wide range of applications such as free surface flows (Löhner et al. 2006; Leroy et al. 2016; Gotoh et al. 2014), hydrodynamic instabilities (Rahmat et al. 2014; Shadloo and Yildiz 2011), multi-phase flows (Rahmat et al. 2016; Szewc et al. 2013; Colagrossi and Landrini 2003), bluff body simulations (Shadloo et al. 2011) and Fluid-Solid Interactions (Rafiee and Thiagarajan 2009; Rahmat et al. 2019; Yang et al. 2014).

In this study, Eqs. 1 and 2 are solved over spatially distributed particles in the solution domain through a smoothing kernel function, \(W(\mathbf {r}_{ij},h)\) or in its concise form, \(W_{ij}\). The kernel function relates particle i with its surrounding neighbor particles j (Monaghan and Kocharyan 1995; Monaghan and Lattanzio 1985), based on the relative distance between these particles \(\mathbf {r}_{ij} = |\mathbf {r}_i - \mathbf {r}_j|\), and the smoothing length, h. There are several kernel functions available in the literature; the Lucy kernel function (Lucy 1977) is used here. The Lucy kernel function is suitable for parallel simulations, so it has been shown in our previous studies showing accurate results for different fluid-solid interactions problems (Rahmat et al. 2019a, b; Alexiadis et al. 2017).

In SPH, any arbitrary variable f can be defined as a summation over discrete particles as

$$\begin{aligned} f_i \simeq \sum _{j=1}^{J_i} {\frac{m_j}{\rho _j} f_j W_{ij}}, \end{aligned}$$
(3)

where \(m_j\) is the mass of the discrete neighboring particles, and \(J_i\) is the number of neighboring particles for particle i. Applying the SPH framework to the continuity and momentum equations, Eqs. 1 and 2 may be written in their discretized form as

$$\begin{aligned}&\dot{\rho }_i = - \sum _{j=1}^{J_i} m_j \mathbf {u}_{ij} \frac{\partial W_{ij}}{\partial \mathbf {x}_i}, \end{aligned}$$
(4)
$$\begin{aligned}&\mathbf {f}_i = - \sum _{j=1}^{J_i} m_i m_j \left( \frac{p_i}{\rho _i^2} + \frac{p_j}{\rho _j^2}\right) \frac{\partial W_{ij}}{\partial \mathbf {x}_i} \nonumber \\&\quad\quad + \sum _{j=1}^{J_i} \frac{m_i m_j \left( \mu _i + \mu _j\right) }{\rho _i \rho _j} \mathbf {u}_{ij} \frac{\partial W_{ij}}{\partial \mathbf {x}_i} + \mathbf {F}_i. \end{aligned}$$
(5)

In Eq. 5, the first term is the pressure gradient and the second one is the dissipation term known as the laminar viscosity model (Morris et al. 1997). In SPH, there are two distinct approaches to evaluate pressure: (1) the Incompressible SPH (ISPH) method which requires solving a pressure Poisson equation (Rahmat and Yildiz 2018; Tofighi et al. 2015; Morris 2000); and (2) the Weakly Compressible SPH (WCSPH) method (Ozbulut et al. 2018; Monaghan and Kocharyan 1995; Fatehi et al. 2019). In the latter approach, the pressure is coupled to the density variations through an Equation Of State (EOS). We use this approach and the so-called Tait EOS (Monaghan and Kos 1999; Ozbulut et al. 2018):

$$\begin{aligned} p = \frac{c_0^2 \rho _0}{\gamma } \bigg [ \left( \frac{\rho }{\rho _0}\right) ^\gamma - 1 \bigg ]. \end{aligned}$$
(6)

where \(c_0\) is a reference speed of sound and set at least one order of magnitude larger than the maximum velocity in the domain, which ensures keeping the density variations below 1 \(\%\). \(\rho _0\) is the reference density set equal to 1000 \(\mathrm {kg}\mathrm {m}^{-3}\) and \(\gamma\) is a coefficient taken equal to (Monaghan 1994; Shadloo et al. 2013).

2.3 The MSM

The Mass Spring Model (MSM) or Lattice Spring Model (LSM) (Kilimnik et al. 2011), also sometimes defined Coarse Grained Molecular Dynamics (CGMD) (Alexiadis 2015) in DMP, is herein utilized to simulate deformable solid objects. Within the MSM framework (Lloyd et al. 2007), these objects are discretized into computational particles and a network of harmonic bonds connecting these particles allows them to move, deform and stretch according to the Newtonian equations of motion under the effect of external forces. In this study, the Mass Spring Model is used to simulate the deformable membrane of the capsule. The harmonic bond potential is used to account for Hookean elasticity between solid particles as

$$\begin{aligned} \mathbf {F}_{i,\mathrm{bond}} = k_b \left( \mathbf {r}_{ij} - \mathbf {r}_0\right) \end{aligned}$$
(7)

where \(k_b\) is the Hookean bond coefficient and \(r_0\) is the equilibrium distance. In this study, we focused on the discretization and implementation of the model, and for the sake of simplicity, we utilized the linear Hookean model. Other non-linear models can be implemented by changing the inter-particle potential, but the link between the non-linear elastic continuum models and non-linear discrete bonds is not as straight-forward as for Hookean elasticity. In the next section, it is shown how the membrane is discretized into computational particles and Eq. 7 is used to model their interactions.

2.4 Coupling of SPH and MSM

The interaction between the solid (MSM particles) and the fluid (SPH particles) is defined by boundary conditions which relate the behaviour of two adjacent materials at the common interface. There are three types of boundary conditions that must be taken into consideration (Esmon 2009), no-penetration, no-slip and continuity of stresses. In continuum mechanics, these conditions are often, respectively, represented as

$$\begin{aligned}&\left( \frac{\partial }{\partial t} \mathbf {u}_f - \mathbf {u}_s\right) \cdot \mathbf {n} = 0, \end{aligned}$$
(8)
$$\begin{aligned}&\left( \frac{\partial }{\partial t} \mathbf {u}_f - \mathbf {u}_s\right) \times \mathbf {n} = 0, \end{aligned}$$
(9)

and

$$\begin{aligned} \sigma _s \mathbf {n} = \sigma _f \left( - \mathbf {n}\right) , \end{aligned}$$
(10)

where \(\mathbf {n}\) is the unit vector normal to the boundary, \(\mathbf {u}_s\) and \(\mathbf {u}_f\) are the displacement of the solid and the velocity of the fluid, respectively; the stress is represented by \(\sigma _s\) and \(\sigma _f\) for the solid and fluid, respectively. Within the DMP numerical framework, ghost SPH particles are assigned to MSM particles at the fluid-solid interface to interact with SPH particles of the fluid. In this way, they are at the same time MSM and SPH particles.

2.5 Numerical algorithm

The time integration is employed using the Velocity Verlet (VV) algorithm with a first-order Euler approach and variable timestep according to the stability condition, \(\Delta t = \zeta h^2/\nu\), where \(\nu\) is the dynamic viscosity equal to \(\nu = \rho / \mu\) and \(\zeta\) is taken to be equal to 0.125 (Alexiadis 2015). Using the VV algorithm, particles velocities are calculated at the intermediate stage:

$$\begin{aligned} \mathbf {u}_\mathrm {i}^*= \mathbf {u}_{\mathrm {i}}^{(n)} + \frac{\Delta t}{2 m_\mathrm {i}} \mathbf {f}_\mathrm {i}^{(n)}. \end{aligned}$$
(11)

Here, the superscript \((*)\) represents an intermediate value and the superscript (n) denotes values at the n-th time step. Then, the density of the particles is updated according to

$$\begin{aligned} \rho _\mathrm {i}^*= \rho _{\mathrm {i}}^{(n)} + \frac{\Delta t}{2} \dot{\rho }_\mathrm {i}^{(n)}, \end{aligned}$$
(12)

where the density variations \(\dot{\rho }\) is calculated according to Eq. 4. In Eq. 4, the density should be updated based on the velocity difference between particles \(\mathbf {u}_\mathrm {ij}\). To prevent poor conservation of total mass due to the lag of the velocity in the VV algorithm, an extrapolated velocity is introduced here as

$$\begin{aligned} \overline{\mathbf {u}}_\mathrm {i}= \mathbf {u}_{\mathrm {i}}^{(n)} + \frac{\Delta t}{m_\mathrm {i}} \mathbf {f}_\mathrm {i}^{(n)}, \end{aligned}$$
(13)

where the velocity difference is now calculated based on \(\mathbf {u}_\mathrm {ij}= (\overline{\mathbf {u}}_\mathrm {i}- \overline{\mathbf {u}}_\mathrm {j})\). The next step is to move particle to their new positions by means of

$$\begin{aligned} \mathbf {x}_\mathrm {i}^{(n+1)} = \mathbf {x}_{\mathrm {i}}^{(n)} + \Delta t \mathbf {u}_\mathrm {i}^{*}. \end{aligned}$$
(14)

At this stage, \(\dot{\rho }_\mathrm {i}^{(n+1)}\), and \(\mathbf {f}_\mathrm {i}^{(n+1)}\) are calculated for the new time step using Eqs. 4 and 5, respectively. Finally, the true velocity and density are calculated, respectively, as

$$\begin{aligned} \mathbf {u}_\mathrm {i}^{(n+1)} = \mathbf {u}_{\mathrm {i}}^*+ \frac{\Delta t}{2 m_\mathrm {i}} \mathbf {f}_\mathrm {i}^{(n+1)}, \end{aligned}$$
(15)

and,

$$\begin{aligned} \rho _\mathrm {i}^{(n+1)} = \rho _{\mathrm {i}}^*+ \frac{\Delta t}{2} \dot{\rho }_\mathrm {i}^{(n+1)}. \end{aligned}$$
(16)

3 Problem setup

Fig. 1
figure 1

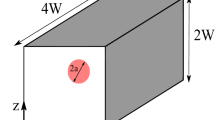
a A 2d schematic of the computational domain; b the structure of the membrane of the capsule; and c 3-D representation of entire domain. Different colors represent different particle types: red, blue, green and white colors illustrate boundary, membrane, outer and inner fluid particles, respectively (color figure online)

Full size image

A schematic of the test case considered in this study is shown in Fig. 1a. The computational domain is a cube with height, width, and depth of \(H=7d\), \(W=2d\) and \(D=2d\), respectively, where d is the diameter of the deformable capsule. The domain consists of two square channels which are connected via a constriction with the length and thickness of \(l_{\rm c} = 2 d\) and \(t_{\rm c}\), respectively. No-slip boundary conditions are applied to the top, bottom, front, rear and constriction walls denoted with solid lines (not shown for front and rear boundaries) while periodic boundary conditions are implemented on the side boundaries, demarcated with dashed lines in Fig. 1a. The capsule is initially located at the center of the left section which has the length of three times of the capsule diameter and fluid particles are arranged on a uniformly-spaced Cartesian grid.

The membrane of the deformable microcapsule is constructed from two concentric spheres with a separation distance of \(h_{\rm t}\). A representation of one of these spheres is shown in Fig. 1b. The spheres are formed by triangles and the computational particles are located on the vertices of these triangles. In order to model the membrane, these particles are connected to their neighboring particles on the same sphere and the adjacent particle on the other sphere with harmonic bonds of constant \(k_{\rm b}\), and to the neighboring particles of the adjacent particle on the other sphere with harmonic bonds of constant \(2/3 k_{\rm b}\). In total, the compliant microcapsule consists of 5124 particles and 25,602 harmonic bonds. Figure 1c illustrates a 3D representation of the entire simulation domain. In total, there are 4 different types of particles in this model: (1) boundary particles (red color), (2) membrane particles (blue color), (3) inner fluid particles (white color), and (4) the outer fluid particles (green color).

4 Results

Considering the dynamics of a compliant microcapsule in a constriction, the inertial force is much smaller than the viscous force, thus the main influential parameter is the capillary number \(\mathrm {Ca} = \mu U r/G_\mathrm{s}\) where r is the radius of the capsule, U is the maximum axial velocity in the constriction and \(G_\mathrm{s}\) is the surface shear elastic modulus equal to \(G_s = \left( 0.5 E/(1+\upsilon )\right) h_t\). It has been shown (Kilimnik et al. 2011; Buxton et al. 2001) that spring network described in previous section can produce an elastic membrane with a Young modulus and Poisson ratio of \(E = 5 k_{\rm b} / \sqrt{3} \delta _\mathrm{ave}\) and \(\upsilon = 1/4\), respectively, where \(\delta _\mathrm{ave}\) is the average length of bonds on the membrane. In addition to capillary number, normalized constriction width, \(\eta = t_{\rm c}/d\), is utilized to describe the confinement of the constriction.

Fig. 2
figure 2

Schematic of the frontal tip and rear tail normalized curvatures of deformed capsule

Full size image

As it has been mentioned earlier, this study provides quantitative measurable parameters for the deformation of microcapsules in constrictions which can be used to identify their mechanical properties in experiments. One quantitative parameter is the deformation index \(D_{\infty, \Lambda }\), where subscript \(\Lambda\) stands for x, y, and z coordinates defined as the maximum elongation of microcapsule in its respective coordinate direction (x, y, and z) normalized by its initial diameter. Other quantitative parameter are frontal tip and rear tail curvatures of microcapsule normalized by the initial radius, \(C_\mathrm{f} = r/R_\mathrm{f}\) and \(C_\mathrm{r} = r/R_\mathrm{r}\), on the xy-plane passing through the center of the channel (see Fig. 2). It should be noted that curvature is assumed to be positive for convex (i.e. frontal side of the capsule in Fig. 2 where the curvature points inwards with respect to the microcapsule) and negative for concave capsule curvatures (i.e. rear side of the microcapsule in Fig. 2 where the curvature point outwards with respect to the microcapsule). After extracting these parameters, they will be analysed for dependency analysis against Ca number. This will determine the sensitivity of these parameters with linear variations of elastic properties of microcapsules. The Pearson R correlation formula (McGraw and Wong 1996) is used here for checking the independency analysis.

In this study, the simulations are carried out on a dimensionless basis and dimensional parameters are normalized using characteristic length d, time d/U, and velocity U, respectively. For the sake of completeness, however, the dimensional properties are also provided here. The density and viscosity of the outer fluid are set equal to \(\rho = 1000\) \(\mathrm {kg} \mathrm {m}^{-3}\) and \(\mu = 0.001\) Pa s, respectively, and the capsule diameter is set to 0.1 mm. Fluid particles are accelerated in the x-direction to maintain a constant fluid velocity in the constriction. The properties of inner and outer fluids such as density and viscosity are set identical, unless stated otherwise.

4.1 Validation and particle resolution study

Fig. 3
figure 3

Validation of present numerical results in simple shear flow against numerical results of Skalak model (C = 1) from (Lac et al. 2004); a steady-state deformation index (\(D_{xy}\)) of capsule as a function of capillary number, b inclination angle (\(\theta / \pi\)) of the capsule as a function of capillary number, and c–f the steady-state deformation of capsule (solid blue lines) compared with those in (Lac et al. 2004) (dashed red lines) at various capillary numbers; c \(\mathrm {Ca} = 0.075\), d \(\mathrm {Ca} = 0.15\), e \(\mathrm {Ca} = 0.30\) and f \(\mathrm {Ca} = 0.60\) (color figure online)

Full size image

The present numerical approach has been extensively tested and validated for a variety of FSI problems such as for modelling cardiovascular systems and deformable materials (Ariane et al. 2017a, b, 2018). For the sake of completeness, however, the numerical method is herein validated against available data in literature. The simple shear flow problem is used for validating the numerical model in a cubic domain with the height of \(H_\mathrm{s} = 5d\), width of \(W_\mathrm{s} = 4d\) and depth of \(D_\mathrm{s} = 4d\). A constant shear rate is provided by setting x-velocity in opposite directions to the top and bottom boundaries while other domain boundaries abide periodic conditions. The rest of simulation conditions are identical with those specified earlier for the present study. Interested readers can refer to our recent publication (Rahmat et al. 2019) for more information about the test-case and further validations.

The deformation of capsules in simple shear flow is quantified using the Taylor deformation \(D_{xy} = \left( \mathcal {H}- \mathcal {D}\right) /\left( \mathcal {H}+ \mathcal {D}\right)\) where \(\mathcal {H}\) and \(\mathcal {D}\) are the major and minor axes of the deformed capsule, and the inclination angle \(\theta / \pi\) defined as the normalized angle between the capsule major axis and the direction of the flow. Here, numerical results are compared with those of Skalak model with the area-dilatation coefficient equal to unity \(\left( C = 1\right)\) from Lac et al. (2004) which is known to be equivalent to the Hookean model (Barthes-Biesel et al. 2002). Figure 3 represents the steady-state Taylor deformation and inclination angle for different capillary numbers (Fig. 3a and b respectively) and the steady-state deformation of capsules at four different capillary numbers. It is observed that both steady-state Taylor deformation index and inclination angle are in good agreement with those from Lac et al. (2004). The comparison of capsule morphology further validates the present numerical results for a wide range of capillary numbers.

Fig. 4
figure 4

Variations of deformation index along the x axis (\({D_{\infty ,x}}\)) as a function of the center of mass (\({x_{\rm c}}\)) of a microcapsule passing through the constriction with simulation conditions equal to \(\eta = 0.5\) at \(\mathrm {Ca} = 0.25\) for four different particle resolutions; \(\xi\)-1 \(= 40 \, \Pi\), \(\xi\)-2 \(= 48 \, \Pi\), \(\xi\)-3 \(= 56 \, \Pi\) and \(\xi\)-4 \(= 64 \, \Pi\) where \(\Pi\) represents the number of particles per unit diameter of the capsule

Full size image

Once the numerical model has been validated, a particle resolution study is carried out to check the dependency of the results with respect to the particle resolution for the present study (the deformation of a microcapsule in constriction). Thus, four particle resolutions of \(\xi\)-1 \(= 40 \, \Pi\), \(\xi\)-2 \(= 48 \, \Pi\), \(\xi\)-3 \(= 56 \, \Pi\) and \(\xi\)-4 \(= 64 \, \Pi\) are considered where \(\Pi\) represents the number of particles per unit diameter of the capsule. Figure 4 shows the variations of deformation index along the x axis (\({D_{\infty ,x}}\)) as a function of capsule center of mass (\({x_{\rm c}}\)) for respective cases with simulation conditions of \(\mathrm {Ca} = 0.25\) and \(\eta = 0.5\). It is observed from Fig. 4 that low resolution cases (\(\xi\)-1 and \(\xi\)-2) over-estimate the deformation index in the constriction. The results converge by increasing the resolution where no significant improvement is observed beyond \(\xi\)-3 which is taken as the optimum resolution throughout this study. It should be noted that the same resolution is used for validating the numerical model discussed earlier for the deformation of capsules in simple shear flow in Fig. 3.

4.2 Effect of capillary number

Fig. 5
figure 5

Variation of deformation index a along the x axis in the direction of the flow (\({D_{\infty ,x}}\)), b along the y axis in the transverse constricted direction (\({D_{\infty ,y}}\)), and c along the z axis (\({D_{\infty ,z}}\)) as a function of the center of mass of a capsule (\({x_\mathrm{c}}\)) through a constriction with \(\eta = 0.5\) for different capillary numbers

Full size image

In this section, the effect of capillary number is investigated for the dynamics of microcapsules in the constriction. In order to isolate the effect of capillary number, the constriction size is taken equal to \(\eta = 0.5\) and capillary number is varied between \(0.005 \le{\rm Ca} \le 2.5\). Figure 5 illustrates the variations of deformation index (a) along the x axis i.e. the direction of the flow (\({D_{\infty ,x}}\)), (b) along the y axis i.e. the constricted transverse direction (\({D_{\infty ,y}}\)) and (c) along the z axis \({D_{\infty ,z}}\) for different capillary numbers as a function of its center of mass (\({x_\mathrm{c}}\)). It is observed that the capsule blocks the constriction for small capillary numbers, i.e. \(\mathrm {Ca} = 0.005\) and \(\mathrm {Ca} = 0.01\). The blockage is due to the stiffness of the membrane that prevents the capsule from being squeezed by the constriction walls. By further increase of the capillary number, hydrodynamic drag at the wake of the capsule and pressure drop push the capsule in the constriction. \({D_{\infty ,x}}\) remains almost constant inside the constriction except when the capsule is at the inlet or exit regions. Towards the exit region, \({D_{\infty ,x}}\) drops significantly reaching its minimum position at \({x_\mathrm{c}} \approx 5.5\), then it increases approaching unity. This behaviour is due to the elastic properties of the microcapsule trying to balance the hydrodynamic forces at the exit region. Further increasing the capillary number results in a drastic increase of \({D_{\infty ,x}}\) at the inlet and larger decrease towards the exit, since high deformability of microcapsule allows the membrane to stretch more in transverse direction as a response to hydrodynamic forces. In Fig. 5b, it is observed that \({D_{\infty ,y}}\) decreases as the capsule approaches the constriction, remains almost constant during the passage, and increases when microcapsule reaches the constriction exit at \({x_\mathrm{c}} \approx 4.6\). Figure 5c also illustrates the expansion of microcapsules along the z axis inside the constriction as a result of available non-confined space representing a similar pattern for all capillary numbers.

Fig. 6
figure 6

Two-dimensional illustration of capsules at arbitrary moments on xy-plane (passing at the center of the channel), in a constriction with \(\eta = 0.5\) for different capillary numbers (Different colors are just used for visual purposes and have no other physical or numerical meanings) (color figure online)

Full size image

Figure 6 represents microcapsules with four different capillary numbers at arbitrary times passing through the constriction (\(\eta = 0.5\)). Except for the smallest capillary number in Fig. 6a (\(\mathrm {Ca} = 0.025\)) which blocks the channel due to high membrane stiffness, all test-cases are squeezed between the constriction walls showing a limiting index of \({D_{\infty ,y}} = 0.42\) as also represented in Fig. 5b. The microcapsule rear tail curvature shifts from a convex shape for \(\mathrm {Ca} = 0.25\) into a concave one for \(\mathrm {Ca} = 2.5\) as a response to the hydrodynamic drag and pressure drop at the wake of the microcapsule competing against its elastic properties. This is further followed by the microcapsule expansion in the transverse direction at the downstream section, forming an oblate shape.

Fig. 7
figure 7

Variation of normalized a frontal tip (\(C_\mathrm{f}\)) and b rear tail (\(C_\mathrm{r}\)) curvatures of microcapsules passing through a constriction with \(\eta = 0.5\) for different capillary numbers as a function of its center of mass (\({x_\mathrm{c}}\))

Full size image

Figure 7 represents variations of normalized frontal tip and rear tail curvatures of microcapsules passing through the constriction with \(\eta = 0.5\) for different capillary numbers as a function of its center of mass (\({x_\mathrm{c}}\)). Despite having different magnitudes, the frontal curvature has almost a constant trend at the first half of the constriction (\({x_\mathrm{c}} < 4\)) except for the largest capillary. The frontal tip curvature drops significantly in the second half of the constriction (\({x_\mathrm{c}} > 4\)) reaching unity. In contrast, the rear tail curvature has larger magnitudes for smaller Capillaries and the rear curvature drops to negative values for large capillary numbers, reaching a minimum value of \(C_\mathrm{r} \approx -5\) for the largest capillary number at \({{x}_{\rm c}} = 5\). This indicates the shift from convex to concave curvatures as also illustrated in Fig. 6d.

Fig. 8
figure 8

Three-dimensional representation of capsule passage through constriction for simulation conditions a \(\mathrm {Ca} = 0.25\) - \(\eta = 0.5\) and b \(\mathrm {Ca} = 2.5\) - \(\eta = 0.5\) at six different simulation times

Full size image

Figure 8 represents three-dimensional illustration of capsule passing through constriction for two different simulation conditions at different simulation times. When capsule approaches the constriction, it expands in the direction of the flow (x-direction) and transverse to the constriction confinement (z-direction) while it is confined by the constriction walls in y direction. Subsequently, the capsule occupies a larger area inside the constriction. The maximum capsule expansion is quantified by comparing the area occupied on the xz-plane with respect to its initial area on the same plane, indicating an increase of 76.5% for \(\mathrm {Ca} = 0.25\), 79.5% for \(\mathrm {Ca} = 0.5\), 84% for\(\mathrm {Ca} = 1.0\), and 100% for \(\mathrm {Ca} = 2.5\). Thus, the larger capillary case has a shorter passage time through the constriction, experiencing a higher drag of flow in its wake. Another reason for a faster passage of capsules at larger capillary numbers is the faster deformation of capsules at the entrance of the constriction due to its highly deformable membrane.

4.3 Effect of channel width

Fig. 9
figure 9

Variation of deformation index a along the x axis in the direction of the flow (\({D_{\infty ,x}}\)), b along the y axis in the transverse (constriction) direction (\({D_{\infty ,y}}\)), and c along the z axis (\({D_{\infty ,z}}\)) as a function of the center of mass of the microcapsule (\({x_\mathrm{c}}\)) for different constriction size (\(\eta\)) and capillary numbers

Full size image

Here, the effect of constriction width is investigated for three different values of \(\eta = 0.5, 0.75\), and 1. The constriction sizes are chosen such that the dynamics of microcapsules are fully observed by providing sufficient deformation to the microcapsules, which will be used for correlating to the mechanical properties as will be explained in Sect. 5. Figure 9 represents the variations of deformation index along the three major axis (a) \({D_{\infty ,x}}\), (b) \({D_{\infty ,y}}\) and (c) \({D_{\infty ,z}}\) for nine different cases with three capillary numbers and three constriction widths as a function of its center of mass (\({x_\mathrm{c}}\)). For the smallest capillary number (\(\mathrm {Ca} = 0.025\)), the microcapsule blocks the constriction for \(\eta = 0.5\), but it passes through wider constrictions showing minimum deformation along the x-axis. The deformation index along the y axis (\({D_{\infty ,y}}\)) indicates that the microcapsule is confined by the constriction walls for small capillary numbers at all constriction sizes. For larger capillary numbers, \({D_{\infty ,x}}\) is larger at narrower constrictions due to the reduction of pressure drop inside the constriction and confinement effects. This also affects the transverse deformation leading to larger \({D_{\infty ,y}}\) at wider constrictions. The deformation index along the z axis (\({D_{\infty ,z}}\)) is highly influenced by the size of the constriction which induces a large deformation on the microcapsules leading to their expansion along the z direction.

Fig. 10
figure 10

Two-dimensional illustration of capsules at arbitrary moments on xy-plane (at the center of the channel), in a constriction with different widths and capillary numbers (Different colors are just used for visual purposes and have no other physical or numerical meanings) (color figure online)

Full size image
Fig. 11
figure 11

Variation of normalized a frontal tip (\(C_\mathrm{f}\)) and b rear tail (\(C_\mathrm{r}\)) curvatures of microcapsules passing through a constriction at different capillary numbers for different positions inside the constriction

Full size image

Figure 10 represents a cross section of the channel on the xy-plane passing through the center of the channel showing two-dimensional profiles of four cases passing through the constriction at arbitrary locations. In Fig. 10a–c, the constriction width is equal to the capsule diameter but Fig. 10d has a narrower constriction size (\(\eta = 0.75\)). Figure 10a shows the microcapsule passing through the constriction with minimum deformation due to the membrane stiffness. At higher capillary numbers, the microcapsule transforms into parachute and bullet shapes as a result of the reduction in elastic modulus of the membrane. It is also observed that at smaller capillary numbers and at the downstream of the constriction, capsule regain its spherical shape since the hydrodynamic effects are not strong enough to compete with the elastic properties. The hydrodynamic forces at the wake of the capsule result in a backward indentation at the rear side at larger capillary numbers. By comparing Fig. 10c and d, it is revealed that the effect of constriction size is more dominant on the deformation of the capsule. This will be further discussed in the next section.

Fig. 12
figure 12

Inverse of the passage time of capsules through the constriction for different capillary numbers and constriction sizes

Full size image

Figure 11 represents the variations of normalized frontal and rear curvatures at different capillary numbers for different positions inside two different constrictions (\(\eta = 0.75\) and \(\eta = 1.0\)). The frontal curvature shows a monotonically increasing trend at \(x_\mathrm{c} = 3.5\) and \(x_\mathrm{c} = 4.0\) in both constriction cases as the capillary number increases. Comparing the magnitudes, higher positive curvatures are obtained at the constriction width of \(\eta = 0.75\) represented by black color in Fig. 11a. Towards the exit region (\(x_\mathrm{c} = 4.5\)), the monotonic increasing trend turns into a decreasing one when the capillary number exceeds \(\mathrm {Ca} = 0.5\) which shows that the elastic properties of the membrane is not strong enough to resist against hydrodynamic forces. Considering the rear tail curvature, it is observed that all cases represent a decreasing trend except at the inlet of the narrower constriction (\(x_\mathrm{c} = 3.5\)). It should also be noted that the rear tail curvature remains positive at the entrance of the constriction but as the capsule moves inside the constriction, the hydrodynamic forces at the wake of the capsule push the membrane and reduce its curvature. This results in a shift in the direction of the rear tail curvature (convex to concave) and membrane inward indentation as depicted in Figs. 6 and 10.

Another important parameter to investigate is the time of passage inside the constriction. Figure 12 represents the inverse of the passage time for the capsules. Here, the inverse of the time is utilized since the passage time for very small capillary cases which block the constriction is infinity, making it difficult to illustrate. The figure represents a monotonically increasing trend as the capillary number increases. It means that more deformable capsules pass through the constriction in a shorter time. There is a clear distinction between passage time of microcapsules in different channel widths showing that the constriction width has more dominant effect on the passage time compared to the capillary number.

There are two main challenges in comparing numerical and experimental results: (1) the effect of initial conditions in numerical cases and (2) the experimental noise especially in microfluidic applications. Here, they are tested in a single case where two off-center microcapsules are initially positioned with the distance of \(\beta = 0.5\) and \(\beta = 1\) (\(\beta\) is the asymmetry parameter measured from channel center-line and normalized with capsule diameter) with the simulation conditions of \(\mathrm {Ca} = 0.25\) and \(\eta = 1.0\). The off-centered feature in taken into account for the experimental noise in which the flowing microcapsule might not travel exactly at the center of the channel. In order to remove the effect of numerical initial conditions, the off-center cases are passed twice from the constriction. Figure 13 represents (a) the deformation index along the x axis (\({D_{\infty ,x}}\)) and (b) and (c) the microcapsule profiles for \(\beta = 0.5\) and \(\beta = 1\), respectively. In addition, a respective centered case is also provided for better comparison (magenta line in Fig. 12). It is observed that the first pass shows a slightly different behaviour, especially for the one with higher asymmetry parameter (\(\beta = 1.0\)), but the second pass data is almost the same as that of the centered one (the magenta color). This shows that the effects of numerical initial conditions are relatively small (by comparing the deformation of the first and second passes) and experimental off-centered noise can be avoided if the constriction is repeated.

Fig. 13
figure 13

Comparison of the data for two off-centered capsules placed 0.5 and 1.0 diameter away from the center-line (\(\beta = 0.5\) and \(\beta = 1.0\)), respectively, with a centered one at \(\mathrm {Ca} = 0.25\) and \(\eta = 1.0\); a the deformation index in the x direction (\({D_{\infty ,x}}\)), b and c the shape of capsules at different arbitrary locations for two passes (black color for the first pass and blue color for the second pass) and the centered case represented by magenta color (color figure online)

Full size image

5 Correlation and dependency analysis

In the previous section, several quantitative parameters e.g. (the inverse of) the passage time of capsules in constriction, the deformation index of capsules in three directions (\({D_{\infty ,x}}\)—along the direction of the flow, \({D_{\infty ,y}}\)—in the direction of the constriction, and \({D_{\infty ,z}}\)—normal to the direction of the flow and constriction), and the frontal tip and rear tail curvatures of microcapsules are introduced and their variations with respect to two effective parameters (\(\mathrm {Ca}\) and \(\eta\)) are analysed. Here, a dependency analysis is provided to check how these parameters are correlated and whether they can be used to extract mechanical properties of microcapsules. Since the mechanical properties are related to the shear elastic modulus, the dependency analysis is performed against capillary number. Subsequently, the Pearson r correlation (McGraw and Wong 1996) is used here

$$\begin{aligned} r_{xy} = \frac{n \, \sum x_{p} y_{p} - \sum x_{p} \sum y_{p}}{\sqrt{n \, \sum {x_{p}}^2 - \left( \sum x_{p}\right) ^2} \sqrt{n \, \sum {y_{p}}^2 - \left( \sum y_{p}\right) ^2}} \end{aligned}$$
(17)

where \(r_{xy}\) is the correlation parameter varying between \(-1 \le r_{xy} \le 1\), x and y parameters denote the measured quantitative parameter (deformation index, curvatures and etc.) and capillary number, respectively, for pth data. The value of \(r_{xy}\) defines the level of correlation between two sets of data (x and y) such that \(r_{xy} = \pm 1\) indicates they are linearly correlated and \(r_{xy} = 0\) represents no correlation. Thus, preferable quantitative parameters are those which their Pearson r correlation factor is close to \(\pm 1\).

To investigate the linear dependency of results with capillary number, the Pearson r correlation is provided in Table 1 for inverse of passage time, deformation index in three different directions at the middle of the constriction (\(x_\mathrm{c} = 4\)), and frontal tip and rear tail curvatures at three different locations (\(x_\mathrm{c} = 3.5, 4\) and 4.5) for three different constriction width cases (i.e., \(\eta = 0.5, 0.75\) and 1). To emphasise on the significance of data, the Pearson r correlation factor is highlighted based on the level of correlation: (1) italics represents high level of linear dependency \(\left( |r_{xy}| > 0.9\right)\), (2) bold indicates mediocre dependency level \(\left( 0.7 < |r_{xy}| \le 0.9\right)\) and (3) boldItalics illustrates low level of dependency in data \(\left( |r_{xy}| \le 0.7\right)\).

Table 1 Pearson r correlation factor for different measurable parameters; the italics represents perfect linear correlation \(\left( |r_{xy}| > 0.9\right)\), while bold \(\left( 0.7 < |r_{xy}| \le 0.9\right)\) and boldItalics \(\left( |r_{xy}| \le 0.7\right)\) represents less correlated relationship
Full size table

Considering the data in Table 1, it can be concluded that the the passage time (t) and the deformation index in the z direction \(\left( {D_{\infty ,z}}\right)\) are not suitable parameters for extracting microcapsule mechanical properties. In contrast, the deformation index in the direction of the flow \(\left( {D_{\infty ,x}}\right)\) is the most effective parameter to extract such correlations. The frontal tip and rear tail curvatures are also effective especially at the inlet region \(\left( x_{\rm c} = 3.5\right)\). This suggests the use of short-length constrictions where the inlet region is the most suitable location to extract curvatures. Considering the curvatures towards the end of the constriction \(\left( x_\mathrm{c} = 4.5\right)\), it is observed that the curvature at the frontal tip does not represent a good correlation while the rear curvature illustrates high level of dependency. Another interesting finding is that the dependency is further promoted by reducing the size of the constriction as it indicates that almost all parameters represent better correlation in \(\eta = 0.5\) compared to larger constrictions.

Although the above correlation analysis is useful in filtering some of the unfavorable parameters, the fabrication and magnitude analysis considerations should also be taken into account. For instance, the deformation index in the y direction \(\left( {D_{\infty ,y}}\right)\) represents a relatively good correlation but the variation of \({D_{\infty ,y}}\) does not change considerably. For instance, \({D_{\infty ,y}}\) varies only between \(\left( 0.42< {D_{\infty ,y}} < 0.44\right)\) and \(\left( 0.52< {D_{\infty ,y}} < 0.70\right)\) for \(\eta = 0.5\) and \(\eta = 0.75\), respectively, for a wide range of capillary number \(0.005< {\rm Ca} < 2.5\). This is particularly important since in many applications, the length scale is in the limit of micrometers and current technology might not be able to accurately measure the values of these parameters. Another consideration which should be taken into account is the width of the constrictions. Despite showing a better dependency for \(\eta = 0.5\) compared to \(\eta = 0.75\) and 1, some technical problems might appear in practice, e.g. microcapsules with larger elastic properties (less deformable ones) might block the constriction as shown earlier.

Considering the above correlation and dependency analysis, one may suggest some manufacturing recommendations for the design and fabrication of microfluidic constrictions to evaluate microcapsule mechanical properties:

  • Since some quantitative parameters such as the frontal and rear curvatures are more dynamic (showing more dependency) at the inlet and exit of the constriction, short-length constrictions are recommended.

  • The size of the constriction should be selected appropriately since quantitative parameters represent better correlations at smaller constrictions while some microcapsules may block those small constrictions. So, a constriction size in the range of 75

  • Considering the magnitude and dependency analysis, \({D_{\infty ,x}}\), frontal tip and rear tail curvatures of the microcapsules are the most linearly correlated parameters which represent considerable variations. These parameters are mostly helpful at the inlet and towards the exit of the constriction.

6 Conclusion

In this paper, the deformation of microcapsules are studies using a hybrid particle-based numerical model using the Smoothed Particle Hydrodynamics (SPH) method and the Mas Spring Model (MSM). The model is validated against available data in literature for the deformation of capsules in shear flow. Then, it is used to simulate the dynamics of microcapsules in micro-constrictions for a wide range of capillary numbers and constriction sizes. The aim of this paper is to provide some quantitative parameters for the dynamics of microcapsules in micro-constrictions correlated with their elastic properties for extracting mechanical properties of microcapsules in experiments.

The dynamics of microcapsules is herein quantified by several parameters such as the deformation index, passage time and the membrane curvature at the frontal tip and rear tail of the microcapsule. It is observed that microcapsules deform easier and pass through the micro-constriction faster at larger capillary numbers, showing more elongation in the direction of the flow. At wider constrictions, capsule elongation is smaller in the direction of the flow for constant capillary cases but they pass through the micro-constriction faster at wider constrictions.

Subsequently, a correlation and dependency analysis is performed for the variation of these quantitative parameters with the capillary number using the Pearson r correlation. Considering the dependency analysis, it is observed that the deformation index along the direction of the flow (\({D_{\infty ,x}}\)) and in the direction of the constriction (\({D_{\infty ,y}}\)), and the curvatures at the frontal tip (\(C_\mathrm{f}\)) and rear tail (\(C_\mathrm{r}\)) are suitable parameters representing better correlations with the capillary number especially in smaller constriction size. In order to reach a comprehensive conclusion, however, other considerations must be taken into account. For instance, the variations of \({D_{\infty ,y}}\) are very small in magnitude and it might be difficult to read its variations for different cases in narrow constrictions accurately. Despite obtaining better correlations at the narrowest constriction (\(\eta = 0.5\)), microcapsules may block the constriction sizes in this range, thus we recommend utilising slightly wider constrictions (\(\eta = 0.75\)) so as to reduce the risk of blockage. Additionally, the frontal tip and rear tail curvatures represent better correlations at the inlet and exit regions of the constriction suggesting that short-length constrictions are more suitable for correlating the dynamic of microcapsules with their mechanical properties.