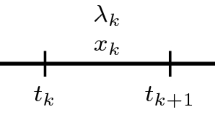Compactness and convergence rates in the combinatorial integral approximation decomposition

Abstract

The combinatorial integral approximation decomposition splits the optimization of a discrete-valued control into two steps: solving a continuous relaxation of the discrete control problem, and computing a discrete-valued approximation of the relaxed control. Different algorithms exist for the second step to construct piecewise constant discrete-valued approximants that are defined on given decompositions of the domain. It is known that the resulting discrete controls can be constructed such that they converge to a relaxed control in the $\hbox {weak}^*$ topology of $L^\infty$ if the grid constant of this decomposition is driven to zero. We exploit this insight to formulate a general approximation result for optimization problems, which feature discrete and distributed optimization variables, and which are governed by a compact control-to-state operator. We analyze the topology induced by the grid refinements and prove convergence rates of the control vectors for two problem classes. We use a reconstruction problem from signal processing to demonstrate both the applicability of the method outside the scope of differential equations, the predominant case in the literature, and the effectiveness of the approach.

1 Introduction

This article concerns the following class of optimization problems

$$\begin{aligned} \begin{aligned} \inf _{x}&j(K(x)) \\ \text {s.t.}&x \in L^\infty (\varOmega _T, V), \\&x(s) \in \{\xi _1,\ldots ,\xi _M\} \subset V \text { for almost all (a.a.) } s \in \varOmega _T \end{aligned} \end{aligned}$$

(P)

for some bounded domain $\varOmega _T \subset {{\mathbb {R}}}^d$, $d \ge 1$. It is an infinite-dimensional and non-smooth optimization problem, in which the distributed optimization variable x is restricted to a finite number of realizations, often also called bangs. The control-to-state operator K solves the dynamics of the underlying system that is controlled. We note that the feasible set of (P) is bounded. However, we cannot generally expect that (P) admits a minimizer because the feasible set of (P) is not closed in the $\hbox {weak}^*$ topology. Apart from control of ODEs and PDEs with discrete-valued control inputs, the problem class (P) also covers problems from image denoising and topology optimization. However, we note that there are also prevalent instances of these problems, where the properties of the control-to-state operator that are required for our analysis do not hold, see for example the problem in [7, Sect. 4.2.2].

Clason et al. treat a similar problem class with a so-called multi-bang control regularization that generalizes an $L^1$-type penalty to promote a corresponding multi-bang solution structure (that is the solution takes the values $\xi _1,\ldots ,\xi _M$) in the series of articles [5,6,7]. Buchheim et al. [4] treat an instance of (P) following the two steps a) discretize (P) into a finite-dimensional integer program (IP), and b) solve the discretized problem with a finite-dimensional IP-technique, namely a branch-and-bound algorithm for convex quadratic integer programs. Their results show that the computational demand may become excessive for fine discretizations. This is unsurprising because the discretized problem is an integer quadratic program (IQP), a class of problems, which is NP-hard in general.

We use the results on convexification reformulations and the combinatorial integral approximation (CIA) decomposition from [12, 15, 21, 23, 24, 26, 27, 36]. The CIA decomposition splits the optimization into

• 1. deriving and solving a continuous relaxation of the problem (P), and

• 2. computing a discrete-valued approximation of the control of the relaxation.

The splitting allows us to take advantage of the infinite-dimensional structure of the problem, which allows to use efficient algorithms to compute approximations of (P). Obviously, the continuous relaxation cannot be solved to optimality in function space on a computer with finite precision. In [16, 22], it is shown that if the minimizers of finite-dimensional approximations of the continuous relaxation approximate a minimizer of the continuous relaxation, the discrete-valued approximation of the relaxed control can be constructed to approximate the infimum of (P). Both steps of the CIA decomposition have been analyzed by means of a reformulation of the problem with binary controls that serve as activation functions of the control realizations $\xi _1$,$\ldots$,$\xi _M$. We follow this procedure and introduce the terms of binary and relaxed control; see [22].

Definition 1.1

The term binary control denotes a measurable function $\omega : \varOmega _T \rightarrow \{0,1\}^M$ with $\sum _{i=1}^M \omega _i = 1$ almost everywhere (a.e.). A measurable function $\alpha : \varOmega _T \rightarrow [0,1]^M$ with $\sum _{i=1}^M \alpha _i = 1$ a.e. in $\varOmega _T$ is called a relaxed control.

Following the literature, we call algorithms that transform continuous-valued variables into discrete-valued ones rounding algorithms.

The proposed approach is advantageous because we can assume that both steps can be executed efficiently. For the second step, different algorithmic approaches exist. We name sum-up rounding (SUR) [24], next-forced rounding (NFR) [14], and the optimization-based ones presented in [2, 37]. All of them take a relaxed control and construct a binary control that is piecewise constant on the cells of a given grid, the so-called rounding grid. If the grid constant, in this case the maximum volume of the grid cells, tends to zero, another quantity, the so-called integrality gap, tends to zero as well. If $\varOmega _T = (t_0,t_f)$ this means that $\sup _{t \in [t_0,t_f]} \Big \Vert \int _0^t \alpha - \omega ^{{{\overline{\varDelta }}}}\Big \Vert \rightarrow 0$ for a relaxed control $\alpha$ and the binary control $\omega ^{{{\overline{\varDelta }}}}$ that was computed on a rounding grid with grid constant ${{\overline{\varDelta }}}$. To avoid ambiguities, we note that we refer to the maximum cell volume in the cells that make up the rounding grid by the symbol ${{\overline{\varDelta }}}$ and the term grid constant. If the operator K exhibits sufficient compactness properties, namely if it maps weakly convergent sequences to norm convergent sequences, and the objective functional is a continuous function of the state vector, we obtain convergence of the objective functional. This gives rise to an optimality principle, which has been shown in [22] for the case of elliptic boundary value problems (BVPs).

The presented approach is closely related to the approximation of control inputs into differential equations or inclusions with so-called chattering controls, a theory, which has been investigated in the optimal control community for several decades. In particular, the Lyapunov convexity theorem [17, 18] and the Filippov-Ważewski theorem [9, 35] are important findings in this context. We also note Tartar’s work [32] because it provides a constructive means to compute discrete-valued controls from continuously-valued ones in Theorem 3. His construction can also be used in the second step of the CIA decomposition. A similar idea is pursued by Gerdts [10, 11] under the name variable time transformation in the one-dimensional – that is the time-dependent – case. In [24, 28], Sager employs this approximation approach in the context of discrete-valued optimal control of ODEs. The results are extended constructively using the aformentioned SUR algorithm in [15, 26] and transferred to evolution equations with semigroup theory in [12, 21]. In [22, 36], the algorithmic approach is transferred to the multi-dimensional setting.

1.1 Contributions

The CIA decomposition has been developed originally for the approximation of control inputs and corresponding solutions of differential equations. We show that it is in fact always applicable to optimization problems, in which distributed optimization variables are passed into compact or completely continuous control-to-state operators and provide a signal processing example that does not involve any differential equation.

The objective corresponding to a relaxed control can be approximated arbitrarily well with discrete-valued control trajectories if the grid size of the rounding grid tends to 0. From a function space point of view, this is independent of the method that is chosen to solve the relaxed optimization problem.

We show that rounding grids induce pseudometrics. Under a regularity assumption on the refinement of the rounding grids, we prove that the induced pseudometrics form a Hausdorff topology. Moreover, this assumption implies a convergence rate for the integer approximation in the $H^{-1}$-norm. We show an improved convergence rate for the state vector approximation for a class of one-dimensional signal filtering approximation problems under a differentiability assumption on the convolution kernel.

We demonstrate computationally that our methodology allows us to obtain high precision approximations of the infimum of (P) without the need to solve a potentially NP-hard discretized problem, which allows for an efficient algorithmic framework and allows for finer discretizations compared to the approach presented in [4].

1.2 Structure of the article

In Sect. 2, we introduce a general formulation of the model problem (P) and derive the relaxation for the first step of the CIA decomposition. In Sect. 3, we introduce rounding algorithms and an approximation property that can be satisfied by suitable algorithms in the second step of the relaxation. We show that this is sufficient to obtain the desired convergence of the objective value by employing compactness properties. In Sect. 4, we motivate and prove a convergence rate of the controls in the space $H^{-1}$. In Sect. 5, we apply the results from Sect. 3 to a model problem from signal processing and prove a convergence rate on the approximated signal under a suitable regularity assumption. Section 6 demonstrates our findings computationally for a variant of the signal processing problem presented in [4], and Sect. 7 draws a conclusion.

1.3 Notation

For a Banach space X, we denote its topological dual space by $X^*$. For an optimization problem (OP), we denote its feasible set by ${\mathcal {F}}_{(OP) }$. We denote the unit simplex by

$$\begin{aligned} {\mathbb {S}}^M :=\left\{ x \in {{\mathbb {R}}}^M : x \in [0,1]^M \text { and } \sum _{i=1}^M x_i = 1 \right\} . \end{aligned}$$

We denote convergence in the $\hbox {weak}^*$ topology by $\rightharpoonup ^*$. We denote the Borel $\sigma$-algebra by ${{\mathcal {B}}}$. We denote the Lebesgue measure on ${{\mathbb {R}}}^m$ by $\lambda _{{{\mathbb {R}}}^m}$. If m is obvious, we abbreviate and simply write $\lambda$. For a set $A \subset {\mathbb {R}}^m$, we write ${{\mathrm{diam}}}A = \sup \{ \Vert x - y\Vert : x,y \in A \}$. For sequences $(a^{(n)})_n \subset [0,\infty )$ and $(b^{(n)})_n \subset [0,\infty )$, we abbreviate the fact that $0 \le c_1 a^{(n)} \le b^{(n)} \le c_2 a^{(n)}$ for global constants $c_1$, $c_2 > 0$ by the Landau notation $b^{(n)} = \varTheta (a^{(n)})$. We highlight that this is a slight deviation from the canonical use of the Landau notation, where only the limiting behavior matters.

2 Standing assumptions and continuous relaxation

Before deriving relaxations and stating our assumptions, we define the term ultraweak-complete continuity, which is tailored to our requirements on the control-to-state operator.

Definition 2.1

Let X and Y be Banach spaces. We call a function $A : X^* \rightarrow Y$ ultraweak-completely continuous if for all sequences $(x^{(n)})_n \subset X^*$, we have that $x^{(n)} \rightharpoonup ^* x$ implies $A(x^{(n)}) \rightarrow A(x)$.

Remark 2.2

An operator $A : X \rightarrow Y$ is called completely continuous if $x^{(n)} \rightharpoonup x$ in X implies $A(x^{(n)}) \rightarrow A(x)$ in Y for Banach spaces X and Y. If X is reflexive and A is linear, this implies compactness of the operator A, that is if the sequence $(x^{(n)})_n \subset X$ is bounded, the sequence $(A(x^{(n)}))_n \subset Y$ has a convergent subsequence. Furthermore, compactness of a linear operator always implies its complete continuity. We define ultraweak-complete continuity analogous to complete continuity but require $\hbox {weak}^*$ convergence for the domain sequence. In particular, we consider $\hbox {weak}^*$ convergence in $L^\infty$ in this manuscript because it is the natural topology to discuss the convergence of the discrete-valued control functions. $\hbox {Weak}^*$ convergence in $L^\infty (\varOmega _T)$ implies weak convergence in $L^p(\varOmega _T)$ for $1 \le p < \infty$ because $(L^p(\varOmega _T))^* \cong L^q(\varOmega _T)$ for $1 \le p < \infty$ and $1/p + 1/q = 1$ by virtue of the canonical map, see [8, Thm IV.1.1], and the continuous embeddings $L^r(\varOmega _T) \hookrightarrow L^s(\varOmega _T)$ for $1 \le s < r \le \infty$. Therefore, completely continuous operators defined on $L^p(\varOmega _T)$, $p \in [1,\infty )$, are ultraweak completely continuous operators on $L^\infty (\varOmega ) \cong (L^1(\varOmega _T))^*$.

If the control-to-state operator K is defined for functions x that take values in ${{\mathrm{conv}}}\{\xi _1,\ldots ,\xi _M\}$ and not only in $\{\xi _1,\ldots ,\xi _M\}$, we can replace the discreteness constraint in (P) by its convex hull and obtain the relaxed problem (Q)

$$\begin{aligned} \begin{aligned} \min _{x}\,&j(K(x)) \\ \text {s.t.}\,&x \in L^\infty (\varOmega _T, V), \\&x(s) \in {{\mathrm{conv}}}\{\xi _1,\ldots ,\xi _M\} \text { for a.a. } s \in \varOmega _T. \end{aligned} \end{aligned}$$

(Q)

Employing the aforementioned algorithms in the second step of the CIA decomposition allows us to compute the discrete-valued approximants of the solution of (Q). However, the algorithms are defined on ${\mathbb {S}}^M$-valued functions. This problem can be circumvented because elements in ${{\mathrm{conv}}}\{\xi _1,\ldots ,\xi _M\}$ can be represented by convex combinations of $\{\xi _1,\ldots ,\xi _M\}$ by construction. We recall that ${{\mathrm{conv}}}\{\xi _1,\ldots ,\xi _M\}$ is compact because $M < \infty$.

In the context of differential equations, the convex coefficients are often used to relax binary activation functions of terms that occur in the right hand side of an ODE or PDE. For example, we may consider the initial value problem (IVP)

$$\begin{aligned} {\dot{y}}(s) = \sum _{i=1}^M \omega _i(s) f(y(s),\xi _i)\text { a.e.},\quad y(0) = y_0 \end{aligned}$$

(2.1)

for binary controls $\omega$. This IVP is equivalent to

$$\begin{aligned} {\dot{y}}(s) = f(y(s),x(s))\text { a.e.},\quad y(0) = y_0 \end{aligned}$$

(2.2)

for all feasible $x(s) \in \{\xi _1,\ldots ,\xi _M\}$ a.e. by means of $x(s) = \sum _{i=1}^M \omega _i(s) \xi _i$ a.e. In this case, the control-to-state operator of the relaxation does not have to be defined for all control functions $x(s) \in {{\mathrm{conv}}}\{\xi _1,\ldots ,\xi _M\}$ a.e. because it is sufficient to analyze the control-to-state operator of (2.1). This strategy is called partial outer convexification in the literature [12, 15, 26]. Thus from now on we consider control-to-state operators that act on the convex coefficients. Therefore, we generalize the relaxation of (P) below. It features a different operator $K_R$ and (R) is equivalent to (Q) if $K_R$ satisfies the identity $K_R(\alpha ) = K\big (\sum _{i=1}^{M} \alpha _i \xi _i\big )$ for all relaxed controls $\alpha$.

$$\begin{aligned} \begin{aligned} \min _{\alpha }\,&j\left( K_R(\alpha )\right) \\ \text {s.t.}\,&\alpha \in L^\infty (\varOmega _T, {{\mathbb {R}}}^M), \\&\alpha (s) \in {\mathbb {S}}^M \text { for a.a. } s\in (t_0,t_f). \end{aligned} \end{aligned}$$

(R)

By requiring that $K_R$ satisfies the identity $K_R(\omega ) = K\big (\sum _{i=1}^{M} \omega _i \xi _i\big )$ for all binary controls $\omega$, we obtain that (R) is a relaxation of (P). We make the following standing assumption on (P).

Assumption 1

• 1. Let $\varOmega _T \subset {{\mathbb {R}}}^d$ be a bounded domain for some fixed $d \in {\mathbb {N}}$.

• 2. Let Y be a Banach space.

• 3. Let $K : \left\{ x \in L^\infty (\varOmega _T, V) \,:\, x(s) \in \{\xi _1,\ldots ,\xi _M\} \text { for a.a. } s \in \varOmega _T \right\} \rightarrow Y$ be a function.

• 4. Let $K_R : L^\infty (\varOmega _T, {{\mathbb {R}}}^M) \rightarrow Y$ be ultraweak-completely continuous.

• 5. Let $K\big (\sum _{i=1}^M \omega _i \xi _i\big ) = K_R(\omega )$ for all binary controls $\omega$.

• 6. Let $j : Y \rightarrow {{\mathbb {R}}}$ be continuous.

• 7. Let the number of discrete control realizations $M \in {\mathbb {N}}$ be fixed.

Remark 2.3

As an alternative to the analysis we present here, one can also analyse the problem (Q) if K is defined on all of $L^\infty (\varOmega _T, V)$. Then, in Assumption 1 one may require that $K : L^\infty (\varOmega _T, V) \rightarrow Y$ is ultraweak-completely continuous. To this end, one generally requires the identification $U^* \cong V$ for some Banach space U and that the space V has the Radon–Nikodym property. Then, this allows to deduce $(L^1(\varOmega _T, U))^* \cong L^\infty (\varOmega _T, V)$, see [8, Thm IV.1.1]. This is a fairly general assumption however and in particular, every reflexive Banach space satisfies this property.

3 Approximation arguments

The approximation arguments generalize work from [16, 22], which analyze the case, where $K_R$ and K are control-to-state operators of the BVPs governed by the Laplace operator. In Sect. 3.1, we introduce important terms for our analysis and recall findings from previous work. Sect. 3.2 derives norm convergence and an optimality principle for the approximation based on Sect. 3.1.

3.1 Definitions and control approximation

The approximation properties in this section are stated for relaxed controls or sequences of them. One should have in mind that the aforementioned algorithms for the second step of the CIA decomposition produce binary controls, or sequences of them, which satisfy these properties. We introduce the terms of rounding grid and admissible sequence of rounding grids.

Definition 3.1

(Rounding grid) A finite partition $\{S_1,\ldots ,S_N\} \subset {\mathcal {B}}$ of the domain $\varOmega _T$ is called a rounding grid. We call ${{\overline{\varDelta }}}:=\max _{i\in \{1,\ldots ,N\}} \lambda (S_i)$ the grid constant of the rounding grid.

Definition 3.2

(Order conserving domain dissection [20, 22]) Let $\varOmega _T$ be a bounded domain. A sequence $\left( \left\{ S_1^{(n)}, \ldots , S_{N^{(n)}}^{(n)}\right\} \right) _n \subset 2^{{{\mathcal {B}}}(\varOmega _T)}$ of rounding grids is called an order conserving domain dissection of $\varOmega _T$ if

• 1. ${{\overline{\varDelta }}}^{(n)} \rightarrow 0$ for the corresponding sequence of grid constants $\big ({{\overline{\varDelta }}}^{(n)}\big )_n$,

• 2. for all n and all $i \in \{1,\ldots ,N^{(n - 1)}\}$, there exist $1 \le j < k \le N^{(n)}$ such that $\bigcup _{\ell =j}^{k} S_\ell ^{(n)} = S_i^{(n-1)}$, and

• 3. the cells $S_j^{(n)}$ shrink regularly, that is there exists $C > 0$ such that for each $S_j^{(n)}$ there exists a ball $B_j^{(n)}$ such that $S_j^{(n)} \subset B_j^{(n)}$ and $\lambda (S_j^{(n)}) \ge C \lambda (B_j^{(n)})$.

Remark 3.3

Definition 3.2 2 is important for the analysis in Sect. 4. Therefore, we postpone a discussion to Sect. 4 and just note here that it can be satisfied by using orderings of the grid cells that are induced by iterates of space-filling curves; see [22]. We note that Definition 3.2 3 is satisfied for isotropic refinements of quasi-uniform meshes; see [22].

We introduce a quantity that is known to tend to zero if the grid constant tends to zero for a sequence of rounding grids and the discrete-valued control functions are constructed with suitable rounding algorithms, which we call integrality gap; see [21, 22].

Definition 3.4

Let $\{S_1,\ldots ,S_N\}$ be a rounding grid and let $\alpha$ and $\omega$ be relaxed controls. Then, we call the quantity

$$\begin{aligned} d(\omega ,\alpha ) :=\max _{k\in \{1,\ldots ,N\}} \left\| \int _{\bigcup _{\ell =1}^k S_\ell } \alpha (s) - \omega (s) {\mathrm {d}}s \right\| _\infty \end{aligned}$$

the integrality gap between $\alpha$ and $\omega$ for this rounding grid.

We will see in Lemma 4.1 that the function d constitutes a pseudometric as mentioned in Sect. 1. We state the main finding on the relationship between the integrality gap, admissible sequences of rounding grids and weak convergence from [22] in the following proposition.

Proposition 3.5

([22, Thm 4.7]) Let an order conserving domain dissection be given with corresponding sequence of integrality gaps $(d^{(n)})_n$. Let $\alpha$ be a relaxed control and $(\omega ^{(n)})_n$ be a sequence of relaxed controls such that

$$\begin{aligned} d^{(n)}(\omega ^{(n)},\alpha ) \rightarrow 0. \end{aligned}$$

Then

$$\begin{aligned} \omega ^{(n)} \rightharpoonup ^* \alpha \text { in } L^\infty (\varOmega _T,{{\mathbb {R}}}^M). \end{aligned}$$

The corollary below follows immediately.

Corollary 3.6

Let the assumptions of Proposition 3.5 hold. Let V be the topological dual space of a Banach space, and let V have the Radon–Nikodym property. Let $x :=\sum _{i=1}^M \alpha _i \xi _i$ and $x^{(n)} :=\sum _{i=1}^M \omega ^{(n)}_i \xi _i$ for $n \in {\mathbb {N}}$. Then, $x^{(n)} \rightharpoonup ^* x$ in $L^\infty (\varOmega _T,V)$.

The literature [14, 15, 23, 26, 27] shows that the aforementioned approximation algorithms admit constants $C > 0$, which are independent of the relaxed control $\alpha$ and the sequence of rounding grids, such that they yield $d^{(n)}(\alpha , \omega ^{(n)}) \le C {{\overline{\varDelta }}}^{(n)}$ for $\omega ^{(n)}$ being produced from $\alpha$ by the algorithm on an admissible sequence of rounding grids. The bounds are usually established for the quantity $\sup _{t\in [0,T]} \big \Vert \int _0^t(\alpha - \omega ^{(n)})\big \Vert _\infty$ for the case $\varOmega _T = (0,T)$ and transfer to multidimensional formulations of the algorithm with the correspondence established in [22, Sect. 4.1]. We note that the bounds on the integrality gap hold for consistent orderings of the grid cells in a) the procedure of the algorithm and b) the increasing union in the evaluation of the integrality gap. Thus, Definition 3.2 and Proposition 3.5 give $\omega ^{(n)} \rightharpoonup ^* \alpha$ and $x^{(n)} \rightharpoonup ^* x$ for an order conserving domain dissection.

3.2 State approximation

The prerequisites on our setting transform the $\hbox {weak}^*$ into norm convergence and convergence of the objective values.

Lemma 3.7

Let $\alpha ^{(n)} \rightharpoonup ^* \alpha$. Then $K_R(\alpha ^{(n)}) \rightarrow K_R(\alpha )$ and $j\big (K_R(\alpha ^{(n)})\big ) \rightarrow j\big (K_R(\alpha )\big )$.

Proof

The claim follows from Assumption 1 and the continuity of j.$\square$

Lemma 3.7 leverages the existence statement on approximating sequences.

Lemma 3.8

Let $\alpha \in {\mathcal {F}}_{(R)}$. Then there exists a sequence $(\omega ^{(n)})_n \subset {\mathcal {F}}_{(R)}$ of binary controls such that

$$\begin{aligned} \omega ^{(n)} \rightharpoonup ^* \alpha \text { in } L^\infty (\varOmega _T,{{\mathbb {R}}}^M) \end{aligned}$$

and

$$\begin{aligned} j(K_R(\omega ^{(n)})) \rightarrow j(K_R(\alpha )). \end{aligned}$$

Proof

We construct an order conserving domain dissection. One possibility is to employ a uniform triangulation with uniform refinements, which imply that Definition 3.2 1 and 3 hold for the induced sequence of rounding grids. We perform the refinement such that each triangle is split up into several smaller triangles. Moreover, we construct the sequence of grid cells of the refined grid by replacing each triangle with the set of triangles into which it was split up. Therefore, Definition 3.2 2 holds for the resulting sequence of rounding grids. Then one may use one of the approximation algorithms like SUR to compute a sequence of binary controls $(\omega ^{(n)})_n \subset {\mathcal {F}}_{(R)}$ on these rounding grids.

Let $d^{(n)}$ denote the integrality gap and ${{\overline{\varDelta }}}^{(n)}$ the grid constant induced by the n-th rounding grid for $n \in {\mathbb {N}}$. By mapping grid cells to intervals that decompose the interval [0, 1](see [22, Sect. 4]), the arguments in [15, 26] imply that there exists $C > 0$ such that

$$\begin{aligned} d^{(n)}(\omega ^{(n)},\alpha ) \le C {{\overline{\varDelta }}}^{(n)} \end{aligned}$$

for all $n \in {\mathbb {N}}$. The uniform refinement gives that $d^{(n)}(\omega ^{(n)},\alpha ) \rightarrow 0$ for $n \rightarrow \infty$. Thus, we apply Proposition 3.5 and obtain

$$\begin{aligned} \omega ^{(n)} \rightharpoonup ^* \alpha \text { in } L^\infty (\varOmega _T,{{\mathbb {R}}}^M) \end{aligned}$$

The second claim follows from Lemma 3.7.$\square$

Starting from Lemma 3.8, we can prove the following optimality principle.

Theorem 3.9

Let Assumption 1 hold. For the optimization problems (P) and (R), it holds true that

$$\begin{aligned} \inf \{ j(K_R(\alpha )) : \alpha \in {\mathcal {F}}_{(R)}\} = \inf \{ j(K(x)) : x \in {\mathcal {F}}_{(P)}\}. \end{aligned}$$

The optimization problem (R) admits a minimizer.

Proof

Since (R) is a relaxation of (P), it suffices to show $\ge$ for the first claim. Let $(\alpha ^{(n)})_n$ be a minimizing sequence for (R). We note that $j(K_R(\alpha ^{(n)})) \rightarrow -\infty$ is possible here. For all $n \in {\mathbb {N}}$ and all $\varepsilon > 0$, we can construct a binary control $\alpha ^{(k_n)} \in {\mathcal {F}}_{(R)}$ such that $j(K_R(\alpha ^{(k_n)})) < j(K_R(\alpha ^{(n)})) + \varepsilon$ by Lemma 3.8. The choice $x^{(k_n)} :=\sum _{i=1}^M \alpha ^{(k_n)}_i \xi _i \in {\mathcal {F}}_{(P)}$ and the identity $K_R(\alpha ^{(k_n)}) = K(x^{(k_n)})$ from the assumptions yield the first claim.

We observe that ${\mathcal {F}}_{(R)}$ is closed with respect to the $\hbox {weak}^*$ topology. To see this, we first apply [32, Theorem 3], which gives that the limit of a $\hbox {weakly}^*$ convergent sequence in ${\mathcal {F}}_{(R)}$ is an a.e. $[0,1]^M$-valued function. The coordinate sequences sum to one a.e. because adding $L^\infty (\varOmega _T)$-functions is a continuous operation with respect to the $\hbox {weak}^*$ topology in both arguments. Moreover, every sequence in ${\mathcal {F}}_{(R)}$ is bounded and thus admits a $\hbox {weak}^*$ accumulation point. Consequently, ${\mathcal {F}}_{(R)}$ is compact with respect to the $\hbox {weak}^*$ topology and the third claim follows from the extreme value theorem as the mapping $j \circ K_R$ is continuous from the $\hbox {weak}^*$ topology of $L^\infty (\varOmega _T, V)$ to ${{\mathbb {R}}}$.$\square$

Remark 3.10

If V is the topological dual space of a Banach space, and V has the Radon–Nikodym property, analogous arguments hold for the relationship between (Q) and (P).

Example 3.11

Considering the solution operator $K_R$ of the IVP (2.1) and the solution operator K of the IVP (2.2), Assumption 1 is satisfied and Theorem 3.9 holds if f is Lipschitz continuous in the first argument by virtue of [21, Thm 3.7].

4 Order-conserving domain dissections and convergence rate

To motivate the results in this section, we consider the first three approximants of the Hilbert curve, a surjective and continuous mapping of the unit interval to the unit square. A facsimile of the figure in [13] is displayed in Fig. 1.

Fig. 1

Hilbert curve iterates approximating $[0,1]^2$. Small numbers indicate the induced orderings of the grid cells along the curve

By inspection of Fig. 1 and the recursive definition of the Hilbert curve iterates, we observe that the ordering of the squares along the curve is preserved from an iterate to the next. This is formulated as Definition 3.2 2 and gives rise to the name order conserving domain dissections for sequences of rounding grids that satisfy this property. Example 4.6 in [22] shows that Proposition 3.5 does not hold true if it is dropped. Moreover, we observe that since the Hilbert curve iterations induce a uniform refinement of the grid cells, Definition 3.2 1 and the regular shrinkage condition Definition 3.2 3 are satisfied as well.

In [22], we have executed the SUR algorithm mentioned above to approximate continuous relaxations of the following elliptic boundary value problem (BVP)

$$\begin{aligned} -\varDelta y = \sum _{i=1}^M \alpha _i f_i,\quad y|_{\partial \varOmega } = 0 \end{aligned}$$

(4.1)

with $\varOmega = (0,1)^2$ for a given control $\alpha$ on the ordering induced by successive Hilbert curve iterates. Again, we denote the grid constant by ${{\overline{\varDelta }}}$. Figure 2 suggests that a convergence rate for the state approximation error may be obtained (in the numerics we observe ${\mathcal {O}}({{\overline{\varDelta }}})$).

Fig. 2

State approximation error for uniformly refined grids along the Hilbert curve approximant-induced orderings (black, dashed), see [22, Fig. 3], with rate $c_2 {{\overline{\varDelta }}}^{(n)}$ (blue, solid)

4.1 Order-conserving domain dissections

Order conserving domain dissections have the advantage that we can conserve the quantity $\int _{S_i^{(n)}} (\alpha - \omega ^{(n)})$ in further grid iterations because the successive integration (or averaging) always happens on partitions of cells from previous iterations; see [20]. Intuitively, one can think of Definition 3.2 2 as a means to maintain spatial coherence of the error quantity in all coordinate directions during the grid refinements. We briefly consider the topology induced by order-conserving domain dissections. A preliminary variant of these results is part of the PhD thesis [19].

Lemma 4.1

(Lemma 8.15 in [19]) Let $1 \le p \le \infty$. It holds that the function $d : L^p(\varOmega _T, {\mathbb {R}}^M) \times L^p(\varOmega _T, {\mathbb {R}}^M) \rightarrow {\mathbb {R}}$ from Definition 3.4 is a pseudometric.

Proof

The symmetry of $\Vert \cdot \Vert _\infty$ implies the symmetry of d. The linearity of the integral, the triangle inequality of $\Vert \cdot \Vert _\infty$, and the subadditivity of ${{\mathrm{ess\,sup}}}$ imply the triangle inequality of d.$\square$

Proposition 4.2

(Proposition 8.17 in [19]) Let $1 \le p \le \infty$. Consider an order conserving domain dissection $\left( \left\{ S^{(n)}_1,\ldots ,S^{(n)}_{N^{(n)}}\right\} \right) _n$ of a bounded domain $\varOmega _T$ with corresponding integrality gaps $(d^{(n)})_n$. Then, the induced family of functions $\nu ^{(n)} : L^p(\varOmega _T) \rightarrow {\mathbb {R}}^+$,

$$\begin{aligned} \nu ^{(n)}(f) :=d^{(n)}(f,0) \end{aligned}$$

is a family of seminorms. The locally convex vector space of $L^p(\varOmega _T)$-functions equipped with the topology determined by the family of seminorms $(\nu ^{(n)})_n$ is Hausdorff, that is it is able to separate points.

Proof

The seminorm properties are induced from the pseudometric properties established in Lemma 4.1. Thus the vector space of $L^p(\varOmega _T)$-functions equipped with the topology induced by $(\nu ^{(n)})_n$ is locally convex. For the Hausdorff property, we verify that if $\nu ^{(n)}(f) = 0$ holds for all $n \in {\mathbb {N}}$ then $f = 0$ a.e.

Let $\nu ^{(n)}(f) = 0$ for all $n \in {\mathbb {N}}$. Thus, for all $n \in {\mathbb {N}}$ and all $k \in \{1,\ldots ,N^{(n)}\}$, we deduce

$$\begin{aligned} \int _{S_k^{(n)}} f\,{\mathrm {d}}\lambda = \int _{\bigcup _{\ell =1}^{k} S_\ell ^{(n)}} f\,{\mathrm {d}}\lambda - \int _{\bigcup _{\ell =1}^{k - 1} S_\ell ^{(n)}} f\,{\mathrm {d}}\lambda = 0 \end{aligned}$$

(4.2)

by definition of $d^{(n)}$ and $0 = \nu ^{(n)}(f) = d^{(n)}(f,0)$.

Since an order conserving domain dissection is a sequence of partitions of the domain $\varOmega _T$, it holds that for all $x \in \varOmega _T$ there exists indices $i_1 \in \{1,\ldots ,N^{(1)}\}$, $i_2 \in \{1,\ldots ,N^{(2)}\}$, $\ldots$ such that $x \in S_{i_k}^{(k)}$ for all $k \in {\mathbb {N}}$.

Moreover, the Definition 3.2 2 gives

$$\begin{aligned} S_{i_1}^{(1)} \supset S_{i_2}^{(2)} \supset \ldots \end{aligned}$$

Combining these inclusions with Definition 3.2 1 and 3 allows us to apply the Lebesgue differentiation theorem, see [31, Corollary 1.7]. This gives the identity

$$\begin{aligned} f(x) = \lim _{n \rightarrow \infty } \frac{1}{\lambda (S^{(n)}_{i_n})} \int _{S^{(n)}_{i_n}} f \,{\mathrm {d}}\lambda \underset{(4.2)}{=} 0 \end{aligned}$$

for a.a. $x \in \varOmega _T$, which means that $f= 0$ a.e., which closes the proof.$\square$

Corollary 4.3

Let $1 \le p \le \infty$. The integrality gaps $d^{(n)}$ induced by order-conserving domain dissections are pseudometrics that equip $L^p(\varOmega _T)$ with a Hausdorff topology.

Corollary 4.4

Let $1 \le p \le \infty$. The integrality gaps $d^{(n)}$ induced by the successive domain decompositions from the approximants of the Hilbert curve are pseudometrics that equip $L^p(\varOmega _T)$ with a Hausdorff topology.

4.2 Control convergence rate in $H^{-1}$

This subsection shows that order-conserving domain dissections allow us to prove a convergence rate for the state vector approximation $y(\omega ^{(n)}) \rightarrow y(\alpha )$. Assume $K_R$ is the solution operator of an elliptic BVP like (4.1). Then the Lax-Milgram lemma and suitable regularity of the right hand side – that is if the $f_i$ are Lipschitz continuous, $f_i \in W^{1,\infty }(\varOmega _T)$ – of an elliptic BVP may yield Lipschitz estimates of the form

$$\begin{aligned} \Vert K_R(\alpha _1) - K_R(\alpha _2)\Vert _{H^1(\varOmega _T)} \le L \Vert \alpha _1 - \alpha _2\Vert _{H^{-1}(\varOmega _T)} \end{aligned}$$

for some $L > 0$. Thus we aim for an estimate on $\Vert \alpha - \omega \Vert _{H^{-1}}$ from bounds on $d(\omega ,\alpha )$ if $\omega$ is a binary control. Regarding the rounding grid one additional regularity assumption is necessary to constrain the ratio of the diameters among the grid cells per rounding grid.

Before stating the estimate, we define a helper function f for $d \in {\mathbb {N}}$ and $0 < \varepsilon \le 1$ as

$$\begin{aligned} f(d,\varepsilon ) :={\left\{ \begin{array}{ll} \frac{1}{2} &{} \text { if } d = 1,\\ \frac{2\varepsilon }{1 + \varepsilon } &{} \text { if } d = 2,\\ 0 &{} \text { if } d \ge 3. \end{array}\right. } \end{aligned}$$

(4.3)

Theorem 4.5

Let $d \ge 1$. Let $\varOmega _T\subset {{\mathbb {R}}}^d$ be a bounded Lipschitz domain. Let $\alpha$ be a relaxed control. Let an order conserving domain dissection be given, and let the ratio between the maximum and minimum diameters of the grid cells be uniformly bounded over the grid iterations, that is let there exist $\rho > 0$ such that for all $n \in {\mathbb {N}}$ and all i, $j \in \{1,\ldots ,N^{(n)}\}$ it holds that $\rho \ge {{\mathrm{diam}}}S_i^{(n)} / {{\mathrm{diam}}}S_j^{(n)}$.

Let $(\beta ^{(n)})_n$ be a sequence of relaxed controls and assume that there exists ${\hat{C}} > 0$ such that $d^{(n)}(\beta ^{(n)}, \alpha ) \le {\hat{C}} {{\overline{\varDelta }}}^{(n)}$ for all $n \in {\mathbb {N}}$. Then, for all $0 < \varepsilon \le 1$ there exist $C(\varepsilon ) > 0$ such that for all grid levels $n\in {\mathbb {N}}$ for which there exists a grid level $1\le n_0(n) \le n$ with ${{\overline{\varDelta }}}^{(n)} =\varTheta (({{\overline{\varDelta }}}^{(n_0(n))})^{\frac{3/2+d/2+f(d,\varepsilon )/d}{1+d/2}})$, we obtain the estimate

$$\begin{aligned} \Vert \alpha - \beta ^{(n)}\Vert _{H^{-1}(\varOmega _T,{\mathbb {R}}^M)} \le C(\varepsilon ) ({{\overline{\varDelta }}}^{(n)})^{\frac{1}{1.5 d + 0.5 d^2 + f(d,\varepsilon )}} \end{aligned}$$

The constant $C(\varepsilon )$ only depends on $\varepsilon$ if $d =2$.

Proof

We show the estimate for each component sequence individually and drop the subscripts i of $\alpha _i$ and $\beta ^{(n)}_i$ throughout the remainder of the proof. Then, the estimate holds by equivalence of the $\ell ^p$-norms on ${\mathbb {R}}^M$ for $p \in [1,\infty ]$.

We have to estimate $\Vert \alpha - \beta ^{(n)}\Vert _{H^{-1}} = \sup \{ \langle \alpha - \beta ^{(n)}, w \rangle : \Vert w\Vert _{H_0^1} \le 1 \}$, where $\langle \cdot , \cdot \rangle$ denotes the duality pairing of $H_0^1(\varOmega _T)$ and $H^{-1}(\varOmega _T)$ (we could more generally also consider $H^1(\varOmega _T)$ and $H^1(\varOmega _T)^*$). Let $(\phi _\delta )_\delta \subset C_0^\infty ({\mathbb {R}}^d, {\mathbb {R}})$ be a family of positive mollifiers, see Definition A.1. Then there exists $C_1 > 0$ such that for all $1\le p\le \infty$, we have

$$\begin{aligned} \Vert \phi _\delta \Vert _{L^p({{\mathbb {R}}}^d)}\le \Vert \phi _\delta \Vert _{L^\infty ({{\mathbb {R}}}^d)} \Vert 1\Vert _{L^1(B_\delta (0))}^{1/p}\le C_1 \delta ^{-d} \delta ^{d/p}= C_1 \delta ^{d/p-d}. \end{aligned}$$

We restrict to the case $w\in H_0^1(\varOmega _T)$ and note that for $H^1(\varOmega _T)$, one needs to work with an extension instead of the extension by 0. This is possible for the assumed Lipschitz domain by virtue of Stein’s extension theorem, see [30, Sect. VI.§3.1 Thm 5]. Let

$$\begin{aligned} \Vert w\Vert _{H_0^1(\varOmega _T)}=\Vert \nabla w\Vert _{L^2(\varOmega _T)}\le 1. \end{aligned}$$

Then, the mollification $w_\delta$ of w,

$$\begin{aligned} w_\delta (x)=(\phi _\delta *w)(x)=\int _{{{\mathbb {R}}}^d} \phi _\delta (z) w(x-z)\,dz, \end{aligned}$$

satisfies the estimate

$$\begin{aligned} \Vert w_\delta -w\Vert _{L^2(\varOmega _T)}\le \Vert \nabla w\Vert _{L^2(\varOmega _T)}\delta \le \delta , \end{aligned}$$

(4.4)

which is proven in Lemma A.2. We combine Young’s convolution inequality with the continuous embedding $H_0^1(\varOmega _T)\hookrightarrow L^p(\varOmega _T)$ for all $1\le p\le \infty$ for $d=1$, for all $1 \le p<\infty$ if $d=2$ and all $1\le p\le 2d/(d-2)$ for $d \ge 3$, see Theorem 5.4 in [1] (Case A for $d \ge 3$, Case B for $d = 2$, Case C for $d = 1$). Then we obtain

$$\begin{aligned} \Vert w_\delta \Vert _{L^\infty (\varOmega _T)}\le \Vert \phi _\delta \Vert _{L^1({{\mathbb {R}}}^d)} \Vert w\Vert _{L^{\infty }(\varOmega _T)} \le C_1 C_2 \end{aligned}$$

for $d=1$ as well as

$$\begin{aligned} \Vert w_\delta \Vert _{L^\infty (\varOmega _T)}\le \Vert \phi _\delta \Vert _{L^q({{\mathbb {R}}}^d)} \Vert w\Vert _{L^{q/(q-1)}(\varOmega _T)} \le C_1 C_2(\varepsilon ) \delta ^{2/(1 + \varepsilon ) - 2} \end{aligned}$$

for $d = 2$ and all $q = 1 + \varepsilon$ with $0 < \varepsilon \le 1$, and we obtain

$$\begin{aligned} \Vert w_\delta \Vert _{L^\infty (\varOmega _T)}\le \Vert \phi _\delta \Vert _{L^{2d/(d+2)}({{\mathbb {R}}}^d)} \Vert w\Vert _{L^{2d/(d-2)}(\varOmega _T)} \le C_1 C_2 \delta ^{1-d/2} \end{aligned}$$

for $d\ge 3$. The constant $C_2$ / $C_2(\varepsilon )$ arises from the continuous embedding of $H^1_0(\varOmega _T) \hookrightarrow L^p(\varOmega _T)$ and depends on $\varepsilon$ if $d = 2$. Using (4.3), we can abbreviate the estimates on $\Vert w_\delta \Vert _{L^\infty (\varOmega _T)}$ as

$$\begin{aligned} \Vert w_\delta \Vert _{L^\infty (\varOmega _T)} \le C_1 C_2(\varepsilon )\delta ^{1-d/2 - f(d,\varepsilon )}. \end{aligned}$$

Moreover, $w_\delta$ has Lipschitz constant $C_1 \delta ^{-d/2}$ because

$$\begin{aligned} \Vert \nabla w_\delta (x)\Vert =\left| \int _{{{\mathbb {R}}}^d} \phi _\delta (z) \nabla w(x-z)\,dz\right| \le \Vert \phi _\delta \Vert _{L^2({{\mathbb {R}}}^d)} \Vert \nabla w\Vert _{L^2(\varOmega _T)} \le C_1 \delta ^{-d/2} \end{aligned}$$

for a.a. $x \in \varOmega _T$.

Now, we consider a rounding grid at level $n_0$ with grid constant ${{\overline{\varDelta }}}^{(n_0)}$ and denote by $H=H(n_0)$ the maximum diameter of its elements. Moreover, we choose $\delta >0$ such that $\delta ^s=H$ for some $s>\max \{1,d/2\}$, which will be adjusted below. Due to the boundedness of the ratio of diameters, the rounding grid at level $n_0$ decomposes $\varOmega _T$ into $N^{(n_0)} \le C_3 H^{-d}=C_3 \delta ^{-sd}$ grid cells for some constant $C_3 > 0$, see Lemma A.4 with $C > 0$ and $\rho > 0$, which are uniformly constant over the iterations by assumption and Definition 3.2 3. Since $w_\delta$ has Lipschitz constant $C_1 \delta ^{-d/2}$, it can be approximated by a piecewise constant function, the cell average, $w_H$ on the rounding grid $\{S_1^{(n_0)},\ldots ,S_{N^{(n_0)}}^{(n_0)}\}$ (having maximal cell diameter $H=\delta ^s$) such that

$$\begin{aligned} \Vert w_\delta -w_H\Vert _{L^\infty (\varOmega _T)} \le \delta ^{s} \Vert \nabla w_\delta \Vert _{L^\infty (\varOmega _T)} \le C_1 \delta ^{s-d/2}, \end{aligned}$$

(4.5)

holds, see Lemma A.3.

We use the abbreviation $I^{(n_0)} :=\{1,\ldots ,N^{(n_0)}\}$. For all $n \ge n_0$, we obtain

$$\begin{aligned}&\left| \int _{\varOmega _T} w_H(x)(\alpha (x) - \beta ^{(n)}(x))\,dx\right| \\&\quad \le \sum _{i=1}^{N^{(n_0)}}\left| \int _{S_i^{(n_0)}} w_H(x) (\alpha (x) - \beta ^{(n)}(x))\,{\mathrm {d}}x\right| \\&\quad \le \sum _{i=1}^{N^{(n_0)}} \Vert w_H\Vert _{L^\infty (\varOmega _T)} \left| \int _{S_i^{(n_0)}} (\alpha (x) - \beta ^{(n)}(x))\,{\mathrm {d}}x\right| \\&\quad \le \Vert w_\delta \Vert _{L^\infty (\varOmega _T)} N^{(n_0)} \max _{i\in I^{(n_0)}} \left| \int _{S_i^{(n_0)}} (\alpha (x) - \beta ^{(n)}(x))\,{\mathrm {d}}x\right| \\&\quad \le C_1C_2(\varepsilon )C_3\delta ^{-sd} \delta ^{1-d/2-f(d,\varepsilon )} \max _{i \in I^{(n_0)}} \left| \int _{S_i^{(n_0)}} (\alpha (x) - \beta ^{(n)}(x))\,{\mathrm {d}}x\right| \end{aligned}$$

for all $0 < \varepsilon \le 1$. Here, the first inequality follows from the triangle inequality. The second inequality follows from the fact that $w_H$ is piecewise constant per grid cell. Because the cell averages $w_H$ do not exceed the extremal values, the estimate $\Vert w_H\Vert _{L^\infty (\varOmega _T)}\le \Vert w_\delta \Vert _{L^\infty (\varOmega _T)}$ holds in the third inequality.

For all $i \in I^{(n_0)}$, we obtain

$$\begin{aligned}&\int _{S_i^{(n_0)}} (\alpha (x)-\beta ^{(n)}(x))\,{\mathrm {d}}x\\&\quad =\int _{\bigcup _{j=1}^i S_j^{(n_0)}} (\alpha (x)-\beta ^{(n)}(x)){\mathrm {d}}s - \int _{\bigcup _{j=1}^{i-1} S_j^{(n_0)}}(\alpha (x)-\beta ^{(n)}(x))\,{\mathrm {d}}x. \end{aligned}$$

Because the grid sequence is an order conserving domain dissection, and in particular Definition 3.2 2 holds, we have the estimate

$$\begin{aligned} \left| \int _{\bigcup _{j=1}^\ell S_j^{(n_0)}} (\alpha (x)-\beta ^{(n)}(x)){\mathrm {d}}x\right| \le d^{(n)}(\beta ^{(n)}, \alpha ) \end{aligned}$$

for all $\ell \in I^{(n_0)}$ and for all rounding grids $n \ge n_0$. Thus, the triangle inequality gives

$$\begin{aligned} \max _{i\in I^{(n_0)}} \left| \int _{S_i^{(n_0)}} (\alpha (x)- \beta ^{(n)}(x)){\mathrm {d}}x\right| \le 2 d^{(n)}(\beta ^{(n)}, \alpha ) \le 2 C_4 {{\overline{\varDelta }}}^{(n)} \end{aligned}$$

in iteration n for $C_4 :={\hat{C}}$ from the prerequisites. We set $C_5(\varepsilon ) :=\max \{C_1,C_1 C_2(\varepsilon ) C_3 2 C_4\}$ and obtain

$$\begin{aligned} \left| \int _{\varOmega _T} w_H(x) (\alpha (x)-\beta ^{(n)}(x))\,dx\right| \le C_5(\varepsilon ) \delta ^{1-(s + 1/2)d-f(d,\varepsilon )}{{\overline{\varDelta }}}^{(n)}. \end{aligned}$$

(4.6)

In iteration $n\ge n_0$, we find $r\ge s$ such that the maximum grid size (diameter) is given by $H_n=\delta ^r$. By Definition 3.2 3 we obtain

$$\begin{aligned} C_7\delta ^{rd} \le {{\overline{\varDelta }}}^{(n)}\le C_6\delta ^{rd} \end{aligned}$$

(4.7)

with constants $C_7 > 0$ and $C_6 > 0$ independent of n.

We combine the estimates above to obtain

$$\begin{aligned}&\left| \int _{\varOmega _T} w(x) (\alpha (x)-\beta ^{(n)}(x)){\mathrm {d}}x \right| \\&\quad \le \Vert w-w_\delta \Vert _{L^2({\varOmega _T})} \Vert \alpha -\beta ^{(n)}\Vert _{L^2({\varOmega _T})} + \Vert w_\delta -w_H\Vert _{L^\infty ({\varOmega _T})} \Vert \alpha -\beta ^{(n)}\Vert _{L^1({\varOmega _T})}\\&\qquad +\left| \int _{\varOmega _T} w_H(x)(\alpha (x)-\beta ^{(n)}(x))\,dx\right| \\&\quad \le \Vert w-w_\delta \Vert _{L^2({\varOmega _T})} \sqrt{\lambda (\varOmega _T)} + \Vert w_\delta -w_H\Vert _{L^\infty ({\varOmega _T})}\lambda (\varOmega _T)\\&\qquad + C_5(\varepsilon ) \delta ^{1-(s + 1/2)d-f(d,\varepsilon )}{{\overline{\varDelta }}}^{(n)} \\&\quad \le C(\varepsilon ) \big ({{\overline{\varDelta }}}^{(n)}\big )^{\frac{1}{rd}} +C(\varepsilon )\big ({{\overline{\varDelta }}}^{(n)}\big )^{\frac{s-d/2}{rd}} +C(\varepsilon )\big ({{\overline{\varDelta }}}^{(n)}\big )^{\frac{1+(r-s-1/2)d -f(d,\varepsilon )}{rd}}, \end{aligned}$$

where

$$\begin{aligned} C(\varepsilon ) :=\max \left\{ \frac{\sqrt{\lambda (\varOmega _T)}}{C_7^{\frac{1}{rd}}}, C_1 \frac{\lambda (\varOmega )}{C_7^{\frac{1}{rd}}}, C_5(\varepsilon ) C_6^{\frac{(s + 1/2)d + f(d,\varepsilon ) - 1 }{rd}}\right\} . \end{aligned}$$

To obtain the second inequality, we have used (4.6) for the third term. For the first and second term, we have applied Hölder’s inequality to estimate $\Vert \alpha - \beta ^{(n)}\Vert _{L^2}$ and $\Vert \alpha - \beta ^{(n)}\Vert _{L^1}$ using the estimate $\Vert \alpha - \beta ^{(n)}\Vert _{L^\infty } \le 1$. Here, $\Vert \alpha - \beta ^{(n)}\Vert _{L^\infty } \le 1$ follows straightforwardly from the fact that $\alpha$ and $\beta ^{(n)}$ are relaxed controls. We may include $\lambda (\varOmega _T)$ into the constants because $\lambda (\varOmega _T) < \infty$ follows from the fact that $\varOmega _T$ is a bounded domain and hence a bounded open subset of ${\mathbb {R}}^d$.

For the third inequality, we note that the first two terms in the $\max$-operation in the definition of $C(\varepsilon )$ follow from the combination of the estimates (4.4) and (4.5) with $\delta \le C_7^{\frac{1}{rd}}\big ({{\overline{\varDelta }}}^{(n)}\big )^{\frac{1}{rd}}$, which follows from (4.7), $\delta > 0$, and the positive exponent $s - d/2$ of $\delta$. The positivity of $s - d/2$ follows from the restrictions on the choice of $\delta$ and s above. The third term follows from (4.6) combined with the upper estimate in (4.7), which can be applied here because the exponent of $\delta$ is negative in (4.6), which follows from $d \ge 1$, $s \ge 1$ and $f(d,\varepsilon ) \ge 0$.

Balancing the terms requires the identities

$$\begin{aligned} 1=s-d/2=1+(r-s-1/2)d\, - f(d,\varepsilon ). \end{aligned}$$

Hence, $s=1+d/2$, $(r-s-1/2)d=f(d,\varepsilon )$ and we obtain

$$\begin{aligned} s=1+d/2,\quad r=s+1/2-f(d,\varepsilon )/d=3/2+d/2 + f(d,\varepsilon )/d. \end{aligned}$$

This gives the estimate

$$\begin{aligned} \Vert \alpha - \beta ^{(n)}\Vert _{H^{-1}(\varOmega _T)} \le 3 C(\varepsilon ) \big ({{\overline{\varDelta }}}^{(n)}\big )^{\frac{1}{1.5 d + 0.5 d^2 + f(d,\varepsilon ) }} \end{aligned}$$

for n such that ${{\overline{\varDelta }}}^{(n)}=\varTheta (\delta ^{rd})$, where $C_7 \delta ^{sd}\le {{\overline{\varDelta }}}^{(n_0)}\le C_6 \delta ^{sd}$ and thus ${{\overline{\varDelta }}}^{(n)} =\varTheta (({{\overline{\varDelta }}}^{(n_0)})^{r/s}) =\varTheta (({{\overline{\varDelta }}}^{(n_0)})^{r/s}) =\varTheta (({{\overline{\varDelta }}}^{(n_0)})^{\frac{3/2+d/2+f(d,\varepsilon )/d}{1+d/2}})$. Note that to derive the estimate, we have made the choice $H_n = \delta ^r$. However, after the balancing identities are solved, r is set to a specific value and s and $H_{n_0}$ dictate the value of $\delta$. The argument holds true with a change in the constant $C(\varepsilon )$ that does not depend on $n_0$ and n if we have $H_n = \varTheta (\delta ^r)$ instead of the definite choice $H_n = \delta ^r$. Combining our insights above, we deduce

$$\begin{aligned} H^d_n = \varTheta ({{\overline{\varDelta }}}^{(n)}) = \varTheta \left( ({{\overline{\varDelta }}}^{(n_0)})^{\frac{3/2+d/2+f(d,\varepsilon )/d}{1+d/2}}\right) = \varTheta \left( (\delta ^{sd})^{\frac{r}{s}}\right) = \varTheta \left( \delta ^{rd}\right) , \end{aligned}$$

which implies that $H_n = \varTheta (\delta ^r)$ indeed holds true and concludes the proof.$\square$

A few remarks are in order here.

Remark 4.6

The proof presented above balances several approximations based on mollification, piecewise averaging and the bound on the integrality gap induced by rounding algorithms. An improved estimate can be obtained under the additional assumption that the grid cells of a rounding grid are ordered along the coordinate axis (time axis) in the case $d = 1$. In this case, one can derive an improved estimate following the lines of [12, 25] that lead to their state space estimate in C([0, T]) into which $W^{1,p}((0,T))$ is continuously embedded. This is shown briefly in the next subsection.

Remark 4.7

We have formulated the proof of Theorem 4.5 for relaxed controls $\beta ^{(n)}$ to do justice to the generality of the argument. However, one should keep in mind that all binary controls are of course relaxed controls as well. We note that for binary controls $\omega ^{(n)}$ produced by the rounding algorithm SUR, we obtain the bound $d^{(n)}(\omega ^{(n)},\alpha ) \le C_4 {{\overline{\varDelta }}}^{(n)}$ for some fixed $C_4 > 0$. In the case $d = 1$, this follows directly from the analysis in [15, 26]. For $d \ge 2$, this follows with the arguments in Section 2 of [22], in particular Proposition 2.4.

Remark 4.8

For the balancing argument to hold, we make an assumption on the grid levels, namely ${{\overline{\varDelta }}}^{(n)} = \varTheta \left( ({{\overline{\varDelta }}}^{(n_0)})^q \right)$ for a specific $q > 1$ depending on d. We show in Proposition 4.9 below that this can be satisfied under under mild assumptions on the grid refinement, namely that the considered maximum grid cell volumes are montonously decreasing and that $\varTheta ({{\overline{\varDelta }}}^{(n)}) = \varTheta ({{\overline{\varDelta }}}^{(n+1)})$.

Proposition 4.9

Let ${{\overline{\varDelta }}}^{(n)} \rightarrow 0$. Let $q > 1$ and $k_1 > 1$ be such that $0 < {{\overline{\varDelta }}}^{(n)} \le {{\overline{\varDelta }}}^{(n - 1)} \le k_1 {{\overline{\varDelta }}}^{(n)}$ for all $n \in {\mathbb {N}}$. Then, there exists $n_1 \in {\mathbb {N}}$ such that for all $n \ge n_1$ it holds that $({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} \le {{\overline{\varDelta }}}^{(1)}$. Moreover, for all $n\ge n_1$ the function

$$\begin{aligned} n_0(n) :=\max \left\{ n_0 \in {\mathbb {N}} \,\Big \vert \, ({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} \le {{\overline{\varDelta }}}^{(n_0)} \right\} \end{aligned}$$

is well-defined and

$$\begin{aligned} {{\overline{\varDelta }}}^{(n)} = \varTheta \left( \left( {{\overline{\varDelta }}}^{(n_0(n))}\right) ^q \right) . \end{aligned}$$

Proof

Since ${{\overline{\varDelta }}}^{(n)}\downarrow 0$, there exists $n_1 \in {\mathbb {N}}$ such that $({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} \le {{\overline{\varDelta }}}^{(1)}$ holds for all $n \ge n_1$. Combining this with the fact that ${{\overline{\varDelta }}}^{(n)} > 0$ for all $n \in {\mathbb {N}}$ yields that $n_0(n)$ is well-defined, which also gives the inequality

$$\begin{aligned} {{\overline{\varDelta }}}^{(n)} \le \left( {{\overline{\varDelta }}}^{(n_0(n))}\right) ^q. \end{aligned}$$

Moreover, we have that ${{\overline{\varDelta }}}^{(n)}\ge \frac{1}{k_1^q} \left( {{\overline{\varDelta }}}^{(n_0(n))}\right) ^q$. To see that this inequality holds, we first note that it is equivalent to $({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} \ge \frac{1}{k_1} {{\overline{\varDelta }}}^{(n_0(n))}$. Then, we argue by contradiction and assume $({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} < \frac{1}{k_1} {{\overline{\varDelta }}}^{(n_0(n))}$. The prerequisites give ${{\overline{\varDelta }}}^{(n_0(n))} \le k_1 {{\overline{\varDelta }}}^{(n_0(n) + 1)}$. Combining both inequalities gives

$$\begin{aligned} ({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} < \frac{1}{k_1}{{\overline{\varDelta }}}^{(n_0(n))} \le {{\overline{\varDelta }}}^{(n_0(n)+1)}, \end{aligned}$$

which implies

$$\begin{aligned} ({{\overline{\varDelta }}}^{(n)})^{\frac{1}{q}} \le {{\overline{\varDelta }}}^{(n_0(n)+1)}. \end{aligned}$$

This contradicts the definition of $n_0(n)$ because $n_0(n) +1 >n_0(n)$. Consequently, we have ${{\overline{\varDelta }}}^{(n)} = \varTheta \left( \left( {{\overline{\varDelta }}}^{(n_0(n))}\right) ^q \right)$ for $n \ge n_1$, which concludes the proof.$\square$

4.3 Improved bound in the one-dimensional case

We consider the case that a rounding algorithm is executed on the discretization $t_0< \ldots < t_N = t_f$ of $[t_0,t_f]$, that is $S_i :=[t_{i-1},t_i)$ for $i \in \{1,\ldots ,N - 1\}$ and $S_N = [t_{N-1},t_N]$ to compute a binary control $\omega$ from a relaxed control $\alpha$. In this case, the integrality gap can be stated independently of the rounding grid, namely

$$\begin{aligned} d_{1D }(\omega , \alpha ) :=\sup _{t\in [0,T]} \left\| \int _0^t \alpha (s) - \omega (s) {\mathrm {d}}s\right\| _\infty , \end{aligned}$$

and the rounding algorithms mentioned in Sect. 1 satisfy $d_{1D }(\alpha , \omega ) \le C {{\overline{\varDelta }}}$ for ${{\overline{\varDelta }}}:=\max \left\{ t_{i} - t_{i-1} \,:\, i \in \{1,\ldots ,N\}\right\}$ for some $C > 0$, which is independent of $\alpha$ and the specific choice of the rounding grid. This follows from

$$\begin{aligned} \max _{i \in \{1,\ldots ,N\}} \left\| \int _{\bigcup _{j=1}^i S_j} \alpha (s) - \omega (s)\,{\mathrm {d}}s\right\| _\infty \le C {{\overline{\varDelta }}}\end{aligned}$$

and the fact that $\alpha - \omega$ is a piecewise monotone function because $\omega$ is piecewise constant and binary-valued. The order of the grid cells (intervals) $S_i$ along the time-axis matters in this case; see [19, 26].

Theorem 4.10

Let $d = 1$. We consider $(0,T) \subset {\mathbb {R}}$ for $T > 0$. Let $\alpha$, $\beta$ be relaxed controls. Let $p \in [1,\infty ]$. Then, $\Vert \alpha - \beta \Vert _{(W^{p}((0,T),{\mathbb {R}}^M))^*} \le {\tilde{C}} d_{1D}(\alpha ,\beta )$ for some ${\tilde{C}} > 0$.

Proof

For $i \in \{1,\ldots ,M\}$, we restrict to the coordinate sequence and drop the subscripts i of $\alpha _i$ and $\beta _i$ below. We abbreviate $W^{1,p} :=W^{1,p}((0,T))$. We compute an estimate on

$$\begin{aligned} \Vert \alpha - \beta \Vert _{(W^{1,p})^*} = \sup \left\{ \left\langle \alpha - \beta , w \right\rangle \,:\, w \in W^{1,p}, \Vert w\Vert _{W^{1,p}} = 1 \right\} , \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes the duality pairing of $(W^{1,p})^*$ and $W^{1,p}$. Let $w \in W^{1,p}$ with $\Vert w\Vert _{W^{1,p}} \le 1$. Since $\alpha - \beta \in L^\infty ((0,T))$, we represent the duality pairing with integration. The one-dimensional domain implies that w has a continuous representative and that the continuous embedding $W^{1,p} \hookrightarrow C([0,T])$ holds, see [1, Thm 5.4]. We use integration by parts and the triangle inequality to deduce

$$\begin{aligned}&\left| \int _0^T w(s) (\alpha (s) - \beta (s))\,{\mathrm {d}}s\right| \\&\quad \le \left| w(T)\int _0^T(\alpha (s) - \beta (s))\,{\mathrm {d}}s\right| + \left| \int _0^T w'(s) \int _0^s \alpha (\tau ) - \beta (\tau ){\mathrm {d}}\tau {\mathrm {d}}s\right| . \end{aligned}$$

The first term of the right hand side is bounded by $C_1 \Vert w\Vert _{W^{1,p}} d_{1D}(\alpha ,\beta )$, where the constant $C_1 > 0$ is due to the continuous embedding $W^{1,p}\hookrightarrow C([0,T])$. The second term is bounded by $C_2 \Vert w\Vert _{W^{1,p}}d_{1D}(\alpha ,\beta )$ for some $C_2 > 0$ by means of Hölder’s inequality, where the constant $C_2 > 0$ is due to the the continuous embeddings $W^{1,p} \hookrightarrow L^p((0,T)) \hookrightarrow L^1((0,T))$.

Combining these estimates for the coordinate sequences with the equivalence of the $\ell ^p$-norms on ${\mathbb {R}}^M$ for $p \in [1,\infty ]$ yields the claim.$\square$

5 Application to signal processing

Let $t_0$, $t_f\in {{\mathbb {R}}}$. We consider the optimization problem

$$\begin{aligned} \begin{aligned} \min _{x}\,&J(x) = \frac{1}{2} \int _{t_0}^{t_f} ((k * x)(t) - f(t))^2 {\mathrm {d}}t \\ \text {s.t.}\,&x \in L^2((t_0,t_f)), \\&x(t) \in \{\xi _1, \ldots , \xi _M\} \subset {{\mathbb {R}}}\text { a.e.\ on } (t_0,t_f). \end{aligned} \end{aligned}$$

(P'')

The problem (P”) constitutes a case where the dynamics of the process are not governed by a differential equation. It arises from (P) by defining $j : L^2((t_0,t_f)) \rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} j(y) :=\frac{1}{2} \Vert y - f\Vert _{L^2}^2 \end{aligned}$$

with the choices $V :={{\mathbb {R}}}$ and $K : L^2((t_0,t_f)) \rightarrow L^2((t_0,t_f))$ as

$$\begin{aligned} K(x) :=k * x \end{aligned}$$

for a fixed filter kernel function $k \in L^1((t_0,t_f))$ and a fixed tracking objective $f \in L^2((t_0,t_f))$. This setting is well-defined by Young’s convolution inequality.

To relate this problem to the analysis of Sect. 3, we define the operator $K_R : L^\infty ((t_0,t_f),{\mathbb {R}}^M) \rightarrow L^2((t_0,t_f))$ through

$$\begin{aligned} K_R(\alpha ) :=K\left( \sum _{i=1}^M\alpha _i\xi _i\right) . \end{aligned}$$

Then, we obtain the following proposition, which implies that Assumption 1 holds for the considered problem.

Proposition 5.1

Let $\varOmega _T :=(t_0,t_f)$. $Y :=L^2((t_0,t_f))$, $V :={\mathbb {R}}$. Let j, K, and $K_R$ defined as above. Then, Assumption 1 holds. Moreover, the operator $K : L^\infty ((t_0,t_f)) \rightarrow L^2((t_0,t_f))$ is ultraweak-completely continuous

Proof

All properties except the ultraweak-complete continuity of K and $K_R$ follow immediately from the definition. The operators K and $K_R$ are linear, the space ${\mathbb {R}}$ is reflexive, and $x^n \rightharpoonup ^* x$ in $L^\infty ((t_0,t_f))$ implies $x^n \rightharpoonup x$ in $L^2((t_0,t_f))$, see also Remark 2.2. Thus, it suffices to know that K and $K_R$ are compact operators, which follows for example from [29, Thm 3.1.17].$\square$

Following Sect. 2, we obtain the relaxation

$$\begin{aligned} \begin{aligned} \min _{x}\,&j(K(x)) = \frac{1}{2} \int _{\varOmega _T} ((k * x)(s) - f(s))^2 {\mathrm {d}}s \\ \text {s.t.}\,&x \in L^2({\varOmega _T}), \\&x(t) \in [\xi _L, \xi _U] \text { a.e.\ on } (t_0,t_f) \end{aligned}. \end{aligned}$$

(Q'')

with $\xi _L :=\min \{\xi _1,\ldots ,\xi _M\}$ and $\xi _U :=\max \{\xi _1,\ldots ,\xi _M\}$. To estimate grid constants for the rounding algorithm a priori, we are interested in estimates on the reconstruction error of the filtered trajectory in $L^2$, that is on

$$\begin{aligned} \Vert k * x - k * x^{{{\overline{\varDelta }}}}\Vert _{L^2((t_0,t_f))}. \end{aligned}$$

Here, $x = x(\alpha )$ denotes a feasible point of (Q”) and $x^{{{\overline{\varDelta }}}} = x(\omega ) = \sum _{i=1}^M \omega _i \xi _i$ the discrete-valued input variable arising from an approximation of x on a rounding grid with grid constant ${{\overline{\varDelta }}}$.

We follow the considerations in Sect. 4.3, and use the function $d_{1D}$ to derive an additional priori estimate. A preliminary version of the result has been obtained as Theorem 9.12 in the PhD thesis [19].

Theorem 5.2

Let $\varOmega _T = (t_0,t_f)$. Let $\alpha$ be a relaxed control and $\omega$ be a binary control. Let $x = \sum _{i=1}^M \alpha _i \xi _i$ and $x^{{{\overline{\varDelta }}}} = \sum _{i=1}^M \omega _i \xi _i$. Let $k \in W^{1,1}({{\mathbb {R}}})$. Let $p \in [1,\infty ]$. Then,

$$\begin{aligned} \Vert k * x - k * x^{{{\overline{\varDelta }}}}\Vert _{L^p((t_0,t_f))} \le C d_{1D}(\omega , \alpha ) \end{aligned}$$

for some $C > 0$ depending on p, $\Vert \xi \Vert _{{{\mathbb {R}}}^M}$, $t_0$, $t_f$, and $\Vert k\Vert _{W^{1,1}}$. For $p = \infty$, the estimate also holds in $C([t_0,t_f])$.

Proof

Let $Y :=W^{1,p}((t_0,t_f))$ and thus $Y^* = (W^{1,p}((t_0,t_f)))^*$. Then,

$$\begin{aligned} (k * (x - x^{{{\overline{\varDelta }}}}))(t)&= \left( k(t - \cdot ), x - x^{{{\overline{\varDelta }}}}\right) _{L^2((t_0,t_f))}\\&= \left\langle k(t - \cdot ), x - x^{{{\overline{\varDelta }}}}\right\rangle _{Y,Y^*} \\&\le \Vert k(t - \cdot )\Vert _{Y}\Vert x - x^{{{\overline{\varDelta }}}}\Vert _{Y^*} \end{aligned}$$

holds for all $t \in (t_0,t_f)$, where the second identity follows from the Riesz–Fréchet representation theorem and the continuous embedding $Y \hookrightarrow L^2((t_0,t_f))$. The inequality follows from the definition of the dual norm.

Clearly, $\Vert k(t - \cdot )\Vert _{Y} \le \Vert k(t - \cdot )\Vert _{W^{1,1}({{\mathbb {R}}})}$ holds for all $t \in (t_0,t_f)$. Moreover,

$$\begin{aligned} \Vert x - x^{{{\overline{\varDelta }}}}\Vert _{Y^*} \le \sum _{i=1}^M |\xi _i| \Vert \alpha _i - \omega _i\Vert _{Y^*} \end{aligned}$$

and the claim follows by virtue of Theorem 4.10 and Hölder’s inequality. $\square$

6 Computational experiments

A discretization transforms (Q) into a finite-dimensional linear-least squares problem which can be solved with standard algorithms for convex optimization problems with box constraints. We name the references [3, 34] which are implemented in the Open-Source library SciPy, see [33], which we use for the computational results in this section.

6.1 The Sum-Up Rounding Algorithm for Control Approximation

We briefly recap the sum-up rounding (SUR) algorithm for one-dimensional problems, which is one possible approximation algorithm in the second step of the CIA decomposition. It is stated in Definition 6.1 below.

Definition 6.1

(Sum-Up-Rounding Algorithm, [24, 26, 28])

Let $t_0< \ldots < t_N = t_f$ discretize $[t_0,t_f]$ with $h :=\max _{i \in \{0, N - 1\}} t_{i+1} - t_i$. For a relaxed control $\alpha \in L^\infty ((0,T),{{\mathbb {R}}}^{M})$, we define the piecewise constant binary control $\omega (\alpha ) : [t_0,t_f] \rightarrow \{0,1\}^{M}$ for $i = 0,\ldots ,N-1$ iteratively by

$$\begin{aligned} \omega (\alpha )_j(t)|_{[t_i, t_{i+1}]} := \left\{ \begin{array}{ll} 1 : &{} j = \underset{k \in \{1,\ldots ,M\}}{{{\mathrm{arg\,max}}}}\int _{t_0}^{t_{i+1}} \alpha _k(t) {\mathrm {d}}t - \int _{t_0}^{t_i} \omega (\alpha )_k(t) {\mathrm {d}}t, \\ 0 : &{} \text { otherwise. } \end{array}\right. \end{aligned}$$

If the maximizing index j is ambiguous, the smallest of the maximizing indices is chosen.

SUR proceeds through the time intervals indexed by $i = 0, \ldots , N - 1$ and computes the approximation for the current interval. The index $j \in \{1,\ldots ,M\}$ identifies an coordinate of the function $\omega$. In the first iteration, the coordinate, in which $\int _{t_0}^{t_1} \alpha$ exhibits the highest value, is set to one in $\omega$ on the interval $[t_0, t_1]$. All other entries of $\omega$ are set to zero in the first interval. This procedure is iterated. For the i-th time interval index, SUR sets $\omega$ to one in the coordinate that exhibits a maximum value of $\int _{t_0}^{t_{i+1}} \alpha - \int _{t_0}^{t_i} \omega$, and to zero in all other coordinates.

As mentioned above, Proposition 3.5, Lemmas 3.7 and 3.8 and Theorem 3.9 hold for approximations constructed by means of SUR. We briefly recap that Proposition 3.5 holds, which yields the other statements.

Proposition 6.2

([26]) For all relaxed controls $\alpha$ and all rounding grids, SUR produces a binary control $\omega$. Furthermore, there exists a constant $C > 0$ such that $d(\alpha ,\omega ) \le C {{\overline{\varDelta }}}$.

We illustrate the behavior of SUR in Fig. 3. We have executed SUR to compute binary controls for two predetermined relaxed controls. The sigmoid function in the left column is approximated very closely by SUR because most of its values are almost binary-valued already. In the bottom image one observes that a finer discretization implies that a difference in norm has to persist when the ascent of the function is approximated more closely. Contrary to the case of the sigmoid function, the difference between the constant function and its SUR approximants in the right column in norm is constant regardless of the chosen discretization. The right column depicts the same effect as [21, Fig. 1].

Fig. 3

Sum-Up Rounding approximation (blue) for functions (black) g(t) (left) and h(t) (right) on coarse (top) and fine grid (bottom)

6.2 Signal processing example

We consider a similar example to the one from [4], which stems from Filtered Approximation in electronics. We introduce a function

$$\begin{aligned} \kappa (t) :=A \left( 1 - \sqrt{2}\exp \left( -\frac{\omega _0 t}{\sqrt{2}}\right) \cos \left( \frac{\omega _0 t}{\sqrt{2}} - \frac{\pi }{4}\right) \right) \end{aligned}$$

We define the convolution kernel for (P) and the reformulations and relaxations thereof as follows

$$\begin{aligned} k(t) :=\left\{ \begin{array}{lc} (-\kappa )'(t) &{} t \ge 0, \\ 0 &{} \text {else,} \end{array}\right. \end{aligned}$$

which yields

$$\begin{aligned} (k * x)(t) = \int _{t_0}^t k(t - \tau ) x(\tau ) {\mathrm {d}}\tau . \end{aligned}$$

We use $t_0 = -1$ and $t_f = 1$ as domain bounds. Regarding the target function f, we set $f(t) :=0.2\cos (2\pi t)$. Assuming that an equidistant discretization of $(t_0,t_f)$ into N intervals, i.e. $t_f - t_0 = N \varDelta$, we obtain a piecewise constant function $x = \sum _{i=1}^M x_i \chi _i$ with $x_i \in {{\mathbb {R}}}$ for $i \in \{1,\ldots ,N\}$ if $\chi _i$ denotes the characteristic function of the i-th interval. This gives

$$\begin{aligned}&\int _{t_0}^{t} \sum _{i=1}^N x_i k (t - \tau )\chi _i(\tau ){\mathrm {d}}\tau \\&\quad = \sum _{i=1}^N x_i \int _{(i-1)\varDelta }^{i\varDelta } k (t - \tau ) {\mathrm {d}}\tau \\&\quad = \sum _{i=1}^N x_i (\kappa (t - (i - 1) \varDelta ) 1_{t \ge (i - 1)\varDelta } - \kappa (t - i\varDelta ) 1_{t \ge i \varDelta }) {\mathrm {d}}\tau . \end{aligned}$$

Setting ${\tilde{g}}(s) :=(\kappa (s) 1_{s \ge 0} - \kappa (s - \varDelta ) 1_{s \ge \varDelta })$, we obtain an IQP similar to the one studied in [4]. We have chosen the parameter values $\omega _0 = \pi$ and $A = 0.1$, see also [4, Fig. 1].

The feasible realizations for the images of x are $\xi _L = \xi _1 = -1$, $\xi _2 = 0$ and $\xi _U = \xi _3 = 1$. We discretize the resulting relaxation (Q) as described above. Then, we solve (Q) using scipy.least_squares, that is with SciPy’s Trust Region implementation (with parameter method=’trf’ – Trust Region Reflective algorithm), see [33]. To apply SUR, we need to compute the convex coefficient functions $\alpha$ from x such that $\sum _{i=1}^M\alpha _i \xi _i = x$. Because this computation is not unique, we have chosen the most intuitive one from our point of view, see also [22], for an elliptic control problem. Specifically, we compute $\alpha (t)$ such that for $t \in [t_0,t_f]$, x(t) is the interpolant between its two neighboring points in $\{\xi _1,\ldots ,\xi _M\}$, that is we select i such that $\xi _i \le x(t) \le \xi _{i+1}$ and set

$$\begin{aligned} \alpha _i(t) :=\frac{\xi _{i+1} - x(t)}{\xi _{i+1} - \xi _i}, \end{aligned}$$

$\alpha _{i+1}(t) :=1 - \alpha _i(t)$ and $\alpha _j(t) :=0$ for $j \notin \{i, i+1\}$. Then, we apply SUR on a sequence of successively refined grids until the rounding grid coincides with discretization grid for the solution of (Q). We note that the convergence holds if the approximation continuous relaxation is not fixed but refined in every iteration as well and the minimizers of the approximations of the continuous relaxation converges to a minimizer of (P); see [22].

6.3 Results

For 256 intervals discretizing $(t_0,t_f)$, we have visualized the results in Fig. 4. The images in the left column show $k * x(\alpha )$ in the first row and $k * x(\omega )$ for $\omega$ being computed for $N = 4$, $N = 32$ and $N = 256$ rounding intervals. The convergence of $k * x(\omega )$ to $k * x(\alpha )$ is clearly visible. The right column shows the solution of (Q”), $x(\alpha )$, in its first row and the SUR approximants $x(\omega )$ for the rounding grids consisting of $N = 4$, $N = 32$ and $N = 256$ intervals.

Fig. 4

Relaxed solution (top) and SUR approximations of x, $k*x$ for $N = 4$, $N = 32$ and $N = 256$ (rows two to four). This is a rework of Figure 10.3 from [19]

For 4096 intervals discretizing $(t_0, t_f)$, we have tabulated the approximation and the relative error in the objective in Table 1. The relative error, which is the relative error of a squared $L^2$-difference, approximately follows a trend proportional to ${{\overline{\varDelta }}}^2$. The convergence to zero can be observed clearly. We consider the execution times of the code on a laptop computer equipped with a Intel(R) Core(TM) i7-6820 CPU clocked at 2.70 GHz. The main part of the computational costs is caused by the solution of (Q”). The costs for the execution of SUR are negligible. The execution time for 4096 intervals is 9222 s. Execution times for $2^i$ intervals, $i\in \{7,\ldots ,12\}$ are tabulated in Table 2.

Parts of the numerical results, in particular preliminary versions of Table 2 and Fig. 4 have been published in the PhD thesis [19].

Table 1 Convergence $j(K(x(\omega ^{{\overline{\varDelta }}}))) \rightarrow j(K(x(\alpha )))$ with convolution and relaxed solution computed on finest grid

Table 2 Execution times of the solution of (Q”) for N intervals discretizing $(t_0,t_f)$. This is Table 10.2 from [19]

7 Conclusion

The computational results in Sect. 6 strengthen our claim that the proposed methodology provides a computationally efficient way to compute discrete-valued distributed variables without the need to use discrete optimization algorithms which might have problems with the high number of variables when fine discretizations of the distributed variables are desired. In the considered function space setting, we achieve

$$\begin{aligned} \inf _{x \in \{\xi _1,\ldots ,\xi _M\}} j(K(x)) = \min _{x \in [\xi _L,\xi _M]} j(K(x)) \end{aligned}$$

and a constructive way to compute a minimizing sequence to the optimum. Finally, we note a shortcoming in the presented theory. To compute solutions of the relaxed problems (Q) or (R) numerically efficiently, it is often necessary to introduce regularization since the problems are usually not strictly convex. Common regularizers like powers $L^p$-norms are not weakly continuous, but only weakly lower semi-continuous, which yields a bounded suboptimality of the form

$$\begin{aligned} \min _{x \in [\xi _L,\xi _M]} j(K(x)) + \lambda R \ge \inf _{x \in \{\xi _1,\ldots ,\xi _M\}} j(K(x)) + \lambda r(x) \ge \min _{x \in [\xi _L,\xi _M]} j(K(x)) + \lambda r(x) \end{aligned}$$

where $r : L^p \rightarrow {{\mathbb {R}}}$ denotes the regularizer and $R :=\sup _{x \in [\xi _L,\xi _M]} r(x)$. Thus, the suboptimality is controlled by the value of coefficient $\lambda$.

Auxiliary statements for Theorem 4.5

Definition A.1

([38, Chap. 1.6]) Let $d \in {\mathbb {N}}$. Let $\phi \in C_0^\infty ({{\mathbb {R}}}^d, {{\mathbb {R}}})$ be a nonnegative function such that ${\text {supp}}\,\phi \subset \overline{B_1(0)}$ and $\int _{{\mathbb {R}}^d} \phi = 1$. Then, the family of functions $(\phi _{\delta })_{\delta > 0}$ with $\phi _\delta (x) :=\frac{1}{\delta ^d} \phi (x/\delta )$ for all $x \in {\mathbb {R}}^n$ is called a family of positive mollifiers.

Lemma A.2

Let $w \in H^1_0(\varOmega _T)$. Let $(\phi _\delta )_\delta$ be a family of positive mollifiers. Let $w_\delta :=\phi _\delta * w$. Then $\Vert w_\delta -w\Vert _{L^2(\varOmega _T)}\le \Vert \nabla w\Vert _{L^2(\varOmega _T)}\delta$.

Proof

We use the the construction of the mollifiers as $\phi _\delta (x) = \frac{1}{\delta ^d} \phi (x/\delta )$ to deduce

$$\begin{aligned} |(\phi _\delta * w)(x) - w(x)|&= \left| \int _{B_\delta (0)} \phi _\delta (y) w(x - y) {\mathrm {d}}y - w(x)\right| \\&= \left| \int _{B_\delta (0)} \phi _\delta (y) w(x - y) {\mathrm {d}}y - \int _{B_\delta (0)} \phi _\delta (y) w(x) {\mathrm {d}}y\right| \\&= \left| \int _{B_\delta (0)} \phi _\delta (y)(w(x - y) - w(x)) {\mathrm {d}}y\right| \\&= \left| \int _{B_1(0)} \delta ^d \phi _\delta (\delta z)(w(x - \delta z) - w(x)) {\mathrm {d}}z\right| \\&= \int _{B_1(0)} \phi (z) \left| \int _0^1 \frac{{\mathrm {d}}}{{\mathrm {d}}s} w(x - s \delta z)|_{s = \tau } {\mathrm {d}}\tau \right| {\mathrm {d}}z. \end{aligned}$$

We insert this expression into the left hand side. Then we use the chain rule for weakly differentiable functions; see [38, Chap. 2.2]. This gives the estimate

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |\phi _\delta * w - w|^2&\le \int _{{{\mathbb {R}}}^d} \int _{B_1(0)} \phi (z)^2 \left| \int _0^1 \frac{{\mathrm {d}}}{{\mathrm {d}}s} w(x - s \delta z)|_{s = \tau } {\mathrm {d}}\tau \right| ^2 {\mathrm {d}}z {\mathrm {d}}x \\&= \int _{{{\mathbb {R}}}^d} \int _{B_1(0)} \phi (z)^2 \left| \int _0^1 \nabla w(x - \tau \delta z)^T (\delta z) {\mathrm {d}}\tau \right| ^2 {\mathrm {d}}z {\mathrm {d}}x \\&\le \int _{B_1(0)} \phi (z)^2 \int _0^1 \int _{{{\mathbb {R}}}^d} |\nabla w(x - \tau \delta z)|^2 \delta ^2{\mathrm {d}}x {\mathrm {d}}\tau {\mathrm {d}}z \\&\le \Vert \nabla w\Vert _{L^2}^2 \delta ^2. \end{aligned}$$

$\square$

Lemma A.3

Let $w \in W^{1,\infty }(\varOmega _T)$. Then, w can be approximated by a piecewise constant function $w_H$ on a grid with (maximum) cell diameter (grid size) H such that $\Vert w - w_H\Vert _{L^\infty (\varOmega _T)} \le \Vert \nabla w\Vert _{L^\infty (\varOmega _T)}H$.

Proof

Let S be a grid cell with diameter less or equal than H. Then, we have for $x \in S$ that

$$\begin{aligned} |w(x) - w_H(x)|&= \left| w(x) \frac{1}{\lambda (S)} \int _S {\mathrm {d}}y - \frac{1}{\lambda (S)} \int _S w(y) \,{\mathrm {d}}y\right| \\&\le \frac{1}{\lambda (S)}\int _S |w(y) - w(x)| \,{\mathrm {d}}y \\&\le \Vert \nabla w\Vert _{L^\infty (\varOmega _T)} \frac{1}{\lambda (S)} \int _S |y - x| \,{\mathrm {d}}y\\&\le \Vert \nabla w\Vert _{L^\infty (\varOmega _T)} H. \end{aligned}$$

$\square$

Lemma A.4

Let $d \in {\mathbb {N}}$. Let $\varOmega _T \subset {\mathbb {R}}^d$ be a bounded domain. Let a rounding grid $S_1,\ldots ,S_N$ be given that decomposes $\varOmega _T$. Assume that there exists $C > 0$ such that for all $j \in \{1,\ldots ,N\}$, there exists a ball $B_j$ such that $\lambda (S_j) \ge C \lambda (B_j)$. Let H, $\rho > 0$ be constants such that ${{\mathrm{diam}}}(S_j) \ge \rho H$. Then,

$$\begin{aligned} N \le \frac{\lambda (\varOmega _T)\varGamma (d/2)2^d}{\pi ^{d/2}\rho ^d C} H^{-d}, \end{aligned}$$

where $\varGamma$ denotes the gamma function.

Proof

Let $j \in \{1,\ldots ,N\}$. Since $S_j \subset B_j$, it holds that $\rho H \le {{\mathrm{diam}}}S_j \le {{\mathrm{diam}}}B_j$. Moreover,

$$\begin{aligned} \lambda (S_j)&\ge C \lambda (B_j) \\&\ge C \frac{\pi ^{d/2}}{\varGamma (d/2)} \left( \frac{{{\mathrm{diam}}}B_j}{2}\right) ^d\\&\ge C \frac{\pi ^{d/2}}{\varGamma (d/2)}\left( \frac{\rho }{2}\right) ^d H^d. \end{aligned}$$

Dividing the volume of $\varOmega _T$ through this lower estimate on the volume of a single grid cell gives

$$\begin{aligned} N&\le \frac{\lambda (\varOmega _T)}{\min _j \lambda (S_j)} \le \frac{\lambda (\varOmega _T)\varGamma (d/2)2^d}{\pi ^{d/2}\rho ^d C} H^{-d}. \end{aligned}$$

$\square$