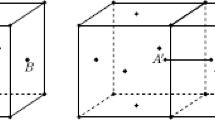Material Affine Connections for Growing Solids

Abstract

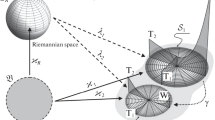
The present paper aims to develop geometrical approach for finite incompatible deformations arising in growing solids. The phenomena of incompatibility is modeled by specific affine connection on material manifold, referred to as material connection. It provides complete description of local incompatible deformations for simple materials. Meanwhile, the differential-geometric representation of such connection is not unique. It means that one can choose different ways for analytical definition of connection for single given physical problem. This shows that, in general, affine connection formalism provides greater potential than is required to the theory of simple materials (first gradient theory). For better understanding of this inconsistence it is advisable to study different ways for material connection formalization in details. It is the subject of present paper. Affine connection endows manifolds with geometric properties, in particular, with parallel transport on them. For simple materials the parallel transport is elegant mathematical formalization of the concept of a materially uniform (in particular, a stress-free) non-Euclidean reference shape. In fact, one can obtain a connection of physical space by determining the parallel transport as a transformation of the tangent vector, which corresponds to the structure of the physical space containing shapes of the body. One can alternatively construct affine connection of material manifold by defining parallel transport as the transformation of the tangent vector, in which its inverse image with respect to locally uniform embeddings does not change. Utilizing of the conception of material connections and the corresponding methods of non-Euclidean geometry may significantly simplify formulation of the initial-boundary value problems of the theory of incompatible deformations. Connection on the physical manifold is compatible with metric and Levi-Civita relations holds for it. Connection on the material manifold is considered in three alternative variants. The first leads to Weitzenböck space (the space of absolute parallelism or teleparallelism, i.e., space with zero curvature and nonmetricity, but with non-zero torsion) and gives a clear interpretation of the material connection in terms of the local linear transformations which transform an elementary volume of simple material into uniform state. The second one allows to choose the Riemannian space structure (with zero torsion and nonmetricity, but nonzero curvature) in material manifold and it is the most convenient way for deriving of field equations. The third variant is based on Weyl manifold with specified volume form and non-vanishing nonmetricity.

Appendices

Appendix. 1. Material Connection

36${}^{\mathbf{\circ}}$ Conventional definitions of operators like gradient, divergence and curl are based on Euclidean parallel transport rule. If u is a vector field in Euclidean space and o is a fixed point then we can transport all values $\textbf{u}(\text{x})$ to o along arbitrary curves, conserving lengths and directions of these vectors. Thus, we can define derivative at o as the relative increment.

In the case of the body manifold if ${u}$ is a vector field on it, then for distinct points $\mathfrak{p}$ and $\mathfrak{q}$ the ‘‘sum’’ ${u}_{\mathfrak{p}}+{u}_{\mathfrak{q}}$ has no sense since values ${u}_{\mathfrak{p}}$ and ${u}_{\mathfrak{q}}$ belong to different fibers of tangent bundle. This implies the difficulty of defining the derivative as a limit of relative increment. We need an extra rule to connect spaces $T_{\mathfrak{p}}\mathfrak{B}$ and $T_{\mathfrak{q}}\mathfrak{B}$. Such the rule is called as parallel transport rule and is defined by an affine connection on $\mathfrak{B}$, which is the mapping

$$\nabla^{B}:{\mathfrak{X}}\,(\mathfrak{B})\times{\mathfrak{X}}\,(\mathfrak{B})\rightarrow{\mathfrak{X}}\,(\mathfrak{B}),\quad({u},{v})\rightarrow\nabla^{B}_{{u}}{v},$$

that satisfies the following axioms [2, 3]:

• ($\nabla_{1}$) $\forall{u},{v},{w}\in{\mathfrak{X}}\,(\mathfrak{B}):\;\nabla^{B}_{{u}+{v}}{w}=\nabla^{B}_{{u}}{w}+\nabla_{{v}}{w}$;

• ($\nabla_{2}$) $\forall{u},{v}\in{\mathfrak{X}}\,(\mathfrak{B})\;\forall f\in C^{\infty}(\mathfrak{B};\mathbb{R}):\;\nabla^{B}_{f{u}}{v}=f\nabla^{B}_{{u}}{v}$;

• ($\nabla_{3}$) $\forall{u},{v},{w}\in{\mathfrak{X}}\,(\mathfrak{B}):\;\nabla^{B}_{{u}}({v}+{w})=\nabla^{B}_{{u}}{v}+\nabla^{B}_{{u}}{w}$;

• ($\nabla_{4}$) $\forall{u},{v}\in{\mathfrak{X}}\,(\mathfrak{B})\;\forall f\in C^{\infty}(\mathfrak{B};\mathbb{R}):\;\nabla^{B}_{{u}}(f{v})=f\nabla^{B}_{{u}}{v}+({u}f){v}$.

Axioms ($\nabla_{1}$) and ($\nabla_{2}$) declare that $\nabla^{B}$ is linear with respect to the lower argument, while axioms ($\nabla_{3}$) and ($\nabla_{4}$) state that $\nabla^{B}$ is additive with respect to the second argument, but not homogeneous. The homogeneity condition is replaced with Leibniz rule. We refer to the value $\nabla^{B}_{{u}}{v}$ as covariant derivative.

In some chart $(U,\varphi)$ on the body the restriction of the connection $\nabla^{B}$ on $U$ can be represented in coordinatewise form. There exist $27$ functions $\Gamma_{jk}^{i}\in C^{\infty}(U;\mathbb{R})$ such that $\nabla^{B}_{\partial_{j}}\partial_{k}=\Gamma_{jk}^{i}\partial_{i}$. Thus, for vector fields ${u}=u^{i}\partial_{i}$ and ${v}=v^{i}\partial_{i}$ on $U$ one gets equality $\nabla^{B}_{{u}}{v}=u^{i}(\partial_{i}v^{k}+v^{j}\Gamma_{ij}^{k})\partial_{k}$. We refer to functions $\Gamma_{jk}^{i}$ as connection symbols.

2. Parallel Transport and Autoparallelism

37${}^{\mathbf{\circ}}$ Material connection $\nabla^{B}$ allows one to introduce linear operators that act between tangent fibers of the body $\mathfrak{B}$ in intrinsic way. Each such operator depends on curve with ends at base points of two fibers and defines the transport of tangent vector along this curve from one fiber to another. With a view to define such operators we consider a vector field ${u}\in{\mathfrak{X}}\,(\mathfrak{B})$ and a smooth curve $\chi:\mathbb{I}\rightarrow\mathfrak{B}$. If $\nabla_{\chi^{\prime}}{u}=0$ then we say that ${u}$ is parallel transported along $\chi$. In a chart on $\mathfrak{B}$, we have first order differential equation $\dot{u}^{b}+u^{c}\dot{\chi}^{a}\Gamma_{ca}^{b}=0$, $b=1,2,3$, If $\mathfrak{p}=\chi(t_{0})$, then one has the following initial condition: ${u}_{\mathfrak{p}}={u}_{0}$. Thus, locally, there exists a unique solution for the Cauchy problem

$$\dot{u}^{b}+u^{c}\dot{\chi}^{a}\Gamma_{ca}^{b}=0,\quad b=1,2,3,$$

$$u_{\mathfrak{p}}^{b}=u_{0}^{b},\quad b=1,2,3.$$

(A1)

This allows us to define parallel transport map $P_{t_{0}}^{t}:T_{\chi(t_{0})}\mathfrak{B}\rightarrow T_{\chi(t)}\mathfrak{B}$ as follows: it transforms each element ${u}_{0}\in T_{\chi(t_{0})}\mathfrak{B}$ to the value ${u}(t)$ of the solution ${u}$ for the Cauchy problem (A1); $P_{t_{0}}^{t}:{u}_{0}\mapsto{u}(t)$.

Parallel transport map allows us to represent covariant derivative as limit of relative increment. If $\mathfrak{p}$ is material point and $\chi$ is a smooth curve on $\mathfrak{B}$ passing through $\mathfrak{p}$, i.e., $\chi(0)=\mathfrak{p}$, then we get

$$\nabla^{B}_{{u}}{v}|_{\mathfrak{p}}=\lim\limits_{h\to 0}\dfrac{P_{h}^{0}{v}_{\chi(h)}-{v}_{\chi(0)}}{h}=\left.\dfrac{d}{dt}P_{t}^{0}{v}_{\chi(t)}\right|_{t=0}.$$

Here $P_{t}^{0}{v}_{\chi(t)}$ is an element of $T_{\chi(0)}\mathfrak{B}$ and the difference $P_{t}^{0}{v}_{\chi(t)}-{v}_{\chi(0)}$ is well-defined since it belongs to $T_{\chi(0)}\mathfrak{B}$.

38${}^{\mathbf{\circ}}$ It may happen that field of infinitesimal generators of curve $\chi:\mathbb{I}\rightarrow\mathfrak{B}$ can be parallel transported along this curve, i.e., the equation $\nabla^{B}_{\chi^{\prime}}\chi^{\prime}=0$ is satisfied identically. In this case we say that the curve $\chi$ isautoparallel. In a smooth chart one gets the system

$$\ddot{\chi}^{q}+\Gamma_{ij}^{q}\dot{\chi}^{i}\dot{\chi}^{j}=0,\quad q=1,2,3.$$

3. Torsion, Curvature, and Nonmetricity

39${}^{\mathbf{\circ}}$ Connection symbols may differ from zero in Euclidean space with respect to curvilinear coordinates as well as in the space $\mathfrak{B}$ with arbitrary material connection. It means that connection symbols $\Gamma_{jk}^{i}$ cannot characterize the geometry, and, therefore, structural inhomogeneity of the body. The deviation of geometry from the Euclidean one is described by tensor fields of torsion $\mathfrak{T}:{\mathfrak{X}}\,(\mathfrak{B})\times{\mathfrak{X}}\,(\mathfrak{B})\rightarrow{\mathfrak{X}}\,(\mathfrak{B})$, Riemann curvature $\mathfrak{R}:{\mathfrak{X}}\,(\mathfrak{B})\times{\mathfrak{X}}\,(\mathfrak{B})\times{\mathfrak{X}}\,(\mathfrak{B})\rightarrow{\mathfrak{X}}\,(\mathfrak{B})$, and nonmetricity $\mathfrak{Q}:{\mathfrak{X}}\,(\mathfrak{B})\times{\mathfrak{X}}\,(\mathfrak{B}\times{\mathfrak{X}}\,(\mathfrak{B})\rightarrow C^{\infty}(\mathfrak{B};\mathbb{R})$, which completely characterize the connection on $\mathfrak{B}$. These fields are defined as follows:

$$\mathfrak{T}({u},{v})=\nabla^{B}_{{u}}{v}-\nabla^{B}_{{v}}{u}-[{u},{v}];$$

(A2)

$$\mathfrak{R}({u},{v},{w})=\nabla^{B}_{{u}}\nabla^{B}_{{v}}{w}-\nabla^{B}_{{v}}\nabla^{B}_{{u}}{w}-\nabla^{B}_{[{u},{v}]}{w};$$

(A3)

$$\mathfrak{Q}({u},{v},{w})=\mathfrak{g}^{B}(\nabla_{{u}}{v},{w})+\mathfrak{g}^{B}({v},\nabla_{{u}}{w})-{u}[\mathfrak{g}^{B}({v},{w})],$$

(A4)

where $[\cdot,\cdot]:{\mathfrak{X}}\,(\mathfrak{B})\times{\mathfrak{X}}\,(\mathfrak{B})\rightarrow{\mathfrak{X}}\,(\mathfrak{B})$ are Lie brackets, $[{u},{v}]f:={u}({v}(f))-{v}({u}(f))$.

In a coordinate frame fields of torsion $\mathfrak{T}$ (A2), curvature $\mathfrak{R}$ (A3) and nonmetricity $\mathfrak{Q}$ (A4) are represented by components

$$\mathfrak{T}_{ij}^{k}=\Gamma_{ij}^{k}-\Gamma_{ji}^{k},$$

(A5)

$$\mathfrak{R}_{ijk}^{t}=\partial_{i}\Gamma_{jk}^{t}-\partial_{j}\Gamma_{ik}^{t}+\Gamma_{jk}^{l}\Gamma_{il}^{t}-\Gamma_{ik}^{l}\Gamma_{jl}^{t},$$

$$-\mathfrak{Q}_{ijk}=\partial_{i}(\mathfrak{g}^{B})_{jk}-\Gamma_{ij}^{m}(\mathfrak{g}^{B})_{mk}-\Gamma_{ik}^{m}(\mathfrak{g}^{B})_{mj},$$

(A6)

where $i,j,k,t=1,2,3$. Formulae (A5) and (A6) imply relations between connection coefficients, torsion and nonmetricity components in coordinate frame [8]:

$$\Gamma_{jk}^{i}=\dfrac{(\mathfrak{g}^{B})^{im}}{2}(\partial_{j}(\mathfrak{g}^{B})_{mk}+\partial_{k}(\mathfrak{g}^{B})_{mj}-\partial_{m}(\mathfrak{g}^{B})_{jk})+\dfrac{(\mathfrak{g}^{B})^{im}}{2}(\mathfrak{T}_{mjk}+\mathfrak{T}_{kmj}+\mathfrak{T}_{jmk})$$

$${}+\dfrac{(\mathfrak{g}^{B})^{im}}{2}(\mathfrak{Q}_{jkm}+\mathfrak{Q}_{kmj}-\mathfrak{Q}_{mjk}),$$

(A7)

where $\mathfrak{T}_{kij}=(\mathfrak{g}^{B})_{km}\mathfrak{T}_{ij}^{m}$. We have the following interpretation of (A7): it is sufficient to define Riemannian metric and independent tensors $\mathfrak{Q}$ and $\mathfrak{T}$ for introducing an affine connection on the manifold $\mathfrak{B}$.

4. Geodesics

40${}^{\mathbf{\circ}}$ Material metric $\text{g}^{B}$ allows to define lengths of curves on $\mathfrak{B}$ which can be regarded as reference lengths of material fibers. If $\chi:{]a,b[}\rightarrow\mathfrak{B}$ is a curve then its length is defined intrinsically as

$$l_{\mathfrak{g}^{B}}(\chi):=\displaystyle\int\limits_{a}^{b}\sqrt{\mathfrak{g}^{B}_{\chi(t)}(\chi^{\prime}(t),\chi^{\prime}(t))}\,dt.$$

In a chart we have $\mathfrak{g}^{B}=(\mathfrak{g}^{B})_{ij}d\mathfrak{p}^{i}\otimes d\mathfrak{p}^{j}$, $\chi(t)=(\chi^{1}(t),\chi^{2}(t),\chi^{3}(t))$ and $\chi^{\prime}(t)=\dot{\chi}^{i}(t)\partial_{i}|_{\chi(t)}$. Then one arrives at the coordinate expression for $l_{\mathfrak{g}^{B}}(\chi)$:

$$l_{\mathfrak{g}^{B}}(\chi)=\displaystyle\int\limits_{a}^{b}L(\chi^{i},\dot{\chi}^{i})\,dt,$$

where $L(\chi^{i},\dot{\chi}^{i})=\sqrt{(\mathfrak{g}^{B})_{ij}(\chi^{1},\chi^{2},\chi^{3})\dot{\chi}^{i}\dot{\chi}^{j}}$ is the Lagrangian density. Consider extremals of the functional $l_{\mathfrak{g}^{B}}(\chi)$: $\delta l_{\mathfrak{g}^{B}}(\chi)=0$. We refer to them as geodesics. The system of the Euler–Lagrange equations has the form

$$\dfrac{\partial L}{\partial\chi^{k}}-\dfrac{d}{dt}\left(\dfrac{\partial L}{\partial\dot{\chi}^{k}}\right)=0,\quad k=1,2,3,$$

and derivation gives the equation of geodesics:

$$\ddot{\chi}^{q}+\dfrac{(\mathfrak{g}^{B})^{qk}}{2}(\partial_{i}(\mathfrak{g}^{B})_{kj}+\partial_{j}(\mathfrak{g}^{B})_{ik}-\partial_{k}(\mathfrak{g}^{B})_{ij})\dot{\chi}^{i}\dot{\chi}^{j}=0,\quad q=1,2,3,$$

where $[(\mathfrak{g}^{B})^{ij}]=[(\mathfrak{g}^{B})_{ij}]^{-1}$.