Delocalized nonlinear vibrational modes of triangular lattices

Abstract

All possible one- and two-component delocalized nonlinear vibrational modes (DNVMs) in triangular lattice are analyzed. DNVMs are obtained considering solely upon the symmetry of the triangular lattice, and thus, they exist regardless the type of interactions between particles. In this work, the nearest-neighbor inter-particle interactions are described by the $\beta$-FPU potential. The one-component DNVMs are periodic in time, while the two-component ones are superposition of the two vibrational modes with, generally speaking, incommensurate frequencies. For many (but not for all) two-component DNVMs, time-periodic solutions can be obtained by a proper choice of the amplitudes of the two constitutive modes. For each DNVM, frequency and energy per particle are reported as the functions of vibration amplitude together with other characteristics.

DNVM construction method

Patterns of particle displacements of different vibrational modes, which are presented in Figs. 1 and 4, were obtained with the aid of the theory of bushes of nonlinear normal modes (BNNMs) [7,8,9] (hereafter bush theory). This theory was developed for studying the nonlinear dynamics of Hamiltonian systems with discrete symmetry. A simplified introduction to this theory without using the apparatus of irreducible representations of point and space symmetry groups is presented in the recent paper [46].

Note that the N-component DNVM in the bush theory is called N-dimensional BNNM.

The bush theory can be regarded as a generalization of the well-known Wigner’s theory [47] used for the classification of normal modes (NMs), which are obtained in the harmonic approximation for small-amplitude atomic vibrations, to the case of large-amplitude vibrations.

Using the methods of group theory, it is possible to find selection rules for the energy exchange between NMs of different symmetry [7,8,9]. These rules lead to the combination of vibrational modes into bushes, which are exact solutions of nonlinear dynamical equations.

The bush theory is based on symmetry-related (group-theoretical) methods only, and therefore, it takes into account anharmonic terms of any type and any strength.

The main ideas of the bush theory are rather simple and can be explained as follows. Any vibrational regime in the system with a given point (for molecules) or space (for crystals) symmetry group $G_0$ can be associated with a certain subgroup G of this group. Indeed, we can act on the displacement pattern corresponding to this mode by all symmetry elements of the group $G_0$ and select those that do not change it. Obviously, the full set of such elements forms a certain subgroup (G) of the group $G_0$. This subgroup, due to the uniqueness of the solution of the classical equations of motion under given initial conditions, does not change in time, in other words, the symmetry of the mode is conserved in time. Note that the last statement is true, provided that the dynamical regime does not lose its stability, which can occur for the case of sufficiently large amplitudes of vibrations.

Thus, we can determine the symmetry group of any given vibrational mode using its displacement pattern. On the contrary, if a certain subgroup (G) of the symmetry group $G_0$ is given, then one can find the pattern of particle displacements, which is invariant with respect to all its symmetry elements. As a result, some symmetry-related restrictions arise on magnitudes and directions of the displacements of different particles.

The importance of the above-mentioned statement that any dynamical regime can be associated with a certain subgroup G of the symmetry group $G_0$ of the lattice in its equilibrium state is determined by the fact that each such subgroup singles out a certain invariant manifold on which some exact solution of nonlinear dynamical equations is realized.

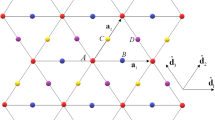
We will explain this idea by considering the one-dimensional bush number 7 from Fig. 1, which we reproduce in Fig. 8 in a different format, indicating with arrows the atomic displacements at a fixed moment. It is essential that all arrows in this figure are of the same length. The symmetry of this displacement pattern is clearly visible. Indeed, in the center of the primitive cell there is an immobile atom, through which the sixth-order symmetry axis perpendicular to the plane passes, as well as the mirror planes passing through this axis and hexagonal coordinate axes. These symmetry elements determine the point group 6mm.

Fig. 8

Displacement pattern for one-dimensional DNVM 7 (see Fig. 1). (Color figure online)

Fig. 9

Displacement pattern for two-dimensional DNVM $\gamma$ (see Fig. 4). (Color figure online)

Since the symmetry group of the triangular lattice is a space (in our case, plane) group, its subgroups can possess primitive cells with different multiplication factors of their volume (in our case, area). The primitive cell of the vibrational state described by the mode 7 is nine times larger than that of the equilibrium state, since each its edge is three times longer than the edges of the primitive cell of the triangular lattice. This is also clear from the number of atoms belonging to the dotted cell in Fig. 8 (9 atoms).

Similarly, one can verify that each of the patterns shown in Figs. 1 and 4 has a certain symmetry group, which is a subgroup of the lattice symmetry group $G_0=p6{mm}$.

If we run the numerical integration of Newton’s dynamical equations for initial atomic displacements corresponding to any pattern in Figs. 1 and 4 with zero initial velocities of all atoms, it is easy to verify that we obtain phase trajectory belonged to a certain invariant manifold. By definition, the invariant manifold is such a set of points of the system’s phase space that starting from any of it, we obtain a phase trajectory, which does not leave this manifold during the unlimited time evolution. This means that the type of atomic displacement pattern does not change in time.

The atomic velocities that were zero at the initial moment become nonzero. The pattern of the velocities of all atoms at any moment of time has the same symmetry as the pattern of atomic displacements, and this symmetry is preserved in time if the considered dynamical regime does not lose stability.

The invariant manifolds obtained in the above way are subspaces of some dimension in the phase space of the system.

Singling out invariant manifolds can be considered as the first stage in the problem of finding exact solutions of nonlinear dynamical equations, since each of such solutions must lie on a certain invariant manifold.

In mathematics, there are no methods for finding invariant manifolds in the general case. However, if the system has a certain group of discrete symmetry, then such a method is proposed by the bush theory. This method reduces the problem to the procedures of singling out subgroups of the symmetry group $G_0$ of the system in equilibrium and finding the displacement patterns that are invariant with respect to these subgroups.

The set of atomic displacements in Fig. 8 is one-parametric, since all arrows, as was already mentioned, possess identical length and transform into each other under the action of the symmetry elements of the group $G_0=p6{mm}$ (the corresponding invariant manifold is one-dimensional).

The corresponding bush defines a certain one-dimensional nonlinear oscillator (its frequency depends on the amplitude), and the length of arrows in displacement pattern changes periodically in time due to the transition of the potential energy of the system to the kinetic one and vice versa.

If we investigate in a similar way the patterns of atomic displacements for all subgroups of the initial symmetry group $G_0=p6{mm}$, then we reveal that the corresponding sets of atomic displacements invariant with respect to them depend on different numbers of arbitrary parameters.

The patterns for bushes in Fig. 4 depend on two arbitrary parameters. They are characterized by two types of arrows of different lengths, as shown in Fig. 9 for the bush $\gamma$. If we expand this pattern over the full set of normal modes, we will see that only two modes make a nonzero contribution to the bush $\gamma$, i.e., it turns out to be two-dimensional vibrational bush. This fact is shown by two adjacent panels in Fig. 4 representing displacement patterns for each of modes of this bush. It describes the system of two interacting nonlinear oscillators.

Considering all different subgroups of the group $G_0$ we find not only one-dimensional and two-dimensional bushes, but also bushes of higher dimensions. The bush theory allows one to obtain the complete list of bushes of different dimensions that can be realized in the given dynamical system with discrete symmetry. Note that the actual listing and studying all such bushes are possible only with the aid of the appropriate computer programs [48].

The bush theory is a generalization of the theory of complete condensates [48,49,50] of primary and secondary order parameters in the theory of structural phase transitions to the case of nonlinear dynamics. This theory was used in many papers for the systems with discrete symmetry of different structures and different physical nature, in particular, for crystals with complex space groups [10, 12, 13, 20, 23, 24, 51,52,53,54,55]. In recent years, bushes of vibrational modes were used to obtain new types of discrete breathers by imposing some localizing functions onto these dynamical objects [15, 16, 56].

In the bush theory, we must distinguish geometrical and dynamical aspects. In the first case, we are talking about the bush structure, which is determined by the set of its modes and does not depend on the type and strength of interatomic interactions. This structure is determined by group-theoretical methods only and does not change during the time evolution of the system. In the second case, we are talking about changing the mode’s amplitudes in time that leads to a periodic or quasiperiodic redistribution of the energy between the modes of a given bush. This process depends substantially on the interatomic interactions in the considered system.

If we excite a certain vibrational mode (by definition, this is the “root” mode), then a number of other (“secondary”) modes are excited due to the force interactions between different modes. Together with the root mode, they form a certain bush whose dimension (m) is equal to the full number of its modes. Other modes of the system are “sleeping” because they possess zero amplitudes. The total energy of the system’s initial excitation turns out to be trapped in a given bush, which for small m represents a Hamiltonian system of significantly lower dimension compared to that of the considered system.

However, with increasing the energy of the initial excitation of a given bush it can lose stability as a consequence of the internal parametric resonance [9, 57,58,59]. Indeed, due to the nonlinearity of the system, the frequencies of vibrational modes depend on their amplitudes, and a certain resonance between the bush modes and some of the sleeping modes can occur. As a result, the previously slept modes wake up and transform into active modes with nonzero amplitudes. A less symmetric bush of greater dimensionality is formed. It is important to emphasize that the bush theory at this stage does not lose its relevance, since some new bush of a greater dimensionality appears, but this is also a bush.

Let us note in conclusion that, being based on group-theoretical methods, the bush theory is rather universal, since it remains valid not only for the models studied with the aid of molecular dynamics, but also for models treated in the framework of the density functional theory [10, 20, 54].