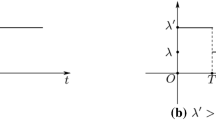1 Introduction

In today’s highly competitive environment, efficient and effective inventory management is necessary to ensure that retailers have a stable supply of products to satisfy fluctuations in market demand. Most customers prefer to obtain products immediately rather than wait for what they have ordered. Insufficient inventory can result in the loss of sales or time-consuming back orders. On the other hand, excess inventory should also be avoided, as it will produce loss of profit due to increased costs. It is important to maintain the right balance of stock in warehouses for shipment to the retailers.

Vendor managed inventory (VMI) is an approach used to streamline supply chain performance, in which the supplier is responsible for optimizing and maintaining the retailers’ inventory levels (for example, see Angulo et al. 2004; Simchi-Levi et al. 2005; and Lee and Seungjin 2008). VMI is a business practice where the retailer provides records of product activities to the supplier for comparison against existing stock levels. Suppliers and retailers together reach an agreement on the maximal and minimal inventory levels. The retailers depend upon the supplier to determine when to replenish their stock based on the data supplied and the vendor’s forecasting of customer demand between these ranges. The main benefits of a VMI system are that it greatly reduces the bullwhip effect and increases the efficiency of inventory management. Information in the VMI system is provided to both the supplier and the individual retailers when deciding upon how much product should be sent and how much should be kept in stock. However, inventory levels are established manually by experienced personnel at some retailers in Taiwan that adopt VMI practice (Chang et al. 2017). The results obtained by manually calculating desired inventory levels may be less effective leading to inefficient inventory management. For example, if the value of the upper level is set too high, or the value of the lower level is set too low, carrying costs will increase, resulting in a financial loss to the company. On the other hand, if the value of the upper level is set too low or the value of the lower level is set too high, the number of deliveries and associated costs will increase. The setting of inappropriate upper and lower level values will increase not only transportation cost, but also the risk of running out of stock. Consequently, the development of a VMI model capable of generating a good replenishment strategy that will lead to more efficient inventory management is important.

Inventory control management has been studied by many researchers. For example, Shahabi et al. (2013) presented integrated mathematical models to coordinate facility location and inventory control for a four-echelon supply chain network consisting of multiple suppliers, warehouses, hubs and retailers, with the objective of minimizing facility location, transportation and the inventory costs. The proposed models simultaneously determined three types of decisions: facility location, assignment of suppliers and retailers to these warehouses, and inventory control decisions. Silva and Gao (2013) formulated a distribution center location model that incorporates joint replenishment inventory costs at the distribution centers and proposed a greedy randomized adaptive search procedure to solve this problem. Coelho et al. (2013) discussed the two most common classification methods for the determination of inventory policy, which define pre-established rules for the replenishment of customer supplies. One type is the order-up-to level (OU) policy (see Archetti et al. 2007; Solyalı and Süral 2008; Michel and Vanderbeck 2012; Adulyasak et al. 2013; Coelho and Laporte 2013b). Under an OU policy, the quantity delivered is that which is needed to fill the inventory capacity whenever a customer is visited. The other is the maximum-level (ML) policy (see Savelsbergh and Song 2008; Raa and Aghezzaf 2009; Hewitt et al. 2013; Coelho and Laporte 2013a; Chu et al. 2017). Under an ML inventory policy, the replenishment level is flexible, but bounded by the capacity available to each retailer.

The demand probability distributions for the customers are known (see Kleywegt et al. 2002, 2004; Aghezzaf 2008; Huang and Lin 2010; Solyalı et al. 2012; Juan et al. 2014; Bertazzi et al. 2015; Roldán et al. 2016), that is to say, the upper and lower inventory levels in bins or storage areas act as parameters in the models, from which the standard deviation of a given probability distribution is usually calculated. Consequently, the planning results may not reflect overall optimality in terms of inventory management, especially for determining and maintaining the optimum level of investment in the inventory. To improve and systemize inventory management, in this study, we develop a method based on the network flow technique to construct a replenishment planning model for the upper-and-lower inventory level control problem. The objective of the proposed model is to minimize the total short-term cost, including the fixed cost (i.e., the cost of regular maintenance for delivery vehicles and salaries for drivers) and the variable costs (i.e., the transportation cost, the stock carrying cost for the supplier and the retailers, and the stock-out cost for the retailers). The model is expected to be a useful tool to assist the planner in making decisions about the optimal upper-and-lower inventory levels. This model is formulated as an integer network flow problem which is characterized as NP-hard (Garey and Johnson 1979) so could be difficult to optimally solve for realistic large-scale problems. To efficiently and effectively solve the model, we also propose a solution algorithm based on the problem decomposition technique.

The rest of the paper is organized as follows: First, the problem is described and assumptions made. The model and the solution algorithm are then proposed. Then, a case study and sensitivity analyses using data from one supplier and a set of retailers in Taiwan are performed. Finally, some conclusions and suggestions for future work are given.

2 The Model

2.1 Problem Description and Assumptions

This study focuses on the development of an inventory control model which considers the upper-and-lower levels of the inventory management problem. The information and conditions of the VMI for the retailers, coupled with the assumptions used for the modelling, which are based on real practices, are summarized below:

  1. (1)

    The VMI strategy which is built based on our proposed model considers one supplier and multiple retailers. The retailers provide information to the supplier about the products carried, and the supplier takes full responsibility to make sure that the retailer has the required level of inventory without any stock-out occasions, with the objective of minimizing the total cost.

  2. (2)

    The (s, S, R) inventory policy, which is a periodic review system, is considered in this study, because of high inventory turnover at the retailers (especially in retail outlets). High inventory turnover in a short period of time tends to produce a short replenishment cycle, with a very short lead time. Therefore, based on the characteristic of the (s, S, R) inventory policy, the length of each review period for replenishment is set to be 1 day and the lead time is set close to zero, meaning that the gap between the time the inventory is checked and the time goods are delivered is very small. In addition, the replenishment planning is designed around a seven-day planning cycle, although the length of the planning cycle can be designed according to real operational data in the future.

  3. (3)

    The demand before performing the distribution and movement of products each day for each retailer is given. The amount of daily demand can be set in advance based on the value provided by the retailer (i.e., data from the client’s computers or the point of sale system) plus the quantity of goods expected to be sold within the lead time. It is assumed that the supplier has sufficient inventory to meet all demands during the replenishment planning period. Negative inventories are not allowed. The total supply of goods is greater than or equal to the total demand of all retailers. In addition, it is also assumed that the supplier is able to deliver goods on time.

  4. (4)

    Each retailer must be visited before its inventory reaches the minimum level. Every day a retailer is visited, the quantity of goods delivered by the supplier is such that the maximum level of inventory is reached at the retailer. It is assumed that the level of inventory at each retailer can never exceed its capacity.

  5. (5)

    For simplicity, all types of goods are transformed into equivalent units and the distances from the supplier to each retailer are given and fixed.

2.2 Modeling Approach

2.2.1 The Logistics-Flow Time-Space Network

As demonstrated by the many successful applications shown in the literature, the time-space network technique is utilized to formulate the movement of goods in terms of time and space between the supplier and all retailers for replenishment planning because of its flexibility and effectiveness. Examples of studies using this approach include those by Haghani and Oh (1996), Yan and Chen (2002), Chardaire et al. (2005), Yan and Shih (2009) and Yan et al. (2014, 2015, 2016, 2017). The logistics-flow time-space network for replenishment planning, as shown in Fig. 1, represents the movement of goods within a specific time period and between certain spatial locations. The horizontal axis represents the supplier warehouse (or the distribution center) and the retail stores in order; the vertical axis stands for the time duration.

Fig. 1
figure 1

Logistics-flow time-space network for replenishment planning

Full size image

Nodes and arcs are two major components in the time-space network. A node, with the exception of a dummy supply node and a collection node, represents a supplier warehouse or a retail store at a specific time. A dummy supply node and a collection node are both used to ensure flow conservation. A supply node contains the total supply in the network. Suppose that the dummy supply node has the total supply of d goods in the system equal to \( \sum \limits_{s=1}^t{q}_s \) for all items supplied by the supplier warehouse during the planning cycle. Note that there are 7 days in the planning cycle in this study (i.e. t = 7). Now suppose that the \( {b}_k^s \) demand for the kth retailer on day s is equal to \( {b}_1^s+{b}_2^s+\dots +{b}_m^s=\sum \limits_{k=1}^m{b}_k^s \). This means that the total demand in the system is equal to \( \sum \limits_{s=1}^t\sum \limits_{k=1}^m{b}_k^s \). By assumption, \( \sum \limits_{s=1}^t{q}_s \) is greater than or equal to \( \sum \limits_{s=1}^t{b}_k^s \). Thus, the demand of a collection node is set as \( -\sum \limits_{s=1}^t{q}_s+\sum \limits_{s=1}^t{b}_k^s \), to produce a balance between network supply and demand. Note that the maximum storage space in a node associated with a retail store (a retailer node) is given. The inventory remaining after demand is satisfied during the planning cycle is collected at the collection node, to balance supply and demand in the network. The arc flows indicate the flow of goods within the network. The arc flow’s lower and upper bounds mean the minimum and maximum number of allowable flow units in the associated arc. The eight types of arcs are defined below.

  1. 1.

    Supply arc

A supply arc, as shown in Fig. 1 (a), connects a dummy supply node to the first node associated with the supplier warehouse. The arc cost is zero because the supply node is viewed as a dummy node. The arc flow’s upper bound is the total amount of goods \( \sum \limits_{j=1}^t{q}_j \) supplied to the supplier warehouse. The arc flow’s lower bound is zero.

  1. 2.

    Dispatch arc

A dispatch arc, as shown in Fig. 1 (b), connects the supplier node to every node associated with a retail store on a specific day. Thus, the amount of goods to be transported must be decided at the supplier node every day. The arc cost is the unit transportation cost, including the cost of transporting an equivalent unit of goods (primarily the incremental cost of fuel consumption and truck maintenance). The arc flow’s upper bound is the retail stock capacity; the arc flow’s lower bound is zero.

  1. 3.

    Holding arc

A holding arc, as shown in Fig. 1 (c)–(d), indicates the holding of goods: (c) at a supplier warehouse or (d) at a retail store. The holding arc cost is the unit stock carrying cost. The arc flow’s upper bound is either the supplier warehouse’ capacity or each retail stock capacity. The arc flow’s lower bound is set to be zero, indicating that no goods are held during the time window.

  1. 4.

    Cycle arc

A cycle arc, as shown in Fig. 1 (e)–(f), functions to show the continuity between two consecutive planning periods: (e) at a supplier warehouse or (f) at a retail store. It connects the end of one period to the beginning of the next period, for the supplier warehouse or each retail store. The arc flow, the arc flow’s upper bound and lower bound, as well as the arc cost, are the same as those of the holding arcs.

  1. 5.

    Shortage arc

A shortage arc, as illustrated in Fig. 1 (g), functions to show a shortage in goods delivered from the supplier warehouse to the retailer on a specific day. It connects the supply node to a retailer node. The arc cost is set to be a large penalty cost in order to avoid having this flow. The arc flow’s upper bound is infinity and the arc flow’s lower bound is zero, indicating that the demand requested by the associated retailer is satisfied.

  1. 6.

    Retailer collection arc

A retailer collection arc, as shown in Fig. 1 (h), connects the last node associated with a retail store to the supplier node. It is used to ensure flow conservation of all collection arc flows in the network. The arc cost is the same as for the supplier dispatch arc. The arc flow’s upper bound is the total amount of remaining goods \( -\sum \limits_{p=1}^t{q}_p+\sum \limits_{p=1}^t{b}_k^p \) from the retailer nodes. The arc flow’s lower bound is zero, meaning that no goods remain at the associated retail store.

  1. 7.

    Supplier collection arc

A retailer collection arc, as shown in Fig. 1 (i), connects the last node associated with the supplier node to the supply node. It is also used to ensure flow conservation for all collection arc flows in the network. The arc flow, the arc flow’s upper bound and lower bound, as well as the arc cost, are the same as those of the supply arc.

  1. 8.

    Retrieval arc

A retrieval arc, as shown in Fig. 1 (j), connects the dummy supply node to the collection node, and is used to decide when goods should be delivered. The arc cost is zero, because no cost is incurred if goods are not delivered. The arc flow’s upper bound is infinity and the arc flow’s lower bound is zero.

To summarize, the supplier dispatch arc, the holding arc and the cycle arc are considered real activities in actual operations; the supply arc, the shortage arc, the retailer/supplier collection arc and the retrieval arc are considered as auxiliary activities used to ensure flow conservation in the network design.

2.3 Model Formulation

Based on the logistics-flow time-space network introduced above, as well as the operating constraints, the model is formulated as an integer network flow problem with side constraints. Before formulating the model, the notations and symbols used in the model formulation are listed.

2.3.1 Notation/Symbols Used in the Model Formulation

Decision variables:

xij:

the arc (i,j) flow in the logistics-flow network;

\( {y}_{\left(j-1\right)j}^u/{y}_{\left(j+6\right)j}^u \):

the value of the upper inventory level for the associated retailer on the holding arc between the (j-1)th time-space point and jth time-space point / on the cycle arc between the (j + 6)th time-space point and jth time-space point in the logistics-flow network;

\( {y}_{\left(j-1\right)j}^l/{y}_{\left(j+6\right)j}^l \):

the value of the lower inventory level for the associated retailer on the holding arc between the (j-1)th time-space point and jth time-space point / on the cycle arc between the (j + 6)th time-space point and jth time-space point in the logistics-flow network;

αj:

an index indicating whether a retailer needs to be replenished by the supplier at the jth time-space point; if αj equals one, it means that the supplier has to provide adequate goods to the associated retailer at the jth time-space point; otherwise (i.e. αj equals zero) the associated retailer does not need to be replenished by the supplier;

Parameters:

cij:

the arc (i,j) cost in the logistics-flow network (if arc (i,j) is a supply/supplier collection/retrieval arc, then cij is zero; if arc (i,j) is a dispatch/retailer collection arc, then cij is the unit transportation cost; if arc (i,j) is a holding/cycle arc, then cij is the unit stock carrying cost; if arc (i,j) is a shortage arc, then cij is a large penalty cost);

p:

the fixed cost incurred by delivering to a retailer, including the driver salary and the regular truck check for replenishing a retailer;

qs:

the supply of goods on day s;

\( {b}_k^s \):

the demand for the kth retailer on day s;

ai:

the supply/demand for the ith node in the logistics-flow network (if node i is the supplier node, then ai > 0; otherwise, ai ≤ 0);

dj:

the amount of demand for the jth time-space point in the logistics-flow network;

fj:

the retail stock capacity associated with the jth time-space point;

uij/lij:

the arc (i,j) flow’s upper/lower bounds in the logistics-flow network;

B:

a very large positive number;

ε:

a very small positive number;

N/A:

the set of all nodes/ arcs in the logistics-flow network;

R:

the set of all nodes for retailers in the logistics-flow network;

RH:

the set of all holding arcs for retailers in the logistics-flow network;

RC:

the set of all cycle arcs for retailers in the logistics-flow network;

E:

the set of all dispatch arcs in the logistics-flow network;

INT:

the set of integers.

2.3.2 Model Formulation

The model is formulated as follows:

$$ \mathit{\operatorname{Min}}\kern1em \sum \limits_{j\in R}p{\alpha}_j+\sum \limits_{ij\in A}{c}_{ij}{x}_{ij}, $$
(1)

subject to

$$ \sum \limits_{j\in N}{x}_{ij}-\sum \limits_{k\in N}{x}_{ki}={a}_i,\kern0.5em \forall i\in N, $$
(2)
$$ {x}_{\left(j-1\right)j}\le {y}_{\left(j-1\right)j}^l+\left(1-{\alpha}_j\right)B,\kern0.5em \forall \left(j-1\right)j\in RH, $$
(3)
$$ {x}_{\left(j-1\right)j}\ge {y}_{\left(j-1\right)j}^l+\varepsilon -{\alpha}_jB,\kern0.5em \forall \left(j-1\right)j\in RH, $$
(4)
$$ {x}_{ij}+{x}_{\left(j-1\right)j}\ge {y}_{\left(j-1\right)j}^u-\left(1-{\alpha}_j\right)B,\kern0.5em \forall ij\in E,\forall \left(j-1\right)j\in RH, $$
(5)
$$ {x}_{ij}+{x}_{\left(j-1\right)j}\le {y}_{\left(j-1\right)j}^u+\left(1-{\alpha}_j\right)B,\kern0.5em \forall ij\in E,\kern0.5em \forall \left(j-1\right)j\in RH, $$
(6)
$$ {x}_{\left(j+6\right)j}\le {y}_{\left(j+6\right)j}^l+\left(1-{\alpha}_j\right)B,\kern0.5em \forall \left(j+6\right)j\in RC $$
(7)
$$ {x}_{\left(j+6\right)j}\ge {y}_{\left(j+6\right)j}^l+\varepsilon -{\alpha}_jB,\kern0.5em \forall \left(j+6\right)j\in RC, $$
(8)
$$ {x}_{ij}+{x}_{\left(j+6\right)j}\ge {y}_{\left(j+6\right)j}^u-\left(1-{\alpha}_j\right)B,\kern0.5em \forall ij\in E,\kern0.5em \forall \left(j+6\right)j\in RH, $$
(9)
$$ {x}_{ij}+{x}_{\left(j+6\right)j}\le {y}_{\left(j+6\right)j}^u+\left(1-{\alpha}_j\right)B,\kern0.5em \forall ij\in E,\forall \left(j+6\right)j\in RH, $$
(10)
$$ {y}_{\left(j-1\right)j}^l\le {y}_{\left(j-1\right)j}^u,\kern0.5em \forall \left(j-1\right)j\in RH, $$
(11)
$$ {y}_{\left(j+6\right)j}^l\le {y}_{\left(j+6\right)j}^u,\kern0.5em \forall \left(j+6\right)j\in RC, $$
(12)
$$ {x}_{ij}\le {f}_j{\alpha}_j,\kern0.5em \forall ij\in E $$
(13)
$$ {\alpha}_j=0\ or\ 1,\kern0.5em \forall j\in R, $$
(14)
$$ 0\le {y}_{\left(j-1\right)j}^u\le f\kern0.5em \mathrm{and}\kern0.5em {y}_{\left(j-1\right)j}^u\in INT,\kern0.5em \forall \left(j-1\right)j\in RH, $$
(15)
$$ 0\le {y}_{\left(j+6\right)j}^u\le f\kern0.5em \mathrm{and}\kern0.5em {y}_{\left(j+6\right)j}^u\in INT,\kern0.5em \forall \left(j+6\right)j\in RC, $$
(16)
$$ {y}_{\left(j-1\right)j}^l\ge 0\kern0.5em \mathrm{and}\kern0.5em {y}_{\left(j-1\right)j}^l\in INT,\kern0.5em \forall \left(j-1\right)j\in RH, $$
(17)
$$ {y}_{\left(j+6\right)j}^l\ge 0\kern0.5em \mathrm{and}\kern0.5em {y}_{\left(j+6\right)j}^l\in INT,\kern0.5em \forall \left(j+6\right)j\in RC, $$
(18)
$$ {l}_{ij}\le {x}_{ij}\le {u}_{ij}\kern0.5em \mathrm{and}\kern0.5em {x}_{ij}\in INT,\kern0.5em \forall ij\in A. $$
(19)

This model is formulated as an integer network flow problem with side constraints. The objective function, (Eq. (1)), used to optimize the short-term total operating cost for replenishment planning, includes a summation of the fixed cost (i.e., the cost of regular maintenance for delivery vehicles and salaries for drivers) and a variable cost (i.e., the transportation cost, the stock carrying cost for supplier and retailers, and the stock-out cost for retailers). Equation (2) ensures flow conservation at every node in the logistics-flow network. Equations (3) and (4) denote whether a retailer needs to be replenished by the supplier at the jth time-space point based on the value of lower inventory level. The Either-Or constraints in this model are constructed by taking into consideration the optimal value of the lower inventory level. To ensure that the Either-Or constraints are automatically satisfied for any solution, a large number B can be added to the right-hand side of such constraints. For example, in Fig. 2, x(j − 1)j is the amount of remaining goods for the associated retailer at the (j-1)th time-space point. If αj = 1, it shows that x(j − 1)j is lower than the value of the lower inventory level, which means that replenishment is needed at the retailer to meet the demand dj at the jth time-space point (i.e., Eq. (3) becomes \( {x}_{\left(j-1\right)j}\le {y}_{\left(j-1\right)j}^l \)). Meanwhile, Eq. (4) \( {x}_{\left(j-1\right)j}\ge {y}_{\left(j-1\right)j}^l+\varepsilon -{\alpha}_jB \) holds true. Otherwise, if αj = 0, it shows that x(j − 1)j is greater than the lower inventory level value, which means that the retailer does not need to be replenished by the supplier at the jth time-space point (i.e., Eq. (3) \( {x}_{\left(j-1\right)j}\le {y}_{\left(j-1\right)j}^l+\left(1-{\alpha}_j\right)B \) holds true and Eq. (4) becomes \( {x}_{\left(j-1\right)j}\ge {y}_{\left(j-1\right)j}^l \)). Similar to Eqs. (3) and (4), Eqs. (5) and (6) denote whether a retailer needs to be replenished by the supplier at the jth time-space point based on the value of upper inventory level. The definitions of Eqs. (7), (8), (9) and (10) are the same as for Eqs. (3), (4), (5) and (6), except that the holding arcs are replaced by the cycle arcs which connect the end of one period (i.e., at the (j + 6)th time-space point) to the beginning of the next period (i.e., at the next jth time-space point) in the replenishment planning cycle. Equations (7) and (8) denote whether a retailer needs to be replenished by the supplier at the (j + 6)th time-space point, based on the lower inventory level value. Similar to Eqs. (5) and (6), Eqs. (9) and (10) denote whether a retailer needs to be replenished by the supplier at the (j + 6)th time-space point based on the upper inventory level value. Equations (11) and (12) ensure that the value of the upper inventory level is greater than or equal to the value of the lower inventory level at every node in the logistics-flow network. Equation (13) denotes that the amount of goods transported between the supplier and each retailer every day does not exceed the retail stock capacity. Equation (14) indicates that all variables that determine whether a retailer needs to be replenished by the supplier in the jth time-space point are either zero or one. Equation (15) holds all the upper inventory level values for a retailer between the (j-1)th time-space point and the jth time-space point in the logistics-flow network within their bounds. Equation (16) holds all the upper inventory level values for a retailer between the (j + 6)th time-space point and the jth time-space point in the logistics-flow network within their bounds. Equations (15) and (16) also ensure the integrality of all variables. Equations (17) and (18) ensure the non-negativity and integrality of the variables. Equation (19) holds all the arc flows within their bounds and ensures the integrality of all variables. Note that the lower bound of a holding arc flow is viewed as the amount of safety stock in Eq. (19), when the proposed model with deterministic demands are applied to the real world where stochastic demands may occur. A stochastic-demand model may be developed as an extension of the deterministic-demand model in future.

Fig. 2
figure 2

Example explaining when a retailer is replenished by the supplier

Full size image

In Taiwan VMI planning, it is assumed that the supplier has sufficient inventory to meet all demands during the replenishment planning period so can replenish the retailers’ stock quickly (assumption point (3)). In addition, the distances between the supplier and the retailers are usually relatively small, less than 40 km. Thus, the lead time is set close to zero in this study (assumption point (2)). Given the afore-mentioned assumptions, seven time units are designed in the network, where each time unit is 1 day. If the proposed model is extended to consider non-zero lead time and/or multiple delivery times per day, the nodes, the arcs, and the length of a time unit in the network coupled with the side constraints have to be modified. Modification of the proposed model to deal with a non-zero lead time and/or multiple delivery times per day can be a direction of research in the future.

3 Solution Algorithm

This model is formulated as an integer network flow problem with side constraints, and is characterized as NP-hard (Garey and Johnson 1979), meaning that it could be difficult to optimally solve for the realistic large-scale problems that occur in practice. We first directly solved the proposed model using the mathematical programming software, CPLEX 11.1. However, for the large problems that occur in practice convergence cannot be obtained within a reasonable time. Therefore, it is necessary to design an efficient algorithm to solve them.

A solution algorithm is developed using a problem decomposition technique, which, coupled with the mathematical programming solver, CPLEX, can efficiently solve realistic large-scale problems within a reasonable solution time. This solution algorithm is primarily designed based on a problem decomposition method, because, for an NP-hard problem the solution time is closely correlated to the problem scale, especially when the scale is large, as is the case in real-world problems.

In addition, according to point (3) in the modeling assumptions, the supplier is able to supply an adequate amount of goods for each retailer during the replenishment period. This means that each sub-problem is independent and thus mathematically feasible. As a result, the original large problem can be decomposed into several smaller sub-problems, each associated with some sub-section of the retailers. These sub-problems are solved sequentially and individually by using CPLEX. The solution algorithm is designed as follows. Several sub-problems are generated in sequence by decomposing the original problem. In particular, the first sub-problem is generated by setting apart a group of retailers. After solving this sub-problem using CPLEX, the solution is fixed and input to the original problem. Then, the second sub-problem is similarly generated for another group of retailers from those remaining. The second sub-problem is solved by using CPLEX and the solution is also affixed to the original problem. The procedure is repeated until the demands for all retailers are satisfied and the final solution is then obtained. The steps are described in detail below.

  1. Step 1:

    Decompose the original problem into a set of sub-problems. Let n sub-problems be generated for different partial sets of retailers. Set i = 1.

  2. Step 2:

    If i > n, go to Step 4; otherwise go to Step 3.

  3. Step 3:

    The ith sub-problem is solved using CPLEX and the solution is affixed to the original problem. Go to Step 2.

  4. Step 4:

    Aggregate the arc flows for the supply arcs, supplier collection arcs and holding arcs at the supplier warehouse in all sub-problems previously solved by using CPLEX.

  5. Step 5:

    Stop the algorithm. The final solution which includes the value of all arc flows in this logistics-flow network is obtained.

It should be mentioned that based on the assumption (point (3)) that the supplier has sufficient inventory to meet all demands during the replenishment planning period, the solution algorithm can solve the model optimally. The reason is as that when the supplier has sufficient inventory, then the replenishment schedule coupled with the upper-and-lower inventory levels of each retailer can be determined independently. There is no crowding out effect between retailers for replenishing the goods from the supplier. Thus, all retailers can be divided into several groups, each containing a number of retailers, and each corresponding to a sub-problem. As a result, the proposed solution algorithm, where the original problem is decomposed into several sub-problems which are then optimally solved using CPLEX, can optimally solve the model by combining the optimal solutions of all sub-problems.

4 Numerical Tests

Some numerical tests are performed to demonstrate how well the proposed model and the solution algorithm may be applied in the real world. The C++ computer language, coupled with the CPLEX 11.1 mathematical programming solver, is used to develop all the necessary programs for building and solving the models. The tests are performed on an Intel® Core(TM) i7 CPU 3.40GHz with 4GB RAM in the environment of Microsoft Windows 7 Professional With Service Pack 1 64-bit. Finally, we perform some sensitivity analyses on the model.

4.1 Data Analysis

Our numerical tests are mainly based on operational data obtained from a major retail company (Firm C) in northern Taiwan. There is one supplier which can be viewed as a distribution center and 50 retail stores for replenishment planning following a schedule designed around a seven-day planning cycle for the numerical tests. Thus, we use a gap of 1 day to construct the trip arcs in the network. Note that the distances from the supplier to each retailer are given and fixed. For ease of testing, all types of goods supplied are transformed into equivalent units, each equivalent to 12 pieces for each commodity. Based on real practices, the maximum carrying capacity of each delivery truck is assumed to be 150 equivalent units. The holding capacity for each retail store is shown in Table 1. The demand data provided by Firm C for all retail stores for the seven-day planning cycle are shown in Table 2. In addition, when applying a deterministic model in real practice where stochastic events may occur, a safety stock amount is usually set, especially for our problem where the lead time is set as zero. In this research, the everyday amount of safety stock (i.e., the lower bound of a holding arc flow) for each retailer is set to be 10% of the amount of demand every day. The user may set a safety stock amount suitable for its own operational requirements in other applications.

Table 1 The holding capacity for each retailer store
Full size table
Table 2 Demand data provided by Firm C for all retailers (equivalent units)
Full size table

All cost data are set as reported by Firm C. The cost of salaries for drivers is set to be NT$1800/day/person. The cost of regular checks for trucks is set to be NT$500/day/truck. The total fixed cost for transportation is thus NT$2300/day/truck. Assuming that a truck can replenish on average of five retailers in 1 day, the fixed cost of replenishing a retailer is NT$460/retailer. Suppose that the average vehicle speed is 30 km/h and the cost for transportation of goods is set to be NT$12.53/km/truck. Assuming that a truck can carry 150 equivalent units of goods, the unit transportation cost is set to be NT$0.084/km/equivalent unit of goods. Thus, the cost of transporting an equivalent unit of goods by truck is calculated as NT$0.084/km/equivalent unit of goods times the conveyance distance from the supplier to a specific retailer. Based on Firm C’s operational experience, the monthly holding cost for stock accounts for about 30% of the average commodity price. According to Firm C’s reports, the average commodity price is approximately NT$200. Therefore, the holding cost is set to be NT$1.97 per equivalent unit of goods per day (i.e., 200 × 0.3 × 12 ÷ 365 = 1.97). In addition, suppose that the stock-out cost accounts for 20% of the average commodity price based on Firm C’s operations. The stock-out cost is set to be NT$480 per equivalent unit of goods (i.e., 200 × 0.2 × 12 = 480).

4.2 Test Results

The size of the test problem is large, including 1810 integer variables, 350 binary variables and 4269 constraints (359 for flow conservation and 3910 others). Before testing, we tried to use CPLEX to directly solve the problem, but a feasible solution could not be found after 1 day. We then employed the solution algorithm to solve the problem. Given that the proposed solution algorithm is primarily solved based on a problem decomposition method, the important issue is how many sub-problems the original problem should be divided into to ensure the greatest efficiency. To find a suitable number of sub-problems in the solution, we tried different numbers of retailers. Table 3 shows the computational results where the original problem is divided into different numbers of sub-problems. Five cases are examined, comprising 25, 10, 5, 2 and 1 sub-problem(s), respectively with 2, 5, 10, 25, and 50 retailers contained in each sub-problem, respectively. As can be seen in Table 3, an optimal solution cannot be found if the number of retailers in each sub-problem exceeds ten (i.e., the number of sub-problems is less than 5). The total cost is always NT$202,778.50 when the number of retailers in each problem is less than ten. The computation times for solving the 25, 10, and 5 sub-problems are 1.37, 12.54 and 2274.65 s, respectively. Therefore, in subsequent tests, the number of retailers per sub-problem is set to be two.

Table 3 Test results for different numbers of sub-problems divided by the original problem
Full size table

Table 4 shows the test results in detail for all kinds of costs as solved by the proposed solution algorithm. It should be noted that the stock-out cost and the retailer collection cost are both zero. The results show that the proposed model and solution algorithm are both efficient and effective. Table 5 shows the statistical test results. The number of replenishments per retailer will be either three or four. The average replenishment quantity for each retailer is between 28 and 65 equivalent units of goods, based on each retailer’s demand. The average value of the upper inventory level for each retailer is between 38 and 125 units, the average value of the lower inventory level is between 4 and 25 units and the average amount of inventory in stock for each retailer is between 23 and 61 units. In addition, the average difference between the replenishment quantity and the value of the upper inventory level for each replenishment is 15.1 equivalent units. Figure 3 shows a chart of the trend of the test results based on the statistical results in Table 5. There is a positive correlation between the relationship among average replenishment, upper inventory level and demand. There is also a trend towards a positive correlation between the average demand and inventory for stock in most retailers. Demand is satisfied by the quantity of supply or the quantity of inventory in stock or both. Therefore, if the average amount of inventory in stock is larger than average amount supplied by the supplier, the relationship between average demand and average amount of inventory in stock is obviously positive.

Table 4 Test results for all kinds of costs (NT$)
Full size table
Table 5 Statistical test results (equivalent units)
Full size table
Fig. 3
figure 3

Test results in trend chart

Full size image

4.3 Sensitivity Analysis

To examine the effect of some essential parameters on the model solution, we perform some sensitivity analyses varying the demand for the retailers, the ratio of holding cost per equivalent unit of goods for the supplier and the retailer, and the amount of safety stock. We also examine the effect obtained by setting the same values for the upper/lower inventory levels for each retailer in the planning period. Sensitivity analyses of other parameters can be similarly performed in the future but are not addressed here to save space. All the tests are carried out using the proposed solution algorithm.

4.3.1 Retail Demand

We evaluate the influence of the retail demand by testing five cases, changes in demand of 80%, 90%, 100%, 110% and 120% of the original demand. As shown in Table 6, the costs, including total cost, fixed cost, transportation costs and supplier holding/cycling cost, increase as the demand increases. The exceptions are for the retailer holding/cycling cost, stock-out cost and retailer collection cost. The results for the stock-out cost and retailer collection cost are the same for all five cases, all being zero. There is about a 10% change in the total cost, fixed cost, transportation cost and supplier holding/cycling cost with an increase in retailer demand of 10%. However, the percentage change in retailer holding/cycling cost seems to be unaffected by the increased demand, probably because the increase is consumed by the customer, so there is almost no increase in the carrying cost for the retailers. The results indicate that retail demand may not have a great influence on the solution in the proposed model. Note that the computation times for all demand scenarios are usually less than 2 s, meaning the proposed algorithm is efficient.

Table 6 Results for different retailer demands
Full size table

4.3.2 The Ratio Between Supplier and Retailer of the Holding/Cycling Cost per Equivalent Unit of Goods

We evaluate the influence of changes in the ratio of the holding cost per equivalent unit of goods between the supplier and the retailer by testing five cases, (1.0:0.8), (1.0:0.9), (1.0:1.0), (1.0:1.1) and (1.0:1.2). As shown in Table 7, the total cost increases as the ratio increases, because of an increase in the holding cost. However, the fixed cost and the transportation cost remain nearly the same regardless of how much the ratio changes. The results show that the fixed cost and the transportation cost are insensitive to the holding cost ratio. In particular, when the ratio decreases from (1.0:1.0) to (1.0:0.9), the retailer holding/cycling cost increases from 25,643.49 to 30,091.36 and the supplier holding/cycling cost simultaneously decreases from 76,229.15 to 67,527.66. The results indicate that it is better for the retailer to stock as many goods as possible when the supplier holding/cycling cost is greater than the retailer holding/cycling cost. On the other hand, when the ratio increases from (1.0:1.0) to (1.0:1.1), the supplier holding/cycling cost increases from 76,229.15 to 82,507.54 and the retailer holding/cycling cost decreases from 25,643.49 to 20,300.46. This indicates that as many goods as possible should be stocked at the supplier warehouse because the retailer holding/cycling cost is greater than the supplier holding/cycling cost. However, when the ratio increases from (1.0:1.1) to (1.0:1.2) or decreases from (1.0:0.9) to (1.0:0.8), the value of supplier holding/cycling cost remains the same, showing that the distribution of goods between the supplier warehouse and the retailer’s stock is in the optimal configuration. Note that the computation times for all cost scenarios are usually less than 5 s.

Table 7 Results for different ratios of the holding cost per equivalent unit of goods between supplier and retailer
Full size table

It should be mentioned that the purpose of this sensitivity analysis is only to observe the difference in solutions resulting from changing the ratio between supplier and retailers of the holding/cycling cost per equivalent unit of goods (via a small change of holding cost at the retailers), so that planners can adjust the holding/cycling cost at the supplier and the retailers. For retailers in Taiwan, who have restrictions on the number of vehicles and drivers in practice, delivery frequency is limited to one trip a day with a lead time of zero, except for special holidays (i.e., such as the Chinese New Year). As a result, the fixed cost and the transportation cost are insensitive to the holding cost ratio. If the proposed model is extended in the future to consider non-zero lead time and/or multiple delivery times per day, it would be interesting to examine how the delivery frequency changes as the holding cost rate varies under deterministic demand scenario.

4.3.3 The Values of the Upper/Lower Inventory Level Are Kept the Same for Each Retailer in the Planning Period

In this section, we evaluate the performance of the proposed model using a new scenario, in which the values of the upper/lower inventory levels are kept the same for each retailer throughout the planning period. In this new scenario, the modified model (NM) is created by adding the four constraints to the original model (OM). The additional four constraints are formulated as follows:

$$ {y}_{\left(j-1\right)j}^u={y}_{j\left(j+1\right)}^u,\kern0.5em \forall \left(j-1\right)j\in RH $$
(20)
$$ {y}_{\left(j+5\right)\left(j+6\right)}^u={y}_{\left(j+6\right)j}^u,\kern0.5em \forall \left(j-1\right)j\in RH,\kern0.5em \forall \left(j+6\right)j\in RC $$
(21)
$$ {y}_{\left(j-1\right)j}^l={y}_{j\left(j+1\right)}^l,\kern0.5em \forall \left(j-1\right)j\in RH $$
(22)
$$ {y}_{\left(j+5\right)\left(j+6\right)}^l={y}_{\left(j+6\right)j}^l,\kern0.5em \forall \left(j-1\right)j\in RH,\kern0.5em \forall \left(j+6\right)j\in RC $$
(23)

Equations (20), (21), (22) and (23) denote the same upper/lower inventory level values for each retailer in the planning period.

The test results are shown in Tables 8 and 9. Table 8 shows the various cost items for the OM and the NM. In addition, Table 9 further shows the detailed upper/lower inventory levels per equivalent unit of goods for each retailer for the NM. As can be seen in Table 8, the value of the total cost obtained with the NM is greater than for the OM. Further analysis of the results shows that with the NM, the fixed cost remains constant compared with the one for the OM while there are slight changes in the values of the transportation cost, the supplier holding/cycling cost and the retailer holding/cycling cost. Furthermore, the transportation cost obtained with the NM is greater than for the OM because of a significant increase in the number of goods transported from the supplier to the retailers, based on the additional four equations. Thus, the retailer holding/cycling cost for the NM is also greater than for the OM. In particular, the stock-out cost and the retailer collection cost obtained with the NM are non-zero, showing that setting uniform values to upper/lower inventory levels will lead to running out of stock or overstocking situations for the retailer. In other words, setting uniform values of upper/lower inventory levels based on the average values over a period of time as performed in past distribution logistics records, will most likely result in a loss caused by running out of stock or overstocking at the retailers. The results indicate the values of the upper/lower inventory levels have a significant influence on the solution and a setting of different upper/lower inventory levels would be more flexible for the supplier and the retailers to manage the stock and the replenishment planning of goods.

Table 8 Results for the same value of the upper/lower inventory levels for each retailer in the planning period
Full size table
Table 9 Test results for different values of the upper/lower inventory levels
Full size table

5 Conclusions

In this study, network flow techniques are employed to develop a replenishment planning model. The objective is to minimize the total short-term cost for replenishment planning by controlling the upper and lower inventory levels. The model can be used to efficiently and effectively decide on the optimal upper-and-lower inventory levels for the planner. Mathematically, this model is formulated as an integer network flow problem with side constraints, which is characterized as NP-hard. Since it is almost impossible to optimally solve the realistic large-scale problems that occur in practice within a limited period of time, we also develop a solution algorithm, based on a problem decomposition technique, which, with the assistance of the mathematical problem solver, CPLEX, can efficiently and effectively solve the problem. To deal with the replenishment schedule coupled with the upper-and-lower inventory levels for all retailers, in this study we not only design a time-space network to formulate the movement of goods between the supplier and all retailers for replenishment planning, but also define the upper-and-lower inventory level control variables (\( {y}_{\left(j-1\right)j}^u/{y}_{\left(j+1\right)j}^u \), \( {y}_{\left(j-1\right)j}^l/{y}_{\left(j+1\right)j}^l \), αj) and related constraints (Eqs. (3)–(13)), based on the problem characteristics. Although the designed time-space network is similar in structure to those discussed in the literature (e.g., Yan and Chen 2002; Yan and Shih 2009; Yan et al. 2014; Yan et al. 2016; Yan et al. 2017;), it differs from previous ones in that it is specifically designed for replenishment scheduling. The upper-and-lower inventory level control variables and related constraints are novel and can be used to formulate practical operational problems. The model is thus able to determine the optimal replenishment schedule and the upper-and-lower inventory levels at every retailer without any lead time.

To test the applicability of model and the solution algorithm in actual operations, a case study based on operating data from a major retail company in northern Taiwan is performed. The case study includes one supplier, a distribution center, and 50 retail stores for replenishment planning. Three sensitivity analyses of essential model parameters are also performed to examine their influence on the solution. The size of the test problem is large, including 1810 integer variables, 350 binary variables and 4269 constraints (359 for flow conservation and 3910 for others). However, it took less than 1 min to complete the solution process for the ten instances. Results indicate that the value of the upper/lower inventory levels for each retailer in the planning period have a significant influence on the solution in the proposed model. The results also show that the proposed model and solution algorithm are both efficient and effective enough to be used in practice and could therefore be useful for both practitioners and researchers.

The main contributions of the paper include the following: 1) we present a novel model for replenishment planning to deal with the upper-and-lower inventory level control problem for retailers in Taiwan; 2) according to the problem characteristics we develop an efficient and effective algorithm, based on a problem decomposition technique, to optimally solve the model; and 3) we conduct numerical tests using real data from a retail company in Taiwan to demonstrate the potential usefulness of the proposed model and solution algorithm in practice. Finally, it should be noted that the proposed solution algorithm may not be able to find an optimal solution if applied to problems where the supplier does not have sufficient inventory to meet all demands during the replenishment planning period. How to evaluate the solution quality and find ways to further improve the solution algorithm can be examined in the future. For ease of modeling we adopt the average demand calculated based on the past distribution logistics records for each retailer in the proposed model. However, the average demand for each retailer can be influenced by many factors and could therefore be stochastic. Hence, how to incorporate stochastic demand for each retailer into the replenishment planning model, to make the upper/lower inventory levels and the replenishment planning more reliable, can be researched in the future.