Appendix
1.1 Local Transformation
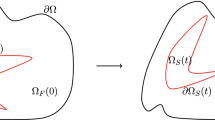
In the proof of Theorem 1.1, since fluid domains of the strong and the weak solution are a priori different, we transform the problem into a common domain. We use the transformation presented in [7] to transform a strong solution to the domain of a weak solution, which is a moving domain, in a way that preserves the divergence-free condition. It is defined by a transformation to a fixed domain as in [36] or [17], which we also need for the construction of regularization. Even though this transformation is by now standard in the literature, here we briefly describe this transformation and recall its main properties for the convenience of the reader and to establish the notation that is used throughout the paper.
According to [17, 36] we can define a transformation \(\mathbf{X }(t):\Omega \rightarrow \Omega \) as the unique solution of the system
$$\begin{aligned} \frac{d}{dt}\mathbf{X }(t,\mathbf{y })=\Lambda (t,\mathbf{X }(t,\mathbf{y })), \qquad \mathbf{X }(0,\mathbf{y })=\mathbf{y }, \qquad \forall \ \mathbf{y }\in \Omega . \end{aligned}$$
where the velocity of change of coordinates \(\Lambda (t,\mathbf{x })\) is a vector field that is smooth in the space variables and divergence-free, and satisfies \(\Lambda =\mathbf{a }(t)+{\varvec{\omega }}(t)\times (\mathbf{x }-\mathbf{q }(t))\) in a neighborhood of S(t) and \(\Lambda =0\) in a neighborhood of \(\partial \Omega \).
Note that the function \(\Lambda \) is a divergence-free extension of the function \(S(t)\ni \mathbf{x }\mapsto \mathbf{a }(t)+{\varvec{\omega }}(t)\times (\mathbf{x }-\mathbf{q }(t))\) to the set \(\Omega \). The construction of the extension \(\Lambda \) is given in [17, Sect. 3] with little correction to the cut-off function \(\chi \), where instead of balls \(\overline{S(t)}\subset B_1\subset B_2\), we choose open sets \(K_1,K_2\) such that \(\overline{S(t)}\subset K_1\subset K_2\subset \Omega \).
We denote
$$\begin{aligned} \Lambda =:\text {Ext}(\mathbf{a }+{\varvec{\omega }}\times (\mathbf{x }-\mathbf{q })). \end{aligned}$$
Here, we assume that \(\mathbf{a }, {\varvec{\omega }}\in L^{\infty }(0,T)\), which is slightly different from assumptions in [17, 36]. Therefore, for existence and uniqueness of solution \(\mathbf{X }\) we need Carathéodory’s theorem (see e.g. [30], Theorem 1.45) instead of the Picard-Lindelöf theorem.
For all \(t\in [0,T]\), the defined transformation \(\mathbf{X }(t)\) is a \(C^{\infty }\) diffeomorphism and the derivatives
$$\begin{aligned} \frac{\partial ^{|\alpha |+i}\mathbf{X }}{\partial t^{i}\partial \mathbf{y }^{\alpha }},\qquad i=0,1\ ,\quad \alpha \in {{\mathbb {N}}}_0^3, \end{aligned}$$
(A.1)
exist and are bounded.
We denote by \(\mathbf{Y }\) the inverse of \(\mathbf{X }\), i.e.
$$\begin{aligned} \mathbf{Y }(t,\cdot )=\mathbf{X }(t,\cdot )^{-1}. \end{aligned}$$
It satisfies the system of differential equations
$$\begin{aligned} \frac{d}{dt}\mathbf{Y }(t,\mathbf{x })=\Lambda ^{(\mathbf{Y })} (t,\mathbf{Y }(t,\mathbf{x })), \qquad \mathbf{Y }(0,\mathbf{x })=\mathbf{x }, \qquad \forall \ \mathbf{x }\in \Omega , \end{aligned}$$
where
$$\begin{aligned} \Lambda ^{(\mathbf {Y })} (t,\mathbf {y }) = -\nabla {\mathbf {X }}(t,\mathbf {y })^{-1}\Lambda (t,\mathbf {X }(t,\mathbf {y })) . \end{aligned}$$
Note that \(\mathbf{Y }\) possesses the same space and time regularity as \(\mathbf{X }\). Furthermore, \(\mathbf{X }\) and \(\mathbf{Y }\) satisfy
$$\begin{aligned} \nabla {\mathbf{X }}(t,\mathbf{y })\nabla {\mathbf{Y }}(t,\mathbf{X }(t,\mathbf{y })) = \text {id} \end{aligned}$$
and are volume-preserving, i.e.
$$\begin{aligned} \det \nabla {\mathbf{X }}(t,\mathbf{y }) = \det \nabla {\mathbf{Y }}(t,\mathbf{x }) = 1, \end{aligned}$$
(A.2)
since \(\mathop {\mathrm{div}}\nolimits \Lambda = 0\).
Then, by Proposition 2.4. in [23], the transformation of the velocity
$$\begin{aligned} \mathbf{U }(t,\mathbf{y }) =\nabla {\mathbf{Y }}(t,\mathbf{X }(t,\mathbf{y }))\mathbf{u }(t,\mathbf{X }(t,\mathbf{y })) \end{aligned}$$
preserves the divergence, i.e.
$$\begin{aligned} \mathop {\mathrm{div}}\nolimits _{\mathbf{y }}\mathbf{U }(t,\mathbf{y }) =\mathop {\mathrm{div}}\nolimits _{\mathbf{x }}\mathbf{u }(t,\mathbf{X }(t,\mathbf{y })), \qquad \forall (t,\mathbf{y })\in \Omega _{F}. \end{aligned}$$
Now, by substituting the transformed solution
$$\begin{aligned} \left\{ \begin{array}{l} \mathbf{U }(t,\mathbf{y })=\nabla {\mathbf{Y }}(t,{\mathbf{X }}(t,\mathbf{y }))\mathbf{u }(t,{\mathbf{X }}(t,\mathbf{y })), \\ P(t,\mathbf{y })=p(t,{\mathbf{X }}(t,\mathbf{y })), \\ \mathbf{A }(t)={{\mathbb {Q}}}^{T}(t)\mathbf{a }(t), \\ {\varvec{\Omega }}(t)={{\mathbb {Q}}}^{T}(t){\varvec{\omega }}(t), \\ {\mathcal {T}}({\mathbf{U }}(t,\mathbf{y }),P(t,\mathbf{y }))={{\mathbb {Q}}}^{T}(t) {{\mathbb {T}}}({{\mathbb {Q}}}(t)\mathbf{U }(t,\mathbf{y }),P(t,\mathbf{y })){{\mathbb {Q}}}(t) \end{array} \right. \end{aligned}$$
in the system of equations (1.12), we get (see [17] or [7])
$$\begin{aligned} \left. \begin{array}{l} \partial _{t}\mathbf{U }+(\mathbf{U }\cdot \nabla )\mathbf{U }-\triangle \mathbf{U }+\nabla P = F, \\ \mathop {\mathrm{div}}\nolimits \mathbf{U }= 0 \end{array} \right\} \;\text {in}\;(0,T)\times \Omega _{F}, \end{aligned}$$
(A.3)
$$\begin{aligned} \mathbf{A }^{\prime }&=-{\varvec{\Omega }}\times \mathbf{A }-\int _{\partial S_{0}}{\mathcal {T}}(\mathbf{U },P)\mathbf{N }\,\mathrm{d}\gamma (\mathbf{y })\qquad \text {in}\;(0,T), \end{aligned}$$
(A.4)
$$\begin{aligned} (I{\varvec{\Omega }})^{\prime }&={\varvec{\Omega }}\times (I{\varvec{\Omega }}) -\int _{\partial S_{0}} ( \mathbf{y }-\mathbf{q }(t))\times {{\mathcal {T}}}(\mathbf{U },P)\mathbf{N }\,\mathrm{d}\gamma (\mathbf{y }) \quad \text {in} \;(0,T), \end{aligned}$$
(A.5)
$$\begin{aligned} \mathbf{U }&= \mathbf{U }_{s}\qquad \text {on}\;(0,T)\times \partial S_0, \qquad \quad \mathbf{U }= 0\qquad \text {on}\;(0,T)\times \partial \Omega , \end{aligned}$$
(A.6)
where \( \mathbf{U }_s = {\varvec{\Omega }}\times \mathbf{y }+ \mathbf{A }\) is the transformed rigid velocity \(\mathbf{u }_s\), \(\mathbf{N }=\mathbf{N }(\mathbf{y })\) is the unit normal at \(\mathbf{y }\in S_0\), directed inside of \(S_0\), \(I={{{\mathbb {Q}}}}^{T}{{\mathbb {J}}}{{{\mathbb {Q}}}}\) is the transformed inertia tensor which no longer depends on time, and
$$\begin{aligned} F = ({\mathcal {L}}-\triangle )\mathbf {U }-{\mathcal {M}}\mathbf {U }-\widetilde{{\mathcal {N}}}\mathbf {U }-({\mathcal {G}}-\nabla )P. \end{aligned}$$
The operator \({\mathcal {L}}\) is the transformed Laplace operator and it is given by
$$\begin{aligned} ({\mathcal {L}}\mathbf{u })_{i}&=\sum _{j,k=1}^{n}\partial _{j}(g^{jk}\partial _k \mathbf{u }_{i})+2\sum _{j,k,l=1}^{n}g^{kl}\Gamma _{jk}^{i}\partial _{l}\mathbf{u }_{j} \nonumber \\&\quad +\sum _{j,k,l=1}^{n}\big (\partial _{k}(g^{kl}\Gamma _{jl}^{i})+\sum _{m=1}^{n}g^{kl}\Gamma _{jl}^{m}\Gamma _{km}^{i}\Big )\mathbf{u} _{j}, \end{aligned}$$
(A.7)
the convection term is transformed into
$$\begin{aligned} ({\mathcal {N}}\mathbf {u })_i = \sum _{j=1}^n \mathbf {u }_j \partial _j \mathbf {u } _i + \sum _{j,k=1}^n \Gamma ^i_{jk} \mathbf {u }_j\mathbf {u }_k = (\mathbf {u }\cdot \nabla \mathbf {u })_i + (\widetilde{{\mathcal {N}}}\mathbf {u })_i, \end{aligned}$$
(A.8)
the transformation of time derivative and gradient is given by
$$\begin{aligned} ({\mathcal {M}} \mathbf{u })_{i} = \sum _{j=1}^n \dot{\mathbf{Y }}_j \partial _j \mathbf{u }_i + \sum _{j,k=1}^n \Big (\Gamma _{jk}^i \dot{\mathbf{Y }}_k + (\partial _k \mathbf{Y }_i)(\partial _j \dot{\mathbf{X }}_k)\Big )\mathbf{u }_j, \end{aligned}$$
(A.9)
and the gradient of pressure is transformed as follows:
$$\begin{aligned} ({\mathcal {G}}p)_{i}=\sum _{j=1}^{n}g^{ij}\partial _{j}p. \end{aligned}$$
(A.10)
Here we have denoted the metric covariant tensor
$$\begin{aligned} g_{ij}=X_{k,i}X_{k,j},\qquad X_{k,i}=\frac{\partial \mathbf{X }_{k}}{\partial \mathbf{y }_{i}}, \end{aligned}$$
(A.11)
the metric covariant tensor
$$\begin{aligned} g^{ij}=Y_{i,k}Y_{j,k}\qquad Y_{i,k}=\frac{\partial \mathbf{Y }_{i}}{\partial \mathbf{x }_{k}}, \end{aligned}$$
(A.12)
and the Christoffel symbol (of the second kind)
$$\begin{aligned} \Gamma _{ij}^{k}=\frac{1}{2}g^{kl}(g_{il,j}+g_{jl,i}-g_{ij,l}),\qquad g_{il,j}=\frac{\partial {g_{il}}}{\partial \mathbf{y }_{j}}. \end{aligned}$$
(A.13)
It is easy to observe that, in particular, the following holds:
$$\begin{aligned} \Gamma _{ij}^{k}=Y_{k,l}X_{l,ij}.\qquad X_{l,ij}=\frac{\partial \mathbf{X }_{l}}{ \partial \mathbf{y }_{i}\partial \mathbf{y }_{j}}. \end{aligned}$$
With little abuse of notation, we identify the operators \({\mathcal {L}},{\mathcal {M}}, \widetilde{{\mathcal {N}}}\) with
$$\begin{aligned}&\left\langle {\mathcal {L}}\mathbf{U }, {\varvec{\psi }}\right\rangle =\int _{\Omega _F(\tau )} \big (\sum _{ijk} (g^{jk}\partial _j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_i + g^{jk}\partial _k\mathbf{U }_i\partial _i{\varvec{\psi }}_j) - \sum _{ijkl} (g^{kl}+\partial _l\mathbf{Y }_k)\Gamma _{li}^j\partial _k\mathbf{U }_{i}{\varvec{\psi }}_j\nonumber \\&\quad + \sum _{ijkl} (g^{kl}\Gamma _{li}^j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_j + g^{jl}\Gamma _{li}^k\mathbf{U }_i\partial _k{\varvec{\psi }}_j) - \sum _{ijklm} (g^{kl}+\partial _k\mathbf{Y }_l)\Gamma _{li}^m\Gamma _{km}^j\mathbf{U }_{i}{\varvec{\psi }}_j \big ), \end{aligned}$$
(A.14)
$$\begin{aligned}&\left\langle {\mathcal {M}}\mathbf{U }, {\varvec{\psi }}\right\rangle = \int _{\Omega _F(\tau )}\sum _{i=1}^n\left( \sum _{j=1}^n \dot{\mathbf{Y }}_j \partial _j \mathbf{u }_i + \sum _{j,k=1}^n \Big (\Gamma _{jk}^i \dot{\mathbf{Y }}_k + (\partial _k \mathbf{Y }_i)(\partial _j \dot{\mathbf{X }}_k)\Big )\mathbf{u }_j\right) {\varvec{\psi }}_i, \end{aligned}$$
(A.15)
$$\begin{aligned}&\left\langle \widetilde{{\mathcal {N}}}\mathbf {U }, {\varvec{\psi }}\right\rangle = \int _{\Omega _F(\tau )} \sum _{i,j,k=1}^n \Gamma ^i_{jk} \mathbf {u }_j\mathbf {u }_k {\varvec{\psi }}_i, \end{aligned}$$
(A.16)
for all \({\varvec{\psi }}\in H^{1}(\Omega _{F}(t))\).
1.2 Reynolds Transport Theorem—Generalization
To prove the weak-strong uniqueness result and the energy equality, we want to cancel the derivation terms from the weak formulations. In the case of smooth functions \(\mathbf{u }\) and \(\mathbf{v }\), by the Reynolds Transport Theorem we have
$$\begin{aligned} \int _{0}^{t}\int _{{\Omega (\tau )}}\big (\mathbf{u }\cdot \partial _t\mathbf{v }+ \mathbf{v }\cdot \partial _t\mathbf{u }\big ) = -\int _{0}^{t}\int _{{\Omega (\tau )}} \nabla (\mathbf{v }\cdot \mathbf{u })\cdot \partial _t\mathbf{X }\, + \int _{{\Omega (t)}}\mathbf{v }(t)\cdot \mathbf{u }(t)\, - \int _{{\Omega (0)}}\mathbf{v }(0)\cdot \mathbf{u }(0). \end{aligned}$$
However, \(\mathbf{u }\) and \(\mathbf{v }\) are not regular enough, and the expression on the left is not well defined. But we can use Lemma 2.4, which states that for \(\mathbf{u }, \mathbf{v }\in {L}^{2}(0,T;{H}^1(\Omega (t)))\) and a coordinate transformation \(\mathbf{X }:\Omega \rightarrow \Omega (t)\), we have
$$\begin{aligned}&\int _{0}^{t}\int _{\Omega (\tau )}\big (\mathbf{u }\cdot \partial _t\mathbf{v }^h + \mathbf{v }\cdot \partial _t\mathbf{u }^h\big )\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \nonumber \\&\quad \rightarrow -\int _{0}^{t}\int _{\Omega (\tau )} \nabla (\mathbf{v }\cdot \mathbf{u })\cdot \partial _t\mathbf{X }\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau + \int _{\Omega (t)}\mathbf{v }(t)\cdot \mathbf{u }(t)\,\mathrm{d}\mathbf{x }\, - \int _{\Omega (0)}\mathbf{v }(0)\cdot \mathbf{u }(0)\,\mathrm{d}\mathbf{x }, \end{aligned}$$
(A.17)
when \(h\rightarrow 0\), for almost every \(t\in [0,T]\). Here \(\mathbf{u }^h\) denotes the regularization of \(\mathbf{u }\) described by (2.16)–(2.18).
Remark A.1
If the domain is fixed, the coordinate transformation \(\mathbf{X }\) is not necessary (\(\mathbf{X }=id\)) and the regularization is standard (convolution in time). Then, by Fubini’s theorem and the properties of the mollifier, we get
$$\begin{aligned} \int _{0}^{t}\int _{\Omega }&\mathbf{u }(\tau )\cdot \partial _t\mathbf{v }^h(\tau )\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau = \int _{0}^{t}\int _{\Omega }\int _{-\infty }^{+\infty } \mathbf{u }(\tau )\cdot \frac{d}{d\tau } j_h(\tau -s)\mathbf{v }(s)\,\, \mathrm{d}s \, \mathrm{d}\mathbf{x }\, \mathrm{d}\tau \nonumber \\ =&\int _{-\infty }^{+\infty }\int _{\Omega }\int _{0}^{t} \frac{d}{d\tau }j_h(\tau -s)\mathbf{u }(\tau )\cdot \mathbf{v }(s)\,\, \mathrm{d}\tau \, \mathrm{d}\mathbf{x }\, \mathrm{d}s \nonumber \\ =&-\int _{0}^{t}\int _{\Omega }\int _{-\infty }^{+\infty } \frac{d}{ds} j_h(s-\tau )\mathbf{u }(\tau )\cdot \mathbf{v }(s)\,\, \mathrm{d}\tau \, \mathrm{d}\mathbf{x }\, \mathrm{d}s \end{aligned}$$
(A.18)
$$\begin{aligned}&{ - \int _{-\infty }^{0}\int _{0}^{t}\int _{\Omega } \mathbf{u }(\tau )\cdot \frac{d}{d\tau }j_h(\tau -s)\mathbf{v }(s)\,\, \mathrm{d}\tau \, \mathrm{d}\mathbf{x }\, \mathrm{d}s } \end{aligned}$$
(A.19)
$$\begin{aligned}&{ - \int _{t}^{+\infty }\int _{0}^{t}\int _{\Omega } \mathbf{u }(\tau )\cdot \frac{d}{d\tau }j_h(\tau -s)\mathbf{v }(s)\,\, \mathrm{d}\tau \, \mathrm{d}\mathbf{x }\, \mathrm{d}s } \end{aligned}$$
(A.20)
$$\begin{aligned}&{ + \int _{0}^{t}\int _{-\infty }^{0}\int _{\Omega } \mathbf{u }(\tau )\cdot \frac{d}{d\tau }j_h(\tau -s)\mathbf{v }(s)\,\, \mathrm{d}\tau \, \mathrm{d}\mathbf{x }\, \mathrm{d}s } \end{aligned}$$
(A.21)
$$\begin{aligned}&{ + \int _{0}^{t}\int _{t}^{+\infty }\int _{\Omega } \mathbf{u }(\tau )\cdot \frac{d}{d\tau }j_h(\tau -s)\mathbf{v }(s)\,\, \mathrm{d}\tau \, \mathrm{d}\mathbf{x }\, \mathrm{d}s } \end{aligned}$$
(A.22)
We see that
$$\begin{aligned} \mathrm{(A.18)} = -\int _{0}^{t}d\tau \int _{\Omega }\partial _t\mathbf{u }^h(\tau )\cdot \mathbf{v }(\tau )\,\,\mathrm{d}\mathbf{x }\end{aligned}$$
and it is easy to prove, by using the Lebesgue differentiation theorem, that
$$\begin{aligned} {\mathrm{(A.19)} + \mathrm{(A.20)} + \mathrm{(A.21)} + \mathrm{(A.22)} } \rightarrow \int _{\Omega }\mathbf{u }(t)\cdot \mathbf{v }(t)\,\,\mathrm{d}\mathbf{x }- \int _{\Omega }\mathbf{u }(0)\cdot \mathbf{v }(0)\,\,\mathrm{d}\mathbf{x }, \qquad h\rightarrow 0, \end{aligned}$$
which ends the proof. In the case of a moving domain the idea of the proof is the same, but the calculation is more complicated because of the changes of variables in the definition of the regularization and before applying Fubini’s theorem.
First we introduce one auxiliary result.
Lemma A.1
Let \(\mathbf{u },\mathbf{v }\) and \(\mathbf{X }\) be as in Lemma 2.4, and let \(\mathbf{Y }\) be the inverse transformation \(\mathbf{Y }(t,\cdot )=\mathbf{X }(t,\cdot )^{-1}\). Then,
$$\begin{aligned} \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }\cdot \partial _t \mathbf{u }^h \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau -\int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }\cdot \partial _t\mathbf{U }_h \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \,\rightarrow \, 0, \qquad h\rightarrow 0, \end{aligned}$$
where
$$\begin{aligned} \mathbf{U }_h(t,\mathbf{x }) = \nabla \mathbf{Y }(t,\mathbf{x })^T \int _{-\infty }^{+\infty } j_h(t-\tau )\nabla \mathbf{X }(\tau ,\mathbf{Y }(t,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(t,\mathbf{x })){\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(t,\mathbf{x })) \,\,\mathrm{d}\tau . \end{aligned}$$
Proof
Since
$$\begin{aligned} \int _{0}^{t}&\int _{\Omega (\tau )} \mathbf{v }\cdot \partial _t\mathbf{u }^h \\&= \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau }\Big ( \int _{-\infty }^{+\infty } j_h(\tau -s) \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\, {\bar{\mathbf{u }}}(s,\mathbf{Y }(\tau ,\mathbf{x })) \,\,\mathrm{d}s \Big ) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \\&= \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau }\Big ( \nabla \mathbf{Y }(\tau ,\mathbf{x })^T \\&\qquad \qquad \int _{-\infty }^{+\infty } j_h(\tau -s)\nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))^T\nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x })){\bar{\mathbf{u }}}(s,\mathbf{Y }(\tau ,\mathbf{x })) \,\,\mathrm{d}s \Big ) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau , \end{aligned}$$
it follows
$$\begin{aligned} \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }\cdot \partial _t \mathbf{u }^h \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau -\int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }\cdot \partial _t\mathbf{U }_h \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau = \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{v }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau } f_h(\tau ,\mathbf{x }) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau , \end{aligned}$$
where
$$\begin{aligned} f_h(\tau ,\mathbf{x })= & {} \nabla \mathbf{Y }(\tau ,\mathbf{x })^T \int _{-\infty }^{+\infty } j_h(\tau -s)\\&\big (\nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))^T\nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x })) - \nabla \mathbf{X }(s,\mathbf{Y }(\tau ,\mathbf{x }))^T\nabla \mathbf{X }(s,\mathbf{Y }(\tau ,\mathbf{x }))\big )\\&{\bar{\mathbf{u }}}(s,\mathbf{Y }(\tau ,\mathbf{x })) \,\mathrm{d}s. \end{aligned}$$
Since \(f_h\rightarrow 0\) strongly in \(\mathbf{L }^2 \mathbf{L }^2\) and the derivatives \(\frac{d}{d\tau }f_h\) are bounded in \(\mathbf{L }^2 \mathbf{L }^2\), it follows that \(\frac{d}{d\tau }f_h\rightarrow 0\) weakly in \(\mathbf{L }^2 \mathbf{L }^2\), so the above expression tends to 0 when \(h\rightarrow 0\). \(\square \)
Now we are able to prove Lemma 2.4.
Proof of Lemma 2.4
As in the fixed domain case, we start with the first term on the left-hand side of (2.19):
$$\begin{aligned} \int _{0}^{t}\int _{\Omega (\tau )}\mathbf{u }\cdot \partial _t\mathbf{v }^h&\,\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau = \int _{0}^{t}\int _{\Omega (\tau )}\mathbf{u }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau } \Big (\nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,{\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\Big )\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \nonumber \\&= \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau } \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,{\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x }) \,\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \end{aligned}$$
(A.23)
$$\begin{aligned}&\quad + \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,\partial _t{\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x })) \,\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \end{aligned}$$
(A.24)
$$\begin{aligned}&\quad + \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\nabla {\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,\partial _t \mathbf{Y }(\tau ,\mathbf{x }) \,\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \end{aligned}$$
(A.25)
The integral (A.24) contains the time derivative of the function \({\bar{\mathbf{v }}}^h\), so we need to combine it with the second term on the left-hand side of (2.19) before passing to the limit. First we change the coordinates. Then we can apply Fubini’s theorem, as follows.
$$\begin{aligned} \int _{0}^{t}\int _{\Omega (\tau )}&\mathbf{u }(\tau ,\mathbf{x })\cdot \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,\partial _t{\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x })) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \nonumber \\&= \int _{0}^{t}\int _{\Omega } \mathbf{u }(\tau ,\mathbf{X }(\tau ,\mathbf{y }))\cdot \nabla \mathbf{X }(\tau ,\mathbf{y })\,\partial _t{\bar{\mathbf{v }}}^h(\tau ,\mathbf{y }) \,\mathrm{d}\mathbf{y }\,\mathrm{d}\tau \nonumber \\&= \int _{0}^{t}\int _{\Omega }\int _{-\infty }^{+\infty } \frac{d}{d\tau }j_h(\tau -s) \nabla \mathbf{X }(\tau ,\mathbf{y }){\bar{\mathbf{u }}}(\tau ,\mathbf{y }) \cdot \nabla \mathbf{X }(\tau ,\mathbf{y }){\bar{\mathbf{v }}}(s,\mathbf{y }) \,\mathrm{d}s\,\mathrm{d}\mathbf{y }\,\mathrm{d}\tau \nonumber \\&= -\int _{-\infty }^{+\infty }\int _{\Omega } {\bar{\mathbf{v }}}(s,\mathbf{y })\cdot \int _{0}^{t} \frac{d}{ds}j_h(s-t) \nabla \mathbf{X }(t,\mathbf{y })^T \nabla \mathbf{X }(t,\mathbf{y }){\bar{\mathbf{u }}}(t,\mathbf{y }) \,\mathrm{d}\tau \,\mathrm{d}\mathbf{y }\, \mathrm{d}s \nonumber \\&= -\int _{0}^{t}\int _{\Omega } {\bar{\mathbf{v }}}(s,\mathbf{y })\cdot \int _{-\infty }^{+\infty } \frac{d}{ds}j_h(s-t) \nabla \mathbf{X }(t,\mathbf{y })^T \nabla \mathbf{X }(t,\mathbf{y }){\bar{\mathbf{u }}}(t,\mathbf{y }) \,\mathrm{d}\tau \,\mathrm{d}\mathbf{y }\, \mathrm{d}s \nonumber \\&\quad + \int _{\Omega (t)}\mathbf{v }(t,\mathbf{x })\cdot \mathbf{u }(t,\mathbf{x })\,\mathrm{d}\mathbf{x }- \int _{\Omega }\mathbf{v }(0,\mathbf{x })\cdot \mathbf{u }(0,\mathbf{x })\,\mathrm{d}\mathbf{x }+ o(h). \end{aligned}$$
(A.26)
The last two equalities are simple consequences of the properties of the mollifier and Lebesgue differentiation theorem (as in the fixed domain case). Next, we calculate (A.26):
$$\begin{aligned} (A.26)&= -\int _{0}^{t}\int _{\Omega (s)} {\bar{\mathbf{v }}}(s,\mathbf{Y }(s,\mathbf{x }))\cdot \int _{-\infty }^{+\infty } \frac{d}{ds}j_h(s-\tau ) \nonumber \\&\quad \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })) {\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\mathrm{d}\tau \,\mathrm{d}\mathbf{x }\, \mathrm{d}s \nonumber \\&\quad = -\int _{0}^{t}\int _{\Omega (s)} {\bar{\mathbf{v }}}(s,\mathbf{Y }(s,\mathbf{x }))\cdot \frac{d}{ds}\Big (\int _{-\infty }^{+\infty } j_h(s-\tau ) \end{aligned}$$
(A.27)
$$\begin{aligned}&\nabla \mathbf{X }(\tau ,Y(s,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })){\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\,\mathrm{d}\tau \Big )\,\mathrm{d}\mathbf{x }\, \mathrm{d}s \nonumber \\&\quad +\int _{0}^{t}\int _{\Omega (s)} {\bar{\mathbf{v }}}(s,\mathbf{Y }(s,\mathbf{x }))\cdot \int _{-\infty }^{+\infty } j_h(s-\tau )\frac{d}{ds}\big (\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T\big ) \end{aligned}$$
(A.28)
$$\begin{aligned}&\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })){\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\,\mathrm{d}\tau \,\mathrm{d}\mathbf{x }\, \mathrm{d}s \nonumber \\&\quad +\int _{0}^{t}\int _{\Omega (s)} {\bar{\mathbf{v }}}(s,\mathbf{Y }(s,\mathbf{x }))\cdot \int _{-\infty }^{+\infty } j_h(s-\tau ) \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T\nonumber \\&\quad \frac{d}{ds}\big (\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })) {\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x }))\big ) \,\,\mathrm{d}\tau \,\mathrm{d}\mathbf{x }\, \mathrm{d}s, \end{aligned}$$
(A.29)
and for (A.27) we get
$$\begin{aligned}&(A.27)\nonumber \\&\quad = -\int _{0}^{t}\int _{\Omega (s)} \mathbf{v }(s,\mathbf{x })\cdot \nabla \mathbf{Y }(s,\mathbf{x })^T \nonumber \\&\qquad \frac{d}{ds}\Big (\int _{-\infty }^{+\infty } j_h(s-\tau )\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })){\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\,\mathrm{d}\tau \Big )\,\mathrm{d}\mathbf{x }\, \mathrm{d}s\nonumber \\&\quad = -\int _{0}^{t}\int _{\Omega (s)} \mathbf{v }(s,\mathbf{x })\cdot \frac{d}{ds} \Big (\nabla \mathbf{Y }(s,\mathbf{x })^T \nonumber \\&\qquad \int _{-\infty }^{+\infty } j_h(s-\tau )\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })){\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\,\mathrm{d}\tau \Big )\,\mathrm{d}\mathbf{x }\, \mathrm{d}s \end{aligned}$$
(A.30)
$$\begin{aligned}&+ \int _{0}^{t}\int _{\Omega (s)} \mathbf{v }(s,\mathbf{x })\cdot \partial _s\nabla \mathbf{Y }(s,\mathbf{x })^T \nonumber \\&\qquad \int _{-\infty }^{+\infty } j_h(s-\tau )\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x })){\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\,\mathrm{d}\tau \,\mathrm{d}\mathbf{x }\, \mathrm{d}s \end{aligned}$$
(A.31)
Now we can let \(h\rightarrow 0\). By Lemma A.1, we have
$$\begin{aligned} \mathrm{(A.30)} + \int \int \mathbf{v }\cdot \partial _t\mathbf{u }^h \rightarrow 0. \end{aligned}$$
The remaining terms do not contain the time derivative of \({\bar{\mathbf{u }}}^h\) or \({\bar{\mathbf{v }}}^h\), so we can directly pass to the limits. Using the property of the transformation \(\mathbf{X }\)
$$\begin{aligned} 0&=\frac{d}{dt}\big ( \nabla \mathbf{X }(t,\mathbf{Y }(t,\mathbf{x }))\nabla \mathbf{Y }(t,\mathbf{x }) \big )\\&= \frac{d}{dt}\big (\nabla \mathbf{X }(t,\mathbf{Y }(t,\mathbf{x })) \big )\nabla \mathbf{Y }(t,\mathbf{x }) + \nabla \mathbf{X }(t,\mathbf{Y }(t,\mathbf{x }))\partial _t\nabla \mathbf{Y }(t,\mathbf{x }), \end{aligned}$$
we get
$$\begin{aligned} (A.23)&= \int _{0}^{t} \int _{\Omega (\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau } \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,{\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x })) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \\&\rightarrow \int _{0}^{t}\int _{\Omega (\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \frac{d}{d\tau } \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,{\bar{\mathbf{v }}}(\tau ,\mathbf{Y }(\tau ,\mathbf{x })) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \\&=-\int _{0}^{t}\int _{\Omega (\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\,\partial _t\nabla \mathbf{Y }(\tau ,\mathbf{x })\,\mathbf{v }(\tau ,\mathbf{Y }(\tau ,\mathbf{x })) \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau , \\ (A.31)&= \int _{0}^{t}\int _{\Omega (s)} \mathbf{v }(s,\mathbf{x })\cdot \partial _s\nabla \mathbf{Y }(s,\mathbf{x })^T \\&\qquad \qquad \int _{-\infty }^{+\infty } j_h(s-\tau )\nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))^T \nabla \mathbf{X }(\tau ,\mathbf{Y }(s,\mathbf{x }))\,{\bar{\mathbf{u }}}(\tau ,\mathbf{Y }(s,\mathbf{x })) \,\mathrm{d}\tau \,\mathrm{d}\mathbf{x }\, \mathrm{d}s \\&\rightarrow \int _{0}^{t}\int _{\Omega (s)} \mathbf{v }(s,\mathbf{x })\cdot \partial _s\nabla \mathbf{Y }(s,\mathbf{x })^T \\&\qquad \qquad \nabla \mathbf{X }(s,\mathbf{Y }(s,\mathbf{x }))^T \nabla \mathbf{X }(s,\mathbf{Y }(s,\mathbf{x }))\, {\bar{\mathbf{u }}}(s,\mathbf{Y }(s,\mathbf{x })) \,\mathrm{d}\mathbf{x }\, \mathrm{d}s \\&= \int _{0}^{t}\int _{\Omega (s)} \nabla \mathbf{X }(s,\mathbf{Y }(s,\mathbf{x })) \partial _s\nabla \mathbf{Y }(s,\mathbf{x })\,\mathbf{v }(s,\mathbf{x })\cdot \mathbf{u }(s,\mathbf{Y }(s,\mathbf{x })) \,\mathrm{d}\mathbf{x }\, \mathrm{d}s. \end{aligned}$$
It follows that
$$\begin{aligned} (A.23)+(A.31)\rightarrow 0, \qquad h\rightarrow 0. \end{aligned}$$
Again, using the properties of the transformation of coordinates we get
$$\begin{aligned}&(A.25)+(A.28) \rightarrow -\int _{0}^{t}\int _{\Omega (\tau )} \nabla \mathbf{v }^T\mathbf{u }\cdot \partial _t\mathbf{X }, \end{aligned}$$
(A.32)
$$\begin{aligned}&(A.29) \rightarrow -\int _{0}^{t}\int _{\Omega (\tau )} \nabla \mathbf{u }^T\mathbf{v }\cdot \partial _t\mathbf{X }. \end{aligned}$$
(A.33)
Hence,
$$\begin{aligned} \begin{aligned}&(A.23) + (A.25) + (A.28) + (A.29) + (A.31)\\&\qquad \rightarrow -\int _{0}^{t}\int _{\Omega _F(\tau )} (\nabla \mathbf{v }^T\mathbf{u }+\nabla \mathbf{u }^T\mathbf{v })\cdot \partial _t\mathbf{X }= -\int _{0}^{t}\int _{\Omega _F(\tau )} \nabla (\mathbf{u }\cdot \mathbf{v })\cdot \partial _t\mathbf{X }. \end{aligned} \end{aligned}$$
(A.34)
Finally, we conclude
$$\begin{aligned}&\int _{0}^{t}\int _{\Omega (\tau )}\mathbf{u }\cdot \partial _t\mathbf{v }^h\,\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau + \int _{0}^{t}\int _{\Omega (\tau )}\mathbf{v }\cdot \partial _t\mathbf{u }^h \,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \\&\qquad \qquad \rightarrow -\int _{0}^{t}\int _{\Omega (\tau )} \nabla (\mathbf{u }\cdot \mathbf{v })\cdot \partial _t\mathbf{X }\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau + \int _{\Omega (t)}\mathbf{v }(t)\cdot \mathbf{u }(t) \,\mathrm{d}\mathbf{x }- \int _{\Omega }\mathbf{v }(0)\cdot \mathbf{u }(0)\,\mathrm{d}\mathbf{x }. \end{aligned}$$
Let us show (A.32) and (A.33):
Since
$$\begin{aligned} \nabla {\bar{\mathbf{v }}}^h \rightarrow \nabla {\bar{\mathbf{v }}} \quad \text {when }h\rightarrow 0 \quad \text {u } L^2L^2, \end{aligned}$$
we have
$$\begin{aligned} (A.25)&= \int _0^t\int _{\Omega _F(\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\nabla {\bar{\mathbf{v }}}^h(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\partial _t\mathbf{Y }(\tau ,\mathbf{x })\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \\&\rightarrow \int _0^t\int _{\Omega _F(\tau )} \mathbf{u }(\tau ,\mathbf{x })\cdot \nabla \mathbf{X }(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\nabla {\bar{\mathbf{v }}}(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\partial _t\mathbf{Y }(\tau ,\mathbf{x })\,\mathrm{d}\mathbf{x }\,\mathrm{d}\tau \\&= \int _0^t\int _{\Omega _F(\tau )} \sum _{ijk}\mathbf{u }_i\partial _j\mathbf{X }_i\partial _k{\bar{\mathbf{v }}}\partial _t\mathbf{Y }_k = \int _0^t\int _{\Omega _F(\tau )} \sum _{ijk}\mathbf{u }_i\partial _j\mathbf{X }_i\frac{d}{d\mathbf{y }_k}(\nabla \mathbf{Y }\mathbf{v })_j\partial _t\mathbf{Y }_k \\&= \int _0^t\int _{\Omega _F(\tau )} \sum _{ijkl}\mathbf{u }_i\partial _j\mathbf{X }_i\frac{d}{d\mathbf{y }_k}(\partial _l\mathbf{Y }_j\mathbf{v }_l)\partial _t\mathbf{Y }_k \\&= \int _0^t\int _{\Omega _F(\tau )} \sum _{ijklm}\mathbf{u }_i\partial _j\mathbf{X }_i(\partial _m\partial _l\mathbf{Y }_j\mathbf{v }_l + \partial _l\mathbf{Y }_j\partial _m\mathbf{v }_l)\underbrace{\partial _k\mathbf{X }_m\partial _t\mathbf{Y }_k}_{(\nabla \mathbf{X }\partial _t\mathbf{Y })_{m}=-\partial _t\mathbf{X }_m} \\&= \int _0^t\int _{\Omega _F(\tau )}( \underbrace{\sum _{ijklm}\mathbf{u }_i\partial _j\mathbf{X }_i\partial _m\partial _l\mathbf{Y }_j\partial _k\mathbf{X }_m\partial _t\mathbf{Y }_k \mathbf{v }_l}_{I} - \underbrace{\sum _{ijlm}\mathbf{u }_i\partial _j\mathbf{X }_i\partial _l\mathbf{Y }_j\partial _t\mathbf{X }_m \partial _m\mathbf{v }_l}_{II}),\\ II&= \sum _{ijlm}\mathbf{u }_i \underbrace{\partial _j\mathbf{X }_i\partial _l\mathbf{Y }_j}_{\delta _{il}} \partial _t\mathbf{X }_m \partial _m\mathbf{v }_l = \sum _{im}\mathbf{u }_i\partial _t\mathbf{X }_m \partial _m\mathbf{v }_i = \nabla \mathbf{v }^T\mathbf{u }\cdot \partial _t\mathbf{X },\\ I&= \sum _{ijklm}\mathbf{u }_i\partial _j\mathbf{X }_i \underbrace{\partial _m\partial _l\mathbf{Y }_j\partial _k\mathbf{X }_m}_{\frac{d}{d\mathbf{y }_k}(\partial _l\mathbf{Y }_j)} \partial _t\mathbf{Y }_k \mathbf{v }_l = \sum _{ijkl}\mathbf{u }_i \underbrace{\partial _j\mathbf{X }_i\frac{d}{d\mathbf{y }_k}(\partial _l\mathbf{Y }_j)}_{= \frac{d}{d\mathbf{y }_k}(\partial _j\mathbf{X }_i\partial _l\mathbf{Y }_j)-\partial _k\partial _j\mathbf{X }_i\partial _l\mathbf{Y }_j} \partial _t\mathbf{Y }_k \mathbf{v }_l\\&= -\sum _{ijkl}\mathbf{u }_i \underline{\partial _k\partial _j\mathbf{X }_i}\partial _l\mathbf{Y }_j \underline{\partial _t\mathbf{Y }_k} \mathbf{v }_l =(*) = -\sum _{ijl}\mathbf{u }_i (\frac{d}{dt}(\nabla \mathbf{X })_{ij}-\partial _t(\nabla \mathbf{X })_{ij}) \partial _l\mathbf{Y }_j\mathbf{v }_l\\&= -\frac{d}{dt}\nabla \mathbf{X }^T\mathbf{u }\cdot \nabla \mathbf{Y }\mathbf{v }+ \partial _t\nabla \mathbf{X }^T\mathbf{u }\cdot \nabla \mathbf{Y }\mathbf{v }, \end{aligned}$$
$$\begin{aligned} (A.25)\rightarrow \int _{0}^{t}\int _{\Omega _F(\tau )}(-\frac{d}{dt}\nabla \mathbf{X }^T\mathbf{u }\cdot \nabla \mathbf{Y }\mathbf{v }+ \partial _t\nabla \mathbf{X }^T\mathbf{u }\cdot \nabla \mathbf{Y }\mathbf{v }- \nabla \mathbf{v }^T\mathbf{u }\cdot \partial _t\mathbf{X }), \end{aligned}$$
(A.35)
$$\begin{aligned} (A.28)&= \int _{0}^{t}\int _{\Omega _F(\tau )} \underbrace{{\bar{\mathbf{v }}}(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))}_{=\nabla \mathbf{Y }(\tau ,\mathbf{x })\mathbf{v }(\tau ,\mathbf{x })} \cdot \int _{-\infty }^{+\infty } j_h(\tau -s)\frac{d}{d\tau }\big (\nabla \mathbf{X }(s,\mathbf{Y }(\tau ,\mathbf{x }))^T\big ) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \nabla \mathbf{X }(s,\mathbf{Y }(\tau ,\mathbf{x })){\bar{\mathbf{u }}}(s,\mathbf{Y }(\tau ,\mathbf{x })) \,\,\mathrm{d}s\,\mathrm{d}\mathbf{x }\, \mathrm{d}\tau \\&= \int _{0}^{t}\int _{\Omega _F(\tau )}\int _{-\infty }^{+\infty } \sum _{ijkl} \mathbf{v }_i\partial _i\mathbf{Y }_j j_h(\tau -s)\frac{d}{d\tau }\partial _j\mathbf{X }_k(s,\mathbf{Y }(\tau ,\mathbf{x })) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \partial _l\mathbf{X }_k(s,\mathbf{Y }(\tau ,\mathbf{x })){\bar{\mathbf{u }}}_l(s,\mathbf{Y }(\tau ,\mathbf{x })) \,\,\mathrm{d}s\,\mathrm{d}\mathbf{x }\, \mathrm{d}\tau \\&= \int _{0}^{t}\int _{\Omega _F(\tau )}\int _{-\infty }^{+\infty } \sum _{ijklm} \mathbf{v }_i\partial _i\mathbf{Y }_j j_h(\tau -s)\partial _m\partial _j\mathbf{X }_k(s,\mathbf{Y }(\tau ,\mathbf{x }))\partial _t\mathbf{Y }_m \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \partial _l\mathbf{X }_k(s,\mathbf{Y }(\tau ,\mathbf{x })){\bar{\mathbf{u }}}_l(s,\mathbf{Y }(\tau ,\mathbf{x })) \,\,\mathrm{d}s\,\mathrm{d}\mathbf{x }\, \mathrm{d}\tau \\&\rightarrow \int _{0}^{t}\int _{\Omega _F(\tau )} \sum _{ijklm} \mathbf{v }_i\partial _i\mathbf{Y }_j \underbrace{\partial _m\partial _j\mathbf{X }_k\partial _t\mathbf{Y }_m }_{\frac{d}{dt}(\nabla \mathbf{X })_{kj}-\partial _t(\nabla \mathbf{X })_{kj}} \underbrace{\partial _l\mathbf{X }_k{\bar{\mathbf{u }}}_l}_{\mathbf{u }_k} \,\,\mathrm{d}s\,\mathrm{d}\mathbf{x }\, \mathrm{d}\tau \\&=-(*)=-\int \int I = \int _{0}^{t}\int _{\Omega _F(\tau )} (\nabla \mathbf{Y }\mathbf{v }\cdot \frac{d}{dt}\nabla \mathbf{X }^T\mathbf{u }-\nabla \mathbf{Y }\mathbf{v }\cdot \partial _t\nabla \mathbf{X }^T\mathbf{u }) \,\mathrm{d}\mathbf{x }\, \mathrm{d}\tau . \end{aligned}$$
It follows
$$\begin{aligned} \mathrm{(A.25)}+ \mathrm{(A.28)} \rightarrow -\int _{0}^{t}\int _{\Omega _F(\tau )} \nabla \mathbf{v }^T\mathbf{u }\cdot \partial _t\mathbf{X }. \end{aligned}$$
It remains to prove (A.29):
$$\begin{aligned} (A.29)&= \int _{0}^{t}\int _{\Omega _F(\tau )} {\bar{\mathbf{v }}}(\tau ,\mathbf{Y }(\tau ,\mathbf{x }))\cdot \int _{-\infty }^{+\infty } j_h(\tau -s)\nabla \mathbf{X }(s,\mathbf{Y }(\tau ,\mathbf{x }))^T\\&\qquad \qquad \qquad \qquad \qquad \qquad \frac{d}{d\tau }\big (\nabla \mathbf{X }(s,\mathbf{Y }(\tau ,\mathbf{x })) {\bar{\mathbf{u }}}(s,\mathbf{Y }(\tau ,\mathbf{x }))\big ) \,\,\mathrm{d}s\,\mathrm{d}\mathbf{x }\, \mathrm{d}\tau \\&= \int _{0}^{t}\int _{\Omega _F(\tau )} \sum _{ijk} {\bar{\mathbf{v }}}_i \int _{-\infty }^{+\infty } j_h(\tau -s)\partial _i\mathbf{X }_j\frac{d}{d\tau }(\partial _k\mathbf{X }_j{\bar{\mathbf{u }}}_k) \\&= \int _{0}^{t}\int _{\Omega _F(\tau )} \sum _{ijkl} {\bar{\mathbf{v }}}_i \int _{-\infty }^{+\infty } j_h(\tau -s)\partial _i\mathbf{X }_j (\partial _l\partial _k\mathbf{X }_j{\bar{\mathbf{u }}}_k + \partial _k\mathbf{X }_j\partial _l{\bar{\mathbf{u }}}_k)\partial _t\mathbf{Y }_l \\&\rightarrow \int _{0}^{t}\int _{\Omega _F(\tau )} \sum _{ijkl} {\bar{\mathbf{v }}}_i \partial _i\mathbf{X }_j \underbrace{(\partial _l\partial _k\mathbf{X }_j{\bar{\mathbf{u }}}_k + \partial _k\mathbf{X }_j\partial _l{\bar{\mathbf{u }}}_k)}_{\frac{d}{d\mathbf{y }_l}(\nabla \mathbf{X }{\bar{\mathbf{u }}})_j=\frac{d}{d\mathbf{y }_l}\mathbf{u }_j=(\nabla \mathbf{u }\nabla \mathbf{X })_{jl}} \partial _t\mathbf{Y }_l \\&= \int _{0}^{t}\int _{\Omega _F(\tau )} {\bar{\mathbf{v }}}\cdot \nabla \mathbf{X }^T \nabla \mathbf{u }\nabla \mathbf{X }\partial _t\mathbf{Y }= \int _{0}^{t}\int _{\Omega _F(\tau )} \underbrace{\nabla \mathbf{X }{\bar{\mathbf{v }}}}_{=\mathbf{v }}\cdot \nabla \mathbf{u }\underbrace{\nabla \mathbf{X }\partial _t\mathbf{Y }}_{=-\partial _t\mathbf{X }} \\&= -\int _{0}^{t}\int _{\Omega _F(\tau )} \mathbf{v }\cdot \nabla \mathbf{u }\partial _t\mathbf{X }= -\int _{0}^{t}\int _{\Omega _F(\tau )} \nabla \mathbf{u }^T \mathbf{v }\cdot \partial _t\mathbf{X }. \end{aligned}$$
\(\square \)
1.3 Weak Formulation—Details
In this subsection we give the remaining technical details of the proof of Proposition 2.1. For simplicity of notation we denote:
$$\begin{aligned} \mathbf{X }={\widetilde{\mathbf{X }}}_2, \, \mathbf{x }=\mathbf{x }_2, \, \mathbf{Y }={\widetilde{\mathbf{X }}}_1, \, \mathbf{y }=\mathbf{x }_1 \end{aligned}$$
and
$$\begin{aligned} (\mathbf{U },P,\mathbf{A },{\varvec{\Omega }}) = (\mathbf{U }_{2},P_{2},\mathbf{A }_{2},{\varvec{\Omega }}_{2}),\, (\mathbf{u },p,\mathbf{a },{\varvec{\omega }}) = (\mathbf{u }_{2},p_{2},\mathbf{a }_{2},{\varvec{\omega }}_{2}). \end{aligned}$$
The fluid time-derivative term.
$$\begin{aligned} \mathbf{u }\cdot \partial _t{\varvec{\varphi }}= \mathbf{U }\cdot \partial _t{\varvec{\psi }}-{\mathcal {M}}\mathbf{U }\cdot {\varvec{\psi }}+ \nabla (\mathbf{U }\cdot {\varvec{\psi }})\cdot \partial _t\mathbf{Y }. \end{aligned}$$
Proof
We have
$$\begin{aligned} \mathbf{u }\cdot \partial _t{\varvec{\varphi }}&= \nabla \mathbf{X }\mathbf{U }\cdot \frac{d}{dt}(\nabla \mathbf{Y }^T{\varvec{\psi }}) \\&= \nabla \mathbf{X }\mathbf{U }\cdot (\partial _t\nabla \mathbf{Y }^T{\varvec{\psi }}+ \nabla \mathbf{Y }^T\partial _t{\varvec{\psi }}+ \nabla \mathbf{Y }^T\nabla {\varvec{\psi }}\partial _t\mathbf{Y }) \\&= \partial _t\nabla \mathbf{Y }\nabla \mathbf{X }\mathbf{U }\cdot {\varvec{\psi }}+ \nabla \mathbf{Y }\nabla \mathbf{X }\mathbf{U }\cdot \partial _t{\varvec{\psi }}+ \nabla \mathbf{Y }\nabla \mathbf{X }\mathbf{U }\cdot \nabla {\varvec{\psi }}\partial _t\mathbf{Y }. \end{aligned}$$
The property of the transformation \(\mathbf{X }\)
$$\begin{aligned} \nabla \mathbf{X }(t,\mathbf{Y }(t,\mathbf{x })))\nabla \mathbf{Y }(t,\mathbf{x })={\mathbb {I}} \end{aligned}$$
(A.36)
implies
$$\begin{aligned} \mathbf{u }\cdot \partial _t{\varvec{\varphi }}= \mathbf{U }\cdot \partial _t{\varvec{\psi }}+ \underbrace{\partial _t\nabla \mathbf{Y }\nabla \mathbf{X }\mathbf{U }\cdot {\varvec{\psi }}}_{I} + \nabla {\varvec{\psi }}^T\mathbf{U }\cdot \partial _t\mathbf{Y }\end{aligned}$$
and by definition of \({\mathcal {M}}\) we have
$$\begin{aligned} {\mathcal {M}}\mathbf{U }\cdot {\varvec{\psi }}= \underbrace{\nabla \mathbf{U }\partial _t\mathbf{Y }\cdot \psi }_{=\nabla \mathbf{U }^T{\varvec{\psi }}\cdot \partial _t\mathbf{Y }} + \underbrace{\nabla \mathbf{Y }\partial _t\nabla \mathbf{X }\mathbf{U }\cdot {\varvec{\psi }}}_{II} + \underbrace{\sum _{ijk}\Gamma _{jk}^i\partial _t\mathbf{Y }_k\mathbf{U }_j{\varvec{\psi }}_i}_{III}. \end{aligned}$$
The identity (A.36) gives
$$\begin{aligned} 0 = \frac{d}{dt}(\nabla \mathbf{Y }\nabla \mathbf{X })_{ij} = (\partial _t\nabla \mathbf{Y }\nabla \mathbf{X })_{ij} + (\nabla \mathbf{Y }\partial _t\nabla \mathbf{X })_{ij} + \sum _{k} \Gamma _{kj}^i\partial _t\mathbf{Y }_k. \end{aligned}$$
Multiplying this equality by \(\mathbf{U }_j{\varvec{\psi }}_i\) and summing over ij, we get
$$\begin{aligned} I = -(II+III) = -{\mathcal {M}}\mathbf{U }\cdot {\varvec{\psi }}+ \nabla \mathbf{U }^T{\varvec{\psi }}\cdot \partial _t\mathbf{Y }. \end{aligned}$$
Finally, we get
$$\begin{aligned} \mathbf{u }\cdot \partial _t{\varvec{\varphi }}&= \mathbf{U }\cdot \partial _t{\varvec{\psi }}-{\mathcal {M}}\mathbf{U }\cdot {\varvec{\psi }}+ \nabla \mathbf{U }^T{\varvec{\psi }}\cdot \partial _t\mathbf{Y }+ \nabla {\varvec{\psi }}^T\mathbf{U }\cdot \partial _t\mathbf{Y }\\&= \mathbf{U }\cdot \partial _t{\varvec{\psi }}-{\mathcal {M}}\mathbf{U }\cdot {\varvec{\psi }}+ \nabla (\mathbf{U }\cdot {\varvec{\psi }})\cdot \partial _t\mathbf{Y }. \end{aligned}$$
\(\square \)
Convective term.
$$\begin{aligned} \mathbf {u }\otimes \mathbf {u }:\nabla {\varvec{\varphi }}= \mathbf {U }\otimes \mathbf {U }:\nabla {\varvec{\psi }}^T - \widetilde{{\mathcal {N}}}\mathbf {U }\cdot {\varvec{\psi }} \end{aligned}$$
Proof
We derive the convective term by using a known identity
$$\begin{aligned} \mathbf{u }\otimes \mathbf{u }:\nabla {\varvec{\varphi }}= \mathop {\mathrm{div}}\nolimits ((\mathbf{u }\cdot {\varvec{\varphi }})\mathbf{u })-(\mathbf{u }\cdot \nabla )\mathbf{u }\cdot {\varvec{\varphi }}. \end{aligned}$$
It is easy to prove (see [23]) that
$$\begin{aligned} \nabla \mathbf{Y }(\mathbf{u }\cdot \nabla )\mathbf{u }={\mathcal {N}}\mathbf{U }, \end{aligned}$$
which implies
$$\begin{aligned} (\mathbf{u }\cdot \nabla )\mathbf{u }\cdot {\varvec{\varphi }}=(\mathbf{u }\cdot \nabla )\mathbf{u }\cdot \nabla \mathbf{Y }^T{\varvec{\psi }}=\nabla \mathbf{Y }(\mathbf{u }\cdot \nabla )\mathbf{u }\cdot {\varvec{\psi }}={\mathcal {N}}\mathbf{U }\cdot {\varvec{\psi }}. \end{aligned}$$
On the other side we conclude
$$\begin{aligned} \mathop {\mathrm{div}}\nolimits ((\mathbf{u }\cdot {\varvec{\varphi }})\mathbf{u })&= \nabla (\mathbf{u }\cdot {\varvec{\varphi }})\cdot \mathbf{u }= \nabla _x(\nabla \mathbf{X }\,\mathbf{U }\cdot \nabla \mathbf{Y }^T{\varvec{\psi }})\cdot \nabla \mathbf{X }\,\mathbf{U }= \nabla _x(\mathbf{U }\cdot {\varvec{\psi }})\cdot \nabla \mathbf{X }\,\mathbf{U }\\&= (\nabla \mathbf{Y }^T\nabla \mathbf{U }^T{\varvec{\psi }}+ \nabla \mathbf{Y }^T\nabla {\varvec{\psi }}^T\mathbf{U })\cdot \nabla \mathbf{X }\,\mathbf{U }= (\nabla \mathbf{U }^T{\varvec{\psi }}+ \nabla {\varvec{\psi }}^T\mathbf{U })\cdot \mathbf{U }\\&=\nabla (\mathbf{U }\cdot {\varvec{\psi }})\cdot \mathbf{U }\\&= \mathbf{U }\cdot \nabla \mathbf{U }\cdot {\varvec{\psi }}+ \mathbf{U }\otimes \mathbf{U }:\nabla \psi ^T. \end{aligned}$$
Therefore,
$$\begin{aligned} \mathbf {u }\otimes \mathbf {u }:\nabla {\varvec{\varphi }}= \mathbf {U }\cdot \nabla \mathbf {U }\cdot {\varvec{\psi }}+ \mathbf {U }\otimes \mathbf {U }:\nabla {\varvec{\psi }}^T - {\mathcal {N}}\mathbf {U }\cdot {\varvec{\psi }}= \mathbf {U }\otimes \mathbf {U }:\nabla {\varvec{\psi }}^T - \widetilde{{\mathcal {N}}}\mathbf {U }\cdot {\varvec{\psi }}. \end{aligned}$$
\(\square \)
Diffusive term.
$$\begin{aligned} \int _{\Omega _F(\tau )} 2\,{{\mathbb {D}}}\mathbf{u }:{{\mathbb {D}}}{\varvec{\varphi }}= \left\langle {\mathcal {L}}\mathbf{U }, {\varvec{\psi }}\right\rangle , \end{aligned}$$
where
$$\begin{aligned} \left\langle {\mathcal {L}}\mathbf{U }, {\varvec{\psi }}\right\rangle= & {} \int _{\Omega _F(\tau )} \big (\sum _{ijk} (g^{jk}\partial _j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_i + g^{jk}\partial _k\mathbf{U }_i\partial _i{\varvec{\psi }}_j) - \sum _{ijkl} (g^{kl}+\partial _l\mathbf{Y }_k)\Gamma _{li}^j\partial _k\mathbf{U }_{i}{\varvec{\psi }}_j\\&\quad + \sum _{ijkl} (g^{kl}\Gamma _{li}^j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_j + g^{jl}\Gamma _{li}^k\mathbf{U }_i\partial _k{\varvec{\psi }}_j) - \sum _{ijklm} (g^{kl}+\partial _k\mathbf{Y }_l)\Gamma _{li}^m\Gamma _{km}^j\mathbf{U }_{i}{\varvec{\psi }}_j \big ). \end{aligned}$$
Proof
We have
$$\begin{aligned} 2{{\mathbb {D}}}\mathbf{u }:{{\mathbb {D}}}{\varvec{\varphi }}= 2{{\mathbb {D}}}\mathbf{u }:\nabla {\varvec{\varphi }}= \nabla \mathbf{u }:\nabla {\varvec{\varphi }}+ \nabla \mathbf{u }^T:\nabla {\varvec{\varphi }}\end{aligned}$$
For the first term we get
$$\begin{aligned} \nabla \mathbf{u }:\nabla {\varvec{\varphi }}&= \sum _{ij} \partial _j\mathbf{u }_{i}\partial _j{\varvec{\psi }}_i = \sum _{ij} \frac{d}{d\mathbf{x }_j}(\nabla \mathbf{X }\mathbf{U })_i\frac{d}{d\mathbf{x }_j}(\nabla \mathbf{Y }^T{\varvec{\psi }})_i\\&= \sum _{ijkl} \frac{d}{d\mathbf{x }_j}(\partial _k\mathbf{X }_i\mathbf{U }_k)\frac{d}{d\mathbf{x }_j}(\partial _i\mathbf{Y }_l{\varvec{\psi }}_l)\\&= \sum _{ijklmp} (\partial _m\partial _k\mathbf{X }_i\mathbf{U }_k +\partial _k\mathbf{X }_i\partial _m\mathbf{U }_k) \underline{\partial _j\mathbf{Y }_m \partial _j\mathbf{Y }_p}(\frac{d}{d\mathbf{y }_p}\partial _i\mathbf{Y }_l{\varvec{\psi }}_l + \partial _i\mathbf{Y }_l\partial _p{\varvec{\psi }}_l)\\&= \underbrace{\sum _{iklmp} g^{mp}\partial _m\partial _k\mathbf{X }_i\partial _{\mathbf{y }_p}\partial _i\mathbf{Y }_l\mathbf{U }_k{\varvec{\psi }}_l}_{I} + \underbrace{\sum _{iklmp} g^{mp}\partial _m\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l\mathbf{U }_k\partial _p{\varvec{\psi }}_l}_{II}\\&\quad +\underbrace{\sum _{iklmp} g^{mp}\partial _k\mathbf{X }_i\partial _{\mathbf{y }_p}\partial _i\mathbf{Y }_l\partial _m\mathbf{U }_k{\varvec{\psi }}_l}_{III} + \underbrace{\sum _{iklmp} g^{mp}\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l\partial _m\mathbf{U }_k\partial _p{\varvec{\psi }}_l}_{IV},\\ II&= \sum _{klmp} g^{mp}(\sum _{i}\partial _m\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l)\mathbf{U }_k\partial _p{\varvec{\psi }}_l = \sum _{klmp} g^{mp}\Gamma _{mk}^l\mathbf{U }_k\partial _p{\varvec{\psi }}_l,\\ IV&= \sum _{klmp} g^{mp}(\sum _{i}\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l)\partial _m\mathbf{U }_k\partial _p{\varvec{\psi }}_l = \sum _{kmp} g^{mp}\partial _m\mathbf{U }_k\partial _p{\varvec{\psi }}_k,\\ III&= \sum _{iklmp} g^{mp}(\partial _p(\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l) - \partial _p\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l)\partial _m\mathbf{U }_k{\varvec{\psi }}_l = -\sum _{klmp} g^{mp}\Gamma _{pk}^l\partial _m\mathbf{U }_k{\varvec{\psi }}_l,\\ I&= \sum _{iklmp} g^{mp}(\partial _p(\partial _m\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l) - \partial _p\partial _m\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l)\mathbf{U }_k{\varvec{\psi }}_l\\&= \underbrace{\sum _{klmp} g^{mp}\partial _p(\Gamma _{mk}^l)\mathbf{U }_k{\varvec{\psi }}_l}_{V} - \underbrace{\sum _{iklmp} g^{mp} \partial _p\partial _m\partial _k\mathbf{X }_i\partial _i\mathbf{Y }_l\mathbf{U }_k{\varvec{\psi }}_l}_{VI},\\ VI&= ([23]) = \sum _{iklmp} g^{mp} \partial _p(\sum _{q}\Gamma _{mk}^q\partial _q\mathbf{X }_i)\partial _i\mathbf{Y }_l\mathbf{U }_k{\varvec{\psi }}_l\\&= \sum _{iklmpq} g^{mp} \partial _p\Gamma _{mk}^q\underline{\partial _q\mathbf{X }_i\partial _i\mathbf{Y }_l}\mathbf{U }_k{\varvec{\psi }}_l + \sum _{iklmpq} g^{mp} \Gamma _{mk}^q\underline{\partial _p\partial _q\mathbf{X }_i\partial _i\mathbf{Y }_l}\mathbf{U }_k{\varvec{\psi }}_l\\&= \underbrace{\sum _{klmp} g^{mp} \partial _p\Gamma _{mk}^l\mathbf{U }_k{\varvec{\psi }}_l}_{= V} + \sum _{klmpq} g^{mp} \Gamma _{mk}^q\Gamma _{pq}^l\mathbf{U }_k{\varvec{\psi }}_l. \end{aligned}$$
It follows
$$\begin{aligned} I&= - \sum _{klmpq} g^{mp} \Gamma _{mk}^q\Gamma _{pq}^l\mathbf{U }_k{\varvec{\psi }}_l. \end{aligned}$$
Hence,
$$\begin{aligned} \nabla \mathbf{u }:\nabla {\varvec{\varphi }}= \sum _{ijk} g^{jk}\partial _j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_i - \sum _{ijkl} g^{kl}\Gamma _{li}^j\partial _k\mathbf{U }_{i}{\varvec{\psi }}_j + \sum _{ijkl} g^{kl}\Gamma _{li}^j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_j - \sum _{ijklm} g^{kl}\Gamma _{li}^m\Gamma _{km}^j\mathbf{U }_{i}{\varvec{\psi }}_j. \end{aligned}$$
Similarly, we get
$$\begin{aligned} \nabla \mathbf{u }^T:\nabla {\varvec{\varphi }}&= \sum _{ij} \partial _i\mathbf{u }_{j}\partial _j{\varvec{\psi }}_i = \sum _{ij} \frac{d}{d\mathbf{x }_i}(\nabla \mathbf{X }\mathbf{U })_j\frac{d}{d\mathbf{x }_j}(\nabla \mathbf{Y }^T{\varvec{\psi }})_i\\&= \sum _{ijkl} \frac{d}{d\mathbf{x }_i}(\partial _k\mathbf{X }_j\mathbf{U }_k)\frac{d}{d\mathbf{x }_j}(\partial _i\mathbf{Y }_l{\varvec{\psi }}_l)\\&= \sum _{ijklmp} ( \partial _m\partial _k\mathbf{X }_j\mathbf{U }_k + \partial _k\mathbf{X }_j\partial _m\mathbf{U }_k )\partial _i\mathbf{Y }_m ( \partial _{j}\partial _i\mathbf{Y }_l{\varvec{\psi }}_l + \partial _i\mathbf{Y }_l\partial _p{\varvec{\psi }}_l\partial _{j}\mathbf{Y }_p)\\&= \underbrace{ \sum _{iklmp} \partial _i\mathbf{Y }_m\partial _m\partial _k\mathbf{X }_j \partial _{j}\partial _i\mathbf{Y }_l\mathbf{U }_k{\varvec{\psi }}_l }_{I'} + \underbrace{ \sum _{iklmp} \partial _i\mathbf{Y }_m\partial _i\mathbf{Y }_l \partial _m\partial _k\mathbf{X }_j\partial _{j}\mathbf{Y }_p\mathbf{U }_k \partial _p{\varvec{\psi }}_l }_{II'}\\&\quad +\underbrace{ \sum _{iklmp} \partial _i\mathbf{Y }_m\partial _k\mathbf{X }_j \partial _{j}\partial _i\mathbf{Y }_l \partial _m\mathbf{U }_k{\varvec{\psi }}_l }_{III'} + \underbrace{ \sum _{iklmp} \partial _i\mathbf{Y }_m \partial _i\mathbf{Y }_l\partial _k\mathbf{X }_j\partial _{j}\mathbf{Y }_p \partial _m\mathbf{U }_k\partial _p{\varvec{\psi }}_l }_{IV'},\\ II'&= \sum _{klmp} g^{ml}\Gamma _{mk}^p\mathbf{U }_k\partial _p{\varvec{\psi }}_l,\\ IV'&= \sum _{klmp} g^{ml}\delta _{pk} \partial _m\mathbf{U }_k\partial _p{\varvec{\psi }}_l = \sum _{klm} g^{ml}\partial _m\mathbf{U }_k\partial _k{\varvec{\psi }}_l,\\ III'&= \sum _{iklmp} \partial _i\mathbf{Y }_m \left( \partial _i (\partial _k\mathbf{X }_j \partial _{j}\mathbf{Y }_l) - \partial _i\partial _k\mathbf{X }_j \partial _{j}\mathbf{Y }_l \right) \partial _m\mathbf{U }_k{\varvec{\psi }}_l = -\sum _{iklm} \partial _i\mathbf{Y }_m \Gamma _{ik}^l \partial _m\mathbf{U }_k{\varvec{\psi }}_l,\\ I'&= \sum _{ijklmp} \partial _i\mathbf{Y }_m \left( \partial _i(\partial _m\partial _k\mathbf{X }_j \partial _{j}\mathbf{Y }_l) - \partial _i\partial _m\partial _k\mathbf{X }_j \partial _{j}\mathbf{Y }_l \right) \mathbf{U }_k{\varvec{\psi }}_l\\&= \underbrace{\sum _{iklmp} \partial _i\mathbf{Y }_m \partial _i\Gamma _{mk}^l\mathbf{U }_k{\varvec{\psi }}_l}_{V'} - \underbrace{\sum _{ijklmp} \partial _i\mathbf{Y }_m \partial _i\partial _m\partial _k\mathbf{X }_j\partial _j\mathbf{Y }_l\mathbf{U }_k{\varvec{\psi }}_l}_{VI'},\\ VI'&= ([23]) =\sum _{ijklmp} \partial _i\mathbf{Y }_m \partial _i(\sum _{q}\Gamma _{mk}^q\partial _q\mathbf{X }_j) \partial _j\mathbf{Y }_l\mathbf{U }_k{\varvec{\psi }}_l\\&= \sum _{ijklmpq} \partial _i\mathbf{Y }_m \partial _i\Gamma _{mk}^q \underline{\partial _q\mathbf{X }_j\partial _j\mathbf{Y }_l} \mathbf{U }_k{\varvec{\psi }}_l + \sum _{ijklmpq} \partial _i\mathbf{Y }_m \Gamma _{mk}^q \underline{\partial _i\partial _q\mathbf{X }_j\partial _j\mathbf{Y }_l} \mathbf{U }_k{\varvec{\psi }}_l\\&= \underbrace{\sum _{iklmp} \partial _i\mathbf{Y }_m \partial _i\Gamma _{mk}^l \mathbf{U }_k{\varvec{\psi }}_l}_{= V'} + \sum _{iklmpq} \partial _i\mathbf{Y }_m \Gamma _{mk}^q\Gamma _{iq}^l \mathbf{U }_k{\varvec{\psi }}_l \end{aligned}$$
It follows
$$\begin{aligned} I'&= - \sum _{iklmpq} \partial _i\mathbf{Y }_m \Gamma _{mk}^q\Gamma _{iq}^l \mathbf{U }_k{\varvec{\psi }}_l. \end{aligned}$$
Therefore,
$$\begin{aligned} \nabla \mathbf{u }^T:\nabla {\varvec{\varphi }}= \sum _{ijk} g^{jk}\partial _k\mathbf{U }_i\partial _i{\varvec{\psi }}_j -\sum _{iklm} \partial _l\mathbf{Y }_k \Gamma _{il}^j \partial _k\mathbf{U }_i{\varvec{\psi }}_j + \sum _{ijkl} g^{jl}\Gamma _{li}^k\mathbf{U }_i\partial _k{\varvec{\psi }}_j - \sum _{ijklm} \partial _k\mathbf{Y }_l \Gamma _{li}^m\Gamma _{km}^j \mathbf{U }_i{\varvec{\psi }}_j \end{aligned}$$
Finally, we get
$$\begin{aligned}&\left\langle {\mathcal {L}}\mathbf{U }, {\varvec{\psi }}\right\rangle :=\int _{\Omega _F(\tau )} 2\,{{\mathbb {D}}}\mathbf{u }:{{\mathbb {D}}}{\varvec{\varphi }}= \int _{\Omega _F(\tau )} \left( \nabla \mathbf{u }:\nabla {\varvec{\varphi }}+ \nabla \mathbf{u }^T:\nabla {\varvec{\varphi }}\right) \\&\quad = \frac{1}{2}\int _{\Omega _F(\tau )} \big (\sum _{ijk} (g^{jk}\partial _j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_i + g^{jk}\partial _k\mathbf{U }_i\partial _i{\varvec{\psi }}_j) - \sum _{ijkl} (g^{kl}+\partial _l\mathbf{Y }_k)\Gamma _{li}^j\partial _k\mathbf{U }_{i}{\varvec{\psi }}_j\\&\qquad + \sum _{ijkl} (g^{kl}\Gamma _{li}^j\mathbf{U }_{i}\partial _k{\varvec{\psi }}_j + g^{jl}\Gamma _{li}^k\mathbf{U }_i\partial _k{\varvec{\psi }}_j) - \sum _{ijklm} (g^{kl}+\partial _k\mathbf{Y }_l)\Gamma _{li}^m\Gamma _{km}^j\mathbf{U }_{i}{\varvec{\psi }}_j \big ). \end{aligned}$$
\(\square \)