Skip to main content
SpringerLink
Log in

Dynamics analysis of timoshenko perforated microbeams under moving loads

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

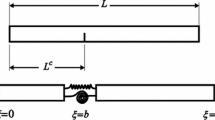
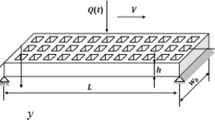
This paper aims to present a modified continuum mathematical model capable on investigation of dynamic behavior and response of perforated microbeam under the effect of moving mass/load for the first time. A size-dependent finite element model with non-classical shape function is exploited to solve the mathematical model and obtain the dynamic response of perforated Timoshenko microbeams under moving loads. To that end, first, equivalent material and geometrical parameters for perforated beam are developed, based on the regular squared perforation configuration. Second, both the stiffness and mass property matrices including the microstructure effect based on modified couple stress theory and Timoshenko first-order shear beam theory are derived for two-node finite element using new shape function. After that, the interaction between the load and beam is modeed and unified with the equation of motion of the beam incorporating mass inertia effects of moving load. The developed procedure is validated and compared. Effects of perforation parameters, moving load velocities, inertia of mass, and the microstructure size parameter on the dynamic response of perforated microbeam structures have been investigated in a wide context. The achieved results are helpful for the design and production of MEMS structures such as frequency filters, resonators, relay switches, accelerometers and mass flow sensors, with perforation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Abdelrahman AA, Eltaher MA, Kabeel AM, Abdraboh AM, Hendy AA (2019) Free and forced analysis of perforated beams. Steel and Composite Structures 31(5):489–502. https://doi.org/10.12989/scs.2019.31.5.489

    Article  Google Scholar 

  2. Abdelrahman AA, Mohamed NA, Eltaher MA (2020) Static bending of perforated nanobeams including surface energy and microstructure effects. Engineering with Computers. https://doi.org/10.1007/s00366-020-01149-x

    Article  Google Scholar 

  3. Abdelrahman, A. A., Eltaher, M. A. (2020). On Bending and Buckling Responses of Perforated Nanobeams including Surface Energy for Different Beams Theories, Engineering with Computers.

  4. Abo-Bakr RM, Eltaher MA, Attia MA (2020) Pull-in and freestanding instability of actuated functionally graded nanobeams including surface and stiffening effects. Engineering with Computers. https://doi.org/10.1007/s00366-020-01146-0

    Article  Google Scholar 

  5. Al-Furjan MSH, Habibi M, Chen G, Safarpour H, Safarpour M, Tounsi A (2020) Chaotic simulation of the multi-phase reinforced thermo-elastic disk using GDQM. Engineering with Computers. https://doi.org/10.1007/s00366-020-01144-2

    Article  Google Scholar 

  6. Alimirzaei S, Mohammadimehr M, Tounsi A (2019) Nonlinear analysis of viscoelastic micro-composite beam with geometrical imperfection using FEM MSGT electro magneto elastic bending, buckling and vibration solutions. Struct Eng Mech 71(5):485–502. https://doi.org/10.12989/sem.2019.71.5.485

    Article  Google Scholar 

  7. Almitani KH, Abdelrahman AA, Eltaher MA (2019) On forced and free vibrations of cutout squared beams. Steel and Composite Structures 32(5):643–655. https://doi.org/10.12989/scs.2019.32.5.643

    Article  Google Scholar 

  8. Almitani KH, Abdelrahman AA, Eltaher MA (2020a) Stability of perforated nanobeams incorporating surface energy effects. Steel and Composite Structures 35(4):555–566. https://doi.org/10.12989/scs.2020.35.4.555

    Article  Google Scholar 

  9. Almitani KH, Abdelrahman AA, Eltaher MA (2020b) Influence of the Perforation Configuration on Dynamic Behaviors of Multilayered Beam Structure. Structures 28:1413–1426. https://doi.org/10.1016/j.istruc.2020.09.055

    Article  Google Scholar 

  10. Arefi M, Pourjamshidian M, Ghorbanpour Arani A (2018) Nonlinear free and forced vibration analysis of embedded functionally graded sandwich micro beam with moving mass. J Sandwich Struct Mater 20(4):462–492. https://doi.org/10.1177/1099636216658895

    Article  Google Scholar 

  11. Areiza-Hurtado M, Vega-Posada CA, Aristizabal-Ochoa JD (2019) Stiffness matrix and loading vector of a two-layer Timoshenko composite beam. Structures 20:20–32. https://doi.org/10.1016/j.istruc.2019.02.014

    Article  Google Scholar 

  12. Asghar S, Naeem MN, Hussain M, Taj M, Tounsi A (2020) Prediction and assessment of nonlocal natural frequencies of DWCNTs: Vibration analysis. Computers and Concrete 25(2):133–144. https://doi.org/10.12989/cac.2020.25.2.133

    Article  Google Scholar 

  13. Aydogdu M (2009) A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Physica E 41(9):1651–1655. https://doi.org/10.1016/j.physe.2009.05.014

    Article  Google Scholar 

  14. Bahrebar M, Lim JB, Clifton GC, Zirakian T, Shahmohammadi A, Hajsadeghi M (2020) Perforated steel plate shear walls with curved corrugated webs under cyclic loading. Structures 24:600–609. https://doi.org/10.1016/j.istruc.2020.01.047

    Article  Google Scholar 

  15. Balubaid M, Tounsi A, Dakhel B, Mahmoud SR (2019) Free vibration investigation of FG nanoscale plate using nonlocal two variables integral refined plate theory. Computers and Concrete 24(6):579–586. https://doi.org/10.12989/cac.2019.24.6.579

    Article  Google Scholar 

  16. Bendenia N, Zidour M, Bousahla AA, Bourada F, Tounsi A, Benrahou KH, Tounsi A (2020) Deflections, stresses and free vibration studies of FG-CNT reinforced sandwich plates resting on Pasternak elastic foundation. Computers and Concrete 26(3):213–226. https://doi.org/10.12989/cac.2020.26.3.213

    Article  Google Scholar 

  17. Bellal M, Hebali H, Heireche H, Bousahla AA, Tounsi A, Bourada F, Tounsi A (2020) Buckling behavior of a single-layered graphene sheet resting on viscoelastic medium via nonlocal four-unknown integral model. Steel and Composite Structures 34(5):643–655. https://doi.org/10.12989/scs.2020.34.5.643

    Article  Google Scholar 

  18. Bendali, A., Labedan, R., Domingue, F., & Nerguizian, V. (2006) “Holes effects on RF MEMS parallel membranes capacitors”, In 2006 Canadian Conference on Electrical and Computer Engineering (pp. 2140–2143). IEEE. https://doi.org/https://doi.org/10.1109/CCECE.2006.277600

  19. Berghouti H, Adda Bedia EA, Benkhedda A, Tounsi A (2019) Vibration analysis of nonlocal porous nanobeams made of functionally graded material. Advances in nano research 7(5):351–364. https://doi.org/10.12989/anr.2019.7.5.351

    Article  Google Scholar 

  20. Bourada F, Bousahla AA, Tounsi A, Bedia EA, Mahmoud SR, Benrahou KH, Tounsi A (2020) Stability and dynamic analyses of SW-CNT reinforced concrete beam resting on elastic-foundation. Computers and Concrete 25(6):485–495. https://doi.org/10.12989/cac.2020.25.6.485

    Article  Google Scholar 

  21. Bourouina H, Yahiaoui R, Sahar A, Benamar MEA (2016) Analytical modeling for the determination of nonlocal resonance frequencies of perforated nanobeams subjected to temperature-induced loads. Physica E 75:163–168. https://doi.org/10.1016/j.physe.2015.09.014

    Article  Google Scholar 

  22. Bousahla AA, Bourada F, Mahmoud SR, Tounsi A, Algarni A, Bedia EA, Tounsi A (2020) Buckling and dynamic behavior of the simply supported CNT-RC beams using an integral-first shear deformation theory. Computers and Concrete 25(2):155–166. https://doi.org/10.12989/cac.2020.25.2.155

    Article  Google Scholar 

  23. Boutaleb S, Benrahou KH, Bakora A, Algarni A, Bousahla AA, Tounsi A, Mahmoud SR (2019) Dynamic analysis of nanosize FG rectangular plates based on simple nonlocal quasi 3D HSDT. Advances in Nano Research 7(3):191. https://doi.org/10.12989/anr.2019.7.3.191

    Article  Google Scholar 

  24. Dai HL, Wang YK, Wang L (2015) Nonlinear dynamics of cantilevered microbeams based on modified couple stress theory. Int J Eng Sci 94:103–112. https://doi.org/10.1016/j.ijengsci.2015.05.007

    Article  MathSciNet  MATH  Google Scholar 

  25. Daikh, A.A., Drai, A., Houari M.S.A, and Eltaher, M.A. Static analysis of multilayer nonlocal strain gradient nanobeam reinforced by carbon nanotubes. Steel and Composite Structures. 36(6), 643–656. https://doi.org/https://doi.org/10.12989/scs.2020.36.6.64.

  26. De Pasquale G, Veijola T, Somà A (2009) Modelling and validation of air damping in perforated gold and silicon MEMS plates. J Micromech Microeng 20(1):015010. https://doi.org/10.1088/0960-1317/20/1/015010

    Article  Google Scholar 

  27. Dehrouyeh-Semnani AM, Bahrami A (2016) On size-dependent Timoshenko beam element based on modified couple stress theory. Int J Eng Sci 107:134–148. https://doi.org/10.1016/j.ijengsci.2016.07.006

    Article  MathSciNet  MATH  Google Scholar 

  28. Draiche K, Bousahla AA, Tounsi A, Alwabli AS, Tounsi A, Mahmoud SR (2019) Static analysis of laminated reinforced composite plates using a simple first-order shear deformation theory. Computers and Concrete 24(4):369–378. https://doi.org/10.12989/cac.2019.24.4.369

    Article  Google Scholar 

  29. Eltaher MA, Hamed MA, Sadoun AM, Mansour A (2014) Mechanical analysis of higher order gradient nanobeams. Appl Math Comput 229:260–272. https://doi.org/10.1016/j.amc.2013.12.076

    Article  MathSciNet  MATH  Google Scholar 

  30. Eltaher MA, El-Borgi S, Reddy JN (2016) Nonlinear analysis of size-dependent and material-dependent nonlocal CNTs. Compos Struct 153:902–913. https://doi.org/10.1016/j.compstruct.2016.07.013

    Article  Google Scholar 

  31. Eltaher MA, Kabeel AM, Almitani KH, Abdraboh AM (2018) Static bending and buckling of perforated nonlocal size-dependent nanobeams. Microsyst Technol 24(12):4881–4893. https://doi.org/10.1007/s00542-018-3905-3

    Article  Google Scholar 

  32. Eltaher MA, Abdraboh AM, Almitani KH (2018) Resonance frequencies of size dependent perforated nonlocal nanobeam. Microsyst Technol 24(9):3925–3937. https://doi.org/10.1007/s00542-018-3910-6

    Article  Google Scholar 

  33. Eltaher MA, Mohamed N (2020a) Nonlinear stability and vibration of imperfect CNTs by Doublet mechanics. Appl Math Comput 382:125311. https://doi.org/10.1016/j.amc.2020.125311

    Article  MathSciNet  MATH  Google Scholar 

  34. Eltaher MA, Mohamed MA (2020b) Vibration of Nonlocal Perforated Nanobeams under General Boundary Conditions. Smart Structures and Systems 25(4):510–514. https://doi.org/10.12989/sss.2020.25.4.501

    Article  Google Scholar 

  35. Eltaher MA, Abdalrahmaan AA (2020) Bending Behavior of squared cutout Nanobeams incorporating Surface Stress Effects. Steel and Composite Structures 36(2):143–161. https://doi.org/10.12989/scs.2020.36.2.143

    Article  Google Scholar 

  36. Eltaher MA, Omar FA, Abdraboh AM, Abdalla WS, Alshorbagy AE (2020) Mechanical Behaviors of Piezoelectric Nonlocal Nanobeam with Cutouts. Smart Structures and Systems 25(2):219–228. https://doi.org/10.12989/sss.2020.25.2.219

    Article  Google Scholar 

  37. Eltaher, M.A., Omar, F.A., Abdalla, W.S., Kabeel, M.A., and A.E. Alshorbagy. (2020b), “Mechanical Analysis of Cutout Piezoelectric Nonlocal Nanobeam including Surface Energy Effects”, Structural Engineering and Mechanics

  38. Eyvazian A, Shahsavari D, Karami B (2020) On the dynamic of graphene reinforced nanocomposite cylindrical shells subjected to a moving harmonic load. Int J Eng Sci 154:103339. https://doi.org/10.1016/j.ijengsci.2020.103339

    Article  MathSciNet  MATH  Google Scholar 

  39. Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16. https://doi.org/10.1016/0020-7225(72)90070-5

    Article  MathSciNet  MATH  Google Scholar 

  40. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710. https://doi.org/10.1063/1.332803

    Article  Google Scholar 

  41. Esen I (2019a) Dynamic response of functional graded Timoshenko beams in a thermal environment subjected to an accelerating load. European Journal of Mechanics-A/Solids 78:103841. https://doi.org/10.1016/j.euromechsol.2019.103841

    Article  MathSciNet  MATH  Google Scholar 

  42. Esen I (2019b) Dynamic response of a functionally graded Timoshenko beam on two-parameter elastic foundations due to a variable velocity moving mass. Int J Mech Sci 153:21–35. https://doi.org/10.1016/j.ijmecsci.2019.01.033

    Article  Google Scholar 

  43. Esen I (2020a) Response of a micro-capillary system exposed to a moving mass in magnetic field using nonlocal strain gradient theory. Int J Mech Sci 188:105937. https://doi.org/10.1016/j.ijmecsci.2020.105937

    Article  Google Scholar 

  44. Esen I (2020b) Dynamics of size-dependent Timoshenko micro beams subjected to moving loads. Int J Mech Sci 175:105501. https://doi.org/10.1016/j.ijmecsci.2020.105501

    Article  Google Scholar 

  45. Farokhi H, Ghayesh MH (2018) Supercritical nonlinear parametric dynamics of Timoshenko microbeams. Commun Nonlinear Sci Numer Simul 59:592–605. https://doi.org/10.1016/j.cnsns.2017.11.033

    Article  MathSciNet  MATH  Google Scholar 

  46. Ferrari, M., Granik, V. T., Imam, A., & Nadeau, J. C. Advances in Doublet Mechanics. 45, Springer Science & Business Media, 1997.

  47. Gao G, Cagin T, Goddard WA III (1998) Energetics, structure, mechanical and vibrational properties of single-walled carbon nanotubes. Nanotechnology 9(3):184. https://doi.org/10.1088/0957-4484/9/3/007

    Article  Google Scholar 

  48. Gao XL, Mahmoud FF (2014) A new Bernoulli-Euler beam model incorporating microstructure and surface energy effects. Zeitschrift für angewandte Mathematik und Physik 65(2):393–404. https://doi.org/10.1007/s00033-013-0343-z

    Article  MathSciNet  MATH  Google Scholar 

  49. Gao XL (2015) A new Timoshenko beam model incorporating microstructure and surface energy effects. Acta Mech 226(2):457–474. https://doi.org/10.1007/s00707-014-1189-y

    Article  MathSciNet  MATH  Google Scholar 

  50. Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech Anal 57(4):291–323. https://doi.org/10.1007/BF00261375

    Article  MathSciNet  MATH  Google Scholar 

  51. Gurtin ME, Murdoch AI (1978) Surface stress in solids. Int J Solids Struct 14(6):431–440

    Article  Google Scholar 

  52. Hadian M, Torabi K, Hadian Jazi S (2020) Nonlinear vibration analysis of an elastically connected double-non-classical Timoshenko microbeam subject to moving particle based on the modified couple stress theory. Journal of the Brazilian Society of Mechanical Sciences and Engineering. https://doi.org/10.1007/s40430-020-02336-z

    Article  Google Scholar 

  53. Hamed MA, Mohamed N, Eltaher MA (2020) Stability Buckling and Bending of Nanobeams including Cutouts. Engineering with Computers. https://doi.org/10.1007/s00366-020-01063-2

    Article  Google Scholar 

  54. Hussain M, Naeem MN, Tounsi A, Taj M (2019) Nonlocal effect on the vibration of armchair and zigzag SWCNTs with bending rigidity. Advances in nano research 7(6):431–442. https://doi.org/10.12989/anr.2019.7.6.431

    Article  Google Scholar 

  55. Hussain M, Naeem MN, Taj M, Tounsi A (2020) Simulating vibration of single-walled carbon nanotube using Rayleigh-Ritz’s method. Advances in nano research 8(3):215–228. https://doi.org/10.12989/anr.2020.8.3.215

    Article  Google Scholar 

  56. Jena SK, Chakraverty S, Malikan M (2019) Implementation of Haar wavelet, higher order Haar wavelet, and differential quadrature methods on buckling response of strain gradient nonlocal beam embedded in an elastic medium. Engineering with Computers. https://doi.org/10.1007/s00366-019-00883-1

    Article  Google Scholar 

  57. Jena SK, Chakraverty S, Malikan M (2020a) Implementation of non-probabilistic methods for stability analysis of nonlocal beam with structural uncertainties. Engineering with Computers. https://doi.org/10.1007/s00366-020-00987-z

    Article  Google Scholar 

  58. Jena SK, Chakraverty S, Malikan M (2020b) Application of shifted Chebyshev polynomial-based Rayleigh-Ritz method and Navier’s technique for vibration analysis of a functionally graded porous beam embedded in Kerr foundation. Engineering with Computers. https://doi.org/10.1007/s00366-020-01018-7

    Article  Google Scholar 

  59. Kahrobaiyan MH, Asghari M, Ahmadian MT (2014) A Timoshenko beam element based on the modified couple stress theory. Int J Mech Sci 79:75–83. https://doi.org/10.1016/j.ijmecsci.2013.11.014

    Article  MATH  Google Scholar 

  60. Karttunen AT, Romanoff J, Reddy JN (2016) Exact microstructure-dependent Timoshenko beam element. Int J Mech Sci 111:35–42. https://doi.org/10.1016/j.ijmecsci.2016.03.023

    Article  Google Scholar 

  61. Karami B, Janghorban M, Tounsi A (2019a) Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Engineering with Computers 35(4):1297–1316. https://doi.org/10.1007/s00366-018-0664-9

    Article  Google Scholar 

  62. Karami B, Janghorban M, Tounsi A (2019b) On pre-stressed functionally graded anisotropic nanoshell in magnetic field. Journal of the Brazilian Society of Mechanical Sciences and Engineering 41(11):495. https://doi.org/10.1007/s40430-019-1996-0

    Article  Google Scholar 

  63. Ke LL, Wang YS (2011) Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos Struct 93(2):342–350. https://doi.org/10.1016/j.compstruct.2010.09.008

    Article  Google Scholar 

  64. Kerid R, Bourouina H, Yahiaoui R, Bounekhla M, Aissat A (2019) Magnetic field effect on nonlocal resonance frequencies of structure-based filter with periodic square holes network. Physica E 105:83–89. https://doi.org/10.1016/j.physe.2018.05.021

    Article  Google Scholar 

  65. Khaniki HB, Hosseini-Hashemi S (2017) The size-dependent analysis of multilayered microbridge systems under a moving load/mass based on the modified couple stress theory. The European Physical Journal Plus 132(5):200. https://doi.org/10.1140/epjp/i2017-11466-0

    Article  Google Scholar 

  66. Khiloun M, Bousahla AA, Kaci A, Bessaim A, Tounsi A, Mahmoud SR (2020) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT. Engineering with Computers 36(3):807–821. https://doi.org/10.1007/s00366-019-00732-1

    Article  Google Scholar 

  67. Khorasani M, Eyvazian A, Karbon M, Tounsi A, Lampani L, Sebaey TA (2020) Magneto-electro-elastic vibration analysis of modified couple stress-based three-layered micro rectangular plates exposed to multi-physical fields considering the flexoelectricity effects. Smart Structures and Systems 26(3):331–343. https://doi.org/10.12989/sss.2020.26.3.331

    Article  Google Scholar 

  68. Koiter WT. Couple stresses in the theory of elasticity. Proc Koninklijke Nederl Akaad van Wetensch 1964;67 https://hal.archives-ouvertes.fr/hal-00852443

  69. Lee HP (1996) Transverse vibration of a Timoshenko beam acted on by an accelerating mass. Appl Acoust 47(4):319–330. https://doi.org/10.1016/0003-682X(95)00067-J

    Article  Google Scholar 

  70. Luschi L, Pieri F (2014) An analytical model for the determination of resonance frequencies of perforated beams. J Micromech Microeng 24(5):055004. https://doi.org/10.1088/0960-1317/24/5/055004

    Article  Google Scholar 

  71. Ma HM, Gao XL, Reddy JN (2008) A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J Mech Phys Solids 56(12):3379–3391. https://doi.org/10.1016/j.jmps.2008.09.007

    Article  MathSciNet  MATH  Google Scholar 

  72. Matouk H, Bousahla AA, Heireche H, Bourada F, Bedia EA, Tounsi A, Benrahou KH (2020) Investigation on hygro-thermal vibration of P-FG and symmetric S-FG nanobeam using integral Timoshenko beam theory. Advances in nano research 8(4):293–305. https://doi.org/10.12989/anr.2020.8.4.293

    Article  Google Scholar 

  73. McFarland AW, Colton JS (2005) Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J Micromech Microeng 15(5):1060. https://doi.org/10.1088/0960-1317/15/5/024

    Article  Google Scholar 

  74. Menasria A, Kaci A, Bousahla AA, Bourada F, Tounsi A, Benrahou KH, Mahmoud SR (2020) A four-unknown refined plate theory for dynamic analysis of FG-sandwich plates under various boundary conditions. Steel and Composite Structures 36(3):355–367. https://doi.org/10.12989/scs.2020.36.3.355

    Article  Google Scholar 

  75. Mindlin, R. D. (1962). Influence of couple-stresses on stress concentrations. COLUMBIA UNIV NEW YORK.

  76. Mindlin RD (1965) Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct 1(4):417–438. https://doi.org/10.1016/0020-7683(65)90006-5

    Article  Google Scholar 

  77. Mirjavadi SS, Afshari BM, Barati MR, Hamouda AMS (2018) Strain gradient based dynamic response analysis of heterogeneous cylindrical microshells with porosities under a moving load. Materials Research Express 6(3):035029. https://doi.org/10.1088/2053-1591/aaf5a2

    Article  Google Scholar 

  78. Mohamed N, Eltaher MA, Mohamed SA, Seddek LF (2019) Energy equivalent model in analysis of postbuckling of imperfect carbon nanotubes resting on nonlinear elastic foundation. Structural Engineering and Mechanics 70(6):737–750. https://doi.org/10.12989/sem.2019.70.6.737

    Article  Google Scholar 

  79. Mohamed N, Mohamed SA, Eltaher MA (2020) Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Engineering with Computers. https://doi.org/10.1007/s00366-020-00976-2

    Article  Google Scholar 

  80. Mohanty A, Varghese MP, Behera RK (2019) Coupled nonlinear behavior of beam with a moving mass. Appl Acoust 156:367–377. https://doi.org/10.1016/j.apacoust.2019.07.024

    Article  Google Scholar 

  81. Nawar MT, Arafa IT, Elhosseiny O (2020) Numerical investigation on effective spans ranges of perforated steel beams. Structures 25:398–410. https://doi.org/10.1016/j.istruc.2020.03.026

    Article  Google Scholar 

  82. Nix WD, Gao H (1998) Indentation size effects in crystalline materials: a law for strain gradient plasticity. J Mech Phys Solids 46(3):411–425. https://doi.org/10.1016/S0022-5096(97)00086-0

    Article  MATH  Google Scholar 

  83. Ozarpa C, Esen I (2020) Modelling the dynamics of a nanocapillary system with a moving mass using the non-local strain gradient theory. Mathematical Methods in the Applied Sciences. https://doi.org/10.1002/mma.6812

    Article  Google Scholar 

  84. Park SK, Gao XL (2008) Variational formulation of a modified couple stress theory and its application to a simple shear problem. Zeitschrift für angewandte Mathematik und Physik 59(5):904–917. https://doi.org/10.1007/s00033-006-6073-8

    Article  MathSciNet  MATH  Google Scholar 

  85. Rajasekaran S, Khaniki HB (2019) Size-dependent forced vibration of non-uniform bi-directional functionally graded beams embedded in variable elastic environment carrying a moving harmonic mass. Appl Math Model 72:129–154. https://doi.org/10.1016/j.apm.2019.03.021

    Article  MathSciNet  MATH  Google Scholar 

  86. Rapaport, D. C., & Rapaport, D. C. R. (2004). The art of molecular dynamics simulation. Cambridge university press.

  87. Rappé AK, Casewit CJ, Colwell KS, Goddard WA III, Skiff WM (1992) UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J Am Chem Soc 114(25):10024–10035. https://doi.org/10.1021/ja00051a040

    Article  Google Scholar 

  88. Rebeiz, G. M. (2004). RF MEMS: theory, design, and technology. John Wiley & Sons.

  89. Reddy JN (2011) Microstructure-dependent couple stress theories of functionally graded beams. J Mech Phys Solids 59(11):2382–2399. https://doi.org/10.1016/j.jmps.2011.06.008

    Article  MathSciNet  MATH  Google Scholar 

  90. Sahu NK, Biswal DK, Joseph SV, Mohanty SC (2020) Vibration and damping analysis of doubly curved viscoelastic-FGM sandwich shell structures using FOSDT. Structures 26:24–38. https://doi.org/10.1016/j.istruc.2020.04.007

    Article  Google Scholar 

  91. Semmah, A., Heireche, H., Bousahla, A. A., & Tounsi, A. (2019). Thermal buckling analysis of SWBNNT on Winkler foundation by non local FSDT. Advances in nano research, 7(2), 89. https://doi.org/https://doi.org/10.12989/anr.2019.7.2.089

  92. Shariati A, Habibi M, Tounsi A, Safarpour H, Safa M (2020) Application of exact continuum size-dependent theory for stability and frequency analysis of a curved cantilevered microtubule by considering viscoelastic properties. Engineering with Computers. https://doi.org/10.1007/s00366-020-01024-9

    Article  Google Scholar 

  93. Sharma JN, Kaur R (2015) Response of anisotropic thermoelastic micro-beam resonators under dynamic loads. Appl Math Model 39(10–11):2929–2941. https://doi.org/10.1016/j.apm.2014.11.019

    Article  MathSciNet  MATH  Google Scholar 

  94. She GL, Liu HB, Karami B (2020) On resonance behavior of porous FG curved nanobeams. Steel Compos. Struct 36:179–186. https://doi.org/10.12989/scs.2020.36.2.179

    Article  Google Scholar 

  95. Sheng GG, Wang X (2017) The geometrically nonlinear dynamic responses of simply supported beams under moving loads. Appl Math Model 48:183–195. https://doi.org/10.1016/j.apm.2017.03.064

    Article  MathSciNet  MATH  Google Scholar 

  96. Şimşek M (2010) Vibration analysis of a single-walled carbon nanotube under action of a moving harmonic load based on nonlocal elasticity theory. Physica E 43(1):182–191. https://doi.org/10.1016/j.physe.2010.07.003

    Article  Google Scholar 

  97. Şimşek M, Aydın M, Yurtcu HH, Reddy JN (2015) Size-dependent vibration of a microplate under the action of a moving load based on the modified couple stress theory. Acta Mech 226(11):3807–3822. https://doi.org/10.1007/s00707-015-1437-9

    Article  MathSciNet  MATH  Google Scholar 

  98. Tawfik M (2008) Dynamics and stability of stepped gun-barrels with moving bullets. Advances in Acoustics and vibration. https://doi.org/10.1155/2008/483857

    Article  Google Scholar 

  99. Tlidji Y, Zidour M, Draiche K, Safa A, Bourada M, Tounsi A, Mahmoud SR (2019) Vibration analysis of different material distributions of functionally graded microbeam. Struct Eng Mech 69(6):637–649. https://doi.org/10.12989/sem.2019.69.6.637

    Article  Google Scholar 

  100. Toupin RA (1964) Theories of elasticity with couple-stress. Arch Ration Mech Anal 17:85–112. https://doi.org/10.1007/BF00253050

    Article  MathSciNet  MATH  Google Scholar 

  101. Wu JJ (2005) Dynamic analysis of an inclined beam due to moving loads. J Sound Vib 288(1–2):107–131. https://doi.org/10.1016/j.jsv.2004.12.020

    Article  MATH  Google Scholar 

  102. Wu Y, Zhang X, Leung AYT, Zhong W (2006) An energy-equivalent model on studying the mechanical properties of single-walled carbon nanotubes. Thin-walled structures 44(6):667–676. https://doi.org/10.1016/j.tws.2006.05.003

    Article  Google Scholar 

  103. Yang FACM, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743. https://doi.org/10.1016/S0020-7683(02)00152-X

    Article  MATH  Google Scholar 

  104. Yang DS, Wang CM (2019) Dynamic response and stability of an inclined Euler beam under a moving vertical concentrated load. Eng Struct 186:243–254. https://doi.org/10.1016/j.engstruct.2019.01.140

    Article  Google Scholar 

  105. Zhang ZJ, Zhang QC, Li FC, Yang JW, Liu JW, Liu ZY, Jin F (2019) Modal characteristics of micro-perforated sandwich beams with square honeycomb-corrugation hybrid cores: A mixed experimental-numerical study. Thin-Walled Structures 137:185–196. https://doi.org/10.1016/j.tws.2019.01.004

    Article  Google Scholar 

  106. Zhang Q, Liu H (2020) On the dynamic response of porous functionally graded microbeam under moving load. Int J Eng Sci 153:103317. https://doi.org/10.1016/j.ijengsci.2020.103317

    Article  MathSciNet  MATH  Google Scholar 

  107. Zine A, Bousahla AA, Bourada F, Benrahou KH, Tounsi A, Adda Bedia EA, Tounsi A (2020) Bending analysis of functionally graded porous plates via a refined shear deformation theory. Computers and Concrete 26(1):63–74. https://doi.org/10.12989/cac.2020.26.1.063

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Karabuk University, Karabuk, Turkey

    Ismail Esen

  2. Mechanical Design & Production Department, Faculty of Engineering, Zagazig University, P.O. Box 44519, Zagazig, Egypt

    Alaa A. Abdelrahman

  3. Mechanical Engineering Department, Faculty of Engineering, King Abdulaziz University, P.O. Box 80204, Jeddah, Saudi Arabia

    Mohamed A. Eltaher

  4. Faculty of Engineering, Zagazig University, Zagazig, Egypt

    Mohamed A. Eltaher

Authors
  1. Ismail Esen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alaa A. Abdelrahman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohamed A. Eltaher
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohamed A. Eltaher.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix

Appendix A

\({{\varvec{N}}}_{{\varvec{w}}}\left({\varvec{x}}\right)\) and \({{\varvec{N}}}_{{\varvec{\phi}}}({\varvec{x}})\) in Eq. (31) are

$$N_{w} \left( x \right) = \left[ {\begin{array}{*{20}c} {N_{w1} } & {\begin{array}{*{20}c} {N_{w2} } & {\begin{array}{*{20}c} {N_{w3} } & {N_{w4} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
$$N_{\phi } \left( x \right) = \left[ {\begin{array}{*{20}c} {N_{\phi 1} } & {\begin{array}{*{20}c} {N_{\phi 2} } & {\begin{array}{*{20}c} {N_{\phi 3} } & {N_{\phi 4} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(A.1)

where

$$N_{w1} = 1 + \frac{1}{{\left( {1 + \Phi } \right)}}\left[ {2\left( \frac{x}{L} \right)^{3} - 3\left( \frac{x}{L} \right)^{2} - \Phi \left( \frac{x}{L} \right)} \right],$$
$$N_{w2} = \frac{L}{{2\left( {1 + \Phi } \right)}}\left[ {2\left( \frac{x}{L} \right)^{3} - \left( {4 + \Phi } \right)\left( \frac{x}{L} \right)^{2} + \left( {2 + \Phi } \right)\left( \frac{x}{L} \right)} \right],$$
$$N_{w3} = \frac{1}{{\left( {1 + \Phi } \right)}}\left[ {3\left( \frac{x}{L} \right)^{2} - 2\left( \frac{x}{L} \right)^{3} + \Phi \left( \frac{x}{L} \right)} \right],$$
(A.2)
$$N_{w4} = \frac{L}{{2\left( {1 + \Phi } \right)}}\left[ {2\left( \frac{x}{L} \right)^{3} + \left( {\Phi - 2} \right)\left( \frac{x}{L} \right)^{2} - \Phi \left( \frac{x}{L} \right)} \right]$$
$$N_{\phi 1} = - \frac{6}{{L\left( {1 + \Phi } \right)}}\left( \frac{x}{L} \right)\left( {1 - \frac{x}{L}} \right)$$
$$N_{\phi 2} = \left[ {1 - \frac{3}{{\left( {1 + \Phi } \right)}}} \right]\left( \frac{x}{L} \right)\left( {1 - \frac{x}{L}} \right),$$
(A.3)
$$N_{\phi 3} = \frac{6}{{L\left( {1 + {\Phi }} \right)}}\left( \frac{x}{L} \right)\left( {1 - \frac{x}{L}} \right),$$
$$N_{\phi 4} = \left[ {1 - \frac{3}{{\left( {1 + \Phi } \right)}}\left( {1 - \frac{x}{L}} \right)} \right]\left( \frac{x}{L} \right)$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Esen, I., Abdelrahman, A.A. & Eltaher, M.A. Dynamics analysis of timoshenko perforated microbeams under moving loads. Engineering with Computers 38, 2413–2429 (2022). https://doi.org/10.1007/s00366-020-01212-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01212-7

Keywords

Search

Navigation