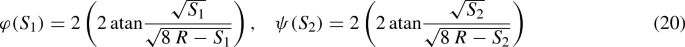1 Introduction

The advent of new manufactory technologies [22, 45, 56], like 3D printing, and the increasing demand for materials with high-performance render desirable design techniques for advanced forms of micro-structured materials have been but little considered heretofore. Accordingly, many research lines have been initiated with the aim of setting up general methods of synthesis of micro-structures for obtaining materials with a macroscopic behavior designed for satisfying given requirements [9, 12, 14, 57, 73, 79, 80, 82]. These materials conceived for fulfilling one or more given functions belong to the set of the generalized continuum materials for which is their microstructure that confers the desired properties. This point of view is what characterizes the so-called metamaterials. Although their first appearance was in the field of electromagnetic and optical applications, soon enough there have been developments also in the mechanical field (see, e.g., [5, 15, 20, 48, 69]). The rationale for the synthesis of such materials is quite ancient. Indeed, the same approach can be found in the synthesis of mechanisms [55, 62, 64, 66] or electric networks [11]. In both cases, there are elemental components with specific properties that, if properly connected to each other, are capable of producing a whole system providing the desired functioning. However, since the introduction of metamaterials is rather recent, a systematic way to design micro-structures is not yet fully developed, as in the case of mechanisms and electric networks. Therefore, the metamaterials proposed up to now in the literature are the results of some researchers’ clever intuition.

Another key aspect concerning the development of metamaterials is the possible multi-disciplinarity of them. Often to obtain the desired results, it is possible to use components with different physical characteristics. Since the design of such materials starts from the functions for which they are conceived, and therefore from the governing equations, because of the analogy between systems of different nature based on these equations [23, 50, 72], it is possible to obtain very particular systems such as piezoelectro-mechanical structures that can be used to shield or reduce vibrations as well as to harvest energy [4, 33, 53].

Typical examples of micro-structured materials that can be used as an archetype for metamaterials are: micropolar materials [8, 10], functionally graded materials [6, 7, 21, 24, 37] cellular materials and foams [47, 61], granular materials [58, 59, 78], lattice materials [2, 3, 35, 36, 38, 49, 71, 74], multi-scale materials [25, 26, 30, 44, 83], materials with non-local properties [31, 46]. Indeed, the changing in a specific way of their microstructure provides a significant alteration in the macroscopic behavior that can be used to obtain high-performances.

A relevant kind of metamaterial is the pantographic structure conceived as an example of material whose behavior can be described with an expression of energy that incorporates terms with the second gradient of the placement function [13, 27, 29, 32, 51, 52, 54, 60, 68, 77]. This is a light material with a huge range of deformation in the elastic regime. Some alternatives of this type of material have been proposed recently for the 1D [18, 42, 76] and 2D case [16, 17].

The pantographic material is made of two straight families of fibers connected to each other with small deformable cylinders (also known as pivots) or hinges to provide a micro-structure that reproduces a pantograph mechanism periodically. In this paper, the micro-structure of a pantographic material is employed locally but using fibers that are not anymore straight. The idea is to generalize the pantographic sheet to obtain a more general theoretical foundation that can be exploited to improve the basic performance of that structure. A numerical identification has been performed to obtain the stiffnesses needed for describing the system in the framework of the bi-dimensional continuous elastic theory following the ideas proposed in [1, 43, 63, 65, 81]. At the end of the paper, an example of topological optimization is presented to illustrate the potentialities of the proposed modeling.

2 Modeling lattice shells

A net constructed by two families of flexible elastic fibers can be described within the purview of the two-dimensional strain-gradient elasticity theory [39, 41, 70, 75]. Herein, the kinematical assumptions made for the network are: i) the fibers are treated as shear undeformable beams, namely their cross sections preserve the orthogonality to the tangent vector at each point of the axis in any configuration; ii) the points where the fiber axes belonging to the two families of curves intersect (joints) share the same position in any configuration; iii) at the joints the only degree of freedom admitted is a relative rotation of the cross sections with respect to the normal vector to the current tangent plane that is the span of the two tangent vectors of the fibers themselves. In this context, the kinematical description of the system is given by the surface, \({\mathcal {S}}\), whose points in the current configuration, \({\varvec{x}}=(x_{1}, x_{2}, x_3) \in \mathbb {R}^{3}\), are expressed in terms of the correspondent points in the reference configuration, \({\varvec{X}}=(X_{1}, X_{2}) \in \varOmega \subset \mathbb {R}^{2}\).

By introducing the components of displacement \(u_{i}\) between the two configurations, the explicit expression of the placement map is expressed by

$$\begin{aligned} {\varvec{x}}=\varvec{\chi }({\varvec{X}})=X_{\alpha }{\mathbf {e}}_{\alpha } +u_{i}({\varvec{X}})\,{\mathbf {e}}_{i} \end{aligned}$$
(1)

where Greek indexes range from 1 to 2 and Latin ones from 1 to 3, the summation convention is adopted for both of them, and the unit vectors \(\{{\mathbf {e}}_{i}\}\) constitute the basis employed to represent the surface \({\mathcal {S}}\). Since the elastic surface considered is assumed to be an infinite distribution of two families of curved fibers, a parametric representation of the central line of these fibers is introduced through the two abscissae \(S_\beta \) in the reference configuration as \({\varvec{X}}={\varvec{X}}(S_\beta )\). Naturally, this representation is inherited by the surface in the current configuration by means of the map (1). Having chosen \(S_\beta \) as a unit-speed parametrization, the reference tangent vectors to the fibers are of unitary length and explicitly

$$\begin{aligned} {\varvec{D}}_\beta ({\varvec{X}})=\frac{\mathrm {d} X_{\alpha }}{\mathrm {d} S_\beta }{\mathbf {e}}_{\alpha } \end{aligned}$$
(2)

Besides, the tangent vectors to the fibers in the current configuration, with the same parametrization, are

$$\begin{aligned} \lambda _\beta ({\varvec{X}})\, {\varvec{d}}_\beta ({\varvec{X}})=\frac{\mathrm {d} \varvec{\chi }}{\mathrm {d} S_\beta }({\varvec{X}}) = {\varvec{F}}({\varvec{X}}) \,{\varvec{D}}_\beta ({\varvec{X}}) \end{aligned}$$
(3)

where \(\lambda _\beta = \Vert {\varvec{F}}\,{\varvec{D}}_\beta \Vert \) and \({\varvec{F}}=\nabla \!_{_{{\varvec{X}}}}\varvec{\chi }\), namely a tensor whose matrix representation has dimension \(3\times 2\), and \({\varvec{d}}_\beta \) are the unit tangent vectors to the fibers in the current configuration. The unit normal field to the surface \({\mathcal {S}}\) is then

$$\begin{aligned} {\varvec{n}}({\varvec{X}})=\frac{{\varvec{d}}_1 \times {\varvec{d}}_2}{\left\| {\varvec{d}}_1\times {\varvec{d}}_2 \right\| } \end{aligned}$$
(4)

In the particular case of orthogonal fibers (\({\varvec{D}}_1 \cdot {\varvec{D}}_2 =0\)), the unit normal vector simplifies in

$$\begin{aligned} {\varvec{n}}({\varvec{X}})=\frac{\varepsilon _{ijk}\, F_{j2}\,F_{k1}\,{\mathbf {e}}_i}{\left\| \varepsilon _{ijk}\,F_{j2}\,F_{k1}\,{\mathbf {e}}_i\right\| } \end{aligned}$$
(5)

where \(\varepsilon _{ijk}\) is the Levi–Civita symbol.

With the intention to model the fibers as Kirchhoff’s rods, for each family of them, a rotation tensor

$$\begin{aligned} {\varvec{R}}_\beta : \{{\mathbf {e}}_i\}\mapsto \{{\varvec{d}}_{\beta },\ {\varvec{n}} \times {\varvec{d}}_{\beta },\ {\varvec{n}}\} \end{aligned}$$
(6)

is introduced to express the cross section orientation of fibers, i.e., beam-like bodies, based on the oriented director triads previously defined. Therefore, the curvature tensor

$$\begin{aligned} {\varvec{W}}_\beta = {\varvec{R}}_\beta ^\top \, \frac{\mathrm {d} {\varvec{R}}_\beta }{\mathrm {d} S_\beta } \end{aligned}$$
(7)

is considered for evaluating, respectively, the twisting and the out-of-plane and geodesic curvatures as follows:

$$\begin{aligned} \kappa _{T\beta }= \left( {\varvec{n}}\times {\varvec{d}}_\beta \right) \cdot \frac{\mathrm {d} {\varvec{n}}}{\mathrm {d} S_\beta }; \quad \kappa _{n\beta }= {\varvec{n}} \cdot \frac{\mathrm {d} {\varvec{d}}_\beta }{\mathrm {d} S_\beta }; \quad \kappa _{g\beta }= - \left( {\varvec{n}}\times {\varvec{d}}_\beta \right) \cdot \frac{\mathrm {d} {\varvec{d}}_\beta }{\mathrm {d} S_\beta } \end{aligned}$$
(8)

The differentiation with respect to the curvilinear abscissa \(S_\beta \) is directly evaluated through Eq. (3) as

$$\begin{aligned} \frac{\mathrm {d} {\varvec{d}}_\beta }{\mathrm {d} S_\beta } = \frac{1}{\lambda _\beta }\left[ \nabla \!_{_{{\varvec{X}}}}{\varvec{F}} \vert {\varvec{D}}_\beta \otimes {\varvec{D}}_\beta + {\varvec{F}}\!\left( \nabla \!_{_{{\varvec{X}}}}{\varvec{D}}_\beta \, {\varvec{D}}_\beta \right) \right] - \frac{\mathrm {d} \lambda _\beta }{\mathrm {d} S_\beta }\frac{{\varvec{d}}_\beta }{\lambda _\beta } \end{aligned}$$
(9)

denoting the above quantities in components as

$$\begin{aligned} \begin{aligned} (\nabla \!_{_{{\varvec{X}}}}{\varvec{F}} \vert {\varvec{D}}_\beta \otimes {\varvec{D}}_\beta )_i&= \frac{\partial F_{i\alpha }}{\partial X_\eta }({\varvec{D}}_\beta )_\eta ({\varvec{D}}_\beta )_{\alpha } \\ (\nabla \!_{_{{\varvec{X}}}}{\varvec{D}}_\beta \, {\varvec{D}}_\beta )_\alpha&= \frac{\mathrm {d}^2 X_{\alpha }}{\mathrm {d} {S_\beta }^2} \end{aligned} \end{aligned}$$

Similarly, the derivative of \({\varvec{n}}\) with respect to \(S_\beta \) can be easily computed.

In the considered framework, a possible choice for the measures of deformation inherited by the presence of the fibers incorporated in the surface \({\mathcal {S}}\) is

  1. 1.

    the fiber stretching

    $$\begin{aligned} \varepsilon _\beta =\lambda _\beta -1 \end{aligned}$$
    (10)
  2. 2.

    the shear distortion angle

    $$\begin{aligned} \gamma =\mathrm {asin} \left( {\varvec{d}}_1 \cdot {\varvec{d}}_2\right) \end{aligned}$$
    (11)
  3. 3.

    the curvature change

    $$\begin{aligned} \varDelta \kappa _{T\beta }=\kappa _{T\beta } -\kappa _{T\beta }^0, \quad \varDelta \kappa _{n\beta }=\kappa _{n\beta } -\kappa _{n\beta }^0, \quad \varDelta \kappa _{g\beta }=\kappa _{g\beta } -\kappa _{g\beta }^0 \end{aligned}$$
    (12)

If the reference configuration is planar \(\kappa _{T\beta }^0=0\), \(\kappa _{n\beta }^0=0\), the only curvature different from zero is the geodesic one that can be calculated as

$$\begin{aligned} \kappa _{g\beta }^0= - \left( {\mathbf {e}}_{3}\times {\varvec{D}}_\beta \right) \cdot \frac{\mathrm {d} {\varvec{D}}_\beta }{\mathrm {d} S_\beta } \end{aligned}$$
(13)

The elastic energy of the lattice shell, which is plane for the reference configuration, can be postulated as

$$\begin{aligned} 2 U\left[ \varvec{\chi }(\cdot )\right] =&\int _{\varOmega } \sum _{\beta =1}^2 K_{e\beta } \left( \lambda _\beta -1\right) ^2 \,\mathrm {d}\varOmega + \int _{\varOmega } K_{s} \gamma ^2 \,\mathrm {d}\varOmega \nonumber \\&+ \int _{\varOmega } \sum _{\beta =1}^2 K_{g\beta } (\kappa _{g\beta } -\kappa _{g\beta }^0)^2 \,\mathrm {d}\varOmega + \int _{\varOmega } \sum _{\beta =1}^2 K_{n\beta } (\kappa _{n\beta })^2 \,\mathrm {d}\varOmega + \int _{\varOmega } \sum _{\beta =1}^2 K_{T\beta } (\kappa _{T\beta })^2 \,\mathrm {d}\varOmega \end{aligned}$$
(14)

where \(K_{e\beta }\), \(K_{s}\), \(K_{g\beta }\), \(K_{n\beta }\), and \(K_{T\beta }\) are positive material parameters representing stretching, shearing, geodesic and normal bending, and twisting stiffness, respectively, for the two families of fibers.

By introducing the skew tensor field

$$\begin{aligned} {\varvec{V}}_\beta = {\varvec{R}}^\top _\beta \, \dot{{\varvec{R}}}_\beta \end{aligned}$$
(15)

where the dot denotes differentiation with respect to the time, the angular velocity pertained to the cross section of the fibers can be evaluated as the components of the axial vector of \({\varvec{V}}_\beta \), namely

$$\begin{aligned} \omega _{\beta 1}= \left( {\varvec{n}}\times {\varvec{d}}_\beta \right) \cdot \dot{{\varvec{n}}}; \quad \omega _{\beta 2}= {\varvec{n}} \cdot \dot{{\varvec{d}}_\beta }; \quad \omega _{\beta 3}= - \left( {\varvec{n}}\times {\varvec{d}}_\beta \right) \cdot \dot{{\varvec{d}}_\beta } \end{aligned}$$
(16)

Considering the particular arrangement of fibers, the kinetic energy can be expressed as follows:

$$\begin{aligned} 2 T \left[ \varvec{\chi }(\cdot ),\dot{\varvec{\chi }}(\cdot )\right] = \int _{\varOmega } \varrho _s ({\dot{u}}_1^2 + {\dot{u}}_2^2 + {\dot{u}}_3^2) \,\mathrm {d}\varOmega + \int _{\varOmega } \sum _{\beta =1}^2\left[ J_{\beta 1} ( {\omega _{\beta 1}})^2 + J_{\beta 2} ( {\omega _{\beta 2}})^2 + J_{\beta 3} ( {\omega _{\beta 3}})^2 \right] \,\mathrm {d}\varOmega \end{aligned}$$
(17)

where \(\varrho _s\) is the apparent mass density per unit area, \(J_{\beta i}\) are inertial parameters that can be evaluated, as a first approximation, as the moments of inertia of the cross section of fibers per unit line, i.e., \(\varrho I_{\beta i}/p_\beta \), where \(\varrho \) is the apparent mass density (per unit volume), \(I_{\beta i}\) are the second moments of area with respect to the directions \({\varvec{D}}_1\), \({\varvec{D}}_2\), \({\mathbf {e}}_3\), and \(p_\beta \) is the pitch between fibers belonging to the \(\beta \) family. All these parameters can be possibly function of \({\varvec{X}}\). The equation that rules the motion, therefore, can be deduced by the principle of the least action, defining the Lagrangian function \(L=U-T\).

3 The case of a cycloidal metamaterial

To analyze the distinctive aspects of the proposed model (say macro-model), both the benefits and the drawbacks, as well as the limit of the range of its applicability, a comparison with a more refined model (referred to as micro-model) is performed for a particular arrangement of fibers. Specifically, the micro-model employs the standard theory of 3D elasticity, making use of a very detailed geometry of the sample at the scale level of the fibers. This kind of modeling is of no use in the real-world applications for the computational burden required. Still, it is beneficial for comparison purposes and to obtain the material parameters needed by the macro-model via a micro–macro-identification procedure, in this case, numerical. Since the considered system might experience large deformation, both the models are nonlinear. The kind of nonlinearities taken into account are geometrical: In the macro-model, they appear in the nonlinear expressions of the deformation measures, being the energy density a quadratic form of them; analogously in the micro-model, the strain tensor is the Green–Saint-Venant one, and the Kirchhoff–Saint-Venant constitutive relationship is resorted to.

Fig. 1
figure 1

Sample with cycloidal fibers: perspective view (top); scheme of the fiber arrangement (bottom)

Full size image

In what follows, a sample with a cycloidal orthogonal net is chosen for its promising mechanical features [67] (see Fig. 1). The fibers have a square cross section of length \(a=1\) mm; the connections between the two families of fibers are cylinders of radius \(r_p=0.45\) mm and height \(h_p=1\) mm. The curves representing the axis of the fibers are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{1} = R \left( \varphi - \sin \varphi \right) +\alpha \\ X_{2} = R \left( 1 - \cos \varphi \right) \end{array}\right. } \end{aligned}$$
(18)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{1} = R \left( \psi - \sin \psi \right) +\beta \\ X_{2} = R \left( 1 + \cos \psi \right) \end{array}\right. } \end{aligned}$$
(19)

where the parameter R is set to be 35 mm, \(\varphi \), and \(\psi \), are specific abscissae along the curves, and \(\alpha \) and \(\beta \) are constants that identify the particular curve belonging to the familyFootnote 1. Indeed, in this fiber arrangement, the two arrays of curves are obtained simply by translating the first curve (passing through \(X_1=0\)) along the \(X_1\) axis of \(\alpha \) or \(\beta \). In the examined case, this translation is equal to R/4, namely 8.75 mm. The whole specimen has a rectangular plan, identifiable with \(\varOmega \), of size \((2 R-s) \times 2 \pi R\), being \(s=4.2\) mm and the bottom left corner has coordinate in the plane \(X_1\)-\(X_2\): (0, s/2). The reason for the choice of such a domain is twofold: i) The fibers nearby \(X_2=0\) and \(X_2=2 R\) become too dense, and therefore, the sample cannot be produced, for example, with a 3D printing process, for the fibers would merge in these zones; ii) on these same lines, the expressions of the curvatures \(\kappa _{g\beta }^0\) are not defined.

The material parameters used for the numerical simulations with the micro-model are typical for the polyamide that can be used in 3D printing, namely: the elastic modulus \(Y=1600\) MPa, the shear modulus G evaluated with the assumption of isotropic material, Poisson’s ratio \(\nu =0.4\), and the mass density \(\rho =930\) kg/\(\hbox {m}^3\).

The material parameters for the macro-model are assumed to be:

$$\begin{aligned} K_{e\beta } = \eta _e \frac{Y A}{p_\beta }, \quad K_{T\beta } = \eta _T \frac{G J_t}{p_\beta }, \quad K_{n\beta } = \eta _n \frac{Y J_{fn}}{p_\beta }, \quad K_{g\beta } = \eta _g \frac{Y J_{fg}}{p_\beta }, \quad K_s = \eta _s \frac{G J_p}{h_p\, p_1 p_2} \end{aligned}$$
(21)

where A is the cross section area of the fibers, \( J_t=0.196\, a^4\) and \(J_{fn}= J_{fg}=a^4/12\) are the torsional and flexural second moment of area of the beam cross sections, and \(J_p = \pi \, r_p^4/2\) is the torsional second moment of area of the pivot. The parameters \(p_\beta \) are the cell size in the orthogonal direction to \({\varvec{D}}_\beta \) (see Fig. 2). Specifically, they are evaluated using the three-dimensional specimen in correspondence of each pivot as the sum of the two half distances between the considered pivot and the adjacent ones on the orthogonal fiber to direction \({\varvec{D}}_\beta \). In Fig. 2, they are plotted as a discrete sequence of circles as a function of \(X_2\)-coordinate. Clearly, since the cycloids are translated along the \(X_1\) axis, the values of \(p_\beta \) are not dependent on \(X_1\). All the curves of the same family have the same \(p_\beta \), keeping fixed the value of \(X_2\). It is worth noting that the extreme values of \(p_\beta \) are sensibly lower than the others because, on the boundaries, only one-half cell must be considered. For this reason, the stiffnesses on those boundaries are larger, entailing a different behavior in these zones, although concentrated on the verges. Besides, in Fig. 2 are also shown trend lines of these quantities obtained as functions proportional to the modulus of the tangent vector to the cycloids (18) and (19) in Cartesian coordinates, namely

$$\begin{aligned} h_{1} = \frac{1}{8}\sqrt{2 R (2 R -X_2)}, \quad h_{2} = \frac{1}{8}\sqrt{2 R X_2} \end{aligned}$$
(22)

The coefficients \(\eta \) are correcting factors to be determined with a micro–macro-identification procedure as done in [28]. The values are listed in Table 1.

Table 1 The tuned coefficients \(\eta \)
Full size table

The distribution of the mass density for the macro-model has been evaluated using the three-dimensional sample. This last has been divided into a finite number of strips along the longitudinal direction, keeping in mind that there is no dependence on \(X_1\), cut in correspondence of the pivots. For each strip, the volume has been computed and then, using the mass density \(\rho \), the mass of the same part. Finally, the mass has been smeared on the corresponding section of the domain \(\varOmega \) to obtain \(\varrho _s\) (see Fig. 3). The parameters \( J_{\beta i}\) are evaluated with formulae analogous to \(K_{T\beta }\), \(K_{n\beta }\), and \(K_{g\beta }\) in Eq. (21) to retrieve the inertia of the cross section fibers per unit area.

For the sake of completeness, the unit tangent vectors to the cycloidal fibers are given in components as follows:

$$\begin{aligned} {\varvec{D}}_{1} \equiv \left( \sqrt{\frac{X_2}{2R}}, \sqrt{1-\frac{X_2}{2R}},0\right) , \quad {\varvec{D}}_{2} = {\varvec{D}}_{1}\times {\mathbf {e}}_3 \end{aligned}$$
(23)

their derivatives with respect to \(S_\beta \) become

$$\begin{aligned} \frac{\mathrm {d} {\varvec{D}}_1}{\mathrm {d} S_1} \equiv \left( \sqrt{\frac{2R-X_2}{16 R^2 \,X_2}}, -\frac{1}{4R},0\right) , \quad \frac{\mathrm {d} {\varvec{D}}_2}{\mathrm {d} S_2} \equiv \left( \sqrt{\frac{X_2}{16 R^2 \,(2R-X_2)}}, \frac{1}{4R},0\right) \end{aligned}$$
(24)

therefore, the curvatures in the reference configuration are given by

$$\begin{aligned} \kappa _{g1}^0 = -\frac{1}{\sqrt{8 R X_2}}, \quad \kappa _{g2}^2 = \frac{1}{\sqrt{8 R (2 R -X_2)}} \end{aligned}$$
(25)
Fig. 2
figure 2

Cell lengths in the orthogonal direction to \({\varvec{D}}_\beta \): \(p_\beta \) evaluated on the 3D specimen (circle markers) and analytical trend lines (gray lines)

Full size image
Fig. 3
figure 3

Distribution of the mass density per unit area

Full size image

3.1 Micro–macro-identification

To determine the material parameters appearing in Eq. (14), two numerical tests are thought devoted to comparing the results of the micro- and macro-models and establishing an equivalence between them. In particular, an inverse analysis is performed to find the correcting factors \(\eta \) defined in Eq. (21), which may make the two models equivalent by an energetic viewpoint and to provide equilibrium shapes as near as possible. The employed approach is explained in detail in [28]. The key idea is to use two or more tests for which some of the energetic contributions of Eq. (14) are complementarily null. In this way, it is possible to find a restricted set of them without affecting the values of the others. The general concept is quite ancient: divide the problem into simpler subproblems and solve them separately. The energetic orthogonality, namely the absence of coupling terms, makes this approach suitable.

The chosen tests are tensile and out-of-plane shear ones. The energies and the equilibrium shapes are obtained by using the finite element method directly exploiting Eq. (14) for the macro-model, while for the micro model, a standard structural mechanics tool supplies the results. The rationale of this selection lies in the fact that in a tensile test are activated primarily only the mechanisms of deformation related to stretching, geodesic bending, and shearing at the macroscopic level. Therefore, the stiffnesses \(K_{e\beta }\), \(K_{g\beta }\), and \(K_{s}\) are mainly involved, being negligible the effects of the others. On the other hand, the sliding motion resulting from the out-of-plane shear test is characterized by deformations pertained to the out-of-plane bending and the twisting of the fibers; thereby, \(K_{n\beta }\) and \(K_{T\beta }\) can be identified.

Fig. 4
figure 4

Equilibrium shape for the tensile test under an imposed displacement \(u_1=R\): a micro-model; b macro-model. Colors indicate the out-of-plane displacement \(u_3\)

Full size image
Fig. 5
figure 5

Equilibrium shape for the tensile test under an imposed displacement \(u_1=R\): comparison through the overlapping of the material lines (black) obtained by the macro-model and the result of the micro-model in colors

Full size image
Fig. 6
figure 6

Energy vs. displacement plot for the tensile test. In the graph, the total energy obtained by the two models are reported. The contributions due to the fibers (with the label beam) and the pivots are also shown

Full size image

The tensile test has been conducted fixing one short edge and imposing a displacement in the \(X_1\) direction on the opposite one from 0 to \(u_1=R\): For the micro model, the displacements have been prescribed at the handles (see Figs. 4, 5 and 6); in the case of the macro-model since it is a second gradient material, also the normal derivative of \(u_3\), namely \(\partial u_{3} / \partial X_{1}\), for the constrained edges has been set to zero to mimic the restraint device employed in the micro model. Since the only parameter involved in the shear deformation at the macro-level is \(K_{s}\), the shear contribution of the energy is settled as an objective function to determine it in the identification procedure. Besides, the energy associated with the beams is taken to identify the rigidity \(K_{e\beta }\) and \(K_{g\beta }\) in a multi-objective procedure of tuning for the two models. In this test, the contributions attributable to the beam deformation primarily are the stretching and the bending on the tangent plane, i.e., geodetic. During the macro-model calibration, the coefficients \(\eta \) related to the remaining stiffnesses are set to one.

Figure 4 displays the equilibrium shape at the end of the test for the two models, while Fig. 5 shows a comparison between the results obtained by overlapping the two final current configurations. The macro-shape is presented by means of material lines that lie in correspondence with the cycloids characterizing the sample. The correspondence between the results is remarkable, at least in the plane \(X_1\)-\(X_2\). During the test, the sample experiences a buckling, as evidenced by the out-of-plane displacement. Although both models are able to predict this kind of behavior, in a more accurate inspection, some little differences can be detected in this component of the displacement. In the micro model, it is evident a small lack of symmetry in the out-of-plane deformation despite the symmetry of the test. This little discrepancy is easily explained by the presence of the non-symmetry in the geometry of the specimen. Indeed, the fibers are not arranged in the same plane and are offset by a certain amount [40]. In Fig. 6, energy contributions of the pivots and the fibers/beams are shown, as well as their total amount for both the models. The match between the graphs is in good agreement until about 25 mm (\(\sim 11.4\)% of the whole length of the sample) where the buckling starts, and then, there is a little difference, due to the complex geometry at the level of fibers, which is not taken into account in the macro-model and it is amplified when the deformations become very large.

Fig. 7
figure 7

Equilibrium shape for the out-of-plane shear test under an imposed displacement of 2R: a micro-model; b macro-model. Colors indicate the out-of-plane displacement

Full size image
Fig. 8
figure 8

Comparison of the displacement \(u_3\) in the out-of-plane shear test under an imposed displacement of 2R: at the middle longitudinal line (a); on one long edge (b)

Full size image
Fig. 9
figure 9

Energy vs. displacement plot for the out-of-plane shear test. In the graph, the total energy obtained by the two models are reported. The contributions due to the fibers (with the label beam) and the pivots are also shown

Full size image

The out-of-plane shear test has been conducted by fixing one short edge and imposing the component of the displacement \(u_3\) on the opposite one from 0 to 2R (see Fig. 7). On the same moving edge, the displacement along \(X_1\) is kept free to avoid the activation of stretching deformation, while \(u_2\) has been constrained to zero. For this test also in the case of the macro-model, the normal derivative of \(u_3\), namely \(\partial u_{3} / \partial X_{1}\), for the constrained edges has been set to zero. In this case, the identification procedure has been performed with a cost function related to the total energy error and the displacement \(u_3\) at the middle longitudinal line. The coefficients \(\eta \) previously determined are currently fixed.

Figure 7 displays the equilibrium shape at the end of the test for the two models. The quantitative comparison is shown in Fig. 8 for the middle longitudinal line and for a long edge of the specimen (the other one is almost equal for symmetry reasons). In Fig. 9, the different energy contributions are exhibited, as well as their total amount for both the models.

The final configuration for the middle longitudinal line in both models is almost coincident (see Fig. 8a). Small deviations are instead perceptible near the long borders and for the energy contributions. The macro-model predicts zero energy in the pivot energy, while a small amount of it is involved in the micro model. This difference is due to the more general deformation of the pivots that at the micro-level also implies not-completely vanishing shear and bending deformations in these connections. These kinds of deformations produce some coupling between the deformations of the two layers of fibers. Therefore, a small discrepancy is also detected in the beam energy contribution. Finally, this complex behavior at the micro-scale produces also a small deviation in the deformation of the long edges, as displayed in Fig. 8b, since the macro-deformation is not dependent on \(X_2\). However, it is possible to conclude that the differences remain small and, therefore, not compromise the predictive abilities of the macro-model.

3.2 Supplementary tests

In this section, some more severe tests are examined to understand the limit of the applicability of the macro-model. The new tests are carried out using the rigidities identified in the previous section.

Fig. 10
figure 10

Equilibrium shape for the in-plane shear test under an imposed displacement of 2R obtained by the micro-model

Full size image
Fig. 11
figure 11

Equilibrium shape for the in-plane shear test under an imposed displacement of 2R obtained by the macro-model

Full size image
Fig. 12
figure 12

Graphs of comparison for the displacement \(u_3\) in the in-plane shear test at the probe points \(P_1\equiv (0.158, 0.0021)\) m and \(P_2 \equiv (0.0614, 0.0679)\) m

Full size image
Fig. 13
figure 13

Energy vs. displacement plot for the in-plane shear test. In the graph, the total energy obtained by the two models are reported. The contributions due to the fibers (with the label beam) and the pivots are also shown

Full size image

Firstly, a second shear test has been performed, fixing one short edge, imposing a displacement in the \(X_2\) direction on the opposite one from 0 to \(u_2=2 R\), and keeping zero the remaining components of the displacement (see Figs. 10, 11). Here, the ratio of stiffnesses is such that after a few millimeters from the starting of the test, an out-of-plane buckling occurs similar to that measured in [19] (see Fig. 12 for the plots of the displacement \(u_3\) associated with two probe points nearby the peaks of the values of the same displacement). It is worth noting that in order to follow the bifurcated equilibrium path, a defect has been introduced as a small distribution of forces at the beginning, which gradually fades as the test progresses. From Figs. 10, 11, and 12, a comparison between the equilibrium shapes provided by the micro and the macro-models can be made. The whole deformation obtained with the macro-model is sufficiently close to that of the micro model to catch the characteristic features. In Fig. 13, the distinct energy contributions are exhibited, as well as their total amount for both the models. The energy related to pivots is remarkably in good agreement for the two models, while the beam energy shows a certain bias (about 10% of the energy at the end of the test). As a matter of fact, by examining the deformation of the pivots, there are no sensible distortions in their shape, and therefore, the predominant torsional deformation hypothesis is confirmed. Most likely, since the kind of material considered is heterogeneous (very stiff at the borders and compliant in the middle), the bias in the energy of the beams can be due to the shear deformation in the beams themselves. Herein the Euler–Bernoulli hypothesis has been made to model the fibers cross sections, namely an internal constraint keeping the fiber cross sections orthogonal to the tangent of their center-line has been assumed. This constraint makes the macro-model fiber energy greater because of an excess of stiffness, as is seen in Fig. 13, thereby relaxing this assumption and considering the shear deformation in the fibers, their energy should decrease. Besides, the offset between the two layers of beams and the lack of symmetry in the equilibrium configuration may play a role in this behavior.

Fig. 14
figure 14

Equilibrium shape for the torsion test: a micro model; b macro-model

Full size image
Fig. 15
figure 15

Energy vs. angle plot for the torsion test. In the graph, the total energy obtained by the two models are reported. The contributions due to the fibers (with the label beam) and the pivots are also shown

Full size image

Thereafter a torsional test is conducted by fixing one short edge and rotating the other side until 3.5 rad with respect to the axis coinciding with the middle longitudinal line of the specimen (see Fig. 14). In this case, also, the equilibrium configurations resulting from the two models are in good agreement. As far as energies are concerned, Fig. 15 displays a good match for the pivot energy until about 3 rad, then a certain amount of discrepancy occurs yet maintaining the quality trend of a softening. Instead, the beam energy has an agreement until about 1.2 rad, then shows a noticeable difference. Probably here, the same effects discussed for the previous test plays a significant role and even amplified after 1.2 rad for the considerable deformations involved.

3.3 Modal analysis

In this section, a modal analysis around the reference configuration has been performed for the micro and the macro-models. Specifically, the first eight vibration modes have been determined. Figures 16, 17, 18, 19, 20, 21, 22 and 23 show a comparison of the modal shapes associated with the natural frequencies for both models. Table 2 lists their natural frequencies with relative errors.

From these results, it is possible to conclude that also from a dynamical point of view, the macro-model is able to capture the salient features, at least in the range of frequency examined.

Table 2 The first eight natural frequencies (Hz)
Full size table
Fig. 16
figure 16

First modal shape: a micro-model; b macro-model

Full size image
Fig. 17
figure 17

Second modal shape: a micro-model; b macro-model

Full size image
Fig. 18
figure 18

Third modal shape: a micro-model; b macro-model

Full size image
Fig. 19
figure 19

Fourth modal shape: a micro-model; b macro-model

Full size image
Fig. 20
figure 20

Fifth modal shape: a micro-model; b macro-model

Full size image
Fig. 21
figure 21

Sixth modal shape: a micro-model; b macro-model

Full size image
Fig. 22
figure 22

Seventh modal shape: a micro-model; b macro-model

Full size image
Fig. 23
figure 23

Eighth modal shape: a micro-model; b macro-model

Full size image

4 An example of stiffness optimization in lattice structures

The specific choice of the cycloidal arrangement of fibers allows us to obtain an attractive material for many applications since it is characterized by a stiff strip in the proximity of the large border and a core, which is very soft, in the middle of the sample. This behavior is a straightforward consequence of the fiber positioning and of their density per unit area. Until now, the connections between fibers have been conceived as identical cylinders. However, one can imagine improving the behavior of that material simply changing the geometry of these cylinders. Indeed, since the values of the shear stiffness \(K_s\) depend on the diameter of the cylindrical connections, it is possible to assume this diameter as a control variable to be optimized in view of the applications for which the material is meant to be used. The limit cases where the fibers belonging to different families i) can freely rotate relative to one another keeping parallel to the tangent plane and ii) are clamped, respectively, associated with \(K_s=0\) and a sufficiently large value of \(K_s\), can be easily obtained substituting the deformable cylinders with hinges and with cylinders having a large diameter whose deformation is negligible. All the intermediate values for \(K_s\) are related to deformable cylinders, possibly with different diameters.

In this section, an example of topology optimization is performed using the control parameter \(K_s\) according to the idea proposed in [34]. In particular, the optimization problem can be formulated in the following way: find the distribution of shear stiffness \(K_s\) for the cycloidal metamaterial, which increases the safety factor relative to failure in elongation.

In this regard, a tensile test is employed to analyze the deformations of the considered system and to minimize the total elongation energy, \(U_e\), by varying the shear stiffness. However, this problem needs some constraints because otherwise the trivial solution \(K_s=0\) (all perfect hinges) is obtained with a significant decrease in the bearing capacity. In this paper, the constraint is imposed on the total bending energy, \(U_b\) in order to preserve its value for the initial distribution of shear stiffness, which is characterized by all the connections geometrically equal, namely they are assumed to be cylinders with the same diameter and height. The reason behind this choice is because the trivial solution implies greater bending energy than that of the initial design (see Fig. 24). Indeed, in the examined case, being the fibers curved, there is a not negligible coupling between the elongation and the bending energy of the fibers and thus decreasing the elongation energy leads to an increase of the bending one. If the bending energy is constrained, it is possible to avoid unnecessary and abnormal storage of energy. Furthermore, the longitudinal reaction, albeit decreases, does not become too low (see Fig. 24). The design problem to solve, hence, can be expressed as

$$\begin{aligned} \min _{K_s} U_e[u_i(K_s)] \qquad \text {subject to } U_b = U_{b}(K_s^0) \end{aligned}$$
(26)

where \(K_s^0\) is the shear stiffness distribution of the initial design. Figure 24 exhibits the results of the optimization through the energy components and the reaction in \(X_1\)-direction. In these plots, it is possible to see a decrease in the maximal elongation energy of about 10%. Figure 25 shows the initial and the optimal distribution of \(K_s\) determined by solving the (26) with the method of moving asymptotes. Using this ‘optimal’ distribution of the stiffness \(K_s\), it is possible to design which connections must be perfect hinges and which ones remain deformable cylinders and possibly change the diameter. Finally, Fig. 26 displays the total energy density for the relevant cases: the initial one, the optimal one, and the trivial one.

Fig. 24
figure 24

Initial, optimal, limit design comparison for the tensile test: a stretching, b bending, c shear energy, and d reaction along \(X_1\) direction

Full size image
Fig. 25
figure 25

Distribution of \(K_s\): a initial and b optimized stiffness

Full size image
Fig. 26
figure 26

Energy density distribution for the tensile test with an imposed displacement of 1 cm: a initial, b optimal, c limit (\(K_s=0\)) case

Full size image

5 Conclusions

In this paper, a new model to describe a system made with narrow and long deformable bodies (referred to as fibers) that in the reference configuration, at rest, are arranged along plane curves forming an orthogonal grid is proposed. The model is an elastic bidimensional continuum body characterized by displacement derivatives up to the second order that qualify it as a strain gradient model. Large deformations are allowed; therefore, the model is nonlinear. Some kinematical assumptions are made up to simplify treatment. Essentially, the fibers are modeled as two infinite distributions of Kirchhoff rods lying on the same surface and are jointed in such a way they exhibit only a relative rotation with respect to the axis normal to the surface in the intersecting points. As a toll for using these simplified hypotheses, the proposed model loses in some circumstances accuracy even though, from a general point of view, remains able to predict the essential aspects involved in the deformation process. On the other hand, only a limited number of rigidities must be identified.

A scrupulous analysis has been carried out for a specific pattern of fibers arranged according to cycloids. Firstly, two tests are performed to implement a micro–macro-numerical identification; secondly, additional two tests are examined to show more explicitly the limit of applicability of the model. To complete the study, modal analysis is executed to investigate the vibrational behavior of the model around the reference configuration.

Finally, a shear stiffness optimization is performed to illustrate how the design of the considered metamaterial could be further improved. The solution of the structural optimization can be adopted to design the connections between fibers to fulfill a prescribed requirement.