Abstract
The modern description of elementary particles, as formulated in the standard model of particle physics, is built on gauge theories1. Gauge theories implement fundamental laws of physics by local symmetry constraints. For example, in quantum electrodynamics Gauss’s law introduces an intrinsic local relation between charged matter and electromagnetic fields, which protects many salient physical properties, including massless photons and a long-ranged Coulomb law. Solving gauge theories using classical computers is an extremely arduous task2, which has stimulated an effort to simulate gauge-theory dynamics in microscopically engineered quantum devices3,4,5,6. Previous achievements implemented density-dependent Peierls phases without defining a local symmetry7,8, realized mappings onto effective models to integrate out either matter or electric fields9,10,11,12, or were limited to very small systems13,14,15,16. However, the essential gauge symmetry has not been observed experimentally. Here we report the quantum simulation of an extended U(1) lattice gauge theory, and experimentally quantify the gauge invariance in a many-body system comprising matter and gauge fields. These fields are realized in defect-free arrays of bosonic atoms in an optical superlattice of 71 sites. We demonstrate full tunability of the model parameters and benchmark the matter–gauge interactions by sweeping across a quantum phase transition. Using high-fidelity manipulation techniques, we measure the degree to which Gauss’s law is violated by extracting probabilities of locally gauge-invariant states from correlated atom occupations. Our work provides a way to explore gauge symmetry in the interplay of fundamental particles using controllable large-scale quantum simulators.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data for figures that support the current study are available at https://doi.org/10.7910/DVN/3RXD5F. Source data are provided with this paper.
Code availability
The codes used for the theoretical curves are available at https://doi.org/10.7910/DVN/3RXD5F.
References
Weinberg, S. The Quantum Theory of Fields: Volume 1, Foundations (Cambridge Univ. Press, 2005).
Gattringer, C. & Lang, C. Quantum Chromodynamics on the Lattice: An Introductory Presentation (Springer, 2009).
Wiese, U.-J. Ultracold quantum gases and lattice systems: quantum simulation of lattice gauge theories. Ann. Phys. 525, 777–796 (2013).
Zohar, E., Cirac, J. I. & Reznik, B. Quantum simulations of lattice gauge theories using ultracold atoms in optical lattices. Rep. Prog. Phys. 79, 014401 (2016).
Dalmonte, M. & Montangero, S. Lattice gauge theory simulations in the quantum information era. Contemp. Phys. 57, 388–412 (2016).
Bañuls, M. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D 74, 1–42 (2020).
Clark, L. W. et al. Observation of density-dependent gauge fields in a Bose–Einstein condensate based on micromotion control in a shaken two-dimensional lattice. Phys. Rev. Lett. 121, 030402 (2018).
Görg, F. et al. Realization of density-dependent Peierls phases to engineer quantized gauge fields coupled to ultracold matter. Nat. Phys. 15, 1161–1167 (2019).
Martinez, E. A. et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516–519 (2016).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).
Surace, F. M. et al. Lattice gauge theories and string dynamics in Rydberg atom quantum simulators. Phys. Rev. X 10, 021041 (2020).
Kokail, C. et al. Self-verifying variational quantum simulation of lattice models. Nature 569, 355–360 (2019); correction 580, E9 (2020).
Dai, H.-N. et al. Four-body ring-exchange interactions and anyonic statistics within a minimal toric-code Hamiltonian. Nat. Phys. 13, 1195–1200 (2017).
Klco, N. et al. Quantum-classical computation of Schwinger model dynamics using quantum computers. Phys. Rev. A 98, 032331 (2018).
Schweizer, C. et al. Floquet approach to \({{\mathbb{Z}}}_{2}\) lattice gauge theories with ultracold atoms in optical lattices. Nat. Phys. 15, 1168–1173 (2019).
Mil, A. et al. A scalable realization of local U(1) gauge invariance in cold atomic mixtures. Science 367, 1128–1130 (2020).
Calzetta, E. A. & Hu, B.-L. B. Nonequilibrium Quantum Field Theory (Cambridge Univ. Press, 2008).
Berges, J. Introduction to nonequilibrium quantum field theory. AIP Conf. Proc. 739, 3–62 (2004).
Halimeh, J. C. & Hauke, P. Reliability of lattice gauge theories. Phys. Rev. Lett. 125, 030503 (2020).
Chandrasekharan, S. & Wiese, U. J. Quantum link models: a discrete approach to gauge theories. Nucl. Phys. B 492, 455–471 (1997).
Coleman, S. More about the massive Schwinger model. Ann. Phys. 101, 239–267 (1976).
Susskind, L. Lattice fermions. Phys. Rev. D 16, 3031–3039 (1977).
Rico, E., Pichler, T., Dalmonte, M., Zoller, P. & Montangero, S. Tensor networks for lattice gauge theories and atomic quantum simulation. Phys. Rev. Lett. 112, 201601 (2014).
Yang, B. et al. Cooling and entangling ultracold atoms in optical lattices. Science 369, 550–553 (2020).
Winkler, K. et al. Repulsively bound atom pairs in an optical lattice. Nature 441, 853–856 (2006).
Jördens, R., Strohmaier, N., Gunter, K., Moritz, H. & Esslinger, T. A Mott insulator of fermionic atoms in an optical lattice. Nature 455, 204–207 (2008).
Altman, E., Demler, E. & Lukin, M. D. Probing many-body states of ultracold atoms via noise correlations. Phys. Rev. A 70, 013603 (2004).
Fölling, S. et al. Spatial quantum noise interferometry in expanding ultracold atom clouds. Nature 434, 481–484 (2005).
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).
Hauke, P., Marcos, D., Dalmonte, M. & Zoller, P. Quantum simulation of a lattice Schwinger model in a chain of trapped ions. Phys. Rev. X 3, 041018 (2013).
Yang, D. Y. et al. Analog quantum simulation of (1+1)-dimensional lattice QED with trapped ions. Phys. Rev. A 94, 052321 (2016).
Zache, T. et al. Dynamical topological transitions in the massive Schwinger model with a θ term. Phys. Rev. Lett. 122, 050403 (2019).
Huang, Y.-P., Banerjee, D. & Heyl, M. Dynamical quantum phase transitions in U(1) quantum link models. Phys. Rev. Lett. 122, 250401 (2019).
Magnifico, G. et al. Symmetry-protected topological phases in lattice gauge theories: topological QED2. Phys. Rev. D 99, 014503 (2019).
Berges, J., Floerchinger, S. & Venugopalan, R. Thermal excitation spectrum from entanglement in an expanding quantum string. Phys. Lett. B 778, 442–446 (2018).
Kogut, J. & Susskind, L. Hamiltonian formulation of Wilson’s lattice gauge theories. Phys. Rev. D 11, 395–408 (1975).
Pichler, T., Dalmonte, M., Rico, E., Zoller, P. & Montangero, S. Real-time dynamics in U(1) lattice gauge theories with tensor networks. Phys. Rev. X 6, 011023 (2016).
Lewenstein, M., Sanpera, A. & Ahufinger, V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-body Systems (Oxford Univ. Press, 2012).
Zohar, E. & Reznik, B. Confinement and lattice quantum-electrodynamic electric flux tubes simulated with ultracold atoms. Phys. Rev. Lett. 107, 275301 (2011).
Banerjee, D. et al. Atomic quantum simulation of dynamical gauge fields coupled to fermionic matter: from string breaking to evolution after a quench. Phys. Rev. Lett. 109, 175302 (2012).
Yang, B. et al. Spin-dependent optical superlattice. Phys. Rev. A 96, 011602 (2017).
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96–192 (2011).
McCulloch, I. P. Matrix Product Toolkit. https://people.smp.uq.edu.au/IanMcCulloch/mptoolkit/ (2015).
Chubb, C. T. & Flammia, S. T. Approximate symmetries of Hamiltonians. J. Math. Phys. 58, 082202 (2017).
Glück, M., Kolovsky, A. R. & Korsch, H. J. Wannier–Stark resonances in optical and semiconductor superlattices. Phys. Rep. 366, 103–182 (2002).
Acknowledgements
We thank J. Berges, Q. J. Chen, Y. J. Deng, S. Jochim and W. Zheng for discussions. We thank Z. Y. Zhou and G. X. Su for their help with the experimental measurements. This work is part of and supported by the National Key R&D Program of China (grant 2016YFA0301603), NNSFC grant 11874341, the Fundamental Research Funds for the Central Universities (special funds for promoting the construction of world-class universities and disciplines), the Anhui Initiative in Quantum Information Technologies, the DFG Collaborative Research Centre ‘SFB 1225 (ISOQUANT)’, the ERC Starting Grant StrEnQTh (project-ID 804305), Q@TN – Quantum Science and Technology in Trento, and the Provincia Autonoma di Trento.
Author information
Authors and Affiliations
Contributions
B.Y., Z.-S.Y., P.H. and J.-W.P. conceived the research; P.H. conceived the theoretical idea; B.Y., Z.-S.Y. and J.-W.P. designed the experiment; B.Y., H.S. and H.-Y.W. performed the experiments and analysed the data; R.O., T.V.Z., J.C.H. and P.H. developed the theory together with B.Y.; and R.O., T.V.Z. and J.C.H. did the numerical simulations. All authors contributed to manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Bryce Gadway, Erez Zohar and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
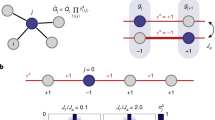
Extended Data Fig. 1 Level structure of a three-site building block (matter–gauge–matter).
The energy manifold of interest is given by the state on the left, which represents a particle pair, and the one on the right, where particles have annihilated while changing the in-between gauge field configuration. In the middle, we show the detuned intermediate processes and states by which these ‘physical’ (that is, gauge-invariant) states are coupled. See main text for nomenclature used in this figure.
Extended Data Fig. 2 Single-site resolved imaging.
a, A staggered-filled 1D chain as our initial state is sketched, which begins with the first site (left part) and ends up with the 75th site (right part). The energy levels are split by a linear magnetic gradient field. Therefore, the internal states |↓⟩ (wavefunction in blue colour) and |↑⟩ (wavefunction in orange colour) of each site can be coupled by a local resonant microwave field. b, Spectroscopic measurement of the site occupation. At each frequency, we average the data over five repetitions, and integrate the signal along the y axis. For simplicity, we show only the beginning site and a few sites at the end of the chain. The blue circles are central positions of the atomic densities along x. According to the spatial position of the image, we plot the staircase structure of the lattice sites in cyan. The lower panel shows the atomic density averages over the measurements on the upper panel, where the amplitude is normalized to the maximum atomic density. The sinusoidal fitting (orange-dashed line) shows the positions of the sites and the staggered structure.
Extended Data Fig. 3 Dynamics in building blocks.
a, Observation of coherent evolution in the building blocks, as sketched above the data. We monitored the dynamics at two different coupling strengths. The solid curves are sinusoidal fitting results, which give oscillation frequencies of 89.3(3) Hz (upper plot) and 57.1(3) Hz (lower plot). Error bars, s.d. The small atom number in the dilute sample leads to larger statistical errors as compared to our many-body experiment reported in the main text. As these data show, the decay of oscillations is insignificant over a range of coupling strengths \(\tilde{t}\), even for values larger than the greatest coupling strength used in the phase transition (\(\mathop{t}\limits^{ \sim }=70\,{\rm{H}}{\rm{z}}\)). b, The oscillation frequency and J2/U have an almost linear relation, which is in excellent quantitative agreement with the theoretical prediction based on the BHM (solid curve).
Extended Data Fig. 4 Quantum phase transition and revival.
Over 240 ms, we ramp the mass as follows: first, from negative to positive; second, from positive to negative, back to the symmetry-unbroken charge-proliferated phase. Error bars, s.d. The recovery of the atoms on even sites indicates the reversibility of this phase transition. The solid curve is a guide for the eye.
Extended Data Fig. 5 Numerical simulations of the phase transition dynamics.
These are calculated by ED (a) and DMRG (b) methods. We monitor the evolution of the deviation of the electric field, which corresponds to the double occupancy (‘doublons’) of the odd sites. a, Simulations of the ideal, fully gauge-invariant QLM, using ED calculations under periodic boundary conditions. b, Simulations of a 1D Bose–Hubbard system modelling our experiment, using the t-DMRG method. The insets show the differences between results for different system sizes and the curve at the largest size (L = 52 for ED and L = 40 for t-DMRG), demonstrating finite-size convergence well below the range of experimental errors.
Extended Data Fig. 6 Correlation length.
Density–density correlation of the final state is plotted against the distance in momentum space. We select the central region with two interfering peaks, where the background has been subtracted from the signal. The solid curve is a Lorentzian fitting of the data. The inset shows the relation between the peak width and the correlation length. The solid curve is calculated for a 1D system with Nddc = 100 sites. The red point represents the correlation length of the final state as shown in Fig. 3a, where the error bars are s.d.
Extended Data Fig. 7 Ramping speed and gauge violation.
a, The phase transition is driven by ramping the mass m and the effective coupling \(\tilde{t}\). We start from a large negative value of mass \(m/\tilde{t}\), retain stronger coupling around the critical point, and end up with a large positive mass. b, Gauge violation against total ramping time calculated with the t-DMRG method in a system with 16 (red), 24 (blue) and 32 (orange) optical-lattice sites. Using the same shape of the ramping curve in a, we change the ramping speed by constraining the total ramping time. The squares points are the maxima of ϵ(t) throughout the dynamics, while the circles represent the gauge violations of the final states. Owing to the coherence of our many-body system, ϵ(t) reaches its maximum around the critical point, and decreases after crossing the critical point (see Fig. 4b).
Extended Data Fig. 8 Dynamics in double wells.
Under the same superlattice configuration, we measure the evolution of three different states in double wells. The initial states are |10⟩ (blue squares), |11⟩ (orange triangles) and |20⟩ (red circles). The state |10⟩ oscillates with almost the full amplitude. The superexchange interaction drives the spin exchange process as expected. In contrast, the atom population remains constant for the state |20⟩. Error bars, s.d. The solid curves are exponentially damped sinusoidal fittings, where the frequency, phase and decay rate are fixed. We find that the oscillation amplitude of tunnelling is almost three orders of magnitude larger than the other two fitting values.
Extended Data Fig. 9 Detecting the gauge-invariant states.
We divide the atoms into double wells and then measure atom tunnelling within each two-site unit. a–d, The dynamics of tunnelling for four different experimental sequences, as sketched in the insets. Five different moments during the phase transition (t = 0, 30, 60, 90, 120 ms) are selected for detecting the gauge-invariant states. Error bars, s.d. We fit the data with a sinusoidal damping function, which has a period of 7.2 ms and an exponential decay constant of 96 ms. The amplitudes of the oscillations in a–d refer to \({A}_{|10\rangle }^{(1)}\), \({A}_{|01\rangle }^{(1)}\), \({A}_{|10\rangle }^{(2)}\) and \({A}_{|01\rangle }^{(2)}\), respectively. These amplitudes are then used for calculating the state probabilities, where the error bars are s.d.
Extended Data Fig. 10 Resolving the population of the states.
For the detection of states |002⟩ and |200⟩, we extract their probabilities from several measurements. There are 64 states that may contribute to the oscillations, which are listed from |000⟩ to |333⟩ as an 8 × 8 square array (left). The amplitudes of these states according to our detection procedures are given by distinct colours (key at bottom right). For example, the state |002⟩ in the third column of the first row only contributes to the first observable \({A}_{|01\rangle }^{(2)}\)+\({A}_{|10\rangle }^{(2)}\) with a factor of 1, while the state |013⟩ at the end of the first row will be recorded by all these observables with the colour-denoted factors. We use seven terms to deduce the lower bound for the probabilities as \({p}_{|\ldots 002\ldots \rangle }+{p}_{|\ldots 200\ldots \rangle }\ge {A}_{|01\rangle }^{(2)}+{A}_{|10\rangle }^{(2)}+{A}_{|01\rangle }^{(1)}+{A}_{|10\rangle }^{(1)}-{\bar{n}}_{c}^{{\rm{o}}}-0.5{\bar{n}}^{{\rm{e}}}-1.5{\bar{n}}_{{\rm{c}}}^{{\rm{e}}}\). Such a relation can be captured from the chequerboard diagram.
Supplementary information
Rights and permissions
About this article
Cite this article
Yang, B., Sun, H., Ott, R. et al. Observation of gauge invariance in a 71-site Bose–Hubbard quantum simulator. Nature 587, 392–396 (2020). https://doi.org/10.1038/s41586-020-2910-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2910-8
This article is cited by
-
Dynamical localization transition in the non-Hermitian lattice gauge theory
Communications Physics (2024)
-
Effective light cone and digital quantum simulation of interacting bosons
Nature Communications (2024)
-
Quantum simulation of fundamental particles and forces
Nature Reviews Physics (2023)
-
Operator growth and Krylov complexity in Bose-Hubbard model
Journal of High Energy Physics (2023)
-
Realizing a 1D topological gauge theory in an optically dressed BEC
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.