1 Introduction

The recording of transient concentration profiles is a most direct way for elucidating mass transfer in nanoporous materials upon uptake and release and during catalytic conversion. The options for attaining this type of information range from single-molecule observation (see the contribution by B. Weckhuysen and colleagues in this Thematic Issue) to the monitoring of the distribution of molecular entities as enabled by, e.g., Magnetic Resonance Imaging (MRI –see W. S. Price et al.) and X-ray Computed Tomography (R. Pini et al.). Over the last two decades, a particularly large gain in information about mass transfer in nanoporous materials has been attained by the application of interference microscopy (Schemmert et al. 1999a; Geier et al. 2001; Schemmert 2001) and IR microscopy (Schueth 1992; Lin et al. 2000; Lehmann et al. 2002; Chmelik 2007) for the recording of the evolution of guest distributions in nanoporous host materials. Both techniques operate, typically, within the time scale of seconds up to minutes and even hours. Compared to interference microscopy (IFM), IR microscopy (IRM) has the great advantage of being able to selectively record concentration profiles of individual molecular species in multi-component systems while the application of IFM is, essentially, restricted to single-component adsorption. IFM, on the other hand, notably exceeds IRM in its spatial resolution, attaining even the sub-micrometer range, while only in optimum cases IRM attains spatial resolution in the range of micrometers. Benefitting from this complementary, IRM and IFM have often been simultaneously applied for one and the same nanoporous host–guest system so that for their application the term microimaging came into common use (Kärger et al. 2014).

After an introduction to the principle of measurement of either technique in Sect. 2, Sect. 3 deals with the investigation of transport resistances on the outer surface of nanoporous materials. Though with already the very first studies comparing uptake and release measurements with measurements of intracrystalline diffusion, evidence of such resistances was provided (Kärger and Caro 1977; Kärger and Ruthven 1989), it was only with the advent of microimaging that a quantification of these resistances based on experimental measurement has become possible.

The measurement of surface barriers did open up, in some way, a new direction of research aiming at a prediction of such resistances by molecular modelling. This aspect of microimaging, namely its potentials of contributing to the development of novel research directions, is in the focus of Sect. 4. The topics presented include the spatially-resolved investigation of guest-induced variations in the host lattice (exemplified with the behavior of benzene in zeolite MFI) and of mass transfer in “mixed-matrix” membranes. The section does, moreover, illustrate the options of IRM and IFM to provide experimental data for correlating mass transfer under equilibrium and non-equilibrium conditions.

The fifth section deals with the potentials of microimaging for investigating mass transfer in multi-component systems, including its application for performance enhancement in heterogeneous catalysis and mass separation.

2 Principle of measurement

Microimaging by both IFM and IRM is based on measurement of the integral \(\underset{0}{\overset{L}{\int }}c(x, y, z;t) dz\) over the guest concentration in observation direction (here assumed the z-direction). Thus one obtains a map of concentrations (more correctly: concentration integrals) in the plane of observation (here the x–y-plane) at the time t of the measurement. L stands for the thickness of the sample under study, which, ideally, is a cuboid. The fact that, by their very nature, both IFM and IRM are not able to provide information about spatial concentration dependencies in three dimensions does not mean any constraint if concentration may be implied to be constant in z direction. Such a situation is given for one- and two-dimensional pore systems, with the observation direction perpendicular to them, and for three-dimensional systems, with the two faces perpendicular to observation direction sealed. In all these cases, the concentration integral simplifies to the product of local concentration and sample thickness L in observation direction. Concentrations are by either technique recorded as relative quantities. Calibration may be easily based on a comparison with the outcome of the measurement (or theoretical prediction) of adsorption isotherms for the given pressure and temperature.

2.1 Microimaging by interference microscopy (IFM)

Monitoring of the density of guest molecules in a nanoporous host material via IFM exploits the fact that the optical density n and, hence, the velocity of the light passing this material, is a function the guest concentration c. This access to the measurement of concentrations and, with their variation, of diffusivities has found widespread application for diffusion measurement with liquid mixtures (Gaffney and Chau 2001; Rashidnia and Balasubramaniam 2002; Sun and Pu 2016). Transfer of this measuring principle to diffusion in zeolites, however, proved to be quite a long way, with first attempts in already as early as 1978 at a device at the Carl-Zeiss-Parent company in Jena, temporarily made available for first attempts (Kärger et al. 1978), with the establishment of a first independent device for this type of measurement in Leipzig (Schemmert et al. 1999a, 1999b). The problems of these early days were mainly related to the difficulties in the activation of single crystals within the optical cell of the interference device, caused by residual amounts of extraneous molecules, giving rise to irregular blockages both in the crystal interior and, notably, on their external surface. It was, essentially, with only the combined application of IFM and IRM that these traces of residual molecules could be identified, as a prerequisite for preventing their presence and thus their disturbing influence (Lehmann et al. 2002).

Schematics of the measuring device for IFM is presented by Fig. 1. Application of IFM for diffusion studies in nanoporous solids has, so far, been based on using a Mach–Zehnder interferometer. It splits the image into two identical images. This allows investigating the interference between a light beam passing the crystal and a beam going through the surrounding gas phase. From the interference pattern, one is able to determine the difference \(\Delta {\varphi }^{L}\) in the phases between the two light beams. Following a pressure step in the surrounding atmosphere, variation in the refractive index of the surrounding atmosphere remains, essentially, negligibly small in comparison with its variation in the nanoporous solid. Via

$$\Delta (\Delta \varphi^{L} (t))\, \propto \,\int\limits_{0}^{L} {\Delta n(t)dz\, \propto \,\int\limits_{0}^{L} {\Delta c(x,y,z,t)dz} }$$
(1)
Fig. 1
figure 1

Experimental set-up and basic principle of interference microscopy for diffusion measurement in nanoporous solids. a Schematic representation of the vacuum system (static) with optical cell containing the sample. b Interference microscope (Carl-Zeiss JENAPOL interference microscope with a Mach–Zehnder type interferometer (Beyer and Schöppe 1965)) with CCD camera on top, directly connected to c the computer. d Basic principle: Changes in intracrystalline concentration by diffusion give rise to changes in the refractive index of the crystal (n1) and, hence, in the phase difference Δφ of the two beams. From this phase difference as appearing in the interference patterns one can evaluate the variation in the intracrystalline concentration via Eq. (1) e Close-up view of the optical cell containing the crystal under study (from (Chmelik et al. 2010b), with permission)

Full size image

variation in the phase shift as appearing in the interference patterns may thus, to a first, linear approximation, be referred to variation in the refractive index and to variation in the concentration integral in observation direction.

2.2 Microimaging by infrared microscopy (IRM)

In IRM, information about the concentration integrals in observation direction is provided by the intensity of characteristic IR bands of the guest molecules. Following the Beer-Lambert law the absorbance can be assumed to be proportional to the concentration of guest molecules (Chmelik et al. 2010a). Although often a linear correlation between the intensity of the IR bands and concentration of the guest molecules is observed, it is highly recommended to verify the correlation by comparing loading dependent IR equilibrium data with a reference adsorption isotherm, e.g. obtained by a gravimetric method. A non-linear trend might e.g. occur at high loadings, for guest molecules with functional groups or strongly adsorbed species and in host-systems with flexible structures. Even in such cases required corrections can be minimized by considering small loading steps only over which a linear correlation between absorbance and concentration exists.

An overview of the various constituents of a measuring device is given by Fig. 2. There are two possibilities of operation. For measuring overall uptake by a single crystal (or a couple of crystals), a single-element (SE) detector is applied. The thus attainable information is comparable to that of ordinary uptake and release experiments, with the important difference that measurement may be performed with an individual crystal, allowing the comparison of the transport properties of different crystals out of the same batch. This type of measurement has, correspondingly, been referred to as mesoscopic (Kärger and Freude 2002). Even without resolving intracrystalline concentration profiles, uptake measurement with single crystals have another great advantage in comparison with bed measurements. Owing to the dramatically enhanced surface-to volume ratio, transient sorption experiments with single crystals remain, essentially, unaffected by disturbing effects of heat release (Heinke et al. 2007a), which, for fast sorption processes in bed experiments, often become the rate-limiting process (Ruthven et al. 1980; Ruthven and Lee 1981).

Fig. 2
figure 2

Fourier-Transform IR microscope (Bruker Hyperion 3000) consisting of a spectrometer (Bruker Vertex 80v) and a microscope with a Focal Plane Array (FPA) detector (Roggo et al. 2005) as a device for micro-imaging, and basic principle of the IR microscopy technique: The optical cell is connected to a vacuum system and mounted on a movable platform under the microscope. As a rule, only one individual crystal is selected for the measurement. Changes in the area under the IR bands of the guest species are related to the guest concentration. The spectra can be recorded as the signal integrated over the whole crystal (or even a couple of crystals) with a single-element detector (SE) for measurement of integral uptake (center) or spatially resolved (with a resolution of up to 2.7 µm in optimum cases) by using an array of detectors (FPA–focal plane array, right) in microimaging (from (Chmelik et al. 2010b), with permission)

Full size image

By use of an array of detectors in the focal plane (“focal plane array (FPA) detector”) IRM, alternatively, allows the spectra over each individual space element (top right of Fig. 2) to be determined. The FPA detector of the device shown in Fig. 2 consists of an array of 128 \(\times\)128 single detectors, each 40  \(\mu\)m \(\times\) 40 \(\mu\)m. Thus, by means of a 15\(\times\) objective, in the crystal under study (positioned in the focal plane) a resolution of 2.7  \(\mu\)m \(\times\) 2.7 \(\mu\)m is gained. However, differing from IFM, IRM does not exactly provide the concentration integral perpendicular to the observation plane. The light is rather focused into the focal plane under a certain angle (about 16° with Bruker Hyperion 3000) which, with increasing sample thickness L, impairs spatial resolution. An example of explicit treatment may, e.g., be found in (Chmelik et al. 2010a).

2.3 Data analysis

With the concentration integral as a function of time t and the position x, y in the plane of observation, IFM and IRM attain coinciding primary information so that data analysis may follow essentially identical routes. We provide, in the following, a short introduction and refer to the more extended treatment in the literature, notably in refs. (Chmelik et al. 2010b; Kärger et al. 2012).

Diffusivities are, as a rule, defined by Fick’s first law.

$$j = - D_{T} \frac{\partial c}{{\partial x}}$$
(2)

as the factor of proportionality between a molecular flux and the concentration gradient, that has given rise to it. In the notation of Eq. (2) we consider single-component diffusion, with the factor of proportionality referred to as Fickian or transport diffusivity, with the latter term indicating that the diffusion process is indeed correlated with a net transport of molecules. Alternatively, the same type of equation may be used for quantitating the diffusion of labelled molecules (by, e.g., using isotopes) within their unlabeled surroundings, ensuring constancy of overall concentration (i.e. of labelled and unlabeled molecules):

$$j^{*} = - D \frac{{\partial c^{*} }}{{\partial x^{ \bullet } }}$$
(3)

Here, \({j}^{*}\) and \({c}^{*}\) stand for the flux and the concentration of labelled molecules. D is referred to as the self- or tracer diffusion coefficient.

While microimaging by both IRM and IFM allows to determine transport (or Fickian) diffusivities by using suitable isotopes (giving different IR bands), IRM gives access to also self- (or tracer) diffusivities.

With Eqs. (2) and (3), knowledge of flux and concentration gradient is seen to give immediate access to the diffusivity. Let us, for simplicity, consider molecular uptake in one dimension, giving rise to subsequent concentration profiles as shown by the central picture on the right of Fig. 2. Concentration gradients appear directly as the slope of the concentration profiles. Flux \(j\left(x,t\right)\) (at position x and time t) results as.

$$j(x,t) \propto \frac{{\int\nolimits_{0}^{x}} {[c(x{^\prime},t_{2} ) - c(x{^\prime},t_{2} )]dx{^\prime}}}{{t_{2} - t_{1} }}$$
(4)

with x = 0 denoting the middle of the crystal. \(\int\nolimits_{0}^{x} {[c(x} {^\prime},t_{2} ) - c(x{^\prime},t_{2} )]dx{^\prime}\) is easily recognized as the area between the concentration profiles at times \({t}_{1}\) and \({t}_{2}\) from x to the crystal center. This area is proportional to the net-amount of molecules, which, during the time interval \({t}_{2}-{t}_{1}\), have passed position x. Flux at position x is nothing else than the ratio between the amount of molecules having passed the plane at position x and the considered time interval \({t}_{2}-{t}_{1}\) as expressed by Eq. (2). t is set equal to \({(t}_{2}-{t}_{1})/2\) with, ideally, \({t}_{2}-{t}_{1}\ll t\).

In practice, diffusivities are more efficiently determined by the application of Fick’s second law.

$$\frac{\partial c}{{\partial t}} = \frac{\partial }{\partial x}\left( {D_{T} \frac{\partial c}{{\partial x}}} \right) = D_{T} \frac{{\partial^{2} c}}{{\partial x^{2} }} + \frac{{dD_{T} }}{dc}\left( {\frac{\partial c}{{\partial x}}} \right)^{2}$$
(5)

The second term in the second equality emerges in consequence of the fact that the transport diffusivity is a function of the guest concentration. For sufficiently small pressure steps and, correspondingly, small concentration intervals covered in uptake and release experiments, this second term becomes negligibly small. Tracer exchange experiments are performed with varying fractions of labelled and unlabeled molecules at constant overall concentration, with the self-diffusivity (as a function of only the overall concentration and, hence, constant) appearing in Eq. (5) in place of the transport diffusivity. In this case, the second term on the right hand side of Eq. (5) does not apply anyway.

Figure 3 provides an example illustrating the determination of the (concentration dependent) transport diffusivity of cyclohexane in nanoporous glass by microimaging via IRM (Titze et al. 2015b). The option to determine concentrations near the surface have made microimaging the only method allowing the direct quantification of transport resistances on the surface of nanoporous solids. These resistances are, commonly, quantified by the relation (Kärger et al. 2012).

$$j_{surf.} = \alpha [c_{eq.} - c_{surf.} (t)]$$
(6)
Fig. 3
figure 3

a Evolution of the transient concentration of cyclohexane in a nanoporous glass during molecular uptake induced by a pressure step from 0 to 0.1 mbar in the surrounding atmosphere, recorded by IRM (circles) at 298 K and comparison with the predictions (solid lines) as resulting from the solution of Fick’s second law, Eq. (5), with the relevant initial and boundary conditions. b Concentration dependence of the transport diffusivity as implied for the prediction of the concentration profiles shown in (a), after (Titze et al. 2015b)

Full size image

with \({j}_{\mathrm{surf}.}\) denoting the flux entering the crystal and with \({c}_{\mathrm{surf}.}(t)\) and \({c}_{\mathrm{eq}.}\) denoting, respectively, the actual concentration close to the surface and the concentration in equilibrium with the external gas phase. The factor of proportionality, \(\alpha\), is a measure of the permeability of the surface barrier and has, accordingly, been introduced under the term surface permeability (Crank 1975; Kortunov et al. 2006; Heinke et al. 2007b; Kärger and Ruthven 2016). Alternatively and, totally equivalently, also the term surface permeance is in use.

With knowledge of the evolution of the concentration profiles, microimaging provides both the actual and the finally attained surface concentrations, \({c}_{\mathrm{surf}.}\left(t\right)\), and \({c}_{\mathrm{eq}.}\), respectively, and, via Eq. (4) with x = L/2, the flux entering the crystal. Thus, with Eq. (6), one is as well able to determine the surface permeability \(\alpha\). Low values of the surface permeability \(\alpha\) are seen to correspond, for a given flux through the surface, to large deviations \({{c}_{\mathrm{surf}.}\left(t\right)-c}_{\mathrm{eq}.}\) of the boundary concentration from the equilibrium value as appearing, e.g., in the profiles shown on the right of Fig. 2. Diverging surface permeabilities require, on the other hand, surface concentrations approaching the equilibrium ones for maintaining physically reasonable (i.e. finite) fluxes through the surface.

Similarly as mentioned already with reference to the diffusivities, also the determination of surface permeability is, due to practical reasons, in general based on the solution of Fick’s second law, Eq. (5), for uptake and release in the appropriate geometry. The relevant boundary condition

$$D_{T} \left( {\frac{\partial c}{{\partial x}}} \right)_{surf.} = \alpha [c_{eq.} - c_{surf.} (t)]$$
(7)

which in this case has to be applied, results by combination of Fick’s first law, Eq. (2), with Eq. (6). It replaces the boundary condition

$$c_{surf.} = c_{eq.}$$
(8)

for negligibly small surface barriers.

3 Measurement of surface barriers

3.1 Barrier vs. diffusion limitation

The method of statistical moments (Kocirik and Zikanova 1974; Dubinin et al. 1975; Barrer 1978) enables a comfortable first-order estimate of the influence of the different transport resistances affecting the rate of molecular uptake and release in terms of the respective time constants. This notably includes (Barrer 1978; Kärger et al. 2012)

$$\tau_{Diff} = \frac{{R^{2} }}{15D}$$
(9)
$$\tau_{Bar} = \frac{R}{3\alpha }$$
(10)

as the time constants of molecular uptake by or release from a sphere of radius R under, respectively, diffusion and barrier limitation. The time constant of overall uptake is simply given by their sum. Equations (9) and (10) remain reasonable approximations for also other particle shapes if

$$R = \frac{3V}{A}$$
(11)

is understood as the radius of a sphere with the same volume-to-surface ratio (\(V/A\)) as the particle under study. With Eqs. (9) and (10), knowledge of intracrystalline diffusivities and surface permeabilities as resulting from microimaging, together with the size of the particle as available by microscopic inspection, are seen to provide direct access to the magnitude of the respective transport resistances.

By plotting the boundary concentration as a function of molecular uptake (Fig. 4a), microimaging allows a novel type of graphic representation (Heinke et al. 2007b; Heinke 2007; Karge and Kärger 2008). The shape of this representation provides direct information about the governing process of mass transfer as illustrated by Fig. 4b, with the two limiting cases of dominating surface resistances (\(\frac{l\alpha }{D}=0.01\)) and dominating diffusion resistances (\(\frac{l\alpha }{D}=100\)). While, under diffusion limitation, boundary concentration assumes, with increasing overall uptake, essentially immediately the equilibrium value, barrier limitation, as the other extreme, gives rise to uniform increase in concentration all over the crystal and, thus, to surface concentration increasing in proportion with overall uptake.

Fig. 4
figure 4

“Heinke-Kärger plots” correlating actual boundary concentration (csurf) and relative uptake (m); a measured along the 8-ring channels of zeolite ferrierite with methanol as a guest molecule for a pressure step from 0 to 10 mbar at room temperature (two symbols for two crystal sides) and b calculated for a plate of thickness 2 l considering mass transport, respectively, under dominating influence of intracrystalline diffusion (lα/D = 100), of surface barriers (lα/D = 0.01), and for comparable influences of intracrystalline diffusion and surface barriers (lα/D = 1). From (Heinke et al. 2007b) with permission

Full size image

Plots of the boundary concentration as a function of overall uptake become, in their final course, straight lines, as exemplified by the data points shown in Fig. 4a. The reciprocal value of the intercept w (0\(\le\) w \(\le\) 1) of these lines with the ordinate may be shown (Heinke et al. 2007b; Heinke 2007; Karge and Kärger 2008) to be approximated by the relation

$$\frac{1}{w} \approx \frac{{\tau_{Diff} + \tau_{Bar} }}{{\tau_{Diff} }}$$
(12)

i. e. by the ratio between the (actual) time constant of uptake or release under the (combined) influence of diffusion and surface permeation (\({\tau }_{\mathrm{Diff}}+{\tau }_{\mathrm{Bar}}\), see Eqs. (9) and (10)) and the time constant under, exclusively, diffusion control (\({\tau }_{\mathrm{Diff}}\), i.e. the time constant attainable if one would succeed in eliminating any surface barriers).

3.2 Revealing the nature of surface barriers

Transport resistances on the external surface of nanoporous solids can be brought about in essentially two different ways. As one limiting case one may consider the formation of a more or less homogeneous layer of dramatically reduced permeability, i.e. with a dramatically reduced diffusivity and/or guest capacity in comparison with the bulk phase. In this case, surface permeation and intracrystalline diffusion must be expected to follow completely different dependencies. This type of barrier formation is commonly referred to as “pore narrowing”. Alternatively, transport resistances may as well emerge by a total blockage of the vast majority of the external surface (i.e. by “pore blocking”), with only a few areas remaining permeable.

In this latter case, by effective medium theory (Tuck 1999), surface permeability may be shown to be correlated with the intracrystalline diffusivity by the relation (Dudko et al. 2004, 2005).

$$\alpha = \frac{2Dr}{{L^{2} }}$$
(13)

where, for simplicity, the permeable areas on the surface are assumed to be circles of radius r in a square-lattice arrangement of mutual distance L. Rearranging Eq. (13) as

$$\frac{\pi }{2}\frac{\alpha }{D}r = \rho_{open}$$
(14)

provides us with an estimate of the fraction \({p}_{\mathrm{open}}\) of unblocked surface area.

As an example, Fig. 5 compares the transport diffusivities and surface permeabilities of propylene at 295 K in a crystal of AlPO-LTA (Schreyeck et al. 1997; Huang and Caro 2010) recorded via microimaging as a function of loading. While both the diffusivity and permeability are found to vary over close to two orders of magnitude, their ratio remains essentially the same. Surface resistance can be concluded, therefore, to be caused by “pore blocking”. With α/D ≈ 2 × 105 m−1 as resulting from the measurements (Fig. 5) and with r ≈ 0.6 nm as a measure of the size of the unit cells and, hence, of the smallest possible hole, with Eq. (14) popen is found to be of the order of 10–4. This means that among about 10,000 “windows” connecting the intracrystalline space with the surroundings, only a single one is permeable. For a given permeation-to-diffusion ratio, with Eq. (14) the percentage of unblocked windows, popen, is seen to increase with increasing “clustering” of the unblocked windows on the crystal surface. This is a consequence of the fact that, for a given fraction popen of open windows, their efficiency for enhancing mass transfer increases with their dispersion.

Fig. 5
figure 5

Transport diffusivities D (squares) and surface permeabilities \(\alpha\) (triangles) of propylene in AlPO-LTA at 295 K, calculated from the transient concentration profiles recorded by microimaging via MFI during molecular uptake (filled symbols) and release (open symbols) induced by a stepwise pressure change in the surrounding atmosphere. From (Hibbe et al. 2012), with permission

Full size image

The same type of barrier formation was revealed in microimaging studies with MOF crystals of type Zn(tbip) (Pan et al. 2006). Here, comparative studies of intracrystalline diffusion and surface permeation did also include a variation of the type of the guest molecule under consideration and the investigation of tracer exchange, i. e. the comparison of self-diffusion and surface permeation under equilibrium conditions. In all these studies (Hibbe et al. 2011), the ratio of surface permeation and intracrystalline diffusion remained constant for one and the same crystal as to be expected on the basis of Eqs. (13) and (14).

On considering different crystals of the same batch, the intracrystalline diffusivities were, essentially, found to remain constant, while surface permeabilities revealed distinct differences, giving rise to also varying diffusivity-to-permeability ratios (Hibbe et al. 2011). This is the expected behaviour since structural variability can be implied to emerge more likely close to the crystal boundary than in its interior. It is interesting to note that, as a rule, surface permeabilities through different faces of one and the same crystal are essentially identical. Surface resistances must be understood to occur in consequence of the conditions, which a nanoporous particle “has seen” during fabrication and subsequent treatment and storage. These conditions are, as a matter of course, expected to be much more similar for different faces of one and the same particle than for different particles, so that this finding is not unexpected.

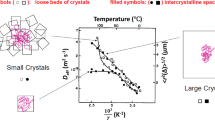
An impressive example illustrating the diversity in the surface permeabilities is provided by Fig. 6. Here, within one and the same batch of nanoporous crystals (SAPO-34 (Cousin Saint Remi et al. 2015)), surface permeabilities of different crystals were found to vary over close to two orders of magnitude, irrespective of the apparent similarity of the crystals.

Fig. 6
figure 6

Batch of crystals of SAPO-34 (left) and surface permeabilities (right) determined with various individual crystals (with sizes from about 40 to 45 m\(\upmu\)) via IFM during uptake of methanol by a pressure step from 0 to 1 mbar at 298 K (right). From (Cousin Saint Remi et al. 2015), with permission

Full size image

Figure 7a shows plots of the boundary concentration as a function of molecular uptake determined via IFM with one and the same crystal of SAPO-34 (“Heinke-Kärger plots”, see Fig. 4) for various probe molecules. The contributions of surface permeation and intracrystalline diffusion to overall mass transfer (represented by the ratios of the respective time constants), as resulting via Eq. (13) from the intercept of these representations with the ordinate, are shown in Fig. 7b. Intracrystalline diffusion and surface permeation in the investigated specimen of SAPO-34 are thus found to be uncorrelated, giving evidence of pore narrowing as the governing mechanism of barrier formation.

Fig. 7
figure 7

Plotting the boundary concentration (csurf) in dependence on molecular uptake (m, “Heinke-Kärger plots”) for assessing the relative influence of diffusion and surface permeation on overall uptake by a single crystal of SAPO-34 (left). The intercept w of the lines with the ordinate (exemplified, with w approximately equal to 0.25, for propanol) provides an estimate of the contribution of the diffusional resistance (\({\tau }_{\mathrm{diff}}\)) to the time constant (\({\tau }_{\mathrm{diff}}+{\tau }_{\mathrm{barr}}\)) of the overall transport resistance (Eq. (12)). The ratios \({\tau }_{\mathrm{barr}}/{\uptau }_{\mathrm{diff}}\) thus derived for all guest molecules considered are shown on the right. From (Cousin Saint Remi et al. 2015), with permission

Full size image

Experimental evidence on the nature of surface barriers is thus seen to be far away from yielding any consistency. Their elucidation remains an attractive topic of future research with, notably, the involvement of sophisticated techniques of structural analysis in addition to diffusion and permeation studies.

4 Novel insight by microimaging

The introduction of microimaging allowed the recording and quantitation of phenomena occurring in nanoporous solids for the very first time. Some of these phenomena have never before been even thought of and, thus, have totally remained out of the focus of investigations. The present section deals with some of them.

4.1 Sticking probabilities

As a key quantity of heterogeneous catalysis with (metal) surfaces, the sticking coefficient (Freund 2008) is defined as the fraction of molecules which, upon colliding with the surface of the catalyst, is not reflected into the gas phase. With the advent of microimaging it has now become possible to also determine experimentally the related information about a nanoporous solid, namely the probability Snp that, upon encountering a nanoporous particle, a molecule shall be able to get through its external surface into its genuine pore space. This probability is, obviously, defined by the ratio.

$$S_{np} = \frac{{j_{in} }}{{j_{gas} }}$$
(15)

with \({j}_{\mathrm{gas}}\) and \({j}_{\mathrm{in}}\) denoting, respectively, the fluxes of molecules colliding with the external surface and propagating into the interior. From kinetic theory of gases (Atkins and Paula 2006) the flux of molecules colliding with a plane surface at pressure p is known to be given by the relation

$$j_{gas} = p \times (2\pi RTM)^{{ - \frac{1}{2}}}$$
(16)

with R and M denoting, respectively, gas constant and molar mass, and with the flux given in the unit \((\mathrm{mol }{\mathrm{s}}^{-1} {\mathrm{m}}^{-2})\), in accordance with the provided list of symbols.

Via microimaging, now also the molecular flux getting from the outer gas phase into the genuine pore space maybe determined, namely by the relation.

$$j_{in} = \alpha \times c_{eq}$$
(17)

with \({c}_{\mathrm{eq}}\) denoting the guest concentration in the particle interior in equilibrium with the surrounding atmosphere. \(\alpha\) is the surface permeability under the conditions of tracer exchange. Equation (17) holds since, under dynamic equilibrium as implied in tracer exchange experiments, the influx (\({j}_{\mathrm{in}}\)) is counterbalanced by the efflux (\(\alpha \times {c}_{\mathrm{eq}}\)). Numerical values attained, in this way, from experimental permeability data range from 0.01 (representing the present upper limit of accessibility) as observed with isobutane on specially pretreated crystals of MFI-type zeolites (Tzoulaki et al. 2008) down to 5\(\times\)10–8 obtained with propane on MOFs of type Zm(tbip) (Chmelik et al. 2009).

4.2 Guest-induced variations in host structure

The structure of nanoporous solids is known to be affected by the presence of guest molecules. This effect has, notably and rather extensively, been investigated with MFI-type zeolites and benzene as guest molecules. Techniques involved include X-ray diffraction analysis (Fyfe et al. 1984; van Koeningsveld et al. 1989), adsorption measurement (Tezel and Ruthven 1990), solid-state NMR (Fyfe et al. 1984, 1988) and molecular dynamics simulations with flexible zeolite lattices (Snurr et al. 1993, 1994). Structural changes were, in particular, found to be accompanied by a redistribution of the guest molecules for loadings above four molecules per unit cell (Song et al. 2005).

With the option to record the variation of the refractive index during guest-induced changes of the host structure, microimaging by interference microscopy has provided a novel tool, which allows the observation of the propagation of such phenomena within the host material (Binder 2013; Kärger et al. 2014; Kärger 2015). Figure 8 shows, as an example, the evolution of the phase shift within an MFI-type zeolite upon adsorption of benzene. Based on the adsorption isotherm recorded in parallel, phase shifts may be translated into respective changes in the guest loading as indicated on the right of the figure.

Fig. 8
figure 8

Two-dimensional maps of the phase shift \(\Delta \varphi\) recorded by IFM during benzene uptake by a crystal of silicalite-1 by a pressure step from 5.0 to 10 mbar. Following the first 265 s of adsorption (a) a second process (associated with a phase transition of the sorbate phase) becomes visible (b). Note, the legend color was changed for better visualization. From (Kärger et al. 2014), with permission

Full size image

Zeolite MFI is known to be traversed by “straight” channels in y- and by “sinusoidal” ones in x-direction, both perpendicular to the longitudinal extension of the crystal. Uptake during the first 200 s (see Fig. 8a) is, correspondingly, observed to occur perpendicular to the longitudinal crystal extension, i.e. in the plane spread by the two channel systems.

Most remarkably, in a second stage (see Fig. 8b) phase shifts are seen to continue in their evolution, now however starting from the far ends of the crystals. Diffusion in this direction, however, is known to be extremely slow since it has to proceed in subsequent shifts along segments alternating between the two channel systems (Kärger 1991; Kärger et al. 2012). Therefore, concentration enhancement cannot be driven by diffusion. It must rather be caused by the structural variation in the host lattice which, in this way, is detected to occur along the longitudinal extension of the crystal, with its far ends as the initial areas of structural variation.

The finding that even after a time span of more than 6 h and, obviously, establishment of overall equilibrium, there are marked deviations from homogeneity of the phase shift nicely corroborates with the message of ref. (Song et al. 2005), predicting a redistribution of the guest molecules. As highly anisotropic molecules, any change in the orientation of the benzene molecules due to variation in their structural arrangement are implied to be accompanied with changes in their refractive index. Since single crystals of type MFI themselves are known to be highly heterogeneous (Kocirik et al. 1998; Schmidt et al. 2007; Karwacki et al. 2009), these heterogeneities must indeed be expected to, finally, occur in also the map of the refractive indices.

4.3 Equilibrium vs. non-equilibrium measurement

IR Microimaging allows the measurement of both the exchange between differently labelled molecules in the nanoporous solid and its surroundings and molecular uptake and release in, essentially, identical experimental devices. It is particularly suited, therefore, for comparative diffusion measurements under equilibrium and non-equilibrium, i.e. of self- and of transport diffusion. Figure 9 shows, as an example of such studies, the self- and transport diffusivities of methanol and ethanol in MOF ZIF-8 as a function of guest concentration (Chmelik 2015).

Fig. 9
figure 9

Adsorption isotherms (a) and loading dependence of transport diffusivity DT (squares) and self- diffusivity D (open circles) for methanol (b) and ethanol (c) in MOF ZIF-8 measured by IRM (298 K) (Chmelik 2015). The corrected diffusivities D0 (filled circles) were calculated via Eq. (22) from the transport diffusivity and the equilibrium isotherms. Full lines are the TST predictions of transport diffusivities and self-diffusivities (implied to coincide, under the given conditions, with the corrected diffusivities) according to Eqs. (24) and (25) After (Chmelik and Kärger 2016) with permission

Full size image

As a remarkable feature, for both systems considered the self- and transport diffusivities are seen to coincide at small loadings. This, however, is the behavior to be expected quite in general since, for sufficiently small loadings, molecular interactions will become negligibly small in comparison with the host–guest interactions so that there is no distinction anymore between equilibrium and non-equilibrium conditions (Prigogine 1997).

A general relation between transport and self-diffusion is, within the Maxwell–Stefan formalism (DeGroot and Mazur 1962; Krishna and Wesselingh 1997; Prigogine 1997; Kärger et al. 2012; Krishna 2014; Kärger and Ruthven 2016), commonly based on the equation (Paschek and Krishna 2001).

(18)

Here, the reciprocal value of the self-diffusivity is understood as a measure of the resistance to be overcome by molecules under the conditions of tracer exchange. This resistance is, obviously, brought about by the influence of the internal pore surface and the friction between counter-diffusing molecules. The latter influence is quantified by the reciprocal value of a parameter Ðii, referred to as the self-exchange diffusivity.

The second contribution, brought about by the interaction with the internal pore space, may be evaluated by considering the gradient in chemical potential as the (genuine) driving force of diffusive fluxes in equilibrium with the resistance experienced by the diffusing molecules

$$fu = - \frac{d\mu }{{dx}}$$
(19)

with \(u\) and \(f\) denoting, respectively, the molecular mean velocity and a friction coefficient reflecting the interaction of the diffusing molecules with the surroundings. With Eq. (19), the diffusive flux may finally be noted as.

$$j = uc = - \frac{RT}{f}\frac{d\ln p}{{d\ln c}}\frac{dc}{{dx{^\prime}}}$$
(20)

where, in the second equality, the chemical potential

$$\mu (c) = \mu_{0} + RT\ln p(c)$$
(21)

is correlated with the (inverse of the) adsorption isotherm \(c(p)\). By comparison with Fick’s first law, Eq. (2), we end up with.

$$D_{T} = \frac{RT}{f}\frac{d\ln p}{{d\ln c}} = D_{0} \frac{d\ln p}{{d\ln c}}$$
(22)

With the second equality, the expression \(\frac{RT}{f}\) has been condensed to \({D}_{0}\), which is referred to as the “corrected” or Maxwell–Stefan diffusivity.

With Eq. (22), the transport diffusivity \({D}_{T}\) is thus found to consist of two constituents. One of them, the term \(\frac{dlnp}{dlnc}\), is referred to as the thermodynamic (correction) factor. It is exclusively determined by thermodynamics. All features of molecular dynamics are contained in the other factor, \({D}_{0}\), which with Eq. (22) has been introduced as being inversely proportional to the friction coefficient. It is therefore 1/\({D}_{0}\) rather than 1/\({D}_{T}\), which has to appear in Eq. (18). In addition to the transport diffusivities ( \({D}_{T}\)) and self-diffusivities (\(D\)), Fig. 9 also displays the values of the corrected diffusivities (\({D}_{0}\)) as resulting, via Eq. (22), from the adsorption isotherms and the transport diffusivities.

For the systems considered in Fig. 9, corrected and self-diffusivities are, most remarkably, found to essentially coincide over the covered range of guest concentration. With Eq. (18) one may therefore immediately conclude that the effect of mutual friction between different guest molecules as expressed by the term is negligibly small in comparison with the resistance experience by the propagating molecules due to the internal surface. This, however, is the expected behavior in view of the close match of the critical diameters of the molecules considered in Fig. 9 with the “windows” between adjacent cages of MOF ZIF-8 (Park et al. 2006). Under such conditions, passage from one cage to the adjacent one may indeed be expected to be the governing step of overall diffusion.

With the application of classical transition state theory (TST) (Gladstone et al. 1941; Ruthven and Derrah 1972; Kärger 1976; Chmelik and Kärger 2016) one may go one step further by using knowledge of the adsorption isotherms for a first-order estimate of the concentration dependencies of the diffusivities. Such an estimate can be based on the proportionality

$$\frac{1}{\tau (c)} \propto \frac{p(c)}{c}$$
(23)

between molecular mean life time within one cage and the ratio between gas pressure and guest concentration. This relation follows from the conception of dynamic equilibrium between the ground state (cage interior) and the activated state (window), with the implications that the population in the windows, being negligibly small, is proportional to the external pressure and that the mean passage time through windows is independent of concentration. Starting with Eq. (23) (see (Gladstone et al. 1941; Ruthven and Derrah 1972; Kärger 1976; Chmelik and Kärger 2016)) self- and transport diffusion may be shown to obey the relations

$$D = D\,(c = 0) \times k\frac{p(c)}{c}$$
(24)

and

$$D_{\text{T}} = D\,(c = 0) \times k\frac{dp}{{dc}}$$
(25)

with

$$k = \left( \frac{c}{p} \right)_{c \to 0} = \left( {\frac{\partial c}{{\partial p}}} \right)_{c \to 0}$$
(26)

denoting the Henry coefficient.

With the full lines included in the representations of the transport and self-diffusivities in Fig. 9b, c, Eqs. (24) and (25) are indeed shown to serve as a useful prediction of their concentration dependences.

With methanol over, essentially, the total range of concentrations and with ethanol up to half pore filling, self-diffusivities in MOF ZIF-8 are seen to exceed the transport diffusivities. The finding that counterdiffusion leads to an enhancement of mass transfer (Chmelik et al. 2010a) in comparison with simple “down-hill” transport diffusion appears, at first sight, to be counterintuitive. However, with , any perceptible resistance through counterdiffusion we had already anyway excluded for the systems under study.

It is, therefore, exclusively the influence of the (thermodynamic) factor \(\frac{dlnp}{dlnc}\), which determines the relationship between transport and self-diffusion—given Eq. (22) and the coincidence of corrected and self-diffusivities for the systems under study. Its magnitude is a function of the shape of the adsorption isotherm. Differing from the conventional Langmuir-type, the S-shape of the adsorption isotherms as appearing from Fig. 9a, is indeed seen to yield values \(\frac{dlnp}{dlnc}<1\) resulting, with Eq. (22), in \({D}_{T}<{D}_{0}\approx D\). Such a tendency may also intuitively be anticipated, given the strong guest-guest interaction in consequence of their large dipolar moment. Giving rise to the typical S-shape of the adsorption isotherm, this interaction may be understood to also reduce the rate of downhill fluxes in comparison with fluxes under uniform overall concentration. For short-chain-length alkanes and alkenes in MOF ZIF-8, with notably smaller dipolar moments, adsorption follows the normal Langmuirian behavior and has, accordingly, been found to give rise to the common situation, with the transport diffusivities exceeding the self- (and corrected) diffusivities (Chmelik and Kärger 2016).

4.4 Monitoring mass transfer in mixed matrix membranes

Information about the distribution of guest molecules and their evolution in time may become particularly enlightening for in-depth studies of mass transfer in complex host systems. Such systems notably include the mixed-matrix membranes (MMMs) (Seoane et al. 2015; Dechnik et al. 2017; Friebe et al. 2017). With the nanoporous particles finely dispersed within a polymer film, MMMs have been developed as a compromise for overcoming, on the one hand side, the limitations in stability of purely inorganic (e.g. zeolite) membranes and, on the other hand, the limitations in selectivity of polymer membranes. Overall mass transfer and selectivity thus results in the interplay of the different phenomena of molecular propagation as occurring in the different constituents. Simulation of this interplay, starting from the elementary processes within the various constituents, has become therefore an important topic of research (Nielsen 1974; Berriot et al. 2003; Papadokostaki et al. 2015; Petropoulos et al. 2015; Schneider et al. 2019). While it is exclusively this overall mass transfer, which is in the focus of the conventional (“macroscopic”) techniques of diffusion measurement like uptake or permeation measurement, microimaging allows insight into also some of these elementary steps of molecular propagation.

Figure 10 introduces into the potentials of such an application of microimging with a model system fabricated by inserting a large MOF crystal of type ZIF-8 into a 6FDA-DAM polymer membrane (Hillock et al. 2008; Zhang et al. 2012). In a series of consecutive pictures of the distribution of CO2 molecules within the system, CO2 is seen to attain its equilibrium value within the MOF ZIF-8 crystal during already the second scan, revealing a much higher diffusivity within the MOF than in the polymer under consideration. CO2 concentration is, moreover, seen to attain its highest values in a region around the interface between MOF ZIF-8 and the polymer. This experimental finding nicely corroborates with predictions of grand canonical Monte Carlo simulations (Semino et al. 2016) that polymer micro-voids, which may be expected to occur predominantly in the vicinity of the interface between the MOF crystal and the polymer bulk phase, give rise to an accumulation of the CO2 molecules (Hwang et al. 2018).

Fig. 10
figure 10

Distribution of CO2 in a model MMM of type ZIF-8@6FDA-DAM, following a pressure step from 0 to 400 mbar at 308 K in the surrounding atmosphere as recorded by IR microimaging. Each image is the average over 8 scans captured during a 3–27 s, b 69–93 s, c 130–154 s, d 183–207, e 237–261 s, f 291–315 s, g 344–368 s, and h 415–439 s after the step in CO2 pressure. Color change from blue to red indicates increase in the CO2 concentration. Reprinted from ref. (Hwang et al. 2018) with permission

Full size image

Microimaging is thus found to provide information about the guest diffusivities in both constituents of the material under study and about an enhancement in guest concentration close to their mutual interface. Incorporation of this type of information is, doubtlessly, a promising route for future refinement of simulation and a continued, knowledge-based improvement of the performance of MMMs.

5 Microimaging with multicomponent systems

5.1 Diffusion pathways affected by Co-adsorption

The advantage of spatially resolved measurement as provided by microimaging becomes particular obvious on considering diffusion phenomena in multicomponent systems. Figure 11 presents, as an example of such studies, a comparison of the evolution of the intracrystalline concentration profiles in a crystal of ferrierite-type zeolite during single-component adsorption (Fig. 11b, c) and during subsequent uptake experiments involving different components (Fig. 11d).

Fig. 11
figure 11

REM picture and schematics of a zeolite crystal of type FER, accommodating two sets of nanoporous channels (a), and transient guest profiles during methanol (b) and ethanol (c) uptake, as well as during methanol uptake (d) as the second step in a two-step experiment, preceded by ethanol uptake over 1.8 h. Variations in the refractive index as shown in Fig. 11d are referred to changes in the methanol concentration. This is justified with the implication that ethanol mobilities are negligibly small in comparison with the methanol mobilities as appearing from the huge differences in the time scales considered in Fig. 11b, c. From (Kärger et al. 2014) with permission

Full size image

It is illustrated by Fig. 11a that zeolites of type ferrierite (FER) are traversed by two sets of mutually intersecting systems of “8-ring” and “10-ring” channels, with cross sections of about 0.43 × 0.55 and 0.34 × 0.48 nm2 (Jacobs and Martens 1987). Uptake of guest molecules (Fig. 11b, c) is, correspondingly, observed to follow, essentially, the notably broader 10-ring channels, with the uptake rate of methanol (with a critical diameter of \(\sim\)0.375 nm) notably exceeding that of ethanol (of \(\sim\)0.47 nm).

On considering molecular uptake of methanol after pre-adsorption of ethanol (Fig. 11d), however, one comes across a remarkable change in the preferred diffusion pathways. Now methanol uptake predominantly occurs along the smaller 8-ring channels, in parallel with a dramatic retardation in uptake kinetics. This redirection of methanol into the much narrower 8-ring channels is, obviously, a consequence of the blockage (the “traffic jam”) in the 10-ring channels affected by ethanol presorption.

5.2 Uphill diffusion and overshooting

Recognizing the gradient in the chemical potential as the genuine driving force, with Eqs. (20) and (22) diffusive fluxes under the conditions of single-component adsorption have been shown to be correlated with the adsorption isotherm via the relation.

$$j = - D_{0} (c)\frac{d\ln p}{{d\ln c}}\frac{dc}{{dx}}$$
(27)

Under the conditions of mixture adsorption with n components, this relation may be generalized to yield, for the diffusive flux of component i,

$$j_{i} = - D_{0i} (c_{1} ...c_{n} )\sum\limits_{j = 1}^{n} {\frac{{\partial \ln p_{i} }}{{\partial \ln c_{j} }}\frac{{dc_{j} }}{dx} = - \sum\limits_{j = 1}^{n} {D_{ij} \frac{{dc_{j} }}{dx}} }$$
(28)

Diffusive fluxes of a given component are thus seen to be brought about by also the concentration gradients of all other components. The diffusion coefficient is replaced by a diffusion matrix, with its elements \({D}_{ij}\) indicating the effect of the concentration gradient of component j on the diffusive flux of component i. This behavior as following with the Maxwell–Stefan formalism of irreversible thermodynamics (Kärger et al. 2012; Krishna 2015, 2016, 2019; Kärger and Ruthven 2016) has now, with the potentials of microimaging, become accessible by direct monitoring.

Two examples of such studies are shown in Fig. 12 (Lauerer et al. 2015). Both are based on the application of microimaging by IFM where, similarly as with the example considered in Sect. 5.1, distinction between the two components is based on the large difference in their diffusivities.

Fig. 12
figure 12

Transient concentration profiles through a single crystal of zeolite ZSM-58 during two-component uptake as recorded by IFM microimaging (a–d) and their prediction via TST following Eq. (28) (e, f). Fig. 12a, b show, respectively, the concentration profile of propene after uptake over 7 h from an external propene atmosphere of 10 mbar and the evolution of the intracrystallien concentration profile of ethane when, subsequently, the propene atmosphere has been replaced by an ethane atmosphere of 200 mbar. Evolution of the concentration profiles of both ethane and CO2 from a mixture of both components with a partial pressure of 200 mbar of each are shown in Figs. 12c and d. All measurements have been performed at room temperature. Figures 12e and f show predictions of the experimentally determined evolutions of the concentration profile of ethane as the “fast” component in a propene-ethane mixture (Fig. 12b) and as the “slow” component in the ethane-CO2 mixture (Fig. 12c). Reprinted under the Creative Commons Attribution License from ref. (Lauerer et al. 2015)

Full size image

Figure 12b shows the evolution of the concentration profiles of ethane in a single crystal of zeolite ZSM-58 upon uptake from a surrounding ethane atmosphere of 200 mbar, after the crystal had been in contact with a propene atmosphere of 10 mbar over 7 h, giving rise to the concentration profile shown in Fig. 12a. Initially, ethane uptake is seen to follow the usual pattern, with a flux in direction of decreasing ethane concentration towards the crystal interior, giving rise to an increasing ethane concentration. This pattern is maintained with also further increasing time so that, after about 10 min, ethane concentration towards the crystal center is going to even exceed the concentration at the boundary. Now, most remarkably, ethane diffusion is seen to be directed towards increasing ethane concentration, i.e. to undergo “up-hill” diffusion. With Eq. (28) and . 12a, b, this effect is easily referred to the influence of the concentration gradient of the second component, namely of propene. This ensures that, irrespective of the change in the sign of the gradient in ethane concentration, the flux continues to be directed into the interior. Only when, with further ethane uptake and increasing slopes in their profiles, both effects finally compensate each other (after about 30 min), the ethane profiles come to a relative standstill. From now on, evolution is controlled by variation in the propene profiles, which is far too slow to allow a reasonable continuation of this type of experiment.

With the transient concentration profiles recorded during the uptake of ethane-CO2 mixtures, Fig. 12c, d consider the essentially opposite situation. Once again, the time dependence is controlled by the diffusion of the ethane molecules. While, in the previous example, the mobility of the second component (namely of propene) was chosen to be negligibly small in comparison to that of ethane, now the opposite is true. With a diffusivity exceeding that of ethane by orders of magnitude, local CO2 concentration can be implied to be, instantaneously, in equilibrium with the given ethane distribution. Thus, each of the profiles shown for CO2 in Fig. 12d emerged under the conditions pertinent to the last profile shown for ethane in Fig. 12b. Differing from Fig. 12a, with a – during the course of our experiment—essentially invariant concentration profile of the slow component (propene), with Fig. 12c we are able to follow the evolution of the distribution of the slow component (now ethane), simultaneously with a decrease in the “over-shooting” of the fast component (CO2) in Fig. 12d.

Similarly as considered already in Sect. 4.3, window diameters in zeolite ZSM-58 are comparable with the size of the ethane molecules as considered in this study. This once again allows the application of TST, now with the jump rates between adjacent cages as a function of the concentration of both components (Lauerer et al. 2015). With the results shown in Fig. 12e, f, TST is found to provide a meaningful prediction of molecular uptake and release under even the by far more complicated situation of multicomponent adsorption.

5.3 Monitoring and evaluating catalytic conversion

By monitoring the evolution of the concentration profiles of all molecules involved in a reaction within a porous catalyst, microimaging by IRM provides us with a novel instrument for the in-depth study of catalytic conversions and knowledge-based performance enhancement. The potentials of such an access are illustrated by Fig. 13. It shows the transient concentration profiles of benzene, during uptake from a benzene-hydrogen atmosphere, by a nickel-loaded porous glass (Enke et al. 2016), accompanied by the formation of cyclohexane emerging as the product of benzene hydrogenation. Measurement is performed with a thin glass platelet with sealed surfaces so that uptake occurs through, exclusively, the edge of the platelet, with the x coordinate showing into its interior.

Fig. 13
figure 13

Hydrogenation of benzene to cyclohexane in a platelet of porous glass with dispersed nickel at 299 K (a) and 348 K (b). After activation, the face at x = 0 is brought into contact with a benzene atmosphere (with excess hydrogen). Data points (circles (A) for benzene, diamonds (B) for cyclohexane) show the evolution of the respective concentration profiles as recorded by IR microimaging. Solid lines are solutions of the diffusion–reaction equations, yielding best fit to the experimental data. With permission from (Titze et al. 2015a)

Full size image

The full lines in Fig. 13 are analytical solutions of the diffusion–reaction equation as resulting from Fick’s second law, Eq. (5), complemented by a reaction term \(\pm kc\). It takes account of benzene conversion into cyclohexane, with k denoting the first-order reaction rate constant (see (Titze et al. 2015a) for details). These solutions are seen to yield reasonable agreement with the experimental data under already quite simplifying assumptions. They include, in particular, coincidence in the diffusivities of both types of molecules and absence of any concentration dependence.

Final attainment of stationary conditions, i.e. of dynamic equilibrium, means coinciding rates of, respectively, benzene uptake, benzene-to-cyclohexane conversion and cyclohexane release. Figure 13 nicely illustrates the acceleration of conversion with increasing temperature, which appears in a significant increase in the uptake and release rates of, respectively, the reactant and product molecules. It is interesting to note that the reactant molecules get close to their final distribution over the catalyst particle (compare, e.g., for 348 K, the two profiles after 2 min) notably faster than the product molecules.

The ratio

$$\eta=\frac{r_{\rm eff}}{r_{\rm int}}=\frac{{\bar{c}}_{\rm reac.}}{c_{\rm react, equ.}}$$
(29)

between the “effective” (i.e. the actual) and the “intrinsic” (i.e. the maximum possible) reaction rates is referred to as the effectiveness factor (Thiele 1939; Haag et al. 1981; Klemm et al. 2002; Dittmeyer and Emig 2008). It is a key number in performance assessment of porous catalysts. The second equality holds for a first-order reaction as considered with the hydrogenation of benzene to cyclohexane, with the reaction rates being proportional to the respective concentrations. \({\bar{c}}_{\mathrm{reac}.}\) and \({c}_{\mathrm{react},\mathrm{equ}.}\) denote, correspondingly, the mean reactant concentration under stationary conditions and its maximum possible value in equilibrium with the surrounding atmosphere (i.e. without any reaction or, equivalently, with the product molecules instantaneously replaced by reactant molecules).

Effectiveness factors are, conventionally, determined by determining reaction rates, as indicated by the first equality in Eq. (29). While \({r}_{\mathrm{eff}}\) is the direct output of the conversion experiments and thus immediately accessible, there is no direct way to experimentally determine \({r}_{\mathrm{int}}\). This is a consequence of the fact that transport resistances can never be totally prevented, which excludes the instantaneous replacement of emerging products by “fresh” reactants. One usually tries to circumvent this problem in a series of measurements, with one parameter (notably the diameter of the catalyst) intentionally varied and all others kept constant. This latter requirement, however, is hardly to be validated by direct experimental evidence (Haag et al. 1981, Garcia and Weisz 1993, Avila et al. 2007, van den Bergh et al. 2010).

The advent of microimaging by IRM offers a solution to this problem. Operating with the single-element detector (SE, see Sect. 2.2 and Fig. 2), IRM is able to record the concentration of each component integrated over the whole catalyst particle. The mean concentration of both the reactant and product molecules within catalyst particles of any shape become thus accessible by direct measurement. In this way, via Eq. (29) and with the relation.

$$c_{react} + c_{prod} \approx c_{react.equ}$$
(30)

approaching the maximum reactant concentration by the sum of the reactant and product molecules under stationary conditions, “one-shot” determination of effectiveness factors has in fact become possible. In Ref. (Chmelik et al. 2018), these potentials have been exploited for the determination of the effectiveness factor of platinum-containing nanoporous glass beads for the hydrogenation of benzene to cyclohexane. Figure 14 illustrates, in a cartoon-like manner, the underlying principle of measurement (Chmelik et al. 2018).

Fig. 14
figure 14

SEM-image of a representative catalyst particle (a) and IR-spectrum (b) showing the bands in the IR spectrum exploited for determining the concentrations of benzene (Bz, green) and cyclohexane (CyH, red) within the catalyst particle during reaction. Inserts refer to the option of spatially resolved concentration measurement by IRM, from (Chmelik et al. 2018), with permission

Full size image

6 Conclusions

Microimaging by the application of interference microscopy (IFM) and of IR microscopy (IRM) has, over the past two decades, found manifold applications for investigating mass transfer phenomena in nanoporous solids. In the very core of their potentials is the ability of monitoring the evolution of concentration profiles within porous solids, induced by a variation in the surrounding atmosphere. So far, such profiles were mainly known from the relevant textbooks like the monographs by Crank (Crank 1975) and (Carslaw and Jaeger 2004). The new options of observation gave rise to the development of a series of measuring concepts with insights into phenomena of guest transport, which, so far, were inaccessible by direct observation. This does, in particular, concern the quantification of transport resistances on the outer surface of the nanoporous particles and, related to this, the probability that, upon colliding with the external surface, a molecule of the surrounding atmosphere continues its diffusion path into the interior of the nanoporous solid.

With the potentials to distinguish between different components, IRM offers the option to record, in addition to molecular fluxes, also chemical conversions. In this way, for the first time effectiveness factors of chemical reactions in porous catalysts have become accessible by direct (“one-shot”) measurement.

The evidence on diffusion and surface permeation in microimaging is based on the observation and measurement of the concentration profiles of the molecules under study and of their variation in time. This provides immediate access to molecular fluxes and, hence, to the phenomena under consideration. This notably minimizes the risk of misinterpretations which, naturally, in experimental studies can never be excluded. In this way, microimaging by IRM and IFM offers good preconditions to serve as a standard procedure for the attainment of reliable diffusion data in porous solids.

Operating with single crystals/particles rather than with particle beds or agglomerates, microimaging is, in addition, able to record the spreading of transport characteristics between the various crystals/particles within one batch. Due to the same reason, however, sample preparation in microimaging turned out to be quite challenging, given the fact that already smallest amounts of impurities in the optical cells could affect the intactness of the host particle under study. In such cases, reliable results can only be attained in a series of experiments with reproducible outcome.

One has to be aware that there are nature-given limits in the applicability of microimaging. This notably includes the spatial resolution, being in the range of fractions of micrometers in IFM and of up to ten micrometers in IRM. Spatially resolved measurements of intracrystalline concentration profiles with particle extensions that do not significantly exceed these limits are therefore anyway excluded. There are, on the other hand, many fundamental problems of mass transfer in complex systems, where microimaging is able to provide important insight. This is even possible by investigating model systems which, in their structure, follow the necessity of the measuring technique rather than the conditions of their practical application. An example of such studies has been presented with the investigation of the dynamics of guest distribution in mixed-matrix membranes on comparing the equilibration rates in the polymer and the microporous “filler”. A rich field of related application will, most likely, open up with hierarchically porous materials where microimaging may help to elucidate the rates of propagation within the various pore space combinations.

The examples provided in this contribution were thought as an illustration of the large variety of information which, with the advent of microimaging, has become possible. Never before the devices used for these studies have been applied in a similar way. Their application for the purposes here described was often accompanied, therefore, by extensive efforts in adopting the measuring conditions to the given requirements, notably including large variations in the temperatures and pressures covered during sample preparation and the experiments. Corresponding developments by already the manufacturers will therefore notably contribute to accelerating further development in the field.