1 Introduction

The contact between metallic bodies occur in many applications [1, 2], and often the contact pressure is so high as to generate plastic deformation, at least at the asperity level [2,3,4,5,6,7,8,9,10,11,12]. In fact, because of surface roughness and the high elastic modulus of most metals, the contact pressure between asperities at short length scale can be very high even when the nominal contact pressure is low. Thus for metals in the area of real contact some plastic flow will almost always occur, at least during the first contact [13].

Metallic seals are used in many applications involving very high fluid pressure differences, and in ultra high vacuum systems. Surface roughness and plastic flow highly affects leakage in metallic seals, since they are key factors in determining the surface separation in the non-contact area. For elastic solids like rubber, contact mechanics theories have been developed for how to predict the fluid leakage rate, and it has been shown that they are in good agreement with experiments [14, 15]. The simplest approach assumes that the whole fluid pressure difference between the inside and outside of the sealed region, occur over the most narrow constrictions (denoted critical junctions), encountered along the largest open percolating non-contact flow channels.

For elastic solids numerical contact mechanics models [16], such as the boundary element model, and the analytic theory of Persson [17, 18], can be used to calculate the surface separation at the critical junction and hence predict fluid leakage rates. For solids involving plastic flow, the surfaces will approach each other more closely than if only elastic deformations would occur. This will reduce the fluid leakage rate [19, 20].

Here we will present the outcome of a study, where we experimentally explore the nature of the plastic deformation of the asperities of a sandblasted aluminum surface, but we believe the results should hold quite generally for other metals (or alloys) of interest such as steel, copper or bronze. We will also present results from numerical simulations of the experimental set-up, based on the boundary element method combined with a simple procedure to include plastic flow. More precisely, we employ the method presented in [21] that assumes an elastoplastic model where a solid deforms elastically until the local pressure reaches a critical stress (the indentation hardness), after which it flows without strain hardening.

Consider the indentation of a nominal flat metal surface with surface roughness by a rigid and perfectly smooth spherical indentor [22]. In the most naive picture of plastic deformation one would expect all the asperities within the indented (spherical cup) region to be plastically flattened. This result follows from the fact that the local pressure acting on an asperity if not flattened would be larger than the indentation hardness as given by the normal force divided by the projected (macroscopic) indentation area. However, it has been known for a long time that the asperities does not flatten out perfectly, but only the upper part of some fraction of the asperities flatten in such a way that the flattened area typically occupy \(50\%\) of the macroscopic indentation area [23,24,25]. This persistence of asperities in indentation experiments can be interpreted as resulting from a indentation hardness which increases as the length scale (or indentation size) decreases, as observed in many experimental studies [26, 27]. This effect could explain our experimental observations if the indentation hardness would be \(\sim 50\%\) higher at the macroasperity level then at the macroscopic level. However, other explanations based on plasticity mechanics of asperity interaction has also been proposed [23, 24, 28,29,30]. Qualitatively, one may say that when an asperity becomes strongly plastically deformed the stress field approach a hydrostatic stress and the asperity therefore becomes resistant to further plastic deformation.

Another important effect which must be considered is that the indentation hardness \(\sigma _\mathrm{P} \approx 3 \sigma _\mathrm{Y}\) refer to full plastic flow. It is well known from studies of, e.g., Johnson [6] and Etison [11, 31] that plastic flow starts at contact pressures \(\sigma \approx 1.1 \sigma _\mathrm{Y}\) much below the indentation hardness \(\sigma _\mathrm{P} \approx 3 \sigma _\mathrm{Y}\), where \(\sigma _\mathrm{Y}\) is the yield stress in elongation. This corresponds (for a spherical indentor) to plastic yielding starting at loads \(\sim 30\) times lower than needed for full plastic flow. It follows that only if the macroscopic indentation is large enough would one expect complete flattening of the asperities in the indented region.

Recently, several studies of surface roughness and plastic flow have been reported using microscopic (atomistic) models [32], or models inspired by atomic scale phenomena that control the nucleation and glide of the dislocations [33,34,35]. These models supply fundamental insight into the complex process of plastic flow, but are not easy to apply to practical systems involving inhomogeneous polycrystalline metals and alloys exhibiting surface roughness on many length scales. The approach we use here is less accurate but easy to implement, and it can be used to estimate the leakage rates of metallic seals. We show that in spite of the simplicity of the description of plastic flow, the numerical simulations give results in good agreement with the experimental data.

2 Experimental

The aluminum block was indented with either a steel ball with \(40 \ \mathrm{mm}\) diameter, or a silicon nitride \(\mathrm{Si}_3 \mathrm{N}_4\) ball with \(33.338 \ \mathrm{mm}\) diameter, or a borosilica glass ball with the diameter \(30 \ \mathrm{mm}\). The normal (indentation) force was \(40 \ \mathrm{kN}\). Indentation was done on a rectangular aluminum block with a polished surface, and on two sandblasted aluminum surfaces. The sandblasting was done with glass beads (spherical particles with smooth surfaces) of diameter ≈ 10 μm for a time ranging from 5 to 8 min using 8 bar air pressure. The topography measurements were performed with Mitutoyo Portable Surface Roughness Measurement device, Surftest SJ-410 with a diamond tip with the radius of curvature R = 1 μm, and with the tip–substrate repulsive force \(F_\mathrm{N}=0.75 \ \mathrm{mN}\). The lateral tip speed was \(v=50\) μm/s and the lateral resolution 0.5 μm. The radius of curvature of the tip was always smaller than the surface curvature radius, which is a necessary condition for reliable measurements of the surface topography [36].

From the the measured surface topography (line scans) \(z=h(x)\) we calculated the one-dimensional (1D) surface roughness power spectra defined by

$$\begin{aligned} C_\mathrm{1D} (q) = {1\over 2 \pi } \int _{-\infty }^\infty dx \ \langle h(x) h(0) \rangle e^{i q x} \end{aligned}$$
(1)

where \(\langle .. \rangle\) stands for ensemble averaging. In the results we show below, we have averaged the powerspectra (and height probability distribution) over several (typically 6) different line scans performed in different directions.

For surfaces with isotropic roughness the 2D power spectrum C(q) can be obtained directly from \(C_\mathrm{1D} (q)\) as described elsewhere [37, 38]. For randomly rough surfaces, all the (ensemble averaged) information about the surface is contained in the power spectrum C(q). For this reason the only information about the surface roughness which enter in contact mechanics theories (with or without adhesion) is the function C(q). Thus, the (ensemble averaged) area of real contact, the interfacial stress distribution and the distribution of interfacial separations, are all determined by C(q) [17, 18]. Note that, the moments of the power spectrum determines the often quoted standard quantities, which are output of most stylus instruments. Thus, for example, the mean-square (ms) roughness amplitude \(\langle h^2 \rangle\) and the ms slope \(\langle (dh/dx)^2\rangle\) are given by

$$\begin{aligned} \langle h^2 \rangle = 2 \int _0^\infty dq \ C_\mathrm{1D}(q), \end{aligned}$$

and

$$\begin{aligned} \langle (dh/dx)^2 \rangle = 2 \int _0^\infty dq \ q^2 C_\mathrm{1D}(q), \end{aligned}$$

respectively.

Since the surface topography was measured only along line scans \(z=h(x)\), for the numerical contact mechanics simulations (see Sect. 4) we produced randomly rough surfaces using the random-phase-method described in Appendix D in Ref. [39]. For generating these surfaces we used the 2D surface roughness power spectra obtained as described above.

3 Experimental Results

We have performed indentation experiments for three different nominally flat aluminum surfaces, one polished and two sandblasted. Before performing the indentation experiments we measured the surface topography \(z=h(x)\) along several \(10 \ \mathrm{mm}\) long tracks, from which we have calculated the 1D surface roughness power spectra using (1).

Figure 1 shows the surface roughness power spectra as a function of the wavenumber (log-log scale) for the sandblasted and polished aluminum surfaces. The root-mean-square (rms) roughness amplitude of the three surfaces are \(h_\mathrm{rms} = 15.8\), 5.8 and 0.3 μm, and the corresponding rms slopes are 0.42, 0.45 and 0.04, respectively. The surfaces have nearly vanishing skewness (\(-0.02\), 0.13 and \(-0.05\)), and the kurtosis (2.7, 2.9 and 3.1) is close to 3 for all the surfaces, as expected for randomly rough surfaces with a Gaussian height probability distribution.

Fig. 1
figure 1

The surface roughness power spectrum as a function of the wavenumber (log–log scale) for two sandblasted aluminum surfaces and one polished aluminum surface. The root-mean-square (rms) roughness amplitude of the three surfaces are \(h_\mathrm{rms} = 15.8\), 5.8 and 0.3 μm. The corresponding rms slopes are 0.42, 0.45 and 0.04, respectively. The surfaces have nearly vanishing skewness and the kurtosis is close to 3 for all the surfaces

Full size image

The aluminum surfaces where indented by steel, ceramic and glass balls. The height profiles of all the ball surfaces (after removing the macroscopic curvature) are shown in Fig. 2. Removing the slope and curvature of the shown height profile segments result in rms-roughness values of 92, 44 and \(17 \ {\mathrm{nm}}\) for the steel, ceramic and glass balls.

Fig. 2
figure 2

The height profile of the steel (black), ceramic (red) and glass (blue) balls. Removing the slope and curvature of the shown height profile segments result in rms-roughness values of 92, 44 and \(17 \ \mathrm{nm}\) for the steel, ceramic and glass balls (Color figure online)

Full size image

The sandblasted surface 1 was squeezed against the steel ball, and the sandblasted surface 2 and the polished surface was squeezed against the ceramic ball and the silica glass ball, in all cases with the normal force \(40 \ \mathrm{kN}\) for 1 min.

Figure 3 shows the surface roughness height profile h(x) of the sandblasted aluminum surface 1 after squeezing it against the steel ball. The spherical cup indentation has nearly the same radius of curvature as the steel ball, and with the indentation diameter \(\approx 0.8 \ \mathrm{cm}\). Also shown in the figure is a line scan from inside the indentation, before and after removing the macroscopic curvature. Note that the high asperities have flat upper surfaces because of plastic flow, while the roughness in the big valleys appears to be left almost unchanged. This is very different from what we observed in Ref. [40] for glassy polymers, in particular polyethylene, where during plastic deformation, the material moved effectively from the top of asperities to the nearby valley, resulting in long wavelength roughness which appeared the same as on the original (undeformed) surface but with smaller amplitude. We attributed this to difference in the stress–strain curves and work-hardening. The aluminum surface is most likely already work-hardened by the production procedure, but we also did experiments on an aluminum block which was first sandblasted and then annealed at T = 500 °C for 2 h; this surface showed similar plastically deformed roughness after indentation as the not annealed aluminum block.

Fig. 3
figure 3

The surface roughness height profile h(x) of the sandblasted aluminum surface 1 after squeezing a steel ball (radius \(R=2 \ \mathrm{cm }\)) against the aluminum block with the axial force \(F_\mathrm{N} = 40 \ \mathrm{kN}\) for 1 min. This result in a spherical cup indentation with nearly the same radius of curvature as the steel ball and with the indentation diameter \(2r_0=\approx 0.8 \ \mathrm{cm}\), giving a macroscopic indentation hardness \(\sigma _\mathrm{P} = F_\mathrm{N}/(\pi r_0^2) \approx 0.8 \ \mathrm{GPa}\). The middle line shows the line scan data from inside the indentation, and the bottom line after removing the macroscopic curvature. Note that the high asperities have flat upper surfaces because of plastic flow

Full size image

Usually the material indentation hardness is defined as the ratio between the external normal force (here \(F_\mathrm{N} = 40 \ \mathrm{kN}\)) and the projected indentation area (here \(A_0 = \pi r_0^2\) with \(r_0 \approx 4 \ \mathrm{mm}\)). This gives \(\sigma _\mathrm{P} \approx 0.8 \ \mathrm{GPa}\) which is in good agreement with other studies, e.g., \(\sigma _\mathrm{P} \approx 1.033\) and \(0.806 \ \mathrm{GPa}\) as found for two different aluminum alloys in Ref. [41]. However, note that the top surface area of the flattened macroasperities occupy only \(\approx 40\%\) of the nominal contact area in Fig. 3, corresponding to an effective indentation hardness \(\sigma _\mathrm{P} \approx 2.0 \ \mathrm{GPa}\). In fact, if a plastically deformed macroasperity contact area is observed at higher magnification, then short wavelength roughness can be observed, and an even smaller fraction than \(\approx 40\%\) of the nominally contact area may be plastically deformed (see also Sect. 5 below). We conclude that most likely the indentation hardness depends on the length scale (or size of the indentor), a fact which is well known from earlier studies using different size of the indentor, or different indentation depth [26]. There are several different reasons for this length-scale dependent hardness, e.g., it may result from a thin work-hardened surface layer.

Figure 4 shows magnified pictures of the surface topography in Fig. 3. The two upper curves are linescans from the sandblasted surface 1 before plastic deformation, and the lower curve shows a linescan from inside the indented region by first removing the macroscopic curvature. Note that the high asperities (at this magnification) appear to have flat upper surfaces because of plastic flow.

Fig. 4
figure 4

The surface roughness height profile h(x) of the sandblasted aluminum surface 1 (top two lines), and after squeezing the steel ball against the aluminium surface (bottom line). The bottom linescan data is from inside the indentation by first removing the macroscopic curvature. Note that the high asperities have flat upper surfaces because of plastic flow.

Full size image

Figure 5 shows the surface roughness height distribution \(P_h\) of a sandblasted aluminum surface 1 before (red line), and after (black line) squeezing the steel ball against the aluminum block. In the latter case the line scan data is from inside the indentation and obtained by first removing the macroscopic curvature. The sharp peak is due to the flat upper surfaces of the plastically deformed asperities.

Fig. 5
figure 5

The surface roughness height distribution \(P_h\) of the sandblasted aluminum surface 1 (red line), and after squeezing the steel ball against the aluminum block (black line). The black line is obtained from the line scan data inside the indentation by first removing the macroscopic curvature. The sharp peak is due to the high asperities have flat upper surfaces (of equal height) because of plastic flow (Color figure online)

Full size image

The blue line in Fig. 6 shows the surface topography of the sandblasted surface 2 after indenting it with the ceramic ball. The linescan is from inside the indented region after removing the surface curvature. Similar result for the polished aluminum surface is shown by the upper green line. The lower green line is the measured surface topography of the polished aluminum surface before indenting it with the ball.

Fig. 6
figure 6

The surface topography of the sandblasted aluminum surface 2 (top blue line), and of the polished surface, indented with a ceramic ball (Silicon nitride, Si3N4) with diameter 33.3 mm. The axial force \(F_\mathrm{N} = 40 \ \mathrm{kN}\) for 1 min. The topography (middle line) is after removing the surface curvature. Also shown is the surface topography of the not indented surface area of the polished ball (bottom green line) (Color figure online)

Full size image

Figure 7 shows a magnified view of segments from the roughness profiles in Fig. 6 (the region between the two vertical lines). Note that the short-wavelength roughness in the plastically deformed region of the sandblasted surface (blue line), is very similar to that in the indented region of the polished surface (upper green line), and slightly larger than that of the original polished surface (green line). The short wavelength roughness (with amplitude ∼ 100 nm) is mainly due to the surface roughness of the ceramic ball (see Fig. 2), but in addition some contribution to the roughness may be due to inhomogeneous plastic flow.

Fig. 7
figure 7

The surface topography in Fig. 6 between the two vertical lines

Full size image

Figure 8 shows the measured surface roughness power spectrum (for the ceramic ball on the sandblasted aluminum surface 2) as a function of the wavenumber (log–log scale) before indentation (blue), and after (black) plastic deformation.

Fig. 8
figure 8

The measured surface roughness power spectrum (for the ceramic ball on the sandblasted aluminum surface 2) as a function of the wavenumber (log–log scale) before indentation (blue), and after (black) plastic deformation (Color figure online)

Full size image

Figure 9 shows the height probability distribution for the sandblasted surface 2 (original surface) (blue), and from inside the indented region after removing the surface curvature (black).

Fig. 9
figure 9

The height probability distribution of the sandblasted surface 2 (blue line), and after indenting it with the ceramic ball (black line). The height probability distribution of the indented surface is from inside the indented region after removing the surface curvature (Color figure online)

Full size image

We have also performed indentation studies using a glass ball. The blue line in Fig. 10 shows the surface roughness height profile h(x) of the sandblasted aluminum surface 2 after squeezing the silica glass ball against the aluminum block. The green line is the same result for the polished aluminum surface and the pink line is the topography of the glass ball. Note that the short wavelength roughness of both the sandblasted and polished aluminum surface are very similar to that of the glass ball. This is due to the plastic imprint of the glass ball roughness in the contact regions with the aluminum surface. Recall that the indentation hardness of the silica glass (about \(6 \ \mathrm{GPa}\), see Ref. [42]) is several times higher than that of the aluminum so mainly the aluminum will flow plastically.

Fig. 10
figure 10

The surface roughness height profile h(x) of the sandblasted aluminum surface 2 after squeezing a glass ball (radius \(R=1.5 \ \mathrm{cm }\)) against the aluminum block with the axial force \(F_\mathrm{N} = 40 \ \mathrm{kN}\) for 1 min (blue line). This result in a spherical cup indentation with nearly the same radius of curvature as the glass ball. The green line is the same result for a polished aluminum surface. The pink line is the topography of the glass ball. In all cases the curvature of the indentation (or the glass ball) is removed (Color figure online)

Full size image

Figure 11 shows the measured surface roughness power spectrum (for the glass ball on the sandblasted surface 2) as a function of the wavenumber (log-log scale) before indentation (blue), and after (black) plastic deformation.

Fig. 11
figure 11

The measured surface roughness power spectrum (for the glass ball on the sandblasted surface 2) as a function of the wavenumber (log–log scale) before indentation (blue), and after (black) plastic deformation (Color figure online)

Full size image

Figure 12 shows the height probability distribution of the sandblasted surface 2 (blue line), and after indenting it with the glass ball (black curve). The height probability distribution of the indented surface is from inside the indented region after removing the surface curvature.

Fig. 12
figure 12

The height probability distribution of the sandblasted surface 2 (blue line), and after indenting it with the glass ball (black curve). The height probability distribution of the indented surface is from inside the indented region after removing the surface curvature (Color figure online)

Full size image

Note that Figs. 8 , 11, and 9, 12, should basically give the same results, as the balls used as indentors have negligible surface roughness. Here, we show the results obtained using both balls, as it constitutes a test about the accuracy and reproducibility of the measurements. The power spectra and the height probability distributions differs slightly because the surface roughness is stochastic, so one expects different results for each topography line scan. If one would average over more line scans the “noise” in the curves would be reduced, but the noise is already small enough that the curves can be compared to the theory prediction (Figs. 15 and 16).

4 Numerical Simulation

We have performed numerical simulations of the plastic deformation of rough surfaces. We use the boundary element method (BEM), which treats the elastic deformations exactly (within the small slope approximation) described in [21], and the plastic deformations is considered within an elastoplastic approximation as described in Ref. [43]. In this model the solid deforms elastically as long as the surface stress is below the indentation hardness \(\sigma _\mathrm{P}\). When the local stress reaches the indentation hardness, the solid flow plastically without work hardening. In the model the plastic flow is taken into account by moving the surface grid point downwards in such a way that the local stress in the plastically deformed area is always equal to the indentation hardness. Figure 13 shows the originally used rough surface and plastically deformed rough surface obtained in the study below. The numerical solution procedure we use is based on spectral theory, and an FFT-accelerated approach is applied to increase the computational efficiency. Inputs to the model is the geometries and roughness of the contacting bodies, their Young’s modulus of elasticity, the Poisson ratios, and the Indentation hardness of the softer of the two surfaces. It predicts the contact pressure distribution and the corresponding elastic and plastic deformations of the contacting bodies. Parameters like the real area of contact, the ratio of plastically deformed to the nominal contact area, can also be deduced by postprocessing the results. This BEM-based elastoplastic approach has also been frequently employed in other works, see e.g. [18, 20, 43,44,45,46,47,48].

Fig. 13
figure 13

A section of size \(1.55 \ \mathrm{mm} \times 1.55 \ \mathrm{mm}\) (full system size \(12.4 \ \mathrm{mm} \times 12.4 \ \mathrm{mm}\)) of the rough surface before and after plastic deformation

Full size image

We have performed calculations for the sandblasted surface 2. Since the topography of this surface was measured only along a line, we first calculated the 2D surface roughness power spectrum from the 1D power spectrum [37, 38]. Next we generated mathematically a randomly rough surface with the power spectrum of surface 2 using the procedure described in Appendix D in Ref. [39]. However, we have not used the full power spectrum as this would result in a surface with roughness over too many length scales or degrees of freedom. Thus, the surface we use has the size \(2048 \times 2048\) grid points, and reproduce the measured power spectrum for \(q < q_1\) with \(q_1 \approx 5\times 10^5 \ \mathrm{m}^{-1}\).

Using a constant (size-independent) indentation hardness (\(\sigma _\mathrm{P} = 0.8 \ \mathrm{GPa}\)), we first simulated the experimental set-up, including the geometry of the spherical indenter, and found, as expected, a spherical-cup indented area where all the asperities are completely flattened. Thus, in order for asperities to persist one must assume that the indentation hardness increases with decreasing size of the indentation.

A feasible way to study the contact mechanics at the asperity level would be to simulate the local contact mechanical behavior at a location somewhere within the macroscopic (spherical cup) indentation area. Therefore, we decided to increase the indentation hardness at the macroasperity level so it become larger than the macroscopic indentation hardness (here defined as the normal load divided by the cross-section area of the macroscopic indentation in Fig. 2), and then simulate the contact between a rigid plane and a deformable nominally flat surface with the roughness obtained from the measurements.

We consider now squeezing a rigid and perfectly flat surface against an elastoplastic solid with the surface roughness obtained as described above. We assume the nominal contact pressure \(1 \ \mathrm{GPa}\) which is similar as the nominal contact pressure acting in the indented region in the experiments. We assume the Young’s elastic modulus \(E=69 \ \mathrm{GPa}\), the Poisson ratio \(\nu = 0.33\), which are typical values for aluminum. We also assume the aluminum indentation hardness \(2.0 \ \mathrm{GPa}\).

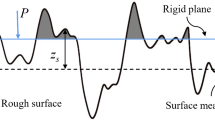
The rough surface has the size \(L\times L\) with \(L\approx 12.5 \ \mathrm{mm}\). In Fig. 14 we show a \(2 \ \mathrm{mm}\) long line scan of the the calculated surface topography. In (a) we show the original surface topography (thin line), and of the plastically deformed profile (thick line). In (b) we show the surface topography during contact with a flat surface (thin line), and of the plastically deformed profile (thick line). Note that in (b) the elastic rebound makes the upper surface of the plastically deformed asperities curved. Note also in (a) that the surface roughness below the plastically deformed region is nearly unchanged. Since the total volume of the solid must be (nearly) unchanged, in reality material must flow also in the tangential direction, which result in some modification of the roughness also in the regions which was not in contact with the flat countersurface. For materials which undergoes work hardening this tangential flow may be very important, but the experiments we did on a sandblasted and then annealed aluminium block (see Sect. 3) gave qualitatively very similar result as for the not annealed block. Still, the plastic flow procedure used in the present paper can not be applied to polymers like polyethylene in Ref. [40] (see also Sect. 5).

Fig. 14
figure 14

Calculated plastic and elastoplastic deformations due to a load corresponding to the nominal contact pressure \(1 \ \mathrm{GPa}\). Depicted in a are the original surface topography (thin line), and the plastically deformed profile (thick line), and depicted in b are the surface topography during contact with a flat surface (thin line), and the plastically deformed profile (thick line)

Full size image

Figure 15 shows the calculated height probability distribution before (blue) and after (black) squeezing (and removing) the rough surface against the flat rigid countersurface. Both the original and plastically deformed surface have similar height distribution as observed in the experiment (compare to Figs. 9 and  12).

Fig. 15
figure 15

The calculated height probability distribution before (blue) and after (black) squeezing the rough surface against a perfectly smooth surface with the nominal contact pressure \(1 \ \mathrm{GPa}\) (Color figure online)

Full size image

Figure 16 shows the calculated surface roughness power spectrum as a function of the wavenumber (log-log scale) before indentation (blue), and after plastic deformation (black). Also shown is the power spectrum of the surface of the solid when in contact with the flat rigid countersurface (gray). Note that for large wavenumber the plastically deformed surface and the surface in contact with the flat rigid surface exhibit the same surface roughness power spectrum. This is due to the fact that the large wavenumber roughness is due to the surface roughness in the regions not in contact with the flat surface, and this part is nearly unchanged. However, the surface area occupied by this (nearly unchanged) surface roughness is smaller than for the original surface, and this explains why the power spectrum for large wavenumbers of the plastically deformed surface is smaller than for the original surface.

Fig. 16
figure 16

The calculated surface roughness power spectrum as a function of the wavenumber (log-log scale) before indentation (blue), and after (black) plastic deformation with the nominal contact pressure \(1 \ \mathrm{GPa}\), and of the deformed surface during indentation (contact pressure \(1 \ \mathrm{GPa}\)) (gray) (Color figure online)

Full size image

In order to compare the measured power spectrum with the calculated ones, we show in Figs. 8 and 11 the measured power spectra on the same wavenumber interval as in Fig. 16. Comparing Fig. 16 with Figs. 8 and 11, we conclude that the calculated power spectrum of the plastically deformed surface is in good agreement with the measured one.

The Persson contact mechanics theory [17] can be used to study the nature of the contact area as we increase the magnification. When we study the interface at the magnification \(\zeta\) we only observe surface roughness with wavenumber \(q < \zeta q_0\), where \(q_0\) is the smallest wavenumber. Thus for \(\zeta = 1\) (or \(\mathrm{log}_{10} \zeta = 0\)) we do not observe any roughness and since the nominal contact pressure \(p=1 \ \mathrm{GPa}\) is below the indentation hardness stress \(\sigma _\mathrm{P} = 2.0 \ \mathrm{GPa}\) there is no plastic deformation, i.e. \(A_\mathrm{el}/A_0 =1\) and \(A_\mathrm{pl}/A_0 =0\). When we increase the magnification we observe surface roughness and the contact area decreases and the contact stress increases until it becomes large enough to induce plastic flow.

Fig. 17
figure 17

The relative contact area \(A/A_0\) as a function of the magnification \(\zeta\) (lower log-scale) or as a function of the wavenumber \(q=\zeta q_0\) (upper log-scale) as obtained using the Persson contact mechanics theory with the power spectrum shown in Fig. 16 (blue line). The relative elastic contact area and plastic contact area are shown separately as the red and green lines, respectively. In the calculation we have used the elastoplastic parameters given in the text (Color figure online)

Full size image

Figure 17 shows the relative contact area \(A/A_0\) as a function of the magnification \(\zeta\) (lower scale) or as a function of the wavenumber \(q=\zeta q_0\) (upper scale) as obtained using the Persson contact mechanics theory with the power spectrum shown in Fig. 16 (blue line). The relative elastic contact area and plastic contact area are shown separately as the red and green lines, respectively. In the calculation we have used the same elastoplastic parameters as in the numerical simulations using the BEM-based approach.

The result in Fig. 17 are consistent with the power spectra shown in Figs. 11, 12, 13, 14, 15, 16. Thus, Fig. 17 shows that the long wavelength roughness components for \(\mathrm{log}_{10}q < 4\) are elastically deformed, and this explain why in this wavenumber region the power spectrum of the plastically deformed surface is close to that of the original surface in Figs. 11, 12, 13, 14, 15, 16. For \(\mathrm{log}_{10}q > 4.4\) the Persson theory predict that the contact is fully plastic which explain why the power spectrum of the plastically deformed surface is the same in and out of contact with the flat surface in this wavenumber region.

5 Discussion

The simple procedure used above to describe the plastic flow produces plastically deformed surfaces with height probability distributions and surface roughness power spectra in semi-quantitative agreement with the experimental data. In our study we used an aluminum block, but the results are probably applicable for other metals as well assuming negligible work hardening so the simple elastoplastic description with a constant indentation hardness is a reasonable approximation. However, the following points need to be taken into consideration:

  1. (a)

    The indentation hardness depends on the length scale. Suppose we indent a solid with a rigid perfectly smooth sphere. If we look at the indentation at low magnification we do not see any surface roughness and we would calculate the indentation hardness \(\sigma _\mathrm{P} = F_\mathrm{N}/A_0\), where \(A_0=\pi r_0^2\) is the projected contact area (a circular area). This is, in fact, the standard definition of the indentation hardness. However, in general we do not make plastic contact everywhere within the apparent (projected) contact area \(A_0\). It is clear from this fact that the indentation hardness at the asperity length scale must be higher than at the macroscopic length scale, as also observed in indentation experiments [26]. If we increase the magnification further we may observe that within the plastically deformed (macro) asperity contact regions there may be regions which are not plastically deformed, corresponding to an even higher indentation hardness at even shorter length scale. To obtain the correct contact mechanics observed at high magnification is is necessary to include the length (or magnification) dependency of the indentation hardness.

    A length dependency of the effective indentation hardness may also result from plasticity mechanics of asperity interaction [23, 24, 28,29,30]. Qualitatively, one may say that when an asperity become strongly plastically deformed the stress field approach a hydrostatic stress and the asperity therefore become resistant to further plastic deformation.

  2. (b)

    At very short length scale the plastic flow may be inhomogeneous. This implies that if one indent a perfectly smooth surface of a solid with a spherical ball with perfectly smooth surface, roughness may be generated in the indented surface area [32].

  3. (c)

    The procedure used above to describe the plastic flow gives plastically deformed surfaces with roughness in relative good agreement with experiment for the aluminum block we used. But this result may hold only if there is no work hardening. The aluminum block we used has probably already undergone strong work hardening during the preparation process, but in another study for an aluminum block first sandblasted and then thermally annealed we observed very similar plastically deformed surface after indentation.

In an earlier study we have found that for some polymers, in particular polyethylene, the plastically deformed surface exhibit a perfectly symmetric Gaussian-like height probability distribution, in contrast to the strongly skewed height distribution we observe for aluminum (see Figs. 9 and 15). In Ref. [40] we suggested that this results from strong work hardening, which may result in flow of materials, from the top of asperities to the nearby wells as indicated in Fig. 18. However, for aluminium we have found the same type of plastic modification of the surface roughness for a surface which was thermally annealed after the sandblasting. However, the work hardening (and the stress–strain relation) for polyethylene is likely very different than for aluminum and this might be the explanation for the difference we observe between metals (here aluminum) and polymers (in particular polyethylene).

Fig. 18
figure 18

Two limiting behavior of the plastic deformation of a surface sinus-roughness-component. a For metals without work hardening (e.g., a material already strongly work hardened) the plastic flow is localized mainly to the region where the solid make contact with the countersurface, here assumed to be a flat rigid surface. b For some polymers like polyethylene the flow of material is more long range, resulting in material transfer to the valley region, effectively resulting in a sinus profile with smaller amplitude. The origin of this effect is not known but may be related to the nature of the stress–strain curve and work hardening

Full size image

The study presented in this paper is relevant for the fluid leakage in metallic seals. Metallic seals are usually made from steel, copper or bronze, and these metals (alloys) usually have work hardened surface layers and should deform plastically in a similar way as the aluminum block studied here. Thus, we believe that the theory approach used here in combination with, e.g. the critical junction theory, may be used to estimate the leakage of metallic seals. Such an (experimental and theory) study is reported elsewhere [49].

6 Summary and Conclusion

We have presented experimental results pertaining to the indentation of rough aluminum surfaces with balls made of steel, ceramic and silica glass. We found that the BEM-based approach, with a simple way to include plasticity within the elastoplastic model description, can be used to predict the height probability distribution and the surface roughness power spectra of the plastically deformed surfaces. The way we include plasticity in our model calculation is very simple. It would be interesting to compare it to the Finite Element Method (FEM), where plasticity effects can be taken into account in a more accurate way. However, such a study could only be performed on a small system as FEM for practical interest system sizes would be very cumbersome. The contact area is of direct importance for seals leakage as it determines when the contact area percolate and the leakage vanishes. This study, combined with findings in [40], indicates that work hardening and the stress–strain relation will strongly affect the nature of the plastically deformed roughness.