Parametric instability of a magnetic pendulum in the presence of a vibrating conducting plate

Abstract

A pendulum with an attached permanent magnet swinging in the vicinity of a conductor is a typical experiment for the demonstration of electromagnetic braking and Lenz’ law of induction. When the conductor itself moves, it can transfer energy to the pendulum. An exact analytical model of such an electromagnetic interaction is possible for a flat conducting plate. The eddy currents induced in the plate by a moving magnetic dipole and the resulting force and torque are known analytically in the quasistatic limit, i.e., when the magnetic diffusivity is sufficiently high to ensure an equilibrium of magnetic field advection and diffusion. This allows us to study a simple pendulum with a magnetic dipole moment in the presence of a horizontal plate oscillating in vertical direction. Equilibrium of the pendulum in the vertical position can be realized in three cases considered, i.e., when the magnetic moment is parallel to the rotation axis, or otherwise, its projection onto the plane of motion is either horizontal or vertical. The stability problem is described by a differential equation of Mathieu type with a damping term. Instability is only possible when the vibration amplitude and the distance between plate and magnet satisfy certain constraints related to the simultaneous excitation and damping effects of the plate. The nonlinear motion is studied numerically for the case when the magnetic moment and rotation axis are parallel. Chaotic behavior is found when the eigenfrequency is sufficiently small compared to the excitation frequency. The plate oscillation typically has a stabilizing effect on the inverted pendulum.

1 Introduction

Time-dependent magnetic fields cause electromagnetic induction, i.e., the generation of eddy currents in a conducting material. Induction is essential for numerous technological applications such as transformers, generators, electric motors and induction heating. A typical experiment of the Lorentz force caused by induction consists of a pendulum with a metal disk that swings next to a magnet [1]. The relative motion between the magnet and the disk leads to the induction of eddy currents that cause a braking of the disk’s motion. However, there are only few cases when the problem of eddy current induction can be solved analytically. For the swinging disk, it seems hardly possible.

Priede et al. [2] have obtained an analytical solution of the induction problem for a magnetic point dipole moving relative to a conducting plate of finite thickness in the limit of low magnetic Reynolds number. Specifically, the cases of a parallel translation of the magnet and its rotation about an axis parallel to the plate surface are considered. Simple analytical expressions for the force and torque exerted on the magnetic dipole are obtained depending on the translation or angular velocity and the components of the magnetic moment. This work was motivated by contactless inductive flow measurement techniques known as the magnetic flywheel and Lorentz force velocimetry. In the former, a magnet (or an arrangement of magnets) can freely rotate about an axis that is parallel to a duct containing a flowing conducting liquid, e.g., a metal melt. The induction in the liquid generates a secondary magnetic field that produces a torque on the magnet. As a result, the magnet spins with an angular velocity indicative of the mean velocity of the conducting liquid [2,3,4]. In Lorentz force velocimetry, the arrangement is similar but the magnet is fixed to a force sensor [5,6,7,8]. The induced drag force on the magnet provides the desired flow velocity.

Although the results from Ref. [2] do not allow one to determine the force and torque acting on the swinging disk pendulum, they provide the basis for an analytical description of these forces for a pendulum with a magnetic dipole bob moving relative to a conducting plate. It seems appropriate to study the dynamics of such a magnetic pendulum as a model problem, especially since pendulum motion provides the basis for more general considerations of oscillation phenomena. For example, the driven torsion pendulum with eddy current brake (Pohl’s wheel) is a common undergraduate physics experiment illustrating forced oscillations, resonance, bifurcation and chaotic motion [9]. Magnetic pendulum motion can also be affected by an interaction with another permanent or electromagnet [10,11,12]. However, the interaction force is then independent of the velocity. Recent works have also considered pendulum setups in external magnetic fields where ferrofluids are used either as magnetic material of the bob itself or as surrounding medium [13, 14].

In the present work, we formulate an analytical model of a magnetic pendulum in the presence of a horizontal conducting plate. To obtain nontrivial dynamics, the pendulum must be driven by a suitable motion of the plate itself. This opens up the possibility of chaotic motion, which is studied in other driven pendulum systems with damping [15,16,17]. Note that a parallel oscillation of the plate always leads to a pendulum oscillation in order to minimize the relative motion. By contrast, a vertical relative motion between plate and the magnetic bob can lead to a vertical Lorentz force that is compensated when the pendulum is vertical. In this case, the more interesting parametric instability is feasible, which has been extensively studied since the pioneering works of Mathieu, Floquet, Hill, Rayleigh [18] and others in the 19th century. The basic mathematical model for parametric instability is Mathieu’s equation, which can be generalized in various ways. Linear stability analyses and results for the equilibrium state are summarized in a recent review paper [19]. Analytical expressions for the stability regions of Mathieu’s equation were studied recently [20]. Parametric instabilities, bifurcations and chaotic motion are not only important in various vibrating mechanical or electromechanical systems, e.g., [21, 22]. They also continue to be of research interest in various pendulum systems [23,24,25,26].

We consider here the configuration where the plate oscillates vertically. Alternatively, one could examine a fixed plate and a vertical oscillation of the pivot, i.e., the classical parametric instability of the pendulum. Although the electromagnetic induction problem is the same, these two configurations differ because of the additional modulation of the gravitational acceleration term.

The paper is structured as follows. The formulation of the mathematical model and definition of the equilibrium conditions are described in the next section. We then analyze the stability limits of the equilibrium state by analytical approximations (harmonic balance method) for weak electromagnetic interaction between the magnet and the plate. These results are verified and extended to stronger electromagnetic interaction by numerical Floquet analysis in Sect. 4. This is followed by numerical investigations of the nonlinear dynamics for a particular orientation of the magnetic dipole moment. We summarize our findings and provide some ideas for further work at the end.

2 Problem definition

2.1 Geometry and physical properties

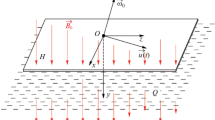
We consider a simple pendulum as sketched in Fig. 1. It is assumed that the pendulum motion is confined to the (x, z)-plane and that the pivot is at the origin of the coordinate system. The bob is magnetic with a magnetic field distribution corresponding to a magnetic point dipole as in Ref. [2]. Notice that the field distribution is realized outside a uniformly magnetized sphere, i.e., the dipole field is not only of purely academic interest. The magnetic dipole moment is $\mathbf {m}$. The bob of mass $m_b$ is connected to the pivot by a massless, inextensible and inflexible rod of length l. The moment of inertia is $m_b l^2$. The flat conducting plate oscillates in z-direction with an amplitude Q and angular frequency $\omega$. In the lower equilibrium position at initial time, the vertical distance h between the plate and the magnet is denoted by P. The plate has an electric conductivity of $\sigma$; its thickness is assumed to be large compared to the distances l, P and Q.

Fig. 1

Sketch of the magnetic pendulum in the presence of a vibrating conducting plate

2.2 Electromagnetic torque

The formulation of the mathematical model requires the computation of the electromagnetic torque acting on the pendulum. To apply the equations provided in Ref. [2], the motion has to be decomposed into its translational and rotational components. The translation is described by the two velocity components $u_x$ and $u_z$. The rotation is characterized by the angular velocity $\varOmega$ around the y-axis. The dipole moment $\mathbf {m}$ has in-plane components $m_x$ and $m_z$ and the out-of-plane component $m_y$. The motion of the pendulum is caused by the in-plane components of the force and the out-of-plane component of the torque on the dipole. We only consider these three components in what follows.

The relevant components of the force and torque acting on the dipole due to the horizontal velocity component $u_x$ are

$$\begin{aligned} F_x= & {} -\frac{\mu _0^2 \sigma u_x}{512 \pi h^3}\left( 3 m_x^2+m_y^2+4 m_z^2\right) ,\nonumber \\ F_z= & {} 0,\nonumber \\ T_y= & {} -\frac{\mu _0^2 \sigma u_x}{128 \pi h^2}\left( m_x^2+ m_z^2\right) , \end{aligned}$$

(1)

where h denotes the vertical distance between magnet and plate surface.

The corresponding terms due to the rotation with angular velocity $\varOmega$ are

$$\begin{aligned} F_x= & {} -\frac{\mu _0^2 \sigma \varOmega }{128 \pi h^2}\left( m_x^2+ m_z^2\right) ,\nonumber \\ F_z= & {} +\frac{\mu _0^2 \sigma \varOmega }{128 \pi h^2} \, m_x m_z,\nonumber \\ T_y= & {} -\frac{\mu _0^2 \sigma \varOmega }{64 \pi h}\left( 2 m_x^2+ m_z^2\right) . \end{aligned}$$

(2)

Finally, the relevant components of force and torque due to the vertical velocity component $u_z$ are

$$\begin{aligned} F_x= & {} 0, \nonumber \\ F_z= & {} -\frac{\mu _0^2 \sigma u_z}{128 \pi h^3}\left( m_x^2+m_y^2+2 m_z^2\right) ,\nonumber \\ T_y= & {} -\frac{\mu _0^2 \sigma u_z}{128 \pi h^2} \, m_x m_z. \end{aligned}$$

(3)

The expressions (3) are not given in Ref. [2] and are derived in “Appendix A”. Equations (1) are also derived in Ref. [27].

The components of the velocity are related to the motion of the pendulum characterized by the displacement angle $\theta$ around the y-axis with $\theta =0$ corresponding to positive z-direction. The horizontal velocity component is

$$\begin{aligned} u_x=\frac{\mathrm{d}}{\mathrm{d}t}l \sin {\theta }. \end{aligned}$$

(4)

Since the magnet is fixed on the rod, its angular velocity is equal to the angular velocity of the pendulum

$$\begin{aligned} \varOmega =\frac{\mathrm{d} \theta }{\mathrm{d}t}. \end{aligned}$$

(5)

The vertical velocity component is related to the distance h between the plate and the magnet, which changes with the displacement of the pendulum and the vertical position of the plate. The position $z_p$ of the plate surface is

$$\begin{aligned} z_p=l+P+Q\sin \omega t. \end{aligned}$$

Since $z_p>l$ is required to prevent collisions between the pendulum and the plate, the distance P must be greater than Q. The distance h is therefore

$$\begin{aligned} h=z_p- l\cos \theta =l+P+Q\sin \omega t- l \cos \theta , \end{aligned}$$

(6)

and the relative vertical velocity is

$$\begin{aligned} u_z=-\frac{\mathrm{d}h}{\mathrm{d}t}=-\omega Q\cos \omega t + \frac{\mathrm{d}}{\mathrm{d}t} l \cos \theta . \end{aligned}$$

(7)

In addition to the linear and angular velocities, the components of the magnetic moment also depend on the displacement angle $\theta$. We denote the orientation of the magnetic dipole moment by the polar and azimuthal angles $\beta$ and $\alpha$ around the y-axis, counted from the equilibrium position $\theta =0$. Zero polar angle $\beta =0$ corresponds to an orientation of the magnetic moment along the y-axis. For $\beta =\pi /2$, the azimuthal angles $\alpha =0$ and $\alpha =\pi /2$ correspond to a dipole moment aligned with the z-axis and x-axis, respectively. With the modulus $M = |\mathbf {m}|$, the components of the dipole moment are

$$\begin{aligned} m_x= & {} M \sin \beta \sin \left( \alpha +\theta \right) , \quad m_y= M \cos \beta ,\nonumber \\ m_z= & {} M \sin \beta \cos \left( \alpha +\theta \right) . \end{aligned}$$

(8)

The y-component of the electromagnetic torque on the pendulum is

$$\begin{aligned} T_{\mathrm{em}}= \sum T_y+l\cos \theta \sum F_x-l\sin \theta \sum F_z, \end{aligned}$$

where the sums contain the corresponding contributions from Eqs. (1–3) with the quantities substituted by expressions (4–8). These substitutions have been done with the Mathematica software [28]. The result is unwieldy and therefore not given explicitly. It consists of a group of terms proportional to $\varOmega ={\dot{\theta }}$ and terms independent of $\varOmega$, i.e.,

$$\begin{aligned} T_{em}= T^{\left( 0\right) } + {\dot{\theta }}\, T^{\left( 1\right) }. \end{aligned}$$

We are interested in the behavior close to the equilibrium $\theta =0$. Therefore, the terms $T^{\left( 0\right) }$ and $T^{\left( 1\right) }$ are linearized with respect to $\theta$. The term $T^{\left( 0\right) }$ has the leading term

$$\begin{aligned} T^{\left( 0\right) } = \frac{\mu _0^2 M^2 \sigma }{256\pi }\frac{\omega Q \cos \omega t \sin 2\alpha \sin ^2\beta }{\left( P+Q\sin \omega t\right) ^2}. \end{aligned}$$

It is independent of $\theta$ and has to vanish in equilibrium $\theta =0$. This is satisfied when $Q=0$, i.e., no oscillation is present. This case is not interesting and will not be studied further.

Other choices leading to an equilibrium $\theta =0$ are $\alpha =0$ or $\alpha =\pi /2$ for arbitrary $\beta$. If we impose $\beta =\pi /2$, these values of $\alpha$ correspond to a vertical or horizontal orientation of the dipole moment. The cases $\alpha =\pi$ and $\alpha =-\pi /2$ are physically equivalent to $\alpha =0$ or $\alpha =\pi /2$ and can therefore be ignored. Finally, $\beta =0$ or equivalently $\beta =\pi$ also represent an equilibrium where the dipole moment is along the out-of-plane or spanwise y-direction. In the following, for simplicity, we focus only on the three cases $\beta =0$ and $\beta =\pi /2$ with $\alpha =0$ or $\alpha =\pi /2$. Considerations given below can also be extended to arbitrary values of the parameter $\beta$.

For the spanwise orientation $\beta =0$ of the dipole moment, the leading terms of $T^{\left( 0\right) }$ and $T^{\left( 1\right) }$ are

$$\begin{aligned} T_s^{\left( 0\right) }= & {} - \theta \, \frac{\mu _0^2 M^2 \sigma }{128\pi }\frac{\omega Q l \cos \omega t }{\left( P+Q\sin \omega t\right) ^3},\\ T_s^{\left( 1\right) }= & {} - \frac{\mu _0^2 M^2 \sigma }{512\pi } \frac{l^2 }{\left( P+Q\sin \omega t\right) ^3}. \end{aligned}$$

For the vertical orientation $\alpha =0$, $\beta =\pi /2$ of the dipole moment, the leading terms of $T^{\left( 0\right) }$ and $T^{\left( 1\right) }$ are

$$\begin{aligned} T_v^{\left( 0\right) }= & {} \theta \, \frac{\mu _0^2 M^2 \sigma }{128\pi }\frac{\omega Q \left( -2l+P+Q\sin \omega t\right) \cos \omega t }{\left( P+Q\sin \omega t\right) ^3},\\ T_v^{\left( 1\right) }= & {} - \frac{\mu _0^2 M^2 \sigma }{128\pi }\left( \frac{l^2 }{\left( P+Q\sin \omega t\right) ^3}\right. \\&\left. + \frac{2 l }{\left( P+Q\sin \omega t\right) ^2}+ \frac{2 }{P+Q\sin \omega t}\right) . \end{aligned}$$

Finally, for the horizontal orientation $\alpha =\pi /2$, $\beta =\pi /2$ of the dipole moment, these terms are

$$\begin{aligned} T_h^{\left( 0\right) }= & {} - \theta \, \frac{\mu _0^2 M^2 \sigma }{128\pi }\frac{\omega Q \left( l+P+Q\sin \omega t\right) \cos \omega t }{\left( P+Q\sin \omega t\right) ^3},\\ T_h^{\left( 1\right) }= & {} - \frac{\mu _0^2 M^2 \sigma }{128\pi }\left( \frac{3 l^2 }{4\left( P+Q\sin \omega t\right) ^3}\right. \\&\left. + \frac{2 l }{\left( P+Q\sin \omega t\right) ^2}+ \frac{4 }{P+Q\sin \omega t}\right) . \end{aligned}$$

The subscripts s, v and h indicate the dipole orientation, i.e., spanwise, vertical and horizontal, respectively.

Note that the cases with the out-of-plane component of dipole moment, i.e., $\beta \ne \pi /2$ and $\alpha =0$ or $\alpha =\pi /2$ can be represented as a superposition:

$$\begin{aligned} T^{\left( 0\right) }= & {} \cos ^2 \beta \, T_i^{\left( 0\right) } +\sin ^2\beta \, T_s^{\left( 0\right) },\\ T^{\left( 1\right) }= & {} \cos ^2 \beta \, T_i^{\left( 1\right) } +\sin ^2\beta \, T_s^{\left( 1\right) }, \end{aligned}$$

where the index $i=v$ for $\alpha = 0$ or $i=h$ for $\alpha = \pi /2$.

2.3 Linearized equation of motion

The change of angular momentum of the pendulum is equal to the applied torque, which is the sum of the torque due to gravity and the electromagnetic torque:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left( l^2 m_b \frac{\mathrm{d}\theta }{\mathrm{d}t} \right) = T_{\mathrm{em}}-m_b g l \sin \theta . \end{aligned}$$

For $T_{em}=0$, $\theta =0$ is a stable equilibrium. By changing the sign of the gravitational acceleration g from positive to negative, $\theta =0$ becomes the unstable equilibrium point corresponding to an inverted pendulum.

The equation of motion is linearized for small $\theta$ to study the behavior near the equilibrium $\theta =0$. Without the electromagnetic torque, the eigenfrequency is $\varOmega _0=\sqrt{|g|/l}$.

For convenience, we define a nondimensional time and four nondimensional parameters, i.e.,

$$\begin{aligned} {\tilde{t}}= & {} \frac{\omega t}{2}, \qquad A=\frac{4 g }{l \omega ^2},\\ B= & {} \frac{2 Q }{l}, \qquad S=\frac{2 P }{l}, \qquad C=\frac{\mu _0^2 M^2 \sigma }{16\pi m_b l^3 \omega }. \end{aligned}$$

Small values of A correspond to high excitation frequencies and negative A to an inverted pendulum. The parameters B and S are length scale ratios with $0\le B<S$. The parameter $C\ge 0$ can be regarded as a ratio between electromagnetic and inertial forces.

Using these parameters, the linearized nondimensional equation of motion can be reduced to the form

$$\begin{aligned} \ddot{\theta } + {\dot{\theta }}\, C \, f_1(t) +\theta \left( A - C \,f_2(t)\right) =0, \end{aligned}$$

(9)

where the tilde over t is suppressed for convenience.

The $\pi$-periodic functions $f_1(t)$ and $f_2(t)$ depend on the orientation of the magnetic moment. For spanwise orientation, they are

$$\begin{aligned} f_1(t)= & {} \frac{1}{2 \left( S+B\sin 2t\right) ^3},\\ f_2(t)= & {} - \frac{2 B\cos 2t}{\left( S+B\sin 2t\right) ^3}. \end{aligned}$$

For vertical orientation these functions take the form

$$\begin{aligned} f_1(t)= & {} \frac{2}{\left( S+B\sin 2t\right) ^3}+\frac{2}{\left( S+B\sin 2t\right) ^2}\\&+\frac{1}{\left. S+B\sin 2t\right. },\\ f_2(t)= & {} \frac{B(-4 +S +B\sin 2t)\cos 2t}{\left( S+B\sin 2t\right) ^3}. \end{aligned}$$

Finally, for horizontal orientation, they are

$$\begin{aligned} f_1(t)= & {} \frac{3}{2\left( S+B\sin 2t\right) ^3}\\&+\frac{2}{\left( S+B\sin 2t\right) ^2} +\frac{2}{\left. S+B\sin 2t\right. },\\ f_2(t)= & {} -\frac{B(2 +S +B\sin 2t)\cos 2t}{\left( S+B\sin 2t\right) ^3}. \end{aligned}$$

3 Analytical stability results

For $C=0$, the problem reduces to the simple pendulum. The stable equilibrium $\theta =0$ corresponds to $A>0$ and the unstable equilibrium $\theta =0$ (inverted pendulum) to $A<0$. We shall determine if the stable equilibrium can be destabilized and, conversely, the unstable equilibrium stabilized by the presence of the oscillating conducting plate.

3.1 Harmonic balance method

The linearized equation of motion (9) has a structure similar to the classical Mathieu equation with linear viscous damping, where $f_1=\text {const.}$ and $f_2=\cos 2t$. In our case, both the stiffness coefficient and the damping coefficient are modulated by anharmonic functions.

Analytical solutions for the Mathieu equation can be sought by exploiting the smallness of the parameter C, e.g., by using an averaging method or a multiple time-scale expansion method with t and Ct as new variables [19]. The solutions can asymptotically grow or decay in time. These methods are possible but will not be pursued further.

When one is only interested in the limits of the unstable parameter region in the (A,C)-plane where the solution grows asymptotically, one can seek for time-periodic solutions in the form of a Fourier series

$$\begin{aligned} \theta = a_0 + \sum _{n=1}^\infty \left( a_n \cos nt+ b_n \sin n t \right) . \end{aligned}$$

(10)

The basic frequency of this Fourier series is half of the driving frequency. It includes Fourier series with basic frequency identical to the driving frequency as a special case.

For the classical undamped Mathieu equation, i.e., $f_1=0$ and $f_2=\cos 2t$, the solution form (10) leads to products of the trigonometric terms. They have to be reduced to pure sine and cosine terms and collected according to their frequency. One thereby obtains a homogeneous system of linear algebraic equations for the expansion coefficients $a_n$ and $b_n$, which is of infinite order. This system separates into four subsets for the coefficients of sines and cosines having either even or odd multiples of the basic frequency, respectively. The nontrivial solvability condition of these subsets requires that the four infinite determinants (called Hill’s determinants) must vanish. Each of these determinants represents a functional relationship between A and C that holds on the neutral parameter set where solutions are neither asymptotically decaying nor growing. For $C=0$, these determinants become purely diagonal and the solvability condition can be fulfilled by requiring that one of the diagonal elements be equal to zero. It occurs at the discrete values $A_n=n^2$, where n represents the integer resonance frequency. The neutral parameter sets in the (A,C)-plane intersect the A-axis at these values. The case $n=1$, known as the principal parametric resonance, corresponds to the subharmonic resonance since the forcing frequency in the term $f_2$ is equal to 2.

For $C>0$, the determinants are no longer purely diagonal and have to be truncated in order to find an approximation of the neutral parameter set. The resulting relations are polynomials in A and C. The terms of higher order omitted by the truncation have to be negligible, which requires $C\ll 1$. It also implies that all $A_n$, except the lowest ones, are excluded, i.e., one can only find an approximation of the neutral parameter set for $A\approx A_n$ if the truncation includes $A_n$ in the determinant for $C=0$. By this approach, one can analytically determine the limits of unstable parameter regions for small values of C. When C is not small, the unstable regions (also called tongues) can only be found by numerical Floquet analysis. More stability results and details of the harmonic balance method can be found in Ref. [19].

For our specific Eq. (9), we use the same representation (10) to determine approximations of the neutral parameter sets in the (A,C)-plane close to the A-axis. For the harmonic balance method to work, the functions $f_1(t)$ and $f_2(t)$ have to be represented as Fourier series expansions at least up to $n=4$. In each of the three cases of the dipole orientation, they are of the form

$$\begin{aligned} \begin{aligned} f_1(t)&= d_0 + d_1 \sin 2t+ d_2 \cos 4 t,\\ f_2(t)&= e_1 \cos 2t+ e_2 \sin 4 t. \end{aligned} \end{aligned}$$

(11)

Terms of higher order are omitted. The coefficients $d_0$, $d_1$, $d_2$ and $e_1$, $e_2$ are obtained analytically using the Mathematica software and listed in the “Appendix B”. They are typically square roots of rational functions of the parameters B and S. The quality of the approximation of $f_1$ and $f_2$ by these expansions deteriorates as the ratio B/S increases, see Fig. 2.

Fig. 2

Functions $f_1(t)$ and $f_2(t)$ and their approximations by truncated Fourier expansion for spanwise dipole orientation and different values of B

Since $f_1$ and $f_2$ contain both sines and cosines, the linear algebraic equations for the coefficients $a_n$ and $b_n$ are no longer decoupled as for the ordinary undamped Mathieu equation. However, the splitting into separate systems for even and odd multiples of the basic frequency still applies since the expansions (11) contain only even frequencies.

We limit our consideration to the simplest representation of $\theta$ in order to find the behavior close to the lowest resonance frequencies. Consider first the case of subharmonic resonance by choosing the solution form

$$\begin{aligned} \theta = a_1 \cos t+ b_1 \sin t. \end{aligned}$$

It is substituted into Eq. (9) with (11) for $f_1$ and $f_2$. Using the Mathematica software one can easily carry out the necessary trigonometric reductions to pure sine and cosine terms. Omitting the higher frequency terms, the result is

$$\begin{aligned} 0= & {} \left[ (2A -2 -C(d_1+e_1)) a_1+ 2 C d_0 b_1\right] \cos t \\&+\left[ (2A -2 +C(d_1+e_1)) b_1- 2 C d_0 a_1\right] \sin t. \end{aligned}$$

This implies that the coefficients of the sine and cosine functions must vanish, which leads to a homogeneous linear system for $a_1$ and $b_1$. Its determinant must be equal to zero for a non-trivial solution. The corresponding quadratic equation has the roots

$$\begin{aligned} A = 1\pm \frac{C}{2} \sqrt{(d_1+e_1)^2-4d_0^2 }. \end{aligned}$$

(12)

These relations hold on the neutral parameter set. For $C>0$, there is an unstable interval of A-values centered on $A=1$ provided that $|d_1+e_1| > 2d_0$.

For the harmonic resonance with basic frequency $n=2$, we choose the solution form

$$\begin{aligned} \theta = a_0+ a_2 \cos 2t + b_2\sin 2t. \end{aligned}$$

This is simpler than for the ordinary undamped Mathieu equation, where the additional terms with $\cos 4t$ and $\sin 4t$ are needed to obtain a nontrivial result for the unstable interval near $A=4$. With this solution, Eq. (9) with (11) for $f_1$ and $f_2$ reduces to

$$\begin{aligned} 0= & {} 2 A a_0 -C(2 d_1+e_1) a_2 \\&+\left[ -2 C e_1 a_0 + 2(A -4) a_2\right. \\&\left. + C(4d_0+2d_2-e_2) b_2 \right] \cos 2t \\&+\left[ - C(4d_0-2d_2+e_2) a_2 +2 (A-4) b_2\right] \sin 2t, \end{aligned}$$

where higher frequency terms have again been omitted. Nonzero solutions for $a_0$, $a_2$ and $b_2$ exist if the determinant of the corresponding linear system vanishes. Evaluation of the determinant gives the condition

$$\begin{aligned} A (4(A-4)^2 -C^2 r_1) - (A-4) C^2 r_2=0 \end{aligned}$$

(13)

with

$$\begin{aligned} r_1= (2d_2-e_2)^2 -16 d_0^2, r_2= 2e_1(2d_1+e_1). \end{aligned}$$

Equation (13) is cubic in A and quadratic in C. For $C=0$, it has a simple root at $A=0$ and a double root at $A=4$. Therefore, we solve this equation for C rather than for A. The result is

$$\begin{aligned} C^2= \frac{4 A (A-4)^2}{r_1 A + r_2 (A-4)}. \end{aligned}$$

(14)

This relation can be approximately solved for A in the vicinity of the three roots for $C = 0$. Assuming $A-4=\varepsilon$ and $|\varepsilon |\ll 1$, the approximate solutions of Eq. (14) are

$$\begin{aligned} \varepsilon =A-4= \pm \frac{C}{2} \sqrt{r_1}. \end{aligned}$$

For $C>0$ there is therefore an unstable interval of A-values centered on $A=4$ provided that $r_1>0$, i.e., $| 2d_2-e_2| > 4d_0$.

Assuming $|A|\ll 1$ in Eq. (14) and keeping the leading terms in A only, the solution is

$$\begin{aligned} A= -\frac{r_2 C^2}{16}. \end{aligned}$$

This solution emanates from the origin of the (A,C)-plane and therefore represents the limit of the unstable range of negative A (inverted pendulum for $C=0$). When $r_2>0$, the stable interval of A values extends to negative A for small positive C, i.e., the inverted position can be stabilized in this case.

3.2 Conditions for subharmonic instability

The obtained criterion $|d_1+e_1| > 2d_0$ on the Fourier coefficients of $f_1(t)$ and $f_2(t)$ defines the subharmonic instability in the limit of small C. The coefficients $d_0$, $d_1$ and $e_1$ are functions of the parameters B and S representing the length ratios that fulfill the geometric constraint $B<S$. Therefore, the conditions for subharmonic instability in the parameter space of B and S can be determined.

To be specific, we focus on the spanwise dipole orientation. The other dipole orientations can be treated in a similar manner and only final results are presented below.

For spanwise dipole orientation, both Fourier coefficients $d_1$ and $e_1$ are negative and $d_0$ is positive, see the “Appendix B”. The critical curve in the (B,S)-plane bounding the region where the instability criterion is satisfied is therefore specified by $2 d_0=-(d_1+e_1)$. This leads to the quadratic equation

$$\begin{aligned} B^2+2 S^2= 3 BS + 4B S^2 -4B^3 \end{aligned}$$

for S with the solutions

$$\begin{aligned} S_1=B \quad \text {and} \quad S_2= \frac{B+4 B^2}{2(1-2B)}. \end{aligned}$$

(15)

The instability criterion is satisfied if $S_1< S <S_2$. This is only valid for $B>1/8$. The critical curve $S_2(B)$ intersects the line $S=B$ at $S=1/8$ and tends to infinity for $B=1/2$.

The other cases of vertical and horizontal orientation of the dipole moment lead to more complicated relations between B and S for the critical curve.

Fig. 3

Critical curves for different dipole orientations according to harmonic balance method in the limit $C\rightarrow 0$ and $A \rightarrow 1$: (a) in the (B, S) parameter plane, (b) in the $(B,S-B)$ parameter plane. Unstable regions are bounded by the line $S-B=0$ and the corresponding critical curves

For the vertical orientation, an analytical expression can be found using $S-B=x$ as new variable. The equation for S(x) becomes

$$\begin{aligned} x(4 S^2 (x-1)+ S (1+10x-4x^2)+x(1-4x+x^2))=0 \end{aligned}$$

with $x=0$ as obvious solution and two nontrivial solutions from the remaining quadratic equation for S(x). Of the latter, only the upper branch is meaningful and leads to an implicit representation of the curve S(B). It intersects the line $S=B$ at $S=1/4$, as can be seen by setting $x=0$ in the quadratic equation for S.

For the horizontal orientation, there appears to be no simple implicit analytical expression. Using $S^2-B^2=x^2$, the two terms

$$\begin{aligned} 8 B x d_0= & {} \sqrt{S^2-x^2} \left( 9 S^2- 3x^2 + 8 x^2(S+x^2)\right) ,\nonumber \\ 4 B x (d_1+e_1)= & {} - 3 (S-x) \nonumber \\&\times \left( 3S^2+4 x^3(1+x)+Sx(3+4x) \right) \nonumber \\ \end{aligned}$$

(16)

have to be equal. Squaring and subtracting them leads to the equation

$$\begin{aligned} 0= & {} (S-x)x^2\left[ 72 S^4-S^3 (27(1-x)-152 x^2) \right. \\&-S^2x (27+168x+64x^2-160x^3)\\&-Sx^2(9+168x+312x^2+128x^3-80x^4) \\&\left. - x^3(9+96x+288x^3+208x^4)\right] , \end{aligned}$$

which has trivial solutions $x=0$ and $S=x$. Finding the nontrivial solutions would require solving the remaining quartic equation for S. Setting $x=0$ in the quartic equation reveals that the critical curve intersects the line $S=B$ at $S=3/8$. The solution is obtained numerically using bisection on the difference between the right-hand sides of Eqs. (16).

In each case, the region of instability is bounded by the critical curve S(B) and the line $S=B$. These regions are shown in Fig. 3a,b for three different dipole moment orientations. Figure 3b also reveals their different asymptotic behavior.

3.3 Conditions for harmonic instability

In the limit of small C, the criterion for instability near $A=4$, i.e., at the driving frequency, is $|2d_2-e_2| > 4d_0$. It appears that in every case the expression $-2 d_2 +e_2$ is positive for $0< B<S$, i.e., the critical curve S(B) satisfies $-2 d_2 +e_2=4d_0$.

Fig. 4

Critical curves for different dipole orientations according to harmonic balance method in the limit $C\rightarrow 0$ and $A \rightarrow 4$: (a) in the (B, S) parameter plane, (b) in the $(B,S-B)$ parameter plane. Unstable regions are bounded by the line $S-B=0$ and the corresponding critical curves

For the spanwise orientation, this condition can be simplified by using $S^2-B^2=x^2$ to

$$\begin{aligned} x^2 (S-x)(2 S^2 + S (2x-1)-x(1+4x))=0. \end{aligned}$$

(17)

For the vertical orientation, the condition becomes

$$\begin{aligned} x^2 (S-x)(2 S^2 - S (2-2x+x^2)-x(2+8x+x^2))=0. \end{aligned}$$

For the horizontal orientation, we obtain

$$\begin{aligned}&x^2 (S-x)(2 S^2 + S (-3+2x+2x^2)\\&\quad -x(3+12x+10x^2))=0. \end{aligned}$$

In each case, the trivial solutions are $x=0$ and $S=x$. The nontrivial solutions are given by the roots of each of the three remaining quadratic equations for S(x) that appear as the last factor on the left-hand sides. Again, only the upper branch is meaningful and leads to an implicit representation of the critical curve S(B). Setting $x=0$ in these quadratic equations, we find the point of intersection of the line $S=B$ and the critical curve at $S=1/2$, $S=1$ and $S=3/2$ for the spanwise, vertical and horizontal orientations, respectively.

The regions of instability are shown in Fig. 4a,b for three different dipole moment orientations. They are bounded by the critical curves S(B) and the line $S=B$. Figure 4b also reveals their different asymptotic behavior.

3.4 Conditions for stability at $A<0$

Stable solutions at small negative A occur provided that $r_2= 2e_1(2d_1+e_1)>0$. For all three cases, one can show that $2d_1+e_1$ is negative for $0<B<S$ by direct calculation and observing that $S >x$, where x is again defined by $x^2=S^2-B^2$.

For this reason, it remains to check that $e_1<0$ in order to have $r_2>0$. It turns out that $e_1$ is negative for any $S>0$ and $0<B<S$ in the cases of spanwise and horizontal dipole moment.

Fig. 5

Regions of instability in the (B,S)-plane obtained by numerical Floquet analysis. Left column corresponds to $A=1$, right column to $A=4$. Orientations of the dipole moment: a, b spanwise, c, d vertical and e, f horizontal

For the vertical orientation, the following expression should be negative for stability

$$\begin{aligned} g=B\left( S^2-B^2\right) ^{3/2} e_1= -2(S-x)(2S+2x-x^2). \end{aligned}$$

Its last factor is zero for $x=S$ at $S=4$, and becomes negative for $x \rightarrow S$ when $S>4$, i.e., g becomes positive. The condition $r_2>0$ for stability is then satisfied for any $0<B<S<4$. For $S>4$, it is not satisfied for all admissible B, since $r_2$ is positive only when B is in the interval

$$\begin{aligned} S^2-2 S -2 -2 \sqrt{1+2S}<B^2 <S^2. \end{aligned}$$

4 Numerical results from the linear stability analysis

For the numerical study of the linear stability of the equilibrium $\theta =0$, we perform a Floquet analysis, i.e., determine a fundamental matrix solution

$$\begin{aligned} {\mathbf {G}}(t)=\left( \begin{matrix} \theta _{1}(t) &{}\quad {\dot{\theta }}_1(t) \\ \theta _{2}(t) &{}\quad {\dot{\theta }}_2(t) \\ \end{matrix} \right) \end{aligned}$$

from two linearly independent solutions $\theta _1$ and $\theta _2$. The differential equations are solved by MATLAB’s ode45 solver [29] with a low relative error tolerance.

The stability is defined by the eigenvalues $\lambda _{1,2}$ of the monodromy matrix

$$\begin{aligned} {\mathbf {M}}={\mathbf {G}}(0)^{-1}{\mathbf {G}}(\pi ), \end{aligned}$$

which determines the evolution over one fundamental oscillation period $\pi$. When the eigenvalue $\lambda _m$ with the largest modulus satisfies $|\lambda _m|>1$, the state $\theta =0$ is unstable.

Our first interest is to check that the analytical predictions for the stability boundaries in the (B,S) parameter plane are correct in the limit $C\rightarrow 0$. This is done by computing the logarithm of $|\lambda _m|$ over range of B and S values with $S>B$ and a fixed small value of C. A contour plot of $\ln |\lambda _m|$ shows the critical curve for the selected value of C as level zero.

This is done in the subharmonic case $A=1$ and the harmonic case $A=4$ considering all three dipole orientations. The results are shown in Fig. 5 for values $C=10^{-3}$ and $C=10^{-2}$. Overall there is a satisfactory agreement between the contour lines $\ln |\lambda _m|=0$ and the analytical curve when C is sufficiently small, i.e., the analytical results are confirmed. Discrepancies appear close to the intersection of the critical curve S(B) with the line $S=B$, and they diminish as C decreases.

For large values of B, the agreement between analytical and numerical results is better for the value $C=10^{-2}$. We attribute this to the finite precision arithmetic in the numerical solution of the differential equation, which may produce somewhat larger inaccuracy when the function $A-C f_2(t)$ has less variation in magnitude over one cycle. This is clearly apparent for the spanwise orientation and $A=1$, where S(B) exhibits a pole at $B=1/2$. It is also noticeable for $A=4$. For the other orientations, there is much less difference between the curves for $C=10^{-3}$ and $C=10^{-2}$.

The stability properties for finite C are investigated for some fixed values of S. We only consider the spanwise orientation for the sake of brevity. The stability boundary is again found as the zero level of $\ln |\lambda _m|$ in the numerical Floquet analysis.

According to harmonic balance method, the relation (14) describes the curve C(A) delimiting the stable range when $C\ll 1$ also for $A<0$. It should provide a good approximation also for finite C when B is fairly small compared to S, since the truncated Fourier expansions (11) are then a good representation of $f_1(t)$ and $f_2(t)$. Figure 6a shows that this is indeed the case for the spanwise orientation and the particular values $B=0.1$ and $S=1/2$. The agreement between numerical and analytical curves is favorable up to $C\approx 0.5$. When B is increased, the differences become more pronounced.

Fig. 6

Results obtained by numerical Floquet analysis for the spanwise dipole orientation and $S=1/2$. a comparison of the critical curve with analytical result (14) for $A<0$ and $B=0.1$; b regions of instability in the (A,C)-plane

Figure 6b shows the numerically obtained stability curves for $S=1/2$ also for positive A. We first note that the stable range for negative A and $C>0$ expands to smaller values of A as B increases. The instability domain originates at $A=1$ for small C. The unstable A-interval expands according to Eq. (12) as C increases although this is not readily apparent due to logarithmic scale of the C axis. Eventually, the unstable A-interval shrinks again and finally disappears at a finite C, i.e., a sufficiently large C prevents instability. The unstable domain also changes with B. It appears when B exceeds the minimal value for instability at the given value of S, which is $B=1/4$ for $S=1/2$ according to Eq. (15), and expands upon increasing B. It also covers negative A values for $B=0.4$.

For the case $S=1$ in Fig. 7a, the limit of the stable range for negative A has the same trends as for $S=1/2$ when B increases. Conditions for instability in the limit of small C are met at $A=1$ when $B>0.319$ and for $A=4$ when $B>0.77$, see Eq.(17), i.e., there are two separate domains for the subharmonic instability (originating at $A=1$) and for the harmonic instability (originating at $A=4$). Both domains expand when B is increased but remain separated. The unstable domain originating at $A=1$ even approaches the stable limit in the range of negative A for $B=0.6$. As for $S=1/2$, a sufficiently large C prevents instability for $A>0$.

Fig. 7

Results obtained by numerical Floquet analysis for the spanwise dipole orientation and $S=1$

5 Pendulum motions with finite amplitude

The expression for the electromagnetic torque without linearization about $\theta =0$ is extremely cumbersome for a general orientation of the dipole moment. For simplicity, we only consider the spanwise orientation. In this case, the nondimensional nonlinear equation of motion is

$$\begin{aligned} \begin{aligned}&\ddot{\theta }+ {\dot{\theta }}\, C \frac{1+3 \sin ^2\theta }{2 \left( 2-2\cos \theta +S+B\sin 2t\right) ^3}\\&\quad +\left( A + C \frac{2 B\cos 2t}{\left( 2-2\cos \theta +S+B\sin 2t\right) ^3} \right) \sin \theta =0. \end{aligned} \end{aligned}$$

(18)

It is solved using the MATLAB ode45 routine.

In the investigation of the nonlinear behavior, we focus on the effects of A and C on the dynamics. A detailed study of all four parameters is beyond the scope of this work. The geometry parameters B and S are selected such that the equilibrium is unstable. Specifically, we choose $B=0.6$ and $S=1$.

For a qualitative characterization of the nonlinear motion, we determine Poincaré sections based on the fundamental period $\pi$ of the forcing frequency, i.e., functions $\theta$ and ${\dot{\theta }}$ at times $t_n=n\pi$ with $n=1,2,\ldots ,N$ should be found from the numerical integration of Eq. (18). By varying C, these sections can be combined to a bifurcation diagram. Specifically, we plot ${\dot{\theta }}$ at various times $t_n=n\pi$ versus C. The results for various A are shown in Figs. 8 and 10.

Fig. 8

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$. Results for two different initial conditions that differ by the signs of $\theta$ and ${\dot{\theta }}$ are shown as full lines and dots, respectively

Fig. 9

Phase planes for different parameters A and C. a shows three periodic orbits for $A=0.3$. Two asymmetric orbits (dotted) correspond to $C=2$ and different initial conditions. The full line is for $C=0.8$. b shows two asymmetric orbits with doubled period at $A=0.25$ and $C=2$

Fig. 10

Bifurcation diagrams based on the angular velocity at times $t_n=n\pi$. Only one initial condition is used

For $A=1$, we find a single subharmonic periodic orbit as soon as $C>0$. This gives rise to two values $\pm {\dot{\theta }}$ of the angular velocity in the Poincaré section. For sufficiently large C, this periodic orbit disappears and only the equilibrium remains as solution. As A is reduced, the threshold for this periodic orbit shifts to a finite value $C>0$, which is shown in Fig. 8b for $A=0.5$. The behavior for large C is qualitatively the same and remains so also for lower values of A.

Figure 8c shows two different periodic orbits in a certain interval of C around $C=2$ at $A=0.3$. These two solution branches are found from two different initial conditions that differ by the signs of $\theta$ and ${\dot{\theta }}$ at time $t=0$. These orbits no longer have the symmetry property ${\dot{\theta }}_n= - {\dot{\theta }}_{n+1}$, i.e., they represent an oscillation of the pendulum that is spatially asymmetric. This is also illustrated by the phase plane in Fig. 9a.

For $A=0.25$ in Fig. 8d, these two asymmetric orbits persist in approximately the same C-interval. In addition, they exhibit a period-doubling in a shorter interval of C that is also located near $C=2$ and shown in Fig. 9b. Increasing or decreasing C from $C=2$ leads first to a disappearance of the period-doubling that is followed by merging of the two asymmetric solution branches.

More complex dynamics is found for values $A=0.2$ and $A=0.1$ shown in Fig. 10. For $A=0.2$, the asymmetric solution branches develop quasiperiodic or chaotic motion in certain C-intervals. To illustrate the asymmetry we show the upper half $({\dot{\theta }}\ge 0)$ and the lower half $({\dot{\theta }}\le 0)$ of the bifurcation diagram for one of the branches side by side. The behavior for the other branch is mirror-symmetric, i.e., it follows by reversing the sign of ${\dot{\theta }}$. One can clearly identify orbits of period four that emerge from the period two orbits as C is increased from $C=1$ or reduced from $C=3$. We have not analyzed the irregular behavior and the apparent periodic windows close to $C=2$ further.

Finally, for $A=0.1$, the behavior is similar to $A=0.2$ upon increasing C from 1, i.e., there are two-period doubling bifurcations, which appear to be followed by chaotic motion. However, in contrast to $A=0.2$, the two asymmetric branches appear to merge near $C\approx 1.3$. Up to $C\approx 2.8$ there is only a single solution branch apparent. This can be identified by comparing Fig. 10c and d. Beyond $C\approx 2.8$ the asymmetric branches persist with chaotic behavior which is subsequently replaced by increasingly regular motion until the two asymmetric period one orbits merge at $C\approx 4.5$. We also note that an orbit with period three is apparent over a relatively large interval around $C=1.8$. For this reason, the irregular motions observed for $A=0.1$ should be chaotic. However, we have not attempted to confirm this by computing Lyapunov exponents.

6 Conclusions

A magnetic pendulum with a dipolar field interacting with a vibrating conducting plate appears to be one of the rare cases where the dissipative electromagnetic interaction can be described analytically for a nontrivial setup. It is studied for the case when the vertical position remains an equilibrium because of the vertical plate vibration. The parametric resonance appears when the nondimensional vibration amplitude B and the nondimensional distance S between the magnet and the plate satisfy certain constraints. They arise from the simultaneous excitation and damping effects on the pendulum by the induction in the plate. The spanwise or out-of-plane orientation of the magnetic moment has comparatively weaker damping than its vertical and horizontal orientations, whereby the constraints on B and S are less strict. For the inverted configuration, the plate vibration tends to stabilize the equilibrium with significantly weaker constraints. These analytical results hold for small electromagnetic interaction parameter C. A numerical Floquet analysis shows that the parametric instability eventually ceases when C is sufficiently large. The pendulum motion with spanwise dipole moment is also studied for finite amplitudes. Bifurcation diagrams with varying C and fixed B and S show that the motion becomes complex and presumably chaotic for sufficiently high excitation frequency. Transitions between statistically symmetric and asymmetric orbits in the chaotic parameter range are also observed.

The present model is based on the quasistatic approximation [30, 31] that applies when rate of change of the magnetic field is slow relative to magnetic diffusion time. Otherwise, the induced eddy currents and resulting force and torque depend not only on the instantaneous relative velocity but retain a memory of the relative motion. The mathematical model must be changed profoundly to include such effects. The complementary problem with a vertically oscillating pivot and a fixed plate can be studied with minimal changes to the present model.

Appendices

Appendix A: Force and torque for vertical dipole motion

The quasistatic approximation [30, 31] is used, i.e., one assumes that the rate of change of the magnetic field is effectively negligible and the induced field is weak by comparison with the imposed field. From Faraday’s law, it follows that the electric field is curl-free, i.e., represented by the negative gradient of the electric potential $\phi$. We consider a horizontally unbounded conducting plate that occupies the half-space $z>h$ and a fixed magnetic dipole located at the origin of the coordinate system. The dipole with magnetic moment $\mathbf {m}$ generates at position $\mathbf {r}$ a magnetic field

$$\begin{aligned} \mathbf {B}=\frac{\mu _0}{4\pi }\left( \frac{3 \mathbf {m}\cdot \mathbf {r} }{r^5}\, \mathbf {r}- \frac{\mathbf {m} }{r^3}\right) . \end{aligned}$$

The plate moves with velocity component $u_z<0$. The induced eddy current density $\mathbf {j}$ in the plate is given by Ohm’s law

$$\begin{aligned} \mathbf {j}=\sigma \left( -\nabla \phi + \mathbf {u}\times \mathbf {B}\right) \end{aligned}$$

for a moving conductor. The magnetic field $\mathbf {B}$ is the unperturbed field of the dipole since the induced field is comparatively small.

Since the velocity is uniform and the magnetic field $\mathbf {B}$ of the dipole is curl-free, the electromotive force $\mathbf {u}\times \mathbf {B}$ is solenoidal. As the currents are solenoidal themselves (according to Ampère’s law), the electric potential satisfies Laplace’s equation in the domain $z>h$. The normal current density $j_z$ vanishes on the plate surface $z=h$, and therefore $\partial \phi /\partial z=0$ on $z=h$. Owing to this homogeneous Neumann boundary condition, the potential is uniform. The Lorentz force density is then

$$\begin{aligned} \mathbf {f}=\mathbf {j}\times \mathbf {B} =\sigma \left( \mathbf {u}\times \mathbf {B}\right) \times \mathbf {B}. \end{aligned}$$

The total Lorentz force and torque on the plate can be found as

$$\begin{aligned} \mathbf {F}=\int _{z>h} \mathbf {f} \, \mathrm{d}V, \qquad \mathbf {T}=\int _{z>h} \mathbf {r} \times \mathbf {f} \, \mathrm{d}V. \end{aligned}$$

The integrands of these expressions were evaluated with the Mathematica software. The integration was performed using cylindrical coordinates. The result is a vertical force opposing the motion of the plate and a torque perpendicular to the magnetic moment and the z-axis. The force and torque on the magnet are equal but opposite to those on the conductor. One obtains the expressions (3) by observing that the velocity of the dipole is also opposite to that of the plate when it moves and the plate is fixed.

Appendix B: Leading Fourier coefficients of the functions $f_1$ and $f_2$

Case of spanwise dipole moment:

$$\begin{aligned} d_0= & {} \frac{1}{4}\, \frac{B^2+2 S^2}{\left( S^2-B^2\right) ^{5/2}}\, , \\ d_1= & {} - \frac{3}{2}\, \frac{SB}{\left( S^2-B^2\right) ^{5/2} }\, , \\ d_2= & {} - \frac{3}{2}\, \frac{B^2}{\left( S^2-B^2\right) ^{5/2} }, \\ e_1= & {} - \frac{2B}{\left( S^2-B^2\right) ^{3/2} },\\ e_2= & {} \frac{8}{B^2}+ \frac{4S}{B^2}\frac{3B^2-2S^2}{\left( S^2-B^2\right) ^{3/2} }. \end{aligned}$$

Case of horizontal dipole moment:

$$\begin{aligned} d_0= & {} \frac{8 B^4+B^2(3-8S-16S^2)+2S^2(3+4S+4S^2)}{4\left( S^2-B^2\right) ^{5/2}}\, , \\ d_1= & {} - \frac{4}{B}- \frac{8B^4(S-1)+8S^5+B^2S(9+8S-16S^2)}{2B\left( S^2-B^2\right) ^{5/2} }\, , \\ d_2= & {} \frac{8(S-1)}{B^2}\\&+ \frac{8B^6{+}40B^2S^3(S{-}1){-}16S^5(S{-}1){+}B^4(-9{+}24S{-}32S^2)}{2B^2\left( S^2{-}B^2\right) ^{5/2}}, \\ e_1= & {} \frac{2}{B} +\frac{2B^2(S-1)-2S^3}{B\left( S^2-B^2\right) ^{3/2} },\\ e_2= & {} -\frac{8(S-1)}{B^2} + \frac{4}{B^2}\, \frac{B^4-3B^2 S (S-1) +2S^3(S-1)}{\left( S^2-B^2\right) ^{3/2} }. \end{aligned}$$

Case of vertical dipole moment:

$$\begin{aligned} d_0= & {} \frac{B^4+B^2(1-2S-2S^2) +S^2(2+2S+S^2)}{\left( S^2-B^2\right) ^{5/2}}\, , \\ d_1= & {} \frac{2}{B}- \frac{2}{B}\, \frac{B^4(S-2)+S^5+B^2S(3+2S-2S^2)}{\left( S^2-B^2\right) ^{5/2} }\, ,\\ d_2= & {} \frac{4(S-2)}{B^2}\\&+ \frac{2}{B^2}\frac{B^6+5B^2S^3(S-2)-2S^5(S-2)+B^4(-3+6S-4S^2)}{\left( S^2-B^2\right) ^{5/2} }, \\ e_1= & {} - \frac{2}{B} -\frac{2B^2(S+2)-2S^3}{B\left( S^2-B^2\right) ^{3/2} },\\ e_2= & {} \frac{8(S+2)}{B^2} - \frac{4}{B^2}\, \frac{B^4-3B^2 S (S+2) +2S^3(S+2)}{\left( S^2-B^2\right) ^{3/2} }. \end{aligned}$$