Distance from the Nucleus to a Uniformly Random Point in the 0-Cell and the Typical Cell of the Poisson–Voronoi Tessellation

Abstract

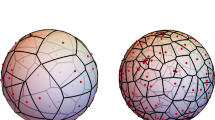
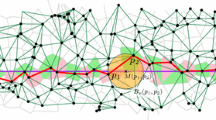
Consider the distances $\tilde{R}_o$ and $R_o$ from the nucleus to a uniformly random point in the 0-cell and the typical cell, respectively, of the d-dimensional Poisson–Voronoi (PV) tessellation. The main objective of this paper is to characterize the exact distributions of $\tilde{R}_o$ and $R_o$. First, using the well-known relationship between the 0-cell and the typical cell, we show that the random variable $\tilde{R}_o$ is equivalent in distribution to the contact distance of the Poisson point process. Next, we derive a multi-integral expression for the exact distribution of $R_o$. Further, we derive a closed-form approximate expression for the distribution of $R_o$, which is the contact distribution with a mean corrected by a factor equal to the ratio of the mean volumes of the 0-cell and the typical cell. An additional outcome of our analysis is a direct proof of the well-known spherical property of the PV cells having a large inball.

Solution of Integral in (41)

Let $a=\frac{d-1}{2}$ and $b=\frac{1}{2}$. From step (a) of (41) and using $I_x(a,b)=\frac{B_x(a,b)}{B(a,b)}$, we have

$$\begin{aligned} p&=\nu _R\int _{R}^{R+\epsilon } B_{{1-\frac{l^2}{(R+\epsilon )^2}}}\left( a,b\right) l^{d-1}\mathrm{d}l, \end{aligned}$$

where $\nu _R=\frac{{d((R+\epsilon )^d-R^d)^{-1}}}{2B\left( a,b\right) }$. We solve the above integral using integration by parts as follows. Let $v=l^{d-1}$ and $u=B_{1-\frac{l^2}{(R+\epsilon )^2}}\left( \frac{d-1}{2},\frac{1}{2}\right)$. We have

$$\frac{\mathrm{d}}{\mathrm{d}l}u=-\frac{2l}{(R+\epsilon )^2}\left( \frac{l^{2}}{(R+\epsilon )^{2)}}\right) ^{b-1}\left( 1-\frac{l^2}{(R+\epsilon )^2}\right) ^{a-1},$$

and thus

$$\begin{aligned} p&=-\nu _R\frac{R^d}{d}B_{1-\frac{R^2}{(R+\epsilon )^2}}\left( a,b\right) \\&\quad + \nu _R\int _R^{R+\epsilon } \frac{l^d}{d} \frac{2l}{(R+\epsilon )^2}\frac{l^{2(b-1)}}{(R+\epsilon )^{2(b-1)}}\left( 1-\frac{l^2}{(R+\epsilon )^2}\right) ^{a-1}\mathrm{d}l. \end{aligned}$$

Now, substituting $\frac{l^2}{(R+\epsilon )^2}=z$, we get

$$\begin{aligned} p&=-\nu _R\frac{R^d}{d}B_{1-\frac{R^2}{(R+\epsilon )^2}}\left( a,b\right) +\nu _R\frac{(R+\epsilon )^d}{d}\int _\frac{R^2}{(R+\epsilon )^2}^1z^{b+\frac{d}{2}-1}(1-z)^{a-1}\mathrm{d}z\\&=-\nu _R\frac{R^d}{d}B_{1-\frac{R^2}{(R+\epsilon )^2}}\left( a,b\right) + \nu _R\frac{(R+\epsilon )^d}{d}\left[ B\left( b+\frac{d}{2}-1,a\right) - B_{\frac{R^2}{(R+\epsilon )^2}}\left( b+\frac{d}{2}-1,a\right) \right] \\&=-\tilde{\nu }_R R^d I_{1-\frac{R^2}{(R+\epsilon )^2}}(a,b) +\tilde{\nu }_R(R+\epsilon )^d\frac{B\left( b+\frac{d}{2},a\right) }{B(a,b)}\left[ 1-I_{1-\frac{R^2}{(R+\epsilon )^2}}\left( b+\frac{d}{2},a\right) \right] \\&{\mathop {=}\limits ^{(a)}}\tilde{\nu }_R(R+\epsilon )^d B_{1-\frac{R^2}{(R+\epsilon )^2}}\left( a,b+\frac{d}{2}\right) -\tilde{\nu }_R R^d I_{1-\frac{R^2}{(R+\epsilon )^2}}(a,b) \end{aligned}$$

where $\tilde{\nu }_R=\frac{1}{2((R+\epsilon )^d-R^d)}$. Step (a) follows using $I_{x}(a,b)=1-I_{1-x}(b,a)$ and $B(a,b)=B(b,a)$.