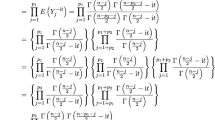Abstract
Lack of independence in the residuals from linear regression motivates the use of random effect models in many applied fields. We start from the one-way anova model and extend it to a general class of one-factor Bayesian mixed models, discussing several correlation structures for the within group residuals. All the considered group models are parametrized in terms of a single correlation (hyper-)parameter, controlling the shrinkage towards the case of independent residuals (iid). We derive a penalized complexity (PC) prior for the correlation parameter of a generic group model. This prior has desirable properties from a practical point of view: (i) it ensures appropriate shrinkage to the iid case; (ii) it depends on a scaling parameter whose choice only requires a prior guess on the proportion of total variance explained by the grouping factor; (iii) it is defined on a distance scale common to all group models, thus the scaling parameter can be chosen in the same manner regardless the adopted group model. We show the benefit of using these PC priors in a case study in community ecology where different group models are compared.



Similar content being viewed by others
References
Dawid A, Lauritzen S (2001) Compatible prior distributions. In: Bayesian methods with applications to sciences, policy and official statistics. Proceedings of the 6th world meeting. International Society for Bayesian Analysis, Office for Official Publications of the European Communities, p 642
Finley AO, Banerjee S, Waldmann P, Ericsson T (2009) Hierarchical spatial modeling of additive and dominance genetic variance for large spatial trial datasets. Biometrics 65(2):441–451. https://doi.org/10.1111/j.1541-0420.2008.01115.x
Frühwirth-Schnatter S, Wagner H (2010) Stochastic model specification search for Gaussian and partial non-Gaussian state space models. J Econom 154(1):85–100. https://doi.org/10.1016/j.jeconom.2009.07.003
Frühwirth-Schnatter S, Wagner H (2011) Bayesian variable selection for random intercept modeling of Gaussian and non-Gaussian data. In: Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, Smith AFM, West M (eds) Bayesian statistics, vol 9. Oxford University Press, Oxford, pp 165–200
Fuglstad GA, Simpson D, Lindgren F, Rue H (2018) Constructing priors that penalize the complexity of Gaussian random fields. J Am Stat Assoc. https://doi.org/10.1080/01621459.2017.1415907
Gelman A (2006) Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Anal 1(3):515–534. https://doi.org/10.1214/06-BA117A
Heino J (2013) Environmental heterogeneity, dispersal mode, and co-occurrence in stream macroinvertebrates. Ecol Evol 3(2):344–355
Kass RE, Raftery AE (1995) Bayes factors. J Am Stat Assoc 90(430):773–795. https://doi.org/10.1080/01621459.1995.10476572
Klein N, Kneib T (2016) Scale-dependent priors for variance parameters in structured additive distributional regression. Bayesian Anal 11(4):1071–1106
Kullback S, Leibler RA (1951) On information and sufficiency. Ann Math Stat 22:79–86
Lamouroux N, Dolédec S, Gayraud S (2004) Biological traits of stream macroinvertebrate communities: effects of microhabitat, reach, and basin filters. J N Am Benthol Soc 23(3):449–466
Lindgren F, Rue H, Lindström J (2011) An explicit link between gaussian fields and gaussian markov random fields: the stochastic partial differential equation approach. J R Stat Soc Ser B (Stat Methodol) 73(4):423–498. https://doi.org/10.1111/j.1467-9868.2011.00777.x
Ovaskainen O, Tikhonov G, Norberg A, Guillaume Blanchet F, Duan L, Dunson D, Roslin T, Abrego N (2017) How to make more out of community data? A conceptual framework and its implementation as models and software. Ecol Lett 20(5):561–576
Riebler A, Held L, Rue H (2012) Estimation and extrapolation of time trends in registry data—borrowing strength from related populations. Ann Appl Stat 6(1):304–333. https://doi.org/10.1214/11-AOAS498
Rue H, Martino S, Chopin N (2009) Approximate Bayesian inference for latent Gaussian models using inte-grated nested Laplace approximations (with discussion). J R Stat Soc B 71(2):319–392
Saville BR, Herring AH (2009) Testing random effects in the linear mixed model using approximate bayes factors. Biometrics 65(2):369–376. https://doi.org/10.1111/j.1541-0420.2008.01107.x
Simpson D, Rue H, Riebler A, Martins TG, Sørbye SH (2017) Penalising model component complexity: a principled, practical approach to constructing priors. Stat Sci 32(1):1–28. https://doi.org/10.1214/16-STS576
Sørbye S, Rue H (2017) Penalised complexity priors for stationary autoregressive processes. J Time Ser Anal 38:923–935 arXiv:1608.08941
Sørbye S, Rue H (2018) Fractional gaussian noise: prior specification and model comparison. Environmetrics 29(5–6):e2457. https://doi.org/10.1002/env.2457
Ventrucci M, Rue H (2016) Penalized complexity priors for degrees of freedom in bayesian \(p\)-splines. Stat Model 16(6):429–453. https://doi.org/10.1177/1471082X16659154
Verbeke G, Molenberghs G (2003) The use of score tests for inference on variance components. Biometrics 59(2):254–262. https://doi.org/10.1111/1541-0420.00032
Warton DI, Blanchet FG, O’Hara RB, Ovaskainen O, Taskinen S, Walker SC, Hui FKC (2015) So many variables: joint modeling in community ecology. Trends Ecol Evol 30(12):766–779. https://doi.org/10.1016/j.tree.2015.09.007
Wisz MS, Pottier J, Kissling WD, Pellissier L, Lenoir J, Damgaard CF, Dormann CF, Forchhammer MC, Grytnes JA, Guisan A et al (2013) The role of biotic interactions in shaping distributions and realised assemblages of species: implications for species distribution modelling. Biol Rev 88(1):15–30
Zuur A, Ieno EN, Walker N, Saveiliev AA, Smith GM (2009) Mixed effects models and extensions in ecology with R. Springer, New York. ISBN: 978-0-387-87457-9
Acknowledgements
Massimo Ventrucci and Daniela Cocchi are supported by the PRIN 2015 Grant Project No. 20154X8K23 (EPHASTAT) founded by the Italian Ministry for Education, University and Research. Gemma Burgazzi is supported by the Project PRIN NOACQUA—responses of communities and ecosystem processes in intermittent rivers a National Relevant Project funded by the Italian Ministry of Education and University (PRIN 2015, Prot. 201572HW8F). The authors thank Maria Franco Villoria and Hȧvard Rue for the stimulating comments received about this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Proofs of results in Sect. 4.2
Proofs of results in Sect. 4.2
Recall the definition of PC prior as an exponential distribution on the distance \(d(\rho )\), with rate parameter \(\lambda \),
If design is balanced then \(m_j=m,\forall j=1,\ldots ,n\); recall that n is the number of groups while m is the number of within group observations. In this case, the distance function in Eq. (5) simplifies to
Fixing \(\lambda =\lambda '/ \sqrt{n}\), the PC prior for \(\rho \) results (by the change of variable rule)
Below, the PC priors in Eqs. (8)–(10) are derived. In each case, the proof is completed by deriving the analytical expression for the term \(\frac{1}{2}|\varvec{R}(\rho )|^{-1}\left| \frac{\partial |\varvec{R}(\rho )|}{\partial \rho }\right| \) and plugging it in (14).
1.1 Exchangeable
Proof of Eq. (8)
Let us consider the compound symmetric matrix \(\varvec{R}(\rho )\) as in (3), where subscript j is removed as we are working under a balanced design. Riebler et al. (2012) showed that
hence the distance function is equal to \(d(\rho ) = \sqrt{-n \log \left\{ (1+(m-1)\rho ) (1-\rho )^{m-1}\right\} }\). The derivative term in (14) is
After some algebraic steps, we obtain
which completes the proof. \(\square \)
1.2 Autoregressive of order one
Proof of Eq. (9)
The PC prior for the lag-one correlation of an AR1 is derived by Sørbye and Rue (2017). Here we extend it to group models having within group correlation matrix \(\varvec{R}(\rho )\) as in (4). It can be shown that
where \(|\varvec{P}| = 1-\rho ^2\). Thus the determinant of the AR1 correlation matrix is
hence the distance function is equal to \(d(\rho ) = \sqrt{-n (m-1) \log (1-\rho ^2)}\). The derivative term in (14) is
After some algebraic steps, we obtain
which completes the proof. \(\square \)
1.3 Ornstein Uhlenbeck
Proof of Eq. (10)
This proof follows straightforwardly from the AR1 case, by recognizing that \(\phi = -\,\log (\rho )\), hence \(\rho = \exp (-\,\phi )\). In this case, the determinant is
and the distance function is equal to \(d(\phi ) = \sqrt{-n (m-1) \log (1-\exp (-\,2\phi ))}\). The derivative term in (14) is
After some algebraic steps, we obtain
which completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Ventrucci, M., Cocchi, D., Burgazzi, G. et al. PC priors for residual correlation parameters in one-factor mixed models. Stat Methods Appl 29, 745–765 (2020). https://doi.org/10.1007/s10260-019-00501-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-019-00501-w