Introduction

In the contemporary era, fuel cell science and technology has evolved into a multidisciplinary discipline that consists of a range of fields including physics, mechanical engineering, molecular chemistry, computational science, electrochemistry and interfacial science, among others. The ultimate aim of many studies in this domain is to develop new and reliable systems of sustainable energy [1, 2].

Fuel cells electrochemically convert the chemical energy that is stored in a given fuel into electrical energy. The main difference between fuel cells and batteries are that fuel cells can provide an uninterrupted power supply, while batteries can only function for a limited period of time [3]. Unlike combustion engines, fuel cells are not limited by Carnot cycle, which offers a maximum efficiency of around 40%. In fact, fuel cells can achieve an efficiency level of around 65% [4,5,6].

At the start of the twentieth century, the temperature of the curvature globe had increased by around 0.6% and 2012 saw one of the highest temperatures on record. Phenomenon such as these have led to global warming concerns, and there is now a worldwide focus on reducing carbon dioxide emissions. One prominent source of such emissions is the combustion engine, and efforts are increasingly being invested in studies that seek to find viable and cost-effective methods of replacing this source of energy. One area that has proven to be particularly promising is fuel cell technology [7, 8].

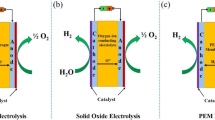
SOFCs are comparable to primary cells in that they are also formed of two electrodes, an anode and a cathode, with an electrolyte sandwiched between the two electrodes [9]. Fuel cells are typically classified according to the electrolyte material properties; however, they can also be categorized according to temperature: low-temperature fuel cells and high-temperature fuel cells. Low-temperature fuel cells operate at a temperature of between 30 °C and 250 °C, and there are five types of these cells: Alkaline fuel cell fuel cells (AFCs), Proton exchange membrane fuel cells (PEMFCs), Direct methanol fuel cells (DMFCs), Direct formic acid fuel cells (DFAFCs) and Solid acid fuel cells (SAFCs), while high-temperature fuel cells operate between 600 °C and 1000 °C and there are three types of these cells: solid oxide fuel cells (SOFCs), proton ceramic fuel cells (PCFCs), and molten carbonate fuel cells (MCFCs) [10,11,12]. In recent years, a significant amount of research effort has been invested in better understanding and addressing the challenges associated with the practical use and commercialization of SOFCs.

The performance of SOFCs is directly impacted by a range of different factors including material composition, fuel stoichiometrics, and geometry. Numerical simulations can be employed to solve complicated problems [13]. As a result of the great strides that have been made in terms of increased computation power and simulation efficiency in recent years, software applications and models have emerged that can be used to verify the effects that various factors—including fuel composition, fuel float rate, anode pressure, cathode strain, and temperature—have on the overall performance of a given fuel cell [14, 15].

Previous studies [16, 17] resulted in the generation of experimental data that modeled the performance of a small button SOFC based on the use of La0.65 Sr0.3 MnO3 and La0.8 Sr0.2 MnO3 nanoceramic powders as cathode materials, yttria-stabilized zirconia, YSZ as cell electrolyte, and NiO–YSZ as anode material. The outputs revealed that a power density in the region of 0.6 W cm−2 could be obtained at a current density of 0.85 A cm−2 at 0.7 V and 800 °C with 1.8 L min−1 hydrogen and 0.6 L min−1 oxygen. There is now a requirement to model the performance of the cell at different current densities, flow rates, and temperatures.

A number of models of varying complexities have been developed for SOFCs [18,19,20,21]. The models that have emerged are typically concerned with ionic transport, mass transport, and electrode kinetics. These models typical facilitate efforts in the areas of SOFC design, optimization, and control.

In previous articles [16, 17] which presented same experimental data for the performance of a small button solid oxide fuel cell, SOFC, based on using La0.65 Sr0.3 MnO3 and La0.8 Sr0.2 MnO3 nanoceramic powders as cathode materials, yttria-stabilized zirconia, YSZ, as cell electrolyte and NiO–YSZ as anode material. It was possible to obtain a power density around 0.6 W cm−2 at a current density of 0.85 A cm−2 at 0.7 V at 800 °C with 1.8 L min−1 hydrogen and 0.6 L min−1 oxygen. Further development requires modeling the cell performance at varying conditions of temperatures, flow rates and current densities.

Several models have been presented for solid oxide fuel cells [18,19,20,21] ranging in complexity from zero-dimensional models. Modeling was generally based on electrode kinetics, mass transport and ionic transport in the electrolyte media. These models are generally needed for design, sealing-up, optimization and control.

Mathematical model

On a basic level, when a fuel cell is connected to an external load, the difference potential across the electrodes within the cell pushes the electrons through an external circuit. However, the underlying processes that form the electrochemical system are relatively complex. While several researchers have focused on the charge transfer that takes place at the interfaces that are formed by the electrolyte and electrodes, understanding in this area remains limited. The operation of SOFCs involves a range of irreversibilities that can lead to different losses. The total resistance of electrodes is influenced by four aspects: concentration polarization resistance, the contact resistance, the internal resistance, and the activation polarization resistance. The internal resistance indicates the electron transport resistance, which is typically measured according to the thickness of the electrode structure and the electronic conductivity. Contact resistance is influenced by the level of contact between the electrolyte structure and the electrode. All restrictive losses represent functions of the local current density. It is possible to reduce potential losses using an appropriate material for the electrode and ensuring that the micro-structural properties of the cells are carefully controlled throughout the manufacturing process.

Our present model is based on the well-known equation of cell potential [18]

$$ V_{{{\text{cell}}}} = \;V_{{{\text{Nernest}}}} - \eta _{{{\text{ohm}}}} - \eta _{{{\text{act}}}} - \eta _{{{\text{dif}}}} = f(i), $$
(1)

where Vcell is the cell voltage, VNernest is the Nernest potential, ηohm is the ohmic polarization, ηact is the activation polarization and ηdif is the diffusion polarization and i is the cell current. Since it has already actual measurements of open-circuit potentials Vocp at different conditions, it can use these instead of VNernest. Therefore, Eq. (1) will be replaced by the following equation

$$ V_{{{\text{cell}}}} = V_{{{\text{ocp}}}} {-} \, \eta_{{{\text{ohm}}}} {-} \, \eta_{{{\text{act}}}} {-} \, \eta_{{{\text{dif}}}} . $$
(2)

The polarization contributions can be estimated as follows:

Ohmic polarization

The cell ohmic resistance is the sum of anode, cathode and electrolyte resistances, Ran, Rcat and Rel, respectively. Each is calculated from Ohm’s second law

$$ Ri = \frac{\sigma i \delta i}{A}, $$
(3)

where \(Ri\) is the resistance contribution of each part, \(\sigma i\) is the specific resistivity, \(\delta i\) is each part thickness and A is the area. As for the electrolyte, the contribution of ionic and electronic resistivities can be estimated from the following equation

$$ \frac{1}{{{\text{Rel}}}} = \frac{1}{{{\text{Rion}}}} + \frac{1}{{{\text{Relec}}}}. $$
(4)

The ionic conductivity of the cell electrolyte is around 0.2 S m−1 [22]. The thickness and electronic resistivities as a function of temperature T in oK of each of the cell components is shown in Table 1.

Table 1 Characteristics of cell components
Full size table

Activation polarization

Activation polarization for simple electrode kinetics is usually expressed by the Butler–Volmer equation [18]

$$ i = \, i_{o} \{ \exp \, (\alpha {-}\exp \, [ - \, (1 - \alpha ) ]\} , $$
(5)

where α is the transfer coefficient, usually taken as 0.5, R is the universal gas constant = 8.314 J mol−1 oK and io is the exchange current. The exchange currents are estimated from the following equations [18]

$$ {\text{i}}_{{{\text{o}},{\text{an}}}} = 0.{25 }\gamma_{{{\text{an}}}} {\text{A exp}}\left( {\frac{ - Eact,an}{{RT}}} \right), $$
(6)
$$ {\text{i}}_{{{\text{o}},{\text{an}}}} = 0.{25 }\gamma_{{{\text{cath}}}} {\text{A exp}}\left( {\frac{ - Eact,cath}{{RT}}} \right), $$
(7)

where Eact is the activation energy for each electrode reaction in J mol−1. γan and γcath are 7 × 109 A m−2 and Eact,an and Eact,cath are 110 and 120 kJ mol−1, respectively [18].

For small over potentials less than 20 mV, the above equations reduce to the following linear equation:

$$ \eta_{{{\text{act}}}} = \frac{RT}{{nFio}}, $$
(8)

and for high over potentials > 100 mV, the equation reduces to the Tafel equation:

$$ \eta_{{{\text{act}}}} = \frac{RT}{{\alpha nF}}\ln \frac{i}{io}. $$
(9)

Diffusion polarization

The diffusion polarization is estimated from the following equation [21]:

$$ \eta_{{{\text{dif}}}} = \frac{RT}{{nF}}\ln \left( {1 - \frac{i}{iL}} \right), $$
(10)

where iL is the limiting current estimated from overall mass transfer coefficient

$$ {\text{i}}_{{\text{L}}} = {\text{nFK}}_{{{\text{ov}}}} {\text{CA}}, $$
(11)

where C is the molar concentration of the reactant, Kov is the combination between the mass transfer coefficients in the gas space above each electrode Kg, and in the porous electrode Kp according to the equation

$$ \frac{1}{Kov} = \frac{1}{Kg} + \frac{1}{Kp}. $$
(12)

Kg in turn can be calculated from the following correlation for laminar gas flow over flat surface [8]

$$ {\text{Sh}} = 0.{648 }\left( {{\text{Re}}} \right)^{{0.{5}}} \left( {{\text{Sc}}} \right)^{{{1}/{3}}} , $$
(13)

where Sh is Sherwood number, \(\frac{Kgd}{D}\), Re is Reynold’s number\(\frac{{\varvec{\uprho}}\mathbf{V}\mathbf{d}}{\mu }\), and Sc is Schmidt number,\(\frac{\mu }{{\varvec{\uprho}}\mathbf{D}}\).

Here, d is the alumina tube diameter, V is the velocity, \(\mu \) is the gas viscosity, \(\rho \) is the gas density, and D is the molar diffusivity of H2 or O2 is the gas phase.

On the other hand Kp is estimated as \(\frac{{\epsilon}D}{\delta }\) [23], where \(\epsilon\) is the electrode porosity.

Gas densities are calculated from the ideal gas law

$$ {\uprho } = \frac{PM}{{RT}} $$
(13)

where P is the absolute pressure and M is gas molecular weight, O2 and H2 viscosities are obtained from ref [24]. The molar diffusivities of O2 and H2 are calculated from the following equation [25]:

$$ DAB = \frac{{10^{( - 4)} \left( {1.084 - 0.249\sqrt {\frac{1}{{{\text{MA}}}} + \frac{1}{{{\text{MB}}}}} } \right)T^{(3/2)} \sqrt {\frac{1}{{{\text{MA}}}} + \frac{1}{{{\text{MB}}}}} }}{{Pr_{AB}^{2} f(KT/\varepsilon_{AB} )}} $$
(14)

where \({r}_{AB}\) and \(f(KT/{\varepsilon }_{AB})\) are given in tabulated forms in ref [25]. Table 2 summarizes the physical properties for O2 and H2 at the given test temperatures.

Table 2 Physical properties of cathode and anode gases
Full size table

Results and discussions

The modeling and simulation of the anode supported planar type of Solid Oxide Fuel Cell was carried out using the equation for calculating the SOFC cell voltage. Testing the model in estimating the cell potential, we selected the conditions of current density of 0.85 A cm−2, cell temperatures of 800 °C, H2 flow rate of 1.8 L min−1 and O2 flow rate of 0.6 L min−1. Table 3 summarizes the cell potential breakdown, which is calculated from the above equations.

Table 3 Characheristics of the experimental cell
Full size table

For comparison, the measured Vcell at these conditions was 0.7 V. This shows that the model in spite of its simplicity estimates the cell potential with reasonable accuracy. The model as such can be used for optimization, control, or investigating of the effects of design parameters on the cell performance (Table 4).

Table 4 Cell Potential breakdown in Volts
Full size table

Conclusion

The goal of this research work is to create a solid oxide fuel cell model and apply the model to analyze the cell 's output by varying various parameters. As there is a direct relation between SOFC design parameters and the performance of a SOFC, it is possible to improve the performance of the cell by optimizing the design parameters. The improved performance of the newly established SOFC model, which can be further strengthened by changing the pressure and thickness of the cell components, is also verified by higher cell power values, average current density and efficiency.