Real and complex supersolvable line arrangements in the projective plane

Abstract

If we regard a set of s lines in ${\mathbb P}^2$ over either the reals or the complex numbers as an algebraic plane curve, then it is an open problem to classify for all s those for which the number $t_2$ of points of multiplicity 2 satisfies $t_2<\lfloor s/2\rfloor$. By the Sylvester–Gallai theorem, there are no nontrivial (i.e., not a pencil or a near pencil) real arrangements with $t_2=0$, but there are complex arrangements with $t_2=0$ and it is an open problem to classify them. In this paper, we initiate a classification of an interesting class of line arrangements called the supersovable line arrangements and give a partial classification for them over the reals or the complex numbers. In particular, we show that a complex line arrangement which is nontrivial cannot have more than 4 modular points and we completely describe those with 3 or 4 modular points.

1 Introduction

Line arrangements have provided useful insight in studying a range of recent problems in algebraic geometry. They have played a fundamental role for studying the containment problem (see [9, 10]), for the bounded negativity problem and H constants [4] and for unexpected curves [6, 7]. The supersolvable arrangements are a particularly tractable subclass of line arrangements which have played a role in the study of unexpected curves [6, 7]. Understanding supersolvable arrangements better should make them even more useful. Thus, the goal of the present paper is to pin down, as much as currently possible, properties of real and complex supersolvable line arrangements.

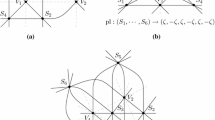
A line arrangement is simply a finite set of $s>1$ distinct lines ${\mathcal L}=\{L_1,\dots , L_s\}$ in the projective plane. A point p is a modular point for ${\mathcal L}$ if it is a crossing point (i.e., a point where two or more of the lines meet) with the additional property that whenever q is any other crossing point, then the line through p and q is $L_i$ for some i. We say ${\mathcal L}$ is supersolvable if it has a modular point (see Fig. 1).

If the s lines of ${\mathcal L}$ are concurrent (i.e., all meet at a point), then ${\mathcal L}$ is supersolvable since it has only one crossing point, and hence, it is modular. Such an arrangement is called a pencil. If ${\mathcal L}$ consists of s lines where exactly $s-1$ of them are concurrent, it is called a near pencil; near pencils are also supersolvable, since every crossing point for a near pencil is modular. For example, consider Fig. 1: Removing any line from the arrangement, other than the line through the two white dots, results in a near pencil. We will refer to pencils and near pencils as being trivial arrangements.

Fig. 1

A supersolvable line arrangement with 2 modular points (shown as white dots)

We refer to the number of lines of an arrangement $\mathcal L$ containing a point as the multiplicity of the point. So crossing points always have multiplicity at least 2. The modular points in Fig. 1 have multiplicity 3, while the other crossing points in the figure have multiplicity 2. For $k\ge 2$, we will use $t_k(\mathcal L)$ to denote the number of crossing points of $\mathcal L$ of multiplicity k.

For example, a pencil of $s\ge 2$ lines has a unique crossing point and it has multiplicity s, so $t_s=1$ and otherwise $t_k=0$. A near pencil of s lines has s crossing points; when $s > 3$, $s-1$ of the s crossing points have multiplicity 2 and one has multiplicity $s-1$ (so $t_2=s-1$, $t_{s-1}=1$ and otherwise $t_k=0$), while if $s=3$ all three crossing points have multiplicity 2 (so $t_2 = 3$ and otherwise $t_k=0$).

It is an open problem to determine which vectors $(t_2,\dots ,t_s)$ can arise for real or complex line arrangements, even for supersolvable line arrangements. It is also an open problem to classify all complex line arrangements with $t_2=0$. By the Sylvester–Gallai theorem [first proved by Melchior [14]; see inequality (2.3)], no nontrivial real line arrangement can have $t_2=0$. However, three nontrivial kinds of complex line arrangements are known with $t_2=0$ (see Sect. 4), but there is no proof that there are no others. Anzis and Tohǎneanu [3] conjectured that a nontrivial complex supersolvable arrangement of s lines has $t_2\ge s/2$, and the first version of the present paper proposed a weaker conjecture, namely that $t_2>0$. After our paper was posted to the arXiv, Abe [1] posted a proof of the Anzis and Tohǎneanu conjecture, thereby showing also that $t_2=0$ is impossible for nontrivial complex supersolvable line arrangements.

The fact that these problems were, at the time of the writing of this paper, also open for the subclass of supersolvable line arrangements motivated this paper. Our approach here is to begin a classification of all supersolvable real or complex line arrangements. The partial classification that we obtain is of interest in its own right. In particular, we show that a complex line arrangement which is nontrivial cannot have more than 4 modular points, we completely describe those with 3 or 4 modular points, and we completely describe those for which the modular points do not all have the same multiplicity. In all of these cases, it happens that $t_2\ge s/2$. This supported our conjecture that $t_2>0$ and the much stronger conjecture of Anzis and Tohǎneanu that $t_2\ge s/2$. (After posting the first version of this paper on the arXiv, Abe and Dimca [2] extended our classification to cover the case of supersolvable line arrangements with exactly two modular points of equal multiplicity, and Abe [1] proved the conjecture of Anzis and Tohǎneanu.)

Given a line arrangement $\mathcal L$, we denote by $\mu _{\mathcal L}$ the number of modular points of $\mathcal L$, so $\mathcal L$ is supersolvable exactly when $\mu _{\mathcal L}>0$. We denote the number of lines of $\mathcal L$ by $s_{\mathcal L}$, the number of crossing points by $n_{\mathcal L}$ and the maximum k such that $t_k(\mathcal L)>0$ by $m_{\mathcal L}$.

We divide supersolvable line arrangements (over any field) into two broad classes. Given a supersolvable line arrangement $\mathcal L$, if it has two or more modular points and they do not all have the same multiplicity, we say $\mathcal L$ is not homogeneous, but if all modular points of $\mathcal L$ have the same multiplicity, we say $\mathcal L$ is homogeneous and m-homogeneous if the common multiplicity is m, in which case we have $m=m_{\mathcal L}$ by Lemma 2.

Our main results are summarized by the following theorem.

Theorem 1

Let $\mathcal L$ be a line arrangement (over any field) with $\mu _{\mathcal L}>0$.

• (a) If $\mathcal L$ is not homogeneous, then either $\mathcal L$ is a near pencil or $\mu _{\mathcal L}=2$; if $\mu _{\mathcal L}=2$, then $\mathcal L$ consists of $a\ge 2$ lines through one modular point, $b>a$ lines through the other modular point, and we have $s_{\mathcal L}=a+b-1$ and $t_2=(a-1)(b-1)$.

• (b) If $\mathcal L$ has a modular point of multiplicity 2, then $\mathcal L$ is trivial.

• (c) If $\mathcal L$ is complex and homogeneous with $m=m_{\mathcal L}>2$, then $1\le \mu _{\mathcal L}\le 4$. If $3\le \mu _{\mathcal L}\le 4$, we have the following possibilities. If $\mu _{\mathcal L}=4$, then $s_{\mathcal L}=6$, $m=3$, $t_2=3$, $t_3=4$ and $t_k=0$ otherwise; up to change of coordinates, $\mathcal L$ consists of the lines $x=0$, $y=0$, $z=0$, $x-y=0$, $x-z=0$ and $y-z=0$ (intuitively, an equilateral triangle and its angle bisectors). And if $\mu _{\mathcal L}=3$, then $m>3$, and up to change of coordinates, $\mathcal L$ consists of the lines defined by the linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$; hence, $s_{\mathcal L}=3(m-1)$, $t_2=3(m-2)$, $t_3=(m-2)^2$, $t_m=3$ and $t_k=0$ otherwise.

The proof of Theorem 1 is as follows. Theorem 1(a,b) follows from Corollary 3. The fact that $1\le \mu _{\mathcal L}\le 4$ in Theorem 1(c) follows from Theorem 7, and when $\mu _{\mathcal L}\ge 3$, the classification in Theorem 1(c) for $m_{\mathcal L}=3$ is done in Sect. 3.2.2, and for $m_{\mathcal L}>3$, it is done in Sect. 3.2.4.

Theorem 1 thus gives a complete classification of supersolvable line arrangements $\mathcal L$ if either there is a modular point of multiplicity 2, or the arrangement is not homogeneous, or the arrangement is homogeneous, defined over $\mathbb {C}$ and has 3 or more modular points. In addition, we give a complete classification of real supersolvable line arrangements with more than 1 modular point (see Sect. 3.4), but our methods only give partial results for the case that $\mu _{\mathcal L}=2$ over $\mathbb C$. For this latter case, we direct the reader to the paper [2] of Abe and Dimca, which builds on our results by finishing the classification for $\mu _{\mathcal L}=2$ over $\mathbb C$. Thus, all that is left for our classification program is the case $\mu _{\mathcal L}=1$. Such cases do occur, but it is still an open problem to classify them. See Sect. 3.3 for some partial results.

The structure of this paper is as follows. In Sect. 2, we recall facts we will use later. In Sect. 3, we study the classification of supersolvable real and complex line arrangements and prove Theorem 7. In Sect. 4, we consider various conjectures related to the occurrence of points of multiplicity 2 on real and complex line arrangements (including Conjectures 12 and 13, now known to be true by Abe [1]), and we demonstrate what our methods can say about these formerly open conjectures (see for example Theorem 18). Finally, in Sect. 5, we discuss the application of supersolvable line arrangements to the occurrence of unexpected plane curves and raise the question of whether all which can occur are already known.

2 Preliminaries

Let ${\mathcal L}=\{L_1,\dots , L_s\}$ be a line arrangement in the projective plane over an arbitrary field K. In this section, we include some well-known results that we use in this paper.

First we have the following combinatorial identity which holds for any field K.

$$\begin{aligned} \left( {\begin{array}{c}s\\ 2\end{array}}\right) = \sum _{k\ge 2}\left( {\begin{array}{c}k\\ 2\end{array}}\right) t_k. \end{aligned}$$

(2.1)

If $K = \mathbb {C}$ and $\mathcal {L}$ is nontrivial, we have the following inequality due to Hirzebruch [12].

$$\begin{aligned} t_2+\frac{3}{4}t_3\ge s + \sum _{k>4}t_k(k-4). \end{aligned}$$

(2.2)

If $K = \mathbb {R}$ and $\mathcal {L}$ is not a pencil, we have the following inequality due to Melchior [14].

$$\begin{aligned} t_2 \ge 3 +\sum _{k\ge 3}(k-3)t_k. \end{aligned}$$

(2.3)

When ${\text {char}}(K)=0$ and $\mathcal {L}$ is supersolvable, we have the following inequality proved in [3, Proposition 3.1].

$$\begin{aligned} t_2\ge 2n_{\mathcal L}-m_{\mathcal L}(s-m_{\mathcal L})-2. \end{aligned}$$

(2.4)

The following result is [15, Lemma 2.1]. For the reader’s convenience, we include a proof.

Lemma 2

Let $\mathcal {L}$ be a supersolvable line arrangement (over any field K) with a modular point p of multiplicity m. If q is a crossing point of multiplicity $n\ge m$, then q is also modular.

Proof

In addition to the line $L=L_{p1}=L_{q1}$ through p and q, $\mathcal {L}$ contains $m-1$ lines through p (denote them by $L_{p2},\dots ,L_{pm}$) and $n-1$ lines through q (denote them by $L_{q2},\dots ,L_{qn}$). Let $r_{ij}$ be the point where $L_{pi}$ intersects $L_{qj}$. Suppose A and B are any two distinct lines in $\mathcal {L}$. Let r be the point where A and B meet. We must show r is on a line in $\mathcal {L}$ through q. If either A or B contain q, then r is on a line in $\mathcal {L}$ through q, so assume neither A nor B contains q.

First say $n>m$. Let $a_j$ be the point where A and $L_{qj}$ meet. Since $q\ne a_j$, we get $n-1$ distinct points $a_j$, each of which is on some line $L_{pi_j}$ since p is modular. But there are only $m-1<n-1$ lines $L_{pi}$, so we must have $i_{j}=i_{j'}$ for some $j\ne j'$, and hence, $A=L_{pi_j}=L_{pi_{j'}}$, so $p\in A$. Likewise $p\in B$, so $r=p\in L$ is on a line in $\mathcal {L}$ through q. (This also shows that $n>m$ implies that every line in $\mathcal {L}$ contains either p or q; i.e., the lines in $\mathcal {L}$ are the $m+n-1$ lines through p and q.)

Now say $n=m$. If both A and B contain p, then $r=p\in L$ is on a line in $\mathcal {L}$ through q. So assume either A or B does not contain p; say $p\not \in A$. But p is modular, so the point r where A and B meet is on $L_{pi'}$ for some $i'$. Again, let $a_j$ be the point where A and $L_{qj}$ meet. Since $q\ne a_j$, we get $n-1$ distinct points $a_j$, each of which is on some line $L_{pi_j}$ since p is modular. If $i_j=i_{j'}$ for some $j\ne j'$, then $A=L_{pi_j}=L_{pi_{j'}}$, so $p\in A$ contrary to assumption. Hence, $i_j\ne i_{j'}$ whenever $j\ne j'$, the $n-1=m-1$ values of $j>1$ map under $j\mapsto i_j$ to all $m-1=n-1$ values of $i>1$; hence, for some $j'$ we have $i'=i_{j'}$, so A meets $L_{pi'}$ at $a_{j'}=r_{i_{j'}j'}=r_{i'j'}\in L_{pi'}$. But A meets $L_{pi'}$ at $r\in L_{pi'}$, so $r=a_{j'}\in L_{qj'}$, so r is on a line in $\mathcal {L}$ through q. Thus, q is modular. $\square$

3 Classifying supersolvable line arrangements

3.1 Supersolvable line arrangements with modular points of multiplicity 2

We first classify all line arrangements, over any field K, having one or more modular points of multiplicity 2, or two (or more) modular points, not all of the same multiplicity. Thus, after this section, we may assume all modular points have the same multiplicity, which is at least 3.

As a corollary of the proof of Lemma 2, we have the following result, which classifies line arrangements with a modular point of multiplicity 2, or where at least two distinct multiplicities occur as multiplicities of modular points.

Corollary 3

Let $\mathcal {L}$ be a supersolvable line arrangement (over any field K) with a modular point p of multiplicity m. If $m=2$, then every crossing point is modular and $\mathcal {L}$ is either a pencil or a near pencil. If $m>2$ and $\mathcal {L}$ has a crossing point q of multiplicity $n>m$, then q is modular, the only modular points are p and q, and $\mathcal {L}$ consists exactly of the m lines through p and the n lines through q (hence $s_{\mathcal L}=m+n-1$).

Proof

Say $m=2$. Then by Lemma 2, every crossing point is modular. Thus, if p is the only modular point, then $\mathcal L$ is a pencil. Now say there is another modular point q. Let L be the line through p and q, and let $L_p\in {\mathcal L}$ be the line through p not through q. First assume q has multiplicity 2. Let $L_q\in {\mathcal L}$ be the line through q not through p. Let r be the point where $L_p$ and $L_q$ cross. Since p and q have multiplicity 2, no point off L other than r is a crossing point of ${\mathcal L}$. In particular, if $A\in {\mathcal L}$ is a line other than L and $L_p$, then A meets $L_p$ away from p, hence at r; i.e., every line in ${\mathcal L}$ other than L contains r. Thus, ${\mathcal L}$ is a near pencil. Now assume q has multiplicity more than 2. Thus, there are at least two lines $B_i\in {\mathcal L}$, $i=1,2$, through q other than L. If $A\in {\mathcal L}$ is a line other than $L_p$ which does not go through q, let $b_i$ be the point where A meets $B_i$. Since $b_1$ and $b_2$ are on A and $A\ne L_p$, at most one of the points $b_i$ can be on $L_p$. Assume $b_1\not \in L_p$. Then $b_1\in L$ (since the only lines of ${\mathcal L}$ through p are L and $L_p$, and p is modular). But $b_1\in B_1$ and $B_1\ne L$ but $B_1$ meets L at q, so $b_1=q$. This contradicts our assumption that A does not go through q. Thus, every line of ${\mathcal L}$ except $L_p$ contains q, so ${\mathcal L}$ is a near pencil.

Now say $m>2$ and $\mathcal {L}$ has a crossing point q of multiplicity $n>m$. Then q is modular by Lemma 2. We saw in the proof of Lemma 2 that the lines in $\mathcal {L}$ are the $m+n-1$ lines through p and q. Thus, there are $n-1>m-1\ge 2$ lines through q other than L, and on each of these $n-1$ lines, there are $m-1\ge 2$ crossing points of multiplicity 2 (these being the points of intersection with the $m-1$ lines through p other than L), and these $(n-1)(m-1)$ crossing points are the only crossing points other than p and q. But a point of multiplicity 2 on one line through q is connected to at most one point of multiplicity 2 on any other line through q, and hence, no point of multiplicity 2 is modular. That is, the only modular crossing points are p and q. $\square$

Proposition 4

Let $\mathcal L$ be a line arrangement (over any field) having one or more modular points, exactly one of which has multiplicity 2 (call this point p). Then $\mathcal L$ is the pencil consisting of the two lines through p.

Proof

If $\mathcal L$ had a crossing point of multiplicity $n>m=2$, then by Corollary 3, $\mathcal L$ is a near pencil, and thus would have n points of multiplicity 2. Thus, $\mathcal L$ has exactly one crossing point, and it has multiplicity 2, so $\mathcal L$ is the pencil consisting of the two lines through p. $\square$

Proposition 5

Let $\mathcal L$ be a line arrangement (over any field) having two or more modular points, at least two of which have multiplicity 2. Then $\mathcal L$ is a near pencil.

Proof

Let p and q be modular points of multiplicity 2. Since $\mathcal L$ is supersolvable, given a crossing point other than p, the line from p to that point is in $\mathcal L$. But p has multiplicity 2, so every crossing point must be on one or the other of the two lines through p. Likewise, every crossing point must be on one or the other of the two lines through q.

Let L be the line through both p and q; thus, $L\in \mathcal L$. Let $L_p$ be the other line in $\mathcal L$ through p, and let $L_q$ be the other line in $\mathcal L$ through q. Let r be the point where $L_p$ and $L_q$ meet. Thus, any crossing point not on L must be on both $L_p$ and $L_q$; i.e., r is the only crossing point not on L. Thus, every line in $\mathcal L$ other than L must contain r, so $\mathcal L$ is a near pencil. $\square$

3.2 Homogeneous supersolvable line arrangements (mostly for ${\text {char}}(K)=0$)

By our foregoing results, we see that it remains to understand supersolvable line arrangements such that all modular points have the same multiplicity m (we say such a supersolvable line arrangement is homogeneous or m-homogeneous) with $m\ge 3$. It follows from Lemma 2 in this case that $t_k=0$ for $k>m$, so $m=m_{\mathcal L}$.

3.2.1 The values of $t_{m_{\mathcal L}}$ that arise for ${\text {char}}(K)=0$

When K is algebraically closed but of finite characteristic, there is no bound to the number of modular points a supersolvable line arrangement can have. (Just take all lines defined over a finite field F of a elements. Then the arrangement has $a^2+a+1$ lines and the same number of crossing points; all are modular and all have multiplicity $a+1$.) In characteristic 0, things are very different, as we show in Theorem 7.

To prove the theorem, we will use the following result.

Proposition 6

For an m-homogeneous supersolvable complex line arrangement $\mathcal L$ with $m=m_{\mathcal L}\ge 3$, no three modular points are collinear.

Proof

Suppose that p, q and r are collinear modular points. Then the line L that contains them is in $\mathcal L$. Moreover, $\mathcal L$ contains $m-1$ additional lines through each of p, q and r. Denote the union of these $m-1$ lines through p by $C_p$. Similarly, we have $C_q$ and $C_r$. The intersection of the curves $C_p$ and $C_q$ is a complete intersection of $(m-1)^2$ points, which are also contained in $C_r$. Since the curves all have degree $m-1$, we see that $C_r$ is in the pencil defined by $C_p$ and $C_q$. That is, the forms $F_p, F_q$ and $F_r$ defining the curves are such that $F_r$ is a linear combination of $C_p$ and $C_q$. we can choose coordinates such that L is $x=0$, p is $x=y=0$, q is $x=z=0$ and r is $y=z=1$. In terms of these coordinates, the restrictions of $F_p,F_q,F_r$ to L are $y^{m-1}$, $z^{m-1}$ and $ay^{m-1}+bz^{m-1}=(y-z)^{m-1}$ for some nonzero constants a and b. Setting $z=1$, we thus see that $ay^{m-1}+b=(y-1)^{m-1}$, so $ay^{m-1}+b$ has a multiple root at $y=1$. This contradicts the fact that the derivative $a(m-1)y^{m-2}+b$ is not 0 at $y=1$. $\square$

Theorem 7

For an m-homogeneous supersolvable complex line arrangement $\mathcal L$ with $m=m_{\mathcal L}\ge 3$, we have $1\le t_m=\mu _{\mathcal L}\le 4$.

Proof

By Lemma 2, we have $t_m=\mu _{\mathcal L}$. First we show that $t_m<7$. Suppose $t_m\ge 7$ for some $m\ge 3$. Each nonmodular crossing point is connected by a line to each of the $t_m\ge 7$ modular points. Since at most two modular points can lie on any line by Proposition 6, we see that each crossing point must have multiplicity at least 4. Also, each modular point has multiplicity $m\ge 6$ since each one connects to each of the others. Thus, $t_2=t_3=0$, but this is impossible by Inequality (2.2).

Next we show that $t_m<6$. Suppose $\mathcal L$ has $t_m=6$. It is enough to show $t_m<6$ under the assumption that every line in ${\mathcal L}$ contains a modular point. (This is because if we let ${\mathcal L}'$ be the line arrangement obtained from ${\mathcal L}$ by deleting all lines not through a modular point, ${\mathcal L}'$ still has $t_{m_{{\mathcal L}'}}=6$.) Since every modular point is on a line in ${\mathcal L}$ through another modular point, we have $m\ge 5$. Every crossing point q of ${\mathcal L}$ also connects to every modular point so has multiplicity at least 3 (since a line can go through at most 2 modular points), with multiplicity exactly 3 if and only if q is 3 lines through pairs of modular points.

There are $2\left( {\begin{array}{c}6\\ 4\end{array}}\right) =30$ possible locations for crossing points of multiplicity 3; hence, $t_3\le 30$. To see this, note that there are $\left( {\begin{array}{c}6\\ 4\end{array}}\right)$ ways to pick 4 of the 6 modular points. There are 3 reducible conics through these 4 points. The singular points of these three conics are crossing points where two lines through disjoint pairs chosen from the 4 points intersect. In order to get a point q of multiplicity 3, the line H through the remaining 2 points of the 6 modular points must contain q. This might not happen for any of the three singular points, but it can be simultaneously true for at most two of the three singular points, since at most two of the singular points can be on the line H. (This is merely because the three singular points cannot be collinear in characteristic 0.) Thus, we get at most $2\left( {\begin{array}{c}6\\ 4\end{array}}\right) =30$ possible locations for crossing points of multiplicity 3.

Now apply Inequality (2.2), using the fact that our assumption (that every line in ${\mathcal L}$ contains a modular point) implies that ${\mathcal L}$ has $(m-5)6+\left( {\begin{array}{c}6\\ 2\end{array}}\right)$ lines:

$$22.5=\frac{3}{4}30\ge \frac{3}{4}t_3\ge ((m-5)6+\left( {\begin{array}{c}6\\ 2\end{array}}\right) )+(m-4)6.$$

For $m\ge 6$, this is $22.5\ge 12m-39\ge 33$; thus, the only possibility for $t_m=6$ is $m=5$. For $m=5$, we see ${\mathcal L}$ has $\left( {\begin{array}{c}6\\ 2\end{array}}\right) =15$ lines and every crossing point has multiplicity at least 3 and at most 5, so from Eq. (2.1) we get:

$$105=\left( {\begin{array}{c}15\\ 2\end{array}}\right) =3t_3+6t_4+10t_5=3t_3+6t_4+60$$

so $15=t_3+2t_4$; hence, $t_3\le 15$. Inequality (2.2) now gives $(3/4)15\ge 15+6$, which is false.

Finally, we show that $t_m<5$. So assume $t_m=5$. Arguing as before, we may assume that every line in ${\mathcal L}$ contains a modular point. We still have that all nonmodular points have multiplicity at least 3, and the 5 modular points have multiplicity $m\ge 4$. Each choice of 4 of the 5 modular points gives 3 possible locations for a triple point; hence, $t_3\le 3(5)=15$. Thus, Inequality (2.2) gives $11.25=(3/4)15\ge (\left( {\begin{array}{c}5\\ 2\end{array}}\right) +(m-4)5)+(m-4)5=10m-30$, which is impossible for $m\ge 5$. For $m=4$, we see ${\mathcal L}$ has $\left( {\begin{array}{c}5\\ 2\end{array}}\right) =10$ lines and every crossing point has multiplicity at least 3 and at most 4, so from Eq. (2.1) we get:

$$45=\left( {\begin{array}{c}10\\ 2\end{array}}\right) =3t_3+6t_4=3t_3+30$$

so $5=t_3$. Inequality (2.2) now gives $(3/4)5\ge 10$, which is false. $\square$

Example 8

For m-homogeneous supersolvable line arrangements over both the complex numbers and the reals, all four cases $1\le t_{m_{\mathcal L}}\le 4$ arise. It is easy to obtain examples with exactly one modular point; see Sect. 3.3. (However, the fact that there are many examples makes it hard to classify them!) It is also easy to obtain examples with exactly two modular points; see Corollary 3. For exactly three modular points, consider the line arrangement defined by the linear factors of $xyz(x^n-y^n)(x^n-z^n)(y^n-z^n)$ for $n\ge 2$. The coordinate vertices are the modular points and have multiplicity $n+2$. For $n=2$, the arrangement is real (see the arrangement of 9 lines shown in Fig. 3); for $n>2$, it is complex but not real. Taking $n=1$, so $xyz(x-y)(x-z)(y-z)$, gives the only example we know over the complexes or reals with exactly four modular points; see Case 2 of Fig. 2. (We thank Ş. Tohǎneanu for pointing out that a line arrangement equivalent to the one defined by the linear factors of $xyz(x^n-y^n)(x^n-z^n)(y^n-z^n)$ for $n=2$ arose as an example in section 3.1.1 of [3], to show that a certain bound on the number of crossing points was sharp. For the line arrangements given by $xyz(x^n-y^n)(x^n-z^n)(y^n-z^n)$, the bound is $t\le d^2+d+1$, where $t=n^2+3n+3$ is the number of crossing points and $d=m_{\mathcal L}-1=n+1$. Thus, we see that $t=d^2+d+1$, so this bound is in fact sharp for all values of n.)

3.2.2 Classifying m-homogeneous $\mathcal L$ for $t_m>1$ and $m=3$

Consider the case of a line arrangement $\mathcal L$ with two or more modular points of multiplicity $m\ge 3$. Since we have at least two modular points, we pick two and call them p and q.

First say $m=3$. We will show that there are three cases, shown in Fig. 2: $\mathcal L$ has either 5, 6 or 7 lines, and either 2, 4 or 7 modular points, respectively. The case of 7 lines occurs only in characteristic 2. The other cases occur for any field.

Clearly, $\mathcal L$ has at least 5 lines: the line L defined by p and q, and in addition lines $p\in L_{pi}$ and $q\in L_{qi}$, for $i=1,2$. No other lines in $\mathcal L$ (if any) can contain p or q. Let $r_1$ be where $L_{p1}$ and $L_{q1}$ meet, and let $r_2$ be where $L_{p2}$ and $L_{q2}$ meet. And let $s_1$ be where $L_{p1}$ and $L_{q2}$ meet, and let $s_2$ be where $L_{p2}$ and $L_{q1}$ meet. Any other line in $\mathcal L$ must intersect the lines $L_{pi}$ and $L_{qi}$ only at $r_1,r_2,s_1,$ or $s_2$.

One possibility is that $\mathcal L$ has only the five lines mentioned above. Alternatively, assume $\mathcal L$ has another line, A. Of the six pairs two points chosen from the four points $r_1,r_2,s_1$ and $s_2$, A must contain either $r_1$ and $r_2$ or $s_1$ and $s_2$ (A cannot contain $r_1$ and $s_1$, for example, because that line is $L_{p1}$). Up to relabeling, the cases $r_1$ and $r_2$ are the same as $s_1$ and $s_2$, so say A contains $r_1$ and $r_2$. Up to projective equivalence, we may assume that $p=(0,0,1)$, $q=(0,1,0)$, $r_1=(1,0,0)$ and $r_2=(1,1,1)$, in which case $s_1=(1,0,1)$ and $s_2=(1,1,0)$. So a second possibility is that $\mathcal L$ has six lines, with A being the sixth line. Note that in this case that $\mathcal L$ has 4 modular points: The points $p,q,r_1$ and $r_2$ are modular, and all have multiplicity 3. The only option for $\mathcal L$ to contain an additional line is for the additional line (call it B) to be the line through $s_1$ and $s_2$. But A is $y-z=0$ and B is $x-y-z=0$, so A and B intersect at the point (2, 1, 1). When the ground field does not have characteristic 2, this is not on any of the three lines through p (or on any of the three lines through q); hence, including B would make $\mathcal L$ not be supersolvable. Thus, when the characteristic is not 2, $\mathcal L$ must either have 5 or 6 lines, and be Case 1 or Case 2 shown in Fig. 2. If the characteristic is 2, the point (2, 1, 1) is on the line through p and q, in which case $\mathcal L$ consists of the 7 lines of the Fano plane, there are 7 crossing points, and all are modular and have multiplicity 3.

Fig. 2

Classification of supersolvable line arrangements with 2 or more modular points (shown as white dots), all of multiplicity $m=3$

3.2.3 Classifying m-homogeneous $\mathcal L$ over $\mathbb {R}$ for $t_m>1$ and $m>3$

Now we consider the case $m\ge 4$ for real line arrangements. So, in addition to the line L through p and q, there are $m-1$ lines through p and $m-1$ lines through q. These lines form a complete intersection (i.e., a grid) of $(m-1)^2$ crossing points. The only other crossing points for these $2m-1$ lines are p and q. Certainly $\mathcal L$ could consist of only these $2m-1$ lines, in which case p and q are the only modular points and we have $t_k=0$ except for $t_m=2$ and $t_2=(m-1)^2$.

The question now is what additional lines can be added to these $2m-1$ while maintaining supersolvability. To answer this, let us choose coordinates so that p becomes (0, 1, 0) and q becomes (1, 0, 0). Thus, the line through p and q is now the line at infinity, and the $m-1$ other lines through p are parallel to the $x=0$ axis, and the $m-1$ other lines through q are parallel to the $y=0$ axis.

Any additional line must avoid p and q, and must intersect the $m-1$ vertical lines only at points where they meet the $m-1$ horizontal lines. By inspection, we can see that this can happen in exactly to ways. First is that the four corners of the grid form a rectangle and the ith vertical line (counting from the left) meets the ith horizontal line (counting up from the bottom) meet on the anti-diagonal of the rectangle (in which case the anti-diagonal can be added to $\mathcal L$). The second way is that the four corners of the grid form a rectangle (as before) and the ith vertical line (counting from the left) meets the ith horizontal line (counting down this time from the top) meet on the main diagonal of the rectangle (in which case the main diagonal can be added to $\mathcal L$). In case both cases hold, both diagonals can be added if and only if m is even.

Thus, there are three cases: $\mathcal L$ has $2m-1$ lines and we have $t_m=2$ and $t_2=(m-1)^2$ but only two modular points, namely p and q; $\mathcal L$ has 2m lines where the additional line is one of the two major diagonals (assuming the lines are spaced correctly) and we still have only two modular points (p and q), with $t_m=2$, $t_2=(m-1)^2-(m-1)+1$; or $\mathcal L$ has $2m+1$ lines where the additional lines are the two major diagonals (assuming the lines are spaced correctly and m is even), in which case either $m=4$ and we have $t_m=3$, $t_2=6$, $t_3=4$ and there are three modular points (p, q and the center of the rectangle), or $m>4$ and we have $t_m=2$, $t_2=(m-1)^2-(2m-1)+2$, $t_3=2m-4$ and $t_4=1$ and there are only two modular points (p and q).

Thus, we have a complete classification of real supersolvable line arrangements when there is more than one modular point of multiplicity at least 3.

3.2.4 Classifying m-homogeneous $\mathcal L$ over $\mathbb {C}$ for $t_m>2$ and $m>3$

Now we consider the case $m\ge 4$ for complex line arrangements with at least 3 modular points. By Theorem 7, the number of modular points cannot be more than 4.

We begin with the case of exactly $t_m=3$ modular points. If $\mathcal L$ has a line that does not contain a modular point, deleting it gives an arrangement which is still supersolvable, so we first assume every line in $\mathcal L$ goes through a modular point.

After a change of coordinates, we may assume that the three modular points, p, q and r, are the coordinate vertices of ${\mathbb P}^2$, so say $p=(0,0,1), q=(0,1,0), r=(1,0,0)$. In addition to the three coordinate axes, $\mathcal L$ must contain $m-2$ lines through each of p, q and r. Let $F_p$ be the form defining the union of these $m-2$ lines through p, other than the coordinate axes. Note that $F_p$ is a form of degree $m-2$ and involves only the variables x and y, hence is $F_p(x,y)$. Likewise we have $F_q(x,z)$ and $F_r(y,z)$ for q and r. Since the coordinate axes are not among the lines defined by $F_p$, $F_q$ or $F_r$, we see that none of these forms is divisible by a variable.

The crossing points for the lines from $F_p$ and the lines from $F_q$ form a complete intersection of $(m-2)^2$ points on which $F_r$ also vanishes, so $F_r=aF_p+bF_q$ for some scalars a and b. The only term that $F_p$ and $F_q$ can have in common is $x^{m-2}$. Thus, in order that all terms involving x cancel in $aF_p+bF_q$ so that $F_r$ involves only y and z, we see that $x^{m-2}$ is the only term in either $F_p$ or $F_q$ involving x. Thus (after dividing by the coefficient of $x^{m-2}$ in each case), we have $F_p=x^{m-2}-\alpha y^{m-2}$ and $F_q=x^{m-2}-\beta z^{m-2}$. By absorbing the $\alpha$ into y and the $\beta$ into z, we get $F_p=x^{m-2}-y^{m-2}$ and $F_q=x^{m-2}-z^{m-2}$, so $F_r=y^{m-2}-z^{m-2}$.

Thus, if every line in $\mathcal L$ goes through one of the three modular points, then the lines in $\mathcal L$ correspond to the linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$. Now we check that no line not through p, q or r can be added to $\mathcal L$ while still preserving supersolvability. If such a line L existed, it would need to intersect every line of $\mathcal L$ in a crossing point. In particular, L must contain one of the $(m-2)^2$ intersection points of the lines from $F_p$ and the lines from $F_q$. Let $n: = m-2$. By an appropriate change of coordinates obtained by multiplying x, y and z by appropriate powers of an nth root of 1, we may assume that L contains (1, 1, 1). Let $\epsilon =\cos (2\pi /n)+\imath \sin (2\pi /n)$ be a primitive nth root of 1. The line L must intersect $y-\epsilon z=0$ at a crossing point (hence at $(\epsilon ^i,\epsilon ,1)$ for some $1 \le i \le n$) and also $y-\epsilon ^2 z=0$ at a crossing point (hence at $(\epsilon ^j,\epsilon ^2,1)$ for some $1 \le j \le n$). The question is whether i and j exist such that these points lie on a line through (1, 1, 1) which does not go through p, q or r.

The lines through (1, 1, 1) are of the form $a(x-z)+b(y-z)=0$. For the line not to go through p, q or r, we need $ab\ne 0$. Thus, we can write the line as $c=(y-z)/(x-z)$ for some $c\ne 0$. For $(\epsilon ^i,\epsilon ,1)$ and $(\epsilon ^j,\epsilon ^2,1)$ both to lie on this line, we must have

$$\begin{aligned} \frac{\epsilon -1}{\epsilon ^i-1}=\frac{\epsilon ^2-1}{\epsilon ^j-1}. \end{aligned}$$

This simplifies to

$$\begin{aligned} \epsilon ^{i-1}(\epsilon +1)=\epsilon ^{j-1}+1. \end{aligned}$$

Thus, the complex norms are equal; i.e., $|\epsilon +1|=|\epsilon ^{j-1}+1|$. But if $\gamma =\cos (\theta )+\imath \sin (\theta )$, the norm $|\gamma +1|$ is a decreasing function of $\theta$ for $0\le \theta \le \pi$, so the only possibilities for $|\epsilon +1|=|\epsilon ^{j-1}+1|$ are $j=2, n$. If $j=2$, then $\epsilon ^{i-1}(\epsilon +1)=\epsilon ^{j-1}+1$ forces $i=1$, so the line through $(\epsilon ^i,\epsilon ,1)$ and $(\epsilon ^j,\epsilon ^2,1)$ then is $x-y=0$, which contains p. If $j=n$, then $\epsilon ^{i-1}(\epsilon +1)=\epsilon ^{j-1}+1=(1+\epsilon )/\epsilon$ forces $\epsilon ^i=1$, and hence, $i=n$, so the line is $x-z=0$, which contains q.

Thus, the only possibility for 3 modular points of multiplicity $m>3$ is (up to choice of coordinates) for the line arrangement to be the lines defined by the linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$.

Now suppose $\mathcal L$ has 4 modular points with $m>3$. We can, up to choice of coordinates, assume that the four points are p, q, r and s, where p, q and r are as above, and $s=(1,1,1)$. If we delete any lines not through p, q and r, then the resulting arrangement must come from the linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$. To get $\mathcal L$, we must add back in lines through s which intersect the lines coming from $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$ only at crossing points for the lines from $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$. But as we just saw there are no such lines. Thus, $\mathcal L$ having 4 modular points with $m>3$ is impossible.

Thus, up to choice of coordinates, the only complex supersolvable line arrangement with 4 modular points is the one we found before; i.e., $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$ with $m=3$, displayed in Case 2 of Fig. 2. And up to choice of coordinates, the only complex supersolvable line arrangements with 3 modular points are given by the linear factors of xyz when $m=2$ and by the linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$ for $m > 3$.

We do not have a classification of complex supersolvable line arrangement with just 1 or 2 modular points, but the case of 2 modular points has now been handled by Abe and Dimca [2]. If for $m\ge 3$ you remove one or more of the linear factors of $y^{m-2}-z^{m-2}$ from the set of linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$, then we get examples of complex supersolvable line arrangement with just 2 modular points. Thus, more examples occur over $\mathbb {C}$ than over $\mathbb {R}$, but it was not clear to us what the full range of possibilities was.

In any case, we have given a full classification over $\mathbb {C}$ for supersolvable line arrangement with 3 or 4 modular points. We discuss the case of 1 modular point in the next section.

3.3 Having a single modular point

The case that there is a single modular point is the hardest to classify and we can give only partial results in this case.

We begin with a lemma.

Lemma 9

Let $\mathcal L$ be a line arrangement (not necessarily supersolvable, not necessarily over the reals). Let m be the maximum of the multiplicities of the crossing points, and let n be the number of crossing points. If $n<2m$, then $\mathcal L$ is either a pencil or near pencil.

Proof

Assume $\mathcal L$ is not a pencil or a near pencil. Let p be a point of multiplicity m and take lines A and B not through p. Then A and the m lines through p give $m+1$ crossing points, and B then gives at least another $m-1$ crossing points, for a total of at least 2m crossing points. $\square$

We now consider the case of a line arrangement $\mathcal L$ with a single modular point, which we assume has multiplicity $m>2$; call it p. By [3], every other crossing point of $\mathcal L$ has multiplicity less than p (because for a supersolvable line arrangement, all points of maximum multiplicity are modular). Assume $\mathcal L$ is not a pencil or a near pencil. Let $\mathcal L'$ be the arrangement obtained from $\mathcal L$ by removing the m lines through p. We can recover $\mathcal L$ by adding to $\mathcal L'$ every line from p to a crossing point of $\mathcal L'$. What is difficult to know is how many lines get added, since one line through p might contain more than one crossing point of $\mathcal L'$. But we see that $t_m=1$ and $t_{k+1}=t_k'$ for all $2<k<m$, where $t_k'$ is the number of crossing points of $\mathcal L'$ of multiplicity k. Even knowing how many lines are in $\mathcal L'$ and the value of $t_k'$ for every k, it is hard to say how many lines are in $\mathcal L$, or what the value of $t_2$ is, except in certain special situations.

Suppose, for example, we know that no two crossing points of $\mathcal L'$ are on the same line through p. Since $\mathcal L'$ has $t_2'+\dots +t_m'$ crossing points and $\mathcal L'$ has $s'$ lines, where $\left( {\begin{array}{c}s'\\ 2\end{array}}\right) =\sum _kt_k'\left( {\begin{array}{c}k\\ 2\end{array}}\right)$ [see (2.1)], we then know that $\mathcal L$ has $s=s'+t_2'+\dots +t_m'$ lines, and then from $\left( {\begin{array}{c}s\\ 2\end{array}}\right) =\sum _kt_k\left( {\begin{array}{c}k\\ 2\end{array}}\right)$, we can determine $t_2$.

Alternatively, start with any line arrangement $\mathcal L'$ (over any field) which is not a pencil or a near pencil. By Lemma 9, $n'\ge 2m'$, where $n'$ is the number of crossing points of $\mathcal L'$ and $m'$ is the maximum of their multiplicities. For a general point p, no line through p will contain more than one crossing point of $\mathcal L'$. Now add to $\mathcal L'$ each line from p to a crossing point of $\mathcal L'$ to get a larger line arrangement $\mathcal L$ of $s=n'+s'$ lines, where $s'$ is the number of lines of $\mathcal L'$. We also know that $t_{k+1}=t_k'$ for all $k>2$, and we can determine $t_2$ from $\left( {\begin{array}{c}s\\ 2\end{array}}\right) =\sum _kt_k\left( {\begin{array}{c}k\\ 2\end{array}}\right)$. Moreover, p is the unique modular point of $\mathcal L$. Note that p has multiplicity $n'\ge 2m'$ and the maximum multiplicity of any other crossing point of $\mathcal L$ is $m'+1<2m'$. Thus, if $\mathcal L$ has another modular point, it has multiplicity $d<n'$; hence, by our classification $\mathcal L$ has $d+n'-1$ lines. But in fact $s'\ge d+1$ since $\mathcal L'$ is not a pencil or near pencil, and $\mathcal L$ has $s=s'+n'>d+1-n'$ lines. Thus, $\mathcal L$ has a unique modular point, namely p. Thus, classifying line arrangements with a unique modular point, even when that point is general, comes down to classifying line arrangements in general.

3.4 Summary

The real supersolvable line arrangements having more than one modular point can be subsumed by one general construction. Take two points, p and q, on a line L. Take $a_p\ge 0$ additional lines through p and $a_q\ge 0$ additional lines through q. This gives a supersolvable line arrangement as long as $a_p+a_q>0$. In addition, if $a_p=a_q\ge 2$ and the obvious collinearity condition obtains, an additional line can be added in two possible ways (shown by the dashed and dashed dotted lines in Fig. 3 in the case of $a_p=a_q=3$). If both can be added separately and if $a_p=a_q$ is odd, both can be added simultaneously. These constructions cover all possible cases of real supersolvable line arrangements with 2 or more modular points.

The case of complex supersolvable line arrangements with more than two modular points is all given, up to choice of coordinates, by the linear factors of $xyz(x^{m-2}-y^{m-2})(x^{m-2}-z^{m-2})(y^{m-2}-z^{m-2})$ for $m\ge 3$.

Fig. 3

A supersolvable line arrangement with 2 modular points of equal multiplicity with possible added lines

4 Points of multiplicity 2 in supersolvable line arrangements

4.1 Questions and conjectures

By Inequality (2.3), every nonpencil real line arrangement has $t_2\ge 3$. More generally, there is the still open Dirac–Motzkin conjecture [8] (now known for $s\gg 0$; see [11]):

Conjecture 10

The inequality $t_2\ge \lfloor s/2\rfloor$ holds for every nonpencil real line arrangement of s lines.

Things over $\mathbb C$ are more complicated. Four types of complex line arrangements with $t_2=0$ are currently known: pencils of 3 or more lines; the lines defined by the linear factors of $(x^n-y^n)(x^n-z^n)(y^n-z^n)$ for $n\ge 3$ (known as the Fermat arrangement, $\mathcal {F}_n$); an arrangement due to Klein [13] with 21 lines and $t_k=0$ except for $t_3=28$ and $t_4=21$; and an arrangement due to Wiman [16] with 45 lines and $t_k=0$ except for $t_3=120$, $t_4=45$ and $t_5=36$ (see [5] for more information about the Klein and Wiman arrangements).

We believe the following question is open.

Question 11

Are there any complex line arrangements with $t_2=0$ other than the four types listed above?

For the case of supersolvable line arrangements, an earlier version of this paper posed the following conjecture.

Conjecture 12

Every nontrivial complex supersolvable line arrangement has $t_2>0$.

A much stronger conjecture was posed by [3].

Conjecture 13

Every nonpencil complex supersolvable line arrangement of s lines has $t_2\ge s/2$.

Recently, Abe [1] has proved Conjecture 13 in full generality. An earlier version of our present paper, which appeared before [1], made some progress toward the conjecture by proving it in some cases. We include these results below, since our methods are very different from those of [1].

In the previous section, we have found all complex supersolvable line arrangements with at least 3 modular points, and for these, $t_2\ge s/2$ holds. Thus, if the conjecture is false, then it must fail for a line arrangement with either one or at most 2 modular points.

It is also interesting to ask:

Question 14

Which nonpencil complex line arrangements of s lines fail to satisfy $t_2\ge \lfloor s/2\rfloor$?

Of course, as noted above, there are nonpencil line arrangements with $t_2=0$, and for these, $t_2\ge \lfloor s/2\rfloor$ fails to hold. Also, by adding or deleting lines from such line arrangements one can sometimes get additional examples. For example, the line arrangement $\mathcal L$ with $s=3n$ lines defined by the linear factors of $(x^n-y^n)(x^n-z^n)(y^n-z^n)$ has $t_2=0$; by adding the line $x=0$, we get a line arrangement $\mathcal L'$ with $s=3n+1$ and $t_2=n$, so $t_2\ge \lfloor s/2\rfloor$ still fails. For another example, each line of the Klein arrangement of 21 lines contains four crossing points of multiplicity 4 and four of multiplicity 3. By removing one line, we thus get an arrangement of $s=20$ lines with $t_4=17$, $t_3=28$ and $t_2=4$, so here too $t_2\ge \lfloor s/2\rfloor$ fails. But this leaves the question: Are there any examples where $t_2\ge \lfloor s/2\rfloor$ fails to hold which do not come in this way from the known examples with $t_2=0$?

If $\mathcal {L}$ is defined over $\mathbb {R}$, [3] proves Conjecture 13 (see [3, Theorem 2.4]). A key step in their proof is [3, Lemma 2.2], a version of which we now state. For the convenience of the reader, we include a slightly simplified version of the proof from [3].

Lemma 15

Let p be a modular point of some multiplicity m in a nonpencil real supersolvable line arrangement $\mathcal {L}$ containing s lines. Then every line in $\mathcal {L}$ not containing p contains a crossing point of multiplicity 2.

Proof

At left in Fig. 4, we see the m lines ($L_1,\dots ,L_m$ enumerated from bottom to top) through p and some line L not through p. To these, we have added a dotted line below $L_1$ and a dashed line above $L_m$. After a change of coordinates, the dotted line becomes $y=0$, the dashed line becomes the line $z=0$ at infinity, L becomes $x=0$ and p becomes the point (1, 0, 0). Thus, in the affine plane as shown at right in Fig. 4, the lines $L_i$ become horizontal lines and L becomes vertical.

Let $p_i$ be the point of intersection of $L_i$ with L. Since p is modular, every line in $\mathcal {L}$ (other than L itself) must intersect L at one of the points $p_i$. We want to show that one of the points $p_i$ has multiplicity 2. Suppose by way of contradiction that the multiplicity of $p_i$ is more than 2 for each i. Thus, we can pick an additional line $H_i$ in $\mathcal {L}$ through $p_i$ for each i. The slope of $H_i$ in the affine picture at right in Fig. 4 is defined and not 0.

For each $i\ne$, the intersection of $H_i$ and $H_j$ must be on one of the lines $L_k$, since p is modular. If the slopes of $H_1$ and $H_m$ have the same sign, it is easy to see that they intersect either above $L_m$ (if the slopes are both positive and $H_1$ has the larger slope, or if the slopes are both negative and $H_1$ has the more negative slope) or below $L_1$ (if the slopes are both positive and $H_m$ has the larger slope, or if the slopes are both negative and $H_m$ has the more negative slope).

Thus, in order for p to be modular, $H_1$ and $H_m$ must have slopes of opposite sign. This means as you go from $H_1$ to $H_2$ and on to $H_m$, there is a least i such that $H_i$ and $H_{i+1}$ have slopes of opposite sign. But this means that $H_i$ and $H_{i+1}$ intersect between $L_i$ and $L_{i+1}$, and hence, that the point of intersection is not on any of the horizontal lines $L_k$, contradicting modularity of p. Thus, at least one of the points $p_i$ must have multiplicity 2. (For example, we could have $p_m$ have multiplicity 2 so there would be no $H_m$, and $H_1,\dots ,H_{m_1}$ could all meet at a point of $L_m$.) $\square$

Fig. 4

At left, a modular point p of multiplicity m in a real supersolvable line arrangement $\mathcal {L}$ and a line L in $\mathcal {L}=\{L_1,\dots ,L_m\}$ not through p, and at right an affine version of the same arrangement after an appropriate change of coordinates moving the dashed line to infinity

We now state and give a simplified proof of a slightly strengthened version of [3, Theorem 2.4].

Theorem 16

Let $\mathcal {L}$ be a real nonpencil supersolvable line arrangement containing s lines. Let p be any modular point of $\mathcal {L}$, and let m be the multiplicity of p. Then $t_2 \ge \max \{s-m,m\}\ge s/2$.

Proof

By Lemma 15, each of the $s-m$ lines in $\mathcal {L}$ not through p contains a point of multiplicity 2. These points are all distinct since if two different lines not through p shared a point of multiplicity 2, no other lines in $\mathcal {L}$ could contain that point; hence, no line through p could contain the point, contradicting modularity of p. Thus, $t_2\ge s-m$. On the other hand, by Inequality (2.3) we have $t_2\ge 3 + (m-3)t_m\ge 3+(m-3)=m$. $\square$

The preceding result prompts the following question:

Question 17

Does every nonpencil supersolvable complex line arrangement of s lines with a modular point of multiplicity m satisfy $t_2 \ge \max \{s-m,m\}$?

Although Conjecture 12 is now known to be true [1], it may be of interest to see how a special case can be obtained using the above methods.

Theorem 18

Let $\mathcal {L}=\{L_1,\ldots ,L_s\}$ be a nontrivial complex line arrangement (i.e., not a pencil or near pencil). Assume that every crossing point of $\mathcal {L}$ has multiplicity equal to 3 or 4. Then the line arrangement $\mathcal {L}$ is not supersolvable.

Proof

Since $\mathcal {L}$ is not a pencil or a near pencil by hypothesis, we can apply Inequality (2.2). In our case, it takes the form: $\frac{3}{4}t_3\ge s$.

By (2.1), we have $s(s-1) = 6t_3+12t_4$.

Suppose that $\mathcal {L}$ is supersolvable. Then, by (2.4), we have $t_2\ge 2n-m(s-m)-2$, where n is the total number of crossings and m is the maximum k such that $t_k>0$. In our case, this gives $0 \ge 2(t_3+t_4) -m(s-m)-2$, where $m = 3$ or $m=4$.

First we assume $m=4$ and obtain a contradiction. We have $2(s-4) +1 \ge t_3+t_4$. This implies $12(s-4) +6 \ge 6(t_3+t_4) \ge 8s+6t_4$. The last inequality follows from the Hirzebruch inequality. So we get $6t_4 + 12(s-4)+6 \ge 6t_3+12t_4 = s(s-1)$, where the last equality follows from (2.1).

This, in turn, gives $12(s-4) +6 \ge 6t_4+8s \ge s(s-1)-12(s-4)-6+8s$. Looking at the first and third terms in this and rearranging terms, we get $s^2-17s+84 \le 0$. But since this quadratic in s has positive leading coefficient and negative discriminant, $s^2-17s+84 > 0$ for every s, giving us the desired contradiction.

The calculation is similar if $m=3$. By (2.4), we get $3(s-3)+2 \ge 2t_3$. Using the Hirzebruch inequality (2.2), we get $9(s-3)+6 \ge 6t_3 \ge 8s$. This forces $s\ge 21$. On the other hand, $s(s-1) = 6t_3$ by (2.1). Hence, we obtain $9(s-3)+6 \ge 6t_3 = s(s-1)$, or equivalently, $(s-3)(s-7) \le 0$. So $3 \le s \le 7$. This is not possible. $\square$

Example 19

We do not know many nontrivial examples of complex line arrangements where every crossing point has multiplicity 3 or 4. We get two examples by taking the lines defined by the linear factors of $(x^n-y^n)(x^n-z^n)(y^n-z^n)$ for $n=3$ and $n=4$. The only other example we know is the one due to Klein [13], having 21 lines with $t_k=0$ except for $t_3=28$ and $t_4=21$.

5 Applications to unexpectedness

One of the most interesting applications of line arrangements in $\mathbb {P}^2$ is to finding unexpected curves. More specifically, given a line arrangement in $\mathbb {P}^2$ one considers the dual arrangement of points. The question then is whether these points admit an unexpected curve. For more details, see [6].

The existence of unexpected curves depends on some properties of the line arrangement. If the arrangement is supersolvable, then [7, Theorem 3.17] proves that there is an unexpected curve through the dual points if and only if $s > 2m$, where s is the number of lines and m is the maximum multiplicity of a crossing point. We now use this characterization to determine which supersolvable arrangements in the classification of Section 3 admit unexpected curves.

5.1 Real line arrangements admitting unexpected curves

First, let us consider a real supersolvable line arrangement $\mathcal {L}$.

If $\mathcal {L}$ has exactly one modular point, then the only arrangement we know which satisfies the condition $s>2m$ is given by considering a regular n-gon for even n and adding the line at infinity. For more details, see [7, Theorem 3.15].

If $\mathcal {L}$ has exactly two modular points, then the only arrangement which admits an unexpected curve is given by the following. Let $m\ge 6$ be even and consider an arrangement of m horizontal and m vertical lines, along with the line at infinity. This is supersolvable with the two modular points of multiplicity $m+1$ at infinity where the horizontal and vertical lines meet the line at infinity. Since there are only $s = 2m+1$ lines, this arrangement does not admit an unexpected curve. But we can add the two diagonals (as in Fig. 3, which shows the case of $m=4$, but in that case there are three modular points) to this arrangement without changing the maximum multiplicity while preserving supersolvability. Now the condition $s=2m+3 > 2(m+1)$ is satisfied, and hence, the new arrangement admits an unexpected curve. This arrangement is a special type of tic-tac-toe arrangement described in [7, Theorem 3.19]. The multiplicities of the two modular points (or three when $m=4$) in this tic-tac-toe arrangement are equal. There are no other supersolvable arrangements with exactly two modular points which admit unexpected curves.

The only other real supersolvable line arrangement admitting an unexpected curve is the Fermat arrangement for $n=2$ with three coordinate axes added. More precisely, this arrangement is defined by $xyz(x^2-y^2)(x^2-z^2)(y^2-z^2)=0$. This has 9 lines and three modular points of multiplicity 4 each. (It is displayed in Fig. 3.)

In summary, except for possibly more supersolvable arrangements with a unique modular point, the only real supersolvable line arrangements which admit an expected curve are listed above. We ask the following question.

Question 20

Are there any other real supersolvable line arrangements (other than the one coming from a regular n-gon) with exactly one modular point whose dual points admit an unexpected curve?

5.2 Complex line arrangements admitting unexpected curves

We now consider complex line arrangements. The only examples known to us of supersolvable arrangements which admit unexpected curves are obtained by adding two or three coordinate axes to the Fermat arrangement $\mathcal {F}_n$. In other words, we are considering the complex line arrangement given by $xy(x^n-y^n)(x^n-z^n)(y^n-z^n)$, or $xyz(x^n-y^n)(x^n-z^n)(y^n-z^n)=0$.

This has $s=3n+\epsilon$ lines, where $\epsilon =2$ or 3 and maximum multiplicity $m=n+2$. Hence, the condition $s>2m$ is satisfied for $\varepsilon =2, n\ge 3$ or $\varepsilon =3, n\ge 2$. In the first case, there is a unique modular point, and in the second case, there are three modular points.

We end with the following question.

Question 21

Are there any other complex supersolvable line arrangements (different from the arrangements coming from the Fermat arrangement described above) whose dual points admit an unexpected curve?