Parametric analysis of a sliding-mode controller to suppress drill-string stick-slip vibration

Abstract

Despite a significant research effort to understand and mitigate stick-slip in drill-strings, this problem yet to be solved. In this work, a comprehensive parametric robustness analysis of the sliding mode controller has hitherto been performed. First, a model verification and extensive parametric analysis of the open-loop model is presented. This is followed by a detailed parametric analysis of the sliding-mode controller based closed-loop system for two cases, (i) an ideal actuator with no delay or constraint and (ii) a realistic actuator with delay or/and constraint. It is shown that though the proposed controller works robustly across a wide range of parameters, in the absence of delay, it fails in the presence of a delay, thereby limiting its practical application. Experimental results are included to support these claims. This work underlines the importance of including the inherent system characteristics during the control design process. Furthermore, the parametric analysis presented here is aimed to act as a blue-print for testing the efficacy of relevant control schemes to be proposed in the future.

1 Introduction

Stick-slip vibration are characterized by phases in which a drill-bit comes to a complete standstill (stick) and phases in which a drill-bit rotates with much larger than nominal angular velocity (slip). This type of vibration often results in excessive bit wear, and is also detrimental for expensive downhole tools of a Bottom Hole Assembly (BHA) [1]. The first rigorous analysis of the stick-slip phenomena was reported in [2]. Since then, to understand this highly nonlinear phenomena, several drill-string models have been proposed in the literature. An overview of these models can be found in [3,4,5]. The key difference in the proposed lumped mass models is the number of degrees-of-freedom (DOF) used to establish a drill-string dynamical model, which vary from 1-DOF pendulum-type to infinite-dimensional described by partial differential equation models. The severity of stick-slip vibration has also been quantified to clearly gauge the magnitude of this problem [6,7,8,9]. As stick-slip vibration is in general detrimental to the structural health of drill-string components as well as to the bore hole stability and Rate of Penetration (ROP), devising strategies to eliminate this torsional vibration has been a key research focus for several decades. As a result, controllers for drilling systems that are capable of maintaining drill-string rotation at a constant angular velocity and the mitigation of torsional (stick-slip) vibration are of huge interest. Due to their simplicity, 1 or 2-DOF pendulum-type models are ideal for controller design [10].

Though controllers for eliminating stick-slip vibration are common in the industry [11], increasingly expanding operating envelopes and the drive for deeper and inclined wells imposes significantly stringent demands that deem the existing controllers ineffective. One of the main reasons for this is the uncertainty in the bit-rock interactions [12, 13]. As such, several bit-rock interaction models have also been proposed, [14,15,16]. With regards to the existing work aiming at understanding of drill-string dynamics [17], bit-rock interactions [18, 19] and quantification of stick-slip vibration, the current research thrust is focused on developing effective control strategies in order to minimize and ideally eliminate stick-slip vibration in drill-strings.

A detailed literature review of the control development to mitigate stick-slip problems in drill-strings can be found in [20]. Some of the more recent and noteworthy approaches include the bit velocity and torque independent stick-slip compensator [21], based on skewed-$\mu$ DK-iteration [22, 23], axial and torsional feedback controllers [24], robust proportional-derivative controllers that maintain constant drill-bit velocity [25], employing different PD-control strategies [26], a Kalman filter based full-state feedback controllers [27], adaptive control in autonomous rotary steerable drilling [28], time-delayed feedback control [29], observer and reference governor based control strategy [30], pole placement technique based on the numerical optimization method [31], a series of cascade sliding hyperplanes [32], linear quadratic regulator [33], and an observer-based output feedback control system [34]. Recently, few attempts have been made by researchers to compare different control methods. Authors in [35] evaluate how three different top-drive feedback controllers influence the occurrence of a stick-slip limit cycle in a rotating drill-string, namely, the industry standard stiff, high-gain controller, SoftTorque, and ZTorque. They have provided a map for each controller indicating the existence and amplitude of oscillations, parametrized in the key friction parameters.

Due to several desirable qualities such as robustness against unpredicted dynamics, model inaccuracies, significant disturbance rejection, broad scope of parametric tuning which includes controlling the Weight On Bit (WOB) as well as having the knowledge of the bit velocity and a broad control bandwidth, sliding-mode controllers have shown a great promise in mitigating stick-slip issues. As such, they are some of the most popular control schemes found in literature to address this particular problem, [36, 37]. A recently proposed sliding-mode control scheme has shown to have effectively eliminated stick-slip vibration both in theory, [38] and in practice, [10]. It should be noted that all these control designs deliver improved stick-slip suppression in the absence of inherent system delay. However, this is not realistic assumption and always there is a delay either on top motor in following the control signal or/and acquired data from the downhole sensors.

In this paper, a recently proposed and experimentally validated sliding-mode controller [10], is used as a candidate to demonstrate the insights offered by the full parametric robustness analysis. The paper is organized as follows: next section describes the drill-string rig that was employed to conduct the supporting experiments included in this paper. It also details the system model, present parameter identification and the model validation procedure adopted herewith. The numerically simulated, parametric analysis results of the open-loop drill-string under changes in WOB, top torque and stiffness are presented in the next section. This is followed by a similar parametric analysis of the drill-string controlled by the sliding-mode controller reported in [10]. Both these sections report analysis without considering the inherent actuator delay encountered in the experimental rig. The effect of this delay on the controlled system is presented in the next section, which presents numerical results for two cases viz: (1) input torque is unconstrained and (2) input torque is constrained. These numerical results are validated via experiments. The last section concludes the paper highlighting key lessons learned.

2 Drill-string rig and system modeling

The schematic diagram of the drill-string assembly employed throughout this work is shown in Fig. 1. This vertical drill-string assembly is housed in the Drill-string Laboratory at the Centre for Applied Dynamics Research (CADR), University of Aberdeen, UK [10, 18]. Details of the drill-string assembly and its derived mathematical model are described in the consequent subsections.

2.1 Rig description

A number of scaled drill-string experimental rigs have been reported in literature [3, 39,40,41]. Most of these drill-string assemblies typically consist of a few meters of slender steel strings that are connected to a motor that drives the drill-string through a specimen-to-be-drilled placed on a rotary table. Also, in most of these assemblies, a BHA is typically a set of discs that are the main source of the WOB. Shakers and brakers are typically employed to gauge bit-rock interaction. Unlike most assemblies reported in literature that are capable of consistently producing one or two types of vibration, the drill-string assembly shown in Fig. 1 has the capability of replicating all major types of vibration encountered in a conventional drill-string, namely, stick-slip, bit-bounce and whirling. Another significant improvement is the actual drilling process. Where most reported rigs employ a brake system, this experimental rig performs real drilling of rock samples and uses commercial PDC bits. The simulation and experimental results presented herewith are based on this drill-string assembly.

Fig. 1

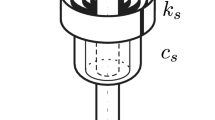
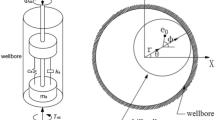
a The 2-DOF lumped-parameter model of the drill-string which shows the upper discs and lower discs and the respective components they represent. b A schematic of the vertical drill-string assembly at the University of Aberdeen explains the principal components viz: actuators (drive motor), BHA, drill-bit, rock sample, sensors attached to record its physical parameters (four component load cell, eddy current probes, LVDT and the top and bottom encoders) and data logging provisions

The main aim of this drill-string assembly is to realistically replicate the different dynamic behaviour exhibited by typical drill-strings. Moreover, this assembly also acts as a test bench to implement, test and validate mathematical models as well as applicable control schemes. The assembly is designed to work with both rigid and flexible shafts. The assembly does not however, replicate the down-hole high-pressure high-temperature conditions, something that is inherently difficult to mimic in a safe laboratory setting. The rigid shaft is used to study the bit-rock interactions, a resulting model for which has been reported in [10, 18]. The flexible shaft setup is used to simulate all the dynamic phenomena including bit bounce, stick-slip and whirling [42]. The rig input torque is powered by a 3-phase AC motor, having an angular velocity range between 0.5 to 1370 rpm, connected to the gearing system. The rotary moment that is produced is transmitted to the bit through the drill-pipe and subsequently to the BHA. The angular velocity of the top as well as the drill-bit are measured using two different encoders, placed on top of the drill-pipe and attached to the BHA. The load-cell which is placed under the rock sample monitors vertical and horizontal forces as well as torque passed from the drill-bit to the rock. All voltage signals from the experimental rig are being sent to the data acquisition card controlled by a LabVIEW graphical interface that is used to monitor the real-time responses of the system. A linear variable differential transformer (LVDT) or a laser sensor depending on the required accuracy is employed to determine the ROP of the bit. An actual field drill-string can be several kilometres long, therefore the rig is designed to accommodate flexible shafts consisting of many layers of thin wires to mimic the mechanical properties of long drill-strings.

2.2 Physical and mathematical model

To ensure that the adopted drill-string model is accurate, adequate and not overcomplicated, a lumped-parameter 2-DOF model is chosen. Several papers have adopted a similar 2-DOF model resulting in meaningful analysis and results, [14, 43]. This drilling system is driven by an electric motor and can be sectioned into two parts viz: (i) the top drive system (rotary table) modeled by the upper disc and (ii) the drilling pipe to the BHA and the drill bit modeled by the lower disc. A simple schematic of this model is shown in Fig. 1a, where the upper disc comprises U is the motor-generated input torque that drives the system, $C_r$ is the viscous damping coefficient of the top drive, $\phi _r$ is the angular position of the top drive and $J_r$ is inertia of the top drive. The drill pipe connects the top drive assembly to the BHA, where C is the torsional damping and K is the torsional stiffness. At the lower disc we have $T_b$, the torque of friction that models the bit-rock interaction, $J_b$, the inertia of the BHA and $\phi _b$, the angular position of the BHA. Following the identification experiments presented in [43], stiffness and damping are approximated to be linear, within the parameter range adopted for the numerical studies. The equation of motion that shows the entire system behaviour is written as:

Fig. 2

a The black line is the time history of the rotary table angular velocity $\dot{\phi }_r$. The red line is the time history of the drill-bit angular velocity $\dot{\phi }_b$. It can be seen that the drill-bit angular velocity reaches 0 - stick phase and then oscillates to 5.2 rad/s - considerably more than the desired angular velocity of 2.6 rad/s (rotary table nominal velocity). b Phase-portrait of the drill-bit (displacement vs velocity) clearly showing the stick-slip phenomena. (Color figure online)

$$\begin{aligned} {\mathop {\phi }\limits ^{..}}_r&= \frac{U}{J_r} - \frac{C_r + C}{J_r}{\mathop {\phi }\limits ^{.}}_r + \frac{C}{J_r}{\mathop {\phi }\limits ^{.}}_b - \frac{K}{J_r}(\phi _r - \phi _b), \end{aligned}$$

(1)

$$\begin{aligned} {\mathop {\phi }\limits ^{..}}_b&= \frac{C}{J_b}{\mathop {\phi }\limits ^{.}}_r -\frac{ C}{J_b}{\mathop {\phi }\limits ^{.}}_b +\frac{K}{J_b}(\phi _r - \phi _b) - \frac{T_b}{J_b}. \end{aligned}$$

(2)

However, the new state of the system can be initialized as follows for the purpose of the controller design:

$$\begin{aligned} x = {({\mathop {\phi }\limits ^{.}}_r, \phi _r - \phi _b,{\mathop {\phi }\limits ^{.}}_b)}^{T} = {( x_1, x_2, x_3)}^{T}, \end{aligned}$$

(3)

which further simplifies the system equation as:

$$\begin{aligned} {\mathop {x}\limits ^{.}}_1&= \frac{U}{J_r} - \frac{C_r + C}{J_r}x_1 + \frac{C}{J_r}x_3 - \frac{K}{J_r}x_2, \end{aligned}$$

(4)

$$\begin{aligned} {\mathop {x}\limits ^{.}}_2&= x_1 - x_3,\end{aligned}$$

(5)

$$\begin{aligned} {\mathop {x}\limits ^{.}}_3&= \frac{C}{J_b}x_1 - \frac{C}{J_b}x_3 + \frac{K}{J_b}x_2 - \frac{T_b}{J_b}. \end{aligned}$$

(6)

2.3 Bit-rock interactions

To capture the interactions between the drill-bit and the formation, different approaches have been taken by researchers such as several variations of Karnopp’s model or frictional and cutting forces at the bit-rock interface considering individual cutters which has been summarised in [44]. The approach we have used here for the control purpose is a common method, which has been reported in literature [15, 38, 45, 46]. The overall bit-rock interactions can be encapsulated into three distinct phases, namely (i) the stick phase in which a drill-bit is stuck with the rock and is not rotating, (ii) the stick-to-slip phase where a drill-bit has accumulated enough energy to just overcome the stiction and begin to slip, and (iii) the slip phase where a drill-bit rotates.

The stick phase terminates when the reaction torque reaches its peak value and therefore, the system is locked between phases (ii) and (iii). Similarly, when the drill bit starts to rotate the system assumes the slip phase. When ${x}_{3} = 0$, the dry friction is approximated by combining a zero band velocity introduced in [47]. This is as follows:

$$\begin{aligned} T_{b} = {\left\{ \begin{array}{ll} \tau _{r}, &{} \text {if}~|{x}_{3}|< \zeta \quad \text {and}\quad |\tau _{r}| \le \tau _{s},\\ \tau _{s}\text {sgn}(\tau _{r}), &{} \text {if}~|{x}_{3}| < \zeta \quad \text {and} \quad |\tau _{r}|> \tau _{s},\\ \mu _{b}R_{b}W_{ob}\text {sgn}({x}_{3}), &{} \text {if}~|{x}_{3}| > \zeta ,\\ \end{array}\right. } \end{aligned}$$

(7)

where the frictional torque during the bit-rock interaction can be formulated as ${\tau }_r=C ({x}_{1}- {x}_{3}) + K ({x}_{2})$ is the reaction torque, ${\tau }_s={\mu }_{sb} R_b W_{ob}$ is the friction torque, ${\mu }_{sb}$ is the static friction coefficient, ${W}_{ob}$ is the WOB, $R_b$ is the drill-bit radius. $J_r$, $J_b$, C, K, $C_{r}$ and $\zeta$ are unchanged system parameters as reported in [10, 43]. Parameters $\mu _{sb}$, $\mu _{cb}$, $R_{b}$, $\gamma _b$ and $\nu _f$ were identified via an experimental procedure detailed in the following subsection.

2.4 Model calibration via experiments

To ensure that simulations carried out using the adopted model agree with the experiments to be performed later, a careful estimation of the physical system parameters was undertaken. This was based on a set of Torque on Bit (TOB)-bit rotational velocity response curves of the system. To obtain the curves, the ${W}_{ob}$ was varied using a number of steel-plates designed and adapted into the experimental rig specifically for this function. Numerical simulations as well as the experiments were carried out for 9 different ${W}_{ob}$ values: [0.85, 1.03, 1.10, 1.22, 1.43, 1.57, 1.88, 2.06, 2.19] kN and 11 different rotational velocities: [0.12, 0.37, 0.50, 1.00, 1.51, 2.64, 3.52, 4.15, 4.92, 5.40, 5.86] rad/s to result in the curves depicted in Fig. 3. The formula for the frictional torque is given by:

$$\begin{aligned} TOB=\mu _{cb} + (\mu _{sb} - \mu _{cb}) e^{{-\gamma }_{b}|{x}_{3}|/{\nu }_{f}}, \end{aligned}$$

(8)

where the dry friction coefficient $\mu _{b} = \mu _{cb} + (\mu _{sb} - \mu _{cb}) e^{{-\gamma }_{b}|{x}_{3}|/{\nu }_{f}}$, $\mu _{cb}$ represents the Coulomb friction coefficient and $0< {\gamma }_{b} < 1$. These relationships are used to compute $\mu _{sb}$, $\mu _{cb}$, $R_{b}$, $\gamma _b$ and $\nu _f$ for each ${W}_{ob}$ curve and are given in below table.

Fig. 3

Numerical TOB-bit rotational velocity response curves (solid lines) for different values of WOB being fitted to the experimental data recorded (dots) for 11 rotational velocities per WOB with drill-string physical parameters used for each of the $W_{ob}$

From these curves, it was seen that the shape of curves for ${W}_{ob}$ value of 1.10 kN, 1.43 kN and 1.88 kN was similar. Thus, an average of the relevant values was obtained from these curves and used as $\mu _{sb}$, $\mu _{cb}$, $R_{b}$, $\gamma _b$ $\nu _f$. The full resulting set of system parameters is given in Table 1. These parameters are used in the simulations presented in this paper.

Table 1 The physical parameters of the drill-string that accurately capture the dynamics of interest

Figure 2b depicts the results of the model simulation for the identified set of parameters. As shown the model effectively replicates the expected behavior of the drill-string. It can be seen from the figure that due to dry friction, the drill-bit gets stuck at 0 rad/s velocity during the sticking phase. At this moment the driving TOB is greater than the torque of friction, the drill-bit gets loosened and starts to rotate speedily with a velocity twice the velocity of the rotary table. This condition is a transition from the stick-to-slip to the slip phase. The drill-bit velocity reduces after a while and then gets stuck again. This phenomenon generates a torsional wave which travels up the drill-string from the drill-bit and oscillates the rotary table accordingly. The drill-bit keeps oscillating around the desired angular velocity but never reaches it, forming a limit cycle.

The next section presents a numerical parametric analysis of the drill-string model. This will provide key insights into the overall behaviour of the drill-string within the scope of stick-slip vibration.

3 Parametric study of the open-loop (uncontrolled) system

In this section the model presented in the Sect. 2.2 has been used to perform an extensive parametric analysis of the open-loop model. For this purpose, three parameters have been identified as the key parameters that will undergo significant variation during the drilling process, namely: (i) WOB - $W_{ob}$ in N, (ii) Input torque - U in Nm, and (iii) Drill-string stiffness -K in Nm/rad. To ensure completeness and relevance of this analysis, sufficiently wide parameter ranges have been adopted. Consequently,

• $W_{ob}$ - [1000, 9200] N

• U - [0, 60] Nm

• K - [0, 25] Nm/rad

Furthermore, to ensure that the analysis is performed over a realistic range of desired rotational velocities, a range of [0, 6] rad/s was selected. The bifurcation diagrams and frequency plots, have been calculated using forward and backward methods, and with zero initial conditions to ensure capturing all possible stable solutions. In addition, 3D basins of attraction have been calculated for selected points in the bifurcation diagrams to capture the co-existence of attractors.

Change in WOB. WOB is a key control parameter used in regulating the ROP of any drilling system. As such, it plays a vital role in the manifestation of stick-slip vibration. Figure 4 presents (a) projection of maximum velocity and (b) vibration frequency of drill-bit when WOB increases from 1000 to 9200 N. Colour red, blue and black mark stick-slip, constant velocity drilling and a stuck drill-bit, respectively. Panel (a) depicts the WOB against the maximum of bit-velocity $max(\dot{\phi }_b)$. It shows that the drill-bit experiences steady drilling for WOB $\le$ 1200 N, from 1200 $\le$ WOB $\le$ 2600 N the drill-bit experiences regions of steady drilling as well as stick-slip, from 2600 $\le$ WOB $\le$ 9000 N the drill-bit experiences stick-slip but no regions of steady drilling and for WOB > 9000 N the drill-bit is stuck. Panel (b) depicts the frequency of the stick-slip vibration of the drill-bit at each WOB. As seen clearly, there is a clear region of between 1200–2600 N, where the drill-bit experiences both steady drilling and stick-slip. The frequency of these stick-slip vibration reduces as WOB is increased and beyond 9000 N, the drill-bit is stuck shown by the frequency of vibration going down to 0 Hz. Basins of attraction depicted in (c)–(f) show that as WOB increases, the drill-string steadily undergoes more and more stick-slip until at the higher limit of 9 kN, where the drill-bit does not rotate and is stuck ($\dot{\phi }_b=0$).

Fig. 4

a Projection of maximum velocity and b vibration frequency of drill-bit when WOB increases from 1000 N to 9200 N. Colour red, blue and black mark stick-slip, constant velocity drilling and a stuck drill-bit, respectively. Panel a depicts the WOB against the maximum of bit-velocity $max(\dot{\phi }_b)$. Panel b presents the frequency of the stick-slip vibration experienced by the drill-bit at each WOB. Basins of attraction depicted in c–f show that as WOB is increases, the drill-string motion steadily experiences more and more stick-slip until at the higher limit of 9 kN, where the drill-bit does not rotate and is stuck ($\dot{\phi }_b=0$)

Change in top torque. The input torque is being a key factor in controlling the dynamics of a drilling system. Intuitively, a low input torque will result in no drilling as some initial torque is required for the drill-bit to overcome the frictional forces arising from the bit-rock interactions. High input torques might result in constant velocity drilling, but this might be limited by physical factors such as structural properties of the drill-string and rating of the top-drive system. Figure 5 depicts (a) projection of maximum velocity and (b) vibration frequency of drill-bit when U increases from 0 to 60 Nm. Panel (a) shows that for input torque less than about 8 Nm, the drill bit is stuck. Beyond 8 Nm, the drill-bit experiences stick-slip vibration with increasing amplitudes of the drill-bit velocity. From about 35 Nm and above, there are regions of constant velocity drilling in addition to the stick-slip vibration and finally, beyond an input torque of about 58 Nm, the stick-slip vibration vanishes and a constant velocity drilling is established. Panel (b) shows that as the input torque is increased, the frequency of stick-slip vibrations, once established, undergoes very little change. 3d basins of attraction depicted in (c)–(f) show that as the input torque is increased, the drill-bit steadily translates from a stuck state, 5 Nm in (c), to a pure stick-slip state, 15 Nm in (d). Further increase in the input torque results in the drill-bit experiencing regions of stick-slip as well as constant velocity drilling as in (e). Finally, with an input torque of 60 Nm, the drill-bit experiences constant velocity drilling for all desired rotational velocities between 0 - 6 rad/s, as shown in (f).

Fig. 5

a Projection of maximum velocity and b vibration frequency of drill-bit when U increases from 0 N to 60 Nm. Colour red, blue and black mark stick-slip, constant velocity drilling and a stuck drill-bit, respectively. Panel a shows the input torque U against the maximum of bit-velocity $max(\dot{\phi }_b)$. Panel b indicates that as the input torque is increased, the frequency of stick-slip vibrations, once established, undergoes very little change. 3-D basins of attraction depicted in c–f show that as the input torque is increased, the drill-bit steadily translates from a stuck state to a pure stick-slip state. (Color figure online)

Change in drill-string stiffness. The drill-string stiffness is another key parameter that governs the dynamics of the system. As the drill-string drills deeper into the surface, its stiffness has the potential to change quite significantly. As a consequence, understanding how the stiffness affects the drill-string dynamics within the scope of stick-slip vibration is important. Figure 6 plots (a) projection of maximum velocity and (b) vibration frequency of drill-bit when k is varied from 1 to 25 Nm/rad. Red indicates stick-slip and blue indicates constant velocity drilling. Panel (a) shows that the drill-bit experiences stick-slip oscillations of virtually a similar magnitude over the entire range of stiffness coefficient considered in this analysis. Panel (b) indicates that with the increase in stiffness, the frequency of the established stick-slip vibration increases steadily. As seen, for all values of stiffness considered in 3D basins of attraction depicted in (c)–(f), the drill-bit experiences constant velocity drilling as well as stick-slip vibration for some values of desired velocity.

Fig. 6

a Projection of maximum velocity and b vibration frequency of drill-bit when k is varied from 1 N to 25 Nm/rad. Colour red and blue mark stick-slip and constant velocity drilling, respectively. As seen, for all values of stiffness considered in 3-D basins of attraction depicted in c–f, the drill-bit experiences constant velocity drilling as well as stick-slip vibrations for some values of desired velocity. (Color figure online)

With these insights, the parametric analysis of the closed-loop system can now be initiated. The next section briefly introduces the sliding-mode controller detailed in [10] and gives the expression for the control input. Parametric analysis in the absence of delay is first presented followed by a detailed settling time analysis.

4 Parametric study of the closed-loop (controlled) system

In this section, we evaluate the efficiency of the the sliding-mode controller presented in [10]. Starting from the ideal system dynamics and accounting for the uncertainty in model parameters, this controller generates a control input that effectively suppresses stick-slip. Note that this controller accounts for parameter uncertainties and would just need estimated parameters.

Fig. 7

The structure of the suggested sliding mode controller. $\Omega _{d}$ is the desired bit rotational velocity and U is the control input computed by the controller

The control structure is shown in Fig. 7 where the control input U is given by:

$$\begin{aligned} U = U_{eq} + U_{sc}, \end{aligned}$$

(9)

where

$$\begin{aligned} U_{eq}= & {} ({\mathop {C}\limits ^{\wedge }}+{\mathop {C}\limits ^{\wedge }}_{r})x_{1}-Cx_{3} + {\mathop {K}\limits ^{\wedge }}x_{2} - {\mathop {J}\limits ^{\wedge }}_{r}\lambda (x_{1} - \Omega _{d}) \nonumber \\&- {\mathop {J}\limits ^{\wedge }}_{r}\lambda (x_{1} - x_{3}) \end{aligned}$$

(10)

and

$$\begin{aligned} {U}_{sc}= & {} -\frac{M_{c}|{x}_{1} - {x}_{3}|s}{|s| + \delta _1exp(-\delta _2\int |{x}_{1} - {x}_{3}|d_t)} \nonumber \\&-\frac{M_{cr}|{x}_{1}|s}{|s| + \delta _1exp(-\delta _2\int |{x}_{1}|d_t)}\nonumber \\&-\frac{M_{k}|{x}_{2}|s}{|s| + \delta _1exp(-\delta _2\int |{x}_{2}|d_t)}\nonumber \\&-\frac{M_{jr}\lambda |{x}_{1} - \Omega _{d}|s}{|s| + \delta _1exp(-\delta _2\int \lambda |{x}_{1} - \Omega _{d}|d_t)}\nonumber \\&-\frac{M_{jr}\lambda |{x}_{1} - {x}_{3}|s}{|s| + \delta _1exp(-\delta _2\int \lambda |{x}_{1} - {x}_{3}|d_t)}-\kappa s, \end{aligned}$$

(11)

and

$$\begin{aligned} {s=(x_1-\Omega _d)+\lambda \int (x_1-\Omega _d)d_t+\lambda \int (x_1-x_3)d_t.} \end{aligned}$$

(12)

Here, ${^\wedge }$ denotes an estimated model parameter and [$\delta _{1}, \delta _{2}, \lambda$] are small positive constants that can be chosen as required. Upper bounds for the estimated parameters used in the proposed sliding-mode controller are given in Table 2.

Table 2 Upper bounds and estimated parameters for the proposed sliding-mode controller

4.1 Closed-loop performance in the absence of delay

Figure 8 shows the time histories of the angular velocity of both the rotary table and drill-bit when the control input (9) is applied to result in a desired velocity of ${\omega }_{d} =$ 2.6 rad/s. The trajectory of the system reaches and stays on the manifold $s =$ 0 asymptotically. The system is in the open-loop state for the first 40 s and as evident from the plots, it experiences significant stick-slip vibration. At 40 s, the controller is engaged and as seen from the plots, the controller effectively eliminates the stick-slip vibration within 20 s of engagement.

Fig. 8

a Time history of the angular velocity of the rotary table and drill-bit without and with the controller engagement. The desired velocity is ${\omega }_{d} =$ 2.6 rad/s. The red trace is for the drill-bit while the black trace is for the top-drive (rotary table). b Phase portrait for bit-velocity and bit-displacement is plotted to show how the stick-slip vibration established in open-loop are eliminated by the implemented sliding-mode controller. c The input torque signal is plotted to show that the control effort is within reasonable practical bounds. (Color figure online)

Fig. 9

a Computed response of the system before the controller is switched on. This response shows stick-slip for all parameter combinations. b Computed response of the system when the controller is engaged. This response shows regions of stick-slip vibration and of constant velocity drilling. Red denotes stick-slip vibration and Blue denotes constant velocity drilling. (Color figure online)

The stiffness K and its estimation used in the sliding-mode design ${\mathop {K}\limits ^{\wedge }}$ are varied against the desired velocity ${\omega }_{d}$, where:

$$\begin{aligned} |{\mathop {K}\limits ^{\wedge }} - K| \le M_{k}. \end{aligned}$$

(13)

As shown in Fig. 9, the controller enables constant velocity drilling for the majority combination of parameters within the range of interest. To gauge how effectively the controller eliminates stick-slip vibration and establishes constant velocity drilling, a thorough settling-time analysis is performed.

4.1.1 Settling time analysis

Stiffness is the system parameter and cannot be changed arbitrarily, but the controller parameter ${\mathop {K}\limits ^{\wedge }}$ (estimated stiffness) can be regulated. It is therefore useful, to analyze and observe the response of different estimated stiffness values to changes in ${\omega }_{d}$ against the settling time ${T}_{s}$. The settling time ${T}_{s}$ estimated in this paper is the time it takes the system to reach and stay within $\pm 5\%$ tolerance of the desired (steady-state) value. In Fig. 10, it can be observed that the shortest settling times for all fixed stiffness values (K) are achieved when the estimated stiffness ${\mathop {K}\limits ^{\wedge }}$ is 2.5 Nm/rad. It can also be observed that higher ${\omega }_{d}$ produces lower settling time for all parameter combinations.

Fig. 10

A set of simulated responses, when ${\omega }_{d}$ is varied against the settling time (${T}_{s}$) for a $K=5\, \text{N}\, \text{m/rad},$ b $K=10\, \text{N}\, \text{m/rad};$ c $K=15\, \text{N}\, \text{m/rad};$ d $K=20\, \text{N}\, \text{m/rad}.$ In these figures black, blue, green, blue and magenta present results for ${\mathop {K}\limits ^{\wedge }}=2.5\, \text{N}\, \text{m/rad},$ ${\mathop {K}\limits ^{\wedge }}=7.5\,\text{N}\, \text{m/rad},$ ${\mathop {K}\limits ^{\wedge }}=12.5\, \text{N}\, \text{m/rad},$ ${\mathop {K}\limits ^{\wedge }}=17.5\,\text{N}\, \text{m/rad},$ and ${\mathop {K}\limits ^{\wedge }}=22.5\,\text{N}\, \text{m/rad},$ respectively. All these results indicate that the system settle faster when the desired velocity increases. (Color figure online)

Note, that these simulations do not take into account the actuator delay present in the system, as revealed from experimental investigations performed in the past, [10, 43]. It is important to mention that this delay as well as other delay components such as those encountered in the sensors and down-hole to surface data transmission, should be considered when designing any realistic control scheme for drilling rigs. As analysis so far in previous sections does not consider this delay, the results can be quite misleading. To clarify this and ensure a full measure of the controller performance, the following section analyzes the impact of the input delay present in the system.

5 Closed-loop performance in the presence of delay

Fig. 11

The structure of the suggested sliding mode controller in presence of the delay. $\Omega _{d}$ is the desired bit rotational velocity and U is the control input computed by the controller

Fig. 12

a Time history of the top-drive (rotary table) angular velocity (black) and the angular velocity of the drill bit (red), before and after the controller being engaged. b Zoomed section of the time history between 95 s to 105 s. c Zoomed section of the un-delayed and delayed control inputs between 95 s to 105 s. d The delayed and un-delayed control inputs to the system. The delayed control input has a lag of 0.4 s. (Color figure online)

In the experimental rig, current from the frequency converter drives the motor after receiving the control torque ${U}_{c}$ sent from the DAQ/Control system (LabView). At the same time, while the frequency converter drives the motor, the converter also produces a signal representing the torque generated by the motor ${U}_{t}$. A resistor converts this into voltage (0–10 V) signal capable of being read by the DAQ/Control system (LabView) that further converts it into an estimated torque ${U}_{e}$ as a percentage of full motor torque capacity. From extensive experiments comparing the motor’s signal output, the controller (${U}_{c}$) and the target (${U}_{t}$), an averaged delay of 0.4 s chosen identified. Furthermore, it was noted that the minimum torque produced by the motor is 22.26 Nm. Therefore, the minimum torque ${U}_{c}$ that can be requested from the frequency converter is zero [43]. To account for this delay, the applied control input signal is shifted by 0.4 s to give: ${U}_{c} (t-0.4)$. The control structure of the system with the delay is shown in Fig. 11.

To confirm the impact of this delay on the controlled system, the same numerical analysis as reported in Fig. 8 was repeated after delaying the control input by an additional 0.4 s. This delay analysis is presented in Fig. 12, where panel (b) shows a zoomed snapshot of the delayed control input compared to the un-delayed one. In Fig. 12a, the system shows stick-slip vibration in open-loop. The controller is engaged after 100 s and it is clear that though the amplitude of the vibration has reduced and the drill-bit velocity does not go to zero (no stick-slip), it does not reach a steady value and instead oscillates at a constant frequency (stable limit cycle). Thus, in the presence of a delay, the controller is not successful in completely eliminating the velocity oscillations and does not result in a constant velocity drilling.

5.1 Constrained and unconstrained inputs

As stated in experimental rig description, only a limited (both upper and lower bounded) torque can be provided to the drill-string once the top-drive is engaged. Similarly, the 3 kW 3-Phase motor used in the experimental rig is capable of supplying an input torque within the range of 22.63–68.46 Nm. Therefore, further analysis will be based on two input conditions:

• constrained input, where control input is between 22.63 Nm and 68.46 Nm,

• unconstrained input with No input constraints.

To be able to quantify and evaluate the sensitivity of the parameter estimation to the system response, a modified Vibration Reduction Factor (VRF) is introduced. This indicates the difference between the amplitudes of the stick-slip vibration seen in the uncontrolled and controlled systems as a percentage of the amplitude seen in the uncontrolled system. The mathematical representation is given by:

$$\begin{aligned} VRF = \dfrac{{A}_{un}-{A}_{c}}{{A}_{un}}~100\%, \end{aligned}$$

(14)

where ${A}_{c}$ is the amplitude of the stick-slip vibration seen in the controlled system and ${A}_{un}$ is the amplitude of the stick-slip vibration seen in the uncontrolled system.

Ideal value for VRF would be 100%, meaning the stick-slip vibration is fully eliminated. Consequently, a positive VRF value less than 100% implies a decrease in vibration of the system response i.e the system response improves. It is also necessary to note that when the VRF value is negative, it implies that the amplitude of the stick-slip vibration manifesting in the controlled system is higher than the amplitude of the stick-slip vibration seen in the uncontrolled one. The VRF analysis is carried out using the nominal system parameters reported at the previous sections except ones which will be explicitly mentioned in this section. Analyzing the response of both the delayed and un-delayed system with constrained control input, in terms of the VRF by varying values of ${\omega }_{d}$ and K but maintaining a fixed ${\mathop {K}\limits ^{\wedge }}$ results in a set of curves plotted in Fig. 13. Figure 14 presents the outcome of this analysis for different fixed estimated stiffnesses. In reference to Equation (13), all chosen control parameters are expected to be within the accepted boundary limit. It is worth noting before going further into the analysis that the nominal values used for specific parameters in the simulations are as follows :

Case 1. Closed-loop performance with and without delay but with constraints.

Analyzing the response of both the delayed and un-delayed system with constrained control input, in terms of the VRF by varying values of ${\omega }_{d}$ and K but maintaining a fixed ${\mathop {K}\limits ^{\wedge }}$ results in a set of curves plotted in Fig. 13. The delayed system responses are plotted on the left panels while their respective un-delayed system responses are plotted on the right panels. As seen clearly from the plots of the un-delayed system responses, the controller is effective in eliminating the stick-slip vibration and attaining a VRF = 100% for any value of stiffness K. On the other hand, for the delayed system, very few parameter combinations (K and ${\mathop {K}\limits ^{\wedge }}$) result in VRF of 100%. Moreover, it is clear that for most cases, the controller is not able to eliminate the stick-slip vibration completely (though it is able to reduce the vibration amplitude) and in some extreme cases, the amplitude of vibration is greater than that observed in the uncontrolled system.

Fig. 13

a–c Computed response of the system with estimated stiffness ${\mathop {K}\limits ^{\wedge }}$ of 2.5, 7.5 and 17.5 Nm/rad, respectively, while the control signal was delayed for 0.4 s and ${\omega }_{d}$ varied against VRF and stiffness changed. d–f Response of the system with their respective same set of parameters but undelayed control signal. All these responses are with constrained input (U) and an upper bound of ${M}_{k}$ of 15

Case 2. Closed-loop performance in the presence of delay but without constrains

Figure 14 shows the VRF plots for the controlled system with delayed and unconstrained control input for four different controller stiffness estimates. It is seen that except for the case where $K=1$ Nm/rad, the controller fails to fully eliminate the stick-slip vibration. In fact, in many cases, the controlled system shows a rapid deterioration of performance that evidently signifies instability.

Fig. 14

a–d Computed response of the system with estimated stiffness ${\mathop {K}\limits ^{\wedge }}$ of 2.5, 7.5, 12.5 and 17.5 Nm/rad, respectively, while the control signal was delayed for 0.4 s and ${\omega }_{d}$ varied against VRF and stiffness changed. All these responses are with unconstrained input (U) and an upper bound of ${M}_{k}$ of 15

To validate the findings of the numerical analysis presented in Fig. 13, a set of experiments were performed. Results of these experiments are reported in the following subsection. As the experimental rig inherently operates with upper and lower bounded control input, the results pertaining to the unconstrained input case (Fig. 14) cannot be practically replicated.

5.2 Experimental validation

As seen from Equation (11), the control gain $\kappa$ is the coefficient of the sliding surface. The parametric analysis presented in the earlier sections was performed under a fixed control gain, $\kappa = 1$. In this section, the effect of change of $\kappa$ on the controller performance (VRF) in presence of actuator delay and control effort constraint is studied experimentally.

In Fig. 15, panels (a), (b), (d) and (e) present the experimentally recorded results while panel (c) plots the numerical simulation results. The experiments are conducted on the experimental rig described previously. In Fig. 15c, the VRF of the controlled system for different system stiffness values (K) is plotted against a change in control gain ($\kappa$). As shown, the change in $\kappa$ has minimal impact on system with higher stiffness ($K\ge 15$ Nm/rad), however, increase of $\kappa$ in all cases decreases the controller efficiency.

The green trace in Fig. 15c (with the nominal value of stiffness; K=10 Nm/rad), depicts the VRFs of the simulated controlled system using the identified model parameters for the experimental rig when $\kappa$ changes. As shown in panels (a)-(b) and (d)-(e) the experimental results are in very close agreement with the numerical results. Here, phase-planes of uncontrolled and controlled system responses are plotted in red and blue respectively for control gains ($\kappa$) of (a) 0.1, (b) 1, (d) 10 and, (e) 100. As expected, the contours in red confirm that the uncontrolled system exhibits stick-slip vibration in all cases. The amplitude of vibration exhibited by the controlled system (plotted in blue) increases when $\kappa$ is increased. This agrees with the numerical simulation results presented in panel (c) (green).

Fig. 15

Experimental results with constrained inputs. Figures show the gain being varied against the VRF with different stiffness values and this was validated experimentally by varying different values of the control gain on stiffness K = 10 Nm/rad: a $\kappa$ = 0.1; b $\kappa$ = 1; d $\kappa$ = 10; e $\kappa$ = 100. (Color figure online)

6 Conclusions

In this paper, we investigated suppression of drill-string torsional vibration while drilling by using a sliding mode controller. As evidenced by the included bifurcation and basins of attraction plots, the work begins by validating the adopted drill-string – bit-rock interaction model via a detailed parametric study over a range of three key drilling parameters namely top torque, Weight-On-Bit and drill-pipe. This was followed by a detailed parametric analysis of the sliding-mode controller’s ability to suppress stick-slip vibration. The controller performance was evaluated in both unconstrained and constrained input conditions. Furthermore, the ideal system (without inherent actuator delay) and the practical system (with an inherent actuator delay of 0.4 s) were analyzed separately.

A modified measure of controller performance called the Vibration Reduction Factor (VRF) was formulated and used to quantify the controller performance. It is shown that the sliding-mode scheme is effective in eliminating the stick-slip vibration in the ideal system (no actuator delay). It is also demonstrated that in presence of actuator delay, the sliding-mode controller goes to instability when the input is unconstrained. However, when the input is constrained, the sliding-mode controller gives a stable performance and effectively eliminates stick-slip vibration within a limited parameter range. This behaviour is predicted by the numerical simulations and is supported by the experimental results, both included in this work.

Future work will focus on extensive experimental studies to expose more detailed nuances of the system’s closed-loop dynamic behaviour, further informing control optimization.