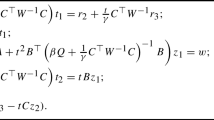Skip to main content
SpringerLink
Log in

Non-conforming Crouzeix-Raviart element approximation for Stekloff eigenvalues in inverse scattering

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

In this paper, we use the non-conforming Crouzeix-Raviart element method to solve a Stekloff eigenvalue problem arising in inverse scattering. The weak formulation corresponding to this problem is non-self-adjoint and indefinite, and its Crouzeix-Raviart element discretization does not meet the condition of the Strang lemma. We use the standard duality technique to prove an extension of the Strang lemma. And we prove the convergence and error estimate of discrete eigenvalues and eigenfunctions using the spectral perturbation theory for compact operators. Finally, we present some numerical examples not only on uniform meshes but also on adaptive refined meshes to show that the Crouzeix-Raviart method is efficient for computing real and complex eigenvalues as expected.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Ainsworth, M., Oden, J.T.: A Posteriori Error Estimates in the Finite Element Analysis. Wiley-Inter science, New York (2011)

    MATH  Google Scholar 

  2. Ainsworth, M.: Robust a posteriori error estimation for nonconforming finite element approximation. SIAM. J. Numer. Anal. 42, 2320–2341 (2005)

    MathSciNet  MATH  Google Scholar 

  3. Alonso, A., Russo, A.D.: Spectral approximation of variationally-posed eigenvalue problems by nonconforming methods. J. Comput. Appl. Math. 223, 177–197 (2009)

    MathSciNet  MATH  Google Scholar 

  4. Andreev, A.B., Todorov, T.D.: Isoparametric finite element approximation of a Steklov eigenvalue problem. IMA. J. Numer. Anal. 24, 309–322 (2004)

    MathSciNet  MATH  Google Scholar 

  5. Armentano, M.G.: The effect of reduced integration in the Steklov eigenvalue problem. Math. Mod. and Numer. Anal. (M2,AN) 38, 27–36 (2004)

    MathSciNet  MATH  Google Scholar 

  6. Armentano, M.G., Padra, C.: A posteriori error estimates for the Steklov eigenvalue problem. Appl. Numer. Math. 58, 593–601 (2008)

    MathSciNet  MATH  Google Scholar 

  7. Armentano, M.G., Duran, R.G.: Asymptotic lower bounds for eigenvalues by nonconforming finit element methods. Electron. Trans. Numer. Anal. 17, 92–101 (2004)

    MATH  Google Scholar 

  8. Babuška, I., Osborn, J.E.: Eigenvalue problems. In: Ciarlet, P.G., Lions, J.L. (eds.) Finite Element Methods (Part I). Handbook of Numerical Analysis, vol. 2, pp 641–787, Elsevier Science Publishers, North-Holand (1991)

  9. Babuška, I., Rheinboldt, W.C.: Error estimates for adaptive finite element computations. SIAM. J. Numer. Anal. 15, 736–754 (1978)

    MathSciNet  MATH  Google Scholar 

  10. Bergman, S., Schiffer, M.: Kernel Functions and Elliptic Differential Equations in Mathematical Physics. Academic Press, New York (1953)

    MATH  Google Scholar 

  11. Bermudez, A., Rodriguez, R., Santamarina, D.: A finite element solution of an added mass formulation for coupled fluid-solid vibrations. Numer. Math. 87, 201–227 (2000)

    MathSciNet  MATH  Google Scholar 

  12. Bernardi, C., Hecht, F.: Error indicators for the mortar finite element discretization of Laplace equation. Math. Comp. 71(240), 1371–1403 (2001)

    MathSciNet  MATH  Google Scholar 

  13. Bi, H., Yang, Y.: A two-grid method of the non-conforming Crouzeix-Raviart element for the Steklov eigenvalue problem. Appl. Math. Comput. 217, 9669–9678 (2011)

    MathSciNet  MATH  Google Scholar 

  14. Boffi, D.: Finite element approximation of eigenvalue problems. Acta Numerica 19, 1–120 (2010)

    MathSciNet  MATH  Google Scholar 

  15. Bramble, J.H., Osborn, J.E.: Approximation of Steklov eigenvalues of non-selfadjoint second order elliptic operators. In: Aziz, A.K. (ed.) Math. Foundations of the Finite Element Method with Applications to PDE, pp. 387–408. Academic, New York (1972)

  16. Brenner, S.C., Sung, L.Y.: Linear finite element methods for planar linear elasticity. Math. Comp. 59, 321–338 (1992)

    MathSciNet  MATH  Google Scholar 

  17. Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, 2nd edn. Springer-Verlag, New York (2002)

    MATH  Google Scholar 

  18. Brenner, S.C., Li, F., Sung, L.: Nonconforming Maxwell eigensolvers. J. Sci. Comput. 40, 51–85 (2009)

    MathSciNet  MATH  Google Scholar 

  19. Bucur, D., Ionescu, I.R.: Asymptotic analysis and scaling of friction parameters. Z. Angew. Math. Phys. (ZAMP) 57, 1042–1056 (2006)

    MathSciNet  MATH  Google Scholar 

  20. Cai, Z., Ye, X., Zhang, S.: Discontinuous Galerkin finite element methods for interface problems: a priori and a posteriori error estimations. SIAM. J. Numer. Anal. 49, 1761–1787 (2011)

    MathSciNet  MATH  Google Scholar 

  21. Cakoni, F., Colton, D., Meng, S., Monk, P.: Stekloff eigenvalues in inverse scattering. SIAM. J. Appl. Math. 76(4), 1737–1763 (2016)

    MathSciNet  MATH  Google Scholar 

  22. Cao, L., Zhang, L., Allegretto, W., Lin, Y.: Multiscale asymptotic method for Steklov eigenvalue equations in composite media. SIAM. J. Numer. Anal. 51, 273–296 (2013)

    MathSciNet  MATH  Google Scholar 

  23. Carstensen, C., Hu, J., Orlando, A.: Framework for the a posteriori error analysis of nonconforming finite elements. SIAM. J. Numer. Anal. 45, 68–82 (2007)

    MathSciNet  MATH  Google Scholar 

  24. Carstensen, C., Hoppe, R.H.W.: Convergence analysis of an adaptive nonconforming finite element method. Numer. Math. 103, 251–266 (2006)

    MathSciNet  MATH  Google Scholar 

  25. Carstensen, C., Gedicke, J.: Guaranteed lower bounds for eigenvalues. Math. Comp. 83, 2605–2629 (2014)

    MathSciNet  MATH  Google Scholar 

  26. Chatelin, F.: Spectral Approximations of Linear Operators. Academic Press, New York (1983)

    MATH  Google Scholar 

  27. Chen, L.: IFEM: an Innovative Finite Element Methods Package in MATLAB. University of California at Irvine, Technical Report (2009)

    Google Scholar 

  28. Ciarlet, P.G.: Basic error estimates for elliptic proplems. In: Ciarlet, P.G., Lions, J.L. (eds.) Finite Element Methods (Part I), pp. 21–343 Handbook of Numerical Analysis, vol, 2, Elsevier Science Publishers, North-Holand (1991)

  29. Conca, C., Planchard, J., Vanninathanm, M.: Fluid and Periodic Structures. Wiley, New York (1995)

    Google Scholar 

  30. Crouzeix, M., Raviart, P.A.: Conforming and nonconforming finite element methods for solving the stationary stokes equations. RAIRO. Anal. Numer. 3, 33–75 (1973)

    MATH  Google Scholar 

  31. Dai, X., Xu, J., Zhou, A.: Convergence and optimal complexity of adaptive finite element eigenvalue computations. Numer. Math. 110, 313–355 (2008)

    MathSciNet  MATH  Google Scholar 

  32. Dauge, M.: Elliptic boundary value problems on corner domains: smoothness and asymptotics of solutions. In: Lecture Notes in Mathematics, vol. 1341. Springer, Berlin (1988)

  33. Dari, E., Durán, R., Padra, C., Vampa, V.: A posteriori error estimators for noconforming finite element methods. RAIRO Model. Math. Anal. Numer. 30, 385–400 (1996)

    MATH  Google Scholar 

  34. Dunford, N., Schwartz, J.T.: Linear Operators. vol. 2: Spectral Theory, Selfadjoint Operators in Hilbert Space. Interscience, New York (1963)

    MATH  Google Scholar 

  35. Falk, R.S.: Nonconforming finite element methods for the equations of linear elasticity. Math. Comp. 57, 529–550 (1991)

    MathSciNet  MATH  Google Scholar 

  36. Garau, E.M., Morin, P.: Convergence and quasi-optimality of adaptive FEM for Steklov eigenvalue problems. IMA. J. Numer. Anal. 31(3), 914–946 (2011)

    MathSciNet  MATH  Google Scholar 

  37. Girault, V., Raviart, P.A.: Finite Element Approximation of the Navier-Stokes Equations Lecture Notes in Mathematics, vol. 749. Berlin, New York (1981)

    Google Scholar 

  38. Grisvard, P.: Elliptic problems in nonsmooth domains boston: Pitman (1985)

  39. Hu, J., Huang, Y., Lin, Q.: The lower bounds for eigenvalues of elliptic operators by Nonconforming finite element methods. J. Sci Comput. 61, 196–221 (2014)

    MathSciNet  MATH  Google Scholar 

  40. Hu, J., Huang, Y.: Lower bounds for eigenvalues of the stokes operator. Adv. Appl. Math. Mech. 5(1), 1–18 (2013)

    MathSciNet  MATH  Google Scholar 

  41. Jerison, D.S., Kenig, C.E.: The Neumann problem on Lipschitz domains. Bull. Amer. Math. Soc. 4, 203–207 (1981)

    MathSciNet  MATH  Google Scholar 

  42. Kufner, A., John, O., Fučik, S.: Function spaces, academia publishing house prague (1977)

  43. Li, Q., Lin, Q., Xie, H.: Nonconforming finite element approximations of the Steklov eigenvalue problems and its lower bound approximations. Appl. Math. 58, 129–151 (2013)

    MathSciNet  MATH  Google Scholar 

  44. Li, M., Lin, Q., Zhang, S.: Extrapolation and superconvergence of the Steklov eigenvalue problems. Adv. Comput. Math. 33, 25–44 (2010)

    MathSciNet  MATH  Google Scholar 

  45. Liu, J., Sun, J., Turner, T.: Spectral indicator method for a non-selfadjoint Steklov eigenvalue problem. J. Sci. Comput. 79, 1814–1831 (2019)

    MathSciNet  MATH  Google Scholar 

  46. Morin, P., Nochetto, R.H., Siebert, K.: Convergence of adaptive finite element methods. SIAM Rev. 44, 631–658 (2002)

    MathSciNet  MATH  Google Scholar 

  47. Oden, J.T., Reddy, J.N.: An Introduction to the Mathematical Theory of Finite Elements. Courier Dover Publications, New York (2012)

    MATH  Google Scholar 

  48. Russo, A.D., Alonso, A.E.: A posteriori error estimates for nonconforming approximations of Steklov eigenvalue problems. Comput. Math. Appl. 62(11), 4100–4117 (2011)

    MathSciNet  MATH  Google Scholar 

  49. Savaré, G.: Regularity results for elliptic equations in Lipschitz domains. J. Funct. Anal. 152, 176–201 (1998)

    MathSciNet  MATH  Google Scholar 

  50. Shi, Z., Wang, M.: Finite Element Methods. Science Press, Beijing (2013)

    Google Scholar 

  51. Strang, G., Fix, G.J.: An Analysis of the Finite Element Method. Prentice-Hall, New York (1973)

    MATH  Google Scholar 

  52. Sun, J., Zhou, A.H.: Finite element methods for eigenvalue problems. CRC Press, Taylor & Francis Group, Boca Raton, London New York (2016)

  53. Verfürth, R.: A Review of a Posteriori Error Estimates and Adaptive Mesh-Refinement Techniques. Wiley-Teubner, New York (1996)

    MATH  Google Scholar 

  54. Xie, H.: A type of multilevel method for the Steklov eigenvalue problem. IMA. J. Numer. Anal. 34, 592–608 (2014)

    MathSciNet  MATH  Google Scholar 

  55. Xie, M., Xie, H., Liu, X.: Explicit lower bounds for stokes eigenvalue problems by using nonconforming finite elements. J.pan J. Indust. Appl. Math. 35(1), 335–354 (2018)

    MathSciNet  MATH  Google Scholar 

  56. Yang, Y., Li, Q., Li, S.: Nonconforming finite element approximations of the Steklov eigenvalue problem. Appl. Numer. Math. 59, 2388–2401 (2009)

    MathSciNet  MATH  Google Scholar 

  57. Yang, Y., Chen, Z.: The order-preserving convergence for spectral approximation of self-adjoint completely continuous operators. Sci. China Ser. A:, Math. 51, 1232–1242 (2008)

    MATH  Google Scholar 

Download references

Acknowledgments

The authors cordially thank the editor and the referees for their valuable comments and suggestions that lead to the improvement of this paper.

Funding

This work is financially supported by the National Natural Science Foundation of China (Grant Nos. 11561014, 11761022).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Guizhou Normal University, Guiyang, 550001, China

    Yidu Yang, Yu Zhang & Hai Bi

Authors
  1. Yidu Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hai Bi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yidu Yang.

Additional information

Communicated by: Aihui Zhou

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Y., Zhang, Y. & Bi, H. Non-conforming Crouzeix-Raviart element approximation for Stekloff eigenvalues in inverse scattering. Adv Comput Math 46, 81 (2020). https://doi.org/10.1007/s10444-020-09818-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10444-020-09818-7

Keywords

Mathematics Subject Classification (2010)

Search

Navigation