Fluid Leakage in Metallic Seals

Abstract

Metallic seals are crucial machine elements in many important applications, e.g., in ultrahigh vacuum systems. Due to the high elastic modulus of metals, and the surface roughness which exists on all solid surfaces, if no plastic deformation would occur one expects in most cases large fluid flow channels between the contacting metallic bodies, and large fluid leakage. However, in most applications plastic deformation occurs, at least at the asperity level, which allows the surfaces to approach each other to such an extent that fluid leakage often can be neglected. In this study, we present an experimental set-up for studying the fluid leakage in metallic seals. We study the water leakage between a steel sphere and a steel body (seat) with a conical surface. The experimental results are found to be in good quantitative agreement with a (fitting-parameter-free) theoretical model. The theory predicts that the plastic deformations reduce the leak-rate by a factor $\approx 8$.

1 Introduction

Seals are a crucial machine element used to confine a high pressure fluid to some given volume. Due to the interfacial surface roughness most seals exhibit leakage [1, 2]. To minimize the leakage, seals are usually made from a soft material, such as rubber (with an elastic modulus of order $E\approx 10 \ \mathrm{MPa}$), which can easily deform elastically and reduce the gap to the counter surface to such an extent that the fluid leakage becomes negligible or unimportant.

For some applications, e.g., involving high temperatures or hot reactive gases, or very high fluid pressures, rubber-like materials cannot be used. In these cases, and in ultra high vacuum systems, seals made from metals are very useful [3,4,5,6].

Metals are elastically very stiff (typical elastic modulus of order $E \approx 100 \ \mathrm{GPa}$), and unless the surfaces are extremely smooth, or the nominal contact pressure extremely high, calculations (assuming purely elastic deformations) show that large non-contact channels would occur at the interface resulting in a large fluid leakage. However, most metals yield plastically at relative low contact pressures, typically of order $\sigma _\mathrm{Y} \approx 1 \ \mathrm{GPa}$. This will allow the contacting surfaces to approach each other, which will reduce the interfacial gap to such an extent that the fluid leakage usually can be neglected.

For purely elastic solids like rubber, contact mechanics theories have been developed for how to predict the fluid leak-rate, and it has been shown that they are in good agreement with experiments [7, 8]. The simplest approach assumes that the whole fluid pressure difference between the inside and outside of the sealed region occurs over the most narrow constrictions (denoted critical junctions) which are encountered along the largest open percolating non-contact flow channels.

For elastic solids numerical contact mechanics models [9], such as the boundary element model, and the analytic theory of Persson [10, 11], can be used to calculate the surface separation at the critical junction and hence predict fluid leakage rates. For solids exhibiting plastic flow, the surfaces will approach each other more closely than if only elastic deformations would occur. This will reduce the fluid leakage rate [12, 13].

We have recently shown how the leakage of static rubber seals can be estimated using the Persson contact mechanics theory combined with the Bruggeman effective medium theory [14,15,16,17,18] (for other approaches, see Refs. [6, 19, 20, 21, 22]). In this paper we apply the theory to metallic seals where plastic deformations are important unless the surfaces are extremely smooth [23,24,25,26].

Experimental studies of plastic deformation of rough metallic and polymeric surfaces was presented in Refs. [27, 28]. Several studies of surface roughness and plastic flow have been reported using microscopic (atomistic) models [29], or models inspired by atomic scale phenomena that control the nucleation and glide of the dislocations [30,31,32,33]. These models supply fundamental insight into the complex process of plastic flow, but are not easy to apply to practical systems involving inhomogeneous polycrystalline metals and alloys exhibiting surface roughness of many length scales. The approach used in this study is less accurate but easy to implement, and it can be used to estimate the leakage rates of metallic seals.

2 Experimental

2.1 Surface Topography

The topography measurements were performed with a Mitutoyo Portable Surface Roughness Measurement device, Surftest SJ-410 with a diamond tip with the radius of curvature $R = 1$ μm, and with the tip–substrate repulsive force $F_\mathrm{N}=0.75 \ \mathrm{mN}$. The lateral tip speed was $v=50$ μm/s.

From the measured surface topography (line scans) $z=h(x)$ we calculated the one-dimensional (1D) surface roughness power spectra defined by

$$\begin{aligned} C_\mathrm{1D} (q) = {1\over 2 \pi } \int _{-\infty }^\infty dx \ \langle h(x) h(0) \rangle e^{i q x} \end{aligned}$$

where $\langle .. \rangle$ stands for ensemble averaging. For surfaces with isotropic roughness, the 2D power spectrum C(q) can be obtained directly from $C_\mathrm{1D} (q)$ as described elsewhere [15, 34, 35]. An approximate transformation can be achieved using $C(q) = C_\mathrm{1D}(q)\pi /q$ [36]. For randomly rough surfaces, all the (ensemble averaged) information about the surface is contained in the power spectrum C(q). For this reason the only information about the surface roughness which enter in contact mechanics theories (with or without adhesion) is the function C(q). Thus, the (ensemble averaged) area of real contact, the interfacial stress distribution and the distribution of interfacial separations, are all determined by C(q) [10, 11, 37,38,−39].

Fig. 1

Schematic picture of the leakage experiment. The dark blue color is water, the light blue color is air and the yellow color is oil. The steel ball (black) is squeezed against the steel seat (green) in part by the applied water pressure, and in part by the steel piston contacting it from on-top (gray cylinder) using an oil based hydraulics system. In the present experiments no force has been applied by the steel piston (Color figure online)

2.2 Leak-Rate Experiment

The aim of the experiment is to measure the fluid (here water) leakage for a ball-seat valve as a function of the applied fluid pressure. In the present set-up we can apply fluid pressures up to $20 \ \mathrm{bar}$ ($2 \ \mathrm{MPa}$), and the pressure can be kept at a constant level even if there is leakage. In this study we are interested in the influence of the surface roughness on the leak-rate. The steel ball we use is very smooth and has a root mean square roughness below $0.1$ μm. We use different seats with varying surface roughness produced by sandblasting. Thus the seat must be easily replaceable.

In the experiments reported below, the ball is squeezed against the seat only by the fluid pressure. However, the experimental set-up also includes the ability to create an additional normal load onto the ball. This additional force is generated by pushing a steel piston against the ball using an oil based hydraulics system. In this work, the steel rod has not been used extensively.

The test chamber, which contains the ball and the seat, can be seen in Fig. 1. Here, the chamber surrounding the ball is filled with water (dark blue color). Purified water is used as the leakage fluid because the low viscosity increases the leakage which makes the measurement more easy and accurate as compared to using a hydraulic oil. Purified water has very few contamination particles which can clog the flow channels. However, if water is used in a hydraulics system one has to be careful to avoid corrosion of all surfaces, including the seat and the ball. In order to keep the water pressure at a constant level a hydraulic accumulator is used to compensate for the (wanted and unwanted) leakage. A pressure sensor measures the actual pressure at the test chamber. When the water pressure crosses a certain threshold the water pump will raise the pressure again. In this way it is possible to keep the water pressure within $\pm 0.5 \ \mathrm{bar}$ ($\pm 0.05 \ \mathrm{MPa}$) of the nominal pressure at every time during the measurement.

The method used to determine the leak-rate depends on the amount of leakage. For very low amounts of leakage the best way is to count the amount of water drops over time. The volume of a single drop can be estimated by repeated measurement of multiple drops. For higher amounts of leakage a measuring cylinder can be used. If the leakage surpasses the typical volume of a measuring cylinder, the leakage is instead determined by measuring its mass using a scale. In this work all three methods have been used. Comparison of different methods in the overlap regions has shown that all three methods deliver comparable results.

Each measurement was repeated five times. Using Gaussian uncertainty propagation we have quantified the uncertainties on derived quantities. Between two consecutive measurements the contact area was cleaned using purified water. If the contact was not been cleaned properly, or if too long time had passed between the cleaning and the start of a measurement, a reduced leak-rate was observed. This was probably due to the accumulation of contamination particles at the sealing contact, which block fluid flow channels.

Fig. 2

A steel ball (radius R) squeezed against a conical surface. The radius of the ball $R=2 \ \mathrm{cm}$ and the cone angle $\theta = 45^\circ$. In the experiments, the axial force $F_\mathrm{N}$ squeezing the ball against the cone surface is due only to the fluid pressure difference between inside and outside the seal, so that $F_\mathrm{N} = \pi r_0^2 p_\mathrm{fluid}$. In some applications, in addition to the fluid pressure force, we applied a force from the steel piston shown in Fig. 1

Fig. 3

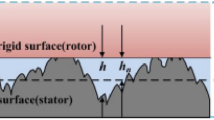
Two limiting cases when a rigid cylinder (black) with radius R is squeezed against a nominal flat halfspace (green). a If the surface roughness amplitude is very small, or the applied force very high, the nominal contact area will be determined by bulk deformations and given by the Hertz contact theory. b In the opposite limit mainly the surface asperities deform (but with a long-range elastic coupling occurring between them). In this limit the pressure profile is Gaussian-like (Color figure online)

Fig. 4

The calculated pressure distributions for a smooth seat surface (red dashed line), and for the rough seat surface (red solid line) for the line load $f_\mathrm{N}=20 \ \mathrm{kN/m}$ (corresponding to the fluid pressure $p_\mathrm{fluid}=20 \ \mathrm{bar}$). For the rough surface we also show the pressure profile for the line load $f_\mathrm{N}=2 \ \mathrm{kN/m}$ (corresponding to the fluid pressure $p_\mathrm{fluid}=2 \ \mathrm{bar}$), multiplied by a factor of 10. In the calculations we used and the effective elastic modulus $E^*=115 \ \mathrm{GPa}$ (Color figure online)

3 Leakage Calculations

The calculation of the fluid leakage in metallic seals involves several steps. First it is necessary to determine the nominal contact pressure profile p(x, y) acting at the interface between the two metallic bodies. This will in general involve both elastic and plastic deformations of the metals. Secondly, one must determine the separation u(x, y) between the surfaces as this will determine the fluid flow channels at the interface. This problem will depend on the pressure profile p(x, y) and on the surface roughness, and the elastoplastic properties of the metals. Finally, one must calculate the fluid flow at the interface in the open (non-contact) channels from the high pressure side to the low pressure side. This is a complex hydrodynamic problem which in general cannot be solved exactly.

3.1 Contact Force

The experimental set-up consists of a steel ball (radius R) and a conical steel body (seat) with the angle $\theta$ defined in Fig. 2. A fluid with the pressure $p_\mathrm{fluid}$ squeezes the ball against the seat. We assume here that there is no other applied force squeezing the ball against the seat. The contact region between the ball and the seat forms a circular region (line contact) with radius $r_0$ (see Fig. 2). Hence, the force squeezing the ball against the seat is $F_\mathrm{N} = \pi r_0^2 p_\mathrm{fluid}$. The force per unit circumferential length is denoted $f_\mathrm{N}$. From Fig. 2, we get

$$\begin{aligned} F_\mathrm{N}= & {} 2 \pi r_0 f_\mathrm{N} \mathrm{cos}\theta \\ R \mathrm{sin}\theta= & {} r_0 \end{aligned}$$

so that

$$\begin{aligned} f_\mathrm{N}={F_\mathrm{N} \over 2 \pi R \mathrm{cos}\theta \mathrm{sin}\theta } \end{aligned}$$

Using $F_\mathrm{N} = \pi r_0^2 p_\mathrm{fluid}$ we get

$$\begin{aligned} f_\mathrm{N} = {1\over 2} R p_\mathrm{fluid} {\mathrm{sin}\theta \over \mathrm{cos}\theta } \end{aligned}$$

(1)

3.2 Hertzian Pressure Profile

If we assume that the contact is Hertz-like we get the pressure distribution [40, 41]

$$\begin{aligned} p=p_0 \left( 1-\left( {x\over a}\right) ^2 \right) ^{1/2} \end{aligned}$$

(2)

where

$$\begin{aligned} p_0= & {} \left( {E^* f_\mathrm{N} \over \pi R}\right) ^{1/2} \end{aligned}$$

(3)

$$\begin{aligned} a= & {} \left( R\delta \right) ^{1/2} \end{aligned}$$

(4)

$$\begin{aligned} f_\mathrm{N}= & {} {\pi \over 4} E^* \delta \end{aligned}$$

(5)

where $E^*$ is the effective Young’s modulus defined by

$$\begin{aligned} {1\over E^*} = {1-\nu _1^2\over E_1}+ {1-\nu _2^2\over E_2} \end{aligned}$$

where $E_1$ and $\nu _1$ are the Young’s modulus and Poisson ratio of the steel seat, and $E_2$ and $\nu _2$ the same quantities for the steel ball.

Using (1) and (3) gives

$$\begin{aligned} p_0 = \left( {E^* p_\mathrm{fluid} \over 2 \pi } {\mathrm{sin}\theta \over \mathrm{cos}\theta }\right) ^{1/2} \end{aligned}$$

(6)

and from (1), (4) and (5)

$$\begin{aligned} a= R \left( {2\over \pi } {p_\mathrm{fluid} \over E^*}{\mathrm{sin}\theta \over \mathrm{cos} \theta }\right) ^{1/2} \end{aligned}$$

(7)

Assuming that both the steel ball and the steel cone (seat) have $E=210 \ \mathrm{GPa}$, $\nu = 0.3$ we get

$$\begin{aligned} E^* = {1\over 2} {E\over 1-\nu ^2} \approx 115 \ \mathrm{GPa} \end{aligned}$$

As an example, if $p_\mathrm{fluid} = 20 \ \mathrm{bar}$, $\theta = 45^\circ$, and $R= 2 \ \mathrm{cm}$ we get $F_\mathrm{N} \approx 1260 \ \mathrm{N}$, and $p_0 \approx 181 \ \mathrm{MPa}$ and the half-width $a\approx 0.07 \ \mathrm{mm}$.

3.3 Gaussian Pressure Profile

When a cylinder with a smooth surface is squeezed against a flat smooth substrate, a rectangular contact region of width 2a is formed with a contact pressure given by the Hertz theory. However, if the substrate has surface roughness the nominal contact region will be larger than predicted by the Hertzian theory.

In a classical study Greenwood an Tripp [42] studied the influence of surface roughness on the elastic contact of rough spheres. They used the Greenwood-Williamson [43] (GW) contact mechanics theory where the elastic coupling between the asperity contact regions is neglected. However, this coupling is very important even for small nominal contact pressures, where the distance between the macroasperity contact regions may be large. The reason is that there are smaller asperities (microasperities) on top of the big asperities, and since the contact pressure in the macroasperity contact region in general is very high, the microasperity contact regions are closely spaced and the elastic coupling between them cannot be neglected. In the present study we will use the Persson contact mechanics theory which includes the elastic coupling between all asperity contact regions in an approximate but accurate way.

We will now show that the pressure distribution will change from parabolic-like for the case of smooth surfaces to Gaussian-like if the surface roughness is large enough. Due to the surface roughness, if the contact pressure p is not too high the interfacial separation u is related to the contact pressure as [37]

$$\begin{aligned} p=p_\mathrm{c} e^{-u/ u_0} \end{aligned}$$

(8)

where $u_0 = \gamma h_\mathrm{rms}$, where $\gamma \approx 0.4$ and where $h_\mathrm{rms}$ is the root-mean-square (rms) roughness amplitude.

For a cylinder with radius R which is squeezed against the flat surface we expect (see Fig. 3)

$$\begin{aligned} u \approx u_1+{x^2 \over 2R} \end{aligned}$$

so that

$$\begin{aligned} p=p_0 e^{-x^2/2s^2}. \end{aligned}$$

(9)

where $s^2 = \gamma R h_\mathrm{rms}$. Using (9) we get

$$\begin{aligned} \int _{-\infty }^\infty dx \ p_0 e^{-x^2/2s^2} = p_0 s ( 2\pi )^{1/2} = f_\mathrm{N} \end{aligned}$$

or

$$\begin{aligned} p_0 = {f_\mathrm{N} \over s (2\pi )^{1/2}} \end{aligned}$$

(10)

We note that (9) holds only as long as the pressure p is so small that the asymptotic relation (8) is valid, but not too small, because then finite size effects become important. In addition, while deriving (9) we have neglected bulk deformations. This is a valid approximation only if $s\gg a$ or $h_\mathrm{rms} \gg \delta$.

Using h_rms = 1.9 μm and $R=2 \ \mathrm{cm}$ gives the standard deviation $s=0.123 \ \mathrm{mm}$. A numerical study using the full $p=p(u)$ relation instead of the asymptotic relation (8), and including bulk deformations, gives a nearly Gaussian stress distribution with the standard deviation $s\approx 0.139 \ \mathrm{mm}$ and the full width at half maximum (FWHM) $\approx 0.33 \ \mathrm{mm}$ (see Fig. 4). These results are close to the prediction $s= (\gamma R h_\mathrm{rms})^{1/2} \approx 0.123 \ \mathrm{mm}$, and the FWHM expected for a Gaussian function, which is $\mathrm{FWHM} = 2 (2 \mathrm{ln} 2)^{1/2} s \approx 2.355 s \approx 0.29 \ \mathrm{mm}$.

Using (1) and (10) we get

$$\begin{aligned} p_0 = {R\over 2 s (2\pi )^{1/2}} {\mathrm{cos}\theta \over \mathrm{sin}\theta } p_\mathrm{fluid} \end{aligned}$$

(11)

For $p_\mathrm{fluid} = 20 \ \mathrm{bar}$ and $s= 0.123 \ \mathrm{mm}$ we get the maximum nominal contact pressure $p_0 \approx 57.4 \ \mathrm{MPa}$.

Note that the asperities act like a compliant layer on the surface of the body, so that contact is extended over a larger area than it would be if the surfaces were smooth and, in consequence, the contact pressure for a given load will be reduced. In reality the contact area has a ragged edge which makes its measurement subject to uncertainty. However, the rather arbitrary definition of the contact width is not a problem when calculating physical quantities like the leakage rate, which can be written as an integral involving the nominal pressure distribution.

Note also that the fact that the nominal contact pressure p(x) is a Gaussian function of x has nothing to do with the fact that randomly rough surfaces has a Gaussian distribution of asperity heights. Rather, it results from the fact that there is an exponential relation between the contact pressure and average interfacial separation (see (8)), and the fact that when bulk deformations can be neglected the average interfacial separation depends quadratic on the lateral coordinate x as long as $x/R<<1$.

3.4 Role of Plastic Deformation

The derivation of the nominal contact pressure profile (9) (and (2)) assumes elastic deformations. The stress-strain curve for the steel 1.4122 used for the seat shows that the stress at the onset of plastic flow (in elongation) is at about $500 \ \mathrm{MPa}$, which is much higher than the maximum stress $p_0$ (and maximum shear stress) at the surface and also below the surface in the ball-seat contact region. Thus for smooth surfaces we expect no macroscopic plastic deformations, and can treat the contact as elastic when calculating the nominal contact pressure distribution. However, the stress in the asperity contact regions is much higher than the nominal contact pressure. Thus, using the power spectrum of the sandblasted seat, and including just the roughness components with wavelength λ > 2 μm, and assuming elastic contact, gives for the nominal contact pressure $p_0 \approx 57 \ \mathrm{MPa}$ the relative contact area [12] $A/A_0 \approx (2/h') (p_0/E^*) \approx 0.003$, where $h'$ is the rms slope. Since the average pressure p in the asperity contact regions must satisfy $p A = p_0 A_0$ or $p=(A_0/A) p_0\approx h'E^*/2$ we get $p \approx 23 \ \mathrm{GPa}$. According to Tabor [44] the penetration hardness is $\sigma _\mathrm{P} \approx 3 \sigma _\mathrm{Y}$, where $\sigma _\mathrm{Y}$ is the (physical) yield stress in tension at about $15\%$ strain, which is about $1\ \mathrm{GPa}$ for the steel 1.4122. Thus $\sigma _\mathrm{P} \approx 3 \ \mathrm{GPa}$ (we use $\sigma _\mathrm{P} \approx 3.5 \ \mathrm{GPa}$ in the calculations presented below). We conclude that the asperities on the seat surface will deform plastically as also observed in optical pictures of the seat surface after removing the steel ball.

However, the derivation of (9) may still be approximately valid if the asperities deform elastically on the length scale which determines the contact stiffness for the (nominal) contact pressures relevant for the calculation of (9). The contact stiffness (or the p(u) relation) for small pressures is determined by the most long wavelength roughness components which deform mainly elastically (see Sect. 4). Nevertheless, a more detail study is necessary to determine the exact influence of plastic flow at the asperity level on the nominal contact pressure profile.

3.5 Leak-Rate Theory

In calculating the fluid (here water) leak-rate we have used the effective medium approach combined with the Persson contact mechanics theory for the probability distribution of surface separations. The most important region for the sealing is a narrow strip at the center of the nominal contact pressure profile, where the contact pressure is highest (and the surface separation smallest), but the study presented below takes into account the full pressure profile p(x).

The basic contact mechanics picture which can be used to estimate the leak-rate of seals is as follows: Consider first a seal where the nominal contact area is a square. The seal separates a high pressure fluid on one side from a low pressure fluid on the other side, with the pressure drop $\Delta P$. We consider the interface between the solids at increasing magnification $\zeta$. At low magnification we observe no surface roughness and it appears as if the contact is complete. Thus studying the interface only at this low magnification we would be tempted to conclude that the leak-rate vanishes. However, as we increase the magnification $\zeta$ we observe surface roughness and non-contact regions, so that the contact area $A(\zeta )$ is smaller than the nominal contact area $A_0 = A(1)$. As we increase the magnification further, we observe shorter wavelength roughness, and $A(\zeta )$ decreases further. For randomly rough surfaces, as a function of increasing magnification, when $A(\zeta )/A_0 \approx 0.42$ the non-contact area percolate [19], and the first open channel is observed, which allow fluid to flow from the high pressure side to the low pressure side. The percolating channel has a most narrow constriction over which most of the pressure drop $\Delta P$ occurs. In the simplest picture one assumes that the whole pressure drop $\Delta P$ occurs over this critical constriction, and if it is approximated by a rectangular pore of height $u_\mathrm{c}$ much smaller than its width w (as predicted by contact mechanics theory), the leak rate can be approximated by [14, 20, 21]

$$\begin{aligned} \dot{Q} = {u_\mathrm{c}^3 \over 12 \eta }\Delta P \end{aligned}$$

(12)

where $\eta$ is the fluid viscosity. The height $u_\mathrm{c}$ of the critical constriction can be obtained using the Persson contact mechanics theory (see Ref. [10, 11, 12, 14, 16, 17, 37]). The result (12) is for a seal with a square nominal contact area.

In this work the Bruggemann effective medium method, which is based on the concept of fluid flow conductivity $\sigma _\mathrm{eff}$, is used to calculate the leak-rate. The fluid flow current

$$\begin{aligned} J_x = - \sigma _\mathrm{eff} {d p_\mathrm{fluid} \over d x} \end{aligned}$$

Since the leak-rate $\dot{Q} = L_y J_x$ we get

$$\begin{aligned} {d p_\mathrm{fluid} \over d x} = -{\dot{Q} \over L_y} {1\over \sigma _\mathrm{eff}} \end{aligned}$$

(13)

Note that $\sigma _\mathrm{eff}$ depends on the contact pressure $p_\mathrm{con}(x)$ and hence on x. In the present case $p_\mathrm{fluid} \ll p_\mathrm{cont}$ and in this case $p_\mathrm{cont} \approx p$, where p(x) is the external applied squeezing pressure (or nominal pressure) given by (9). Integrating (13) over x gives

$$\begin{aligned} \Delta P = {\dot{Q} \over L_y} \int _{-\infty }^{\infty } dx \ {1\over \sigma _\mathrm{eff}(p(x))} \end{aligned}$$

where $\Delta P$ denotes the fluid pressure drop from inside to outside the seal, and where we have used that $\dot{Q}$ is independent of x as a result of fluid volume conservation. For the Hertz contact pressure profile, where $p(x) = 0$ for $x>a$ and $x<a$, we get with $y=x/a$:

$$\begin{aligned} \Delta P = \dot{Q} {2a \over L_y} \int _0^1 dy \ {1\over \sigma _\mathrm{eff}(p (y))} \end{aligned}$$

where

$$\begin{aligned} p_\mathrm{c} (y)=p_0 \left( 1-y^2\right) ^{1/2} \end{aligned}$$

For the Gaussian pressure profile (9) using $y=x/s$ we get

$$\begin{aligned} \Delta P = \dot{Q} {2s \over L_y} \int _0^\infty dy \ {1\over \sigma _\mathrm{eff}(p (y))} \end{aligned}$$

(14)

where

$$\begin{aligned} p (y)=p_0 e^{-y^2/2}. \end{aligned}$$

From (14) we get the fluid leak-rate (volume per unit time)

$$\begin{aligned} \dot{Q} = {L_y \over 2s} {\Delta P \over \int _0^\infty dy \ \sigma ^{-1}_\mathrm{eff}(p (y))} \end{aligned}$$

(15)

This theory takes into account all the fluid flow channels and not just the first percolating channel observed with increasing magnification. The dependency of the leak-rate on the fluid viscosity $\eta$ and the fluid pressure difference $\Delta P$ given by (11) is the same in the more accurate approach. Similar, the leak-rate is proportional to $L_y/L_x$ (where $L_x=2s$ in the present case) in this approach. Comparison of the prediction of the Bruggeman effective medium theory for the leak-rate with exact numerical studies has shown the effective medium theory to be remarkably accurate in the present context [19].

3.6 Accounting for Plastic Deformations

In the present study we are interested in metallic seals and in this case plastic deformation of the solids is very important. Plastic flow is a complex topic but two very simple approaches have been proposed to take into account plastic deformations in the context of metallic seals. One approach, which is simple to implement when using actual realizations of the rough surfaces (as done in most numerically treatments, e.g., using the boundary element method [11]), is to move surface grid points vertically in such a way that the stress in the plastically deformed region is equal to (or below) the penetration hardness.

Another approach, which is more convenient in analytic contact mechanics theories, is based on smoothing the surface in wavevector space (see [14, 16, 17]). Thus, if two solids are squeezed together with the pressure $p_0$ they will deform elastically and, at short enough length scale, plastically. If the contact is now removed the surfaces will be locally plastically deformed. Assume now that the surfaces are moved into contact again at exactly the same position as the original contact, and with the same squeezing pressure $p_0$ applied. In this case the solids will deform purely elastically and the Persson contact mechanics theory can be (approximately) applied assuming that the surface roughness power spectrum $C_\mathrm{pl}(q)$ of the (plastically) deformed surface is known.

An expression for $C_\mathrm{pl}(q)$ can be obtained as follows. Let us consider the contact between two elastoplastic bodies with nominal flat surfaces, but with surface roughness extending over many decades in length scale, as is almost always the case. Assume that the applied (nominal) contact pressure $p_0$ is smaller than the penetration hardness $\sigma _\mathrm{P}$ of the solids. When we study the contact between the solids at low magnification we do not observe any surface roughness, and since $p_0 < \sigma _\mathrm{P}$ the solids deform purely elastically at this length scale. As we increase the magnification we observe surface roughness and the (elastic) contact area decreases. At some magnification the pressure $p=p_0 A_0/A(\zeta )$ may reach the penetration hardness and at this point all the contact regions are plastically deformed. In general, depending on the magnification $\zeta$, some fraction of the contact area involves elastic deformations, while the other fraction has undergone plastic deformation. Thus we can write the contact area $A(\zeta ) = A_\mathrm{el}(\zeta )+A_\mathrm{pl}(\zeta )$. The Persson contact mechanics theory predicts both $A_\mathrm{el}(\zeta )$ and $A_\mathrm{pl}(\zeta )$ (see Ref. [10]).

In Refs. [45, 46] we have shown that $C_\mathrm{pl}(q)$ can be obtained approximately using (with $\zeta = q/q_0$, where $q_0$ is the smallest wavenumber)

$$\begin{aligned} C_\mathrm{pl} (q)= \left[ 1-\left( {A_\mathrm{pl} (\zeta ) \over A^0_\mathrm{pl}}\right) ^6\right] C(q), \end{aligned}$$

(16)

where $A^0_\mathrm{pl}=F_\mathrm{N}/\sigma _\mathrm{P}$ is the contact area assuming that all contact regions have yielded plastically so the pressure in all contact regions equal the penetration hardness $\sigma _\mathrm{P}$. The basic picture behind this definition is that surface roughness at short length scales gets smoothed out by plastic deformation, resulting in an effective cut-off of the power spectrum for large wave vectors (corresponding to short distances). Assuming elastic contact and using the power spectrum (16) result in virtually the same (numerical) contact area $A(\zeta )$, as a function of magnification $\zeta$, as predicted for the original surface using the elastoplastic contact mechanics theory, where $A(\zeta ) = A_\mathrm{el}(\zeta )+A_\mathrm{pl}(\zeta )$.

The smoothing of the surface profile at short length scale allows the surfaces to approach each other and will reduce the height $u_\mathrm{c}$ of the critical constriction. By using the plastically deformed surface roughness power spectrum (16) this effect is taken into account in a simple approximate way.

It is not clear which of the two ways to include plastic flow described above is most accurate. In the first approach the solids deform plastically only in the region where they make contact, but this procedure does not conserve the volume of the solids. The second approach does conserve the volume but smooth the surfaces everywhere, i.e., even in the non-contact region. However, this does not influence the area of real contact, and it has a relative small influence on the surface separations in the big fluid flow channels, which mainly determine the fluid leakage rate (see Ref. [12] for a discussion of this).

Fig. 5

The (measured) 2D surface roughness power spectrum of the sandblasted steel cone surface (red line) and of the steel ball (green line). The rms roughness are 1.9 μm and 0.8 μm, respectively. The rough cone has the rms slope 0.4 (Color figure online)

Fig. 6

The relative elastic $A_\mathrm{el}/A_0$ (red line) and relative plastic $A_\mathrm{pl}/A_0$ (green line) contact area as a function of the magnification $\zeta$. The red dotted line is the relative contact area without plasticity. In the elastoplastic calculation we use the penetration hardness $\sigma _\mathrm{P} = 3.5 \ \mathrm{GPa}$. For the effective Young’s modulus $E^* = 115 \ \mathrm{GPa}$ and the nominal contact pressure $p_0=50 \ \mathrm{MPa}$ (Color figure online)

Fig. 7

The (measured) 2D surface roughness power spectrum of the sandblasted steel cone (seat) surface (blue line), and the (calculated) power spectrum of the plastically deformed cone surface (green solid line) (Color figure online)

Fig. 8

The measured (red squares) and the calculated water leak-rate as a function of the water pressure difference. The green line is the result including plastic deformation, and the blue line assuming only elastic deformation. The steel ball is squeezed against the sandblasted conical surface (seat) only by the water pressure so increasing the water pressure also increases the normal force squeezing the ball against the seat’s surface (Color figure online)

Fig. 9

The measured (red squares) and the calculated (green line) water leak-rate as a function of the water pressure difference. The theory curve includes the plastic deformation (Color figure online)

Fig. 10

The calculated surface separation at the critical junction as a function of the water pressure. The green line is the result including plastic deformation, and the blue line assuming only elastic deformation

Fig. 11

The time dependency of the measured leak rate for the sandblasted seat at the water pressure $p_\mathrm{water} = 1 \ \mathrm{bar}$ (red squares) and $p_\mathrm{water} = 10 \ \mathrm{bar}$ (green squares). For the $p_\mathrm{water} = 10 \ \mathrm{bar}$ case an additional normal force of $8.5 \ \mathrm{kN}$ was squeezing the ball against the seat. The decrease in the leakage rate with increasing time is likely due to clogging of flow channels by contamination particles (Color figure online)

4 Experimental Results and Analysis

Figure 5 shows the (measured) 2D surface roughness power spectrum of the sandblasted seat’s surface (red line) and of the steel ball (green line). The rms roughness are $1.9$ μm and $0.8$ μm, respectively. The rough cone has the rms slope 0.4. The smooth seat has anisotropic roughness (not shown), resulting from the grinding process which introduced wear tracks in the circumferential direction. These wear tracks are easily observed with the naked eyes, and shows up in the power spectrum in the radial direction as the two sharp peaks around $q\approx 10^5 \ \mathrm{m}^{-1}$ (not shown). Since the theory we use to analyze the experimental data assumes randomly rough surfaces (but it can be generalized to include periodic roughness [47]), in this paper we consider only the seat with the sandblasted surface (red line), which is randomly rough to a good approximation.

Figure 6 shows the (calculated) relative elastic $A_\mathrm{el}/A_0$ (red line) and relative plastic $A_\mathrm{pl}/A_0$ (green line) contact area as a function of the magnification $\zeta$ (lower log-scale) and the wavenumber q (upper log-scale). The red dotted line is the relative contact area without plasticity. In the elastoplastic calculation we use the penetration hardness $\sigma _\mathrm{P} = 3.5 \ \mathrm{GPa}$, and the effective Young’s modulus $E^* = 115 \ \mathrm{GPa}$ and the nominal contact pressure $p_0=50 \ \mathrm{MPa}$. Note that the long wavelength roughness is elastically deformed, but already at the magnification $\zeta \approx 100$ all the contact area is observed to be plastically deformed. The magnification $\zeta \approx 100$ corresponds to the wavenumber $q=\zeta q_0 \approx 10^5 \ \mathrm{m}^{-1}$ or the wavelength $\lambda = 2\pi /q \approx 60$ μm. Thus all the contact regions observed with, e.g., an optical microscope (with the optimal resolution determined by the wavelength of light, $\lambda \approx 1$ μm), are plastically deformed.

Figure 7 shows the (measured) 2D surface roughness power spectrum of the sandblasted steel seat’s surface (red line, from Fig. 5), and the (calculated) power spectrum of the plastically deformed seat’s (green solid line) as obtained using (16).

Figure 8 shows the measured (red squares) and the calculated water leak-rate as a function of the water pressure difference. The green line is the result including plastic deformation, and the blue line assuming only elastic deformation. The steel ball is squeezed against the sandblasted seat only by the water pressure so increasing the water pressure also increases the normal force squeezing the ball against the seat’s surface. This will reduce the interfacial separation at the critical junctions, and hence the leak rate, and this explains why the leak rate does not increase proportional to the fluid pressure difference $\Delta P$ as otherwise expected.

Note that including the plastic deformation results in a drastic reduction, by roughly a factor of 8, in the (calculated) fluid leak-rate. The theory prediction with the plastic deformation included is in very good agreement with experiments. This is shown in greater detail in Fig. 9. We note that all the parameters which enter in the theory, like surface roughness power spectrum or elastoplastic modulus, have been measured directly so there is no fitting parameter in the theory calculation.

The leak-rate depends on the separation at the critical constriction as $u_\mathrm{c}^3$. Thus the reduction in the leak-rate by a factor of $\approx 8$ when including the plastic deformation imply that the separation $u_\mathrm{c}$ decreases with a factor of $\approx 2$. This is in good agreement with the result shown in Fig. 10 which shows the calculated surface separation at the critical junction as a function of the water pressure. The green line is the result including plastic deformation, and the blue line assuming only elastic deformation.

Figure 10 shows that if there would be contamination particles in the fluid of micrometer size they could clog the flow channels and hence reduce the fluid leakage rate with increasing time. In spite of the fact we used purified water we did observe a dependency of the leak-rate on time. This may be due to dust particles in the water, which could not be completely avoided as the experiments was performed in the normal atmosphere. Other possible reasons for the contamination are internal leakage from the air side or the oil side or corrosion of the materials. To illustrate this effect, in Fig. 11 we show the measured time dependency of the measured leak-rate for the sandblasted seat at the water pressure $p_\mathrm{water} = 1 \ \mathrm{bar}$ (red squares) and $p_\mathrm{water} = 10 \ \mathrm{bar}$ (green squares). The steel ball is squeezed against the smooth seat by the water pressure, but for the $p_\mathrm{water} = 10 \ \mathrm{bar}$ case an additional normal force of $8.5 \ \mathrm{kN}$ was applied via the piston in Fig. 1. The decrease in the leakage rate with increasing time may be due to clogging of flow channels by contamination particles.

The leak rates in this work have been estimated using the total amount of leakage during 10 minutes. The time-variation in the leakage rate due to clogging of flow channels by particles in not included in the theory presented in this work and introduces another uncertainty to the experimental results.

5 Summary and Conclusion

We have investigated the role of plastic deformation in the leak-rate of metallic seals. We found that plastic deformation increases the area of real contact and reduces the interfacial separation at the critical constriction, which reduces the leak rate by roughly a factor of 8. Our experimental results show a nonlinear dependency of leak-rate with fluid pressure difference, due to a dependency of the applied axial force on the fluid pressure. The theoretical results, based on the Persson’s contact mechanics theory in combination with the Bruggeman effective medium theory are in good agreement with measured data for the leak-rate as a function of the fluid pressure. The measured leak-rate decreases with increasing time, which we interpret as resulting from clogging of critical constrictions by impurities present in the water.