TOuNN: Topology Optimization using Neural Networks

Abstract

Neural networks, and more broadly, machine learning techniques, have been recently exploited to accelerate topology optimization through data-driven training and image processing. In this paper, we demonstrate that one can directly execute topology optimization (TO) using neural networks (NN). The primary concept is to use the NN’s activation functions to represent the popular Solid Isotropic Material with Penalization (SIMP) density field. In other words, the density function is parameterized by the weights and bias associated with the NN, and spanned by NN’s activation functions; the density representation is thus independent of the finite element mesh. Then, by relying on the NN’s built-in backpropogation, and a conventional finite element solver, the density field is optimized. Methods to impose design and manufacturing constraints within the proposed framework are described and illustrated. A byproduct of representing the density field via activation functions is that it leads to a crisp and differentiable boundary. The proposed framework is simple to implement and is illustrated through 2D and 3D examples. Some of the unresolved challenges with the proposed framework are also summarized.

1 Introduction

Topology optimization (TO) is now a well-established field encompassing numerous methods including Solid Isotropic Material with Penalization (SIMP)-based optimization (Bendsoe and Sigmund 2003; Bendsoe et al. 2008; Sigmund 2001; Chandrasekhar et al. 2020), level set methods (Wang et al. 2003), evolutionary methods (Xie and Steven 1993) and topological sensitivity methods (Suresh 2013; Deng and Suresh 2015; Mirzendehdel et al. 2018; Mirzendehdel and Suresh 2015a). The variety of TO methods not only has added richness to the field but also offers design engineers several TO options to choose from.

The objective of this paper is to explore yet another TO method that differs from the above established methods in its construction. The proposed method relies on the popular Solid Isotropic Material with Penalization (SIMP) mathematical formulation, but uses a neural network’s activation functions (Gurney 1997) to represent the SIMP density. In other words, the density function is parameterized by the weights and bias associated with the NN, and spanned by NN’s activation functions; the density representation is thus independent of the finite element mesh. While prior works (see Section 2) have used neural networks (NN) to accelerate topology optimization, the objective here is to directly execute topology optimization using NN. The proposed framework is discussed in Section 3, followed by a description of the algorithm in Section 4. In Section 5, several numerical experiments are carried out to establish the validity, robustness and other characteristics of the method. Open research challenges, opportunities and conclusions are summarized in Section 6.

2 Literature review

Given the objective of this paper, the literature review is limited here to recent work on exploiting NN for TO. The primary strategy thus far is to use NN, and more broadly machine learning (ML) techniques, to accelerate TO through data-driven training, and image processing. For example, an encoder-decoder convolutional neural network (CNN) was used in Banga et al. (2018) to accelerate TO, based on the premise that a large data set spanning multiple loads and boundary conditions can help establish a mapping from problem specification to an optimized topology. The authors of Sosnovik and Oseledets (2019) also employed a CNN, but they established a mapping from intermediate TO results to the final optimized structure, thereby once again accelerating TO. A data-driven approach for predicting optimized topologies under variable loading cases was proposed in Ulu et al. (2016), where the binary images of optimized topologies are used as training data; then, a feed-forward neural net was employed to predict the optimized topology under different loading conditions. In Lei et al. (2019), the authors proposed ML models based on support vector regression and K-nearest neighbors to generate optimal topologies in a moving morphable component framework. Recently, a data-driven conditional generative adversarial network (GAN) was used (Nie et al. 2020) to generate optimized topologies based on input vector specification. The authors of Yu et al. (2019) used a CNN trained with a data set containing optimized topologies in conjunction with a GAN to generate optimal topologies, while the authors of Lin et al. (2018) used a ML framework to recognize and substitute evolving features during the optimization process, thereby improving the convergence rate. An encoder-decoder framework was proposed in Zhang et al. (2019) to learn optimized designs at various loading conditions, as a surrogate to gradient-based optimization. A recent effort that seeks to capture optimized topologies using NN is reported in Hoyer et al. (2019); they used CNNs to obtain an image prior of the optimized designs, and the prior was then post-processed to obtain optimized topologies.

In this paper, instead of using NN (or broadly ML techniques) as a training/acceleration tool, we directly execute topology optimization using NN. The primary concept is to use NN’s activation functions to represent the SIMP-based density field. Then, by relying on the NN’s backpropogation and a conventional finite element solver, the density field is optimized. A byproduct of representing the density field via activation functions is that it leads to a crisp and differentiable boundary, with implicit filtering. These and other characteristics of the method are demonstrated later through numerical experiments.

3 Proposed method

3.1 Overview

We will assume that a design domain with loads and restraints have been prescribed (for example, see Fig. 1). The objective here is to find, within this design domain, a topology of minimal compliance and desired volume. We will also assume that the domain has been discretized into finite elements for structural analysis.

Fig. 1

A classic topology optimization problem

The method discussed in this paper builds upon the popular SIMP formulation for topology optimization (TO) (Bendsoe and Sigmund 2003). In particular, the TO problem is converted into a continuous optimization problem using an auxiliary density field ρ defined over the domain. Assuming the volume constraint is active, as is typically assumed in such compliance minimization problems (Sigmund 2001), the topology optimization problem can be posed as (Bendsoe and Sigmund 2003; Bendsoe et al. 2008; Sigmund 2001):

$$ \begin{array}{@{}rcl@{}} \underset{\boldsymbol{\rho}}{\text{minimize}} &&\boldsymbol{u}^{\boldsymbol{\top}}\boldsymbol{K}(\boldsymbol{\rho})\boldsymbol{u} \end{array} $$

(1a)

$$ \begin{array}{@{}rcl@{}} \text{subject to} &&\boldsymbol{K}(\boldsymbol{\rho})\boldsymbol{u} = \boldsymbol{f} \end{array} $$

(1b)

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{e} \rho_{e} v_{e} = V^{*} \end{array} $$

(1c)

where u is the displacement field, K is the finite element stiffness matrix, f is the applied force, ρ_e is the density associated with element e, v_e is the volume of the element, and V^∗ is the prescribed volume.

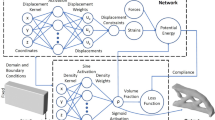
While the density field is typically represented using the finite element mesh, in this paper, it will be constructed independently via activation functions associated with a neural network (NN). In other words, given any point in the domain, the NN will output a density value (see Fig. 2). Using this transformation, we convert the constrained optimization problem in (1) into an unconstrained penalty problem by constructing a loss function (as explained later in Section 3.4). The loss function is minimized by employing standard machine learning (ML) techniques. The methodology and various components of the framework are described in the remainder of this section. We note that in ML, optimization is often referred to as training, sensitivity analysis as backpropagation, and iteration as epoch.

Fig. 2

Overview of the proposed TOuNN framework in 2D

3.2 Neural network

While there are various types of neural networks (NN), we employ here a simple fully connected feed-forward NN (Bishop 2006). The input to the network is either 2-dimensional (x, y) for 2D problems, or 3-dimensional (x, y, z) for 3D problems (see Fig. 3). The output of the NN is the density value ρ at that point. In other words, the NN is simply an evaluator that return the density value for any point within the domain; the value returned will depend on the weights, bias and activation functions, as described below.

Fig. 3

The architecture of the proposed neural net for 2D problems

The NN itself consists of a series of hidden layers associated with activation functions such as leaky rectified linear unit (LeakyReLU) (Goodfellow et al. 2016; Lu et al. 2019) coupled with batch normalization (Ioffe and Szegedy 2015) (this is illustrated in Fig. 3 for 2D problems; see description below). The final layer of the NN is a classifier layer with a softMax activation function that ensures that the density lies between 0 and 1.

As illustrated in Fig. 3, the NN typically consists of several hidden layers (depth); each layer may consist of several activation functions (height). By varying these two, one can increase the representational capacity of the NN. As an example, Fig. 4 illustrates a NN with a single hidden layer of height 2. Observe that each connection within the NN is associated with a weight, and each node is associated with an activation function and a bias. The output of any node is computed as follows. In Fig. 4, the value of $z_{1}^{[1]}$ is first computed as $z_{1}^{[1]} = w_{11}^{[1]}x + w_{21}^{[1]}y + b_{1}^{[1]}$, where $w_{ij}^{[k]}$ is the weight associated to the j th neuron in layer k from the i th neuron in the previous layer, and $b^{[k]}_{j}$ is the bias associated with the j th neuron in the k th layer. Then, the output $a_{1}^{[1]}$ of the node is computed as $a_{1}^{[1]} = \sigma (z_{1}^{[1]})$ where σ is the chosen activation function. For example, the ReLU activation function is defined as follows: σ(z) ≡ max(0,z). In this paper, we will rely on a variation of the ReLU, namely, LeakyReLU (Lu et al. 2019) that is differentiable. This and other differentiable activation functions are supported by various NN software libraries such as pyTorch (Paszke et al. 2019).

Fig. 4

Illustration of a simple network with one hidden layer of height 2

The final layer, as mentioned earlier, is a softMax function that scales the outputs from the hidden layers to values between 0 and 1. For example, in Fig. 4, we have $\psi _{1}^{[2]} = \frac {e^{z_{1}^{[2]}}}{ e^{z^{[2]}_{1}} + e^{z^{[2]}_{2}}}$. The softMax function has many outputs as inputs; however, we will use only the first output, and interpret it as the density field $(\rho = \psi _{1}^{[2]})$; the remaining outputs are disregarded, but can be used, for example, in a multi-material setting.

As should be clear from the above description, once the activation function is chosen, the output ρ(x,y) is defined globally, and determined solely by the weights and bias. We will denote the entire set of weights and bias by w. Thus, the optimization problem using the NN may be posed as:

$$ \begin{array}{@{}rcl@{}} \underset{\boldsymbol{w}}{\text{minimize}} &&\boldsymbol{u}^{\mathsf{T}}\boldsymbol{K}(\boldsymbol{w})\boldsymbol{u} \end{array} $$

(2a)

$$ \begin{array}{@{}rcl@{}} \text{subject to} && \boldsymbol{K}(\boldsymbol{w})\boldsymbol{u} = \boldsymbol{f} \end{array} $$

(2b)

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{e} \rho_{e} (\boldsymbol{w}) v_{e} = V^{*} \end{array} $$

(2c)

The element density value ρ_e(w) in the above equation is the density function evaluated at the center of the element.

3.3 Finite element analysis

For 2D finite element analysis, we use a regular 4 node quad element, and fast Cholesky factorization based on the CVXOPT library (Andreassen et al. 2011). For 3D, we use a regular 8 node hexahedral element, and an assembly free deflated finite element solver (Yadav and Suresh 2014; Mirzendehdel and Suresh 2015b). Note that the FE solver is outside of the NN (see Fig. 2), and is treated as a black-box by the NN. During each iteration, the density at the center of each element is computed by the NN, and is provided to the FE solver. The FE solver compute the stiffness matrix for each element based on the density evaluated at the center of the element. Note that, since the density function can be evaluated at multiple points within each element, it is possible to use advanced integration schemes to compute a more accurate estimate of element stiffness matrices; this is however not pursued in this paper. The assembled global stiffness matrix is then used to compute the displacement vector u, and the un-scaled compliance of each element:

$$ J_{e} = \{u_{e}\}^{T}[K]_{0}\{u_{e}\} $$

(3)

This will be used in sensitivity calculations as explained later on. The total compliance is given by:

$$ J = \sum\limits_{e} {\rho_{e}^{p}} J_{e} $$

(4)

where p is the usual SIMP penalty parameter.

3.4 Loss function

In this section, we describe how the optimization problem is solved using standard NN capabilities. While the optimization is usually carried out using optimality criteria (Bendsøe and Sigmund 1995) or MMA (Svanberg 1987), here we will rely on neural networks (NN). NNs are designed to minimize an unconstrained loss function using built-in procedures such as Adam optimization (Kingma and Ba 2015). We therefore convert the constrained minimization problem in (1) into an unconstrained minimization problem by relying on the penalty formulation (Nocedal and Wright 2006) to define the loss function as:

$$ L(\boldsymbol{w}) = \frac { \boldsymbol{u}^{\mathsf{T}}\boldsymbol{K}\boldsymbol{u}} {J^{0}} + \alpha \left( \frac{\sum \limits_{e} \rho_{e} v_{e} }{V^{*}} - 1\right)^{2} $$

(5)

where α is a penalty parameter, and J⁰ is the initial compliance of the system, used here for scaling. As described in Nocedal and Wright (2006), the solution of the constrained problem is obtained by minimizing the loss function as follows. Starting from a small positive value for the penalty parameter α, a gradient-driven step is taken to minimize the loss function. Then, the penalty parameter is increased and the process is repeated. Observe that, in the limit $\alpha \rightarrow \infty$, when the loss function is minimized, the equality constraint is satisfied and the objective is thereby minimized (Nocedal and Wright 2006). In practice, a maximum value of 100 is usually assigned for α (Nocedal and Wright 2006); the complete update scheme is described later in Algorithm 1. Other methods such as the augmented Lagrangian (Nocedal and Wright 2006) may also be used to convert the equality-constrained problem into an equivalent unconstrained problem. While this paper largely focuses on an equality-constrained topology optimization problems using NN, more recently, researchers have also solved generic optimization problems with inequality constraints using NN (Kervadec et al. 2019; Márquez-Neila et al. 2017). Adapting these techniques for TO is a topic of future research.

3.5 Sensitivity analysis

We now turn our attention to sensitivity analysis, a critical part of any optimization framework including NN. NNs rely on backpropagation (Rumelhart et al. 1986) to analytically compute (Baydin et al. 2017; Ruder 2016; Abadi et al. 2016; Paszke et al. 2019) the sensitivity of loss functions with respect to the weights and bias. This is possible since the activation functions are analytically defined, and the output can be expressed as a composition of such functions.

Thus, in theory, once the network is defined, no additional work is needed to compute sensitivities; it can be computed automatically (and analytically) via backpropogation! However, in the current scenario, the FE implementation is outside of the NN (see Fig. 2). Therefore, we need to compute some of the sensitivity terms explicitly.

Note that the sensitivity of the loss function with respect to a particular design variable w_i is given by:

$$ \frac{\partial L}{\partial w_{i}} = \sum\limits_{e} \frac{\partial L}{\partial \rho_{e}} \frac{\partial \rho_{e}}{\partial w_{i}} $$

(6)

The second term $\frac {\partial \rho _{e}}{\partial w_{i}}$ can be computed analytically by the NN through backpropagation since the density dependence on the weights is entirely part of the NN. On the other hand, the first term involves both the NN and the FE black-box, and must therefore be explicitly provided. Note that:

$$ \frac{\partial L}{\partial \rho_{e}} = \frac{1}{J^{0}} \frac{\partial}{\partial \rho_{e}} (\boldsymbol{u}^{\mathsf{T}}\boldsymbol{K}\boldsymbol{u}) + \frac{2 \alpha v_{e}}{V^{*}} \left( \frac{\sum\limits_{k} \rho_{k} v_{k}}{V^{*}} - 1 \right) $$

(7)

Further, recall that (Bendsoe and Sigmund 2013), (Sigmund 2001):

$$ \frac{\partial}{\partial \rho_{e}} (\boldsymbol{u}^{\mathsf{T}}\boldsymbol{K}\boldsymbol{u}) = -p \rho_{e}^{p-1} J_{e} $$

(8)

where J_e is the element-wise un-scaled compliance defined earlier. Thus, one can now compute the desired sensitivity as follows:

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial w_{i}} &=& \frac{1}{J^{0}}\left[ -p \sum\limits_{e} \rho_{e}^{p-1} J_{e} \frac{\partial \rho_{e}}{\partial w_{i}} \right]\\&+& \left[ \frac{2 \alpha}{V^{*}} \left( \frac{\sum\limits_{k} \rho_{k} v_{k}}{V^{*}} - 1 \right) \sum\limits_{e} \frac{\partial \rho_{e}}{\partial w_{i}} v_{e}\right] \end{array} $$

(9)

Due to the compositional nature of the NN, the gradient is typically stabilized using gradient clipping (Pascanu et al. 2012).

4 Algorithm

In this section, the proposed framework is summarized through an explicit algorithm. We will assume that the NN has been constructed with a desired number of layers, nodes per layer and activation functions. Here, we use pyTorch (Paszke et al. 2019) to implement the NN. The weights and bias of the network are initialized using Glorot normal initialization (Glorot and Bengio 2010).

The first step in the algorithm is to sample the domain at the center of each element; this is followed by the initialization of the penalty parameter α and the SIMP parameter p. In the main iteration, the element densities are computed using the NN using the current values of w. These densities are then used by the FE solver to solve the structural problem, and to compute the un-scaled element compliances J_e defined in (3). Further, in the first iteration, a reference compliance J⁰ is also computed for scaling purposes. Then, the loss function is computed using (5) and the sensitivities are computed using (9). The weights w are then updated using the built-in optimizer (here Adam optimizer). This is followed by an update of the penalty parameter α. Finally, we use the continuation scheme where the parameter p is incremented to avoid local minima (Rojas-Labanda and Stolpe 2015; Sigmund and Petersson 1998). The process is then repeated until termination. In typical mesh-based density optimization, the algorithm terminates if the maximum change in element density is less than a prescribed value. Here, since the density is a globally function, the algorithm is set to terminate if the percentage of gray elements (elements with densities between 0.05 and 0.95) 𝜖_g = N_gray/N_total is less than a prescribed value. Through experiments, we observed that this criteria is robust and consistent with the formulation.

Further, once the algorithm terminates, the density function can be sampled at a finer resolution to extract crisp boundaries, as illustrated below through numerical experiments. Finally, one can easily and accurately compute the gradient of the density field to compute, for example, boundary normals.

5 Numerical experiments

In this section, we conduct several numerical experiments to illustrate the TOuNN framework and algorithm. The 2D implementation is in Python, and uses the pyTorch library (Paszke et al. 2019) for the neural network. The 3D implementation is in C++, and uses the C++ implementation of pyTorch. The default parameters in the implementation are as follows.

• The material properties were E = 1, E_min = 1e^− 6 and ν = 0.3.

• A mesh size of 60 × 30 was used for all 2D experiments, unless otherwise stated.

• The NN is composed of 5 layers with 20 nodes (neurons) per layer, for both 2D and 3D, unless otherwise specified. The number of design variables, i.e., the size of w, is 1782, which corresponds approximately to the total number of 2D elements in a 60 × 30 mesh; this is equal the number of design variables in typical SIMP-based formulations.

• The LeakyReLU was chosen as the activation function for all nodes.

• The learning rate for the Adam optimizer was set at the recommended value of 0.01 (Smith 2018).

• A threshold value for gradient clipping was also set at the recommended value of 0.1 (Pascanu et al. 2012).

• The α parameter is updated as follows: α₀ = 0.1, α_max = 100 and Δα = 0.05.

• The p parameter is updated as follows: p₀ = 2.0, p_max = 4 and Δp = 0.01..

• The termination criteria were as follows: $\epsilon _{g}^{*} = 0.035$; a maximum of 499 iterations is also imposed..

• After termination, the density in each element was sampled on a 15 × 15 grid to extract the topology.

All experiments were conducted on a Intel i7 - 6700 CPU @ 2.6 Ghz with 16 GB of RAM. Through the experiments, we investigate the following.

• 1. Validation: The first task to validate the TOuNN framework by comparing the computed topologies for standard 2D benchmark problems, against those obtained via established methods (Andreassen et al. 2011). Typical convergence plots for the loss function, objective and constraint are also included..

• 2. Computational Cost: Typical computational costs are tabulated and compared..

• 3. NN Dependency: Next, we vary the NN size (depth and width), and study its impact on the computed 2D topologies..

• 4. Mesh Dependency: Similarly, we vary the FE mesh size in 2D and study its impact on the topology..

• 5. High Resolution Boundary: Boundary extraction via post-process sampling of the density field is illustrated through examples.

• 6. Three-dimensional: The proposed methodology is demonstrated using a 3D example.

• 7. Design and Manufacturing Constraints: Finally, we explore extension of the presented framework to include manufacturing constraints that render the obtained designs manufacturable.

5.1 Validation

We begin by comparing the topologies obtained from the proposed framework, against those obtained using the popular 88-line implementation of SIMP-based optimization (Andreassen et al. 2011). With the default parameters listed above, and with a filtering radius of 2.0 (Andreassen et al. 2011), the results are summarized in Fig. 5, where $v_{f}^{*}$ is the desired volume fraction. We observe that although the topologies are sometimes different (due to the infinitely many solutions), the compliances are marginally lower (better) for the TOuNN framework. The number of finite element operations is also summarized for each example. The sharpness of the boundary for the TOuNN framework stems from the analytic representation of the density field.

Fig. 5

Validation of TOuNN

Typical convergence plots for the mid-loaded cantilever beam is illustrated in Fig. 6, and the convergence plot for the Michell beam is illustrated in Fig. 7. In the two figures, the relative number of gray elements denotes the ratio of elements with densities between 0.05 and .95, to the total number of elements, i.e., 𝜖_g = N_gray/N_total. As described at the beginning of this section, optimization terminates when 𝜖_g < 0.035.

Fig. 6

Convergence plots for the problem in Fig. 5 mid-cantilever

Fig. 7

Convergence plots for the problem in Fig. 5 Michell beam

Finally, Table 1 summarizes the number of FE iterations for all 5 examples, for a wide range of volume fractions. We could not observe any pattern. However, for the distributed load problem, the algorithm failed to converge for two of the volume fractions. This is discussed further later in the paper.

Table 1 The number of iterations for various examples; asterisk denotes lack of convergence

5.2 Computational cost

Next, we briefly summarize the computational costs in TOuNN. Recall that the framework (see Fig. 2) can be separated into the following components:

• 1. Forward : Computing density values at the sampled points, a.k.a, forward propagation.

• 2. FEA : Finite element analysis to compute displacements, compliance, etc.

• 3. Wt.Update : Computing the loss function, gradient clipping and updating weights through backpropagation (includes sensitivity analysis).

• 4. Other : Computing the convergence criteria and other book-keeping tasks.

Table 2 summarizes the time taken for each example, and for each of the components. For the default mesh size of 60 × 30, FEA consumes approximately 50% of the total computation. For larger mesh sizes, the percentage increases as one would expect. We note that the cost of each TOuNN iteration is roughly twice the cost of each iteration in the 88-line code (Andreassen et al. 2011).

Table 2 Time taken in seconds for each component of the framework, for each example

5.3 NN size dependency

The functional representation of a neural network (here the density function) is global and highly non-linear, and evades simple characterization (Arora et al. 2016; Cybenko 1989; Sontag 1998). It is therefore difficult to predict a priori the minimum size of the neural network (depth and height) required to capture a particular topology, except in trivial scenarios. One such scenario is illustrated in Fig. 8a where the expected topology is a tensile bar. Due to the simplicity of the topology a neural network with a single hidden layer with a single node (size: 1 × 1) is sufficient to capture the topology of volume fraction 0.4 as illustrated in Fig. 8b. The number of design variables, i.e., the size of w, associated with this 1 × 1 network is 7.

Fig. 8

The tensile load problem; a neural net of size 1 × 1 is sufficient to capture the topology

As expected, for other non-trivial scenarios, a larger NN is required. To illustrate, we compute the topology for the tip-cantilever problem posed in Fig. 5, with varying neural net size (depth and height), keeping everything else at default values, as listed at the beginning of this section. The results are summarized in Fig. 9, where a NN: 2 × 8 (114) implies that the neural network has 2 layers, with each layer having 8 nodes, and the total number of design variables is 114. The algorithm did not converge when the NN size was too small (2 × 8). We observe that the complexity of the resulting topology remains unchanged with increasing NN size, while the computational cost (as captured by seconds/iteration) is weakly dependent on the NN size. It is a reasonable to expect that the minimum feature size will depend on the size of the neural network; further investigation is needed to validate this hypothesis.

Fig. 9

Optimized topologies for the tip-loaded cantilever beam, for varying neural net size: depth × height, with number of design variables in parenthesis

5.4 Effect of mesh size

We next briefly study the effect of the mesh size on the computed topology; all other parameters were kept constant at default values. Since the density field is independent of the mesh, the computed topology can also be expected to be independent of the mesh (provided the disretization is fine enough to capture the underlying physics). This can be observed in the results illustrated in Fig. 10.

Fig. 10

Impact of mesh size on the computed topology

5.5 High resolution boundary

One of the key challenges in TO is boundary resolution. This is often achieved by increasing the size of the mesh (which increases the computational cost), or by employing multi-resolution schemes (Nguyen et al. 2010; Groen et al. 2017). In the proposed framework, one can extract a high resolution boundary at no additional cost as follows. First the optimization is carried out; then the optimized (i.e. trained) weights, i.e., w^∗, are used to sample the domain at a fine resolution as illustrated in Fig. 11.

Fig. 11

High resolution boundary is extracted by first optimizing, and then using the optimized weights to sample the density at a high resolution

5.6 Extension to 3D

We now consider the implementation of the TOuNN framework to 3D. To achieve this, the fundamental changes are as follows: (1) we add an input neuron corresponding to the z coordinate and (2) we use a 3D FEA solver; this is illustrated in Fig. 12. All other aspects of the NN remain unchanged.

Fig. 12

Implementation of TOuNN in 3D

To validate the 3D implementation, we consider the edge cantilever beam problem (Liu and Tovar 2014) posed in Fig. 13a. The domain is discretized by a 15 × 30 × 9 hexahedral mesh. The topology obtained and the compliance using the code provided by Liu and Tovar (2014) are illustrated in Fig. 13b. In our formulation we used an identical mesh; all other parameters including the NN size were set at default values. The computed topology and compliance are illustrated in Fig. 13c. For this example, the 3D TOuNN framework takes fewer iterations and leads to a design with comparable compliance. Further, the number of finite elements is 4050, while the size of NN, i.e., the number of design variables, is 1800.

Fig. 13

a 3D edge cantilever (Liu and Tovar 2014). b Computed topology using Liu and Tovar (2014). c Computed topology using 3D TOuNN

5.7 Design and manufacturing constraints

Typically, design and manufacturing constraints are imposed in TO through projection operators (Vatanabe et al. 2016) that act on the density field ρ. Similarly, in the current formulation, we introduce input and output projection operators as illustrated in Fig. 14. As explained below, certain types of constraints can be handled as input projections, and others as output projections.

Fig. 14

Input and output projections can be used to impose design/manufacturing constraints

5.7.1 Symmetry

First we consider classic symmetry constraints within this framework. To enforce symmetry about, say, the x axis passing through (x₀,y₀), we transform the y coordinate as follows:

$$ y \leftarrow y_{0} + |y - y_{0} | $$

(10)

In other words, we treat symmetry as an input projection. No other change is needed to the framework. As an example, Fig. 15 illustrates imposing symmetry about the y axis for a tip-loaded cantilever beam. For comparison, see Fig. 5 where the symmetry was not imposed. Imposing symmetry results in a 13% increase in compliance.

Fig. 15

Symmetry about the y axis for a tip-cantilever beam

5.7.2 Non-design region

We now consider the non-design constraint where material should not be removed from certain a region Ω_N. Essentially, the density value should be forced to a value of 1 in this region. However, to facilitate backward propagation, i.e., sensitivity analysis, we treat this as an output projection via a functional approximation of the max operator:

$$ \rho \leftarrow 0.5(\rho + |1-\rho| ) \quad \{x,y\} \in {\Omega}_{N} $$

(11)

As an example, Fig. 16a illustrates the Michell beam problem with a non-design constraint, where material should not be removed from an annular region as shown. The computed topology is illustrated in Fig. 16b. Imposing this constraint results in a 14% increase in compliance, compared with the design without this constraint in Fig. 5.

Fig. 16

a Michell beam problem with a non-design constraint. b Optimized topology that satisfies the constraint

5.7.3 Extrusion

The final constraint explored here is extrusion in 3D, where the cross section of the topology must not change along the extruded direction. Extrusion constraint can be easily implemented here as an input projection. Specifically, suppose the extruded direction is x, then the x input is simply discarded in the 3D NN architecture; everything else remains the same (including the use of 3D FEA):

$$ (y,z) \leftarrow (x,y,z) $$

(12)

As an example, Fig. 17a illustrates a simple design problem in 3D; the desired volume fraction is 0.5. Figure 17b illustrates the optimized topology without extrusion constraint, while Fig. 17c illustrates the topology with an extrusion constraint along x. The extrusion constraint leads to a 6% increase in compliance, but takes fewer iterations.

Fig. 17

a A 3D beam problem. b Optimized topology without extrusion constraint. c Optimized topology with extrusion constraint along x

6 Opportunities and challenges

There are several extensions and opportunities that we foresee. A possible extension is multi-material topology optimization; this would entail extending the NN output to multiple dimensions. A potentially rich opportunity is in the infinitely differentiable density function. This translate into accurate computation of boundary normal, that could be useful in several applications.

We also observed some challenges. For example, the lack of detailed features in the computed topologies (see Fig. 5) could be of concern in certain applications. This limitation directly stems from the use of global activation functions in TOuNN. It may be possible to overcome this by exploring other activation functions.

A second (and related) challenge is the handling of distributed loads. For example, consider the distributed load problem in Fig. 18; the topologies computed via 88-line (Andreassen et al. 2011) and TOuNN are also illustrated. While the 88-line code (Andreassen et al. 2011) converged to a possible solution (with gray regions), TOuNN failed to converge due to the imposed termination criteria of requiring close to zero gray elements. Alternate termination criteria suitable for our framework are being explored. One simple solution, we observed, was to increase the penalization factor; alternately, one can penalize presence of gray elements through the loss function.

Fig. 18

Distributed loads leads to gray regions, and may therefore fail to converge

In this paper, a simple volume-constrained compliance minimization was explored; extensions to handle other objectives with multiple constraints are currently being explored (see Kervadec et al. 2019; Márquez-Neila et al. 2017).

An open and interesting question is the geometric interpretation of the NN design variables. However, even for the simple tensile bar problem in Fig. 8a where a NN of 1 × 1 was used, it was difficult to geometrically interpret the weights and bias values. This can be attributed to the use of non-linear softMax function at the output. Alternate output functions need to be explored.

Checkerboard patterns commonly occur in SIMP-based topology optimization (Díaz and Sigmund 1995; Sigmund and Maute 2013), and restriction methods such as filtering, perimeter control, etc. are often used in this context (Sigmund and Petersson 1998). However, in the current formulation, no checkerboard patterns were observed in any of the experiments. However, it is possible that checkerboard might begin to appear if the NN size is increased significantly; further investigation is needed.

In conclusion, in this paper, a direct topology optimization framework using a conventional neural network (NN) was proposed. The salient features of the framework are: (1) the direct use of NN’s activation functions, (2) exploiting built-in backpropogation for sensitivity analysis, (3) implicit filtering, (4) sharpness of the boundary, and (5) scope for relearning. The framework was validated and characterized through several benchmark problems in 2D and 3D. However, several challenges remain as highlighted above.