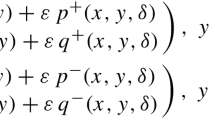Bifurcations of Zeros in Translated Families of Functions and Applications

Abstract

In this paper, we study the creation of zeros in a certain type of families of functions. The families studied are given by the difference of two basic functions with a translation made in the argument of one of these functions. The problem is motivated by applications in the 16th Hilbert problem and its ramifications. Here, we apply the results obtained to the study of bifurcations of critical periods in the Loud family of quadratic centers.

A Appendix

We put in the Appendix some classical results that we need, as well as some specific technicalities

1.1 A.1 Classical Results

We start with Goursat’s version of the implicit function theorem which requires continuous differentiability only with respect to the variable that we isolate.

Theorem A.1

[3] Let X be an open subset of ${\mathbb {R}}^{n}$ and let W be an open subset of ${\mathbb {R}}^{k}$. Consider (x₀, w₀) ∈ X × W and ${\Phi }:X\times W\to {\mathbb {R}}^{k}$ be such that

• (a) Φ(x₀, w₀) = 0;

• (b) Φ(x, w) is continuous on X × W;

• (c) ∂_wΦ(x,⋅) is continuous on W, for all x ∈ X;

• (d) ∂_wΦ(x₀, w₀) is surjective.

Then there exist a neighborhood X₁ × W₁ of (x₀, w₀) and a function ϕ : X₁ → W₁ such that ϕ(x₀) = w₀ and for every (x₁, w₁) ∈ X₁ × W₁ we have Φ(x₁, w₁) = 0 if and only if w₁ = ϕ(x₁). Moreover, ϕ is continuous.

Lemma A.2

Let {f_μ}_μ∈U be a continuous family of functions on (0, s₀) and let K ⊂ U be a compact set. Then $\lim _{s\to 0^{+}}f_{\mu }(s)=\ell (\mu )$, uniformly on μ ∈ K, if and only if $\lim _{(\mu ,s)\to (\hat \mu , 0^{+})}f_{\mu }(s)=\ell (\hat \mu )$, for every $\hat \mu \in K$.

Proof

Assume that $\lim _{s\to 0^{+}}f_{\mu }(s)=\ell (\mu )$, uniformly on μ ∈ K. Then μ↦ℓ(μ) is continuous on K. Let us show now that, under the uniformity assumption, f_μ(s) tends to $\ell (\hat \mu )$, as $(s,\mu )\longrightarrow (0^{+},\hat \mu )$. Consider a given ε > 0. Then, thanks to the claim, there exists a neighborhood $\mathscr U$ of $\hat \mu$ such that $\left |{\ell (\mu )-\ell (\hat \mu )}\right |<\varepsilon /2$ for all $\mu \in \mathscr U$. Furthermore, on account of the uniformity, there exists δ > 0 such that $\left |{f_{\mu }(s)-\ell (\mu )}\right |<\varepsilon /2$ for all s ∈ (0, δ) and $\mu \in \mathscr U$. Consequently,

$$ \left|{f_{\mu}(s)-\ell(\hat\mu)}\right|\leqslant \left|{f_{\mu}(s)-\ell(\mu)}\right|+\left|{\ell(\mu)-\ell(\hat\mu)}\right|<\varepsilon,\text{ for all } s\in(0,\delta) \text{ and } \mu\in \mathscr U, $$

and so $\lim _{(\mu ,s)\to (\hat \mu , 0^{+})}f_{\mu }(s)=\ell (\hat \mu ),$ as desired. Suppose now that $\lim _{(\mu ,s)\to (\hat \mu , 0^{+})}f_{\mu }(s)=\ell (\hat \mu )$, for every $\hat \mu \in K$. Then the map (s, μ)↦f_μ(s) extends continuously to [0, s₀/2] × K, which is compact. So the map is uniformly continuous, which clearly implies that $\lim _{s\rightarrow 0^{+}}f_{\mu }(s)=\ell (\mu )$ is uniform on K. This proves the result. □

It will be convenient in order to apply the implicit function theorem, to work with functions defined in an open neighborhood of the origin. For that reason, we extend monotone function $\hat f_{\mu }$ defined on a one-sided neighborhood of the origin to an odd function $\hat f_{\mu }$ defined in a full neighborhood of the origin.

Lemma A.3

Let {f_μ}_μ∈U be a continuous family of functions on (0, s₀) with $\lim _{s\to 0^{+}}f_{\mu }(s)=0$ uniformly on U. For each μ ∈ U, we define

$$ \hat f_{\mu}(s)=\left\{\! \begin{array}{cl} f_{\mu}(s),&\text{ if $s\in (0,s_{0})$,} \\ 0, &\text{ if $s=0$,} \\ -f_{\mu}(-s),&\text{ if $s\in (-s_{0}, 0)$.} \end{array} \right. $$

Then $\{\hat f_{\mu }\}_{\mu \in U}$ is a continuous family of functions on (−s₀, s₀). If in addition s↦f_μ(s) is monotonous on (0, s₀), for all μ ∈ U, then $\{\hat f^{-1}_{\mu }\}_{\mu \in U}$ is a continuous family of functions on (−s₁, s₁), for some s₁ > 0.

Proof

The continuity of $(s,\mu )\longmapsto \hat f_{\mu }(s)$ at some $(\hat s,\hat \mu )\in (0,s_{0})\!\times U$ is obvious, for $\hat s\neq 0$, whereas, for $\hat s=0$, it follows by applying Lemma A.2. Suppose additionally that f_μ is monotonous on (0, s₀) for all μ ∈ U. Then $\hat f_{\mu }$ is monotonous on (−s₀, s₀) for all μ ∈ U. Accordingly $(s,\mu )\longmapsto (\hat f_{\mu }(s),\mu )$ is an injective continuous map from the open set $(-s_{0},s_{0})\!\times U\subset \mathbb {R}^{k}$ to $\mathbb {R}^{k}$. Then, by the Domain Invariance Theorem, it follows that there exists s₁ > 0 such that $\{\hat f^{-1}_{\mu }\}_{\mu \in U}$ is a continuous family of functions on (−s₁, s₁). Hence, the result is proved. □

1.2 A.2 Technicalities

Recall (4) that ω is a deformation of the logarithmic function. The first claim of the following lemma is the deformation of the fomula for the logarithm of a product for the function ω.

Lemma A.4

The following hold:

• (a) ω(ab; α) = a^−αω(b; α) + ω(a; α),

• (b) $\frac {1}{\omega (s;\alpha )}\to \frac {|\alpha |-\alpha }{2}$, as s → 0⁺ uniformly on α ≈ 0,

• (c) Let α↦λ(α) be a continuous map at α = 0. Then 1 ≺₀s^λ(α)ω(s; α), if and only if λ(0) > 0.

• (d) $|\frac {\partial \omega }{\partial \alpha }/\omega ^{2}|$ is bounded.

Proof

The equality in (a) is straightforward taking the definition of ω(s; α) into account. The assertion in (b) follows easily from the inequality $\omega (s;\alpha )\geqslant \inf (-\log s,1/|\alpha |)$, cf. [18, S3]. Concerning (c), the sufficiency follows writing the compensator as $\omega (s;\alpha )=F(\alpha \log s)\log s$, where $F(x)\!:=\frac {e^{-x}-1}{x}$, and using that $|{F(x)}|\leqslant e^{|x|}$ for all $x\in \mathbb {R}.$ To show the necessity we use Lemma A.2, which implies that $\lim _{(\alpha ,s)\to (\hat \alpha , 0^{+})} s^{\lambda (\alpha )}\omega (s;\alpha )=0$ for any $\hat \alpha \in [-\delta ,\delta ]$ with δ > 0 sufficiently small. Clearly this is not possible if $\lambda (0)\leqslant 0$ because then $s^{\lambda (0)}\omega (s;0)=s^{\lambda (0)}\log s$ tends to $-\infty$ as s→0⁺. Thus λ(0) > 0, and so (c) follows. Claim (d) follows from Lemma 4.1.1 in [8]. □

Remark A.5

If $\lim _{s\to 0^{+}}{\Psi }_{1}(s;\mu )=L(\mu )$ and $\lim _{s\to 0^{+}}{\Psi }_{2}(s;\mu )=0$, with both limits being uniform on μ, then $\lim _{s\to 0^{+}}{\Psi }_{1}\bigl ({\Psi }_{2}(s;\mu );\mu \bigr )=L(\mu )$, uniformly on μ.

We shall deal with two types of families of admissible functions, $\{s^{\lambda }\}_{\lambda >0}$ and {sω(s; α)}_{α≈ 0}, both defined in principle, for s > 0. It is clear that each function f_λ(s) = s^λ in the first family is monotonously increasing and that, by applying Lemma A.3, {f_λ}_{λ> 0} and $\{f_{\lambda }^{-1}\}_{\lambda >0}$ can be continuously extended to (−s₀, s₀) for some s₀ > 0. It is obvious in addition that $f_{\lambda }^{-1}(s)=s^{1/\lambda }$. In the following result we show analogous properties for the second family.

Lemma A.6

Set f_α(s) = sω(s; α). Then the following hold:

• (a) f_α(ab) = a^1−αf_α(b) + bf_α(a),

• (b) There exists s₀ > 0 and ε > 0 such that {f_α}_{α∈(−ε, ε)} is a continuous family of monotonous increasing functions on (0, s₀) with $\lim _{s\to 0^{+}}f_{\alpha }(s)=0$, uniformly on α ∈ (−ε, ε). In addition $\{f^{-1}_{\alpha }\}_{\alpha \in (-\varepsilon ,\varepsilon )}$ is a continuous family of functions on (0, s₀), with $\lim _{s\to 0^{+}}f^{-1}_{\alpha }(s)=0$, uniformly on α ∈ (−ε, ε).

• (c) $f_{\alpha }^{-1}(s)\sim _{0} \frac {s\kappa (\alpha )}{\omega (s;\alpha /(1-\alpha ))}$, where $\kappa (\alpha )\!:=(1-\alpha ) \alpha ^{\frac {\alpha +|\alpha |}{2(1-\alpha )}}.$

Proof

The equality in (a) is straightforward taking the definition of ω(s; α) into account. The monotonicity in (b) follows using that, by (b) in Lemma A.4, $f_{\alpha }^{\prime }(s)=-1+(1-\alpha )\omega (s;\alpha )$ tends to $+\infty$ as (α, s) → (0, 0⁺). The fact that f_α(s) tends to zero as s → 0⁺ uniformly on α is a consequence of (c) in Lemma A.4. Taking this into account, the assertion concerning $f_{\alpha }^{-1}$ follows by applying Lemma A.3. In order to show (c), setting $\alpha ^{\prime }\!:=\frac {\alpha }{1-\alpha }$, we first claim that

$$ {\Psi}_{1}(s;\alpha)\!:=\left.\frac{f_{\alpha}^{-1}(u)}{\frac{u}{\omega(u;\alpha^{\prime})}}\right|_{u=f_{\alpha}(s)}=\frac{\omega\bigl(s\omega(s;\alpha);\alpha^{\prime}\bigr)}{\omega(s;\alpha)} $$

tends to κ(α) as s→0⁺ uniformly on α ≈ 0. Note that (c) will follow once we prove this claim. Indeed, since $\lim _{s\to 0^{+}}f^{-1}_{\alpha }(s)=0$ uniformly on α ≈ 0 by (b), we get the desired conclusion, by applying Remark A.5, with ${\Psi }_{2}(s;\alpha )=f^{-1}_{\alpha }(s).$

In order to prove the claim, we apply Lemma A.2. To this end note that $\kappa (\alpha _{0})=(1-\alpha _{0})\alpha _{0}^{\frac {\alpha _{0}}{1-\alpha _{0}}}$, if α₀ > 0, κ(0) = 1 and κ(α₀) = 1 − α₀, if α₀ < 0. If α₀≠ 0, then, by definition,

$$ \frac{\omega\bigl(s\omega(s;\alpha);\alpha^{\prime}\bigr)}{\omega(s;\alpha)} =\frac{s^{-\alpha^{\prime}}\left( \frac{s^{-\alpha}-1}{\alpha}\right)^{-\alpha^{\prime}}-1}{s^{-\alpha}-1}\frac{\alpha}{\alpha^{\prime}}, $$

which clearly tends to 1 − α₀, as (α, s)→(α₀, 0⁺), in case that α₀ < 0. If α₀ > 0, then for convenience we write the above equality as

$$ \begin{array}{@{}rcl@{}} \frac{\omega\bigl(s\omega(s;\alpha);\alpha^{\prime}\bigr)}{\omega(s;\alpha)} \!&=&\!\frac{s^{-\alpha^{\prime}+\alpha\alpha^{\prime}}(1-s^{\alpha})^{-\alpha^{\prime}}{-}\alpha^{-\alpha^{\prime}}}{s^{-\alpha}(1-s^{\alpha})}\frac{\alpha^{1+\alpha^{\prime}}}{\alpha^{\prime}}{=}\frac{s^{-\alpha}(1{-}s^{\alpha})^{-\alpha^{\prime}}-\alpha^{-\alpha^{\prime}}}{s^{-\alpha}(1-s^{\alpha})}(1-\alpha)\alpha^{\alpha^{\prime}}\\ &=&\frac{(1-s^{\alpha})^{-\alpha^{\prime}}-\alpha^{-\alpha^{\prime}}s^{\alpha}}{1-s^{\alpha}}(1-\alpha)\alpha^{\alpha^{\prime}}, \end{array} $$

which tends to $(1-\alpha _{0})\alpha _{0}^{\frac {\alpha _{0}}{1-\alpha _{0}}}$, as (α, s)→(α₀, 0⁺). It only remains to see that $\frac {\omega (s\omega (s;\alpha );\alpha ^{\prime })}{\omega (s;\alpha )}\longrightarrow 1$ as (α, s)→(0, 0⁺). With this aim in view, some manipulations show that

$$ \begin{array}{@{}rcl@{}} \frac{\omega\bigl(s\omega(s;\alpha);\alpha^{\prime}\bigr)}{\omega(s;\alpha)}\!&-&\!1+\alpha {=}\frac{\bigl(s\omega(s;\alpha)\bigr)^{-\alpha^{\prime}}-1}{\alpha^{\prime}}\frac{\alpha}{s^{-\alpha}-1}-1+\alpha =(1-\alpha)\left( \frac{s^{-\alpha^{\prime}}\left( \frac{s^{-\alpha}-1}{\alpha}\right)^{-\alpha^{\prime}}-1}{s^{-\alpha}-1}-1\right)\\ \!&=&\!(1{-}\alpha)\left( \frac{\left( \frac{1-s^{\alpha}}{\alpha}\right)^{-\alpha^{\prime}}-s^{\alpha}}{1-s^{\alpha}}-1\right) {=}(1{-}\alpha)\frac{\left( \frac{1-s^{\alpha}}{\alpha}\right)^{-\alpha^{\prime}}-1}{1-s^{\alpha}} {=}\frac{\omega\bigl(\omega(s;-\alpha);\alpha^{\prime}\bigr)}{\omega(s;-\alpha)},\!\! \end{array} $$

(30)

where we take $\alpha ^{\prime }=\frac {\alpha }{1-\alpha }$ into account several times. Note that

$$ \frac{\omega\bigl(\omega(s;-\alpha);\alpha^{\prime}\bigr)}{\omega(s;-\alpha)}= \frac{\omega\bigl(x;\alpha^{\prime}\bigr)}{x}, \text{ with } x=\omega(s;-\alpha)\longrightarrow +\infty, \text{ as } (\alpha,s)\longrightarrow (0, 0^{+}), $$

(31)

due to $\omega (s;\alpha )\geqslant \inf (-\log s,1/|\alpha |).$ Moreover, $\omega (s;\alpha )=F(\alpha \log s)\log s$, where recall that $F(x)=\frac {e^{-x}-1}{x}$ verifies that $|{F(x)}|\leqslant e^{|x|}$, for all $x\in \mathbb {R}.$ Accordingly, for x > 1 and $\alpha ^{\prime }\in [-\frac {1}{2},\frac {1}{2}]$, we can assert that

$$ \left|\frac{\omega(x;\alpha^{\prime})}{x} \right|\leqslant\frac{\log x}{x^{1-|\alpha^{\prime}|}}\leqslant\frac{\log x}{x^{1/2}}. $$

Hence, $\frac {\omega (x;\alpha ^{\prime })}{x}\longrightarrow 0$, as $x\longrightarrow +\infty$, uniformly on $\alpha ^{\prime }\in [-\frac {1}{2},\frac {1}{2}]$. This, together with (31), implies that

$$ \frac{\omega\bigl(\omega(s;-\alpha);\alpha^{\prime}\bigr)}{\omega(s;-\alpha)}\longrightarrow 0 \text{ as $(\alpha,s)\longrightarrow (0, 0^{+})$} $$

because $\alpha ^{\prime }=\frac {\alpha }{1-\alpha }\longrightarrow 0$ as α→0. Therefore, on account of (30), we finally obtain

$$ \frac{\omega\bigl(s\omega(s;\alpha);\alpha^{\prime}\bigr)}{\omega(s;\alpha)}-1=\frac{\omega\bigl(\omega(s;-\alpha);\alpha^{\prime}\bigr)}{\omega(s;-\alpha)}-\alpha\longrightarrow 0 \text{ as $(\alpha,s)\longrightarrow (0, 0^{+}),$} $$

as desired. This proves the claim and so the result follows. □

Remark A.7

By Lemma A.3, each family $\{s^{\alpha }\}_{\alpha >0}$ and {sω(s; α)}_{α≈ 0} extends to a continuous family of homeomorphisms $\{\hat f_{\alpha }\}$ on (−s₀, s₀) with $\hat f_{\alpha }(0)=0$. Their respective inverses form also a continuous family of functions $\{\hat f^{-1}_{\alpha }\}_{\alpha }$ on (−s₁, s₁) for some s₁ > 0. In the sequel, by an abuse of notation and when there is no risk of ambiguity, we will denote $\hat f$ and $\hat f^{-1}$ by f and f^− 1, respectively.

Lemma A.8

The Dulac time T₋(s; F) of the Loud family (5) restricted to the line D + F = 0 between the transverse sections {x = 0} parametrized by $\sigma (s)=\left (0,\frac {1-s}{\sqrt {F(F-1)}}\right )$ and {y = 0, x < 0} satisfies the following:

• (a) For every F₀ > 3/2, there is δ > 0, such that $T_{-}(s;F)=T_{00}(F)+T_{01}(F)s^{r(F)}+{\mathcal {F}}_{r(F_{0})+\delta }^{\infty }(F=F_{0})$ with $r(F)=\frac {1}{2(F-1)}$ and

  $$T_{01}(F)=-F^{-\frac{F}{F-1}}2^{\frac{1}{2(F-1)}}\sqrt{F(F-1)}\sqrt{\pi}\frac{\Gamma(1-r(F))}{\Gamma(\frac{1}{2}-r(F))}.$$

  In particular, T₀₁(F) = −(F − 2)U₀₁(F) with U₀₁(2) > 0.

• (b) $T_{-}(s;F)=T_{00}(F)+T_{01}(F)s^{r(F)}+T_{101}s\omega \left (s;\frac {F-2}{F-1}\right )+T_{100}(F)s+{\mathcal {F}}_{3/2-\delta }^{\infty }(F=2)$ with T₁₀₁(2) > 0.

Proof

We perform the projective change of coordinates $(u,v)=\phi (x,y)=(1-\sqrt {F(F-1)}\frac {y}{1-Fx},\frac {1}{1-Fx})$ which brings the Loud vector field (x − 1)y∂_x + (x + F(y² − x²))∂_y into $X_{F}=\frac {1}{v}[P_{F}(u,v)u\partial _{u}+Q_{F}(u,v)v\partial _{v}]$ where $P_{F}(u,v)=\sqrt {\frac {F-1}{F}}(u-2)(v-1)$ and $Q_{F}(u,v)=\frac {1}{\sqrt {F(F-1)}}(u-1)((F-1)v+1)$ and the transverse sections x = 0 and y = 0 into v = 1 and u = 1 respectively. The hyperbolicity ratio of the saddle of X_F at (u, v) = (0, 0) is $r(F)=\frac {1}{2(F-1)}<1$ for F > 3/2. This gives us the announced expansion in (a). Let us now compute the coefficient T₀₁(F). In the coordinate chart (u, v) the parametrization σ(s) translates into σ(s) = (s, 1) and we can take the parametrization τ(s) = (1, s) in the target transverse section. By applying [7, Theorem A], after some tedious but straightforward computations, we obtain that

$$ \begin{array}{@{}rcl@{}} T_{01}(F)&=&F^{-\frac{F}{F-1}}\left( -\sqrt{F(F-1)}+\frac{1}{2}\sqrt{\frac{F}{F-1}}{{\int}_{0}^{1}}\left( (1-\frac{u}{2})^{-1-r(F)}-1\right)\frac{du}{u^{1+r(\mu)}}\right)\\ &=&-F^{-\frac{F}{F-1}}2^{\frac{1}{2(F-1)}}\sqrt{F(F-1)}\sqrt{\pi}\frac{\Gamma(1-r(F))}{\Gamma(\frac{1}{2}-r(F))} \end{array} $$

thanks to the formula ${{\int \limits }_{0}^{1}}\left ((1-\frac {u}{2})^{-a}-1\right )\frac {du}{u^{a}}=\frac {2^{a-1}\sqrt {\pi }{\Gamma }(2-a)}{(1-a){\Gamma }(\frac {3}{2}-a)}-\frac {1}{1-a}$ in which appears the Gamma function Γ. In particular, $\frac {\Gamma (1-r(F))}{\Gamma (\frac {1}{2}-r(F))}=\frac {\sqrt {\pi }}{2}(F-2)+O((F-2)^{2})$.

To prove (b), it suffices to take F ≈ 2 where the announced asymptotic expansion holds by [13, Theorem A]. In fact, we have $T_{-}(s)=T_{00}+T_{01}s^{r}+T_{10}s+T_{02}s^{2r}+{\mathcal {F}}_{2r_{0}+\delta }(r=r_{0})$ if $r_{0}>\frac {1}{2}$ and T₁₀₁ = (1 − 2r)T₀₂, T₁₀₀ = T₁₀ + T₀₂ so that

$$T_{101}|_{F=2}=\lim\limits_{r\to\frac{1}{2}}(1-2r)T_{02}=-\lim\limits_{r\to\frac{1}{2}}(1-2r)T_{10}.$$

By [14, Theorem A]

$$T_{10}=-\sigma_{120}\left( \frac{\sigma_{121}}{\sigma_{120}Q(0,\sigma_{120})}+\frac{\sigma_{111}}{L_{1}(\sigma_{120})}\hat B_{1}(1/r-1,\sigma_{120})\right),$$

with

$$L_{1}(u)={\exp{\int}_{0}^{u}}\left( \frac{P(0,z)}{Q(0,z)}+\frac{1}{r}\right)\frac{dz}{z}=(1+(F-1)u)^{2F}$$

and

$$B_{1}(u)=L_{1}(u)\partial_{1}Q^{-1}(0,u)=-\sqrt{F(F-1)}(1+(F-1)u)^{2F-1}.$$

Since $1-(1/r-1)=\frac {1-2r}{-r}$ we have that

$${-}\lim\limits_{r\to\frac{1}{2}}(1{-}2r)T_{10}{=}{-}\frac{\sigma_{120}^{2}\sigma_{111}}{2L_{1}(\sigma_{120})}B_{1}^{\prime}(0)|_{F=2}{=}\frac{\sigma_{120}^{2}\sigma_{111}}{L_{1}(\sigma_{120})}\sqrt{F(F-1)}(2F-1)(F\!-1)|_{F=2}>0$$

using [14, Theorem B.1] in the first equality. □