1 Introduction

Carbon nanotubes (CNTs), large molecular wires of carbon, are important structures at the nanoscale. Estimates vary as to exactly how strong a carbon nanotube is, but experiments have already shown that the tensile strength of these materials is more than 40 times higher than that of quality steel and, by some estimates, a nanotube thread thinner than human hair can hold a trailer. Nanotechnology scientists pointed out that CNTs are not only the most powerful materials ever made, but are among the most powerful materials that can be made in the future [1,2,3,4].

Double-walled carbon nanotubes (DWCNTs) are an insoluble nanostructure similar to single-walled carbon nanotubes (SWCNTs) that can be suspended and dispersed based on a combination of ultrasonic and surfactant vibration. Such a special class of nanostructures includes two CNTs, one is nested into another. In contrast to SWCNTs, the advantage of utilizing DWCNTs is the ability of combination of functionality and solubility [5]. The wondrous characteristics of CNTs, such as good tensile resistance, high elastic modulus and the carbon nature of nanotubes, have resulted in enormous efforts into the efficiency and proliferation of nanotube growth processes over the last decade. Generally, the investigations on CNTs can be divided into three branches; studies on the chemistry, physics and mechanical properties of CNTs [6,7,8,9,10,11,12,13,14,15] and those focused on the static/dynamic behavior of CNTs. In the category of mechanics, Theodosiou and Saravanos [16] developed molecular mechanics with mixing in finite element method (FEM) to model CNTs. Garg et al. [17] found an equivalent orthotropic elastic model for multi-walled carbon nanotubes (MWCNTs) using FEM which simulated large deformations and their nonlinear responses. Based on nonlinear structural mechanics, Pantano et al. [18] analyzed SWCNTs and MWCNTs by employing shell elements and modeled the van der Waals forces using some special interaction elements. More importantly, to show the importance of van der Waals (vdW) interaction, they incorporated wrinkles into the CNTs. Deformation and axial compression of SWCNTs and MWCNTs were reported by Pantano et al. [19, 20]. On the basis of FEM utilizing shell elements, bending, stability and post-stability of CNTs were estimated. Several articles by Li and Chou can be found in which they assessed the natural frequencies of CNTS [21], the axial stability based on multiscale modeling in combination of atomistic CNTs and FEM continuum matrix [22] and the vibrational response of MWCNTs [23]. By means of multiscale modeling, Li and Chou [24] published the results of their research originated from merging a polymer macroscale matrix and the CNTs atomic scale. By establishing molecular mechanics, Li and Chou also investigated the elastic stability and bending behavior of CNTs [25, 26]. Ru [27] investigated the static stability of a DWCNT resting in a polymer foundation under axial compressive loads. The vdW interactions between two tubes were considered, and the elastic matrix was supposed to follow the Winkler model. The displacement field was assumed on the basis of the Donnell shell theory, and the obtained stability relation was analytically solved based on Navier’s technique. Axial stability analysis of CNTs by means of molecular mechanics was studied by Chang et al. [28]. They confirmed that an armchair CNT has less stability than a zigzag CNT. On the other hand, they proved that the vdW interaction slightly affects the results of axial buckling of DWCNTs. Qian et al. [29] examined the effects of curvature on axially compressed hinged DWCNTs assuming small diameter and curvature dependency on the vdW pressures. The buckling behavior of an embedded multi-walled carbon nanotube bridged was investigated by Liew et al. [30]. The simply supported boundary condition was applied on the nanotubes, and the bifurcation was analyzed with and without the presence of vdW effects. Zhang et al. [31] developed the energy method for static stability of a lengthy DWCNT placed on a soft substrate. The nanotubes were exposed to far-field hydrostatic compression. Wang et al. [32] proposed a solid shell element to calculate the critical stability value of DWCNTs subject to axial compressive loads. The element sufficiently modeled the effects of transverse shear deformations which is significant in nanotubes with small aspect ratios. Their outcomes were compared to a molecular dynamics (MD) simulation which led to an acceptable match between the results of two approaches. Ranjbartoreh et al. [33] inspected a pivot DWCNT surrounded by an elastic environment subjected to an axial compressive load. Wang et al. [34] presented an eccentric compressive load on a DWCNT to consider the critical buckling conditions. The model was based on an elastic foundation, and the Galerkin technique was employed to solve the resulting relations. Temperature impact on a longitudinally compressed DWCNT was studied by Yao and Han [35]. The linear Donnell shell relation was utilized to derive the governing equations, and the system was embedded in hinged boundaries at both ends. Using a molecular mechanics method, Lu et al. [36] analyzed a DWCNT under static stability conditions in a thermal environment. They showed that the temperature effects decrease the stability strength of the nanotubes. Lu et al. [37] studied a shell theory on the basis of an interatomic potential to examine buckling of DWCNTs. Their results exhibited that the vdW interaction has no significantly impact on the DWCNTs’ deformation in the post-buckling state. Hwang et al. [38] considered MD simulation for a MWCNT exposed to a longitudinal load. In a special research, Mohammadimehr et al. [39] examined pivot DWCNTs under static stability condition placed on an elastic matrix. They employed the Timoshenko beam approach to derive the governing equations and used nonlocal elasticity theory in order to evaluate the small-scale effects. Shima [40] analyzed the nonlinear static buckling of CNTs. Elishakoff and Bucas [41] modeled a DWCNT in a clamped-free condition subjected to a concentric axial force and employed the Bubnov–Galerkin technique to present critical buckling modes. Axial stability of pinned CNTs assuming thin beam theory nested on an elastic foundation with respect to the Timoshenko beam approach was inspected by Berrabah et al. [42] within the framework of stress-driven approach of Eringen’s nonlocal elasticity. Timesli et al. [43] predicted the critical buckling modes for an axially compressed MWCNT by applying Donnell’s shell theory. Chemi et al. [44] determined the critical buckling modes for a DWCNT assuming the Timoshenko beam model and nonlocal elasticity theory. The nanotubes were nested on an elastic matrix, and different chirality was then considered. The results showed that the buckling loads depend remarkably on the chirality of the nanotubes.

Following previously published research, this paper will step forward with the analysis of DWCNTs. More obviously, the first attempt of examining the impact of eccentricity on a DWCNT is addressed in this research. Although DWCNTs should be concentric, eccentricity can likely occur during the production of DWCNTs, because such a deviation cannot be easily controlled. There have been some researches which studied the physics of eccentricity among nano-shells/tubes [45, 46].

The main objective of the current study is to present the effect of eccentricity on the static stability of double-walled carbon nanotubes with reference to the nonlocal approach of strain gradient theory through investigating the effects of nonlocal stress and size reduction separately. With the aid of Lagrangian strains and the variational principle, the classical beam theory assumption is applied through the energy method. The van der Waals interaction bettween two CNTs is applied linearly on the basis of the Lennard–Jones model. The numerical findings are presented based on the analytical approach and compared to the results of published works in the literature for the sake of validation. Finally, to investigate the effects of different parameters/conditions on the static stability of DWCNTs, some qualitative analyses are presented graphically.

2 Theoretical specimen

2.1 Beam model

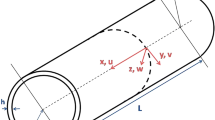
A Cartesian coordinate system is adopted in Fig. 1 for a DWCNT in which an eccentricity can be observed. The dedicated symbols based on the defined coordinate system are: internal radius of the outer tube based on the coordinate origin (\(S_{i})\), internal radiuses of the inner and outer tubes (\(r_{i}\) and \(R_{i})\), exterior diameter of the inner tube (d), exterior diameter of the outer tube (D), thickness of inner tube (h), thickness of the outer tube (H) and the eccentricity distance c.

Fig. 1
figure 1

Three-dimensional (a) and cross section (b) of the DWCNT

Full size image

The kinematic motion of the DWCNTs’ nodes can be investigated by means of the classical beam model as

$$\begin{aligned} \left\{ \begin{array}{c} u_{1i}\left( {x,z} \right) \\ u_{3i} \left( {x,z} \right) \\ \end{array} \right\} =\left\{ {{\begin{array}{*{20}c} {u_{i} \left( x \right) -z\frac{\mathrm{d}w_{i} \left( x \right) }{\mathrm{d}x}} \\ {w_{i} \left( x \right) } \\ \end{array} }} \right\} ; \quad {i}=1,2, \end{aligned}$$
(1)

where u(x) and w(x) are mid-surface displacements, and \(u_{1i} \) and \(u_{3i} \) denote the point’s displacements in the x and z directions, respectively. In addition, the thickness direction is denoted by z. Furthermore, it is noted that the index 1 is associated with the outer tube and the index 2 with the inner one.

Using Lagrangian strains and assuming Eq. (1), the linear static strain tensor can be derived as

$$\begin{aligned} \left\{ {\varepsilon _{xxi} } \right\} =\left\{ {\frac{\mathrm{d}u_{i} }{\mathrm{d}x}-z\frac{\mathrm{d}^{2}w_{i} }{\mathrm{d}x^{2}}} \right\} ;\quad { i}=1,2. \end{aligned}$$
(2)

The stress resultants in the local framework are shown as

$$\begin{aligned} \left\{ {N_{xxi} } \right\} =\int _z {\left\{ {\sigma _{xxi} } \right\} \mathrm{d}z} =E_{i} \int _{A_{i}} {\left\{ {\frac{\mathrm{d}u_{i} }{\mathrm{d}x}-z\frac{\mathrm{d}^{2}w_{i} }{\mathrm{d}x^{2}}} \right\} \mathrm{d}} {A}_{{i}} ;\quad {i}=1,2, \end{aligned}$$
(3)
$$\begin{aligned} \left\{ {M_{xxi} } \right\} =\int _z {\left\{ {\sigma _{xxi} z} \right\} \mathrm{d}z} =E_{i} \int _{A_{i} } {\left\{ {z\frac{\mathrm{d}u_{i} }{\mathrm{d}x}-z^{2}\frac{\mathrm{d}^{2}w_{i} }{\mathrm{d}x^{2}}} \right\} \mathrm{d}} {A}_{\mathrm{i}} ;\quad {i}=1,2, \end{aligned}$$
(4)

in which the moment and in-plane static stress resultants are \(M_{x} \), and \( N_{x} \), respectively, and \(E_{i}\) represents the elastic modulus.

The cross-sectional moments of inertia for the DWCNT can be written as

$$\begin{aligned} I_{c1}= & {} \int _{A_{1} } {z^{2}\mathrm{d}A_{1} } +c^{2}\int _{A_{1} } {\mathrm{d}A_{1} }, \end{aligned}$$
(5)
$$\begin{aligned} I_{c2}= & {} \int _{A_{1} } {z^{2}\mathrm{d}A_{2} }, \end{aligned}$$
(6)

where A is the cross-sectional area of the nanotubes.

The variational principle can be expressed as

$$\begin{aligned} \delta \Pi _{i} =\int {\left( {\delta K_{i} -\left( {\delta U_{i} +\delta W_{i} } \right) } \right) \mathrm{d}V} =0 ; \quad {i}=1,2, \end{aligned}$$
(7)

in which \(\delta U, \delta K\) and \(\delta W\) symbolize the first variations of strain potential energy, kinetic energy and the work done by the external forces, respectively.

Thereby, the strain energy may be expanded as

$$\begin{aligned} U_{i}= & {} \frac{1}{2}\int _0^{L_{i} } {\int _{A_{i} } {\left( {\sigma _{xxi} \varepsilon _{xxi} } \right) \mathrm{d}A_{i} \mathrm{d}x} } =0 ;\quad { i}=1,2, \end{aligned}$$
(8)
$$\begin{aligned} \delta U_{i}= & {} \frac{1}{2}\int _0^{L_{i} } {\int _{A_{i} } {\left( {\sigma _{xxi} \frac{\mathrm{d}\delta u_{i} }{\mathrm{d}x}-\sigma _{xxi} z\frac{\mathrm{d}^{2}\delta w_{i} }{\mathrm{d}x^{2}}} \right) } } \mathrm{d}A_{i} \mathrm{d}x=0 ;\quad {i}=1,2, \end{aligned}$$
(9)
$$\begin{aligned} \delta U_{i}= & {} \frac{1}{2}\int _0^{L_{i} } {\left[ {\frac{\mathrm{d}}{\mathrm{d}x}\left( {N_{xxi} \delta u_{i} } \right) -\frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}\left( {M_{xxi} \delta w_{i} } \right) } \right] \mathrm{d}x} =0 ;\quad {i}=1,2, \end{aligned}$$
(10)

in which \(\sigma \) and \(\varepsilon \) denote the static stress and strain tensors, respectively, and \(\delta \) is the symbol of variation.

2.2 vdW interaction

The Lennard–Jones (LJ) model is adopted here to describe the vdW interaction between two nanotubes. Thereby, it is assumed that the vdW forces between the tubes are in opposite direction with the same absolute values as in [27, 39]:

$$\begin{aligned} P_{1} \left( x \right) \times S_{i} =-P_{2} \left( x \right) \times r_{i}, \end{aligned}$$
(11)

in which \(S_{i}\) is calculated by the following geometrical relation:

$$\begin{aligned} S_{i} =c\times \cos \left( \theta \right) +\sqrt{R_{i}^{2}-c^{2}\times \sin ^{2}\left( \theta \right) } \;\; ;\;\; 0\le c<\left[ {R_{i} -r_{i} } \right] . \end{aligned}$$
(12)

As is geometrically detailed in Fig. 1a, the distance between the centers of the two CNTs (offset distance) is symbolized with c. \(P_{1}\) and \(P_{2}\) are the pressures exerted on both nanotubes’ corresponding points. Additionally, it is assumed that the pressure created by vdW bonds at any point x on the exterior CNT is a function of the distance between the exterior and the interior CNTs at that point:

$$\begin{aligned} P_{1} \left( x \right) =g\left[ {\delta \left( x \right) } \right] , \end{aligned}$$
(13)

in which \(g\left[ {\delta \left( x \right) } \right] \) defines the function of the space \(\delta \left( x \right) \) which may be a nonlinear or linear function. Based on the LJ model and examining the linear relation of \(g\left[ {\delta \left( x \right) } \right] \), the distributed pressure on the outer tube can be derived as [27, 39]

$$\begin{aligned} P_{1} \left( x \right) =h\left[ {K_{O} \left( {w_{1} -w_{2} } \right) } \right] , \end{aligned}$$
(14)

where \(K_{O}\) is the vdW modulus value.

Substituting Eq. (14) into Eq. (11), one gets [27, 39]

$$\begin{aligned} P_{2} \left( x \right) =-\frac{S_{i} }{r_{i} }hK_{O} \left( {w_{1} -w_{2} } \right) . \end{aligned}$$
(15)

The works done by the external loads and their variations are written as

$$\begin{aligned} W_{1}= & {} \frac{1}{2}\int _0^{L_{1} } {\left[ {N_{xx1} \left( {\frac{\mathrm{d}w_{i} }{\mathrm{d}x}} \right) ^{2}+hK_{O} \left( {w_{1} -w_{2} } \right) ^{2}} \right] } \mathrm{d}x, \end{aligned}$$
(16)
$$\begin{aligned} W_{2}= & {} \frac{1}{2}\int _0^{L_{2} } {\left[ {N_{xx2} \left( {\frac{\mathrm{d}w_{2} }{\mathrm{d}x}} \right) ^{2}-\frac{S_{i} }{r_{i} }hK_{O} \left( {w_{1} -w_{2} } \right) ^{2}} \right] } \mathrm{d}x, \end{aligned}$$
(17)
$$\begin{aligned} \delta W_{1}= & {} \int _0^{L_{1} } {\left[ {N_{xx1} \frac{\mathrm{d}w_{1} }{\mathrm{d}x}\frac{d\delta w_{1} }{\mathrm{d}x}+hK_{O} \left( {w_{1} -w_{2} } \right) \delta w_{1} } \right] } \mathrm{d}x, \end{aligned}$$
(18)
$$\begin{aligned} \delta W_{2}= & {} \int _0^{L_{2} } {\left( {N_{xx2} \frac{\mathrm{d}w_{2} }{\mathrm{d}x}\frac{\mathrm{d}\delta w_{2} }{\mathrm{d}x}-\frac{S_{i} }{r_{i} }hK_{O} \left( {w_{1} -w_{2} } \right) \delta w_{2} } \right) } \mathrm{d}x, \end{aligned}$$
(19)

where \(N_{xx1} \) and \(N_{xx2} \) equal to \(N_{0}\) demonstrate the critical axial buckling load of the DWCNTs.

Applying \(\delta \Pi _{i} =0\) gives the governing equations as

$$\begin{aligned}&\delta u_{i} =0\;:\frac{\mathrm{d}N_{xxi} }{\mathrm{d}x}=0 ;\quad { i}=1,2, \end{aligned}$$
(20)
$$\begin{aligned}&\delta w_{1} =0\;:-\frac{\mathrm{d}^{2}M_{xx1} }{\mathrm{d}x^{2}}+N^{0} \frac{\mathrm{d}^{2}w_{1} }{\mathrm{d}x^{2}}-hK_{O} \left( {w_{1} -w_{2} } \right) =0, \end{aligned}$$
(21)
$$\begin{aligned}&\delta w_{2} =0\;:-\frac{\mathrm{d}^{2}M_{xx2} }{\mathrm{d}x^{2}}+N^{0} \frac{\mathrm{d}^{2}w_{2} }{\mathrm{d}x^{2}}+\frac{S_{i} }{r_{i} }hK_{O} \left( {w_{1} -w_{2}} \right) =0. \end{aligned}$$
(22)

2.3 Small-scale effects

In the case of mechanical analysis of nanoscale structures like CNTs, the influence of size-dependency, as a vital effect, should be taken into consideration. This paper uses the nonlocal strain gradient continuum theory (NSGT) to address this phenomenon as [47]

$$\begin{aligned} \left( {1-\mu \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}} \right) \sigma _{ij} ={C}_{{ijkl}} \left( {1-l^{2}\frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}} \right) \varepsilon _{kl} ; \left\langle {\mu \hbox {(nm)}^{2}=\left( {e_{0} a} \right) ^{2}} \right\rangle , \end{aligned}$$
(23)

where l is assigned to exhibit the hardening effect named gradient parameter and \(\mu \) is defined to mark the atomic interaction called stress nonlocality. Additionally, the carbon–carbon bond length is denoted by a, and \(e_{0}\) is a specific length in nanomaterials. Both l and \(\mu \) depend directly on the micro/nano-material’s physical, natural and mechanical conditions, such as boundary conditions or geometrical dimensions and are not material constants [48, 49].

Integrating stress and strain parts in Eq. (23) based on the \(\int _A {z\mathrm{d}A} \) and substituting Eqs. (2) and (4) into the obtained relation, the static moment stress resultants in the nonlocal state are found to be [50,51,52,53,54,55,56,57,58,59]

$$\begin{aligned} M_{xxi} -\mu \frac{\mathrm{d}^{2}M_{xxi} }{\mathrm{d}x^{2}}=-E_{i} I_{ci} \left( {1-l^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}} \right) \frac{\mathrm{d}^{2}w_{i} }{\mathrm{d}x^{2}};\quad { i}=1,2. \end{aligned}$$
(24)

Based on Eqs. (21) and (22) and re-writing these equations regarding the first terms and replacing the resulting relations into the second term of Eq. (24), Eq. (24) will lead to

$$\begin{aligned} M_{xx1}= & {} \mu \left( {N^{0} \frac{\mathrm{d}^{2}w_{1} }{\mathrm{d}x^{2}}-hK_{O} \left( {w_{1} -w_{2} } \right) } \right) -E_{1} I_{c1} \left( {1-l^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}} \right) \frac{\mathrm{d}^{2}w_{1} }{\mathrm{d}x^{2}}, \end{aligned}$$
(25)
$$\begin{aligned} M_{xx2}= & {} \mu \left( {N^{0} \frac{\mathrm{d}^{2}w_{2} }{\mathrm{d}x^{2}}+\frac{S_{i} }{r_{i} }hK_{O} \left( {w_{1} -w_{2} } \right) } \right) -E_{2} I_{c2} \left( {1-l^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}} \right) \frac{\mathrm{d}^{2}w_{2} }{\mathrm{d}x^{2}}. \end{aligned}$$
(26)

2.4 Stability equations of the DWCNT

In the current research work, it is presumed that the pre-buckling axial forces are identical for both CNTs. Substituting Eqs. (25) and (26) into Eqs. (21) and (22) yields the stability equations in displacement form as

$$\begin{aligned}&E_{1} I_{c1} \left( {\frac{\mathrm{d}^{4}w_{1} }{\mathrm{d}x^{4}}-l^{2} \frac{\mathrm{d}^{6}w_{1} }{\mathrm{d}x^{6}}} \right) +N^{0}\left( {\frac{\mathrm{d}^{2}w_{1} }{\mathrm{d}x^{2}}-\mu \frac{\mathrm{d}^{4}w_{1} }{\mathrm{d}x^{4}}} \right) \nonumber \\&\quad -\,hK_{O} \left[ {\left( {w_{1} -w_{2} } \right) -\mu \left( {\frac{\mathrm{d}^{2}w_{1} }{\mathrm{d}x^{2}}-\frac{\mathrm{d}^{2}w_{2} }{\mathrm{d}x^{2}}} \right) } \right] =0 , \end{aligned}$$
(27)
$$\begin{aligned}&E_{2} I_{c2} \left( {\frac{\mathrm{d}^{4}w_{2} }{\mathrm{d}x^{4}}-l^{2} \frac{\mathrm{d}^{6}w_{2} }{\mathrm{d}x^{6}}} \right) +N^{0}\left( {\frac{\mathrm{d}^{2}w_{2} }{\mathrm{d}x^{2}}-\mu \frac{\mathrm{d}^{4}w_{2} }{\mathrm{d}x^{4}}} \right) \nonumber \\&\quad +\,\frac{S_{i} }{r_{i} }hK_{O} \left[ {\left( {w_{1} -w_{2} } \right) -\mu \left( {\frac{\mathrm{d}^{2}w_{1} }{\mathrm{d}x^{2}}-\frac{\mathrm{d}^{2}w_{2} }{\mathrm{d}x^{2}}} \right) } \right] =0. \end{aligned}$$
(28)

3 Solution process

As far as the obtained stability relations are linear (referring to Eqs. (27) and (28)), hence, the stability equations can be analytically solved using the following solution method [60]

$$\begin{aligned} w_{i} \left( {x,t} \right) =\zeta \left( x \right) \exp \left( {i\omega t} \right) ;\quad {i}=1,2 , \end{aligned}$$
(29)

in which \(\omega \) and \(\zeta \left( x \right) \) are the natural frequency and the fundamental mode shape. In order to achieve the problem solution, the boundary conditions are presented in Table 1.

Table 1 Boundary conditions (BCs) of the problem
Full size table

The mode shapes correspond to each type of boundary conditions in Table 1 can be described as below:

$$\begin{aligned} \hbox {For}\,\hbox {SS}:\zeta \left( x \right) =\sin \left( {\alpha x} \right) \end{aligned}$$
(30)
$$\begin{aligned} \hbox {For}\,\hbox {CC}:\zeta \left( x \right) =\sin ^{2}\left( {\alpha x} \right) \end{aligned}$$
(31)

in which \(\alpha =\frac{m\pi }{L}\), m defines the half-wave number (in this paper \(m=1\)). By substituting Eq. (29) into Eqs. (27) and (28), and performing some manipulations and simplifications, Eqs. (27) and (28) reduce to a set of algebraic equations as follows:

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {K_{11} } &{}\quad {K_{12} } \\ {K_{21} } &{}\quad {K_{22} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {w_{1} } \\ {w_{2} } \\ \end{array} }} \right\} =0 , \end{aligned}$$
(32)

where \(K_{ij}\) is the stiffness matrix.

Table 2 Results of hinged–hinged boundary conditions in comparison with the available literature
Full size table
Table 3 Results of clamped–clamped boundary conditions in comparison with the available literature
Full size table

A nontrivial solution to estimate the critical stability value could be achieved by setting \(\det \left[ {\int _0^L {\left( {K_{ij} \cdot \zeta \left( x \right) } \right) \mathrm{d}x} } \right] =0\), then, based on some computations, the numerical values of the critical stability of CNTs in a non-concentric geometry can be presented.

4 Numerical results

In this section, at first, by reducing the obtained equations (32) into the stability equation of an SWCNT, the problem is solved for the sake of justification of the presented formulation. As a matter of fact, there is no reference to validate Eq. (32), because no research analysis on an eccentric DWCNT exists in the literature. To this end, Tables 2 and 3 [61, 62] are presented in which the critical buckling load is computed for an SWCNT by assuming various nonlocal parameters and a variety of the nanotube’s length. Table 2 tabulates the SS end conditions results, and Table 3 reports those of fully clamped end conditions. As it is found, in both cases, with an increase in the length of the nanotubes, the results of other references and present work get closer to each other. Also, the difference in the results of the smallest length value is acceptable. On the other hand, it is pointed out that for smaller amounts of the nonlocal parameter, the difference is smaller.

The mechanical properties of the DWCNT used in the simulation are [39, 42, 63, 64]

  • \(E_{1}= E_{2}=5500\) nN/nm\(^{{2}}\), \(\nu _{{1}}= \nu _{{2}}=0.19\), \(K_{O}=99.1866693\) nN/nm\(^{{3}}\),

  • \(H=h=0.66\) Å, \(D=219\) Å, \(d=136\) Å (1 Å \(= 0.1\) nm), \({0}\le {c}\le 0.349\;\hbox {nm}\).

The main goal of this study is to investigate the eccentricity effect on the stability of DWCNTs by considering the variations of system parameters such as nonlocal/ gradient coefficients, length to diameter ratio (aspect ratio) and different boundary conditions. In fact, it is interesting to know if the nanotubes have some eccentricity due to the manufacturing process, since the detection of this geometrical imperfection is very difficult and costly, how this geometrical deviation does affect the mechanical behavior of such important nanostructures, and if its impact is predicted to be meaningful, what kind of results are expected? For this purpose, we first consider the effect of the fundamental parameter c in a given interval against the changes of the nonlocal parameter according to Fig. 2. The values provided for the nonlocal parameter are according to the reported values in the literature (\(e_{0}a = 0.05538\) nm [39], \(e_{0}a= 0.11664\) nm [65], \(e_{0}a =0.5\) to 2 nm [66]). The assumed values, which are also credible, were evaluated and validated. It should be noted that the nonlocal parameter strongly depends on the conditions of the problem, e.g., the type of end conditions. It can be seen from the plotted curves that the increase in the non-centrality of the nanotubes increases their stability against the in-plane axial forces. Interestingly, this increasing effect is the same for all nonlocal coefficients, while the slope is almost the same for all nonlocal parameters. On the other hand, increasing from \(c = 0.2\) nm onwards, the critical load would be steeper. It is possible to interpret this consequence in the critical load which is caused by the increase in offset rate. Physically, as the eccentricity value of the two nanotubes increases, due to the increase in the surface moment of inertia for the outer tube, the rigidity of the outer tube relative to the coordinate origin gets larger which may lead to the higher stability of the DWCNT.

Fig. 2
figure 2

The influence of eccentricity (c) on the critical axial buckling load of the DWCNTs (\(l=h, L= 5D, SS{-}ss\)) considering different stress nonlocality (ea)

Full size image

As illustrated in Figs. 3a, b, this paper considers double-walled nanotubes with opposite boundary conditions. In the first figure, the tubes are centered and in the second one are out of center, and the variations of the strain gradient hardening parameter are also investigated. The opposite boundary conditions mean that the boundary conditions in the inner nanotube would be different from the outer tube. In all previous studies on DWCNTs, it has been assumed that the tubes have similar boundary conditions on each side. On the contrary, in the present study, XX-xx indexing is used by which we will demonstrate two different edge conditions for nanotubes. The lowercase letters are dedicated to the boundary conditions of the inner tube and uppercase letters for the boundary conditions of the outer tube. For example, SS-cc means that the outer tube is hinged at both ends and the internal CNT is clamped and completely fixed on both ends. Of course, the discussion is purely theoretical, and it should be kept in mind that the boundary condition is the type of behavior of the beams at the edges; the mechanism and type of implementation of these models of boundary conditions in reality are not in the scope of this paper. As can be seen, the smallest critical load occur when both nanotubes are hinged on both sides, and the highest stability occurs when the outer tube has fully fixed boundary conditions. Interestingly, the effect of the inner tube’s boundary condition is negligible compared to those of the outer tube. This means that when the outer nanotube has clamped boundaries, it does not make much difference to the conditions which the inner nanotube has at its both ends. In addition, considering the comparison of Figs. 3a, b, it is important to know that when the nanotubes are not concentric, the effect of the type of the inner tube’s boundary condition is less important. This consequence can be understood from the difference between the results of the SS-ss boundary condition and SS-cc one in both figures. The difference in the results when two tubes are centered is greater than when they are off-center.

Fig. 3
figure 3

a The influence of gradient parameter (l) on the critical axial buckling load of the DWCNTs (\(l^{*}=l/h, L=10D\)) as the eccentricity is \(c=0\). b The influence of the gradient parameter (l) on the critical axial buckling load of the DWCNTs (\(l^{*}=l/h, L=10D\)) as the eccentricity is \(c=0.1\) nm

Full size image

To investigate the effect of nonlocal parameter variations on the contrasting boundary conditions, Figs. 4a, b are plotted in two concentric and non-concentric situations of the nanotubes. First, it is found that by increasing the value of the nonlocal parameter, the important result obtained in the previous figure is not true here. That is, at larger values of the nonlocal parameter, the response of the outer tube’s boundary condition is not the criterion of behavior of the whole system and the different boundary conditions for the inner tube give different answers. It is worth mentioning that the more flexible boundary condition for the inner nanotube results in an increase in the critical load at larger values of the nonlocal parameter. Of course, when the nanotubes are off-center we will not get the result completely and the inner tube’s boundary condition becomes negligible when the outer tube is fixed. In addition, it is interesting to note that when the external nanotube has an edge-locking condition, the softening effect of the nonlocal parameter is much more noticeable. This can be seen from the larger negative slope of the CC-ss and CC-cc curves. The important point in these two figures is that when the nonlocal parameter increases, the results of SS-cc and SS-ss get closer to each other and vice versa, the results of CC-cc with CC-ss are farther apart. This outcome may approve the huge dependency of the nonlocal parameter on the boundary conditions.

Fig. 4
figure 4

a The influences of nonlocal parameter (\(e_{0}a\)) versus the critical axial buckling load of the DWCNTs (\(l=h, L=10D\)) as the eccentricity is \(c=0.\) b The influences of nonlocal parameter (\(e_{0}a\)) versus the critical axial buckling load of the DWCNTs (\(l=h, L=10D\)) as the eccentricity is \(c=0.1\) nm

Full size image

Figures 5a, b are shown to complement the discussion of this study. For this aim, in the first diagram, the problem is analyzed at the scale of a moderately thick nanotubes, \(L = 5D\), and in the second figure at the scale of almost thin nanotubes, \(L = 20D\). As it turns out, while the tubes are larger, they possess less stability. However, the conclusion is that, in the case of the longer nanotubes, any increase of eccentricity will further affect the stability of the system. This conclusion can be found from the larger slope of the CC results in Fig. 5b. It is also germane to point out that for the higher degree of non-centrality, the type of boundary conditions of the internal tube is generally negligible. This means that, the results of SS-ss correspond to SS-cc and vice versa in both figures at \(c = 0.3\) nm. Therefore, it can be concluded that when the eccentricity of the nanotubes gets larger, it is no longer necessary to have the exact type of the inner tube’s boundary condition and it is only necessary to know the outer tube’s boundary behavior.

Fig. 5
figure 5

a The influences of eccentricity (c) versus the critical axial buckling load of the DWCNTs (\(l=h, L=5D\)) considering different edge conditions. b The influences of eccentricity (c) versus the critical axial buckling load of the DWCNTs (\(l=h, L=20D\)) considering different edge conditions

Full size image

5 Conclusions

This paper presented a novel analysis on the DWCNTs assuming the non-concentric conditions where the deviation affects the stability of the nanomaterials. The DWCNT was simulated as an Euler–Bernoulli beam model and treated nanoscale dimensions based on the second strain gradient and nonlocal theories. To connect the outer and inner tubes, the Lennard–Jones approach was employed to provide the van der Waals forces. Closed-form solution techniques are the best choice to deal with the considered system of linear equations due to brevity in their procedure. Therefore, this paper used an efficient method to present the numerical outcomes for both clamped and hinged boundary conditions. Finally, the numerical results delivered some valuable points listed below which can be beneficial for designing the smart electronic and medical equipment using DWCNTs.

  • If the nanotubes’ eccentricity is higher, the mechanical stability is higher.

  • In the local analysis of carbon nanotubes, when the outer tube has clamped boundaries, the criterion of the system behavior is the external tube’s boundary condition and the system response will be based on it. However, this is not true in the nonlocal analysis and for large values of the nonlocal parameter.

  • Being off-center in the DWCNTs dramatically reduces the effect of the inner tube’s boundary condition.