Anderson–Kitaev spin liquid

Abstract

The bond-disordered Kitaev model attracts much attention due to the experimental relevance in α-RuCl₃ and A₃LiIr₂O₆ (A = H, D, Ag, etc.). Applying a magnetic field to break the time-reversal symmetry leads to a strong modulation in mass terms for Dirac cones. Because of the smallness of the flux gap of the Kitaev model, a small bond disorder can have large influence on itinerant Majorana fermions. The quantization of the thermal Hall conductivity κ^xy/T disappears by a quantum Hall transition induced by a small disorder, and κ^xy/T shows a rapid crossover into a state with a negligible Hall current. We call this immobile liquid state Anderson–Kitaev spin liquid (AKSL). Especially, the critical disorder strength δJ_c1 ~ 0.05 in the unit of the Kitaev interaction would have many implications for the stability of Kitaev spin liquids.

Introduction

The Kitaev model¹ is one of the greatest examples of two-dimensional (2D) solvable models of quantum spin liquids (QSLs)^2,3,4, especially in the perspective of spin-orbital-entangled physics^5,6. This model has a bond-dependent anisotropic interaction, which brings about exchange frustration and realizes gapped and gapless spin liquid states depending on its parameters. Amazingly, this interaction can be furnished in materials with a strong spin–orbit coupling⁷. Iridates and α-RuCl₃ are prominent examples of candidate materials for the Kitaev model^8,9,10, and thus are called Kitaev materials. As a hallmark, the half-integer quantization of the thermal Hall conductance has been observed in α-RuCl₃ with a magnetic field¹¹, suggesting the fractionalization of spin degrees of freedom predicted from the Kitaev model. However, it is also known that these honeycomb materials cannot fully be understood by the original (pure) Kitaev model^12,13. While other diagonal or offdiagonal interactions might be important in real materials¹⁴, the importance of disorder has been ignored in these materials until recently^15,16,17. Indeed, experiments in A₃LiIr₂O₆ (A = H, Ag, etc.) show a universal scaling in the field dependence of the heat capacity^5,18, which strongly suggests the existence of disorder^19,20. The candidate ground states must be disordered QSLs, and the absence of long-range order can be attributed to the critical role of disorder.

In fact, the role of disorder in QSLs itself is a long-standing problem because of the absence of a solvable model, except for limited cases²¹. We propose a disordered Kitaev model as a "numerically” solvable model for the disordered QSL, where we can treat the magnetic field effect within the perturbation theory. Thus, this study is not only a model investigation for the disordered Kitaev materials like A₃LiIr₂O₆ (A = H, D, Ag, etc.)^5,18,22, but also a systematic examination of a numerically solvable disordered QSL, which would be an attempt towards the universal understanding of various disordered QSLs. Especially, since most QSLs are unsolvable, an unbiased study of disordered QSLs was impossible in the previous method.

Moreover, the bond-disordered Kitaev model with an applied magnetic field is not an “analytically” solvable problem. While it seems that the problem is reduced to the Anderson localization of symmetry class D with a short-range correlated disorder²³, we discovered that this is not the end of the story. The nontrivial part comes from the third-order perturbation in an applied field because the computation of the “disorder” in the time-reversal-breaking term requires diagonalization¹. This nonlocal operation makes the disorder long-range correlated. Such a long-range correlated random mass disorder could be a relevant perturbation²⁴, and a simple renormalization group analysis may fail. Treating the long-range correlated disorder essentially requires a large-scale calculation and the extrapolation to the thermodynamic limit, which were numerically difficult in the finite-size Monte Carlo methods^25,26. For these reasons, we invented a powerful numerical method based on the kernel polynomial method (KPM)²⁷ to overcome the difficulty.

From the materials side, the dispersion of low-energy excitations of H₃LiIr₂O₆ is a mystery. Although the behavior of the heat capacity of H₃LiIr₂O₆ without a magnetic field⁵ is partially explained by the bond-disordered Kitaev model¹⁷, the T²-dependence of the heat capacity of H₃LiIr₂O₆ with a magnetic field⁵, which suggests the linear dispersion of the low-energy density of states (DOS)⁵, has never been described by an unbiased calculation. Such heat capacity behaviors are phenomenologically explained by the random-singlet theory with a Dzyaloshinskii–Moriya (DM) interaction¹⁹. However, it is not clear whether the DM interaction is important in H₃LiIr₂O₆, and symmetric Kitaev–Γ interactions may be a dominant consequence of the spin–orbit coupling. We rather try to explain the observed linear dispersion with an applied field from the bond-disordered Kitaev model. Indeed, an unbiased numerical simulation of the bond disorder is not only theoretically nontrivial but also experimentally important.

The Anderson transition (or quantum Hall transition) is visible in a Kitaev spin liquid (KSL) by applying a small magnetic field. The quantized thermal Hall conductivity serves as an order parameter, which must go to zero in the large-disorder limit. This limit without a linear slope of the thermal Hall conductivity is named Anderson–Kitaev spin liquid (AKSL). The transition between KSL and AKSL is nothing but a transition between different Hall plateaus. Although we defined the transition in 2D, the transition may be observable even in three-dimensional (3D) generalizations^28,29 (mobility edge).

In this article, we simulate the bond-disordered Kitaev model to see a crossover between KSL and AKSL, especially from the topological transition in the thermal Hall effect^11,25,30. We discovered that the quantized thermal Hall effect is not as stable as expected from the Anderson transition with a short-range correlated disorder.

Results

Magnetic field effect

The pure Kitaev model on the honeycomb lattice can be defined from Fig. 1a. The bonds parallel to the red, green, and blue ones are x-, y-, and z-labeled bonds, respectively. The Hamiltonian is

$${H}_{0}=-J\mathop {\sum}\limits_{\langle jk\rangle \in \gamma }{\sigma }_{j}^{\gamma }{\sigma }_{k}^{\gamma },$$

(1)

where 〈jk〉 means a nearest-neighbor (NN) bond, and J > 0. γ = x, y, or z is determined by a bond label. This model is known to be solvable by representing ${\sigma }_{j}^{\gamma }$ by Majorana fermions $i{b}_{j}^{\gamma }{c}_{j}$. This representation still works even if we introduce bond disorder as follows:

$${H}_{{\rm{bond}}}=-\mathop {\sum}\limits_{\langle jk\rangle \in \gamma }{J}_{jk}{\sigma }_{j}^{\gamma }{\sigma }_{k}^{\gamma },$$

(2)

where J_jk = J ± δJ is a bond-dependent hopping, and δJ > 0 is the strength of bond disorder. This model is still numerically solvable if we can assume that the ground state is 0-flux when δJ is in the perturbative regime. Under this assumption, all the states with a vison, which is defined as a pair of neighboring π-flux vortices excited by flipping the sign of a single bond, are assumed to be the "first” excited states from the ground state flux sector. This is how the perturbation theory works for this Kitaev model. We employ Kitaev’s trick to solve these Hamiltonians with an applied magnetic field¹.

Fig. 1: Schematic phase diagram.

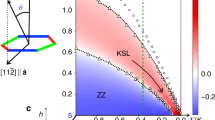
a Directional dependence of the bond interaction and the NNN hopping arising for Majorana fermions under the magnetic field. b ${\Delta }_{\min }=\min ({\Delta }_{{\rm{vison}}})$ versus disorder strength δJ. After the gap closing around δJ = δJ_c2, the flux sector becomes vison glass. c κ^xy versus disorder strength δJ. From δJ > δJ_c1, the crossover to the AKSL is observed and κ^xy/T finally reaches 0 around δJ/J = 1.

Let us first review the perturbation for the pure Kitaev model with a magnetic field

$$H={H}_{0}+V.$$

(3)

$$V=-\mathop {\sum}\limits_{j}\left({h}^{x}{\sigma }_{j}^{x}+{h}^{y}{\sigma }_{j}^{y}+{h}^{z}{\sigma }_{j}^{z}\right),$$

(4)

where ${\bf{h}}={({h}^{x},{h}^{y},{h}^{z})}^{t}$ is an applied magnetic field.

It is well known that V can be treated by the third-order perturbation¹. The result after introducing itinerant Majorana fermions c_j is

$${H}_{{\rm{eff}}}=\frac{iJ}{2}\mathop {\sum}\limits_{\langle jk\rangle }{c}_{j}{c}_{k}+\frac{i\tilde{\kappa }}{2}\mathop {\sum}\limits_{\langle \langle kl\rangle \rangle }{c}_{k}{c}_{l}+({\text{four-fermion}}\, {\text{terms}}).$$

(5)

$$\tilde{\kappa }=\frac{3{h}^{x}{h}^{y}{h}^{z}}{48{\alpha }_{0}^{2}{J}^{2}},$$

(6)

where α₀ = 0.262433 in the thermodynamic limit for the 0-flux state, and α₀J is a vison gap in the uniform case. The determination of the prefactor follows a mean-field solution³¹. The direction of the next-nearest-neighbor (NNN) bond 〈〈kl〉〉 is defined clockwise as shown in Fig. 1a around the site j. A site connected by the γ-bond from j is called γ[j] for γ = x, y, and z, as shown in Fig. 1a. We define $\tilde{h}={h}^{x}{h}^{y}{h}^{z}/48$.

Kitaev’s trick

Next, let us include binary disorder as H = H_bond + V. Following Kitaev¹, we can always do perturbation from any random H_bond by a formula

$${H}_{{\rm{eff}}}^{(3)}={\Pi }_{0}V{G}_{0}^{\prime}({E}_{0})V{G}_{0}^{\prime}({E}_{0})V{\Pi }_{0},$$

(7)

where Π₀ is a projection onto the ground state flux sector, ${G}_{0}^{\prime}(E)$ is an unperturbed Green function constructed from H_bond with the ground state flux sector excluded from the Hilbert space, and E₀ is an initial energy. Since H_bond is solvable by Majorana fermions, it is in principle possible to calculate ${G}_{0}^{\prime}(E)$ numerically to exhaust every term appearing in the third order. For example, a Green function for excited states is efficiently obtained by KPM²⁷ numerically. However, this strategy is surely overkill for our problem.

A much simpler solution is to use a trick introduced by Kitaev. Though we still need an O(N⁴) calculation cost to decide all terms by usual matrix diagonalization, where N is the number of sites, there is no need for matrix exponentiation or integration. Kitaev’s trick is done by replacing ${G}_{0}^{\prime}({E}_{0})$ by − (1 − Π₀)/Δ_vison, assuming that the virtual state energy is constant determined just by a vison gap Δ_vison. This is a bold approximation to simplify the problem drastically, but as we will see essential features, such as the modulation of the mass term, can be captured even within Kitaev’s approximation.

In this way, a typical third-order term is as follows:

$${H}_{{\rm{eff}}}=\frac{i}{2}\mathop {\sum}\limits_{\langle jk\rangle }{J}_{jk}{c}_{j}{c}_{k}+\frac{i}{2}\mathop {\sum}\limits_{\langle \langle kl\rangle \rangle }{\tilde{\kappa }}_{kl}{c}_{k}{c}_{l}+\cdots$$

(8)

where ${\tilde{\kappa }}_{kl}$ depends on the intermediate site j in the third-order perturbation process. Seen from j, $\tilde{\kappa }$ can be calculated by replacing $3/{({\alpha }_{0}J)}^{2}$ by 1/(Δ_xΔ_y) + 1/(Δ_yΔ_z) + 1/(Δ_zΔ_x), where Δ_γ is the energy of the vison excited by flipping the sign of the bond between j and γ[j].

$${\tilde{\kappa }}_{kl}={\tilde{\kappa }}_{j}=\frac{\tilde{h}}{{\Delta }_{x}{\Delta }_{y}}+\frac{\tilde{h}}{{\Delta }_{y}{\Delta }_{z}}+\frac{\tilde{h}}{{\Delta }_{z}{\Delta }_{x}}.$$

(9)

We note that three bonds have the same value of ${\tilde{\kappa }}_{kl}$ around j. Thus, the disorder simply modulate the mass term of Dirac cones via random NNN hoppings, and the problem is still solvable numerically.

In this case, four-fermion terms are short-ranged and we have just ignored them as we are only interested in the Hall conductivity in the h → 0 limit. Though we will assume the ground state of H_bond to be 0-flux in the following discussions, the perturbation can be done from any flux configuration. We note that a second-order perturbation in h is ignored because it just renormalizes bond-dependent hoppings J_jk and does not break the time-reversal symmetry. Indeed, there is a priori no way to determine the ratio of the coefficients of the second- and third-order perturbations, although we can always use a mean-field solution of the pure Kitaev model to estimate it³¹. As stressed in the Introduction, the computation by Kitaev’s trick is an essential part of this study, producing long-range correlation in the mass disorder.

Thermal conductivity

We only consider zero temperature and ignore thermal flux fluctuations above the 0-flux sector. Lieb’s theorem³² no longer applies, but we can expect it to be applicable on average. Anyway, the calculation is relevant only in the regime where the flux gap is not closed by thermal fluctuation or bond disorder (δJ < δJ_c2 in Fig. 1b, c).

We employed Kitaev’s trick to calculate a Majorana spectrum with an external magnetic field for each quenched bond disorder. From this, we can compute an inplane thermal Hall conductivity κ^xy(T), especially behavior of κ^xy/T at T → 0. Here xy does not coincide with the Cartesian axis but means a transverse component of the thermal conductivity.

As described in Methods, the thermal Hall conductivity can be computed directly by the Kubo formula. However, we can alternatively use the so-called noncommutative Chern number (NCCN)³³, which is defined by a spectral projector for occupied free fermions. This formula is advantageous because it is proven to become integer after disorder average with some conditions, whereas it only makes sense in the thermodynamic limit.

$${\rm{Ch}}=-\frac{2\pi i}{{L}^{2}}\ {\rm{tr}}\left\{{P}_{F}\left[[{r}_{1},{P}_{F}],[{r}_{2},{P}_{F}]\right]\right\},$$

(10)

where P_F is a spectral projector, i.e. the projection operator onto the occupied states, and L is a linear scale of the system. This formula must agree with the Kubo formula in the thermodynamic limit by a well-known relation ${\kappa }^{xy}/T=\pi {k}_{B}^{2}{\rm{Ch}}/(12\hslash )$ for Majorana fermions. We note that there are other ways to detect the topological nontriviality^34,35,36.

After taking an average of Ch ∝ κ^xy/T over a number of disorder configurations, we plot a physical thermal Hall conductivity as a function of δJ. The error bar is estimated from a statistical deviation. From now on we set $\hbar$ = k_B = J = 1.

Numerical results

We first note that, since we only include the third-order perturbation, the results here are not simply comparable with experiments. However, it was proposed that the contribution from h^xh^yh^z can be picked up by applying an inplane magnetic field³⁷, so we only take an odd component under every sign change (h^x ↦ − h^x, h^y ↦ − h^y, and h^z ↦ − h^z) of the three components of h from total κ^xy. From now on we denote κ^xy as an odd component under every sign change and ignore other components.

The approximate correspondence between the Kubo formula and NCCN is confirmed for the pure Kitaev model (see Fig. 2a). We note that Haar-random vectors are used in this calculation, but are not used in the following as described in Supplementary Methods and Supplementary Fig. 1. From here we will prefer NCCN to the Kubo formula because we can use KPM to approximate the spectral projector P_F to avoid diagonalization. We note that the application of KPM to the Kubo formula requires efforts³⁸.

Fig. 2: Main results.

a Kubo formula versus NCCN. NCCN-Diag means that the Chern number is calculated by diagonalization, while NCCN-KPM means that the Chern number is calculated by KPM with ${M}^{\prime}=512$ and R = 100. In order to put errorbars, random vectors are chosen to be Haar-random. Only $L\,\mathrm{mod}\,\,6=2,\ 4$ is plotted. The ordinary periodic boundary condition is used. b Mean and minimum values of flux gaps calculated by KPM. The error bar is smaller than the line width and only plotted for L = 10. KPBC is used. c NCCN calculated by diagonalization (solid lines) and KPM (scatter plots). N_sample = 24 is used for the diagonalization. For KPM we used R = 24, and N_sample = 360. KPBC is used. d NCCN calculated by KPM and the value extracted for L → ∞. The margin of error at 5% significance level is used for the ribbon for the extrapolation. Error bars are standard errors (SE) if not mentioned.

Next, we would move on to a large-scale calculation by Kitaev’s trick. We only take (Kitaev’s) L × L periodic boundary condition (for spins) from L = 10, where the vison gap gets close to the thermodynamic limit. As long as we are interested in the topological property, the h → 0 limit does not have to be taken. We set ${h}^{x}={h}^{y}={h}^{z}\equiv h={\Delta }_{\min }$, where ${\Delta }_{\min }$ is the minimum vison gap for each disorder configuration. In order to reduce the finite-size effect, we adopt Kitaev’s torus basis where the finite-size effects cancel out, which is defined from a torus basis (Ln₁, Ln₂ + n₁)¹. We call it Kitaev’s periodic boundary condition (KPBC) for simplicity. The NCCN formula for KPBC has to be modified as described in Supplementary Methods. This arbitrary choice of boundary conditions does not matter in the thermodynamic limit. The averaged 〈κ^xy〉/T for T → 0 is shown as a function of δJ, and drops rapidly to 0 from the quantized value as the disorder strength δJ grows. From here 〈κ^xy〉/T is plotted in the unit of a quantum π/12. We used R = 24 vectors to approximate the trace³⁹.

The mean and minimum values of vison gaps are plotted for each δJ in Fig. 2b. When δJ > δJ_c2 ~ 0.3, the vison gap approaches 0 for some plaquette, and the 0-flux ground state is destabilized. We tentatively define δJ_c2 as the point where ${\Delta }_{\min }=0.05$. From here, the perturbation from the 0-flux sector cannot be justified. Moreover, some flux sectors get almost degenerate and the first-order perturbation in h now becomes relevant. Beyond this point, a quantized thermal Hall current is no longer a well-defined notion. Flux excitations and (itinerant) Majorana fermions are not separable, and the discussion based only on free Majorana fermions breaks down.

When δJ ≪ δJ_c2, the calculation by Kitaev’s trick can be justified. Fig. 2c shows NCCN calculated by diagonalization (line plot) and KPM (scatter plot). These two methods agree well. From the data of KPM we extrapolated the thermodynamic limit. The finite-size data are fit by exponential functions, and extracted the converged value for L → ∞. The extrapolation is plotted in Fig. 2d and the thermodynamic limit is shown in a line plot with a ribbon. Around δJ = δJ_c1 = 0.05, NCCN deviates from unity, which suggests the existence of the topological transition into the gapless phase. For the calculations we took N_sample = 360 quenched disorder samples and used M = 1024, and R = 24, where M is the expansion order of KPM.

Local density of states

When δJ ≪ δJ_c2, free Majorana fermions are only relevant low-energy excitations, and we can use many tools of free fermions to discuss properties of the transition, such as DOS and a localization length. DOS around the ground state can be measured from the information of the 0-flux sector. As is often the case, we only calculated local density of states (LDOS), instead. LDOS for a site i is defined as follows²⁷:

$${\rho }_{i}(\varepsilon )=\mathop{\sum }\limits_{k = 1}^{N}{\left|\langle i| k\rangle \right|}^{2}\delta (\varepsilon -{\varepsilon }_{k}),$$

(11)

where $\left|i\right\rangle$ is a site basis, and $\left|k\right\rangle$ is an eigenstate of the Hamiltonian with an energy ε = ε_k.

The nonlocality of Majorana fermions does not matter as averaged LDOS approximates DOS well enough. Both of the quantities are easily computed using KPM, and LDOS is enough for our purpose. The ratio of the arithmetic and geometric means of LDOS also works as the order parameter of an Anderson transition instead of the localization length. From the gapped Dirac spectrum (see Fig. 3a) the LDOS becomes gapless as the disorder strength increases. In the gapless region, DOS behaves linearly around ε = 0 (see Fig. 3b–d). The localization in Fig. 3b–d is clear from the discrepancy between the arithmetic and geometric averages of LDOS. Details are included in Supplementary Methods.

Fig. 3: Arithmetic and geometric means of LDOS.

a δJ = 0.0. b δJ = 0.1. c δJ = 0.2. d δJ = 0.3. For every figure L = 100, R = 24, and N_sample = 360.

Discussion

Even in a finite-size calculation, the transition between KSL and AKSL was well-observed and the schematic phase diagram in Fig. 1c was confirmed. From the extrapolation, δJ_c1 is very small and δJ_c1/J ~ 0.05. δJ_c1/J ≪ α₀ ~ 0.26 suggests the fragility of KSL. The fragility potentially explains the observed sample dependence of the half-integer quantized thermal Hall effect in α-RuCl₃⁴⁰. There is a possibility that δJ_c1/J → 0 as $h/{\Delta }_{\min }\to 0$, which means that the bond disorder in the Kiteav model is a relevant perturbation²⁴. After the transition, the V-shaped behavior of DOS completely agrees with an observed linear low-energy DOS for H₃LiIr₂O₆ with an applied magnetic field⁵.

It was proposed that the spin-polarized scanning tunneling microscopy (SP-STM) could be a local probe for edge states of the Kitaev model⁴¹. During the crossover to AKSL, edge states should disappear gradually and thus SP-STM should be a good probe for the topological transition.

The $h/{\Delta }_{\min }\to 0$ limit must be taken carefully. A small $h/{\Delta }_{\min }$ suffers from the finite-size effect, so we need to increase N according to the $h/{\Delta }_{\min }\to 0$ limit, as described in Supplementary Methods and Supplementary Fig. 2. Whether or not δJ_c1/J → 0 in this limit is an important future problem. We note that the vortex disorder is known to be relevant, so the introduction of random vortices may change the universality⁴².

The fragility of the quantization has many implications to experiments. Disorder always exists in real materials, especially in any 2D layered system, and even in clean samples of α-RuCl₃ stacking faults must exist⁴³. Thus, the situation is quite similar to that of the fractional quantum Hall effect (FQHE). The observation of FQHE requires a really clean sample, and the recently observed quantized thermal Hall current of FQHE is more sensitive to disorder⁴⁴. The sensitivity also resembles unconventional superconductors⁴⁵. It might be universal in strongly correlated systems. Thus, we need to reconsider the importance of cleanness for the topological order in general. Further discussions can be found in Supplementary Discussion.

Note added

After the early version of the present paper on arXiv, a finite-temperature calculation of the disordered Kitaev models has been reported⁴⁶.

Methods

We would like to introduce the KPM^27,47,48. KPM is used twofold in this work. The first is for the vison gap calculation and the second is for the Chern number calculation. The calculation cost for the former is O(N²) and for the latter O(N).

Vison gap calculation

First, let us consider a Majorana Hamiltonian with the following form.

$$H=\frac{1}{4}\mathop {\sum}\limits_{j,k}{{\mathcal{H}}}_{jk}{c}_{j}{c}_{k},$$

(12)

where ${\mathcal{H}}$ is a Hermitian matrix. For Majorana fermions c_j, ${\mathcal{H}}$ has a form ${\mathcal{H}}=iA$, where A is a real skew-symmetric matrix. From now on, we assume ${\mathcal{H}}$ to be the ones considered in the main text, either with or without a magnetic field. The eigenvalues of the N × N matrix ${\mathcal{H}}$ is denoted by E_k with k = 1, …, N.

A Green function can be expanded by a Chebyshev polynomial T_m(x) as follows:

$${G}_{jj}(E+i\varepsilon )=i\frac{{\tilde{\mu }}_{0}+2\mathop{\sum }\nolimits_{m = 1}^{M-1}{\tilde{\mu }}_{m}\exp [-im\arccos (E/s)]}{\sqrt{{s}^{2}-{E}^{2}}}.$$

(13)

$${\tilde{\mu }}_{m}={g}_{m}\langle j| {T}_{m}({\mathcal{H}}/s)| j\rangle .$$

(14)

$${g}_{m}=\frac{\sinh [\lambda (1-m/M)]}{\sinh \lambda },$$

(15)

where λ = 4.0 was used in the Lorentz kernel g_m. M is the expansion order and m = 0, …, M − 1. ε is a small parameter which goes to 0 when M → ∞. The scaling factor s is necessary so that the spectrum of the Hamiltonian ${\mathcal{H}}/s$ falls within the domain of the Chebyshev polynomials [−1, 1]. We note that this expression is for diagonal components, but almost the same is true for offdiagonal components. We simply set $s={E}_{\max }+0.1$, where ${E}_{\max }$ is the maximal eigenvalue.

Elements of Chebyshev moments ${T}_{m}({\mathcal{H}}/s)$ can be computed recursively by using T_m(x) = 2xT_m−1(x) − T_m−2(x) and T_2m+i(x) = 2T_m(x)T_m+i(x) − T_i(x) for i = 0, 1. The total O(N²) cost is required to compute all the necessary elements.

From the expanded Green function, we can compute the energy change by the local modification of the Hamiltonian ${\mathcal{H}}\to {\mathcal{H}}+\delta {\mathcal{H}}$. We define

$${\mathcal{D}}(E)=\det [1+G(E)\delta {\mathcal{H}}].$$

(16)

By extending this function to a complex number, the energy difference, i.e. vison gap Δ_vison, can be computed as follows:

$${\Delta }_{{\rm{vison}}}=\frac{1}{\pi }{\int\nolimits_{-\infty }^{\infty }}F(E)\mathop {\text{lim}}\limits_{\varepsilon \to 0}{\rm{Im}}\ {\mathrm{log}}\,[{\mathcal{D}}(E+i\varepsilon )]dE,$$

(17)

where F(E) is a Fermi-Majorana function at zero temperature.

$$F(E)=-\mathop {\text{lim}}\limits_{\beta \to \infty }\frac{1}{2}\tanh \frac{\beta E}{2}=\vartheta (-E)-\frac{1}{2}.$$

(18)

The evaluation of the integral in the Green function requires fast Fourier transformation (FFT) or discrete cosine transformation (DCT)²⁷. Using this, the integral is reduced to a discrete weighted sum of the Fermi(-Majorana) function evaluated at some specific points. The discretization size $\tilde{M}$ for the summation was set $\tilde{M}=2M$ for simplicity. We compared M = 64, 128, 256, 512, 1024, and 2048. Among these, we found that M = 1024 has the best performance for our purpose, where the error is always about 0.01J.

KPM can reproduce the vison gap with an enough precision and reduce the computational cost to O(N) with a truncation algorithm^49,50,51. However, later we found that the truncation causes a problem in our simulation, and thus we used the abovementioned O(N²) algorithm without a truncation^27,47,48.

Chern number calculation

A Kubo formula for κ^xy at zero temperature is reduced to the generalized Thouless-Kohmoto-Nightingale-den Nijs (TKNN) formula⁵² for noninteracting Majorana Hamiltonians:

$${\kappa }^{xy}=\frac{\hslash {\pi }^{2}{k}_{B}^{2}T}{6{L}^{2}}\mathop{\sum }\limits_{m,n}\vartheta (-{\varepsilon }_{m})\frac{2{\rm{Im}}[\langle m| {v}_{1}| n\rangle \langle n| {v}_{2}| m\rangle ]}{{\left({\varepsilon }_{m}-{\varepsilon }_{n}\right)}^{2}},$$

(19)

where m and n label eigenvalues of ${\mathcal{H}}$, ε_m and ε_n, corresponding to eigenstates $\left|m\right\rangle$ and $\left|n\right\rangle$, respectively^53,54. ϑ(x) is a Heaviside theta and ${v}_{\alpha }=i[{\mathcal{H}},{r}_{\alpha }]/\hslash$ is a velocity operator along the α-direction. We define a position operator r_α for the n_α-direction for α = 1, 2. A gravitomagnetic term should be added to derive this formula. We note the generalized formula without a translation symmetry was originally discussed by Kitaev¹ using a flow of unitary matrices and extended by Kapustin and Spodyneiko⁵⁵. This Kubo-TKNN formula is nothing but a real-space formulation of the Chern number calculation.

However, as mentioned in the main text, it is better to use a noncommutative Chern number (NCCN) Eq. (10)³³ to compute the same quantity in the thermodynamic limit. Though Eq. (10) makes sense only in the thermodynamic limit, we can make use of a discretized version, which exponentially converges to the thermodyanamic limit by an artificial k-space quantization of a size L × L. This version can be derived by replacing the commutator³³ as follows:

$$-i[{r}_{\alpha },{P}_{F}]\mapsto \mathop{\sum }\limits_{q = -Q}^{Q}{c}_{q}{e}^{-iq\Delta {r}_{\alpha }}{P}_{F}{e}^{iq\Delta {r}_{\alpha }},$$

(20)

where Δ = 2π/L, c₀ = 0 and c_q = −c_−q are determined to hold $x-\mathop{\sum }\nolimits_{q = -L/2}^{L/2}{c}_{q}{e}^{iq\Delta x}=O({\Delta }^{L})$, and Q ≤ L/2. Thus, we can expect that these two methods to compute κ^xy may agree with a large L, while the Hall conductivity and the Chern number are a priori different quantities. We fixed Q = 15 for L > 30 because otherwise the calculation cost becomes O(N³).

The spectral projector P_F can be rewritten as:

$${P}_{F}=-\frac{1}{2\pi i}{\oint _{{\mathcal{C}}}}\frac{1}{{\mathcal{H}}-E}dE,$$

(21)

where ${\mathcal{C}}$ is a contour which encloses every negative eigenvalue of ${\mathcal{H}}$. The integrant is nothing but a Green function, and can be expanded by KPM.

It is better to use the following Fermi function instead of approximating a spectral projector directly.

$${P}_{F}^{{\rm{eff}}}=F({\mathcal{H}}/s)=\vartheta (-{\mathcal{H}}/s)-\frac{1}{2}.$$

(22)

Due to the particle-hole symmetry, this deformation also gives a correct Chern number. This expression can again be expanded by Chebyshev polynomials. Especially, the Fermi function has been expanded as

$${f}_{m}={\int\nolimits_{-1}^{1}}\frac{dx}{\pi \sqrt{1-{x}^{2}}}{T}_{m}(x)F(x).$$

(23)

$$F(x)={f}_{0}+2\mathop{\sum }\limits_{m = 1}^{{M}^{\prime}-1}{f}_{m}{T}_{m}(x),$$

(24)

where ${M}^{\prime}$ is a cutoff of the expansion for NCCN³⁹. We used the Jackson kernel for the Chern number:

$${g}_{m}^{\prime}=\frac{({M}^{\prime}-m+1)\cos \frac{\pi m}{{M}^{\prime}+1}+\sin \frac{\pi m}{{M}^{\prime}+1}\cot \frac{\pi }{{M}^{\prime}+1}}{{M}^{\prime}+1},$$

(25)

where $m=0,\ldots ,{M}^{\prime}-1$. We here used ${M}^{\prime}=512$, instead. Thus,

$${P}_{F}^{{\rm{eff}}} \sim {g}_{0}^{\prime}{f}_{0}{T}_{0}({\mathcal{H}})+2\mathop{\sum }\limits_{m = 1}^{{M}^{\prime}-1}{g}_{m}^{\prime}{f}_{m}{T}_{m}({\mathcal{H}}).$$

(26)

This can indeed be evaluated with a calculation cost of O(N). Detailed information for the O(N) approximation is included in Supplementary Methods.