A systematic approach for COVID-19 predictions and parameter estimation

Abstract

The world is currently facing a pandemic called COVID-19 which has drastically changed our human lifestyle, affecting it badly. The lifestyle and the thought processes of every individual have changed with the current situation. This situation was unpredictable, and it contains a lot of uncertainties. In this paper, the authors have attempted to predict and analyze the disease along with its related issues to determine the maximum number of infected people, the speed of spread, and most importantly, its evaluation using a model-based parameter estimation method. In this research the Susceptible-Infectious-Recovered model with different conditions has been used for the analysis of COVID-19. The effects of lockdown, the light switch method, and parameter variations like contact ratio and reproduction number are also analyzed. The authors have attempted to study and predict the lockdown effect, particularly in India in terms of infected and recovered numbers, which show substantial improvement. A disease-free endemic stability analysis using Lyapunov and LaSalle’s method is presented, and novel methods such as the convalescent plasma method and the Who Acquires Infection From Whom method are also discussed, as they are considered to be useful in flattening the curve of COVID-19.

1 Introduction

The novel coronavirus COVID-19 has caused a drastic change in human lifestyle and behavior. The World Health Organization (WHO) declared COVID-19 a public health emergency on January 30, 2020 and a pandemic on March 11, 2020 [1]. The International Committee on Taxonomy of Viruses (ICTV) named the virus severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [6]. It is a class of β-coronavirus and has many potential natural, intermediate, and final hosts [7]. This virus spreads quite quickly [2] and already has outbreaks in various parts of the world [4],[5]. As of August 23, 2020, the total reported cases in India numbered 3,080,483 with 2,313,510 recoveries and 57,263 deaths [15] with a recovery rate of 72.83%. Population plays a significant role in any epidemic, especially in the case of COVID-19, where the rate of transmission is high [3]. So, for a country like India with a huge population, it is a herculean task to prevent its spread. Due to some strict and preventive actions taken by the administration, the infection rate has been lowered as compared to other countries. As stated, as of August 23, 2020, the recovery rate had improved significantly to 72.83%, with a lower death rate of 2.3% [17]. In India the process of unlock was started beginning on June 1, 2020 in different phases, namely unlock 1 and unlock 2, with the unlock 3 process currently taking place. As a result the reproduction number R₀ has been reduced from 1.36 to 1.13 and is directly affected by the infected population. The current situation shows that 90% of the cases are limited to 10 states of India, and the government is increasing testing and monitoring in these states. The Indian government is now more focused on testing. As a result, as of now 35,292,220 tests have been conducted while 801,147 tests are performed on a daily basis [17].

The delayed recognition of symptoms has a great effect on the increasing number of infected people [3]. It is essential to minimize the spread of the virus; hence, estimating the size of the pandemic by monitoring and tracking it is useful for health services [8]. To predict the dynamic spread of the virus, deterministic models have been used. The Susceptible-Infectious-Recovered (SIR) model can be applied for different levels of complexity to describe the flow between compartments using differential equations [9]. These deterministic mathematical models have considered parameter variations such as infection rate, recovery rate, confirmed cases, and recovered cases. This paper presents modeling and analysis of the SIR model for COVID-19 in terms of disease spread, maximum number of infected individuals, and number of deceased individuals. Simulation results have been discussed with lockdown policy and parameter variations to determine the number of infected and recovered cases in India.

The remainder of the paper is organized as follows. In Section 2, SIR mathematical models with different conditions are discussed. In Section 3, the mathematical analysis is discussed to determine the effects of the disease. Disease-free and endemic Lyapunov stability are discussed in Section 4. Section 5 presents the simulation results and discussion, while Section 6 discusses novel methods to limit the disease. In Section 7, the impact of the disease and the situation during unlock on India are discussed, while the conclusions are drawn in Section 8.

1.1 Highlights of the paper

The main features of the paper are as follows:

• 1. A brief mathematical analysis has been done in terms of size of disease spread, speed of spread, maximum number of infectious persons, and parameter variations (refer to Section 3).

• 2. Disease-free and endemic equilibria stabilities have been discussed using a Lyapunov function (refer to Section 4).

• 3. A model-based prediction and parameter estimation method has been used for the disease spread and end date of the epidemic in India (refer to Section 5).

• 4. A solution-based analysis has been done to attempt to limit the pandemic spread and flatten the infection curve. Novel prevention methods such as convalescent plasma therapy, Who Acquires Infection From Whom (WAIFW), and the light switch method are discussed (refer to Section 6).

2 The Susceptible-Infectious-Recovered (SIR) mathematical model

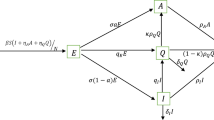
SIR is a fundamental model widely used in the analysis of a disease spread. To calculate the infection parameter and reproduction number for the disease, a time-varying SIR model has been used [10]. The SIR model consists of three compartments known as Susceptible, Infectious, and Recovered. The population which is not infectious falls under susceptible, and for COVID-19 the entire population [11] may get the infection, as there is no vaccine yet. An individual in the susceptible level moves into the infectious level when that individual is in close proximity to or contacting an infected person [12]. As the disease is contagious, the number of infected people continuously increases, which makes individuals in the susceptible level more likely to become infected and move to the infected level. The recovered level represents those who are no longer infectious [10]. Figure 1 represents the SIR model.

Fig. 1

Block diagram of the SIR model

2.1 SIR model with no migration

The SIR model is used with the following assumptions:

• 1. The population remains constant.

• 2. The rate of infection is directly proportional to contacts/touches.

• 3. A constant rate of infectious persons will recover/die.

The mathematical equations of the SIR model are as follows:

$$ \frac{\text{d}S}{\text{d}t} = - r I S $$

(1)

where r is the rate of contact and, based on the second assumption, people become infected. Therefore, $\frac {dS}{dt}$ is negative.

$$ \frac{\text{d}I}{\text{d}t} = \ r\ I\ S - a\ I $$

(2)

where a is constant. The infectious level increases because individuals in the susceptible level will be infected.

$$ \frac{\text{d}R}{\text{d}t} = \ a\ I $$

(3)

For analyzing the model, the initial conditions are assumed as

S = S₀, I = I₀, and R = 0

According to the first assumption, we get the following equation:

$$ \frac{\text{d}S}{\text{d}t} + \frac{\text{d}I}{\text{d}t} + \frac{\text{d}R}{\text{d}t} = 0\ $$

(4)

$$ S + I + R = S_{0} + \ I_{0} $$

(5)

2.2 SIR model with migration

The main factor in disease spread is the size of the population. When individuals in the population are moving around, the number of infected cases will increase and result in an epidemic [13]. In the SIR model, we consider the migration effect with the following assumptions:

• 1. The susceptible population does not move around in space.

• 2. The infectious population migrates randomly at a constant rate.

• 3. The removed/recovered population does not move in space.

Taking these assumptions into consideration, we can focus only on the infectious migrating because they increase the contact ratio as they travel and move around. Since the migrating population is dependent on both time and space, a partial derivative analysis is required. The SIR equations with migration become

$$ \frac{\partial S}{\partial t} = \ - r\ I\ S $$

(6)

$$ \frac{\partial I}{\partial t} = \ r\ I\ S - a\ I + D\ \frac{\partial^{2}I}{\partial x^{2}} $$

(7)

where D is the constant rate of diffusion, and x is the space in which the individuals in the population are moving.

$$ \frac{\partial R}{\partial t} = \ a\ I $$

(8)

Since this SIR model is a function of time and space, a new variable y must be introduced in the following form:

$$ y = x - C\ t $$

(9)

Here C is the traveling speed, and its value plays an important role in spreading disease in the migrated population.

The derivative of Eq. (9) with respect to time can be written as

$$ \frac{\text{d}y}{\text{d}t} = \ - C $$

(10)

After dividing (1) and (2) by (10), we get

$$ 0 = C\ \frac{\text{d}S}{\text{d}y} - I\ S $$

(11)

$$ 0 = \ \frac{\mathrm{d}^{2}I}{\mathrm{d}y^{2}} + C\ \frac{\text{d}I}{\text{d}y} + I\ (\ S - \ \frac{1}{R_{0}}) $$

(12)

To analyze (11) and (12), consider some initial values. From (9):

If$\ y \rightarrow - \infty$, it means past values, i.e., before the occurrence of the disease; then $I \rightarrow 0\textit {and}\ S \rightarrow 1$.

If $\rightarrow \infty$, it means future values; i.e., $I \rightarrow 0$ with time, and the value of S also changes with time. This will be further analyzed in Section 3.

2.3 Vital dynamics of the SIR model

Let μ be the birth and death rate in a population N, such that

$$ N = S + I + R $$

(13)

Equations (1), (2), and (3) are modified as follows:

$$ \frac{\text{d}S}{\text{d}t} = \ - r\ I\ S + \ \mu\ - \mu\ S $$

(14)

$$ \frac{\text{d}I}{\text{d}t} = \ r\ I\ S - a\ I - \ \mu\ I $$

(15)

$$ \frac{\text{d}R}{\text{d}t} = \ a\ I - \ \mu\ R $$

(16)

Normally in a practical system, the birth rate is higher compared to the death rate. Hence, the contact ratio and reproduction number also change in the population.

2.4 SIR model with vaccines/tablets

Suppose a tablet with 10,000 units/day has been developed. This factor can be introduced in (1) and (3) as

$$ \frac{\text{d}S}{\text{d}t} = \ - r\ I\ S - 10,000 $$

(17)

$$ \frac{\text{d}R}{\text{d}t} = \ a\ I + 10,000 $$

(18)

In the case of COVID-19, no vaccines have been developed yet, and for this reason the entire population is considered to be in the susceptible level. The goal is to take susceptible individuals and convert them into recovered individuals with vaccination. The value of $\frac {\text {dS}}{\text {dt}}$ decreases while $\frac {\ \text {dR}}{\text {dt}}$ increases over time. Equation (2) indicates that vaccines may not affect individuals who are already infected, as the term S is present in it. This results in increasing $\frac {\text {dI}}{\text {dt}}$.

3 Analysis of COVID-19 using SIR model

3.1 The spread of the disease

From (1), it can be seen that, since r, I, and S are positive, in order for $\frac {\text {dS}}{\text {dt}}$ to be negative, S should be less than or equal to S₀, i.e., S≤ S₀.

Substituting the above condition in (2), we get

$$ \frac{\text{d}I}{\text{d}t} \leq I\ (\ r\text{\ \ }S_{0} - a)\ $$

(19)

If the value of infectious I increases from initial value I₀, the epidemic will occur.

If ${\ S}_{0} > \frac {a}{r}$, then the disease will spread.

Therefore, the contact ratio is represented by

$$ \frac{a}{r}\ = \ \frac{1}{q} $$

(20)

where q is the contact ratio.

The contact ratio is the fraction of the population who come into contact with infected individuals. The second level of transmission can also spread the disease, which depends on the reproductive ratio (also known as reproduction number) given by

$$ R_{0} = r\ \frac{S_{0}}{a} $$

(21)

where R₀ represents the number of secondary infections in the population caused by the initial primary infection. If one person has the disease, then the R₀ value indicates the number of individuals this person will spread the disease to on average. For the seasonal flu, the value of R₀ is between 1.5 to 2, but for COVID-19, R₀ is between 3 to 4.

For this disease, the whole population is taken as susceptible, and the value of the reproduction number R₀ is high as compared to other diseases.

3.2 Maximum number of infectious individuals

Determining the number of infected individuals is very helpful in planning and distributing health resources. When (2) is divided by (1), we get

$$ \frac{\text{d}I}{\text{d}S} = \frac{\ r\ I\ S - a\ I}{- r\ I\ S} $$

(22)

$$ \frac{\text{d}I}{\text{d}S} = \ - 1 + \frac{\ a}{r\ S} $$

(23)

$$ \frac{\text{d}I}{\text{d}S} = \ - 1 + \frac{\ 1}{q\ S} $$

(24)

After integrating (12) and substituting the initial values, we get

$$ I + S - \ \frac{1}{q}\ln{S = \ \ }I_{0\ } + \ S_{0} - \ \frac{1}{q}\ln S_{0} $$

(25)

From (24), $\frac {\text {d}I}{\text {d}S}$ will be zero when $S = \ \frac {1}{q}$. Putting this value of S in (25), we get the maximum number of infectious as

$$ I_{\max} = \ I_{0} + \ S_{0} - \frac{1}{q}\left( 1 + {ln(}{qS_{0}} \right)) $$

(26)

Substituting R₀ = q S₀ in (26), we get

$$ I_{\max} = \ I_{0} + \ S_{0} - \frac{1}{q}\left( 1 + {ln(}R_{0} \right) $$

(27)

$$ I_{\max} = \ I_{0} + \ S_{0} - f(x) $$

(28)

where $f\left (x \right ) = \frac {1}{q}\left (1 + {ln(}R_{0} \right ))$

From (28), it can be observed that $f\left (x \right )$ is a logarithmic function which is subtracted from almost the entire population.

For COVID-19, the contact ratio q is very high, especially during the period where symptoms might not be observed. Therefore, the value of $f\left (x \right )$ will be very low, and I_max can be written as

$$ I_{\max} = \ I_{0} + \ S_{0} $$

(29)

Hence for COVID-19, the maximum number of infectious individuals can be calculated using (29), which will result in a very big number.

3.3 Size of the disease spread

When the spread of the disease is stopped, this means that the number of infected individuals has gone down to zero or I = 0.

Substituting the value I = 0 in (5) and (25), we get

$$ R_{\text{end}} = \ I_{0} + S_{0} - \ S_{\text{end}} $$

(30)

$$ S_{\text{end}} - \frac{1}{q}\ln S_{\text{end}}\ = \ I_{0} + S_{0} - \ \frac{1}{q}\ln S_{0} $$

(31)

where R_end and S_end are the end values of R and S. In (30), the value of S_end determines the size of the disease spread.

Substituting the value of S_end from (31) into (30), we get

$$ R_{\text{end}} = 2\ \left( I_{0} + S_{0} \right) + \ \frac{1}{q}\ln{(S_{\text{end}}} - S_{0}) $$

(32)

From (32), it is evident that the value of S_end will be very small. This is due to the fact that the contact ratio value q is very high for COVID-19.

3.4 Speed of the disease spread in migration

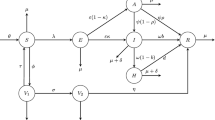
The speed of disease spread in a population is an important factor to consider when making policies and utilizing other resources in an epidemic [14]. The spread of the disease takes place more in the migrated population; therefore, the SIR model with migration is used for the analysis.

If $y \rightarrow - \infty$, meaning past values, i.e., before disease occurs, are used, then $I \rightarrow 0$ and $S \rightarrow 1$ are used as initial values. A linearization process has been used by introducing a new parameter P, which is a constant with a small value given by

$$ S = 1 - P $$

(33)

Substituting the value of S from (33) in (11) and (12), we get

$$ - C\ \frac{\text{d}P}{\text{d}y} - I\ S = 0 $$

(34)

$$ \frac{\mathrm{d}^{2}I}{\mathrm{d}y^{2}} + C\ \frac{\text{d}I}{\text{d}y} + I\ \left( \ 1 - \ \frac{1}{R_{0}} \right) = 0 $$

(35)

Phase plane analysis gives the solution of a traveling wave. The migration of a population can be assumed to be a traveling wave having both time and space. Therefore, the traveling speed using this method can be represented by

$$ C\ = 2\ \sqrt{1 - \frac{1}{R_{0}}} $$

(36)

Equation (36) clearly shows that for COVID-19 the traveling speed can be controlled by controlling the reproduction number R₀, i.e., the secondary infection, or in other words by reducing the average number of individuals infected. The secondary transmission condition may occur when a partial or full restriction is removed. Hence, R₀ will continue changing, and it will be far from 1. From the above model with different aspects of COVID-19, it is clear that the key parameter that must be controlled is contact ratio q.

3.5 Parameter estimation method

Let the model be described by the following differential equation:

$$ x^{\prime} = f(x,\theta) $$

(37)

where $\lbrack 0,\ t_{\max \limits }\rbrack$ is a time interval with initial value (0) = x₀.

The disease data over the time interval are given by

$$ \left( t_{1},g\left( x^{\left( 1 \right)} \right) \right), \left( t_{2},g\left( x^{\left( 2 \right)} \right) \right).........\left( t_{p},g\left( x^{\left( p \right)} \right) \right) $$

(38)

where the function g(x) is called the observable function of the state variables. To fit the data we consider values of the solution $x\left (t,\theta \right )$. Since initial condition x₀ is fixed, we consider it as a part of parameter 𝜃. Now the data points can be denoted as

$$ y = ((g\left( x^{\left( 1 \right)} \right),(g\left( x^{\left( 2 \right)} \right)\ldots\ldots.(g\left( x^{\left( p \right)}) \right) $$

(39)

The squared sum of errors (SSE) is given by

$$ SSE(\theta)= (d(g\left( x\left( t,\theta \right) \right),y)^{2} $$

(40)

In the nonlinear least squares method, the value of $\widehat {\theta }$ for model parameter 𝜃 is selected such that SSE(𝜃) is minimized.

4 Disease-free and endemic equilibria using Lyapunov-LaSalle’s method

As time goes on, the spread of the disease will eventually stop, and the infectious population should become zero. To find stability, the solution does not change in time, as implied by the following assumptions:

$$ \frac{\text{d}S}{\text{d}t} = \frac{\text{d}I}{\text{d}t}= 0 $$

(41)

Substituting the above assumptions into (14) and (15) yields the following equations:

$$ \frac{\text{d}S}{\text{d}t} = \ - r\ I\ S + \ \mu\ - \mu\ S = 0 $$

(42)

$$ \frac{\text{d}I}{\text{d}t} = \ r\ I\ S - a\ I - \ \mu\ I = 0 $$

(43)

Then the feasible region for the model is G = {((S,I) ∈R²)},0 ≤ S + I ≤ 1}. The model shows the equilibrium in this region. For (38) and (39), two possible equilibria are

• (i) P₀ = (1,0), i.e., disease-free equilibrium

• (ii) P^∗ = (S^∗,I^∗), i.e., endemic equilibrium

where $S^{*} = \frac {\mu + a}{r}$ and $I^{*} = \frac {\mu \lbrack \ r - \left (\mu + a \right )\rbrack }{r(\mu + a)}$.

If $R_{0} = \frac {r}{\mu + a}$ a < 1, P^∗ falls outside the feasible region G and corresponds to P₀ when R₀ = 1.

If R₀ < 1, all solutions converge to disease-free equilibrium P₀. P₀ is globally stable in region G by the method of Lyapunov-LaSalle.

Let the Lyapunov function $L\ \left (S,I \right ) = I$. Its derivative along with a solution $\left (S\left (t \right ),\ I\left (t \right ) \right )$ is

$$ \frac{\text{d}L}{\text{d}t} = \frac{\text{d}I}{\text{d}t} = I\left( \ \text{r}S - a - \mu \right) \leq I(r - a - \mu)\ \leq 0 $$

(44)

According to LaSalle’s invariance principle,

$$ K = \{(S,I) \in G,\ \frac{\text{d}L}{\text{d}t} = 0\ \} $$

(45)

From (44), $\frac {\text {d}L}{\text {d}t} = 0$ when (1) I = 0 and (2) R₀ = 1 and $S = \frac {\mu + a}{r}$.

In both cases the only compact invariant set in the set K is the singleton {P₀}. This means all solutions in G will converge to P₀. The existence of Lyapunov function L and of global convergence implies the local stability of P₀. Therefore, P₀ is globally stable in G.

5 Results and discussion

The SIR model has been simulated with different situations and parameter variations to analyze the effect of COVID-19. The parameter variations such as contact ratio and reproduction number have been chosen to analyze the effect of the disease worldwide. Based on administrative policies, the effect of COVID-19 in India has also been discussed using recent data [17]. Collected data up to April 28, 2020 have been used for simulation purposes [15]. All simulations have been done in MATLAB.

5.1 Case I: without lockdown

As discussed in Section 3, contact ratio and reproduction number are the key parameters in the spread of COVID-19 worldwide. Figure 2a–c shows the comparison in terms of SIR model parameters for several countries with an initial transmission rate.

Fig. 2

Worldwide effect. a Susceptible population, b Infectious, c Recovered

Figure 3 shows the spread of COVID-19 in India starting from the first case reported on January 30, 2020. From Fig. 3 it is evident that with the initial transmission rate of 2.28 the number of infectious could be very large and could move to the next stage of disease transmission, i.e., community transmission.

Fig. 3

Spread of COVID-19 in India before lockdown

5.2 Case II: effects of lockdown in India

To avoid the spread of COVID-19, the administration of India decided to implement a lockdown on March 25, 2020. This decision was made 55 days after finding the first case in India. The main goal of the lockdown was to control the contact ratio and reproduction number, which was initially 2.28. As per the data on April 11, 2020, the reproduction number (reproduction rate) was reduced to 1.55, and it was further reduced to 1.36 on April 21, 2020 [17]. As the contact among individuals was reduced significantly due to the lockdown, the reproduction rate evidently decreased. Figures 4 and 5 show a substantial decrease in the number of infectious persons. The number of recovered individuals also increased significantly. As of April 28, 2020, the recovery rate had improved by 22.3% in India [17].

Fig. 4

The spread of COVID-19 in India after the lockdown, with R₀ = 1.55. a Susceptible, b Infectious, c Recovered

Fig. 5

The spread of COVID-19 in India after the lockdown with R₀ = 1.36. a Susceptible, b Infectious, c Recovered

The unlock process began in the country on June 1, 2020 in different phases. As the unlock process has proceeded, the reproduction number has changed, which directly affects the infectious population. As per the latest data available on August 23, 2020, the reproduction number R₀ has reduced from 1.36 to 1.13 [17]. The analysis with the updated reproduction number in terms of model parameters is shown in Fig. 6a–c.

Fig. 6

The spread of COVID-19 in India after the lockdown with R₀ = 1.13. a Susceptible, b Infectious, c Recovered

5.3 Case III: effect of light switch method in India

Since lockdown cannot be implemented infinitely, an alternative method was needed which not only can bring back a normal human lifestyle but can also limit the disease spread. The light switch method was used in the post-COVID-19 period with normal activities like those before the disease occurred.

Figure 7 represents the infectious population curve after using the light switch method. There is an increase in the contact ratio parameter, which is expected as part of the resumed normal human lifestyle after the lockdown. Table 1 shows the analysis of Fig. 7 in terms of the infected population during weekdays.

Fig. 7

Infection spread of COVID-19 in India with light switch method

Table 1 Analysis of COVID-19 effect after lockdown in India

From Table 1, it is clear that the reduced contact ratio directly affects the infectious population and helps in flattening the infectious curve. The contact ratio of 20% signifies the importance of a strict social distancing rule in the population that is not infected yet.

5.4 Case IV: analysis using parameter estimation method

Our objective is to estimate the parameters r (rate of contact) and a (recovery rate), which can help in limiting the spread of COVID-19. Figure 8a, b shows the artificially generated data obtained by adding noise to the parameters that can affect the disease spread. These results also show the best fit values of the parameters to be r = 0.0096 and a = 0.1006.

Fig. 8

a Data on I and N artificially generated by adding noise. b Fitting results of I and N to the artificial data

6 Prevention methods to limit COVID-19 spread (flattening the curve)

According to the World Health Organization (WHO), it may take 12 to 15 months for a COVID vaccine to be developed and commercialized. Most of the analysis is now focused on limiting the spread of the disease by trying to flatten the curve of the infectious population. Here we discuss a few methods on how to flatten the curve of the disease.

6.1 Convalescent plasma therapy

Convalescent refers to a person who has recovered from a disease, and plasma refers to the yellow liquid part of the blood that contains antibodies. In the beginning of this year, China implemented this therapy on some groups of people suffering from COVID-19, and they showed positive results. Figure 9 shows the block flow diagram of the convalescent plasma method.

Fig. 9

Block flow diagram of convalescent plasma therapy

Convalescent plasma therapy is described as follows. If a person is infected with COVID-19, during the phase of the illness, the immune system of the patient will be active and will produce antibodies into the bloodstream. These antibodies react and try to deactivate the virus. This makes the immune system stronger, which helps in fighting the virus more effectively until the patient recovers from the disease. The plasma of the recovered individual is infused into another individual who is suffering from the same disease. The antibodies present in that plasma will enhance the ability of the immune system in fighting the virus at a faster rate. As a result, the infected patient will recover much faster using this treatment compared to other treatments. This treatment is helpful in reducing the number of infected people and increasing the recovery rate. Hence, the epidemic curve tends to become flat.

6.2 Who Acquires Infection From Whom (WAIFW) method

To limit COVID-19’s spread and to flatten the epidemic curve, exact contact tracing is required. The WAIFW method can be used with a contact matrix to trace the exact contacts. Administrations have started implementing mobile data apps with a unique Quick Response (QR) code to show the COVID-19 history of the individual carrying this QR code. This code would then be used to provide permissions to the user to enter facilities such as offices, movie theaters, hospitals, educational institutions, restaurants, religious places, and other public locales. The unique QR code will help in tracing the areas the individual has attended and providing treatment to this individual if he becomes infected. The code would also be able to identify individuals who may have been in close contact with the infected person who was later diagnosed with COVID-19 to provide them with treatment before they come in contact with more people.

6.3 Light switch method

In the current situation to limit the spread of COVID-19, many administrative policies have been implemented that have badly affected our lives. Figure 2b shows the worldwide effect of COVID-19, which is expected to remain for a long period of time. The main goal of this method is to reduce the contact ratio and reproduction number while maintaining a normal human life routine. The following are some of the measures that may be taken to implement this method:

• 1. Workplaces and essential services should be opened 24/7, and a shift-wise policy may be adopted to reduce the number of individuals in the premises at all times.

• 2. Offices should have different time schedules, which as a result will reduce the number of people in buses, metros, and other modes of transport.

• 3. People should perform tasks online if possible, e.g., working from home, online meetings, home delivery of essential items, digital banking, etc.

Table 1 shows the effect of the light switch method. When the contact ratio is at q = 50%, it is evident that the number of infected individuals in the population is decreased. This would not only help in minimizing the infectious peak on the epidemic curve but would also give some additional time to administration to more effectively utilize the health resources.

6.4 Community immunity

The main idea is to increase the immunity of the susceptible population so that they do not fall victim to this disease easily. COVID-19 mostly infected people belonging to an age group of 50 to 60 years old. In the case of the Spanish flu epidemic, natural development of community immunity reduced the spread [1], and a similar approach can be followed now. Offices, workplaces, and other public organizations must perform periodic testing and monitoring of their employees’ health. Administration may also issue immunization cards and make them required for essential services such as booking a train or purchasing flight tickets. This can help in reducing the size of the infected population significantly.

7 Impact of COVID-19 on India

India is the second most populated country (after China) in the world. Population plays an important role in disease spread. Using impressive administration policies, India has done quite well in managing the spread of COVID-19 as compared to other countries, and it was able to achieve a recovery rate of 22.3% as of April 28, 2020 [17]. As per recent studies, India is now the most favorable country for investment in sectors like trade, technology, manufacturing [16], and many others, and the day is not far when it would become a new center of world trade. Also, during the lockdown, users of online learning apps, online meeting apps, and digital transactions have drastically increased [16], which would herald the beginning of a new work culture in the society. The COVID-19 virus has a unique feature of its spike protein which helps this virus to change its structure with time. A vaccine would not have a strong effect in fighting this virus due to its mutation process. Because of all these challenges, we now have to live with COVID-19 for a long time, as we do with the human immunodeficiency virus (HIV), and we must also follow some rules like social distancing, wearing a face mask, using hand sanitizer, and avoiding crowded areas.

7.1 Unlock situation

India started the process of unlock on June 1, 2020. This unlock process is quite similar to the light switch method which was discussed in Section 6.2. During the process of unlock, the government has given some exemptions for places of work and other public places. Following the government advisory, the daily life and work culture in the country have been changed in terms of working hours of offices, use of public transport, etc. Most of the states are now doing lockdown on weekends to avoid or slow down the spread of the disease. The education system is badly affected by COVID-19, and as a result, most of the schools and universities are delivering online education. The Indian government has decided to issue a digital health card under the Digital Health Mission, which would be helpful in tracing and testing.

8 Conclusion

In this paper, mathematical analyses of COVID-19 have been done in terms of disease spread, maximum number of infected individuals, and size and speed of the disease spread in migration. These analyses are helpful in predicting the number of infected individuals and the reproduction number for the disease using a time-varying SIR model. This may lead to better utilization of health resources. Disease-free time and endemic equilibria have been discussed by choosing a Lyapunov function for the model. Prevention methods like convalescent plasma therapy and the light switch method are also discussed to limit the disease spread and help in flattening the epidemic curve. A COVID-19 vaccine has yet to be developed; therefore, most countries have used a lockdown policy. The effect of lockdown in India has been discussed in Section 4 and was found to have reduced the reproduction number to 1.36. It was also evident that the lockdown policy resulted in decreasing the number of infected people, compared to the situation in countries which did not implement this policy [15]. A comparison of susceptible, infectious, and recovered individuals has been done by varying the contact ratio and reproduction number under different conditions, i.e., with and without lockdown and under the light switch method. It can be concluded that by utilizing the light switch method there would be no infected person in 234 days, while normally it would take around a year to eradicate the disease. Since it is still unknown when a vaccine will be available for each and every human being, one way of reducing the spread of the disease is to live with it by making our immune systems stronger and by using proper protective equipment.