Addressing the lack of measurements in the subsea environment by using a model scheduling Kalman filter coupled with a robust adaptive MPC

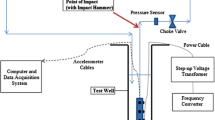
Abstract

Electric submersible pumps (ESPs) are one of the most widespread oil artificial lifting technologies. In the operation of an ESP there are a large number of parameters that must be monitored and held within operational constraints in order to guarantee stable and optimal operation. Manual control is subject to sub-optimal production and constant violation of operational limits, that can cause either a reduction in ESP lifetime or premature failure. Therefore, a proper automation strategy must be applied to support operators in order to ensure the best production rate with less energy cost. Previous literature has proposed the use of linear MPC based on system identification, however all relevant system variable measurements were considered available. In this paper, the problem of losing measurements of the state variables due to the aggressive subsea environment is addressed. We show that a non-adaptive single linear model strategy lacks in quality for state estimation and, therefore, a robust MPC is not possible under this configuration. In this work, an adaptive constrained MPC coupled with a model scheduling Kalman filter (MSKF) is proposed. Two model scheduling strategies based on linear interpolation of a pre-set number of local models are proposed and compared to successive linearization at every sampling time, based on Taylor series expansion of the nonlinear model. All strategies guarantee model accuracy and model stability over the whole operational range. The proposed scheduling strategies presented similar performance compared to the successive linearization strategy, avoiding the need of obtaining a local linear model at each sampling time.

Appendices

Appendix A. ESP process model

The ESP process model considered in the present work was proposed by Pavlov et al. (2014) and adapted by Binder et al. (2015) in order to improve its fidelity to a real well. The model is a third-order nonlinear differential–algebraic system of equations. The set of differential equation is derived by considering the system of a hydraulic transmission line with pressure loss due to friction along pipes and pressure boost due to the ESP:

$$\frac{d{p}_{bh}}{dt} =\frac{({q}_{r}-q) {\beta }_{1}}{{V}_{1}}$$

(15)

$$\frac{d{p}_{wh}}{dt} = \frac{\left(q-{q}_{c}\right) {\beta }_{2}}{{V}_{2}}$$

(16)

$$\frac{dq}{dt} =\frac{1}{M}\left({p}_{bh}-{p}_{wh}-\rho g {h}_{w}-\Delta {p}_{f}+\rho g H\right)$$

(17)

The well productivity index is considered constant on the operation time scale, so the reservoir inflow rate is:

$${q}_{r}= PI \left({p}_{r}-{p}_{bh}\right)$$

(18)

It is considered that there is always a pressure loss across the choke valve, so no backflow is allowed and the flow rate can be calculated by:

$${q}_{c}= { C}_{c} z \sqrt{{p}_{wh}-{p}_{m}}$$

(19)

The pressure drop in each pipe section comes from Darcy–Weisbach considering the Fanning friction factor for smooth pipe and turbulent flow:

$${F}_{i} = 0.158\frac{\rho {L}_{i} {q}^{2}}{{D}_{i} {A}_{i}^{2}}{\left(\frac{\mu }{\rho {D}_{i} q}\right)}^{1/4}$$

(20)

So the pressure drop in the well is the sum of both friction factors, $\Delta {p}_{f}={F}_{1}+{F}_{2}$. It is assumed that the fluid proprieties (i.e., density and viscosity) are constant across the ESP, so the multi-stage pump can be modeled as a number of single-stages. Moreover, the fluid is considered incompressible; therefore, the affinity laws presented by Takacs (2009) are valid and the pump equations are:

$${q}_{0}=\frac{q}{{C}_{q}}\left(\frac{{f}_{0}}{f}\right)$$

(21)

$$H={C}_{H}{H}_{0}{\left(\frac{f}{{f}_{0}}\right)}^{2}$$

(22)

$$P = {C}_{P}{P}_{0}{\left(\frac{f}{{f}_{0}}\right)}^{3}$$

(23)

$${p}_{p,in }= {p}_{bh} - \rho g {h}_{1}-{F}_{1}$$

(24)

The model parameter values considered in the present study are shown in Table 9.

Table 9 Model parameters (Binder et al. 2015)

${H}_{o}$ and ${P}_{0}$ in Eqs. (22) and (23), respectively, are head and power characteristic curves of the pump at a reference frequency ${f}_{0}$ and for water as a fluid ($\mu =1 cP$). ${C}_{q}$, ${C}_{H}$ and ${C}_{P}$ in Eqs. (21), (22) and (23) are viscosity correction factors for flow, head and power. The characteristic curves and the viscosity correction factors are polynomial functions (Binder et al. 2015):

$$R\left(x\right)={\sum }_{i=0}^{4}{c}_{i}{x}^{i}$$

(25)

where $x$ denotes ${q}_{0}$ for the characteristic curves and $\mu$ the viscosity correction factor.

Appendix B. System linearization strategy

The linearization strategy followed the Taylor series expansion truncated in the first order element, resulting in the following linear system written in the matrix form:

$$\begin{array}{c}\frac{d{\varvec{x}}\left(t\right)}{dt}={\varvec{A}}{\varvec{x}}\left(t\right)+{\varvec{B}}{\varvec{u}}\left(t\right)\\ {\varvec{y}}\left(t\right)={\varvec{C}}{\varvec{x}}\left(t\right)+{\varvec{D}}{\varvec{u}}\left(t\right)\end{array}$$

(26)

in which ${\varvec{x}}$, ${\varvec{u}}$ and ${\varvec{y}}$ are respectively state, input and output variables in a reference state deviation notation.

$${\varvec{x}}=\left(\begin{array}{c}{p}_{bh}-{p}_{bh}^{*}\\ {p}_{wh}-{p}_{wh}^{*}\\ q-{q}^{*}\end{array}\right)$$

(27)

$${\varvec{u}}=\left(\begin{array}{c}f-{f}^{*}\\ z-{z}^{*}\end{array}\right)$$

(28)

$${\varvec{y}}=\left(\begin{array}{c}{p}_{p,in}-{p}_{p,in}^{*}\\ P-{P}^{*}\end{array}\right)$$

(29)

Let $d{\varvec{x}}\left(t\right)/dt$ be represented by a function of ${\varvec{x}}$ and ${\varvec{u}}$, such as:

$$\frac{d{\varvec{x}}\left(t\right)}{dt}=\mathcal{F}\left({\varvec{x}},{\varvec{u}}\right)$$

(30)

The elements of matrices ${\varvec{A}}$, ${\varvec{B}}$, ${\varvec{C}}$ and ${\varvec{D}}$ can be calculated by the analytical derivatives of $\mathcal{F}$ and ${\varvec{y}}$ over ${\varvec{x}}$ and ${\varvec{u}}$:

$${a}_{i,j}={\left.\frac{\partial {\mathcal{F}}_{i}}{\partial {x}_{j}}\right|}_{{{\varvec{x}}}^{*},{{\varvec{u}}}^{*}}, {b}_{i,j}={\left.\frac{\partial {\mathcal{F}}_{i}}{\partial {u}_{j}}\right|}_{{{\varvec{x}}}^{*},{{\varvec{u}}}^{*}}, {c}_{i,j}={\left.\frac{\partial {y}_{i}}{\partial {x}_{j}}\right|}_{{{\varvec{x}}}^{\boldsymbol{*}},{{\varvec{u}}}^{*}}, {d}_{i,j}={\left.\frac{\partial {y}_{i}}{\partial {u}_{j}}\right|}_{{{\varvec{x}}}^{*},{{\varvec{u}}}^{\boldsymbol{*}}}$$

(31)

The elements of the Jacobian matrix, ${\varvec{A}}$, are:

$$\begin{gathered} a_{{1,1}} = - PI~\beta _{1} /V_{1} \hfill \\ a_{{1,2}} = 0 \hfill \\ a_{{1,3}} = - \beta _{1} /V_{1} \hfill \\ a_{{2,1}} = 0 \hfill \\ a_{{2,2}} = - \frac{{\beta _{2} }}{{V_{2} }}\left( {\frac{{C_{c} z^{*} }}{2}\frac{1}{{\sqrt {p_{{wh}}^{*} - p_{m}^{*} } }}} \right) \hfill \\ a_{{2,3}} = \beta _{2} /V_{2} \hfill \\ a_{{3,1}} = 1/M \hfill \\ a_{{3,2}} = - 1/M \hfill \\ a_{{3,3}} = - \frac{{F_{1}^{'} - F_{2}^{'} }}{M} + \frac{{\rho gC_{H} }}{M}\left( {\frac{{f^{*} }}{{f^{0} }}} \right)^{2} \left( {C_{{1,H0}} + 2C_{{2,H0}} q^{*} \frac{{f^{*} }}{{C_{q} f_{0} }}} \right)\frac{{f^{*} }}{{C_{q} f_{0} }} \hfill \\ \end{gathered}$$

(32)

The elements of matrix ${\varvec{B}}$ are:

$$\begin{gathered} b_{{1,1}} = 0 \hfill \\ b_{{1,2}} = 0 \hfill \\ b_{{2,1}} = 0 \hfill \\ b_{{2,2}} = - \frac{{\beta _{2} }}{{V_{2} }}C_{c} \sqrt {p_{{wh}}^{*} - p_{m}^{*} } \hfill \\ a_{{3,1}} = 1/M \hfill \\ a_{{3,2}} = - 1/M \hfill \\ \end{gathered}$$

(33)

The elements of matrix ${\varvec{C}}$ are:

$$\begin{gathered} c_{{1,1}} = 1 \hfill \\ c_{{1,2}} = 0 \hfill \\ c_{{2,1}} = F_{1} \hfill \\ c_{{2,2}} = 0 \hfill \\ c_{{3,1}} = 0 \hfill \\ c_{{3,2}} = \frac{{C_{P} ~f^{*} }}{{C_{q} ~f_{0} }}\left( {\frac{{f^{*} }}{{f_{0} }}} \right)^{3} \left[ {C_{{1,P0}} + 2C_{{2,P0}} \frac{{q^{*} ~f^{*} }}{{C_{q} ~f_{0} }} + 3C_{{3,P0}} \left( {\frac{{q^{*} ~f^{*} }}{{C_{q} ~f_{0} }}} \right)^{2} } \right] \hfill \\ \end{gathered}$$

(34)

Finally, the elements of matrix ${\varvec{D}}$ are:

$$\begin{gathered} d_{{1,1}} = 0 \hfill \\ d_{{1,2}} = 0 \hfill \\ d_{{2,1}} = C_{P} \left( {\frac{{f^{*} }}{{f_{0} }}} \right)^{3} \left[ {C_{{1,P0}} + 2C_{{2,P0}} \frac{{q^{*} ~f^{*} }}{{C_{q} ~f_{0} }} + 3C_{{3,P0}} \left( {\frac{{q^{*} ~f^{*} }}{{C_{q} ~f_{0} }}} \right)^{2} } \right] \hfill \\ d_{{2,2}} = 0 \hfill \\ \end{gathered}$$

(35)

In which,

$${F}_{i}^{^{\prime}}=0.158\frac{2\rho {L}_{i}{q}^{*}}{{D}_{i}{A}_{i}^{2}}{\left(\frac{\mu }{\rho {D}_{i}{q}^{*}}\right)}^{1/4}+\frac{0.158}{4}\frac{\rho {L}_{i}{{q}^{*}}^{2}}{{D}_{i}{A}_{i}^{2}}{\left(\frac{\mu }{\rho {D}_{i}{q}^{*}}\right)}^{-3/4}\left(\frac{-\mu }{\rho {D}_{i}{{q}^{*}}^{2}}\right), i=\mathrm{1,2}$$

(36)

It is noteworthy that a relative deviation approach enhances the controllability of the system. This is a normalization strategy to deal with the different order of magnitude of the variables. The system notation adopting the relative deviation is:

$$\begin{array}{c}\frac{d{\varvec{z}}\left(t\right)}{dt}=\widehat{{\varvec{A}}}{\varvec{z}}\left(t\right)+\widehat{{\varvec{B}}}{\varvec{\mu}}\left(t\right)\\ {\varvec{w}}\left(t\right)=\widehat{{\varvec{C}}}{\varvec{z}}\left(t\right)+\widehat{{\varvec{D}}}{\varvec{\mu}}\left(t\right)\end{array}$$

(37)

in which ${\varvec{z}}$, ${\varvec{\mu}}$ and ${\varvec{w}}$ are, respectively, state, input and output variables in a reference state relative deviation notation.

$${\varvec{z}}=\left(\begin{array}{c}\frac{{p}_{bh}-{p}_{bh}^{*}}{{p}_{bh}^{*}}\\ \frac{{p}_{wh}-{p}_{wh}^{*}}{{p}_{wh}^{*}}\\ \frac{q-{q}^{*}}{{q}^{*}}\end{array}\right)$$

(38)

$${\varvec{\mu}}=\left(\begin{array}{c}\frac{f-{f}^{*}}{{f}^{*}}\\ \frac{z-{z}^{*}}{{z}^{*}}\end{array}\right)$$

(39)

$${\varvec{w}}=\left(\begin{array}{c}\frac{{p}_{p,in}-{p}_{p,in}^{*}}{{p}_{p,in}^{*}}\\ \frac{P-{P}^{*}}{{P}^{*}}\end{array}\right)$$

(40)

Taking the system in a reference deviation notation, it is possible to find the equivalent matrices in the fractional reference deviation by applying the following transformations:

$${\widehat{a}}_{i,j}={a}_{i,j}\frac{{x}_{j}^{*}}{{x}_{i}^{*}}$$

(41)

$${\widehat{b}}_{i,j}={b}_{i,j}\frac{{u}_{j}^{*}}{{x}_{i}^{*}}$$

(42)

$${\widehat{c}}_{i,j}={c}_{i,j}\frac{{x}_{j}^{*}}{{y}_{i}^{*}}$$

(43)

$${\widehat{d}}_{i,j}={d}_{i,j}\frac{{u}_{j}^{*}}{{y}_{i}^{*}}$$

(44)

in which ${\widehat{a}}_{i,j}$, ${\widehat{b}}_{i,j}$, ${\widehat{c}}_{i,j}$ and ${\widehat{d}}_{i,j}$ are the elements of matrices $\widehat{{\varvec{A}}}$, $\widehat{{\varvec{B}}}$, $\widehat{{\varvec{C}}}$ and $\widehat{{\varvec{D}}}$, respectively.