Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-23T20:57:32.812Z Has data issue: false hasContentIssue false
  • English
  • Français

The integral cohomology of the Hilbert scheme of points on a surface

Part of: Cycles and subschemes Fiber spaces and bundles

Published online by Cambridge University Press:  04 November 2020

Burt Totaro Open the ORCID record for Burt Totaro [Opens in a new window]
Burt Totaro*
Affiliation:
UCLA Mathematics Department, Box 951555, Los Angeles, CA90095-1555,USA; E-mail: totaro@math.ucla.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if X is a smooth complex projective surface with torsion-free cohomology, then the Hilbert scheme 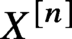$X^{[n]}$ has torsion-free cohomology for every natural number n. This extends earlier work by Markman on the case of Poisson surfaces. The proof uses Gholampour-Thomas’s reduced obstruction theory for nested Hilbert schemes of surfaces.

Keywords

Hilbert scheme of pointsintegral cohomologyChow motive

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes)
Secondary: 55R80: Discriminantal varieties, configuration spaces
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e40
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Atiyah, M., K-Theory (W. A. Benjamin, New York, 1967).Google Scholar
Atiyah, M. and Hirzebruch, F., ‘Vector bundles and homogeneous spaces’, in Proc. Sympos. Pure Math., vol. 3 (American Mathematical Society, 1961), 7–38.Google Scholar
Auel, A., Colliot-Thélène, J.-L., and Parimala, R., ‘Universal unramified cohomology of cubic fourfolds containing a plane’, in Brauer Groups and Obstruction Problems (Palo Alto, 2013) (Birkhäuser, 2017), 29–56.CrossRefGoogle Scholar
de Cataldo, M. A. and Migliorini, L., ‘The Douady space of a complex surface’, Adv. Math. 151 (2000), 283–312.CrossRefGoogle Scholar
de Cataldo, M. A. and Migliorini, L., ‘The Chow groups and the motive of the Hilbert scheme of points on a surface’, J. Alg. 251 (2002), 824–848.CrossRefGoogle Scholar
Ellingsrud, G. and Strømme, S., ‘On the homology of the Hilbert scheme of points in the plane’, Invent. Math. 87 (1987), 343–352.CrossRefGoogle Scholar
Gholampour, A. and Thomas, R. P., ‘Degeneracy loci, virtual cycles and nested Hilbert schemes. I’, Tunisian J. Math. 2 (2020), 633–665.CrossRefGoogle Scholar
Gorchinskiy, S. and Orlov, D., ‘Geometric phantom categories’, Publ. Math. IHES 117 (2013), 329–349.CrossRefGoogle Scholar
Göttsche, L., ‘Hilbert schemes of points on surfaces’, in Proceedings of the International Congress of Mathematicians (Beijing, 2002), vol. 2 (Higher Education Press, Beijing, 2002), 483–494.Google Scholar
Li, Wei-Ping and Qin, Zhenbo, ‘Integral cohomology of Hilbert schemes of points on surfaces’, Comm. Anal. Geom. 16 (2008), 969–988.CrossRefGoogle Scholar
Markman, E., ‘Integral generators for the cohomology ring of moduli spaces of sheaves over Poisson surfaces’, Adv. Math. 208 (2007), 622–646.CrossRefGoogle Scholar
Totaro, B., ‘The integral cohomology of the Hilbert scheme of two points’, Forum Math. Sigma 4 (2016), e8, 20 pp.CrossRefGoogle Scholar
Totaro, B., ‘The motive of a classifying space’, Geometry and Topology 20-4 (2016), 2079–2133.CrossRefGoogle Scholar