Abstract
In this paper, the geometric dislocation density tensor and Burgers vector are studied using an elastic–plastic decomposition of Laplace stretch \(\varvec{\mathcal {U}}\). The Laplace stretch arises from a \(\mathbf {QR}\) decomposition of the deformation gradient and is very useful, as one can directly and unambiguously measure its components by performing experiments. The geometric dislocation density tensor \({\tilde{\mathbf {G}}}\) is obtained using the classical argument of failure of a Burgers circuit in a suitable configuration \(\tilde{\kappa }_p\) where the deformation of a body is solely due to the movement of dislocations. The geometric features of space \(\tilde{\kappa }_p\) are explored. It is shown that the derived geometric dislocation tensor is related to the torsion of \(\tilde{\kappa }_p\), which serves as a measure of incompatibility in this space. Additionally, \({\tilde{\mathbf {G}}}\) vanishes only when the space \(\tilde{\kappa }_p\) is compatible. A balance law for geometric dislocations is derived taking into account the effect of the dislocation flux and source dislocations. The physical meaning of the plastic Laplace stretch, and consequently, of the derived geometric dislocation tensor proves to be particularly useful in the classification of dislocations. Finally, the significance of the dislocation density tensor is discussed. The derived geometric dislocation density tensor could be specifically useful in developing a strain-gradient and size-dependent theory of plasticity.



Similar content being viewed by others
Notes
Originally proposed by Bilby et al. [5].
Note that \(\varvec{\mathcal {R}}\) is different from the rotation tensor \(\mathbf {R}\) obtained from polar decomposition of \(\mathbf {F}\).
This measure for GND density is same as the one derived in Cermelli and Gurtin [9].
The Gram-Schmidt procedure does not specify the 1 coordinate direction nor the 12 coordinate plane, based upon which the other coordinate directions are determined. Therefore, one can potentially have a non-unique set of bases for an experimenter’s frame of reference. This issue is resolved by re-indexing the deformation gradient using a strategy whereby the selected 1 direction undergoes the least amount of transverse shear, and the selected 12 coordinate plane experiences least amount of in-plane shear. This re-indexed deformation gradient is denoted by \(\varvec{\mathcal {F}}\), whose construction is developed in a paper soon to be published. In fact, the re-indexed deformation gradient \(\varvec{\mathcal {F}}\) is decomposed into \(\varvec{\mathcal {R}}\) and \(\varvec{\mathcal {U}}\). This is merely a problem of selecting the ‘correct’ set of bases. Deformation gradients \(\mathbf {F}\) and \(\varvec{\mathcal {F}}\) essentially contain the same information.
Although it is indeed possible for bodies made up of a rigid plastic material to undergo a plastic only deformation, such a constitutive relation is too restrictive.
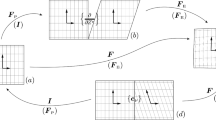
Such cases appear whenever the deformation gradient is upper-triangular, e.g., a uniaxial or a biaxial tension.
Note that in this case, elongation along the 1 direction is \(a=1\).
References
Acharya, A.: A counterpoint to Cermelli and Gurtin’s criteria for choosing the ‘correct’ geometric dislocation tensor in finite plasticity. In: IUTAM Symposium on theoretical, computational and modelling aspects of inelastic media, pp. 99–105. Springer (2008)
Acharya, A., Bassani, J.L.: Lattice incompatibility and a gradient theory of crystal plasticity. J. Mech. Phys. Solids 48(8), 1565–1595 (2000)
Barber, J.R.: Elasticity. Springer, Berlin (1992)
Bilby, B.A., Bullough, R., Smith, E.: Continuous distributions of dislocations: a new application of the methods of non-Riemannian geometry. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 231(1185), 263–273 (1955)
Bilby, B. A., Gardner, L. R. T., Stroh, A. N.: Continuous distributions of dislocations and the theory of plasticity. In: Proceedings of the 9th international congress of applied mechanics, volume 8, pp. 35–44. University de Bruxelles, Brussels (1957)
Bullough, R., Bilby, B.A.: Continuous distributions of dislocations: surface dislocations and the crystallography of martensitic transformations. Proc. Phys. Soc. Sect. B 69(12), 1276 (1956)
Burgers, J. M.: Physics.–Some considerations on the fields of stress connected with dislocations in a regular crystal lattice. I. In: Selected Papers of JM Burgers, pp. 335–389. Springer, Berlin (1995)
Casey, J., Naghdi, P.M.: A remark on the use of the decomposition \(\mathbf{F}=\mathbf{F}^e\mathbf{F}^p\) in plasticity. J. Appl. Mech. 47(3), 672–675 (1980)
Cermelli, P., Gurtin, M.E.: On the characterization of geometrically necessary dislocations in finite plasticity. J. Mech. Phys. Solids 49(7), 1539–1568 (2001)
Acharya, A. A counterpoint to Cermelli and Gurtin’s criteria or choosing the ‘correct’ geometric dislocation tensor in finite plasticity. In: IUTAM Symposium on Theoretical, Computational and Modelling Aspects of Inelastic Media, pp. 99–105 (2008)
Clayton, J.D.: On anholonomic deformation, geometry, and differentiation. Math. Mech. Solids 17(7), 702–735 (2012)
Clayton, J.D.: Differential Geometry and Kinematics of Continua. World Scientific, Singapore (2015)
Dafalias, Y.F.: Plastic spin: necessity or redundancy? Int. J. Plast 14(9), 909–931 (1998)
Davini, C., Parry, G.P.: On defect-preserving deformations in crystals. Int. J. Plast 5(4), 337–369 (1989)
Davini, C., Parry, G.P.: A complete list of invariants for defective crystals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 432(1886), 341–365 (1991)
Fleck, N.A., Muller, G.M., Ashby, M.F., Hutchinson, J.W.: Strain gradient plasticity: theory and experiment. Acta Metall. Mater. 42(2), 475–487 (1994)
Freed, A.D., le Graverend, J.B., Rajagopal, K.R.: (2019): A decomposition of Laplace stretch with applications in inelasticity. Acta Mech. 230(9), 3423–3429 (2019)
Freed, A.D., Srinivasa, A.R.: Logarithmic strain and its material derivative for a QR decomposition of the deformation gradient. Acta Mech. 226(8), 2645–2670 (2015)
Freed, A.D., Zamani, S.: On the use of convected coordinate systems in the mechanics of continuous media derived from a QR factorization of F. Int. J. Eng. Sci. 127, 145–161 (2018)
Gao, H., Huang, Y., Nix, W.D., Hutchinson, J.W.: Mechanism-based strain gradient plasticity-I. Theory. J. Mech. Phys. Solids 47(6), 1239–1263 (1999)
Ghosh, P., Srinivasa, A.R.: Development of a finite strain two-network model for shape memory polymers using QR decomposition. Int. J. Eng. Sci. 81, 177–191 (2014)
Green, A.E., Naghdi, P.M.: Some remarks on elastic-plastic deformation at finite strain. Int. J. Eng. Sci. 9(12), 1219–1229 (1971)
Gupta, A., Steigmann, D.J., Stölken, J.S.: On the evolution of plasticity and incompatibility. Math. Mech. Solids 12(6), 583–610 (2007)
Gurtin, M.E.: The Burgers vector and the flow of screw and edge dislocations in finite-deformation single-crystal plasticity. J. Mech. Phys. Solids 54(9), 1882–1898 (2006)
Iwasawa, K.: On some types of topological groups. Ann. Math. pp. 507–558 (1949)
Jiang, J., Zhang, T., Dunne, F.P., Britton, T.B.: Deformation compatibility in a single crystalline Ni superalloy. Proc. R. Soc. A Math. Phys. Eng. Sci. 472(2185), 20150690 (2016)
Kondo, K.: Non-Riemannian geometry of imperfect crystals from a macroscopic viewpoint. Mem. Unif. Stud. Basic Probl. Eng. Sci. Means Geom. 1, 6–17 (1955)
Kröner, E.: Allgemeine kontinuumstheorie der versetzungen und eigenspannungen. Arch. Ration. Mech. Anal. 4(1), 273 (1959)
Fox, N.: A continuum theory of dislocations for single crystals. IMA J. Appl. Math. 2(4), 285–298 (1966)
Eshelby, J.D.: The continuum theory of lattice defects. Solid State Phys. 3, 79–144 (1956)
Kuroda, M., Tvergaard, V.: A finite deformation theory of higher-order gradient crystal plasticity. J. Mech. Phys. Solids 56(8), 2573–2584 (2008)
Le, K.C., Stumpf, H.: On the determination of the crystal reference in nonlinear continuum theory of dislocations. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 452(1945), 359–371 (1996)
Lee, E.H.: Elastic-plastic deformation at finite strains. J. Appl. Mech. 36(1), 1–6 (1969)
Lembo, M.: On the determination of deformation from strain. Meccanica 52(9), 2111–2125 (2017)
Leon, S.J., Björck, Å., Gander, W.: Gram-Schmidt orthogonalization: 100 years and more. Numer. Linear Algebra Appl. 20(3), 492–532 (2013)
Lubarda, V.A.: Constitutive theories based on the multiplicative decomposition of deformation gradient: Thermoelasticity, elastoplasticity, and biomechanics. Appl. Mech. Rev. 57(2), 95–108 (2004)
McLellan, A.G.: Finite strain coordinates and the stability of solid phases. J. Phys. C: Solid State Phys. 9(22), 4083 (1976)
McLellan, A.G.: The classical thermodynamics of deformable materials. Cambridge University Press, Cambridge (1980)
Naghdi, P.M.: A critical review of the state of finite plasticity. Zeitschrift für angewandte Mathematik und Physik ZAMP 41(3), 315–394 (1990)
Naghdi, P.M., Srinivasa, A.R.: Characterization of dislocations and their influence on plastic deformation in single crystals. Int. J. Eng. Sci. 32(7), 1157–1182 (1994)
Nix, W.D., Gao, H.: Indentation size effects in crystalline materials: a law for strain gradient plasticity. J. Mech. Phys. Solids 46(3), 411–425 (1998)
Nye, J.F.: Some geometrical relations in dislocated crystals. Acta Metall. 1(2), 153–162 (1953)
Paul, S., Freed, A.D.: A simple representation of compatibility condition for finite deformation using a Gram-Schmidt factorization of the deformation gradient. Acta Mech. 231, 3289–3304 (2020)
Rodriguez, E.K., Hoger, A., McCulloch, A.D.: Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27(4), 455–467 (1994)
Schubert, H.: Memoirs of the unifying study of the basic problems in engineering sciences by means of geometry, volume I, by a study group of sixteen members. chairman Dr. Ing. Kazuo Kondo Prof. ad Univ. Tokio). XV+ 690 S. m. zahlr. Abb. Tokio 1955. Gakujutsu Bunken Fukyu-kai. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 37(5-6):237–237 (1957)
Simo, J.C.: A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: Part i. Continuum formulation. Comput. Methods Appl. Mech. Eng. 66(2), 199–219 (1988)
Srinivasa, A.R.: On the use of the upper triangular (or QR) decomposition for developing constitutive equations for Green-elastic materials. Int. J. Eng. Sci. 60, 1–12 (2012)
Vujosevic, L., Lubarda, V.: Finite-strain thermoelasticity based on multiplicative decomposition of deformation gradient. Theoret. Appl. Mech. 28(29), 379–399 (2002)
Yavari, A., Goriely, A.: Riemann-Cartan geometry of nonlinear dislocation mechanics. Arch. Ration. Mech. Anal. 205(1), 59–118 (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Paul, S., Freed, A.D. Characterizing geometrically necessary dislocations using an elastic–plastic decomposition of Laplace stretch. Z. Angew. Math. Phys. 71, 196 (2020). https://doi.org/10.1007/s00033-020-01420-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-020-01420-7