Friction-induced vibration considering multiple types of nonlinearities

Abstract

The friction-induced vibration of a novel 5-DoF (degree-of-freedom) mass-on-oscillating-belt model considering multiple types of nonlinearities is studied. The first type of nonlinearity in the system is the nonlinear contact stiffness, the second is the non-smooth behaviour including stick, slip and separation, and the third is the geometrical nonlinearity brought about by the moving-load feature of the mass slider on the rigid belt. Both the linear stability of the system and the nonlinear steady-state responses are investigated, and rich dynamic behaviours of the system are revealed. The results of numerical study indicate the necessity of the transient dynamic analysis in the study of friction-induced-vibration problems as the linear stability analysis fails to detect the occurrence of self-excited vibration when two stable solutions coexist in the system. The bifurcation behaviour of the steady-state responses of the system versus some parameters is determined. Additionally, the significant effects of each type of nonlinearity on the linear stability and nonlinear steady-state responses of the system are discovered, which underlie the necessity to take multiple types of nonlinearities into account in the research of friction-induced vibration and noise.

1 Introduction

Friction-induced vibration is widespread in mechanical systems as well as in everyday life, e.g. the sound of bowed instruments, the squeaking windscreen wiper, the chattering machine tools, the stick–slip oscillations of drill strings and the automobile brake noise [1,2,3]. Among them, the automobile brake noise attracts great attention of engineers and researchers due to its noise impact and scientific intricacy of this problem [3].

There have been a number of published studies which revealed rich dynamic behaviours in the friction-excited systems. Popp et al. [4, 5] studied discrete and continuous models exhibiting a stick–slip phenomenon, and rich bifurcation and chaotic behaviours were observed. Elmaian et al. [6] investigated the friction-induced vibration of a 3-DoF model that displayed three distinct dynamic states, i.e. stick, slip and separation, and the variations of time ratios of the three states in the whole process with the system parameters which can be linked to the appearance of different categories of noises. Zhang et al. [7] used a flexible pin-on-disc system to simulate how squeal noise could be generated in frictional contact and the features of time-varying squeal because of periodic friction coefficient were studied. Kruse et al. [8] explored the effect of joints on the stability and bifurcation behaviour of a system subject to friction-induced flutter. Brunetti et al. [9] studied the dynamics of a periodic modular lumped model in which each module consists of a mass in frictional contact with the moving belt and a mass linked with the adjacent modules. Pilipchuk et al. [10] examined the non-stationary effects in friction-induced vibration of a two-degree-of-freedom brake model. It was found that the system responses experienced qualitative transitions due to the linearly deceasing velocity of the belt. Wei et al. [11] established a 3-DoF dynamic model of a brake system consisting of two-layer pads and a rigid disc and the bifurcation and chaotic behaviour of system responses dependent on the variation of brake pressure, and the parameters of double-layer pads were observed. Denimal et al. [12] proposed a new method called the Generalized Model Amplitude Stability Analysis to identify the contributions of unstable modes involved in the nonlinear self-excited vibration response and to estimate the limit cycles. Lima and Sampaio [13] analysed a multiphysics system with stick–slip oscillations where a mechanical subsystem interacts with an electromagnetic subsystem. Papangelo et al. [14] presented multiple localized vibration states in a chain of weakly coupled friction-excited oscillators. Von Wagner et al. [15] analysed the stability behaviour of a disc brake model with a wobbling disc. Sui and Ding [16] investigated the instability of a pad on disc in moving interactions and carried out a stochastic analysis. In the works [17, 18], both the numerical simulation on the low-degree-of-freedom models and the experimental validation on the real test rigs concerning the friction-induced vibration of systems were implemented.

There are two main categories of methods for the analysis of friction-induced-vibration problems, i.e. the complex eigenvalue analysis (CEA) and the transient dynamic analysis (TDA). The linear complex eigenvalue approach is often employed for the stability analysis of the steady-sliding state. If at least one of the eigenvalues of the linearized system has positive real part, the steady-sliding state becomes unstable and the system will show self-excited vibration. Hoffmann et al. [19] used a 2-DoF model to clarify the mechanism of mode-coupling instability of friction-induced vibration. It was observed that as the friction coefficient increases, the imaginary parts of eigenvalues coalesce and one real part becomes positive, which indicates the occurrence of self-excited vibration in the system. Ouyang and Mottershead [20] introduced the velocity-dependent friction with the Stribeck effect into the moving-load model for the vibration of a car disc brake. The dynamic instability of the system was identified by solving a nonlinear complex eigenvalue problem. Kang [21] analytically investigated the mode-coupling instability of a stationary disc and two stationary brake pads with circumferential friction under steady-sliding condition. Liu et al. [22] investigated the effects of key parameters on the dynamic instability of a finite element brake model by employing the CEA method. Because the CEA allows all unstable eigenvalues to be found in one run and is thus computationally efficient, it becomes a standard analysis tool to predict brake squeal propensity in industry [23,24,25].

The transient dynamic analysis of friction-induced vibration has been performed by numerous researchers. Li et al. [26] examined the dynamics of a 2-DoF model with nonlinear contact stiffness and the effects of separation and reattachment on the vibration amplitudes of dynamic responses were studied. Liu and Ouyang [27] studied the friction-induced vibration of a slider on an elastic disc spinning at time-varying speeds and observed that the time-varying disc speed could be a cause for unstable vibration. Sinou [28] studied the transient and stationary self-excited vibration in a nonlinear finite element model of a disc brake. Soobbarayen et al. [29] presented a numerical analysis of the influence of the loading conditions on the vibration and acoustic responses of a finite element model. The numerical results showed that a sufficiently fast ramp loading can destabilize a stable configuration predicted by the stability analysis. Papangelo et al. [30] investigated the subcritical bifurcation of a slider-on-belt system in the case of a weakening–strengthening friction law, and the results showed that there was a range of the belt velocity where two stable solutions coexisted, i.e. a stable sliding equilibrium and a stable stick–slip limit cycle. Zhang et al. [31] examined the dynamics of a 4-DoF friction oscillator and found the CEA under-predicts the instability of the system due to its inability to detect the subcritical Hopf bifurcation. From the studies above, the drawbacks of the CEA method for the analysis of nonlinear friction-induced vibration can be observed. Firstly, the CEA may miss the dynamic instabilities in some situations, e.g. when subcritical Hopf bifurcation exists. Secondly, the real part and imaginary part of an unstable eigenvalue do not necessarily describe the amplitude and frequency of the steady-state response of the system.

The nonlinearities in friction-induced-vibration problems can originate from multiple sources, e.g. nonlinear contact stiffness [26, 28, 31,32,33], non-smooth behaviours including stick–slip and contact/separation [6, 27, 34,35,36,37]. Although quite a few published papers on friction-induced vibration took the nonlinearities into account, a comprehensive analysis of the effects of multiple types of nonlinearities on the friction-induced self-excited vibration is still lacking. In this paper, the dynamics of a 5-DoF friction-excited slider-on-moving-belt model is studied, in which three representative types of nonlinearities in the friction-induced-vibration problems are present. The first type of nonlinearity is the nonlinear contact stiffness, the second is the non-smooth behaviours including stick, slip and separation, and the third is the geometrical nonlinearity brought about by the moving-load feature of the slider on the belt. Both the linear stability of the system and the steady-state responses are investigated by means of the CEA and the TDA, respectively.

The rest of the paper is arranged as follows. In Sect. 2, the system configuration of the slider-on-belt model is introduced and the equations of motion for the system in three different states: slip, stick and separation, are derived. The conditions for the transitions among these states are determined. In Sect. 3, the procedures of the linear stability analysis and numerical simulation scheme of the transient dynamic analysis are stated. In Sect. 4, the numerical study of the linear stability and nonlinear steady-state responses of the system is conducted, where the effects of each type of nonlinearity are examined. Finally, in Sect. 5 the important conclusions are drawn.

2 The mechanical model and dynamic equations

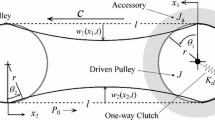
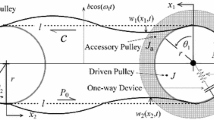
The model of the 5-DoF frictional system is shown in Fig. 1, which consists of two parts, i.e. the mass slider and the belt. The point mass slider, with mass M, is constrained by a spring $k_{1}$ and a damper $c_{1}$ in the horizontal direction and a damper $c_{2}$ in the vertical direction. Besides, a spring $k_{3}$ at 45 degree relative to the horizontal direction, which couples the vibration in the two directions, is connected to the slider. The belt, with mass m and rotational inertia about the mass centre J, is moving at a constant speed $v$ around two wheels what are constrained by a set of spring–damper system ($k_{4}$, $c_{4}$) in the horizontal direction and two sets of spring–damper systems ($k_{5}$, $c_{5}$ and $k_{6}$, $c_{6}$) in the vertical direction. The vertical spring–damper systems, which are located at the centres of the two wheels at distances $l_{1}$ and $l_{2}$ from the mass centre of the belt, respectively, also constrain the rotational motion of the belt. A preload $F$ is applied to press the slider to be in frictional contact with the moving belt, and Coulomb’s law of friction is utilized to model the friction force on the interface. The contact between the slider and the belt is assumed to be unilateral, and a combination of a linear spring $k_{2}$ and a nonlinear spring $k_{\text{nl}}$ with cubic stiffness is used to model the contact stiffness. In this model, the horizontal and vertical motion of the slider, as well as the horizontal, vertical and rotational motion of the belt, is investigated. Without loss of generality, the slider is assumed to be right above the mass centre of the belt at zero displacements.

Fig. 1

The model of the 5-DoF frictional system

The equations of motion of the 5-DoF system can be written as,

$$ \left\{ {\begin{array}{*{20}l} {M\ddot{x}_{1} + c_{1} \dot{x}_{1} + k_{1} x_{1} + \frac{1}{2}k_{3} x_{1} - \frac{1}{2}k_{3} y_{1} = F_{\text{T}} } \hfill \\ {M\ddot{y}_{1} + c_{2} \dot{y}_{1} - \frac{1}{2}k_{3} x_{1} + \frac{1}{2}k_{3} y_{1} + F = F_{\text{N}} } \hfill \\ {m\ddot{x}_{2} + c_{4} \dot{x}_{2} + k_{4} x_{2} = - F_{\text{T}} } \hfill \\ {m\ddot{y}_{2} + c_{5} \left( {\dot{y}_{2} + l_{1} \dot{\varphi }} \right) + k_{5} \left( {y_{2} + l_{1} \varphi } \right) + c_{6} \left( {\dot{y}_{2} - l_{2} \dot{\varphi }} \right) + k_{6} \left( {y_{2} - l_{2} \varphi } \right) = - F_{\text{N}} } \hfill \\ {J\ddot{\varphi } + c_{5} \left( {\dot{y}_{2} + l_{1} \dot{\varphi }} \right)l_{1} + k_{5} \left( {y_{2} + l_{1} \varphi } \right)l_{1} - c_{6} \left( {\dot{y}_{2} - l_{2} \dot{\varphi }} \right)l_{2} - k_{6} \left( {y_{2} - l_{2} \varphi } \right)l_{2} = F_{\text{N}} \left( {x_{1} - x_{2} } \right)} \hfill \\ \end{array} } \right. $$

(1)

where $F_{\text{T}}$ and $F_{\text{N}}$ represent the tangential friction force and the normal force between the slider and the belt, respectively. As the system may experience non-smooth behaviours including slip, stick and separation, $F_{\text{T}}$ and $F_{\text{N}}$ will take different forms in distinct states of motion.

When the slider is in contact with belt, in the states of slip and stick, the normal force is the resultant force of the linear spring $k_{2}$ and the nonlinear spring $k_{\text{nl}}$, i.e.

$$ F_{\text{N}} = k_{2} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right) + k_{\text{nl}} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right)^{3} . $$

(2)

The friction force takes different forms in the states of slip and stick. In the state of slip, the friction force is expressed as,

$$ F_{\text{T}} = {\text{sgn}}\left( {v_{\text{r}} } \right)\mu_{\text{k}} F_{\text{N}} . $$

(3)

where $v_{\text{r}} = v + \dot{x}_{2} - \dot{x}_{1}$ and $\mu_{\text{k}}$ is coefficient of kinetic friction. The condition for the system to stay in the state of slip is,

$$ \left\{ {\begin{array}{*{20}c} {v_{\text{r}} \ne 0} \\ {F_{\text{N}} > 0} \\ \end{array} } \right. $$

(4)

In the state of stick, the friction force serves to sustain the relative static state, i.e. $v_{\text{r}} = 0$, and thus can be obtained from the equations of motion of the system, as shown in Eq. (1). As the absolute belt velocity here is $v + \dot{x}_{2}$, which is not known a priori, the tangential velocity of the slider $\dot{x}_{1}$ during sticking is not known a priori either. In the following, a method to derive the state variables and the friction force during sticking is presented.

Firstly, it is obtained from $v_{\text{r}} = 0$ that

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{2} = \dot{x}_{1} - v} \hfill \\ {\ddot{x}_{2} = \ddot{x}_{1} } \hfill \\ {x_{2} \left( t \right) = x_{1} \left( t \right) - x_{1} \left( {t_{\text{s}} } \right) - v \times \left( {t - t_{\text{s}} } \right) + x_{2} \left( {t_{\text{s}} } \right)} \hfill \\ \end{array} } \right. $$

(5)

where $t_{\text{s}}$ is the time at the onset of stick. Then, by adding the third equation in Eq. (1) into the first equation in Eq. (1), it is obtained that

$$ M\ddot{x}_{1} + m\ddot{x}_{2} + c_{1} \dot{x}_{1} + c_{4} \dot{x}_{2} + \left( {k_{1} + \frac{1}{2}k_{3} } \right)x_{1} - \frac{1}{2}k_{3} y_{1} + k_{4} x_{2} = 0 $$

(6)

By substituting Eq. (5) into Eq. (6), the terms involving $x_{2}$, $\dot{x}_{2}$, $\ddot{x}_{2}$ in Eq. (6) can be eliminated, i.e.

$$ \left( {M + m} \right)\ddot{x}_{1} + \left( {c_{1} + c_{4} } \right)\dot{x}_{1} + \left( {k_{1} + \frac{1}{2}k_{3} + k_{4} } \right)x_{1} - \frac{1}{2}k_{3} y_{1} = c_{4} v + k_{4} \left[ {x_{1} \left( {t_{\text{s}} } \right) + v \times \left( {t - t_{\text{s}} } \right) - x_{2} \left( {t_{\text{s}} } \right)} \right] $$

(7)

Similarly, the expression of $x_{2}$ in Eq. (5) is substituted into other equations in Eq. (1) to eliminate the terms involving $x_{2}$. Therefore, the original 5-DoF equations of motion involving $x_{1}$, $y_{1}$, $x_{2}$, $y_{2}$, $\varphi$ and their velocities and accelerations are converted into a 4-DoF equations of motion involving $x_{1}$, $y_{1}$, $y_{2}$, $\varphi$ and their velocities and accelerations, in the state of stick. By integrating the 4-DoF equations of motion, the values of $x_{1}$, $y_{1}$, $y_{2}$, $\varphi$ (also including velocities and accelerations) during sticking are obtained, and the values of $x_{2}$ (also including velocity and acceleration) during sticking can also be acquired from Eq. (5). Besides, the value of friction force during sticking can be derived from the first or the third equation in Eq. (1). The condition for the system to stay in the state of stick is,

$$ \left\{ {\begin{array}{*{20}l} {|F_{\text{T}} | \le \mu_{\text{s}} F_{\text{N}} } \hfill \\ {F_{\text{N}} > 0} \hfill \\ \end{array} } \right. $$

(8)

where $\mu_{\text{s}}$ is the coefficient of static fn.

While in the state of separation, the slider and the belt are not in contact, therefore $F_{\text{N}} = 0,$ $F_{\text{T}} = 0$. The condition for the system to stay in the state of separation is,

$$ y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} < 0 $$

(9)

With the formulations of $F_{\text{T}}$ and in each of the three states obtained, the equations of motion for each of the states are determined. After separation, the condition Eq. (9) is monitored for re-contact. Re-contact happens when the slider’s vertical motion becomes equal to the vertical motion of the belt at the contact point. And a very short-lived impact force is considered to act between the slider and the belt within a tiny time duration of $\left( {t_{r}^{ - } ,t_{r}^{ + } } \right)$. The method for determining the values of the dynamic state variables immediately after re-contact, which was given in [38], is employed in this paper. For simplification, an assumption for the re-contact is that the impact is perfectly plastic. Suppose the impulse at $t_{r}$ is $p$ and based on the theorem of conservation of momentum, the velocity jump for the slider and the belt due to the impact can be thus obtained as,

$$ \dot{y}_{1} \left( {t_{r}^{ + } } \right) - \dot{y}_{1} \left( {t_{r}^{ - } } \right) = \frac{p}{M} $$

(10)

$$ \dot{y}_{2} \left( {t_{r}^{ + } } \right) - \dot{y}_{2} \left( {t_{r}^{ - } } \right) = - \frac{p}{m} $$

(11)

$$ \dot{\varphi }\left( {t_{r}^{ + } } \right) - \dot{\varphi }\left( {t_{r}^{ - } } \right) = \frac{{p \cdot \left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)}}{J} $$

(12)

For perfectly plastic impact, the slider has the same vertical velocity as that of the belt at the contact point at time $t_{r}^{ + }$ therefore

$$ \dot{y}_{1} \left( {t_{r}^{ + } } \right) = \dot{y}_{2} \left( {t_{r}^{ + } } \right) - \left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)\dot{\varphi }\left( {t_{r}^{ + } } \right) $$

(13)

By substituting Eqs. (10–12) into Eq. (13), the values of the impulse $p$ and the state variables immediately after re-contact can be obtained, which are,

$$ p = \frac{{\dot{y}_{2} \left( {t_{r}^{ - } } \right) - \dot{y}_{1} \left( {t_{r}^{ - } } \right) - \left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)\dot{\varphi }\left( {t_{r}^{ - } } \right)}}{{\frac{1}{M} + \frac{1}{m} + \frac{{\left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)^{2} }}{J}}} $$

(14)

$$ \dot{y}_{1} \left( {t_{r}^{ + } } \right) = \dot{y}_{1} \left( {t_{r}^{ - } } \right) + \frac{{\dot{y}_{2} \left( {t_{r}^{ - } } \right) - \dot{y}_{1} \left( {t_{r}^{ - } } \right) - \left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)\dot{\varphi }\left( {t_{r}^{ - } } \right)}}{{M\left[ {\frac{1}{M} + \frac{1}{m} + \frac{{\left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)^{2} }}{J}} \right]}} $$

(15)

$$ \dot{y}_{2} \left( {t_{r}^{ + } } \right) = \dot{y}_{2} \left( {t_{r}^{ - } } \right) - \frac{{\dot{y}_{2} \left( {t_{r}^{ - } } \right) - \dot{y}_{1} \left( {t_{r}^{ - } } \right) - \left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)\dot{\varphi }\left( {t_{r}^{ - } } \right)}}{{m\left[ {\frac{1}{M} + \frac{1}{m} + \frac{{\left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)^{2} }}{J}} \right]}} $$

(16)

$$ \dot{\varphi }\left( {t_{r}^{ + } } \right) = \dot{\varphi }\left( {t_{r}^{ - } } \right) + \frac{{\left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)\left[ {\dot{y}_{2} \left( {t_{r}^{ - } } \right) - \dot{y}_{1} \left( {t_{r}^{ - } } \right) - \left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)\dot{\varphi }\left( {t_{r}^{ - } } \right)} \right]}}{{J\left[ {\frac{1}{M} + \frac{1}{m} + \frac{{\left( {x_{1} \left( {t_{r} } \right) - x_{2} \left( {t_{r} } \right)} \right)^{2} }}{J}} \right]}} $$

(17)

3 Linear stability analysis and transient dynamic analysis

3.1 Linear stability analysis

In this section, the procedure to carry out the linear stability analysis is introduced. Firstly, the equilibrium points of the system are determined by solving the nonlinear static equations. Then, the equations of motion of the system are linearized around the equilibrium points and a linearized system is derived. Finally, the eigenvalues of linearized system are calculated to determine the stability of the steady-sliding state for various values of key parameters.

3.1.1 Equilibrium points

By setting all the terms involving velocity and acceleration in the equations of motion for the state of slip to zero, the nonlinear algebraic equations whose solutions are the equilibrium points are obtained as

$$ \left[ {\begin{array}{*{20}c} {k_{1} + \frac{1}{2}k_{3} } & { - \frac{1}{2}k_{3} } & 0 & 0 & 0 \\ { - \frac{1}{2}k_{3} } & {\frac{1}{2}k_{3} } & 0 & 0 & 0 \\ 0 & 0 & {k_{4} } & 0 & 0 \\ 0 & 0 & 0 & {k_{5} + k_{6} } & {k_{5} l_{1} - k_{6} l_{2} } \\ 0 & 0 & 0 & {k_{5} l_{1} - k_{6} l_{2} } & {k_{5} l_{1}^{2} + k_{6} l_{2}^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {y_{1} } \\ {x_{2} } \\ {y_{2} } \\ \varphi \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {a_{1} } \\ {a_{2} } \\ {a_{3} } \\ {a_{4} } \\ {a_{5} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ { - F} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] $$

(18)

where

$$ a_{1} = - \mu_{\text{k}} \left[ {k_{2} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right) + k_{\text{nl}} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right)^{3} } \right] $$

$$ a_{2} = - k_{2} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right) - k_{\text{nl}} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right)^{3} $$

$$ a_{3} = \mu_{\text{k}} \left[ {k_{2} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right) + k_{\text{nl}} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right)^{3} } \right] $$

$$ a_{4} = k_{2} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right) + k_{\text{nl}} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right)^{3} $$

$$ a_{5} = - \left( {x_{1} - x_{2} } \right)\left[ {k_{2} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right) + k_{\text{nl}} \left( {y_{2} - \left( {x_{1} - x_{2} } \right)\varphi - y_{1} } \right)^{3} } \right] $$

By solving Eq. (18), the equilibrium points can be determined.

3.1.2 Complex eigenvalue analysis

By linearizing the nonlinear equations of motion around the equilibrium points, a linearized system results:

$$ {{{\mathbf{M}}\ddot{\bar{\mathbf{x}}}}} + {{{\mathbf{C}}\dot{\bar{\mathbf{x}}}}} + {{{\mathbf{K}}\bar{\mathbf{x}}}} = 0 $$

(19)

where ${\bar{\mathbf{x}}} = {\mathbf{x}} - {\mathbf{x}}_{\text{e}}$, ${\mathbf{x}} = \left[ {x_{1} ,y_{1} ,x_{2} ,y_{2} ,\varphi } \right]^{\text{T}}$, ${\mathbf{x}}_{\text{e}} = \left[ {x_{{1{\text{e}}}} ,y_{{1{\text{e}}}} ,x_{{2{\text{e}}}} ,y_{{2{\text{e}}}} ,\varphi_{\text{e}} } \right]^{\text{T}}$ is an equilibrium point. The mass matrix, damping matrix and stiffness matrix of the linearized system are,

$$ {\mathbf{M}} = {\text{diag}}\left( {M,M,m,m,J} \right) $$

$$ {\mathbf{C}} = \left[ {\begin{array}{*{20}c} {c_{1} } & 0 & 0 & 0 & 0 \\ 0 & {c_{2} } & 0 & 0 & 0 \\ 0 & 0 & {c_{4} } & 0 & 0 \\ 0 & 0 & 0 & {c_{5} + c_{6} } & {c_{5} l_{1} - c_{6} l_{2} } \\ 0 & 0 & 0 & {c_{5} l_{1} - c_{6} l_{2} } & {c_{5} l_{1}^{2} + c_{6} l_{2}^{2} } \\ \end{array} } \right] $$

$$ {\mathbf{K}} = \left[ {\begin{array}{*{20}l} {k_{1} + \frac{1}{2}k_{3} + \varLambda \mu_{\text{k}} \varphi_{\text{e}} } \hfill & { - \frac{1}{2}k_{3} + \varLambda \mu_{\text{k}} } \hfill & { - \varLambda \mu_{\text{k}} \varphi_{\text{e}} } \hfill & { - \varLambda \mu_{\text{k}} } \hfill & {\varLambda \mu_{\text{k}} \left( {x_{1} - x_{2} } \right)} \hfill \\ { - \frac{1}{2}k_{3} + \varLambda \varphi_{\text{e}} } \hfill & {\frac{1}{2}k_{3} + \varLambda } \hfill & { - \varLambda \varphi_{\text{e}} } \hfill & { - \varLambda } \hfill & {\varLambda \left( {x_{1} - x_{2} } \right)} \hfill \\ { - \varLambda \mu_{\text{k}} \varphi_{\text{e}} } \hfill & { - \varLambda \mu_{\text{k}} } \hfill & {k_{4} + \varLambda \mu_{\text{k}} \varphi_{\text{e}} } \hfill & {\varLambda \mu_{\text{k}} } \hfill & { - \varLambda \mu_{\text{k}} \left( {x_{1} - x_{2} } \right)} \hfill \\ { - \varLambda \varphi_{\text{e}} } \hfill & { - \varLambda } \hfill & {\varLambda \varphi_{\text{e}} } \hfill & {\varLambda + k_{5} + k_{6} } \hfill & { - \varLambda \left( {x_{1} - x_{2} } \right) + k_{5} l_{1} - k_{6} l_{2} } \hfill \\ { - \varPi } \hfill & {\varLambda \left( {x_{1} - x_{2} } \right)} \hfill & \varPi \hfill & { - \varLambda \left( {x_{1} - x_{2} } \right) + k_{5} l_{1} - k_{6} l_{2} } \hfill & {\varLambda \left( {x_{1} - x_{2} } \right)^{2} + k_{5} l_{1}^{2} + k_{6} l_{2}^{2} } \hfill \\ \end{array} } \right] $$

and

$$ \begin{aligned} \varLambda = k_{2} + 3k_{\text{nl}} \left[ {y_{{2{\text{e}}}} - \left( {x_{{1{\text{e}}}} - x_{{2{\text{e}}}} } \right)\varphi_{\text{e}} - y_{{1{\text{e}}}} } \right]^{2} \hfill \\ \varPi = k_{2} \left[ {y_{{2{\text{e}}}} - y_{{1{\text{e}}}} - 2\varphi_{\text{e}} \left( {x_{{1{\text{e}}}} - x_{{2{\text{e}}}} } \right)} \right] + k_{\text{nl}} \left\{ { - 3\varphi_{\text{e}} \left( {x_{{1{\text{e}}}} - x_{{2{\text{e}}}} } \right)\left[ {y_{{2{\text{e}}}} - \left( {x_{{1{\text{e}}}} - x_{{2{\text{e}}}} } \right)\varphi_{\text{e}} - y_{{1{\text{e}}}} } \right]^{2} + } \right.\left. {\left[ {y_{{2{\text{e}}}} - \left( {x_{{1{\text{e}}}} - x_{{2{\text{e}}}} } \right)\varphi_{\text{e}} - y_{{1{\text{e}}}} } \right]^{3} } \right\} \hfill \\ \end{aligned} $$

Then, the eigenvalues of the linearized system above are calculated. If the real parts of all the eigenvalues are negative, the equilibrium point corresponding to the steady-sliding state is stable. If at least one of the eigenvalues has a positive real part, the equilibrium point is unstable, which leads to self-excited vibration in the nonlinear system.

3.2 Transient dynamic analysis

Because $F_{\text{T}}$ and $F_{\text{N}}$ take different mathematical forms in distinct states of motion, the dynamic system in question is non-smooth, which brings about a difficulty in numerical integration. To obtain the whole time histories of the dynamic responses of the system, the fourth-order Runge–Kutta method [39] is employed to calculate the responses in every single state, while conditions for the transition of states are monitored at each time step. Within the time step in which the transition of states occurs, the bisection method is employed to capture the precise transition time instant. After the transition point, the state changes and the original set of equations of motion is replaced by another one. The details of the algorithm for the transient dynamic analysis are described in the form of a flowchart in Appendix.

4 Numerical study

4.1 Stability analysis

According to the procedure given in Sect. 3.1, the stability of the system at the equilibrium point is analysed in this section, where the effects of different types of nonlinearities are examined. As the focus of this paper is on the effects of nonlinearities on the friction-induced dynamics, some basic parameters are assigned constant values if not specified otherwise, which are listed in Table 1.

Table 1 The values of the constant system parameters

The results show that the mode-coupling instability arises in the system with the variations of parameter values; namely, the imaginary parts of two eigenvalues coalesce, and one of the real parts becomes positive. In Figs. 2 and 3, the complex eigenvalues of a pair of modes as a function of the friction coefficient $\mu_{\text{k}}$ with a different nonlinear contact stiffness $k_{\text{nl}}$ are exhibited. For each value of $k_{\text{nl}}$, the mode-coupling instability occurs in the system with the increase of $\mu_{\text{k}}$. The value of the friction coefficient at which the instability occurs can be called the critical friction coefficient. The comparison between the results of different $k_{\text{nl}}$ indicates that a larger nonlinear contact stiffness leads to a smaller critical friction coefficient for the instability. Besides, the comparison between Figs. 2 and 3 suggests that the preload also influences the critical friction coefficient. The relationship between the critical friction coefficient and the preload is depicted in Fig. 4, from which it is seen that the critical friction coefficient for the instability decreases with the increase in the preload.

Fig. 2

Stability analysis of the system with a different nonlinear contact stiffness $k_{\text{nl}}$ when the preload $F = 100{\text{N}}$: a frequencies and b growth rates

Fig. 3

Stability analysis of the system with a different nonlinear contact stiffness $k_{\text{nl}}$ when the preload $F = 1000\,{\text{N}}$: a frequencies and b growth rates

Fig. 4

The critical friction coefficient $\mu_{\text{k}}$ for the instability as a function of the preload $F$

Next, the effect of the geometrical nonlinearity (GN) in the system on the stability is investigated. The geometrical nonlinearity in the system is produced by the combination of the relative motion between the slider and the belt with the rotational motion of the belt. In Fig. 5, the critical friction coefficient for the instability as a function of the preload when the rotational motion of the belt is not considered, i.e. without the geometrical nonlinearity, is compared with that of the original 5-DoF system, i.e. with the geometrical nonlinearity. It is clearly observed that the critical friction coefficient for the instability with the geometrical nonlinearity is quite smaller than without. In another word, the geometrical nonlinearity promotes the occurrence of the instability. Besides, another effect of the geometrical nonlinearity on the stability is found. Figure 6 shows the complex eigenvalues analysis results of the system in the two situations, i.e. with and without geometrical nonlinearity, when $F = 1000{\text{N}}$, $l_{1} = 0.1\,{\text{m}}$, $l_{2} = 0.3\,{\text{m}}$. It is seen that the system with the geometrical nonlinearity exhibits more complex behaviour of instability than without. For the system without the geometrical nonlinearity, there is only one instability when $\mu_{\text{k}}$ is larger than its critical value. For the system with the geometrical nonlinearity, however, two instabilities arise (the real parts of two pairs of conjugate eigenvalues become positive) when $\mu_{\text{k}}$ is within a certain range and one of the instabilities disappears for large value of $\mu_{\text{k}}$. This example indicates that the geometrical nonlinearity increases the complexity of the instability in the system.

Fig. 5

The effect of the geometrical nonlinearity (GN) on the critical friction coefficient $\mu_{\text{k}}$ for the instability

Fig. 6

The effect of the geometrical nonlinearity on the system instability: a, b with the geometrical nonlinearity and c, d without the geometrical nonlinearity. ($F = 1000\,{\text{N}}$,$l_{1} = 0.1\,\,{\text{m}}$, $l_{2} = 0.3\,\,{\text{m}}$)

Lastly, the nonlinearity with respect to the non-smooth behaviours has no effect on the stability of the system at the equilibrium point because the system is in the state of slip near the equilibrium point.

4.2 Nonlinear steady-state responses

In this section, the nonlinear steady-state responses of the system are investigated by means of the transient dynamic analysis. The values of the basic system parameters are the same as those in Table 1. The effects of different types of nonlinearities on the steady-state responses of the system are examined.

4.2.1 The characteristics of the steady-state responses of the system

Firstly, the time responses of the system under three different values of $\mu_{\text{k}} \left( {0.3, 1.4, 2.5} \right)$ with $\mu_{\text{s}} = 3$, $k_{\text{nl}} = 10^{4} \,\,{\text{N}}/\,{\text{m}}$ and $F = 200\,{\text{N}}$ are obtained in Fig. 7. For each $\mu_{\text{k}}$, the solutions of the nonlinear algebraic equations in Eq. (18) consist of a solution of real numbers and a pair of solutions of conjugate complex numbers. The solution of real numbers is the equilibrium point of the system, which is,

Fig. 7

The time responses of the system under three different values of $\mu_{\text{k}} \left( {0.3, 1.4, 2.5} \right)$ with $\mu_{\text{s}} = 3$, $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$ and $F = 200{\text{N}}$ from two different initial conditions: a, c, e near the equilibrium point and b, d, f far from the equilibrium point

$$ {\mathbf{x}}_{\text{e}} = \left[ { - 0.0042\,\,{\text{m}}, - 0.0304\,\,{\text{m}}, - 0.0036\,\,{\text{m}}, - 0.0061\,\,{\text{m}}, - 0.0001\,{\text{rad}}} \right]^{\text{T}} ,\quad {\text{for}}\,\mu_{\text{k}} = 0.3, $$

$$ {\mathbf{x}}_{\text{e}} = \left[ { - 0.0053\,\,{\text{m}}, - 0.0263\,\,{\text{m}}, - 0.0147\,\,{\text{m}}, - 0.0053\,\,{\text{m}},0.0026\,{\text{rad}}} \right]^{\text{T}} ,\quad {\text{for}}\,\mu_{\text{k}} = 1.4, $$

$$ {\mathbf{x}}_{\text{e}} = \left[ {0.0124\,\,{\text{m}}, - 0.0233\,\,{\text{m}}, - 0.0232\,\,{\text{m}}, - 0.0046\,\,{\text{m}},0.0041\,{\text{rad}}} \right]^{\text{T}} \quad {\text{for}}\,\mu_{\text{k}} = 2.5. $$

It is worth noting that a mode-coupling instability happens in the system with the increase of $\mu_{\text{k}}$. The eigenvalues of the coupled modes for the three values of $\mu_{\text{k}}$ are $\left[ { - 0.05 \pm 100{\text{i}}, - 0.04 \pm 89.4{\text{i}}} \right]$, $\left[ { - 0.05 \pm 98.7{\text{i}}, - 0.048 \pm 93.7{\text{i}}} \right]$ and $\left[ {11.98 \pm 102.6{\text{i}}, - 12.08 \pm 102.6{\text{i}}} \right]$, respectively; therefore $\mu_{\text{k}} = 0.3$ and $1.4$ lead to a stable equilibrium point, and $\mu_{\text{k}} = 2.5$ leads to an unstable equilibrium point. In Fig. 7, the exhibited time responses for each value of $\mu_{\text{k}}$ are acquired from two different initial conditions, i.e. one near the equilibrium point and the other far from the equilibrium point. When $\mu_{\text{k}} = 0.3$, the dynamic responses from both initial conditions approach the equilibrium point, indicating there is only one stable solution for the system responses, i.e. the equilibrium point. When $\mu_{\text{k}} = 2.5$, the dynamic responses from both initial conditions approach the same limit cycle, indicating there is only one stable solution for the system responses, i.e. the limit cycle vibration. When $\mu_{\text{k}} = 1.4$, however, the two initial conditions lead to different steady-state responses. The dynamic responses from the initial condition near the equilibrium point approach the equilibrium point, while the dynamic responses from the initial condition far from the equilibrium approach the limit cycle vibration, which indicates the coexistence of two stable solutions in the system. This example shows that the linear stability analysis at the equilibrium point in the friction-excited system fails to detect the occurrence of self-excited vibration when the system is bi-stable, which can only be found out by a transient dynamic analysis.

In Fig. 8, the steady-state limit cycle vibration when $\mu_{\text{k}} = 1.4$ and $\mu_{\text{k}} = 2.5$ is further compared in terms of the contact forces, the phase plots and the frequency spectra. It is deduced from Fig. 8a, c, e that the steady-state dynamic responses of the system when $\mu_{\text{k}} = 1.4$ are periodic with the frequency of around $1.58\,{\text{Hz}}$, while Fig. 8b, d, f demonstrates that the steady-state dynamic responses when $\mu_{\text{k}} = 2.5$ are non-periodic. Therefore, the system responses bifurcate with the variation of $\mu_{\text{k}}$ and the bifurcation behaviour of the system with the given parameter values is displayed in Fig. 9, which shows the values of $x_{1}$ at the transition points from slip to stick. It shows that the system has periodic steady-state responses when $0.9 \le \mu_{\text{k}} < 1.8$ and non-periodic responses when $0.4 \le \mu_{\text{k}} < 0.9$ or $1.8 \le \mu_{\text{k}} < 3$. Besides, an index is defined to measure the intensity of steady-state vibration of the system, which is,

$$ L_{\text{s}} = \mathop \sum \limits_{i = 1}^{5} \frac{{\mathop \smallint \nolimits_{T} \left[ {\left( {X_{i} - X_{{i{\text{e}}}} } \right)^{2} } \right]{\text{d}}t}}{T} $$

(20)

where $X_{i} \left( {i = 1,2,3,4,5} \right)$ represents the dynamic response $x_{1}$, $y_{1}$, $x_{2}$, $y_{2}$, $\varphi$, respectively; $X_{{i{\text{e}}}}$ is the value of the equilibrium point and $T$ represents a time period in the steady state. Index $L_{\text{s}}$ as a function of $\mu_{\text{k}}$ is shown in Fig. 10, from which it is observed that the system has a single stable equilibrium point when $\mu_{\text{k}} < 0.4$ and a single stable limit cycle when $\mu_{\text{k}} > 1.5$, while two stable steady-state solutions coexist when $\mu_{\text{k}} \in \left[ {0.4, 1.5} \right]$.

Fig. 8

The steady-state limit cycle vibration in terms of the contact forces, the phase plots and the frequency spectra: a, c, e $\mu_{\text{k}} = 1.4$ and b, d, f $\mu_{\text{k}} = 2.5$

Fig. 9

The bifurcation behaviour of the steady-state limit cycle vibration of the system

Fig. 10

Index $L_{\text{s}}$ as a function of $\mu_{\text{k}}$

4.2.2 The effects of nonlinearities on the steady-state responses of the system

First of all, the effects of the nonlinear contact stiffness on the steady-state responses are investigated. With different values of $k_{\text{nl}}$ and the same values of other parameters as those in Sect. 4.2.1, the bifurcation behaviours of the steady-state limit cycle vibration of the system, which reveal the periodicity of the steady-state responses with the variation of $\mu_{\text{k}}$, are shown in Fig. 11. By comparing the results in Fig. 11 with those in Fig. 9, it is observed that the bifurcation behaviours of the steady-state responses when $k_{\text{nl}} = 0$ and $k_{\text{nl}} = 10^{4} \,\,{\text{N}}/\,{\text{m}}$ are alike, while the bifurcation behaviour of the steady-state responses when $k_{\text{nl}} = 10^{7} \,\,{\text{N}}/\,{\text{m}}$ is quite different. Figure 11(a) shows that the system in the case of $k_{\text{nl}} = 0$ also has periodic steady-state responses when $0.9 \le \mu_{\text{k}} < 1. 8$, except $\mu_{\text{k}} = 1.3$. Besides, the system when $k_{\text{nl}} = 0$ has stable periodic limit cycle vibration at $\mu_{\text{k}} = 0.05$, which is different from the result of the system with $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$. Figure 11b demonstrates that the system has periodic steady-state responses when $0.75 \le \mu_{\text{k}} \le 2.9$ or $\mu_{\text{k}} = 0.1$, and the values of $x_{1}$ at the transition points from slip to stick are approximately identical when $\mu_{\text{k}}$ lies in the above range, as shown in the figure, indicating that the system responses in the above range of $\mu_{\text{k}}$ are close. In Fig. 12, index $L_{\text{s}}$ as the function of $\mu_{\text{k}}$ with three values of $k_{\text{nl}}$, i.e. $k_{\text{nl}} = 0$, $10^{4} \,\,{\text{N}}/\,{\text{m}}$ and $10^{7} \,{\text{N}}/\,{\text{m}}$, is depicted. The range of $\mu_{\text{k}}$ in which two stable steady-state solutions (the equilibrium point and the limit cycle) coexist in the system is identified, which is $\left[ {0.4, 1.5} \right]$ for both $k_{\text{nl}} = 0$ and $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$, and $\left( {0, 0.6} \right]$ for $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$. Besides, the values of $L_{\text{s}}$ as the function of $\mu_{\text{k}}$ roughly reflect the intensity of steady-state vibration of the system at different values of $\mu_{\text{k}}$. For $k_{\text{nl}} = 0$ and $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$, the steady-state vibration generally gets stronger for larger values of $\mu_{\text{k}}$. For $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$, however, the steady-state vibration is weaker when $0.75 \le \mu_{\text{k}} \le 2.9$, namely, when the system has periodic oscillations, than that when the system has non-periodic oscillations. Based on the above observations, it is concluded that the nonlinearity from the contact stiffness has a significant effect on the steady-state responses of the system.

Fig. 11

The bifurcation behaviours of the steady-state limit cycle vibration of the system with different values of $k_{\text{nl}}$ a $k_{\text{nl}} = 0$ and b $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$

Fig. 12

Index $L_{\text{s}}$ as a function of $\mu_{\text{k}}$ for the system with different values of $k_{\text{nl}}$

Secondly, the effects of the geometrical nonlinearity in the system on the steady-state responses are investigated. To reveal the effects of the geometrical nonlinearity, the steady-state responses of the system without the geometrical nonlinearity are calculated and compared with the results of the original system with the geometrical nonlinearity. In Fig. 13, the bifurcation behaviours of the steady-state limit cycle vibration of the system without the geometrical nonlinearity are plotted. It is seen that the system experiences nearly unchanged periodic oscillations when $\mu_{\text{k}}$ varies within $\left[ {0.38, 2.95} \right]$ in the case of $k_{\text{nl}} = 0$ and $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$, and the representative phase-plane plots of the periodic oscillations are depicted in Fig. 13d, e. In the case of $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$, the system has non-periodic steady-state responses when $\mu_{\text{k}}$ is very small and similar periodic responses as $\mu_{\text{k}}$ varies within $\left[ {0.05, 2.95} \right]$. The representative phase-plane plot of the periodic responses is depicted in Fig. 13f, which is different from those in the case of $k_{\text{nl}} = 0$ and $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$. Index $L_{\text{s}}$ as a function of $\mu_{\text{k}}$ for the system without the geometrical nonlinearity is presented in Fig. 14, which shows a much more steady pattern of the values of $L_{\text{s}}$ with the variation of $\mu_{\text{k}}$ than the counterpart of the system with the geometrical nonlinearity. Besides, the steady-state responses with different values of preload $F$ when $\mu_{\text{k}} = 2.5$ and $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$ in the two situations, i.e. with and without the geometrical nonlinearity, are calculated, and the bifurcation behaviours and index $L_{\text{s}}$ are shown in Fig. 15. By the comparison between the results in the two situations, it is clearly seen that the system responses with the geometrical nonlinearity experience more fluctuations than those without the geometrical nonlinearity as preload $F$ varies, in terms of the periodicity and intensity of the steady-state vibration. Based on the above observations, it is concluded that the geometrical nonlinearity has a significant effect on the steady-state responses of the system, and the system responses in the presence of geometrical nonlinearity are more changeable with the variations of parameters (e.g. $\mu_{\text{k}}$ and $F$) than those without geometrical nonlinearity.

Fig. 13

The bifurcation behaviours of the steady-state limit cycle vibration (a–c) and phase-plane plots when $\mu_{\text{k}} = 2$ (d–f) for the system without the geometrical nonlinearity: a, d $k_{\text{nl}} = 0$, b, e $k_{\text{nl}} = 10^{4} \,{\text{N}}/\,{\text{m}}$ and c, f $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$

Fig. 14

Index $L_{\text{s}}$ as a function of $\mu_{\text{k}}$ for the system without the geometrical nonlinearity

Fig. 15

The bifurcation behaviour and index $L_{\text{s}}$ of the steady-state responses as the function of the preload $F$ for the system when $\mu_{\text{k}} = 2.5$ $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$ in the two situations: a, c with the geometrical nonlinearity and b, d without the geometrical nonlinearity

Thirdly, the effects of the non-smooth behaviours on the steady-state responses of the system are investigated. Many previous studies [7, 8, 31, 40] only took the state of relative sliding into account when investigating the dynamics of frictional systems, while the states of stick and separation will actually happen in the vibration of frictional systems because of the discontinuous friction force and the unilateral contact. To reveal the effects of the non-smooth behaviours including stick–slip and contact/separation on the steady-state responses of the system, the dynamic responses when the non-smooth behaviours are not considered, i.e. there exists the single state of relative sliding in the vibration, are calculated and compared with the results of the original system. In Fig. 16, the dynamic responses of the system in the two situations, i.e. including and excluding the non-smooth behaviours, are depicted for comparison, where $\mu_{\text{k}} = 2.5$, $\mu_{\text{s}} = 3$, $k_{\text{nl}} = 10^{7} \,{\text{N}}/\,{\text{m}}$, $F = 800{\text{N}}$ and the values of other basic parameters are the same as those in Table 1 except $k_{4} = k_{5} = k_{6} = 5 \cdot 10^{6} \;\,{\text{N}}/\,{\text{m}}$ in this example. From this figure, it is observed that the amplitudes of dynamic responses when excluding the non-smooth behaviours are much larger than those when including the non-smooth behaviours in the vibration. It should be noted here the contact between the slider and the belt is assumed to be bilateral (i.e. maintained) when the non-smooth behaviours are excluded; therefore, normal force $F_{\text{N}}$ is allowed to become negative. With the values of other parameters unchanged and $\mu_{\text{k}}$ as the control parameter, the bifurcation behaviour and index $L_{\text{s}}$ of the steady-state responses in the two situations are plotted in Fig. 17. In the bifurcation diagram for the situation when the non-smooth behaviours are excluded, the values of $x_{1}$ when $\dot{x}_{1} = 0$ at each $\mu_{\text{k}}$ are displayed, which indicate that the steady-state dynamic responses are periodic for all $\mu_{\text{k}} \ge 1.4$. The bifurcation diagram for the situation when the non-smooth behaviours are included, however, shows that the steady-state dynamic responses are non-periodic for most values of $\mu_{\text{k}}$. Another difference between the results in these two situation is that the limit cycle vibration appears from very small $\mu_{\text{k}}$ (0.15) when the non-smooth behaviours are included, while in the situation of excluding non-smooth behaviours, the limit cycle vibration arises from $\mu_{\text{k}} = 1.4$, which is only slightly smaller than the critical friction coefficient for the instability of the equilibrium point that is $1.735$ in this example, as indicated in Fig. 17c. Besides, the values of index $L_{\text{s}}$ in these two situations in Fig. 17c demonstrate that the steady-state vibration when excluding non-smooth behaviours is much stronger than that when the non-smooth behaviours are included. Based on the above observations, it is concluded that the nonlinearity of the non-smooth behaviours in the system also has a significant effect on the steady-state responses of the system. Therefore, it is indispensable to incorporate all non-smooth behaviours including stick, slip and separation in order to accurately acquire the dynamic responses of the frictional systems.

Fig. 16

Comparisons of the system responses including and excluding the non-smooth behaviours: a $x_{1}$, b $y_{1}$ and c $F_{\text{N}}$

Fig. 17

The bifurcation behaviour and index $L_{\text{s}}$ of the steady-state responses as the function of $\mu_{\text{k}}$: a the bifurcation behaviour when including non-smooth behaviours, b the bifurcation behaviour when excluding non-smooth behaviours and c index $L_{\text{s}}$ in the two situations

The unstable eigenfrequencies obtained from the CEA are usually regarded as the frequencies of the self-excited vibration in the brake system in industry, which may not be accurate as the nonlinearities in the brake system can cause the frequencies of the self-excited vibration to be quite different from the unstable eigenfrequencies in the linearized system. To clarify their differences, the frequencies of the steady-state responses are compared with the unstable eigenfrequencies in the linearized system in a numerical example, where the values of other parameters are the same as those in Fig. 17. The colour in Fig. 18 indicates the response amplitude, and the dark marked lines exhibit the unstable eigenfrequencies in the linearized system with the variation of $\mu_{\text{k}}$. It is observed from Fig. 18a that the frequencies of the steady-state responses in this nonlinear frictional system deviate markedly from the unstable eigenfrequencies in the linearized system. To reveal the effects of each type of nonlinearity, the comparisons are also made when a single type of nonlinearity exists in the system and displayed in Fig. 18b–d, which show that the frequencies of the steady-state responses are close to the unstable eigenfrequencies in the situation of the single geometrical nonlinearity, while in the situations of the single nonlinearity of contact stiffness and the single nonlinearity of non-smooth behaviours, there exist larger differences between the frequencies of the steady-state responses and the unstable eigenfrequencies.

Fig. 18

The frequencies of the steady-state responses of the system and unstable eigenfrequency of the linearized system a with all three types of nonlinearities, b with the single nonlinearity of contact stiffness, c with the single geometrical nonlinearity and d with the single nonlinearity of non-smooth behaviours

5 Conclusions

In this work, the dynamics of a novel 5-DoF mass-on-belt frictional model with three different types of nonlinearities is investigated. The first type of nonlinearity is the nonlinear contact stiffness, the second is the non-smooth behaviour including stick, slip and separation, and the third is the geometrical nonlinearity caused by the moving-load feature of the mass on the rigid belt. Both the linear stability of the system and the nonlinear steady-state responses are studied. The effects of each type of nonlinearity on the system dynamics are revealed. Based on the observations from the numerical study, the following conclusions are reached,

• 1. The mode-coupling instability arises in the system with the increase in the coefficient of kinetic friction $\mu_{\text{k}}$. The critical friction coefficient for the instability decreases with the increase in the preload.

• 2. The nonlinearity of contact stiffness and the geometrical nonlinearity have significant effects on the linear stability of the system. The increase in nonlinear contact stiffness leads to the decrease in critical friction coefficient for the instability. The presence of geometrical nonlinearity contributes to the decrease in critical friction coefficient for the instability and increases the complexity of the instability in the system.

• 3. There is coexistence of two stable solutions, i.e. the equilibrium point and the limit cycle vibration, in the system in a certain range of $\mu_{\text{k}}$, and the linear stability analysis fails to detect the occurrence of self-excited vibration when the system is bi-stable, which can only be found out by the transient dynamic analysis. Besides, the bifurcation behaviour of the steady-state responses of the system with the variation of $\mu_{\text{k}}$ is found.

• 4. Each of the three different types of nonlinearities has significant effects on the steady-state responses of the system, which are demonstrated in the numerical study.

• 5. Frequencies of the steady-state responses in this nonlinear frictional system deviate markedly from the unstable eigenfrequencies of the linearized system, and each type of nonlinearity has different effects on the deviation of vibration frequencies from the unstable eigenfrequencies.

Appendix

The flowchart of the algorithm for the transient dynamic analysis of the system is shown in Fig. 19.

Fig. 19

The flowchart of the algorithm for the transient dynamic analysis of the system