Abstract
Each of our theories of mental representation provides some insight into how the mind works. However, these insights often seem incompatible, as the debates between symbolic, dynamical, emergentist, sub-symbolic, and grounded approaches to cognition attest. Mental representations—whatever they are—must share many features with each of our theories of representation, and yet there are few hypotheses about how a synthesis could be possible. Here, I develop a theory of the underpinnings of symbolic cognition that shows how sub-symbolic dynamics may give rise to higher-level cognitive representations of structures, systems of knowledge, and algorithmic processes. This theory implements a version of conceptual role semantics by positing an internal universal representation language in which learners may create mental models to capture dynamics they observe in the world. The theory formalizes one account of how truly novel conceptual content may arise, allowing us to explain how even elementary logical and computational operations may be learned from a more primitive basis. I provide an implementation that learns to represent a variety of structures, including logic, number, kinship trees, regular languages, context-free languages, domains of theories like magnetism, dominance hierarchies, list structures, quantification, and computational primitives like repetition, reversal, and recursion. This account is based on simple discrete dynamical processes that could be implemented in a variety of different physical or biological systems. In particular, I describe how the required dynamics can be directly implemented in a connectionist framework. The resulting theory provides an “assembly language” for cognition, where high-level theories of symbolic computation can be implemented in simple dynamics that themselves could be encoded in biologically plausible systems.


Similar content being viewed by others
Notes
The LOT’s focus on structural rules is consistent with many popular cognitive architectures that use production systems (Anderson et al. 1997, 2004; Newell 1994), although the emphasis on in most LOT models is on the learning and computational level of analysis, not the implementation or architecture.
The problem is also faced by some connectionist models. For instance, Rogers and McClelland (2004), a connectionist model of semantics, builds in relations (e.g.
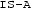 ,
,  ,
, 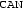 ) and observable attributes (e.g.
) and observable attributes (e.g.  ,
, 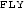 ,
,  ) as activation patterns on individual nodes. There, the puzzle is: what precisely makes it the case that activation in one node means (whatever that means)
) as activation patterns on individual nodes. There, the puzzle is: what precisely makes it the case that activation in one node means (whatever that means) 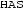 as opposed to
as opposed to  ?
?Although this notion is controversial—see Hoffman et al. (2015) and the ensuing commentary.
Curiously, an isomorphism into real number is not the only one possible for physics—it has been argued that physical theories could be stated without numbers at all (Field 2016).
The general idea of finding a formal internal representation satisfying observed relations has close connections to model theory (Ebbinghaus and Flum 2005; Libkin 2013), as well as the solution of constraint satisfaction problems specified by logical formulas (satisfiability modulo theories) (Davis and Putnam 1960; Nieuwenhuis et al. 2006).
One simple “non-halting” combinator is
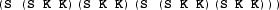 .
.However, the general time complexity of this interface is not apparent to me at least.
Intuitively, more data is needed than in the simple Fish transitive inference cases because the
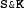 model does not inherently know it is dealing with a dominance hierarchy. Cases of dominance hierarchies in animal cognition may have a better chance of being innate, or at least higher prior than other alternatives.
model does not inherently know it is dealing with a dominance hierarchy. Cases of dominance hierarchies in animal cognition may have a better chance of being innate, or at least higher prior than other alternatives.Fodor and Pylyshyn (2014) notes there is no imagistic representation of a concept like “squareness”, or the property that all squares, a problem that Berkeley (1709) struggled with in understanding the origin and form of abstract knowledge. Anderson (1978) shows how perceptual propositional codes might account for geometric concepts like the structure of the letter “R” and how imagistic and propositional codes can made similar behavioral predictions (see also, e.g. Pylyshyn 1973).
A mathematical function, for instance mapping the world to a representation, is continuous if boundedly small changes in the input give rise to boundedly small changes in the output.
My inclination is that Putnam’s argument tells us primarily about the meaning of the word “meaning” rather than anything substantive about the nature of mental representations (for a detailed cognitive view along these lines in a different setting, see Piantadosi 2015). It is true that intuitively the meaning of a term should include something about its referent; it is not clear that our intuitions about this word tell us anything about how brains and minds actually work. In other words, Putnam may just be doing lexical semantics, a branch of psychology, here—if his point is really about the physical/biological system of the brain, it would be good to know what evidence can be presented that convincingly shows so.
References
Abe, H., & Lee, D. (2011). Distributed coding of actual and hypothetical outcomes in the orbital and dorsolateral prefrontal cortex. Neuron, 70(4), 731–741.
Abelson, H., & Sussman, G. (1996). Structure and interpretation of computer programs. Cambridge, MA: MIT Press.
Amalric, M., Wang, L., Pica, P., Figueira, S., Sigman, M., & Dehaene, S. (2017). The language of geometry: Fast comprehension of geometrical primitives and rules in human adults and preschoolers. PLoS Computational Biology, 13(1), e1005273.
Anderson, J. R. (1978). Arguments concerning representations for mental imagery. Psychological Review, 85(4), 249.
Anderson, J. R., Bothell, D., Byrne, M. D., Douglass, S., Lebiere, C., & Qin, Y. (2004). An integrated theory of the mind. Psychological Review, 111(4), 1036.
Anderson, J. R., Matessa, M., & Lebiere, C. (1997). Act-r: A theory of higher level cognition and its relation to visual attention. Human-Computer Interaction, 12(4), 439–462.
Aydede, M. (1997). Language of thought: The connectionist contribution. Minds and Machines, 7(1), 57–101.
Barsalou, L. W. (1999). Perceptions of perceptual symbols. Behavioral and Brain Sciences, 22(04), 637–660.
Barsalou, L. W. (2008). Grounded cognition. Annual Review Psychology, 59, 617–645.
Barsalou, L. W. (2010). Grounded cognition: Past, present, and future. Topics in Cognitive Science, 2(4), 716–724.
Battaglia, P. W., Hamrick, J. B., & Tenenbaum, J. B. (2013). Simulation as an engine of physical scene understanding. Proceedings of the National Academy of Sciences, 110(45), 18327–18332.
Beer, R. D. (2000). Dynamical approaches to cognitive science. Trends in Cognitive Sciences, 4(3), 91–99.
Bennett, C. H. (1995). Logical depth and physical complexity. The Universal Turing Machine A Half-Century Survey, pp 207–235.
Berkeley, G. (1709). An essay towards a new theory of vision.
Blackburn, P., & Bos, J. (2005). Representation and inference for natural language: A first course in computational semantics. Center for the Study of Language and Information.
Block, N. (1987). Advertisement for a semantics for psychology. Midwest Studies in Philosophy, 10(1), 615–678.
Block, N. (1997). Semantics, conceptual role. The Routledge Encylopedia of Philosophy.
Bonawitz, E. B., van Schijndel, T. J., Friel, D., & Schulz, L. (2012). Children balance theories and evidence in exploration, explanation, and learning. Cognitive Psychology, 64(4), 215–234.
Bongard, M. M. (1970). Pattern Recognition. New York: Hayden Book Co.
Boole, G. (1854). An investigation of the laws of thought: On which are founded the mathematical theories of logic and probabilities. London, UK: Walton and Maberly.
Bowman, S. R., Manning, C. D., & Potts, C. (2015). Tree-structured composition in neural networks without tree-structured architectures. arXiv preprint arXiv:1506.04834.
Bowman, S. R., Potts, C., & Manning, C. D. (2014a). Learning distributed word representations for natural logic reasoning. arXiv preprint arXiv:1410.4176.
Bowman, S. R., Potts, C., & Manning, C. D. (2014b). Recursive neural networks can learn logical semantics. arXiv preprint arXiv:1406.1827.
Bratko, I. (2001). Prolog programming for artificial intelligence. New York: Pearson.
Brigandt, I. (2004). Conceptual role semantics, the theory theory, and conceptual change.
Bubic, A., Von Cramon, D. Y., & Schubotz, R. I. (2010). Prediction, cognition and the brain. Frontiers in Human Neuroscience, 4, 25.
Cardone, F., & Hindley, J. R. (2006). History of lambda-calculus and combinatory logic. Handbook of the History of Logic, 5, 723–817.
Carey, S. (1985). Conceptual change in childhood.
Carey, S. (2009). The Origin of Concepts. Oxford: Oxford University Press.
Carey, S. (2015). Why theories of concepts should not ignore the problem of acquisition. Disputation: International Journal of Philosophy., 7, 41.
Chalmers, D. (1990). Why fodor and pylyshyn were wrong: The simplest refutation. In: Proceedings of the twelfth annual conference of the cognitive science society, Cambridge, mass (pp. 340–347).
Chalmers, D. J. (1992). Subsymbolic computation and the chinese room. The symbolic and connectionist paradigms: Closing the gap, (pp. 25–48).
Chalmers, D. J. (1994). On implementing a computation. Minds and Machines, 4(4), 391–402.
Chalmers, D. J. (1996). Does a rock implement every finite-state automaton? Synthese, 108(3), 309–333.
Chater, N., & Oaksford, M. (1990). Autonomy, implementation and cognitive architecture: A reply to fodor and pylyshyn. Cognition, 34(1), 93–107.
Chater, N., & Oaksford, M. (2013). Programs as causal models: Speculations on mental programs and mental representation. Cognitive Science, 37(6), 1171–1191.
Chater, N., & Vitányi, P. (2003). Simplicity: A unifying principle in cognitive science? Trends in Cognitive Sciences, 7(1), 19–22.
Chater, N., & Vitányi, P. (2007). Ideal learning of natural language: Positive results about learning from positive evidence. Journal of Mathematical Psychology, 51(3), 135–163.
Chomsky, N. (1956). Three models for the description of language. IRE Transactions on Information Theory, 2(3), 113–124.
Chomsky, N. (1957). Syntactic Structures. The Hague: Mouton.
Church, A. (1936). An unsolvable problem of elementary number theory. American Journal of Mathematics, 58(2), 345–363.
Church, A., & Rosser, J. B. (1936). Some properties of conversion. Transactions of the American Mathematical Society, 39(3), 472–482.
Clapp, L. (2012). Is even thought compositional? Philosophical Studies, 157(2), 299–322.
Conant, R., & Ashby, R. (1970). Every good regulator of a system must be a model of that system\(\dagger \). International Journal of Systems Science, 1(2), 89–97.
Costa Florêncio, C. (2002). Learning generalized quantifiers. In: M. Nissim (Ed.), Proceedings of the ESSLLI02 Student Session (pp. 31–40). University of Trento.
Craik, K. J. W. (1952). The nature of explanation (Vol. 445). CUP Archive.
Craik, K. J. W. (1967). The nature of explanation. CUP Archive.
Curry, H. B., & Feys, R. (1958). Combinatory logic, volume i of studies in logic and the foundations of mathematics. Amsterdam: North-Holland.
Dale, R., & Spivey, M. J. (2005). From apples and oranges to symbolic dynamics: A framework for conciliating notions of cognitive representation. Journal of Experimental & Theoretical Artificial Intelligence, 17(4), 317–342.
Davies, D., & Isard, S. D. (1972). Utterances as programs. Machine Intelligence, 7, 325–339.
Davis, E. (1990). Representations of commonsense knowledge. San Mateo, CA: Morgan Kaufmann Publishers Inc.
Davis, E., & Marcus, G. (2016). The scope and limits of simulation in automated reasoning. Artificial Intelligence, 233, 60–72.
Davis, M., & Putnam, H. (1960). A computing procedure for quantification theory. Journal of the ACM (JACM), 7(3), 201–215.
Depeweg, S., Rothkopf, C. A., & Jäkel, F. (2018). Solving bongard problems with a visual language and pragmatic reasoning. arXiv preprint arXiv:1804.04452.
Ditto, W. L., Murali, K., & Sinha, S. (2008). Chaos computing: Ideas and implementations. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 366(1865), 653–664.
Drews, C. (1993). The concept and definition of dominance in animal behaviour. Behaviour, 125(3), 283–313.
Ebbinghaus, H.-D., & Flum, J. (2005). Finite model theory. New York: Springer.
Edelman, S. (2008a). On the nature of minds, or: Truth and consequences. Journal of Experimental and Theoretical AI, 20, 181–196.
Edelman, S. (2008b). A swan, a pike, and a crawfish walk into a bar. Journal of Experimental & Theoretical Artificial Intelligence, 20(3), 257–264.
Edelman, S., & Intrator, N. (2003). Towards structural systematicity in distributed, statically bound visual representations. Cognitive Science, 27(1), 73–109.
Edelman, S., & Shahbazi, R. (2012). Renewing the respect for similarity. Frontiers in Computational Neuroscience, 6, 45.
Ediger, B. (2011). cl—a combinatory logic interpreter. http://www.stratigery.com/cl/.
Erdogan, G., Yildirim, I., & Jacobs, R. A. (2015). From sensory signals to modality-independent conceptual representations: A probabilistic language of thought approach. PLoS Computer Biology, 11(11), e1004610.
Falkenhainer, B., Forbus, K. D., & Gentner, D. (1986). The structure-mapping engine. Department of Computer Science, University of Illinois at Urbana-Champaign.
Feldman, J. (2000). Minimization of Boolean complexity in human concept learning. Nature, 407(6804), 630–633.
Feldman, J. (2003a). Simplicity and complexity in human concept learning. The General Psychologist, 38(1), 9–15.
Feldman, J. (2003b). The simplicity principle in human concept learning. Current Directions in Psychological Science, 12(6), 227.
Feldman, J. (2012). Symbolic representation of probabilistic worlds. Cognition, 123(1), 61–83.
Field, H. (2016). Science without numbers. Oxford: Oxford University Press.
Field, H. H. (1977). Logic, meaning, and conceptual role. The Journal of Philosophy, 74(7), 379–409.
Fitch, W. T. (2014). Toward a computational framework for cognitive biology: Unifying approaches from cognitive neuroscience and comparative cognition. Physics of Life Reviews, 11(3), 329–364.
Fodor, J. (1975). The language of thought. Cambridge, MA: Harvard University Press.
Fodor, J. (1997). Connectionism and the problem of systematicity (continued): Why smolensky’s solution still doesn’t work. Cognition, 62(1), 109–119.
Fodor, J. (2008). LOT 2: The language of thought revisited. Oxford: Oxford University Press.
Fodor, J., & Lepore, E. (1992). Holism: A shopper’s guide.
Fodor, J., & McLaughlin, B. P. (1990). Connectionism and the problem of systematicity: Why Smolensky’s solution doesn’t work. Cognition, 35(2), 183–204.
Fodor, J., & Pylyshyn, Z. (1988). Connectionism and cognitive architecture: a critical analysis, Connections and symbols. Cognition, 28, 3–71.
Fodor, J., & Pylyshyn, Z. W. (2014). Minds without meanings: An essay on the content of concepts. New York: MIT Press.
Frege, G. (1892). Über sinn und bedeutung. Wittgenstein Studien, 1, 1.
French, R. M. (2002). The computational modeling of analogy-making. Trends in Cognitive Sciences, 6(5), 200–205.
Gallistel, C., & King, A. (2009). Memory and the computational brain. New York: Wiley Blackwell.
Gallistel, C. R. (1998). Symbolic processes in the brain: The case of insect navigation. An Invitation to Cognitive Science, 4, 1–51.
Gardner, M., Talukdar, P., & Mitchell, T. (2015). Combining vector space embeddings with symbolic logical inference over open-domain text. In 2015 aaai spring symposium series (Vol. 6, p. 1).
Gayler, R. W. (2004). Vector symbolic architectures answer jackendoff’s challenges for cognitive neuroscience. arXiv preprint arXiv:cs/0412059.
Gayler, R. W. (2006). Vector symbolic architectures are a viable alternative for Jackendoff’s challenges. Behavioral and Brain Sciences, 29(01), 78–79.
Gelman, S. A., & Markman, E. M. (1986). Categories and induction in young children. Cognition, 23(3), 183–209.
Gentner, D. (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science, 7(2), 155–170.
Gentner, D., & Forbus, K. D. (2011). Computational models of analogy. Wiley interdisciplinary reviews: cognitive science, 2(3), 266–276.
Gentner, D., & Markman, A. B. (1997). Structure mapping in analogy and similarity. American Psychologist, 52(1), 45.
Gentner, D., & Stevens, A. L. (1983). Mental models.
Gertler, B. (2012). Understanding the internalism–externalism debate: What is the boundary of the thinker? Philosophical Perspectives, 26(1), 51–75.
Gierasimczuk, N. (2007). The problem of learning the semantics of quantifiers. In Logic, Language, and Computation, pp. 117–126.
Goldman, A. I. (2006). Simulating minds: The philosophy, psychology, and neuroscience of mindreading. Oxford: Oxford University Press.
Goodman, N., Mansinghka, V., Roy, D., Bonawitz, K., & Tenenbaum, J. (2008a). Church: A language for generative models. In Proceedings of the 24th conference on uncertainty in artificial intelligence, uai 2008 (pp. 220–229).
Goodman, N., Tenenbaum, J., Feldman, J., & Griffiths, T. (2008b). A Rational Analysis of Rule-Based Concept Learning. Cognitive Science, 32(1), 108–154.
Goodman, N. D. (1972). A simplification of combinatory logic. The Journal of Symbolic Logic, 37(02), 225–246.
Goodman, N. D., Tenenbaum, J. B., & Gerstenberg, T. (2015). Concepts in a probabilistic language of thought. In: Margolis & Lawrence (Eds.), The conceptual mind: New directions in the study of concepts. MIT Press: New York.
Goodman, N. D., Ullman, T. D., & Tenenbaum, J. B. (2011). Learning a theory of causality. Psychological Review, 118(1), 110.
Gopnik, A., & Meltzoff, A. N. (1997). Words, thoughts, and theories. New York: Mit Press.
Gopnik, A., & Wellman, H. M. (2012). Reconstructing constructivism: Causal models, bayesian learning mechanisms, and the theory theory. Psychological Bulletin, 138(6), 1085.
Gordon, R. M. (1986). Folk psychology as simulation. Mind & Language, 1(2), 158–171.
Graves, A., Wayne, G., & Danihelka, I. (2014). Neural turing machines. arXiv preprint arXiv:1410.5401.
Greenberg, M., & Harman, G. (2005). Conceptual role semantics.
Grefenstette, E. (2013). Towards a formal distributional semantics: Simulating logical calculi with tensors. arXiv preprint arXiv:1304.5823.
Griffiths, T., Chater, N., Kemp, C., Perfors, A., & Tenenbaum, J. (2010). Probabilistic models of cognition: exploring representations and inductive biases. Trends Cogn. Sci, 14(10.1016).
Grosenick, L., Clement, T. S., & Fernald, R. D. (2007). Fish can infer social rank by observation alone. Nature, 445(7126), 429–432.
Grover, A., Zweig, A., & Ermon, S. (2019). Graphite: Iterative generative modeling of graphs. In International conference on machine learning (pp. 2434–2444).
Grünwald, P. D. (2007). The minimum description length principle. New York: MIT press.
Hadley, R. F. (2009). The problem of rapid variable creation. Neural Computation, 21(2), 510–532.
Harman, G. (1987). (Non-solipsistic) Conceptual Role Semantics. In E. Lepore (Ed.), New directions in semantics. London: Academic Press.
Harnad, S. (1990). The symbol grounding problem. Physica D: Nonlinear Phenomena, 42(1–3), 335–346.
Hauser, M. D., Chomsky, N., & Fitch, W. T. (2002). The faculty of language: What is it, who has it, and how did it evolve? Science, 298(5598), 1569–1579.
Hegarty, M. (2004). Mechanical reasoning by mental simulation. Trends in Cognitive Sciences, 8(6), 280–285.
Heim, I., & Kratzer, A. (1998). Semantics in generative grammar. Malden, MA: Wiley-Blackwell.
Hindley, J., & Seldin, J. (1986). Introduction to combinators and\(\lambda \)-calculus. Cambridge, UK: Press Syndicate of the University of Cambridge.
Hoffman, D. D., Singh, M., & Prakash, C. (2015). The interface theory of perception. Psychonomic Bulletin & Review, 22(6), 1480–1506.
Hofstadter, D. R. (1980). Gödel Escher Bach. New Society.
Hofstadter, D. R. (1985). Waking up from the boolean dream. Metamagical Themas, (pp. 631–665).
Hofstadter, D. R. (2008). I am a strange loop. Basic books.
Hopcroft, J., Motwani, R., & Ullman, J. (1979). Introduction to automata theory, languages, and computation (Vol. 3). Reading, MA: Addison-Wesley.
Horsman, C., Stepney, S., Wagner, R. C., & Kendon, V. (2014). When does a physical system compute? In Proc. r. soc. a (Vol. 470, p. 20140182).
Hsu, A., & Chater, N. (2010). The logical problem of language acquisition: A probabilistic perspective. Cognitive Science, 34(6), 972–1016.
Hsu, A., Chater, N., & Vitányi, P. (2011). The probabilistic analysis of language acquisition: Theoretical, computational, and experimental analysis. Cognition, 120(3), 380–390.
Hummel, J. E., & Holyoak, K. J. (1997). Distributed representations of structure: A theory of analogical access and mapping. Psychological Review, 104(3), 427.
Hutter, M. (2005). Universal artificial intelligence: Sequential decisions based on algorithmic probability. New York: Springer.
Jackendoff, R. (2002). Foundation of language-brain, meaning, grammar, evolution. Oxford: Oxford University Press.
Jacobson, P. (1999). Towards a variable-free semantics. Linguistics and Philosophy, 22(2), 117–185.
Jaeger, H. (1999). From continuous dynamics to symbols. In Dynamics, synergetics, autonomous agents: Nonlinear systems approaches to cognitive psychology and cognitive science (pp. 29–48). World Scientific.
Jay, B., & Given-Wilson, T. (2011). A combinatory account of internal structure. The Journal of Symbolic Logic, 76(03), 807–826.
Jay, B., & Kesner, D. (2006). Pure pattern calculus. In Programming languages and systems (pp. 100–114). Springer.
Jay, B., & Vergara, J. (2014). Confusion in the church-turing thesis. arXiv preprint arXiv:1410.7103.
Johnson, K. E. (2004). On the systematicity of language and thought. Journal of Philosophy, CI, 111–139.
Johnson-Laird, P. N. (1977). Procedural semantics. Cognition, 5(3), 189–214.
Johnson-Laird, P. N. (1983). Mental models: Towards a cognitive science of language, inference, and consciousness (No 6). New York: Harvard University Press.
Katz, Y., Goodman, N., Kersting, K., Kemp, C., & Tenenbaum, J. (2008). Modeling semantic cognition as logical dimensionality reduction. In Proceedings of Thirtieth Annual Meeting of the Cognitive Science Society.
Kearns, J. T. (1969). Combinatory logic with discriminators. The Journal of Symbolic Logic, 34(4), 561–575.
Kemp, C. (2012). Exploring the conceptual universe. Psychological Review, 119, 685–722.
Kemp, C., & Tenenbaum, J. (2008). The discovery of structural form. Proceedings of the National Academy of Sciences, 105(31), 10687.
Kemp, C., Tenenbaum, J. B., Griffiths, T. L., Yamada, T., & Ueda, N. (2006). Learning systems of concepts with an infinite relational model. In Aaai (Vol. 3, p. 5).
Kemp, C., Tenenbaum, J. B., Niyogi, S., & Griffiths, T. L. (2010). A probabilistic model of theory formation. Cognition, 114(2), 165–196.
Kipf, T., Fetaya, E., Wang, K.-C., Welling, M., & Zemel, R. (2018). Neural relational inference for interacting systems. In International conference on machine learning (icml).
Kipf, T., et al. (2020). Deep learning with graph-structured representations.
Koopman, P., Plasmeijer, R., & Jansen, J. M. (2014). Church encoding of data types considered harmful for implementations.
Kushnir, T., & Xu, F. (2012). Rational constructivism in cognitive development (Vol. 43). New York: Academic Press.
Kwiatkowski, T., Goldwater, S., Zettlemoyer, L., & Steedman, M. (2012). A probabilistic model of syntactic and semantic acquisition from child-directed utterances and their meanings. In: Proceedings of the 13th conference of the european chapter of the association for computational linguistics (pp. 234–244).
Kwiatkowski, T., Zettlemoyer, L., Goldwater, S., & Steedman, M. (2010). Inducing probabilistic ccg grammars from logical form with higher-order unification. In: Proceedings of the 2010 conference on empirical methods in natural language processing (pp. 1223–1233).
Lake, B. M., Salakhutdinov, R., & Tenenbaum, J. B. (2015). Human-level concept learning through probabilistic program induction. Science, 350(6266), 1332–1338.
Laurence, S., & Margolis, E. (2002). Radical concept nativism. Cognition, 86(1), 25–55.
Lee, M. D. (2010). Emergent and structured cognition in bayesian models: comment on griffiths et al and mcclelland et al. Update, 14, 8.
Levin, L. A. (1973). Universal sequential search problems. Problemy Peredachi Informatsii, 9(3), 115–116.
Levin, L. A. (1984). Randomness conservation inequalities; information and independence in mathematical theories. Information and Control, 61(1), 15–37.
Levine, S., Finn, C., Darrell, T., & Abbeel, P. (2016). End-to-end training of deep visuomotor policies. The Journal of Machine Learning Research, 17(1), 1334–1373.
Li, F.-F., Fergus, R., & Perona, P. (2006). One-shot learning of object categories. IEEE Transactions on Pattern Analysis and Machine intelligence, 28(4), 594–611.
Li, M., & Vitányi, P. (2008). An introduction to Kolmogorov complexity and its applications. New York: Springer.
Liang, P., Jordan, M., & Klein, D. (2010). Learning Programs: A Hierarchical Bayesian Approach. In Proceedings of the 27th International Conference on Machine Learning.
Libkin, L. (2013). Elements of finite model theory. New York: Springer.
Lind, D., & Marcus, B. (1995). An introduction to symbolic dynamics and coding. Cambridge: Cambridge University Press.
Loar, B. (1982). Conceptual role and truth-conditions: comments on harman’s paper:”conceptual role semantics”. Notre Dame Journal of Formal Logic, 23(3), 272–283.
Lu, Z., & Bassett, D. S. (2018). A parsimonious dynamical model for structural learning in the human brain. arXiv preprint arXiv:1807.05214.
Mahon, B. Z. (2015). What is embodied about cognition? Language, Cognition and Neuroscience, 30(4), 420–429.
Marcus, G. F. (2003). The algebraic mind: Integrating connectionism and cognitive science. New York: MIT press.
Margolis, E., & Laurence, S. (1999). Concepts: Core readings. New York: The MIT Press.
Markman, E. M. (1991). Categorization and naming in children: Problems of induction. New York: Mit Press.
Marr, D. (1982). Vision: A computational investigation into the Human Representation and Processing of Visual Information. London: W.H. Freeman & Company.
Marr, D., & Poggio, T. (1976). From understanding computation to understanding neural circuitry. MIT AI Memo 357.
Martin, A. E., & Doumas, L. A. (2018). Predicate learning in neural systems: Discovering latent generative structures. arXiv preprint arXiv:1810.01127.
Martinho, A., & Kacelnik, A. (2016). Ducklings imprint on the relational concept of “same or different”. Science, 353(6296), 286–288.
McClelland, J. L., Botvinick, M. M., Noelle, D. C., Plaut, D. C., Rogers, T. T., Seidenberg, M. S., et al. (2010). Letting structure emerge: Connectionist and dynamical systems approaches to cognition. Trends in Cognitive Sciences, 14(8), 348–356.
McNamee, D., & Wolpert, D. M. (2019). Internal models in biological control. Annual Review of Control, Robotics, and Autonomous Systems, 2(1), 339–364. https://doi.org/10.1146/annurev-control-060117-105206.
Miller, G. A., & Johnson-Laird, P. N. (1976). Language and perception. New York: Belknap Press.
Mody, S., & Carey, S. (2016). The emergence of reasoning by the disjunctive syllogism in early childhood. Cognition, 154, 40–48.
Mollica, F., & Piantadosi, S. T. (2015). Towards semantically rich and recursive word learning models. In Proceedings of the Cognitive Science Society. http://colala.berkeley.edu/papers/mollica2015towards.pdf
Montague, R. (1973). The Proper Treatment of Quantification in Ordinary English. Formal. Semantics, (pp 17–34).
Mostowski, M. (1998). Computational semantics for monadic quantifiers. Journal of Applied Nonclassical Logics, 8, 107–122.
Murphy, G. L., & Medin, D. L. (1985). The role of theories in conceptual coherence. Psychological Review, 92(3), 289.
Neelakantan, A., Roth, B., & McCallum, A. (2015). Compositional vector space models for knowledge base inference. In 2015 aaai spring symposium series.
Newell, A. (1994). Unified theories of cognition. Cambridge, MA: Harvard University Press.
Newell, A., & Simon, H. A. (1976). Computer science as empirical inquiry: Symbols and search. Communications of the ACM, 19(3), 113–126.
Nickel, M., & Kiela, D. (2017). Poincaré embeddings for learning hierarchical representations. In Advances in Neural Information Processing Systems (pp. 6338–6347).
Nieuwenhuis, R., Oliveras, A., & Tinelli, C. (2006). Solving sat and sat modulo theories: From an abstract davis-putnam-logemann-loveland procedure to dpll (t). Journal of the ACM (JACM), 53(6), 937–977.
Nilsson, N. J. (2009). The quest for artificial intelligence. Cambridge: Cambridge University Press.
Okasaki, C. (1999). Purely functional data structures. Cambridge: Cambridge University Press.
Osherson, D. N., Smith, E. E., Wilkie, O., Lopez, A., & Shafir, E. (1990). Category-based induction. Psychological Review, 97(2), 185.
Overlan, M. C., Jacobs, R. A., & Piantadosi, S. T. (2016). A hierarchical probabilistic language-of-thought model of human visual concept learning. In Proceedings of the Cognitive Science Society. http://colala.berkeley.edu/papers/overlan2016hierarchical.pdf
Overlan, M. C., Jacobs, R. A., & Piantadosi, S. T. (2017). Learning abstract visual concepts via probabilistic program induction in a language of thought. Cognition, 168, 320–334. http://colala.berkeley.edu/papers/overlan2017learning.pdf
Penn, D. C., Holyoak, K. J., & Povinelli, D. J. (2008). Darwin’s mistake: Explaining the discontinuity between human and nonhuman minds. Behavioral and Brain Sciences, 31(02), 109–130.
Piantadosi, S. T. (2011). Learning and the language of thought. Unpublished doctoral dissertation, MIT. Retrieved from http://colala.berkeley.edu/papers/piantadosi2011learning.pdf
Piantadosi, S. T. (2015). Problems in the philosophy of mathematics: A view from cognitive science. In E. Davis & P. J. Davis (Eds.), Mathematics, substance and surmise: Views on the meaning and ontology of mathematics. Springer. http://colala.berkeley.edu/papers/piantadosi2015problems.pdf.
Piantadosi, S. T., & Jacobs, R. (2016). Four problems solved by the probabilistic Language of Thought. Current Directions in Psychological Science, 25, 54–59. http://colala.berkeley.edu/papers/piantadosi2016four.pdf.
Piantadosi, S. T., Tenenbaum, J., & Goodman, N. (2012). Bootstrapping in a language of thought: a formal model of numerical concept learning. Cognition, 123, 199–217. http://colala.berkeley.edu/papers/piantadosi2012bootstrapping.pdf.
Piantadosi, S. T., Tenenbaum, J., & Goodman, N. (2016). The logical primitives of thought: Empirical foundations for compositional cognitive models. Psychological Review, 123, 392–424. http://colala.berkeley.edu/papers/piantadosi2016logical.pdf.
Pierce, B. C. (2002). Types and programming languages. New York: MIT press.
Plate, T. A. (1995). Holographic reduced representations. IEEE transactions on Neural Networks, 6(3), 623–641.
Pollack, J. B. (1989). Implications of recursive distributed representations. In Advances in neural information processing systems (pp. 527–536).
Pollack, J. B. (1990). Recursive distributed representations. Artificial Intelligence, 46(1), 77–105.
Putnam, H. (1975). The meaing of meaning. In Philosophical Papers, Volume II: Mind, Language, and Reality. Cambridge: Cambridge University Press.
Putnam, H. (1988). Representation and reality (Vol. 454). Cambridge: Cambridge Univ Press.
Pylyshyn, Z. W. (1973). What the mind’s eye tells the mind’s brain: A critique of mental imagery. Psychological Bulletin, 80(1), 1.
Quine, W. V. (1951). Main trends in recent philosophy: Two dogmas of empiricism. The philosophical review (pp. 20–43).
Rips, L., Asmuth, J., & Bloomfield, A. (2006). Giving the boot to the bootstrap: How not to learn the natural numbers. Cognition, 101, 51–60.
Rips, L., Asmuth, J., & Bloomfield, A. (2008a). Do children learn the integers by induction? Cognition, 106, 940–951.
Rips, L., Asmuth, J., & Bloomfield, A. (2013). Can statistical learning bootstrap the integers? Cognition, 128(3), 320–330.
Rips, L., Bloomfield, A., & Asmuth, J. (2008b). From numerical concepts to concepts of number. Behavioral and Brain Sciences, 31, 623–642.
Rips, L. J. (1975). Inductive judgments about natural categories. Journal of Verbal Learning and Verbal Behavior, 14(6), 665–681.
Rips, L. J. (1989). The psychology of knights and knaves. Cognition, 31(2), 85–116.
Rips, L. J. (1994). The psychology of proof: Deductive reasoning in human thinking. New York: Mit Press.
Rocktäschel, T., Bosnjak, M., Singh, S., & Riedel, S. (2014). Low-dimensional embeddings of logic. In Acl workshop on semantic parsing.
Rogers, T., & McClelland, J. (2004). Semantic cognition: A parallel distributed processing approach. Cambridge, MA: MIT Press.
Romano, S., Salles, A., Amalric, M., Dehaene, S., Sigman, M., & Figueira, S. (2018). Bayesian validation of grammar productions for the language of thought. PLoS One, 2, 311.
Romano, S., Salles, A., Amalric, M., Dehaene, S., Sigman, M., & Figueria, S. (2017). Bayesian selection of grammar productions for the language of thought. bioRxiv, 141358.
Rothe, A., Lake, B. M., & Gureckis, T. (2017). Question asking as program generation. In Advances in neural information processing systems (pp. 1046–1055).
Rule, J. S., Tenenbaum, J. B., & Piantadosi, S. T. (2020). The child as hacker. Trends in Cognitive Sciences.
Rumelhart, D., & McClelland, J. (1986). Parallel distributed processing. Cambridge, MA: MIT Press.
Runge, C. (1901). Über empirische funktionen und die interpolation zwischen äquidistanten ordinaten. Zeitschrift für Mathematik und Physik, 46(224–243), 20.
Salakhutdinov, R., Tenenbaum, J., & Torralba, A. (2010). One-shot learning with a hierarchical nonparametric bayesian model.
Schmidhuber, J. (1995). Discovering solutions with low kolmogorov complexity and high generalization capability. In Machine learning proceedings 1995 (pp. 488–496). Elsevier.
Schmidhuber, J. (2002). The speed prior: a new simplicity measure yielding near-optimal computable predictions. In International conference on computational learning theory (pp. 216–228).
Schmidhuber, J. (2007). Gödel machines: Fully self-referential optimal universal self-improvers. In Artificial general intelligence (pp. 199–226). Springer.
Scholten, D. (2010). A primer for Conant and Ashby’s good-regulator theorem [Unpublished].
Scholten, D. L. (2011). Every good key must be a model of the lock it opens.
Schönfinkel, M. (1967). On the building blocks of mathematical logic. From Frege to Gödel (pp 355–366).
Searle, J. R. (1980). Minds, brains, and programs. Behavioral and Brain Sciences, 3(03), 417–424.
Searle, J. R. (1990). Is the brain a digital computer? In Proceedings and addresses of the american philosophical association (Vol. 64, pp. 21–37).
Sellars, W. (1963). Science, perception, and reality.
Shalizi, C. R., & Crutchfield, J. P. (2001). Computational mechanics: Pattern and prediction, structure and simplicity. Journal of Statistical Physics, 104(3–4), 817–879.
Shastri, L., Ajjanagadde, V., Bonatti, L., & Lange, T. (1996). From simple associations to systematic reasoning: A connectionist representation of rules, variables, and dynamic bindings using temporal synchrony. Behavioral and Brain Sciences, 19(2), 326–337.
Shepard, R. N., & Chipman, S. (1970). Second-order isomorphism of internal representations: Shapes of states. Cognitive Psychology, 1(1), 1–17.
Shipley, E. F. (1993). Categories, hierarchies, and induction. The Psychology of Learning and Motivation, 30, 265–301.
Sinha, S., & Ditto, W. L. (1998). Dynamics based computation. Physical Review Letters, 81(10), 2156.
Siskind, J. (1996). A Computational Study of Cross-Situational Techniques for Learning Word-to-Meaning Mappings. Cognition, 61, 31–91.
Sloutsky, V. M. (2010). From perceptual categories to concepts: What develops? Cognitive Science, 34(7), 1244–1286.
Smolensky, P. (1988). The constituent structure of connectionist mental states: A reply to fodor and pylyshyn. The Southern Journal of Philosophy, 26(S1), 137–161.
Smolensky, P. (1989). Connectionism and constituent structure. Connectionism in perspective (pp. 3–24).
Smolensky, P. (1990). Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial Intelligence, 46(1), 159–216.
Smolensky, P. (2012). Subsymbolic computation theory for the human intuitive processor. In Conference on computability in europe (pp. 675–685).
Smolensky, P., Lee, M., He, X., Yih, W.-t., Gao, J., & Deng, L. (2016). Basic reasoning with tensor product representations. arXiv preprint arXiv:1601.02745.
Smolensky, P., & Legendre, G. (2006). The Harmonic Mind. Cambridge, MA: MIT Press.
Solomonoff, R. J. (1964a). A formal theory of inductive inference. Part I. Information and Control, 7(1), 1–22.
Solomonoff, R. J. (1964b). A formal theory of inductive inference: Part II. Information and Control, 7(2), 224–254.
Spivey, M. (2008). The continuity of mind. Oxford: Oxford University Press.
Stay, M. (2005). Very simple chaitin machines for concrete ait. Fundamenta Informaticae, 68(3), 231–247.
Steedman, M. (2001). The syntactic process. Cambridge MA: MIT Press.
Steedman, M. (2002). Plans, affordances, and combinatory grammar. Linguistics and Philosophy, 25(5–6), 723–753.
Stone, T., & Davies, M. (1996). The mental simulation debate: A progress report. Theories of theories of mind (pp. 119–137).
Tabor, W. (2009). A dynamical systems perspective on the relationship between symbolic and non-symbolic computation. Cognitive Neurodynamics, 3(4), 415–427.
Tabor, W. (2011). Recursion and recursion-like structure in ensembles of neural elements. In Unifying themes in complex systems. proceedings of the viii international conference on complex systems (pp. 1494–1508).
Tabor, W., Juliano, C., & Tanenhaus, M. K. (1997). Parsing in a dynamical system: An attractor-based account of the interaction of lexical and structural constraints in sentence processing. Language and Cognitive Processes, 12(2–3), 211–271.
Tenenbaum, J., Kemp, C., Griffiths, T., & Goodman, N. (2011). How to grow a mind: Statistics, structure, and abstraction. Science, 331(6022), 1279–1285.
Tenenbaum, J. B., Griffiths, T. L., & Kemp, C. (2006). Theory-based bayesian models of inductive learning and reasoning. Trends in Cognitive Sciences, 10(7), 309–318.
Tenenbaum, J. B., Kemp, C., & Shafto, P. (2007). Theory-based bayesian models of inductive reasoning. Inductive reasoning: Experimental, developmental, and computational approaches (pp. 167–204).
Tiede, H. (1999). Identifiability in the limit of context-free generalized quantifiers. Journal of Language and Computation, 1(1), 93–102.
Touretzky, D. S. (1990). Boltzcons: Dynamic symbol structures in a connectionist network. Artificial Intelligence, 46(1), 5–46.
Trask, A., Hill, F., Reed, S. E., Rae, J., Dyer, C., & Blunsom, P. (2018). Neural arithmetic logic units. In Advances in neural information processing systems (pp. 8035–8044).
Tromp, J. (2007). Binary lambda calculus and combinatory logic. Randomness and Complexity, from Leibniz to Chaitin, 237–260.
Turing, A. M. (1937). Computability and \(\lambda \)-definability. The Journal of Symbolic Logic, 2(04), 153–163.
Ullman, T., Goodman, N., & Tenenbaum, J. (2012). Theory learning as stochastic search in the language of thought. Cognitive Development.
van Benthem, J. (1984). Semantic automata. In J. Groenendijk, D. d. Jongh, & M. Stokhof (Eds.), Studies in discourse representation theory and the theory of generalized quantifiers. Dordrecht, The Netherlands: Foris Publications Holland.
Van Der Velde, F., & De Kamps, M. (2006). Neural blackboard architectures of combinatorial structures in cognition. Behavioral and Brain Sciences, 29(01), 37–70.
Van Gelder, T. (1990). Compositionality: A connectionist variation on a classical theme. Cognitive Science, 14(3), 355–384.
Van Gelder, T. (1995). What might cognition be, if not computation? The Journal of Philosophy, 92(7), 345–381.
Van Gelder, T. (1998). The dynamical hypothesis in cognitive science. Behavioral and brain sciences, 21(05), 615–628.
Wagner, E. G. (1969). Uniformly reflexive structures: on the nature of gödelizations and relative computability. Transactions of the American Mathematical Society, 144, 1–41.
Watter, M., Springenberg, J., Boedecker, J., & Riedmiller, M. (2015). Embed to control: A locally linear latent dynamics model for control from raw images. In Advances in neural information processing systems (pp. 2746–2754).
Wellman, H. M., & Gelman, S. A. (1992). Cognitive development: Foundational theories of core domains. Annual Review of Psychology, 43(1), 337–375.
Whiting, D. (2006). Conceptual role semantics.
Wisniewski, E. J., & Medin, D. L. (1994). On the interaction of theory and data in concept learning. Cognitive Science, 18(2), 221–281.
Wolfram, S. (2002). A new kind of science (Vol. 1). Wolfram Media Champaign, IL.
Wong, Y. W., & Mooney, R. J. (2007). Learning synchronous grammars for semantic parsing with lambda calculus. In Annual meeting-association for computational linguistics (Vol. 45, p. 960).
Woods, W. A. (1968). Procedural semantics for a question-answering machine. In Proceedings of the December 9-11, 1968, fall joint computer conference, part I (pp. 457–471).
Woods, W. A. (1981). Procedural semantics as a theory of meaning. (Tech. Rep.). DTIC Document.
Xu, F. (2019). Towards a rational constructivist theory of cognitive development. Psychological Review, 126(6), 841.
Xu, F., & Tenenbaum, J. (2007). Word learning as Bayesian inference. Psychological Review, 114(2), 245–272.
Yildirim, I., & Jacobs, R. A. (2012). A rational analysis of the acquisition of multisensory representations. Cognitive Science, 36(2), 305–332.
Yildirim, I., & Jacobs, R. A. (2013). Transfer of object category knowledge across visual and haptic modalities: Experimental and computational studies. Cognition, 126(2), 135–148.
Yildirim, I., & Jacobs, R. A. (2014). Learning multisensory representations for auditory-visual transfer of sequence category knowledge: a probabilistic language of thought approach. Psychonomic bulletin & review (pp. 1–14).
Zettlemoyer, L. S., & Collins, M. (2005). Learning to Map Sentences to Logical Form: Structured Classification with Probabilistic Categorial Grammars. In UAI (pp. 658–666).
Zhang, Z., Cui, P., & Zhu, W. (2020). Deep learning on graphs: A survey. IEEE Transactions on Knowledge and Data Engineering.
Zylberberg, A., Dehaene, S., Roelfsema, P. R., & Sigman, M. (2011). The human turing machine: A neural framework for mental programs. Trends in Cognitive Sciences, 15(7), 293–300.
Acknowledgements
I am extremely grateful to Goker Erdogan, Tomer Ullman, Hayley Clatterbuck, Shimon Edelman, and Ernest Davis for providing detailed comments and suggesting improvements on an earlier draft of this work. Josh Rule contributed greatly to this work by providing detailed comments on an early draft, important discussion, and important improvements to Churiso’s implementation. Noah Goodman, Josh Tenenbaum, Chris Bates, Matt Overlan, Celeste Kidd, and members of the computation and language lab and kidd lab provided useful discussions relevant to these ideas. Research reported in this publication was supported by the Eunice Kennedy Shriver National Institute of Child Health & Human Development of the National Institutes of Health under award number R01HD085996-01 and award 2000759 from the National Science Foundation, Division of Research on Learning. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The author is also grateful to support from the network grant provided by the James S. McDonnell Foundation to S. Carey, “The Nature and Origins of the Human Capacity for Abstract Combinatorial Thought.”
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Sketch of Universality
Appendix A: Sketch of Universality
It may not be obvious that any statement about the relation between objects can be encoded into an LCL system. Here, I sketch a simple proof that this is possible when we are allowed to define what function composition means. My focus is on the high-level logic of the proof while attempting to minimize the amount of notation required. Let’s suppose that we are given an arbitrary base fact like,

We may re-write this into binary constraints, with a single variable on the left and a single function application on the right, by introducing “dummy” variables  ,
,  , etc:
, etc:

This is akin to Chomsky normal form for a context-free grammar.
The challenge then is to find a mapping from symbols to combinators that satisfies these expressions. A difficulty to note is that some variables, like  , may appear on the left and the right, meaning that their combinator structure must be the output of a function (appearing on the left) as well as a function that itself does something useful (on the right). To address this, the proof sketch here will assume that we are allowed to define the way functions are applied. For instance, instead of requiring
, may appear on the left and the right, meaning that their combinator structure must be the output of a function (appearing on the left) as well as a function that itself does something useful (on the right). To address this, the proof sketch here will assume that we are allowed to define the way functions are applied. For instance, instead of requiring  \(\rightarrow \)
\(\rightarrow \) , we will replace the function application
, we will replace the function application  with our own custom one,
with our own custom one,  . When
. When  , we are left with ordinary function application. I do not determine here if requiring
, we are left with ordinary function application. I do not determine here if requiring  permits universal isomorphism. But we can show that if we are free to choose
permits universal isomorphism. But we can show that if we are free to choose  , we can satisfy any constraints.
, we can satisfy any constraints.
With this change, we can re-write our base facts as,

With this addition, we can take each of the symbols ( and
and  ) and give them each an integer with Church encoding. Standard schemes for this can be found in Pierce (2002). Integers in Church encoding also support addition, subtraction, and multiplication. We may therefore view these facts as a set of integer-values, where
) and give them each an integer with Church encoding. Standard schemes for this can be found in Pierce (2002). Integers in Church encoding also support addition, subtraction, and multiplication. We may therefore view these facts as a set of integer-values, where  is a function from two (integer) arguments to a single (integer) outcome:
is a function from two (integer) arguments to a single (integer) outcome:

Note that at this point we may check if the facts are logically consistent—they may not state, for instance, that  \(\rightarrow \)
\(\rightarrow \) ,
,  \(\rightarrow \)
\(\rightarrow \) , and
, and  \(\ne \)
\(\ne \) .
.
Assuming consistency, we may then explicitly encode the facts by setting  to be a polynomial which encodes these facts. To see how this is possible, suppose we have constraints
to be a polynomial which encodes these facts. To see how this is possible, suppose we have constraints

It is well-known that in one dimension, any set of x, y points can be approximated by a polynomial. The same holds for two dimensions, with a variety of available techniques. This means that we can set  to be the combinator that implements the polynomial mapping each \(\alpha _i\), \(\beta _i\) to \(\gamma _i\) with the desired accuracy.
to be the combinator that implements the polynomial mapping each \(\alpha _i\), \(\beta _i\) to \(\gamma _i\) with the desired accuracy.
An alternative to 2D polynomials is to use Gödel numbering to convert the two-dimensional problem to a one-dimensional one. If  first converts its arguments to a single integer, for instance \(2^{\alpha _i} 3^{\beta _i}\), then the problem of finding the right polynomial reduces to a one-dimensional interpolation problem. Explicit solutions then exist, such as this version of Lagrange’s solution to the general problem,
first converts its arguments to a single integer, for instance \(2^{\alpha _i} 3^{\beta _i}\), then the problem of finding the right polynomial reduces to a one-dimensional interpolation problem. Explicit solutions then exist, such as this version of Lagrange’s solution to the general problem,

To check this, note that when \(i=j\), the fractions inside the product cancel and the coefficient for \(\gamma _j\) becomes 1. However, when \(i \ne j\), then there will be some numerator term which is zero, canceling out all of the other \(\gamma _m\). Together, these give the output of  as \(\gamma _i\) when given \(\alpha _i\) and \(\gamma _i\) as input.
as \(\gamma _i\) when given \(\alpha _i\) and \(\gamma _i\) as input.
Note that this construction does not guarantee sensible generalizations when running  on new symbols. The specific patterns of generalization will depend on how symbols are mapped to integers, but more problematically, polynomial interpolation famously exhibits chaotic or wild behavior on points other than those that are fixed, a fact known as Runge’s phenomenon (Runge 1901). As a result, the polynomial mapping should be taken only as an existence proof that some mapping of combinators will be able to satisfy the base facts, or the combinatory logic can in principle encode any isomorphism when we define function application with
on new symbols. The specific patterns of generalization will depend on how symbols are mapped to integers, but more problematically, polynomial interpolation famously exhibits chaotic or wild behavior on points other than those that are fixed, a fact known as Runge’s phenomenon (Runge 1901). As a result, the polynomial mapping should be taken only as an existence proof that some mapping of combinators will be able to satisfy the base facts, or the combinatory logic can in principle encode any isomorphism when we define function application with  .
.
Rights and permissions
About this article
Cite this article
Piantadosi, S.T. The Computational Origin of Representation. Minds & Machines 31, 1–58 (2021). https://doi.org/10.1007/s11023-020-09540-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11023-020-09540-9


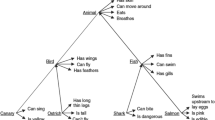


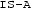 ,
,  ,
, 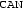 ) and observable attributes (e.g.
) and observable attributes (e.g.  ,
, 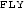 ,
,  ) as activation patterns on individual nodes. There, the puzzle is: what precisely makes it the case that activation in one node means (whatever that means)
) as activation patterns on individual nodes. There, the puzzle is: what precisely makes it the case that activation in one node means (whatever that means) 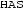 as opposed to
as opposed to  ?
?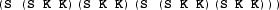 .
.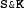 model does not inherently know it is dealing with a dominance hierarchy. Cases of dominance hierarchies in animal cognition may have a better chance of being innate, or at least higher prior than other alternatives.
model does not inherently know it is dealing with a dominance hierarchy. Cases of dominance hierarchies in animal cognition may have a better chance of being innate, or at least higher prior than other alternatives.