Abstract
Shear strength is a crucial property of soils regarded as its intrinsic capacity to resist failure when forces act on the soil mass. This study proposes an advanced meta-leaner to discern the shear strength property and generate a reliable estimation of the ultimate shear strength of the soil. The proposed model is named as metaheuristic-optimized meta-ensemble learning model (MOMEM) and aims at helping geotechnical engineers accurately predict the parameter of interest. The MOMEM was established with the integration of the artificial electric field algorithm (AEFA) to dynamically blend the radial basis function neural network (RBFNN) and multivariate adaptive regression splines (MARS). In the framework of forming MOMEM, the AEFA consistently monitor the learning phases of the RBFNN and MARS in mining soil shear strength property through optimizing their controlling parameters, including neuron number, Gaussian spread, regularization coefficient, and kernel function parameter. Simultaneously, RBFNN and MARS are stacked via a linear combination method with dynamic weights optimized by the AEFA metaheuristic. The one-tail t test on 20 running times affirmed that with the greatest mean and standard deviation of RMSE (mean = 0.035 kg/cm2; Std. = 0.005 kg/cm2), MAE (mean = 0.026 kg/cm2; Std. = 0.004 kg/cm2), MAPE (mean = 7.9%; Std. = 1.72%), and R2 (mean = 0.826; Std. = 0.055), the MOMEM is significantly superior to other artificial intelligence-based methods. These analytical results indicate that MOMEM is an innovative tool for accurate calculating soil shear strength; thus, it provides geotechnical engineers with reliable figures to significantly increase soil-related engineering design.
Similar content being viewed by others
1 Introduction
The soil shear strength can be defined as the magnitude of shear stress that soil is capable of withstanding [1]. In civil engineering, the shear strength of soils is fundamental for describing their susceptibility to applied pressures from building loads and construction machines/equipment. Geotechnical engineers use shear strength of soil as an essential factor to evaluate the stability of structure on or embedded in the ground, such as retaining walls, embankments, airfield pavements, and foundations of a high-rise building [2]. Therefore, obtaining an accurate estimation of the shear strength of soil is a highly important task in various geotechnical designs [3,4,5].
In practice, computing this parameter of interest faces various difficulties. It is because the mapping function between the shear strength and soil properties has been proved to be complicated [6,7,8,9,10,11,12]. Freitag [13] found that there is a complicated dependency between soil strength and properties of moisture content and bulk density; thus, estimation of soil strength based on such factors is by no means an easy task. Conventional estimations of shear strength are dependent of in the values of the cohesion (c) and the angle of internal friction (φ). However, there are inconsistencies in the values of the cohesion and the angle of internal friction for a particular soil [14].
Fredlund et al. [15] attempted to capture the variation of the soil shear via a soil-water characteristic curve and the saturated shear parameters of soil [15]. However, the closed-form predictions are not applicable to all types of soils. Gao et al. [3] pointed out that the shear strength of soil varies significantly with different soil types. Moreover, performing laboratory tests (e.g., applied triaxial equipment) to estimate the shear strength of soils is also found to be both time-consuming and costly due to the employments of instruments as well as highly trained technicians [16].
Due to such challenges, alternative methods based on advanced machine learning models have been recently proposed to deal with the task of soil shear strength prediction. Based on existing samples collected from laboratory tests, intelligent models can be developed and train to perform shear strength calculations automatically and instantly. Based on a direct comparison between actual testing outcomes and results predicted by those intelligent models, the reliability of machine learning models can be objectively judged.
Adaptive neuro-fuzzy inference system (ANFIS) has been employed to predict the shear strength of unsaturated soils [17]. This fuzzy neural network model is shown to be a capable tool for dealing with the problem of interest. A hybrid model consisting of artificial neural networks and support vector machines with various ensemble strategies (i.e., voting, bagging, and stacking) has been proposed by Chou and Ngo [18] to compute the strength of fiber-reinforced soil. Chen et al. [19] proposed a modified linear regression method for modeling the variation of shear strength based on soil properties. Mbarak et al. [20] predict the undrained shear strength of soil with the utilizations of random forest, gradient boosting and stacked models.
Recently, metaheuristic approaches have been increasingly harnessed to create intelligent models to copy with the task at hand. Pham et al. [21] replaced the conventional gradient descent based algorithm used for training ANFIS models by well-established metaheuristic algorithms, including particle swarm optimization and genetic algorithm. Tien Bui et al. [22] recently combines the least square support vector machine and metaheuristic method of cuckoo search optimization for predicting the shear strength parameter of soft soil. Moayedi et al. [23] investigated the feasibility of spotted hyena optimizer and ant lion optimization for training neural networks used for estimating the soil parameter of interest. Nhu et al. [24] establish an integrated model of support vector regression and particle swarm optimization relying on various soil features such as moisture, density, components, void ratio, and water content. The dragonfly algorithm, whale optimization algorithm, invasive weed optimization, elephant herding optimization, shuffled frog leaping algorithm, salp swarm algorithm, and wind-driven optimization models have been employed to construct capable neural network-based prediction models [25, 26]; Metaheuristic has shown their capability of improving predictive accuracy of neural network models by annihilating the drawback of conventional backpropagation and gradient descent methods [27,28,29].
Besides, in the fields of data science and civil engineering, there is an increasing trend of applying ensemble learning methods to solve complex data modeling tasks [18, 30,31,32,33]. This novel approach of machine learning employs multiple learning paradigms to construct combined models featuring excellent predictive capability. Ensemble models have been shown to attain better prediction accuracy and alleviate the overfitting phenomenon [34,35,36,37]. A machine learning ensemble is generally constructed by aggregating results produced by several alternative models; therefore, the trained ensemble model often has good flexibility in data modeling and strong resilience to noise [38,39,40].
Following these two trends of research, this study proposes a novel metaheuristic optimized machine learning ensemble approach for predicting the soil shear strength. The ensemble includes the two capable individual machine learning methods of the radial basis function neural network (RBFNN) [41, 42] and multivariate adaptive regression splines (MARS) [43, 44] which are powerful tools for nonlinear and multivariate data modeling. The two techniques also present different types of machine learning; thus, they are likely to contribute their reciprocal strengths and cover weakness of each other in building a meta-ensemble model with an outstanding efficiency [45]. In this integrated framework, individual RBFNN and MARS models are trained and their prediction results are combined via the stacking aggregation method [35].
In addition to simultaneously tuning hyper-parameters for constituent models in the ensemble model, the weights of each individual model’s output must be determined adaptively. The training phase of the proposed meta-ensemble model is further enhanced by the employment of the artificial electric field algorithm (AEFA)—a state-of-the-art metaheuristic approach. The AEFA [46] is inspired by the concept of the electric field, charged particles, and the Coulomb’s law of electrostatic force. This algorithm has achieved competitive performances against other optimization methods in terms of both solution quality and convergence speed. Hence, the AEFA surely optimizes the performance of the stacking method-based ensemble model by simultaneously searching for the most suitable set of hyper-parameter values and weights of constituent models.
A dataset of 249 data samples collected from the geotechnical investigation process in Hanoi (Vietnam) is used to train and test the proposed approach. The variables of the depth of the sample, sand percentage, loam percentage, clay percentage, moisture content percentage, wet density, dry density, void ratio, liquid limit, plastic limit, plastic index, and liquidity index are employed as influencing factors.
All in all, the goal of this research is to construct and verify a hybrid Metaheuristic-optimized meta-ensemble learning model, denoted as MOMEM, to enhance the prediction accuracy of the soil shear strength. The contribution of this study is multifold: (1) a novel machine learning ensemble for predicting soil shear strength is proposed; (2) the model is adaptively constructed with the employment of the AEFA metaheuristic; (3) a superior predictive performance is achieved compared to other benchmark machine learning models. The rest of the study is organized as follows: the collected dataset is described in the second section. The next section reviews the research method, followed by a section that presents the newly developed machine learning framework. Experimental results and comparisons are reported in the fifth section. The final section provides several concluding remarks of the study.
2 The collected dataset
The dataset used in the present study was collected at the geotechnical investigation phase of the Le Trong Tan Geleximco Project, located in the west of Hanoi, Vietnam (Fig.1). The site investigation was conducted in April 2009. This project covers an area of approximately 135 ha, which was used for the construction of low-rise housing, high-rise housing, public infrastructures, and entertainment centers. In order to gather information on the soil conditions, the boring-based soil sampling is utilized. The boreholes are drilled by means of slurry (a mixture of bentonite and water), and thin-walled metal tubes to ward off soil collapses. The soil samples with a diameter of 91 mm are gathered by the method of piston samplers. The sample collection process complies with the Vietnamese national standards of the TCXDVN-194-2006 (High Rise Building—Guide for Geotechnical Investigation), the TCN-259-2000 (the procedure for soil sampling by boring methods).
There were 65 boreholes with a total of 249 soil samples collected from the geotechnical investigation process. The depth of the collected soil samples ranges from 1.20 to 39.5 m. The factors measured from soil samples are (1) depth of sample (m), (2) sand percentage (%), (3) loam percentage (%), (4) clay percentage (%), (5) moisture content percentage (%), (6) wet density (g/cm3), (7) dry density (g/cm3), (8) void ratio, (9) liquid limit (%), (10) plastic limit (%), (11) plastic index (%), and (12) liquidity index. These 12 factors are employed as conditioning variables to estimate the shear strength of the soil. Descriptive statistics of the soil variables in this study are shown in Table 1. Figure 2 graphically presents a correlation of soil-shear-strength with its conditioning factors.
3 Methodology
3.1 Radial basis function neural network (RBFNN)
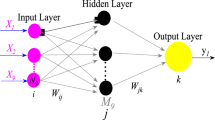
A typical structure of a RBFNN model [41, 42] used for nonlinear function approximation consists of three layers and is graphically presented in Fig. 3. The first layer has a number of neurons equal to the number of influencing factors, which is equal to 12 in this study. The next layer comprises a set of radial basis function (RBF) neurons, which are basic units of information processing. This neuron employs the RBF, which is an attenuation, central-radial symmetry, non-negative, non-linear function. It is noted that all functions that are dependent only on the distance from a center vector are radially symmetric about that vector. The last layer, which is the output layer, yields the network output by performing a linear combination of outputs produced by units in the second layer.
The RBF used in the second layer is mathematically presented as follows [47]:
where \(v\) and \(\sigma\) denote the parameter of position and width, respectively, of the RBF nodes.
It is proper to note that the number of output neurons in this study is 1, which is the shear strength of the soil. Accordingly, the soil shear string can be computed via the RBFNN model as follows [48,49,50]:
where x = (x1, x2, …, xu) denotes an u-dimensional vector; x − νj is Euclidean distance between the center of the jth hidden node and a data point; wj represents the connecting weight from the jth hidden node to output layer; b is the bias term; Nn denotes the number of hidden neurons; \(\varphi_{j} \left( \bullet \right)\) is the radial basis function of the jth hidden note.
It is noted that the model construction phase of the RBFNN model requires a proper determination of the number of neurons (Nn) and the RBF width (σ). An appropriate set of Nn and σ ensures the success of establishing a robust RBFNN model used for soil shear strength estimation. The parameter Nn dictates the architecture of the inference model, resulting to either the over-fitted (in case of too many RBF nodes assigned) or under-fitted model with low accuracy (in case of having a small number of RBF nodes) [51, 52]. Additionally, the parameter σ affects the influence of RBF nodes on each data point; therefore, it determines the generalization of the prediction model.
3.2 Multivariate adaptive regression splines
MARS was developed by Friedman [43], which is formed by fitting basic function (term) to distinct intervals of input variables. In general, splines (also called piecewise polynomials) have pieces smoothly connected with joining points called knots (k). MARS uses two-sided truncated power functions as spline basis functions, described as Eqs. (3) and (4):
where \(\begin{array}{*{20}c} {(q} \\ \end{array} \ge 0)\) is the degree the resultant function estimate; \([]_{ + }\) indicates to take positive values.
An interaction term is yielded by multiplying an existing term with a truncated linear function having a new attribute. Accordingly, both the existing term and the newly created interaction term are involved in the construction MARS model. The search for new terms is limited in a maximum order of the user. The formula of interaction term and the general MARS function can be referred to Eqs. (5) and (6), respectively:
where Km is the number of truncated linear functions multiplied in the mth term. Km is less than maximum interaction among variables Imax that is pre-defined by the user. xv(m,j) is the input variable corresponding to the jth truncated linear function in the mth term; km,j is the knot value of xv(m,j); sm,j is the selected sign + 1 or − 1; \(\hat{y}\) is the dependent variable predicted by the MARS model; c0 is a constant; Tm(x) is the mth term, which may be a single spline basis functions; and cm is the coefficient of the mth term.
A MARS model is constructed through a two-stage process including a forward phase and backward phase. The forward phase adds terms until the maximum number of terms is reached which is pre-assigned by users (Tmax). This phase aims at reducing the sum-of-squares residual error and tends to result in the complex and over-fitted model. Hence, it needs to have a backward phase to remove the redundant terms with less impact on the model’s generalization. The generalized cross-validation (GCV) was introduced as a criterion to recognize those redundant terms as shown in Eq. (7):
where n is the number of data patterns. C(M) is a dynamic complexity penalty defined as Eq. (8):
where M is the number of terms in Eq. (8); the parameter d is a penalty for each term added into the model and pre-assigned by the user. Notably, a suitable value of d can lead to an under-fitted or over-fitted model with poor generalizability [53,54,55]. In general, Tmax, Imax, and d are regarded as essential factors to control the MARS model’s performance.
3.3 Artificial electric field algorithm
Artificial electric field algorithm was developed by [46] which is inspired by the Coulomb’s law of electrostatic force, stated that an electrostatic force between two charged particles is directly proportional to the product of their charges and inversely proportional to the square of the distance between their positions. In the AEFA, an agent is regarded as a charged particle and its strength is measured by electric charge. A particle can either attract or repel others by an electrostatic force which is used as a means of communication channel among particles. A particle with better fitness will possess a greater electrostatic force. In the AEFA, the attractive electrostatic force is regulated that a charged particle with the greatest charge attract all other particles of lower charge and move slowly in the search space. Figure 4 presents the flowchart of the AEFA.
The AEFA first randomly locates of N particles in d-dimensional search space with the position of ith particle presented as Xi = [x 1i , x 2i , x 3i , …, x di ] with \(i \in [1, 2, 3, \ldots , N]\). The position of the particle ith at time t is given by the following equation:
The location of the best particle with the greatest fitness is denoted by Pbest = Xbest. The force acting on the charge ith from charge jth is calculated as follows:
where Qi(t) and Qj(t) are the charges of ith and jth particle at any time t, respectively; K(t) is the Coulomb’s constant at any time t; ϵ is a positive constant; and Rij(t) is the Euclidian distance between the ith particles and the jth particle. The Coulomb’s constant K(t) is given as follows:
where α and K0 are a constant value and initial value, respectively; iter is the current iteration and maxiter is the maximum number of iterations.
The total electric force acts on the ith particle by all the other particles is given by the following equation:
where rand() is an uniform random number in the range of [0 1].
The electric field of the ith particle at any time t is given by the following equation:
The acceleration of the ith particle at any time t is given by the following equation:
where Mi(t) is the unit mass of the ith particle at any time t. The velocity and position of the ith particle are updated as follows:
where rand() is a uniform random number in the interval [0, 1].
The charge of a particle is calculated based on the fitness functions with an assumption of equal charge for all particles as shown in Eq. (10). Fundamentally, the charge of the best particle should have the greatest value while other particles have charge values in the range of [0 1]. Hence, the particle with a larger charge has a greater force for the best fitness value:
where fiti is the fitness value of ith particle at any time t; best(t) = min(fiti(t)) and worst(t) = max(fiti(t)).
4 The proposed metaheuristic-optimized meta-ensemble learning model for soil-shear-strength estimation
This section describes the overall structure of the metaheuristic optimized machine learning ensemble, named as MOMEM, used for predicting the soil shear strength. The proposed model consists of the RBFNN and MARS machine learning models. The construct a robust prediction approach, the AEFA metaheuristic is employed to optimize the hyper-parameters of the RBFNN and MARS. Besides, the dynamic weight values for model members involved in the ensemble MOMEM are also automatically determined by the AEFA method. The general workflow of the proposed MOMEM for estimating the shear of soil is presented in Fig. 5.
4.1 Initiative phase
As presented in Fig. 5, the initialization phase uses purely the training data for the construction. Since greater numeric ranges tend to result in undesirable bias in the construction of a machine learning model; therefore, all attribute values are converted into the same range of [0, 1] so that these attributes are fed to the construction process of a machine learning with the equal weight. Herein, the convertion uses the normalization method with the equation presented in Eq. (20). It is worth noticing that the study employed 10-cross validation method to divide the whole dataset. Hence, the training dataset is the result of gathering 9 of 10-crossing folds. The remaining fold is used for testing the trained machine learning model. The training dataset is then partitioned into two sets; one set with 70% of data patterns is employed to trained model; another set with the remaining 30% of data patterns is used to validate the newly trained model:
where xi,j is a data value of the attribute jth, xj,min is the lowest value for the attribute jth, xj,max is the highest value for the attribute jth, and x trani,j is the transformed value of the attribute jth.
Parameters in the MOMEM are composed of a number of member inference models integrated into and their controlling parameters. Hence, the framework of blending machine learners leads to an increase of parameter numbers along with the increase of involved inference models. In this study, reciprocal merits of the MARS and RBFNN are blended to establish the MOMEM, there are seven parameters (Nn, σ, Mmax, d, Imax, α, and β) that need to be simultaneously fine-tuned to attain the optimal configuration of MOMEM with ultimate generalizability. In this phase, each of all seven parameters initially was assigned many random values in an extensive range to have an evaluation basis for the searching loop at the next phase. The searching boundary for each parameter is set to be sufficiently large to cover all potentially suitable values of concerned parameters and shown in Table 2.
4.2 Searching phase
At steps 1.1 and 1.2, member models will receive values of parameter generated by the AEFA searching engine to proceed with the construction of inference models by using partitioned training data that is processed at the previous phase. This is the construction process of many model candidates and thus inevitably consumes time most compared to other steps. Further, more inference models blended in this meta-ensemble learning framework will entail more computational time. In the MOMEM, particularly, the RBFNN model and MARS model are established independently with AEFA-assigned parameter values (Nn and σ) and (Mmax, Imax and d), respectively. Eventually, the trained models generate the prediction values of all data points for training and testing sets. It should be emphasized that these parameter values purposely attain the greatest prediction accuracy for the proposed meta-learning model, the MOMEM, rather than individual models. It is important to note that many new models are created to potentially replace the old ones at each iteration.
As mentioned previously, the final prediction values of the MOMEM is calculated by summing up the predictive values of blended member models multiplied with their dynamic weight of the corresponding models. Notably, values of dynamic weights (α and β) express the influencing level of the corresponding constituent models on the final prediction values of the MOMEM which are tuned by the AEFA searching engine in the standardized range of [0, 1] as shown in Table 3. Formulas of merging predictive values are expressed in Eq. (21). It is noted that the traditional stacking ensemble method; all member models are assumed to have an equal role, which is expressed by the average weight assigned [56]. These subjective average values may diminish the generalizability of the ensemble model. Further, the AEFA searching engine can automatically discard any member models by assigning a dynamic weight of 0 if it recognizes those models undermine the accuracy of the MOMEM. At that time, the MOMEM becomes a single hybrid machine learner:
where pMNVIM, pRBFNN, and pLSVR indicate the prediction values of the MOMEM, RBFNN, and MARS, respectively; α and β are the dynamic weight of the RBFNN and MARS, respectively.
Setting an appropriate objective function for the AEFA searching engineer is crucial to obtain a robust meta-learner successfully. Many joined individual models along with the support of the AEFA are likely to purely minimize the training error that causes the final model to be trapped at the over-fitting problem. It is worth noticing that this well-fitting model has poor generalizability since it is over-trained with a high-complex degree to fit the training data only [57]. Inspired by successes of other works [58,59,60,61], this study put forward an objective function expressed by a sum of validation error and training error, as shown in Fig. 5. The present study prefers to employ the root mean square error (RMSE) for the objective functions because this evaluation criterion has an additional feature of reducing the number of large biases between actual values predictive values. The AEFA searching engine thus needs to reduce the sum of RMSE of training and validation concurrently as shown in Eq. (22). The offered objective function is thus expected to alleviate the effect of over-fitting, increase the generalizability of the MOMEM, and reduce the number of large undesirable biases. Hence the concerned issued may be stroked efficiently:
The set of parameter values (Nn, σ, Mmax, Imax, d, α, and β) will be synchronously adjusted by the transformation procedure of AEA. A bad set of values is replaced by better ones based on the obtained values of the objective function. Therefore, the values of tuning parameters will be progressively improved after each loop. Accordingly, the learnability and generalizability of the MOMEM are progressively improved after each searching loop. The AEFA will select the best tuning parameters, i.e., for each searching loop, those that provide the lowest value of fitness function. The AEFA shall memorize the suitable sets of parameters and extend the searching loop to meeting the stopping criterion. This study used the iteration number of 50 as the stopping criterion.
4.3 Optimal meta-learner and application phase
The searching process halts when the stopping condition is met, indicating that the optimal set of tuning parameters (Nn, σ, Mmax, Imax, d, α, and β) is available to train MOMEM with the entire training dataset. The trained MOMEM is then saved to perform prediction tasks for the testing phase or generate prediction value for new data input. It is recommended to update and re-train when having enough number of new data. More data of soil-shear-strength enable MOMEM to further discover more underline features of soil-shear-strength thus reaching closer to the underlying function of soil’s shear strength.
5 Experimental results and discussions
5.1 Performance evaluation criteria
The performance of an AI-based inference model should be evaluated and compared based on many criteria that are required to cover different aspects comprehensively. This ensures the conclusion of the assessment to be reliable. This study uses root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and determination of coefficient (R2) to benchmark performance of the MOMEM against other models.
In detail, MAPE displays the model accuracy in the type of percentage that spots the high errors of the small actual values. RMSE highlights the undesirably sizable biases among actual values and predictive values, while MAE gives an average of the prediction bias with equal weight to all errors. The greater models will attain smaller values of RMSE and MAE. Meanwhile, R2 indicates the capability of the model in reasonably inferring future outcomes with the highest value of 1. Formulae of RMSE, MAPE, MAE, and R2 are expressed as Eqs. (23)–(26):
where SST= total of sum square errors; SSR = sum of square residual errors; pi = predicted value; yi = actual value; \(\bar{y}\) = average of actual value; and n = number of data patterns.
5.2 Experimental results and discussion
In order to avoid the bias in the data partition process, a tenfold cross-validation approach is applied for the splitting dataset [62]. Thus, all data patterns will be in turn assigned in both training and testing sets. Since this study compares AI-inference models based on statistical methods with mean and standard deviation, all models will perform the prediction task on 20 run times. Hence, the ten crossing folds are used twice. The models were run in MATLAB environment version 2018a [63].
Table 3 displays the performance of the MOMEM on the soil-shear-strength for 20 run times. As seen in the table, the MOMEM attains a very high accuracy for inferring values of soil-shear-strength which is expressed by the relatively low average values of RMSE (0.035 kg/cm2), MAPE (7.94%), and MAE (0.026 kg/cm2) in the testing phase. Further, the low values of the standard deviation of those criteria strongly confirm that the high performance of MOMEM is retained stable and exiguously affected by the data partition. Interestingly, there are a slight difference between the values of evaluation criteria between the testing phase and the training phase. Particularly, the absolute deviations of MAPE and RMSE at the two phases are only 0.25% and 0.003 (kg/cm2), respectively. These facts indicate that the over-fitting issue is addressed efficiently in the MOMEM by summarizing the training and validation errors in the objective function.
Sets of parameter values found on 20 run times are shown in Table 4. Surprisingly, the values of all parameters vary in large ranges. Especially, the optimal spread of Gaussian function in RBFNN lies from 0.018 to 4.979 while the maximum number of neurons is 60 that is as many as ten times of minimum number, respectively. Those changes are obviously interpreted as to grasp the different characters of each training and validation dataset. Apparently, the chance of the trial-and-error method or experience-based parameter setting to successfully determine the optimal configuration of MOMEM is limited.
As exhibited in Fig. 6, there is a change of the member model’s role in the MOMEM which is identified by the values of α and β found in a range of [0 0.997]. Especially, the RBFNN absolutely dominated the MARS in the construction of MOMEM in the 16th run when α and β are found as 0.997 and 0, respectively. Inversely, the RBFNN was discarded in the final MOMEM in the 12th run and the 17th run. The values of dynamic weights assigned to be 0 dedicated that the corresponding constituent model (RBFNN or MARS) was recognized to impair the accuracy of the MOMEM model; thus, the final prediction values of the MOMEM were produced by the only one of two constituent models (RBFNN or MARS). Accordingly, the MOMEM becomes a pure hybrid of the AEFA with the RBFNN or with the MARS, abbreviated as AEFA-RBFNN and AEFA-MARS, respectively.
It is worth noticing that found values of parameters lie in the middle of pre-defined ranges, indicating the boundary of each range was sufficient to cover all the potential values of parameters. Figure 7 exhibits the convergence curves of the particular run, which demonstrated the AEFA to have a rapid convergence. In detail, the optimal values were able to be found at approximately iteration 35 out of 50, which affirmed that the fittest values are always determined before the stopping condition is met.
5.3 Result comparison and discussion
It is necessary to compare the performance of the developed models against that of other AI-based inference models so that the role of techniques in MOMEM is clearly clarified. RBFNN, MARS, generalized regression neural network (GRNN), and support vector regression with Gaussian function (kernel function) (SVRgau) are selected because they present a different type of machine learner and highly perceived in solving engineering-related issues in the literature. AEFA-MARS and AEFA-RBFNN, and traditional MARS + RBFNN ensemble models are selected in the comparison to quantify the contribution of each technique integrated into MOMEM. All models were run on MATLAB environment 2018a [63] with the trial-and-error method to find the potentially suitable configuration. The interface platforms are presented in Fig. 8.
The statistical results shown in Table 5 have demonstrated the proposed model, MOMEM, as the greatest model by achieving the greatest values in terms of RMSE (0.035 kg/cm2), MAPE (7.94%), MAE (0.026 kg/cm2). Those values are much lower than that of the second-best model, the AEFA-RBFNN, which attains values of RMSE, MAPE, MAE of 0.039 kg/cm2, 9.05%, 0.029 kg/cm2, respectively, in the testing phase. As measured, there are at least 11.4 and 11.5% improvement in terms of RMSE and MAE, respectively, when using MOMEM to predict soil-shear-strength rather than the use of the AEFA-RBFNN and the AEFA-MARS (third-best model). Notably, in machine learning, the generalizability of a model is the first priority since it presents the ability of the model to infer new facts. It is thus acceptable as MOMEM obtained higher values of RMSE (0032 kg/cm2), MAE (0.026 kg/cm2), MAPE (7.69%) than the AEFA-RBFNN and the AEFA-MARS in the training phase.
In comparison with traditional the MARS + RBFNN ensemble model, MOMEM expresses as a dominant model because it reduces values of RMSE and MAE up to 16 and 23%, respectively. These numbers affirmed that the AEFA searching engine and re-defined dynamic weights already fulfilled the gap of performance of the traditional ensemble method. The statistical results revealed that using conventional single machine learners, including the MARS, RBFNN, GRNN, and SVRgau, models are not efficient in diminishing of bias in predicting soil-shear-strength.
A cause-and-effect relationship between the soil’s shear strength and its attributes will lead to a high value of R2, meaning that the MOMEM mapped a closer underlying function of soil’s shear strength by gaining the greatest value of R2 (0.864 and 0.826 for training and testing phase, respectively). In other words, 82.6% of data patterns can be inferred by MOMEM-mapped function while it is only 77.7% for the second-best model, the AEFA-RBFNN. Figure 9 presents the actual-versus-prediction value of all data patterns in the testing phase. Generally, the obtained results have firmly proved a possibility of boosting the accuracy of soil-shear-strength estimate by integrating the AEFA in the fusion of the MARS and the RBFNN.
5.4 One-tail t test method for examining the mean difference
This study further conducted a one-tailed t test to test for the significant differences of the MOMEM’s performance in estimating shear strength of soil against that of other AI models. The one-tailed t test was calculated on the root mean absolute error (RMSE) values with an equal size of 20 samples (run times) and unknown variances. It is worth noting that the RMSE sample is assumed to have a normal distribution. The procedure for implementing one-tailed t test is as follows:
-
\(H_{0}{:}\quad {\text{MAPE}}_{\text{MOMEM}} - {\text{MAPE}}_{\text{others}} = 0\)
-
\(H_{1}{:}\quad {\text{MAPE}}_{\text{MOMEM}} - {\text{MAPE}}_{\text{others}} < 0\)
where n is the number of samples (n = 20); ν is the degree of freedom; s 21 and s 22 are the unbiased estimators of the variances of the two samples; the denominator of t is the standard error of the difference between two means \(\bar{x}_{1}\) and \(\bar{x}_{2}\) (average).
Calculated results with a confidence level of 95% (α = 0.05) are presented in Table 6. For all cases, t statistic < − t-critical one-tailed (− 1.69), indicating MOMEM significantly outperformed other models in reducing RMSE values of soil-shear-strength. This conclusion may be manifested in Fig. 10. In conjunction with a robust performance demonstrated as analyzed above, the MOMEM has no request for setting up its configuration in the soil-shear-strength estimate process. In general, Analysis results support the MOMEM as the best choice for civil engineers; this model is able to yield reliable estimate values of soil’s shear strength.
In order to achieve efficiency, the construction of the MOMEM using the hybrid of several AI techniques inevitably increases the complexity of the model structure. Thus, the MOMEM needs more computation time than other models in the model construction process. Considering the many obtained benefits, including significantly improved prediction accuracy of soil-shear-strength and user-friendliness, the additional computation time is justified and acceptable.
6 Concluding remarks
The shear strength is the maximum resistance or stress that a particular soil can offer against failure over its improper surface loading. The shear strength of soils is essential for any stability analysis. Therefore, it is crucial to determine the reliable values of soil-shear-strength. A novel meta-learner was created based on the framework, called Metaheuristic-optimized meta-ensemble learning model (MOMEM) which was a combination of the RBFNN, the MARS, and the AEFA search engine. In the MOMEM, AEFA applies its optimization procedure to organize suitable configuration of the inference model member, including RBFNN (Nn and σ) and MARS (Mmax, Imax, and d) through adjusting model’s control parameters. Simultaneously, AEFA finetunes the model weights of RBFNN and MARS (α and β) to eventually generate prediction values of the MOMEM which is calculated by the sum of member models predictive values multiplied with their corresponding model weights.
The performance of the MOMEM is validated based on 240 data patterns of soil-shear-strength that were collected during the site investigation in the Le Trong Tan Project, Hanoi, Vietnam. The statistical results of 20 run times based on a tenfold cross-validation technique display that MOMEM is the best model in predicting shear strength of soil by attaining greatest values in terms of RMSE (mean = 0.035 kg/cm2; Std. = 0.005 kg/cm2), MAE (mean = 0.026 kg/cm2; Std. = 0.004 kg/cm2), MAPE (mean = 7.9%; Std. = 1.72%), and R2 (mean = 0.826; Std. = 0.055). The one-tail t test endorsed that the obtained results are significantly better than that of other comparative AI models, including variants of the RBFNN, the MARS, the conventional RBFNN + MARS ensemble, and the SVReg.
The findings demonstrated that the AEFA searching engine can autonomously determine the best set of parameter values to adaptively exploit features of each training dataset. The AEFA is able to recognize and discard a model member that damages the accuracy of the MEMOM. At that time, the MEMOM becomes a purely single hybrid model of a metaheuristic algorithm and a machine learner. In summary, the AEFA plays an integral role in selecting the merits of RBFNN and MARS to make them the best fit in the MOMEM.
This study is the first to put forward a novel stacking techniques-based ensemble model of hybridizing MARS and RBFNN that represent different types of learners in the field of machine learning for sharing reciprocal merits in the meta-ensemble model. Additionally, the present study lifted the operation of ensemble model to a higher level by integrating a robust metaheuristic optimization algorithm, AEFA, to ascertain automatically attaining the maximum performance of the model combination. With the success of employing MOMEM for addressing the soil-shear-strength prediction problem, this study further contributes a novel framework of establishing metaheuristic stacking technique-based ensemble model which is expected to inspire scholars to create new models for solving other practical problems.
Despite possessing many advantages, the MOMEM also has two weaknesses: First, the MOMEM performs the inference process as a black box since the mapped functions of soil-shear-strength is not visually formulated. Second, the model construction needs a long time due to the optimization process and two inference models involved in the trained process. However, the computational time problem can be sharply shortened by using modern high-speed computers. Further, once the optimal model is found, it can quickly infer the outcome of new data patterns and saved for use in a long time. The saved model should be updated with new data points collected which is also a work for authors to implement in the future.
References
Das BM, Sobhan K (2013) Principles of geotechnical engineering. Cengage Learning, Stamford. ISBN-10:1133108660
Vanapalli SK, Fredlund DG (2000) Comparison of different procedures to predict unsaturated soil shear strength. In: Advances in Unsaturated Geotechnics, Proceedings. Sessions Geo-Denver 2000, Geotech. Special Publ, vol. 99. pp 195–209 ASCE, Reston, Virginia
Gao Y et al (2020) Predicting shear strength of unsaturated soils over wide suction range. Int J Geomech 20(2):04019175
Li X et al (2019) Learning failure modes of soil slopes using monitoring data. Probab Eng Mech 56:50–57
Eid HT, Rabie KH (2017) Fully softened shear strength for soil slope stability analyses. Int J Geomech 17(1):04016023
Katte V, Blight G (2012) The roles of solute suction and surface tension in the strength of unsaturated soil. Springer, Berlin
Leong EC, Nyunt TT, Rahardjo H (2013) Triaxial testing of unsaturated soils. Springer, Berlin
Eslami A, Mohammadi A (2016) Drained soil shear strength parameters from CPTu data for marine deposits by analytical model. Ships Offshore Struct 11(8):913–925
Yavari N et al (2016) Effect of temperature on the shear strength of soils and the soil–structure interface. Can Geotech J 53(7):1186–1194
Ching J, Hu Y-G, Phoon K-K (2016) On characterizing spatially variable soil shear strength using spatial average. Probab Eng Mech 45:31–43
Cao Z, Wang Y (2014) Bayesian model comparison and characterization of undrained shear strength. J Geotech Geoenviron Eng 140(6):04014018
Chen C et al (2019) The drying effect on xanthan gum biopolymer treated sandy soil shear strength. Constr Build Mater 197:271–279
Freitag DR (1971) Methods of measuring soil compaction. In: Barnes KK et al (eds) Compaction of agricultural soils. ASAE, St. Joseph, pp 47–103
Ohu JO et al (1986) Shear strength prediction of compacted soils with varying added organic matter contents. Trans ASAE 29(2):351–0355
Fredlund DG, Vanapalli SK, Pufahl DE (1995) Predicting the shear strength function for unsaturated soils using the soil-water characteristic curve. In: Proceedings of the first international conference on unsaturated soils, UNSAT ‘95, Paris, France,1995, vol 1, pp 63–69. http://flash.lakeheadu.ca/~svanapal/papers/new%20papers/paris95.pdf. Accessed 31 Aug 2020
Nam S et al (2011) Determination of the shear strength of unsaturated soils using the multistage direct shear test. Eng Geol 122(3):272–280
Hashemi Jokar M, Mirasi S (2017) Using adaptive neuro-fuzzy inference system for modeling unsaturated soils shear strength. Soft Comput 22(13):4493–4510
Chou J-S, Ngo N-T (2018) Engineering strength of fiber-reinforced soil estimated by swarm intelligence optimized regression system. Neural Comput Appl 30(7):2129–2144
Chen L-H et al (2019) Accurate estimation of soil shear strength parameters. J Cent South Univ 26(4):1000–1010
Mbarak WK, Cinicioglu EN, Cinicioglu O (2020) SPT based determination of undrained shear strength: regression models and machine learning. Front Struct Civ Eng 14(1):185–198
Pham BT et al (2018) Prediction of shear strength of soft soil using machine learning methods. CATENA 166:181–191
Tien Bui D, Hoang N-D, Nhu V-H (2019) A swarm intelligence-based machine learning approach for predicting soil shear strength for road construction: a case study at Trung Luong National Expressway Project (Vietnam). Eng Comput 35(3):955–965
Moayedi H et al (2019) Spotted hyena optimizer and ant lion optimization in predicting the shear strength of soil. Appl Sci 9(22):4738
Nhu V-H et al (2020) A hybrid computational intelligence approach for predicting soil shear strength for urban housing construction: a case study at Vinhomes Imperia project, Hai Phong city (Vietnam). Eng Comput 36(2):603–616
Moayedi H et al (2019) Novel nature-inspired hybrids of neural computing for estimating soil shear strength. Appl Sci 9(21):4643
Moayedi H et al (2020) Hybridizing four wise neural-metaheuristic paradigms in predicting soil shear strength. Measurement 156:107576
Ojha VK, Abraham A, Snášel V (2017) Metaheuristic design of feedforward neural networks: a review of two decades of research. Eng Appl Artif Intell 60:97–116
Han F et al (2019) A survey on metaheuristic optimization for random single-hidden layer feedforward neural network. Neurocomputing 335:261–273
Khan A et al (2019) An alternative approach to neural network training based on hybrid bio meta-heuristic algorithm. J Ambient Intell Humaniz Comput 10(10):3821–3830
Nguyen H et al (2020) A comparative study of empirical and ensemble machine learning algorithms in predicting air over-pressure in open-pit coal mine. Acta Geophys 68:325–336
Prayogo D et al (2019) Combining machine learning models via adaptive ensemble weighting for prediction of shear capacity of reinforced-concrete deep beams. Eng Comput 36:1135–1153
Arabameri A et al (2019) Novel ensembles of COPRAS multi-criteria decision-making with logistic regression, boosted regression tree, and random forest for spatial prediction of gully erosion susceptibility. Sci Total Environ 688:903–916
Kadavi PR, Lee C-W, Lee S (2018) Application of ensemble-based machine learning models to landslide susceptibility mapping. Remote Sens 10(8):1252
Dang V-H et al (2019) Enhancing the accuracy of rainfall-induced landslide prediction along mountain roads with a GIS-based random forest classifier. Bull Eng Geol Environ 78(4):2835–2849
Kuncheva LI (2014) Combining pattern classifiers: methods and algorithms. Wiley, New York (Printed in the United States of America)
Rokach L (2010) Ensemble-based classifiers. Artif Intell Rev 33(1):1–39
Rokach L (2005) Ensemble methods for classifiers. In: Maimon O, Rokach L (eds) Data mining and knowledge discovery handbook. Springer US, Boston, pp 957–980
Zaherpour J et al (2019) Exploring the value of machine learning for weighted multi-model combination of an ensemble of global hydrological models. Environ Model Softw 114:112–128
Zhang X, Mahadevan S (2019) Ensemble machine learning models for aviation incident risk prediction. Decis Support Syst 116:48–63
Pham BT et al (2019) Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: hybrid machine learning approaches. CATENA 175:203–218
Broomhead DS, Lowe D (1988) Radial basis functions, multi-variable functional interpolation and adaptive networks. Technical report. Royal Signals and Radar Establishment
Chen S, Cowan CFN, Grant PM (1991) Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans Neural Netw 2(2):302–309
Friedman JH (1991) Multivariate adaptive regression splines. Ann Stat 19(1):1–67
Friedman JH, Roosen CB (1995) An introduction to multivariate adaptive regression splines. Stat Methods Med Res 4(3):197–217
Zhou Z-H (2012) Ensemble methods: foundations and algorithms. CRC Press, Boca Raton
Yadav A (2019) AEFA: artificial electric field algorithm for global optimization. Swarm Evol Comput 48:93–108
Hoang N-D, Tien Bui D (2017) Slope stability evaluation using radial basis function neural network, least squares support vector machines, and extreme learning machine. In: Samui P, Sekhar S, Balas V E (eds) Handbook of neural computation. Academic Press, Cambridge, pp 333–344
Musavi MT et al (1992) On the training of radial basis function classifiers. Neural Netw 5(4):595–603
Cheng M-Y, Cao M-T, Wu Y-W (2015) Predicting equilibrium scour depth at bridge piers using evolutionary radial basis function neural network. J Comput Civ Eng 29(5):04014070
Cha Y-J, Choi W, Büyüköztürk O (2017) Deep learning-based crack damage detection using convolutional neural networks. Comput Aided Civ Infrastruct Eng 32(5):361–378
Yang Y-K et al (2013) A novel self-constructing radial basis function neural-fuzzy system. Appl Soft Comput 13(5):2390–2404
Kopal I et al (2019) Radial basis function neural network-based modeling of the dynamic thermo-mechanical response and damping behavior of thermoplastic elastomer systems. Polymers 11:1074
Fernando SL et al (2012) A hybrid device for the solution of sampling bias problems in the forecasting of firms’ bankruptcy. Expert Syst Appl 39(8):7512–7523
Kriner M (2007) Survival analysis with multivariate adaptive regression splines, in Mathematic, Information and Statistics Department, Munchen University. Dissertation, LMU Munich
Tien Bui D, Hoang N-D, Samui P (2019) Spatial pattern analysis and prediction of forest fire using new machine learning approach of Multivariate Adaptive Regression Splines and Differential Flower Pollination optimization: a case study at Lao Cai province (Viet Nam). J Environ Manag 237:476–487
Chou J-S, Pham A-D (2013) Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr Build Mater 49:554–563
Bishop CM (2006) Pattern recognition and machine learning (information science and statistics). Springer, New York
Cheng M-Y, Cao M-T, Herianto JG (2020) Symbiotic organisms search-optimized deep learning technique for mapping construction cash flow considering complexity of project. Chaos Solitons Fractals 138:109869
Nguyen T-D et al (2019) A success history-based adaptive differential evolution optimized support vector regression for estimating plastic viscosity of fresh concrete. Eng Comput. https://doi.org/10.1007/s00366-019-00899-7
Hoang N-D, Nguyen Q-L (2019) A novel method for asphalt pavement crack classification based on image processing and machine learning. Eng Comput 35(2):487–498
Chou J-S, Pham A-D (2017) Nature-inspired metaheuristic optimization in least squares support vector regression for obtaining bridge scour information. Inf Sci 399:64–80
Orenstein T, Kohavi Z, Pomeranz I (1995) An optimal algorithm for cycle breaking in directed graphs. J Electron Test 7(1–2):71–81
MathWorks (2019). https://mathworks.com/products/matlab.html. Accessed 15 Apr 2019
Acknowledgements
We would like to thank the Geleximco group JSC (Hanoi, Vietnam) and the Foundation Engineering and Underground Construction (FECON) JSC (Vietnam) for providing the data for this research.
Funding
Open Access funding provided by University Of South-Eastern Norway.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The collected dataset
Sample | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | Y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 | 2.00 | 36.30 | 28.19 | 34.88 | 33.41 | 1.87 | 1.40 | 0.94 | 46.16 | 28.65 | 17.51 | 0.27 | 0.46 |
2 | 5.30 | 25.67 | 49.76 | 24.57 | 42.15 | 1.76 | 1.24 | 1.17 | 47.78 | 31.01 | 16.77 | 0.66 | 0.32 |
3 | 8.80 | 22.24 | 48.19 | 29.41 | 35.59 | 1.84 | 1.36 | 0.99 | 39.60 | 23.86 | 15.74 | 0.75 | 0.34 |
4 | 1.80 | 18.23 | 53.89 | 27.78 | 27.66 | 1.90 | 1.49 | 0.81 | 36.19 | 23.01 | 13.18 | 0.35 | 0.48 |
5 | 6.80 | 24.48 | 51.60 | 23.82 | 49.75 | 1.70 | 1.14 | 1.37 | 54.12 | 38.22 | 15.90 | 0.73 | 0.22 |
6 | 9.80 | 19.41 | 53.50 | 27.06 | 46.33 | 1.72 | 1.17 | 1.30 | 49.78 | 36.22 | 13.57 | 0.75 | 0.24 |
7 | 2.80 | 13.52 | 58.41 | 27.51 | 34.40 | 1.85 | 1.38 | 0.96 | 41.18 | 25.94 | 15.24 | 0.56 | 0.33 |
8 | 7.00 | 15.83 | 57.91 | 26.26 | 36.07 | 1.78 | 1.31 | 1.06 | 41.65 | 26.35 | 15.30 | 0.64 | 0.28 |
9 | 11.00 | 8.55 | 63.02 | 28.43 | 37.84 | 1.83 | 1.33 | 1.03 | 44.97 | 28.25 | 16.72 | 0.57 | 0.24 |
10 | 14.80 | 13.17 | 58.57 | 28.25 | 45.37 | 1.74 | 1.19 | 1.25 | 50.11 | 33.99 | 16.12 | 0.71 | 0.22 |
11 | 3.50 | 11.13 | 59.17 | 29.70 | 34.28 | 1.84 | 1.37 | 0.97 | 41.22 | 26.35 | 14.87 | 0.53 | 0.37 |
12 | 8.00 | 21.93 | 49.79 | 28.28 | 45.33 | 1.74 | 1.20 | 1.24 | 51.05 | 34.96 | 16.09 | 0.64 | 0.24 |
13 | 11.00 | 12.97 | 59.78 | 27.24 | 40.02 | 1.75 | 1.25 | 1.15 | 45.98 | 30.12 | 15.86 | 0.62 | 0.26 |
14 | 1.80 | 16.72 | 53.36 | 29.88 | 24.51 | 1.92 | 1.54 | 0.76 | 32.65 | 20.33 | 12.32 | 0.34 | 0.48 |
15 | 6.50 | 29.15 | 42.97 | 27.89 | 40.99 | 1.75 | 1.24 | 1.16 | 46.51 | 29.66 | 16.85 | 0.67 | 0.27 |
16 | 11.50 | 37.93 | 33.25 | 28.81 | 38.75 | 1.76 | 1.27 | 1.12 | 43.12 | 26.97 | 16.14 | 0.73 | 0.39 |
17 | 1.50 | 14.24 | 57.03 | 28.73 | 28.74 | 1.94 | 1.50 | 0.80 | 38.65 | 24.53 | 14.12 | 0.30 | 0.48 |
18 | 4.50 | 13.55 | 59.17 | 27.28 | 38.52 | 1.81 | 1.31 | 1.07 | 42.36 | 31.35 | 11.01 | 0.65 | 0.36 |
19 | 12.00 | 12.32 | 58.95 | 28.73 | 39.51 | 1.79 | 1.29 | 1.10 | 44.32 | 27.37 | 16.95 | 0.72 | 0.24 |
20 | 14.00 | 24.76 | 50.16 | 25.07 | 31.83 | 1.88 | 1.42 | 0.90 | 37.69 | 25.63 | 12.06 | 0.51 | 0.31 |
21 | 1.30 | 10.58 | 39.17 | 50.21 | 23.09 | 1.90 | 1.55 | 0.76 | 35.44 | 18.42 | 17.02 | 0.27 | 0.52 |
22 | 7.50 | 13.81 | 55.86 | 30.34 | 44.15 | 1.75 | 1.21 | 1.23 | 50.09 | 33.19 | 16.90 | 0.65 | 0.28 |
23 | 12.50 | 26.50 | 44.98 | 28.52 | 41.07 | 1.78 | 1.26 | 1.14 | 48.55 | 32.25 | 16.31 | 0.54 | 0.26 |
24 | 14.00 | 12.01 | 57.02 | 29.79 | 35.46 | 1.86 | 1.37 | 0.98 | 41.25 | 26.56 | 14.70 | 0.61 | 0.37 |
25 | 2.00 | 13.63 | 58.00 | 28.37 | 27.79 | 1.91 | 1.50 | 0.81 | 37.02 | 23.12 | 13.90 | 0.34 | 0.50 |
26 | 8.00 | 23.87 | 46.07 | 29.67 | 47.01 | 1.72 | 1.17 | 1.31 | 53.17 | 37.42 | 15.75 | 0.61 | 0.35 |
27 | 12.00 | 21.91 | 48.82 | 29.27 | 45.94 | 1.72 | 1.18 | 1.29 | 50.32 | 35.66 | 14.66 | 0.70 | 0.33 |
28 | 2.30 | 10.65 | 59.12 | 29.63 | 24.95 | 1.92 | 1.53 | 0.77 | 36.25 | 20.34 | 15.92 | 0.29 | 0.50 |
29 | 6.30 | 17.10 | 53.02 | 29.88 | 41.09 | 1.71 | 1.21 | 1.22 | 44.34 | 29.82 | 14.51 | 0.78 | 0.18 |
30 | 10.30 | 14.88 | 57.32 | 27.79 | 38.23 | 1.76 | 1.28 | 1.12 | 43.00 | 26.34 | 16.66 | 0.71 | 0.27 |
31 | 13.10 | 15.60 | 59.41 | 24.98 | 30.69 | 1.76 | 1.34 | 1.01 | 36.11 | 20.02 | 16.09 | 0.66 | 0.30 |
32 | 2.80 | 9.10 | 60.63 | 29.59 | 28.93 | 1.91 | 1.48 | 0.82 | 38.54 | 25.47 | 13.07 | 0.26 | 0.55 |
33 | 6.80 | 22.65 | 48.36 | 28.99 | 38.83 | 1.74 | 1.25 | 1.14 | 42.36 | 28.56 | 13.80 | 0.74 | 0.25 |
34 | 9.80 | 19.12 | 52.79 | 28.09 | 47.06 | 1.71 | 1.16 | 1.31 | 53.12 | 36.91 | 16.20 | 0.63 | 0.35 |
35 | 14.80 | 15.63 | 56.92 | 27.25 | 43.51 | 1.73 | 1.20 | 1.24 | 48.53 | 33.25 | 15.28 | 0.67 | 0.29 |
36 | 2.00 | 10.02 | 60.89 | 27.44 | 25.34 | 1.95 | 1.56 | 0.74 | 36.21 | 21.33 | 14.88 | 0.27 | 0.52 |
37 | 5.00 | 13.89 | 56.35 | 29.76 | 32.60 | 1.88 | 1.42 | 0.91 | 38.56 | 24.55 | 14.01 | 0.57 | 0.27 |
38 | 10.30 | 11.57 | 58.74 | 29.70 | 44.10 | 1.76 | 1.22 | 1.21 | 49.91 | 34.05 | 15.85 | 0.63 | 0.36 |
39 | 14.00 | 18.55 | 51.81 | 29.64 | 39.96 | 1.76 | 1.25 | 1.15 | 45.23 | 30.25 | 14.98 | 0.65 | 0.35 |
40 | 2.00 | 21.15 | 44.53 | 34.22 | 31.91 | 1.87 | 1.41 | 0.92 | 45.05 | 27.24 | 17.81 | 0.26 | 0.55 |
41 | 5.60 | 7.76 | 42.62 | 49.63 | 35.64 | 1.86 | 1.37 | 0.97 | 44.52 | 25.53 | 18.99 | 0.53 | 0.37 |
42 | 8.00 | 13.15 | 59.07 | 27.78 | 46.60 | 1.73 | 1.18 | 1.28 | 51.02 | 34.16 | 16.86 | 0.74 | 0.30 |
43 | 12.50 | 34.73 | 41.42 | 23.86 | 37.04 | 1.79 | 1.31 | 1.06 | 41.52 | 27.89 | 13.64 | 0.67 | 0.31 |
44 | 14.80 | 32.45 | 38.82 | 28.73 | 46.81 | 1.73 | 1.18 | 1.28 | 49.62 | 36.98 | 12.64 | 0.78 | 0.28 |
45 | 5.00 | 45.76 | 25.59 | 28.65 | 40.83 | 1.80 | 1.28 | 1.12 | 46.25 | 30.24 | 16.01 | 0.66 | 0.33 |
46 | 9.00 | 32.68 | 37.58 | 29.75 | 35.08 | 1.80 | 1.33 | 1.03 | 38.69 | 24.52 | 14.17 | 0.75 | 0.27 |
47 | 1.50 | 21.45 | 48.92 | 29.62 | 28.36 | 1.92 | 1.50 | 0.81 | 36.52 | 23.36 | 13.16 | 0.38 | 0.46 |
48 | 3.00 | 16.29 | 57.33 | 26.37 | 25.21 | 1.94 | 1.55 | 0.75 | 32.63 | 19.61 | 13.02 | 0.43 | 0.43 |
49 | 7.50 | 12.70 | 58.70 | 28.60 | 34.56 | 1.87 | 1.39 | 0.95 | 42.36 | 26.58 | 15.78 | 0.51 | 0.33 |
50 | 3.30 | 22.34 | 47.67 | 29.99 | 25.36 | 1.90 | 1.52 | 0.79 | 36.32 | 21.25 | 15.07 | 0.27 | 0.51 |
51 | 6.50 | 10.82 | 60.04 | 29.14 | 35.61 | 1.85 | 1.36 | 0.98 | 40.23 | 26.35 | 13.88 | 0.67 | 0.30 |
52 | 9.80 | 11.87 | 58.93 | 29.20 | 38.36 | 1.78 | 1.28 | 1.11 | 43.23 | 26.62 | 16.61 | 0.71 | 0.26 |
53 | 9.00 | 16.63 | 55.27 | 28.10 | 30.20 | 1.92 | 1.47 | 0.84 | 34.55 | 23.03 | 11.52 | 0.62 | 0.30 |
54 | 4.30 | 11.35 | 59.35 | 29.30 | 37.84 | 1.82 | 1.32 | 1.04 | 42.51 | 28.54 | 13.97 | 0.67 | 0.32 |
55 | 1.60 | 25.60 | 45.28 | 27.50 | 26.61 | 1.95 | 1.54 | 0.76 | 35.24 | 22.15 | 13.09 | 0.34 | 0.51 |
56 | 7.00 | 20.04 | 52.97 | 26.99 | 40.17 | 1.79 | 1.28 | 1.11 | 47.00 | 32.52 | 14.48 | 0.53 | 0.29 |
57 | 3.80 | 10.93 | 59.59 | 29.05 | 40.30 | 1.74 | 1.24 | 1.18 | 46.81 | 31.29 | 15.53 | 0.58 | 0.32 |
58 | 1.30 | 15.51 | 39.00 | 45.49 | 33.05 | 1.87 | 1.41 | 0.93 | 47.05 | 27.95 | 19.10 | 0.27 | 0.54 |
59 | 7.80 | 25.39 | 46.33 | 28.21 | 41.33 | 1.78 | 1.26 | 1.14 | 48.92 | 32.12 | 16.81 | 0.55 | 0.34 |
60 | 5.00 | 9.20 | 60.91 | 29.76 | 32.69 | 1.88 | 1.41 | 0.91 | 39.83 | 25.35 | 14.48 | 0.51 | 0.36 |
61 | 2.00 | 10.85 | 59.44 | 29.71 | 25.69 | 1.95 | 1.55 | 0.74 | 36.26 | 19.65 | 16.61 | 0.36 | 0.45 |
62 | 8.00 | 70.77 | 19.89 | 8.98 | 18.38 | 1.85 | 1.56 | 0.72 | 23.12 | 18.02 | 5.10 | 0.07 | 0.42 |
63 | 11.80 | 76.05 | 14.97 | 8.98 | 20.05 | 1.84 | 1.54 | 0.74 | 23.00 | 18.98 | 4.03 | 0.27 | 0.39 |
64 | 14.80 | 68.84 | 21.25 | 9.86 | 21.51 | 1.87 | 1.54 | 0.75 | 24.15 | 17.33 | 6.82 | 0.61 | 0.41 |
65 | 3.20 | 28.47 | 42.28 | 29.25 | 44.86 | 1.74 | 1.20 | 1.25 | 49.21 | 32.56 | 16.65 | 0.74 | 0.35 |
66 | 2.00 | 20.61 | 51.47 | 27.92 | 27.36 | 1.91 | 1.50 | 0.81 | 36.54 | 22.36 | 14.18 | 0.35 | 0.47 |
67 | 3.80 | 13.94 | 56.79 | 29.27 | 38.91 | 1.78 | 1.28 | 1.10 | 44.56 | 28.25 | 16.31 | 0.65 | 0.29 |
68 | 7.80 | 20.88 | 52.47 | 26.65 | 37.04 | 1.83 | 1.33 | 1.04 | 43.96 | 29.54 | 14.41 | 0.52 | 0.32 |
69 | 11.40 | 15.62 | 54.56 | 29.79 | 39.01 | 1.81 | 1.30 | 1.08 | 42.63 | 29.56 | 13.07 | 0.72 | 0.36 |
70 | 14.80 | 23.96 | 47.38 | 28.66 | 42.98 | 1.77 | 1.24 | 1.18 | 47.24 | 31.32 | 15.92 | 0.73 | 0.34 |
71 | 1.40 | 26.20 | 48.19 | 25.58 | 26.20 | 1.91 | 1.51 | 0.79 | 35.26 | 19.56 | 15.70 | 0.42 | 0.49 |
72 | 5.00 | 16.68 | 53.92 | 29.39 | 31.51 | 1.86 | 1.41 | 0.91 | 39.25 | 22.51 | 16.74 | 0.54 | 0.32 |
73 | 14.00 | 29.28 | 42.05 | 28.68 | 39.19 | 1.81 | 1.30 | 1.07 | 44.12 | 28.02 | 16.10 | 0.69 | 0.29 |
74 | 3.00 | 12.51 | 58.57 | 28.56 | 30.92 | 1.87 | 1.42 | 0.90 | 36.25 | 23.21 | 13.04 | 0.59 | 0.34 |
75 | 11.00 | 22.61 | 52.00 | 25.40 | 30.28 | 1.87 | 1.43 | 0.89 | 35.69 | 19.15 | 16.54 | 0.67 | 0.37 |
76 | 14.00 | 22.19 | 47.94 | 29.87 | 39.21 | 1.74 | 1.25 | 1.16 | 42.15 | 30.14 | 12.01 | 0.76 | 0.27 |
77 | 1.60 | 13.64 | 58.55 | 27.81 | 20.57 | 1.95 | 1.62 | 0.67 | 32.69 | 16.52 | 16.17 | 0.25 | 0.44 |
78 | 4.00 | 20.94 | 50.37 | 28.68 | 47.73 | 1.72 | 1.16 | 1.32 | 53.23 | 37.22 | 16.01 | 0.66 | 0.30 |
79 | 9.00 | 11.83 | 58.98 | 29.19 | 43.72 | 1.74 | 1.21 | 1.24 | 48.77 | 32.09 | 16.68 | 0.70 | 0.31 |
80 | 14.00 | 34.26 | 39.16 | 26.06 | 45.45 | 1.72 | 1.18 | 1.28 | 50.56 | 36.12 | 14.44 | 0.65 | 0.33 |
81 | 3.80 | 11.25 | 59.56 | 29.19 | 37.09 | 1.76 | 1.29 | 1.10 | 40.23 | 28.56 | 11.67 | 0.73 | 0.29 |
82 | 1.80 | 13.98 | 56.52 | 27.47 | 29.72 | 1.90 | 1.47 | 0.85 | 36.58 | 25.24 | 11.34 | 0.39 | 0.48 |
83 | 8.80 | 23.62 | 51.84 | 24.54 | 43.35 | 1.73 | 1.21 | 1.24 | 49.21 | 33.12 | 16.09 | 0.64 | 0.29 |
84 | 14.20 | 24.54 | 50.00 | 25.19 | 48.93 | 1.71 | 1.15 | 1.35 | 54.01 | 38.67 | 15.34 | 0.67 | 0.26 |
85 | 2.50 | 15.21 | 55.97 | 28.83 | 38.88 | 1.75 | 1.26 | 1.14 | 43.23 | 29.63 | 13.59 | 0.68 | 0.32 |
86 | 7.00 | 11.84 | 57.66 | 29.85 | 31.03 | 1.90 | 1.45 | 0.87 | 37.44 | 22.24 | 15.20 | 0.58 | 0.31 |
87 | 2.20 | 10.33 | 60.81 | 28.86 | 28.33 | 1.87 | 1.45 | 0.86 | 33.65 | 23.65 | 10.00 | 0.47 | 0.41 |
88 | 6.80 | 59.44 | 30.31 | 10.25 | 32.22 | 1.82 | 1.38 | 0.95 | 34.25 | 27.97 | 6.28 | 0.68 | 0.40 |
89 | 2.70 | 24.55 | 47.70 | 27.62 | 40.54 | 1.75 | 1.24 | 1.17 | 44.25 | 33.62 | 10.63 | 0.65 | 0.31 |
90 | 2.80 | 15.44 | 45.25 | 39.21 | 29.88 | 1.91 | 1.47 | 0.84 | 42.16 | 24.11 | 18.05 | 0.32 | 0.46 |
91 | 5.00 | 13.29 | 59.53 | 27.18 | 41.46 | 1.75 | 1.24 | 1.18 | 48.22 | 32.94 | 15.28 | 0.56 | 0.34 |
92 | 7.00 | 15.95 | 55.82 | 28.23 | 45.12 | 1.73 | 1.19 | 1.26 | 50.14 | 34.93 | 15.22 | 0.67 | 0.26 |
93 | 11.00 | 9.76 | 63.24 | 27.00 | 47.08 | 1.73 | 1.18 | 1.28 | 53.44 | 36.63 | 16.81 | 0.62 | 0.29 |
94 | 14.80 | 10.18 | 59.56 | 29.83 | 44.23 | 1.74 | 1.21 | 1.23 | 50.93 | 35.16 | 15.77 | 0.57 | 0.24 |
95 | 3.10 | 28.96 | 42.50 | 28.43 | 31.05 | 1.85 | 1.41 | 0.91 | 39.65 | 27.51 | 12.14 | 0.29 | 0.44 |
96 | 4.00 | 27.53 | 43.89 | 28.58 | 29.27 | 1.89 | 1.46 | 0.85 | 36.12 | 20.14 | 15.98 | 0.57 | 0.38 |
97 | 11.80 | 7.67 | 63.65 | 28.68 | 46.02 | 1.72 | 1.18 | 1.28 | 51.18 | 34.56 | 16.63 | 0.69 | 0.25 |
98 | 14.80 | 42.55 | 27.65 | 29.80 | 40.78 | 1.72 | 1.22 | 1.20 | 46.12 | 30.15 | 15.96 | 0.67 | 0.26 |
99 | 2.30 | 14.06 | 57.15 | 28.79 | 28.82 | 1.93 | 1.50 | 0.80 | 37.25 | 23.51 | 13.74 | 0.39 | 0.52 |
100 | 6.00 | 30.40 | 41.58 | 28.02 | 44.99 | 1.72 | 1.19 | 1.27 | 50.01 | 33.19 | 16.82 | 0.70 | 0.22 |
101 | 12.30 | 45.79 | 25.52 | 28.69 | 47.82 | 1.72 | 1.16 | 1.32 | 52.12 | 36.19 | 15.93 | 0.73 | 0.27 |
102 | 14.30 | 41.87 | 35.87 | 22.23 | 38.66 | 1.81 | 1.31 | 1.06 | 42.19 | 28.33 | 13.86 | 0.75 | 0.28 |
103 | 2.70 | 23.15 | 50.13 | 26.73 | 36.59 | 1.81 | 1.33 | 1.04 | 42.36 | 29.63 | 12.73 | 0.55 | 0.36 |
104 | 6.30 | 18.47 | 52.01 | 29.52 | 43.12 | 1.75 | 1.22 | 1.21 | 48.56 | 32.16 | 16.40 | 0.67 | 0.26 |
105 | 11.80 | 14.19 | 56.65 | 28.76 | 46.53 | 1.72 | 1.18 | 1.29 | 48.52 | 41.21 | 7.31 | 0.73 | 0.31 |
106 | 1.80 | 16.79 | 53.78 | 29.43 | 27.03 | 1.91 | 1.51 | 0.80 | 35.20 | 20.04 | 15.16 | 0.46 | 0.50 |
107 | 6.00 | 34.30 | 38.04 | 27.66 | 48.30 | 1.71 | 1.15 | 1.34 | 53.21 | 37.12 | 16.10 | 0.69 | 0.24 |
108 | 8.80 | 38.84 | 32.94 | 28.22 | 47.08 | 1.71 | 1.16 | 1.32 | 53.21 | 37.12 | 16.09 | 0.62 | 0.25 |
109 | 2.00 | 30.56 | 39.49 | 29.86 | 30.24 | 1.90 | 1.46 | 0.86 | 37.11 | 23.02 | 14.09 | 0.51 | 0.37 |
110 | 4.30 | 23.64 | 50.53 | 25.20 | 27.62 | 1.89 | 1.48 | 0.83 | 38.23 | 22.31 | 15.92 | 0.33 | 0.49 |
111 | 1.80 | 22.46 | 48.35 | 28.90 | 30.42 | 1.90 | 1.46 | 0.87 | 39.81 | 24.12 | 15.70 | 0.40 | 0.49 |
112 | 5.50 | 28.66 | 44.73 | 26.61 | 49.20 | 1.71 | 1.15 | 1.35 | 54.12 | 37.82 | 16.30 | 0.70 | 0.29 |
113 | 9.20 | 9.84 | 60.57 | 29.58 | 37.72 | 1.79 | 1.30 | 1.08 | 45.02 | 29.52 | 15.50 | 0.53 | 0.29 |
114 | 14.00 | 30.70 | 41.45 | 27.85 | 46.31 | 1.73 | 1.19 | 1.28 | 49.81 | 34.16 | 15.65 | 0.78 | 0.27 |
115 | 2.00 | 13.43 | 54.97 | 31.60 | 28.29 | 1.90 | 1.48 | 0.83 | 37.52 | 20.02 | 17.51 | 0.47 | 0.50 |
116 | 6.00 | 21.85 | 53.59 | 24.56 | 26.77 | 1.91 | 1.50 | 0.80 | 32.69 | 19.77 | 12.93 | 0.54 | 0.35 |
117 | 2.80 | 10.52 | 40.79 | 48.65 | 35.74 | 1.81 | 1.33 | 1.03 | 46.22 | 27.41 | 18.81 | 0.44 | 0.46 |
118 | 7.80 | 7.48 | 42.30 | 50.21 | 25.60 | 1.90 | 1.51 | 0.80 | 37.82 | 19.75 | 18.08 | 0.32 | 0.50 |
119 | 3.00 | 16.76 | 48.46 | 34.74 | 49.65 | 1.72 | 1.15 | 1.36 | 57.11 | 39.85 | 17.27 | 0.57 | 0.36 |
120 | 5.00 | 12.65 | 60.36 | 26.99 | 43.20 | 1.76 | 1.23 | 1.20 | 50.22 | 34.22 | 16.01 | 0.56 | 0.34 |
121 | 8.80 | 6.79 | 63.63 | 29.57 | 43.99 | 1.73 | 1.20 | 1.25 | 46.52 | 36.52 | 10.00 | 0.75 | 0.28 |
122 | 11.80 | 31.46 | 40.81 | 27.73 | 38.42 | 1.82 | 1.32 | 1.05 | 45.12 | 28.33 | 16.78 | 0.60 | 0.33 |
123 | 14.80 | 10.48 | 57.69 | 29.93 | 29.31 | 1.91 | 1.47 | 0.83 | 37.99 | 24.52 | 13.47 | 0.36 | 0.48 |
124 | 1.80 | 19.30 | 44.99 | 35.71 | 35.84 | 1.81 | 1.33 | 1.03 | 45.19 | 27.02 | 18.18 | 0.49 | 0.44 |
125 | 4.80 | 21.82 | 53.27 | 24.90 | 40.18 | 1.76 | 1.26 | 1.14 | 44.99 | 29.19 | 15.80 | 0.70 | 0.25 |
126 | 8.80 | 10.46 | 61.29 | 28.25 | 38.43 | 1.82 | 1.32 | 1.05 | 43.12 | 27.00 | 16.12 | 0.71 | 0.26 |
127 | 3.00 | 17.26 | 54.91 | 27.83 | 31.08 | 1.88 | 1.43 | 0.88 | 36.75 | 21.05 | 15.70 | 0.64 | 0.24 |
128 | 5.50 | 19.87 | 50.22 | 29.92 | 33.53 | 1.86 | 1.39 | 0.93 | 37.21 | 24.36 | 12.85 | 0.71 | 0.28 |
129 | 9.80 | 68.67 | 15.60 | 8.79 | 40.19 | 1.76 | 1.25 | 1.14 | 44.02 | 38.41 | 5.61 | 0.32 | 0.39 |
130 | 3.10 | 28.96 | 42.50 | 28.43 | 31.05 | 1.85 | 1.41 | 0.91 | 39.65 | 27.51 | 12.14 | 0.29 | 0.44 |
131 | 2.30 | 14.06 | 57.15 | 28.79 | 28.82 | 1.93 | 1.50 | 0.80 | 37.25 | 23.51 | 13.74 | 0.39 | 0.52 |
132 | 2.70 | 23.15 | 50.13 | 26.73 | 36.59 | 1.81 | 1.33 | 1.04 | 42.36 | 29.63 | 12.73 | 0.55 | 0.36 |
133 | 1.80 | 16.79 | 53.78 | 29.43 | 27.03 | 1.91 | 1.51 | 0.80 | 35.20 | 20.04 | 15.16 | 0.46 | 0.50 |
134 | 2.00 | 30.56 | 39.49 | 29.86 | 30.24 | 1.90 | 1.46 | 0.86 | 37.11 | 23.02 | 14.09 | 0.51 | 0.37 |
135 | 4.30 | 23.64 | 50.53 | 25.20 | 27.62 | 1.89 | 1.48 | 0.83 | 38.23 | 22.31 | 15.92 | 0.33 | 0.49 |
136 | 1.80 | 22.46 | 48.35 | 28.90 | 30.42 | 1.90 | 1.46 | 0.87 | 39.81 | 24.12 | 15.70 | 0.40 | 0.49 |
137 | 2.30 | 12.74 | 58.76 | 28.51 | 23.66 | 1.97 | 1.59 | 0.70 | 34.23 | 19.26 | 14.97 | 0.29 | 0.54 |
138 | 2.50 | 15.20 | 55.88 | 28.56 | 26.32 | 1.92 | 1.52 | 0.78 | 35.84 | 21.24 | 14.60 | 0.35 | 0.46 |
139 | 3.50 | 17.01 | 50.93 | 27.99 | 25.99 | 1.93 | 1.53 | 0.77 | 36.25 | 21.25 | 15.00 | 0.32 | 0.51 |
140 | 2.50 | 12.09 | 59.67 | 28.24 | 31.25 | 1.87 | 1.43 | 0.89 | 40.36 | 27.12 | 13.24 | 0.31 | 0.49 |
141 | 2.00 | 17.64 | 51.50 | 30.86 | 29.02 | 1.94 | 1.51 | 0.80 | 36.21 | 22.65 | 13.56 | 0.47 | 0.45 |
142 | 4.50 | 23.03 | 48.68 | 28.28 | 31.21 | 1.87 | 1.42 | 0.90 | 36.95 | 23.25 | 13.70 | 0.58 | 0.31 |
143 | 2.50 | 10.76 | 59.26 | 29.88 | 32.22 | 1.84 | 1.39 | 0.94 | 41.14 | 25.36 | 15.78 | 0.43 | 0.44 |
144 | 2.00 | 25.19 | 47.73 | 27.08 | 26.32 | 1.92 | 1.52 | 0.78 | 35.84 | 21.24 | 14.60 | 0.35 | 0.47 |
145 | 1.40 | 16.34 | 55.51 | 27.31 | 30.26 | 1.88 | 1.44 | 0.88 | 37.41 | 26.58 | 10.83 | 0.34 | 0.45 |
146 | 1.20 | 19.72 | 51.68 | 28.21 | 28.42 | 1.90 | 1.48 | 0.83 | 35.68 | 21.21 | 14.47 | 0.50 | 0.42 |
147 | 2.80 | 36.69 | 36.43 | 26.73 | 25.69 | 1.91 | 1.52 | 0.78 | 33.21 | 19.63 | 13.58 | 0.45 | 0.45 |
148 | 1.80 | 19.21 | 49.54 | 28.92 | 25.60 | 1.93 | 1.54 | 0.76 | 32.14 | 21.32 | 10.82 | 0.40 | 0.47 |
149 | 1.80 | 22.33 | 42.06 | 29.77 | 27.54 | 1.93 | 1.52 | 0.79 | 38.51 | 22.14 | 16.37 | 0.33 | 0.52 |
150 | 2.00 | 25.21 | 32.99 | 28.04 | 27.44 | 1.96 | 1.53 | 0.77 | 36.52 | 23.32 | 13.20 | 0.31 | 0.47 |
151 | 1.80 | 26.67 | 45.02 | 27.25 | 26.33 | 1.96 | 1.55 | 0.74 | 36.25 | 21.25 | 15.00 | 0.34 | 0.45 |
152 | 2.50 | 16.70 | 53.41 | 29.06 | 30.54 | 1.90 | 1.45 | 0.86 | 36.25 | 21.36 | 14.89 | 0.62 | 0.33 |
153 | 3.80 | 29.41 | 42.97 | 27.62 | 30.12 | 1.86 | 1.43 | 0.90 | 40.92 | 24.99 | 15.93 | 0.32 | 0.45 |
154 | 2.20 | 16.20 | 56.64 | 27.01 | 28.32 | 1.90 | 1.48 | 0.84 | 38.54 | 24.21 | 14.33 | 0.29 | 0.51 |
155 | 3.80 | 21.43 | 48.94 | 29.60 | 27.51 | 1.88 | 1.48 | 0.83 | 39.88 | 23.16 | 16.72 | 0.26 | 0.45 |
156 | 3.80 | 34.76 | 37.27 | 27.97 | 32.20 | 1.90 | 1.44 | 0.89 | 39.75 | 25.33 | 14.42 | 0.48 | 0.38 |
157 | 1.80 | 29.24 | 45.92 | 24.84 | 28.13 | 1.90 | 1.48 | 0.83 | 37.48 | 23.12 | 14.36 | 0.35 | 0.46 |
158 | 3.80 | 32.61 | 41.37 | 26.03 | 31.27 | 1.87 | 1.43 | 0.89 | 38.77 | 26.02 | 12.76 | 0.41 | 0.42 |
159 | 1.80 | 33.56 | 37.53 | 28.91 | 25.61 | 1.90 | 1.52 | 0.79 | 37.02 | 21.20 | 15.82 | 0.28 | 0.51 |
160 | 4.00 | 27.53 | 43.89 | 28.58 | 29.27 | 1.89 | 1.46 | 0.85 | 36.12 | 20.14 | 15.98 | 0.57 | 0.38 |
161 | 11.80 | 7.67 | 63.65 | 28.68 | 46.02 | 1.72 | 1.18 | 1.28 | 51.18 | 34.56 | 16.63 | 0.69 | 0.25 |
162 | 6.00 | 30.40 | 41.58 | 28.02 | 44.99 | 1.72 | 1.19 | 1.27 | 50.01 | 33.19 | 16.82 | 0.70 | 0.22 |
163 | 7.80 | 25.79 | 48.37 | 25.50 | 48.02 | 1.71 | 1.15 | 1.34 | 51.22 | 36.95 | 14.28 | 0.78 | 0.24 |
164 | 5.50 | 28.66 | 44.73 | 26.61 | 49.20 | 1.71 | 1.15 | 1.35 | 54.12 | 37.82 | 16.30 | 0.70 | 0.29 |
165 | 9.20 | 9.84 | 60.57 | 29.58 | 37.72 | 1.79 | 1.30 | 1.08 | 45.02 | 29.52 | 15.50 | 0.53 | 0.29 |
166 | 14.00 | 30.70 | 41.45 | 27.85 | 46.31 | 1.73 | 1.19 | 1.28 | 49.81 | 34.16 | 15.65 | 0.78 | 0.27 |
167 | 6.30 | 13.11 | 58.71 | 27.51 | 43.92 | 1.73 | 1.20 | 1.25 | 49.22 | 36.19 | 13.03 | 0.59 | 0.28 |
168 | 10.30 | 13.63 | 54.96 | 28.62 | 40.09 | 1.75 | 1.25 | 1.16 | 46.89 | 32.12 | 14.77 | 0.54 | 0.34 |
169 | 6.50 | 21.56 | 50.21 | 27.38 | 36.25 | 1.79 | 1.31 | 1.06 | 41.36 | 29.58 | 11.78 | 0.57 | 0.34 |
170 | 10.50 | 13.23 | 53.82 | 26.39 | 40.20 | 1.74 | 1.24 | 1.17 | 44.22 | 28.67 | 15.55 | 0.74 | 0.32 |
171 | 14.80 | 16.64 | 53.94 | 29.42 | 36.21 | 1.84 | 1.35 | 1.00 | 41.12 | 27.00 | 14.12 | 0.65 | 0.34 |
172 | 6.80 | 22.89 | 48.87 | 28.25 | 34.12 | 1.85 | 1.38 | 0.96 | 41.36 | 26.58 | 14.78 | 0.51 | 0.26 |
173 | 9.80 | 31.54 | 36.89 | 28.50 | 45.32 | 1.71 | 1.18 | 1.29 | 50.22 | 39.63 | 10.59 | 0.54 | 0.29 |
174 | 9.80 | 40.07 | 31.09 | 26.61 | 27.25 | 1.93 | 1.52 | 0.78 | 32.14 | 21.32 | 10.82 | 0.55 | 0.30 |
175 | 8.50 | 24.18 | 46.43 | 29.39 | 47.41 | 1.72 | 1.17 | 1.30 | 51.25 | 36.36 | 14.89 | 0.74 | 0.29 |
176 | 4.80 | 26.59 | 43.60 | 29.75 | 45.66 | 1.74 | 1.19 | 1.26 | 50.23 | 34.26 | 15.97 | 0.71 | 0.30 |
177 | 5.40 | 19.24 | 48.83 | 29.17 | 33.62 | 1.84 | 1.38 | 0.96 | 41.25 | 25.33 | 15.92 | 0.52 | 0.27 |
178 | 5.80 | 18.87 | 52.62 | 28.52 | 28.39 | 1.90 | 1.48 | 0.82 | 32.12 | 21.36 | 10.76 | 0.65 | 0.35 |
179 | 6.20 | 25.56 | 44.77 | 29.48 | 33.41 | 1.82 | 1.37 | 0.98 | 40.31 | 25.33 | 14.98 | 0.54 | 0.26 |
180 | 14.20 | 27.45 | 46.11 | 26.44 | 30.21 | 1.84 | 1.42 | 0.91 | 37.54 | 21.51 | 16.03 | 0.54 | 0.28 |
181 | 5.20 | 14.20 | 56.20 | 29.60 | 34.60 | 1.86 | 1.38 | 0.96 | 41.11 | 27.53 | 13.58 | 0.52 | 0.25 |
182 | 9.80 | 7.14 | 62.95 | 29.91 | 38.52 | 1.76 | 1.27 | 1.13 | 43.21 | 28.54 | 14.67 | 0.68 | 0.19 |
183 | 14.20 | 23.25 | 47.86 | 26.59 | 42.55 | 1.73 | 1.21 | 1.23 | 44.95 | 33.58 | 11.37 | 0.79 | 0.21 |
184 | 3.20 | 23.81 | 48.89 | 27.09 | 30.54 | 1.87 | 1.43 | 0.89 | 35.24 | 24.12 | 11.12 | 0.58 | 0.34 |
185 | 6.30 | 25.41 | 48.30 | 26.28 | 34.19 | 1.85 | 1.38 | 0.97 | 38.74 | 22.60 | 16.14 | 0.72 | 0.33 |
186 | 9.80 | 17.86 | 52.41 | 29.73 | 34.63 | 1.77 | 1.31 | 1.05 | 40.36 | 26.11 | 14.25 | 0.60 | 0.31 |
187 | 7.80 | 29.66 | 43.22 | 27.12 | 37.19 | 1.81 | 1.32 | 1.04 | 39.85 | 27.22 | 12.63 | 0.79 | 0.23 |
188 | 11.80 | 29.46 | 45.71 | 24.84 | 37.83 | 1.83 | 1.32 | 1.04 | 42.62 | 26.97 | 15.65 | 0.69 | 0.33 |
189 | 7.80 | 29.19 | 44.35 | 24.86 | 32.25 | 1.87 | 1.41 | 0.92 | 38.51 | 22.66 | 15.85 | 0.60 | 0.36 |
190 | 7.80 | 32.54 | 44.20 | 23.26 | 45.32 | 1.72 | 1.19 | 1.27 | 47.23 | 32.52 | 14.70 | 0.87 | 0.21 |
191 | 11.80 | 34.20 | 39.46 | 26.34 | 46.33 | 1.73 | 1.18 | 1.28 | 48.93 | 32.95 | 15.98 | 0.84 | 0.20 |
192 | 15.80 | 27.92 | 48.11 | 23.97 | 36.23 | 1.82 | 1.34 | 1.02 | 43.82 | 27.99 | 15.83 | 0.52 | 0.33 |
193 | 14.80 | 42.55 | 27.65 | 29.80 | 40.78 | 1.72 | 1.22 | 1.20 | 46.12 | 30.15 | 15.96 | 0.67 | 0.26 |
194 | 12.30 | 45.79 | 25.52 | 28.69 | 47.82 | 1.72 | 1.16 | 1.32 | 52.12 | 36.19 | 15.93 | 0.73 | 0.27 |
195 | 14.30 | 41.87 | 35.87 | 22.23 | 38.66 | 1.81 | 1.31 | 1.06 | 42.19 | 28.33 | 13.86 | 0.75 | 0.28 |
196 | 6.30 | 18.47 | 52.01 | 29.52 | 43.12 | 1.75 | 1.22 | 1.21 | 48.56 | 32.16 | 16.40 | 0.67 | 0.26 |
197 | 11.80 | 14.19 | 56.65 | 28.76 | 46.53 | 1.72 | 1.18 | 1.29 | 48.52 | 41.21 | 7.31 | 0.73 | 0.31 |
198 | 6.00 | 34.30 | 38.04 | 27.66 | 48.30 | 1.71 | 1.15 | 1.34 | 53.21 | 37.12 | 16.10 | 0.69 | 0.24 |
199 | 8.80 | 38.84 | 32.94 | 28.22 | 47.08 | 1.71 | 1.16 | 1.32 | 53.21 | 37.12 | 16.09 | 0.62 | 0.25 |
200 | 7.00 | 26.67 | 47.00 | 26.33 | 42.14 | 1.76 | 1.24 | 1.19 | 47.99 | 36.11 | 11.88 | 0.51 | 0.32 |
201 | 14.60 | 22.91 | 48.02 | 27.91 | 43.25 | 1.72 | 1.20 | 1.25 | 49.62 | 35.54 | 14.08 | 0.55 | 0.32 |
202 | 14.30 | 18.62 | 52.99 | 28.30 | 40.15 | 1.75 | 1.25 | 1.16 | 44.36 | 29.85 | 14.51 | 0.71 | 0.27 |
203 | 6.80 | 21.88 | 50.81 | 27.31 | 45.23 | 1.70 | 1.17 | 1.30 | 47.12 | 31.32 | 15.80 | 0.88 | 0.23 |
204 | 11.00 | 21.10 | 50.27 | 28.63 | 37.25 | 1.82 | 1.33 | 1.03 | 41.11 | 26.14 | 14.97 | 0.74 | 0.30 |
205 | 4.20 | 13.53 | 58.01 | 28.30 | 41.07 | 1.77 | 1.25 | 1.15 | 43.99 | 30.18 | 13.81 | 0.79 | 0.21 |
206 | 9.20 | 19.16 | 52.31 | 28.47 | 38.22 | 1.78 | 1.29 | 1.10 | 42.20 | 28.22 | 13.98 | 0.72 | 0.27 |
207 | 4.50 | 19.95 | 51.80 | 28.25 | 38.52 | 1.76 | 1.27 | 1.13 | 40.11 | 26.32 | 13.79 | 0.88 | 0.27 |
208 | 8.00 | 12.36 | 59.41 | 28.24 | 31.25 | 1.87 | 1.43 | 0.89 | 36.21 | 24.63 | 11.58 | 0.57 | 0.26 |
209 | 14.00 | 26.04 | 46.84 | 27.12 | 32.52 | 1.85 | 1.40 | 0.94 | 39.58 | 23.21 | 16.37 | 0.57 | 0.26 |
210 | 3.80 | 23.80 | 44.94 | 26.83 | 29.32 | 1.89 | 1.46 | 0.86 | 34.54 | 24.36 | 10.18 | 0.49 | 0.52 |
211 | 7.20 | 53.22 | 35.77 | 9.92 | 24.84 | 1.96 | 1.57 | 0.71 | 26.32 | 21.58 | 4.74 | 0.69 | 0.38 |
212 | 6.50 | 27.18 | 43.97 | 28.84 | 34.42 | 1.86 | 1.38 | 0.96 | 39.50 | 27.36 | 12.14 | 0.58 | 0.32 |
213 | 7.80 | 23.11 | 48.78 | 28.11 | 35.99 | 1.81 | 1.33 | 1.03 | 42.21 | 25.65 | 16.56 | 0.62 | 0.34 |
214 | 13.80 | 21.41 | 50.84 | 27.75 | 31.20 | 1.86 | 1.42 | 0.91 | 38.51 | 22.03 | 16.48 | 0.56 | 0.36 |
215 | 15.80 | 32.35 | 39.35 | 26.30 | 35.47 | 1.86 | 1.37 | 0.98 | 40.01 | 26.96 | 13.05 | 0.65 | 0.33 |
216 | 19.80 | 22.90 | 52.21 | 24.89 | 32.20 | 1.86 | 1.41 | 0.91 | 36.43 | 22.94 | 13.48 | 0.69 | 0.31 |
217 | 35.50 | 59.97 | 28.01 | 9.42 | 28.88 | 1.82 | 1.41 | 0.91 | 33.11 | 26.55 | 6.56 | 0.36 | 0.41 |
218 | 24.60 | 30.05 | 46.46 | 23.49 | 33.54 | 1.81 | 1.36 | 0.99 | 37.94 | 25.20 | 12.74 | 0.65 | 0.27 |
219 | 28.00 | 29.44 | 42.01 | 28.40 | 35.19 | 1.86 | 1.37 | 0.97 | 39.22 | 27.18 | 12.04 | 0.67 | 0.35 |
220 | 15.20 | 21.48 | 51.05 | 26.89 | 33.50 | 1.86 | 1.40 | 0.93 | 40.01 | 24.12 | 15.90 | 0.59 | 0.33 |
221 | 17.00 | 26.88 | 48.53 | 24.59 | 35.17 | 1.85 | 1.37 | 0.98 | 40.67 | 26.35 | 14.32 | 0.62 | 0.34 |
222 | 25.40 | 28.62 | 41.82 | 25.18 | 35.15 | 1.81 | 1.34 | 1.01 | 37.94 | 23.16 | 14.78 | 0.81 | 0.34 |
223 | 27.80 | 28.51 | 41.91 | 29.58 | 33.11 | 1.84 | 1.38 | 0.95 | 38.75 | 26.20 | 12.55 | 0.55 | 0.33 |
224 | 31.80 | 28.25 | 48.63 | 23.12 | 37.85 | 1.81 | 1.32 | 1.05 | 41.02 | 28.70 | 12.33 | 0.74 | 0.36 |
225 | 5.80 | 33.00 | 40.16 | 26.84 | 38.42 | 1.76 | 1.27 | 1.12 | 45.12 | 30.08 | 15.04 | 0.55 | 0.32 |
226 | 9.80 | 23.16 | 52.02 | 24.83 | 36.20 | 1.84 | 1.35 | 0.99 | 38.43 | 22.94 | 15.48 | 0.86 | 0.25 |
227 | 13.80 | 26.46 | 44.40 | 29.15 | 33.20 | 1.87 | 1.40 | 0.93 | 36.58 | 24.14 | 12.45 | 0.73 | 0.34 |
228 | 17.80 | 28.75 | 41.37 | 29.85 | 30.20 | 1.87 | 1.44 | 0.88 | 35.02 | 23.99 | 11.03 | 0.56 | 0.37 |
229 | 21.80 | 25.55 | 49.61 | 24.84 | 36.32 | 1.82 | 1.34 | 1.02 | 40.02 | 26.99 | 13.03 | 0.72 | 0.31 |
230 | 25.80 | 24.41 | 45.98 | 29.61 | 32.20 | 1.87 | 1.41 | 0.91 | 37.28 | 23.85 | 13.43 | 0.62 | 0.34 |
231 | 29.80 | 27.04 | 42.98 | 29.97 | 29.76 | 1.88 | 1.45 | 0.87 | 36.89 | 21.02 | 15.87 | 0.55 | 0.37 |
232 | 32.80 | 29.08 | 41.68 | 29.10 | 39.77 | 1.80 | 1.29 | 1.10 | 43.19 | 31.05 | 12.13 | 0.72 | 0.34 |
233 | 5.80 | 49.10 | 38.42 | 12.48 | 32.27 | 1.86 | 1.41 | 0.91 | 35.02 | 28.95 | 6.07 | 0.55 | 0.41 |
234 | 9.80 | 31.86 | 44.65 | 23.49 | 30.08 | 1.90 | 1.46 | 0.86 | 36.22 | 21.23 | 15.00 | 0.59 | 0.35 |
235 | 13.80 | 13.85 | 56.82 | 29.33 | 37.05 | 1.81 | 1.32 | 1.04 | 42.99 | 28.31 | 14.68 | 0.60 | 0.34 |
236 | 35.80 | 33.93 | 39.51 | 26.56 | 26.85 | 1.90 | 1.50 | 0.81 | 36.88 | 23.20 | 13.69 | 0.27 | 0.46 |
237 | 37.50 | 52.50 | 35.84 | 11.66 | 30.46 | 1.82 | 1.40 | 0.92 | 33.98 | 27.82 | 6.16 | 0.43 | 0.42 |
238 | 39.50 | 31.91 | 40.25 | 27.84 | 27.63 | 1.90 | 1.49 | 0.82 | 38.02 | 23.99 | 14.02 | 0.26 | 0.42 |
239 | 21.80 | 25.81 | 46.15 | 28.04 | 40.15 | 1.76 | 1.26 | 1.15 | 46.05 | 34.12 | 11.93 | 0.51 | 0.33 |
240 | 25.80 | 28.27 | 46.89 | 24.84 | 31.23 | 1.90 | 1.45 | 0.87 | 38.01 | 24.41 | 13.60 | 0.50 | 0.37 |
241 | 29.80 | 30.35 | 41.60 | 28.05 | 34.82 | 1.87 | 1.38 | 0.95 | 39.05 | 25.44 | 13.61 | 0.69 | 0.35 |
242 | 33.80 | 26.51 | 47.16 | 26.33 | 26.85 | 1.89 | 1.49 | 0.81 | 37.05 | 20.19 | 16.86 | 0.39 | 0.43 |
243 | 24.80 | 30.60 | 44.43 | 24.97 | 32.22 | 1.87 | 1.42 | 0.91 | 39.02 | 22.42 | 16.60 | 0.59 | 0.34 |
244 | 25.80 | 36.24 | 35.85 | 27.91 | 28.03 | 1.87 | 1.46 | 0.85 | 35.66 | 20.19 | 15.47 | 0.51 | 0.36 |
245 | 29.80 | 21.71 | 51.03 | 27.26 | 41.29 | 1.76 | 1.24 | 1.17 | 46.00 | 32.95 | 13.05 | 0.64 | 0.32 |
246 | 32.80 | 25.50 | 44.92 | 29.58 | 30.47 | 1.88 | 1.44 | 0.88 | 35.22 | 24.01 | 11.21 | 0.58 | 0.35 |
247 | 35.80 | 26.45 | 52.14 | 21.41 | 33.75 | 1.85 | 1.39 | 0.95 | 38.02 | 25.00 | 13.03 | 0.67 | 0.36 |
248 | 11.00 | 45.31 | 42.36 | 9.42 | 33.36 | 1.82 | 1.37 | 0.97 | 35.95 | 29.25 | 6.70 | 0.61 | 0.35 |
249 | 8.00 | 16.35 | 54.42 | 29.14 | 41.23 | 1.75 | 1.24 | 1.17 | 44.36 | 30.21 | 14.15 | 0.78 | 0.19 |
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cao, MT., Hoang, ND., Nhu, V.H. et al. An advanced meta-learner based on artificial electric field algorithm optimized stacking ensemble techniques for enhancing prediction accuracy of soil shear strength. Engineering with Computers 38, 2185–2207 (2022). https://doi.org/10.1007/s00366-020-01116-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-020-01116-6