Abstract
We study the dependence of the spectral gap for the generator of the Ginzburg–Landau dynamics for all \(\mathcal O(n)\)-models with mean-field interaction and magnetic field, below and at the critical temperature on the number N of particles. For our analysis of the Gibbs measure, we use a one-step renormalization approach and semiclassical methods to study the eigenvalue-spacing of an auxiliary Schrödinger operator.
Similar content being viewed by others
1 Introduction and Main Results
1.1 \({\mathcal {O}}(n)\)-model
The model we are concerned with in this article is the generator of the Ginzburg–Landau dynamics, or Langevin dynamics, of the mean-field \({\mathcal {O}}(n)\)-model in the critical and supercritical regime \(\beta \ge n\), as defined precisely in Section 2. Our objective is to study the scaling of the spectral gap in terms of the system size N, for all the numbers of components \(n\ge 1\), and including the cases with or without external magnetic field, in the low temperature and critical regime, extending the study of the subcritical regime \(\beta < n\) in [BB19]. When \(\beta <n\), the spectral gap of the generator remains open uniformly in N and for any number of components n, in the full temperature range.
The mean-field \({\mathcal {O}}(n)\)-model is defined by the energy function
acting on spin configurations \(\sigma : \{1,..,N\} \rightarrow {\mathbb {S}}^{n-1}\) where \(\Delta _{\text {MF}}\) is the mean-field Laplacian and \(h \in {\mathbb {R}}^n\) an external magnetic field. For our study of spectral gaps, we consider the Ginzburg–Landau dynamics associated with the Gibbs measure \(d\rho \propto e^{-\beta H(\sigma )}\) with Hamilton function (1.1). The inverse temperature parameter \(\beta \) is such that lower temperatures (higher \(\beta \)) favors alignment of spins. The study of mean-field \({\mathcal {O}}(n)\)-models is motivated by the fact that their behavior approximates that of the full \({\mathcal {O}}(n)\)-model on high-dimensional tori [Ell85, LLP10].
1.2 State of the art and motivation
The study of spectral gaps in \({\mathcal {O}}(n)\) models is a popular problem that has received a lot of attention over the last decades. The study of logarithmic Sobolev (and other functional) inequalities is a classical and very effective tool to study concentration of measures and to quantify the relaxation rates, i.e. the mixing properties, of the dynamics. In particular, the spectral gap (the speed of relaxation) is determined by the constant in the Log-Sobolev inequalities. We define the spectral gap to be the size of the gap between 0 and the rest of the spectrum of the associated generator L, defined in (2.3). The gap then can be also characterized by
where \({\text {Var}}_\rho \) is the variance relative to the equilibrium measure \(\rho \). All these quantities will be specified for our setting in the following section. For further background on functional inequalities see [Gro93, BE85, Led99, Led01, GZ03, ABC+00] and references therein.
There are only few general approaches for the study of spectral gaps of spin systems, using log-Sobolev inequalities, available and many of them rely on an asymptotic study of log-Sobolev inequalities [LY93, SZ92a, SZ92b, SZ92c] or [MO13] for a more recent result in that direction. In the article [BB19], a simpler proof for a log-Sobolev inequality was provided for bounded and unbounded spin systems and sufficiently high temperatures. The novelty of the approach in [BB19] is the combination of the study of log-Sobolev inequalities with a simple renormalization group approach to decompose the stationary measure in a way that makes it accessible to simple Bakry-Émery techniques.
Inspired by the method in [BB19], we invoke the same one-step renormalization group procedure to reduce the high-dimensional problem to the study of a low-dimensional renormalized measure and a fluctuation measure. In the subcritical regime \(\beta < n\), which is the regime analyzed in [BB19], the renormalization of the equilibrium measure is particularly efficient, since the renormalized potential is strictly convex such that the Bakry-Émery criterion can be directly applied to this measure and implies that the spectral gap remains open. This renormalization group method has recently also been successfully applied in the study of the spectral gap for hierarchical spin models [BB] and for a lattice discretization of a massive Sine-Gordon model [BB20].
The low temperature regime, which is the regime we are concerned about within this article, has a non-convex renormalized potential. In this regime, after a single renormalization step, the renormalized potential is not convex. This makes the asymptotic analysis much more difficult and requires new methods:
While we analyze the Ising model, \(n=1\), without magnetic field, directly using explicit criteria for spectral gap and log-Sobolev inequalities [BG99, BGL14], we heavily use the equivalence between the generator of the Ginzburg–Landau dynamics and a Schrödinger operator to analyze multi-component,\(n \ge 2\), \({\mathcal {O}}(n)\)-models. This analysis builds heavily upon ideas by Simon [Sim83, CFKS87] and Helffer–Sjöstrand [HS85, HS87] who developed effective semiclassical methods to study the low-lying spectrum of Schrödinger operators in the semiclassical limit (which in our case corresponds to \(N \rightarrow \infty \)). These results are discussed thoroughly in the final chapters of [NH05]. In this article however, we have to study the spectrum of Schrödinger operators beyond the harmonic approximation. In this case, the limiting operator is not explicitly diagonalizable anymore and the spacing between eigenvalues is no longer linear in the semiclassical parameter N, the number of spins.
The mixing time of the Glauber dynamics of the mean-field Ising model \(({\mathcal {O}}(1))\) without magnetic field has been carefully analyzed in [DLP09a, DLP09b]. There it is shown-among others- that the mixing time in the subcritical regime \(\beta <1\) is \(N \log (N)\), the scaling at the critical point \(N^{3/2}\) for \(\beta =1\) and in the supercritical regime \(\beta >1\) it is exponential growing in N. This is to be compared to a spectral gap that remains open for \(\beta <1\), closes like \(N^{-1/2}\) for \(\beta =1\) and closes exponentially fast also for \(\beta >1\). Thus, the mixing time for the Glauber dynamics are -up to a factor 1/N- comparable to our findings on the spectral gap, cf. Theorem 1.
Our main result on the mean-field Ising model in the supercritical regime \(\beta >n\) is stated in the following Theorem:
Theorem 1
(Spectral gap–Supercritical Mean-field Ising models, \(\beta >1\)). Let N be the number of spins and n the number of components. For the supercritical mean-field Ising model (\(n=1, \beta >1\)), the spectral gap \(\lambda _N\) of the generator
-
for the case of small magnetic fields \(\vert h \vert < h_{\text {c}}\), closes as \(N \rightarrow \infty \) exponentially fast,
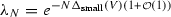 . In particular, for magnetic fields \(h \in [0,h_{\text {c}})\)$$\begin{aligned} \Delta _{\mathrm{small}}(V) = \int _{\gamma _1(\beta )}^{\gamma _2(\beta )} \beta \left( \varphi -{\text {tanh}}(\beta \varphi +h) \right) d \varphi \end{aligned}$$
. In particular, for magnetic fields \(h \in [0,h_{\text {c}})\)$$\begin{aligned} \Delta _{\mathrm{small}}(V) = \int _{\gamma _1(\beta )}^{\gamma _2(\beta )} \beta \left( \varphi -{\text {tanh}}(\beta \varphi +h) \right) d \varphi \end{aligned}$$where \(\gamma _1(\beta ) \le \gamma _2(\beta ) \in {{\mathbb {R}}}\) are the two smallest numbers satisfying the condition
$$\begin{aligned} \gamma (\beta ) = \tanh (\gamma (\beta ) \ \beta +h). \end{aligned}$$ -
For critical magnetic fields \(\vert h\vert =h_{\text {c}}\), the spectral gap does not close faster than \(\Theta (N^{-1/3})\) anymore.
-
Finally, for strong magnetic fields \(\vert h\vert > h_{\text {c}}\), it is bounded away from zero uniformly in N.
where \(h_{c}=\sqrt{\beta (\beta -1)}- {\text {arccosh}}(\sqrt{\beta }).\)
In the case of supercritical multi-component systems (\(n\ge 2, \beta >n\)) without magnetic fields, it is the rotational invariance of the model that leads to a closing spectral gap as N tends to infinity. To capture this property, we call a function \(f:({\mathbb {S}}^n)^N \rightarrow {{\mathbb {R}}}\) radial, if it is only a function of the norm of the mean spin \(\vert {\bar{\sigma }} \vert .\) Our main results for all multi-component systems in the supercritical regime \(\beta >n\) are summarized in the following Theorem:
Theorem 2
(Spectral gap–Supercritical Mean-field \({\mathcal {O}}(n)\)-models, \(\beta >n\ge 2\)). Let N be the number of spins and n the number of components. For the supercritical mean-field \({\mathcal {O}}(n)\)-models(\(n \ge 2, \beta >n\)), the spectral gap \(\lambda _N\) of the generator
-
closes as \(\lambda _N=\Theta (N^{-1})\) if there is no external magnetic field \(h=0\), but remains open \(\lambda _N= \Theta (1)\) for radial functions.
-
is bounded away from zero uniformly in the number of spins for all \(h \in {\mathbb {R}}^n\backslash \{0\}.\)
We also analyze the behavior of the spectral gap at the critical point \(\beta =n\) and \(h=0\). Using a discrete Fourier analysis approach implemented in Section 6 for the Ising case \(n=1\) and a direct asymptotic analysis for all higher component systems \(n \ge 2\), we find a different asymptotic of the spectral gap from both the supercritical \(\beta >n\) (exponentially fast closing) and subcritical \(\beta <n\) (spectral gap remains open) regimes:
Theorem 3
(Spectral gap–Critical Mean-field \({\mathcal {O}}(n)\) models, \(\beta =n\)). For all critical, \(\beta =n\), \(h=0\) mean-field \({\mathcal {O}}(n)\)-models the spectral gap closes as \(\lambda _N=\Theta (N^{-1/2})\). In particular, the rate \(N^{-1/2}\) is attained for the magnetization
We emphasize that at the critical points (\(\beta =n\), \(h=0\)), the gap does no longer close once a non-zero magnetic field is present:
Theorem 4
(Spectral gap–Mean-field \({\mathcal {O}}(n)\) models, \(\beta =n\), \(h \ne 0\) ) For all, \(\beta =n\) and \(h \ne 0\), the spectral gap of all mean-field \({\mathcal {O}}(n)\)-models remains open.
The proof of Theorem 4 is along the lines of Theorem 1 in the regime \(h > h_{\text {c}}\) and follows from Proposition 4.2 in the Ising-case, \(n=1\), and in the multi-component case, \(n \ge 2\), from Proposition 5.4.
1.3 Organization of the article
The article is organized as follows:
-
In Section 2 we introduce the mean-field \({\mathcal {O}}(n)\)-model.
-
In Section 3 we introduce the renormalized methods.
-
In Section 4 we analyze the mean-field Ising model in the supercritical regime \(\beta >1\) and prove Theorem 1.
-
In Section 5 we analyze the higher-component mean-field \({\mathcal {O}}(n)\)-models in the supercritical regime \(\beta >n\) and prove Theorem 2.
-
In Section 6 we study the critical regime and prove both Theorems 3 and 4.
-
Our article contains an appendix that contains technical details and further details on numerical methods.
Notation We write \(f(z) = {\mathcal {O}}(g(z)) \) to indicate that there is \(C>0\) such that \(\left|f(z) \right|\le C \left|g(z) \right|\) and  for \(z \rightarrow z_0\) if there is for any \(\varepsilon >0\) a neighbourhood \(U_{\varepsilon }\) of \(z_0\) such that \(\left|f(z)\right|\le \varepsilon \left|g(z) \right|.\) We say that \(f(z) = \Theta (g(z))\) if there are \( k_1, k_2>0\) and \(z_0\) such that for all \(z \ge z_0\) we have \(k_1 g(z) \le f(z) \le k_2 g(z).\) The expectation with respect to a measure \(\mu \) is written denoted by \({\mathbb {E}}_{\mu }(X).\) The normalized surface measure on the n sphere is denoted as \(dS_{{\mathbb {S}}^{n}}.\) We write \(\mathbb {1}\) to denote a vector or matrix whose entries are all equal to one and \({\text {id}}\) for the identity map. Finally, we introduce the notation \([N]:=\left\{ 1,...,N \right\} .\) The eigenvalues of a self-adjoint matrix A shall be denoted by \(\lambda _1(A)\le ... \le \lambda _N(A)\).
for \(z \rightarrow z_0\) if there is for any \(\varepsilon >0\) a neighbourhood \(U_{\varepsilon }\) of \(z_0\) such that \(\left|f(z)\right|\le \varepsilon \left|g(z) \right|.\) We say that \(f(z) = \Theta (g(z))\) if there are \( k_1, k_2>0\) and \(z_0\) such that for all \(z \ge z_0\) we have \(k_1 g(z) \le f(z) \le k_2 g(z).\) The expectation with respect to a measure \(\mu \) is written denoted by \({\mathbb {E}}_{\mu }(X).\) The normalized surface measure on the n sphere is denoted as \(dS_{{\mathbb {S}}^{n}}.\) We write \(\mathbb {1}\) to denote a vector or matrix whose entries are all equal to one and \({\text {id}}\) for the identity map. Finally, we introduce the notation \([N]:=\left\{ 1,...,N \right\} .\) The eigenvalues of a self-adjoint matrix A shall be denoted by \(\lambda _1(A)\le ... \le \lambda _N(A)\).
2 The Mean-Field \({\mathcal {O}}(n)\)-Model
We study the mean-field \({\mathcal {O}}(n)\)-model with spin configuration \(\sigma : [N] \rightarrow {\mathbb {S}}^{n-1}\) and introduce the mean-field Laplacian \((\Delta _{\text {MF}}\sigma )(x):= \tfrac{1}{N}\sum _{y \in [N]} \left( \sigma (y)-\sigma (x)\right) .\)
The mean spin is defined as \({\overline{\sigma }}:=\tfrac{1}{N} \sum _{x \in [N]} \sigma (x).\) The energy of a spin configuration \(\sigma \) is given by the Curie–Weiss Hamiltonian
where the constant vector \(h \in {\mathbb {R}}^n\) represents an external magnetic field and \(\beta \) is the inverse temperature of the system. The critical temperature for the \({\mathcal {O}}(n)\)-models is \(\beta =n\) and we study both regimes: the supercritical regime \(\beta >n \) and the critical regime \(\beta =n\).
The dynamics we consider is the continuous-time Ginzburg–Landau dynamics
to the invariant distribution of the mean-field \({\mathcal {O}}(n)\)-model which is the Gibbs measure \(d\rho (\sigma ):=e^{- \beta H(\sigma )} /Z \ dS^{\otimes N}_{{\mathbb {S}}^{n-1}}(\sigma )\) with normalizing constant Z. The operators \(\Delta ^{(x)}_{{\mathbb {S}}^{n-1}}\) defined by \(\langle f,-\Delta ^{(x)}_{{\mathbb {S}}^{n-1}}f \rangle :=\langle \nabla ^{(x)}_{{\mathbb {S}}^{n-1}}f,\nabla ^{(x)}_{{\mathbb {S}}^{n-1}}f\rangle \) and \(\nabla ^{(x)}_{{\mathbb {S}}^{n-1}}\) are the Laplace-Beltrami and gradient operator on \({\mathbb {S}}^{n-1}\) acting on spin i, respectively. We recall that for the Ising model \(n=0\) and a function \(F:{\mathbb {S}}^0 \rightarrow {\mathbb {R}}\), the gradient is given by \((\nabla _{{\mathbb {S}}^0} F)(\sigma )=F(\sigma )-F(-\sigma ).\) The \(L^2\left( ({\mathbb {S}}^{n-1})^N\right) \)-adjoint of the generator of the Kramers–Smoluchowski equation (2.2) is the generator
Studying the operator L on the weighted space \(L^2\left( ({\mathbb {S}}^{n-1})^N, \ d\rho \right) \) makes this generator self-adjoint. The quadratic form of the generator (2.3) is just a rescaled Dirichlet form
3 Renormalized Measure and Mathematical Preliminaries
We start with the definition of entropy with respect to probability measures:
Definition 3.1
(Entropy). For a probability measure \(\mu \) on some Borel set \(\Omega \) the entropy \({\text {Ent}}_{\mu }(F)\) of a positive measurable function \(F:\Omega \rightarrow {\mathbb {R}}_{\ge 0}\) with \(\int _{\Omega } F(x) \log ^+(F(x)) \ d\mu (x)< \infty \) is defined as
Instead of studying the generator of the dynamics directly, we apply a one step renormalization first [BBS19, Sec. 1.4]:
Definition 3.2
(Renormalized quantities). The renormalized single spin potential \(V_n\) associated with the mean-field \( {\mathcal {O}}(n)\)-model for \(\varphi \in {\mathbb {R}}^n\) is defined as
where I is the modified Bessel function of the first kind. The N-particle renormalized measure is defined for a normalizing constant \(\nu _N^{(n)}\) by
Definition 3.3
(Fluctuation measure). For any \(\varphi \in {\mathbb {R}}^n,\) there is a probability measure \(\mu _{\varphi }\), the fluctuation measure, on \(\left( {\mathbb {S}}^{n-1}\right) ^N\) defined as
A straightforward calculation shows that the stationary measure \(d\rho \) can be decomposed into the fluctuation and renormalized measure such that \({\mathbb {E}}_{\rho }(F)= {\mathbb {E}}_{\nu _N}({\mathbb {E}}_{\mu _{\varphi }}(F)).\)
Example 1
In the case of the Ising model \((n=1)\) the renormalized potential is
For the XY model \((n=2)\) the renormalized potential reads
where I is the modified Bessel function of the first kind.
For the Heisenberg model \((n=3)\) one finds
For the N-asymptotic study of eigenvalues we observe that the renormalized potential grows quadratically at infinity such that \(\Delta V_n \in L^{\infty }({\mathbb {R}}^n).\)
The Ginzburg–Landau dynamics dynamics for the renormalized measure is then given by the self-adjoint operator \(L_{\text {ren}}:D(L_{\text {ren}}) \subset L^2({\mathbb {R}}^n, d\nu _N) \rightarrow L^2({\mathbb {R}}^n, d\nu _N)\), satisfying
The renormalized generator \(L_{\text {ren}}\) satisfies
The renormalized Schrödinger operator with null space spanned by \(e^{-NV_n} \) is the operator defined by conjugation \(- \Delta _{{\text {ren}}} = e^{-NV_n/2} L_{\text {ren}} e^{NV_n/2}\)
Definition 3.4
(LSI and SGI). Let \(\mu \) be a Borel probability measure on \({\mathbb {R}}^n\). We say that \(\mu \) satisfies a logarithmic Sobolev inequality LSI(k) iff
for all smooth functions f. The LSI(k) implies [Led99, Prop. 2.1] that \(\mu \) satisfies a spectral gap inequality SGI(k)
Thus, in light of the characterisation (1.2), the spectral gap of \(L_{\text {ren}}\) is by (3.8) precisely the constant in the SGI of the renormalized measure.
Remark 1
If f vanishes outside a set \(\Omega \) of measure \(\mu (\Omega ) <1\) and if \(\mu \) satisfies a SGI(k) then
For Borel probability measures \(\mu \) on \({\mathbb {R}}\) there is an explicit characterization of the measures satisfying a LSI [BG99, Theorem 5.3]:
Any such measure \(\mu \) satisfies a LSI(k) iff there exist absolute constants \(K_0=1/150\) and \(K_1=468\) such that the optimal value k in the LSI(k) satisfies \(K_0(D_0+D_1)\le 1/k \le K_1(D_0+D_1)\) for finite \(D_0\) and \(D_1\). Let m be the median of \(\mu \) and \(p(t) \ dt\) the absolutely continuous part of \(\mu \) with respect to Lebesgue measure. The constants \(D_0\) and \(D_1\) are given by
For constants
one defines the Muckenhoupt number [Muc72] \(B:={\text {max}}(B_0,B_1).\) The measure \(\mu \) satisfies then a SGI with optimal constant \(c=1/k\) if and only if B is finite in which case
[BGL14, Theorem 4.5.1].
Remark 2
The proof given in [BG99, Theorem 5.3] shows that the characterization of LSI constants holds true not only by splitting at the median: Instead, there is \(\varepsilon >0\) such that for any \(\zeta \) for which \(\mu ((-\infty ,\zeta ]), \mu ([\zeta ,\infty )) \in (1/2-\varepsilon ,1/2+\varepsilon )\) the above characterization (3.11) holds true when the median m is replaced by \(\zeta .\) The same is, up to an unimportant adaptation of the lower bound in (3.13), for the SGI as well, cf. [GR01, Prop. 3.2 + 3.3].
We continue by observing that the fluctuation measures satisfy a LSI(\(\tfrac{2}{\gamma _n}\)) independent of h or \(\varphi \). This follows for \(n=1\) with \(\gamma _n = 4\) from a simple application of the tensorization principle to the classical bound on the Bernoulli distribution [ABC+00, Led01, SC97]. For number of components \(n \ge 2\) one can use the results from [ZQM11].
Proposition 3.5
Let the renormalized measure \(\nu _N\) satisfy a LSI(\(\lambda \)), then the full equilibrium measure \(\rho \) satisfies a LSI
and if the renormalized measure \(\nu _N\) satisfies a SGI(\(\lambda \)), then the equilibrium measure \(\rho \) satisfies a SGI
Proof
The proof of the SGI is as follows: For the SGI we obtain the decomposition
To bound the second term in the above estimate, we compute using the Cauchy–Schwarz inequality and the spectral gap inequality for fluctuation measures \(\mu _{\varphi }\) on the sphere, defined by (3.4) such that, see [BB19, Theorem 1, (11)–(15)],
We then use that by the explicit expression (3.2)
Inserting this into (3.15) we find that
Thus, we have using Cauchy–Schwarz that
We can then use that by Cauchy–Schwarz again
Finally, inserting this into (3.17) and using the LSI for the fluctuation measure, we find
which after inserting this bound into (3.14) implies the claim. To prove the LSI we follow [BB19] and write
For the second term we have from applying the Cauchy–Schwarz inequality:
By doubling the variables \(\sigma _x, \sigma _x'\), we write
where in the last two lines we applied CS inequality and used that \( | \sigma _x - \sigma _x'|\le 2\). Then
This gives
Overall we have
\(\square \)
4 The Mean-Field Ising Model
Without loss of generality, we assume \(h \ge 0\) when studying the Ising model. We define the critical magnetic field strength in the Ising model
for temperatures \(\beta \ge 1\) as the supremum of all \(h>0\) such that \(x = \tanh (\beta x+h)\) has three distinct solutions for \(x \in [-1,1].\) In particular \(h_c(\beta )\) is monotone with respect to the inverse temperature \(\beta \).
The critical magnetic field strength is chosen in such a way that for fields \(h<h_c(\beta )\) there are two potential wells in the renormalized potential landscape, see Figure 1, whereas for \(h \ge h_c(\beta )\) there is only one, see Figure 2 in subsection 4.3 where this case is discussed.
4.1 Lower bound on spectral gap in weak field \(h< h_c(\beta )\) regime
We start by showing that the inverse spectral gap in the Ising model in the case of subcritical magnetic fields, i.e. \(h<h_c(\beta ),\) converges at most exponentially fast to zero as the number of spins, N, increases.
We start by showing a LSI with exponential constant for the renormalized measure. This implies by Prop. 3.5 that such an LSI must also hold for the full many-particle measure \(d\rho .\)
Proposition 4.1
(LSI for \(\nu _N\))
Let \(\beta >1\) and \(h<h_c(\beta )\) such that \(V_1\) is a double well potential where the depth of the smaller well is denoted by \(\Delta _{\mathrm{small}}(V),\) cf. Fig. 1. The mean-field Ising model satisfies a LSI Footnote 1
Footnote 1

Proof
The renormalized potential \(V_1\) has on \([0,\infty )\) a global minimum with positive second derivative at some \(\varphi _{\text {min}}\) satisfying \(\varphi _{\text {min}} = \tanh (\beta \varphi _{\text {min}}+h).\) This follows since the renormalized potential (3.2) reduces to
and the critical points of this potential are easily found to satisfy \(\varphi = \tanh (\beta \varphi +h),\) see also [BBS19, Lemma 1.4.6]. For small temperatures, i.e. \(\beta \rightarrow \infty ,\) one has 
We first consider \(h=0\): In this case, the median of the renormalized measure is located precisely at \(\varphi =0\) and \(\varphi _{\text {min}}>0\) is one of the two non-degenerate global minima of the renormalized potential (the other minimum is located at \(-\varphi _{\text {min}}\) by axisymmetry).
An application of Laplace’s principle, see [Won01, Ch. II,Theorem 1], shows that for all \(x>0:\)
The supremum of (4.1) is attained at \(x=\varphi _{\text {min}}\) such that
Here, we used that for \(x> \varphi _{\text {min}}\) we get by Laplace’s principle

and thus \(\lim _{N \rightarrow \infty } \tfrac{\log \left( -\log \left( \nu _N [x,\infty ) \right) \right) }{N}=0.\)
On the other hand, if \(x \in (0,\varphi _{\text {min}})\) then, again by Laplace’s principle,  and thus \(\lim _{N \rightarrow \infty } \tfrac{\log \left( -\log \left( \nu _N [x,\infty ) \right) \right) }{N}=0\) as well. The case \(x=\varphi _{\text {min}}\) can be treated analogously. Hence, we obtain for the constant \(D_1\) as in (3.11)
and thus \(\lim _{N \rightarrow \infty } \tfrac{\log \left( -\log \left( \nu _N [x,\infty ) \right) \right) }{N}=0\) as well. The case \(x=\varphi _{\text {min}}\) can be treated analogously. Hence, we obtain for the constant \(D_1\) as in (3.11)

The symmetry of the distribution for \(h=0\) implies then that \(D_0=D_1\).
We now consider \(h>0\): The renormalized potential possesses a unique global minimum at some \(\varphi _{\text {min}}\) and the median of the renormalized measure converges to this point \(\varphi _{\text {min}}\), see Fig. 1, as Laplace’s principle implies
Hence, it suffices to verify the LSI bounds (3.11) for \(m=\varphi _{\text {min}}\) as argued in Remark 2.
Arguing as in (4.2) yields for \(h>0\) and \(x< \varphi _{\text {min}}:\)
which shows  by taking x to be the minimum of the smaller well of the renormalized potential. For the constant \(D_1\) we get on the other hand for \(x>\varphi _{\text {min}}\), since the renormalized potential is monotonically increasing on \([\varphi _{\text {min}},\infty ),\)
by taking x to be the minimum of the smaller well of the renormalized potential. For the constant \(D_1\) we get on the other hand for \(x>\varphi _{\text {min}}\), since the renormalized potential is monotonically increasing on \([\varphi _{\text {min}},\infty ),\)
such that \(D_1\) is negligible compared with \(D_0.\) \(\quad \square \)
4.2 Upper bound on spectral gap in weak field \(h<h_c(\beta )\) regime
The upper bound on the spectral gap is obtained by finding an explicit trial function saturating the SGI. For this construction, we use the notation and results of Lemma B.1.
In order to fix ideas first, we assume \(h=0\). We start by observing that the mean spin \({\overline{\sigma }}\) can only take values in the set \({\mathcal {M}}:=\left\{ -1, -1+2/N,...,1 \right\} .\) The weights of the stationary measure \(d\rho \) are given by functions \(\eta _N:{\mathcal {M}} \rightarrow {\mathbb {R}}\)
where we used (2.1).
We also introduce trial functions \(f_N: \left\{ \pm 1 \right\} ^N \rightarrow {\mathbb {R}}\) for the spectral gap inequality given by
with indicator function \(\mathbb {1}\) and \(\gamma _3(\beta )\) is the largest solution to \(\varphi = \tanh (\beta \varphi +h).\) Since \(f_N\) depends only on the mean spin, we can identify them with functions \(g_N:{\mathcal {M}} \rightarrow {\mathbb {R}}\)
For the \(L^2\) norm of the \(f_N\) we find
where Z is the normalization constant of the full measure \(d\rho \). For the gradient of \(f_N\) we find
Hence, for some \(C>0\)
Using (3.10) with \(\mu (\Omega ) = \tfrac{1}{2}\) implies by comparing (4.7) with (4.8) that the constant \(\gamma \) in the SGI is bounded from below by
We recall from the discussion in Lemma B.1 that the continuous approximation \(\eta _N(i)\) attains its maximum in the limit at \(i= \gamma _3(\beta )\) and the summand \(\frac{1}{\eta _N(i)}\) in the second sum attains its maximum in the limit at \(i= 0\).
Thus it suffices to study the asymptotic of the logarithm of the leading order summands in (4.9) using the asymptotic behaviour of \(\zeta _{N} := \partial _s \log (\eta _{N}(s))\) given in (B.1)

Here, we used integration of the inverse function to obtain the last line and (3.5) in the last one. In the case of a positive weak magnetic field \(h \in (0, h_c(\beta ))\) we choose a trial function \(f_{N,h}: \left\{ \pm 1 \right\} ^N \rightarrow {\mathbb {R}}\) given by
Proceeding as above in (4.7) we obtain for the \(L^2\) norm the lower bound
For the Dirichlet form we find, as for (4.8), for some \(C>0\)
We can apply (3.10) with \(\mu (\Omega ) = \tfrac{1}{1-\varepsilon }\) for some \(\varepsilon >0\) since the trial function (4.10) vanishes to the right of the global maximum such that by comparing (4.11) with (4.12) the constant \(\gamma \) in the SGI is bounded from below by
The weight \(\eta _{N,h}(i)\) in the first sum attain their maximum (in the limit) at \(i=\gamma _1(\beta )\) and the summands \(\frac{1}{\eta _{N,h}(i)}\) in the second sum attain their maximum at \(i=\gamma _2(\beta )\).
To explicitly state an upper bound on the spectral gap it suffices to study the asymptotic of the logarithm of the leading order summands

4.3 Spectral gap in strong magnetic field regime \(h> h_{c}(\beta )\)
Next, we study the case of strong magnetic fields for the Ising model, that is \(V_1'\) has at most one root, for \(\beta >1\). We also include the case \(\beta =1\) and \(h \ne 0\). Unlike in the case of weak magnetic fields, in which case the constant in the LSI for the renormalized measure is exponentially increasing in the number of spins, the spectral gap of the renormalized measure is now linearly increasing in the number of spins. Responsible for this uniform gap is the local uniform convexity at the minimum of the renormalized potential. More precisely, we have
Thus, \(V_1''(\varphi )=0\) yields \(\varphi _{\pm }= \frac{-h \pm {\text {arccosh}}(\sqrt{\beta })}{\beta }.\) Inserting this into \(V_1'(\varphi _{\pm })=0\) implies that \(h_{\pm }=\pm {\text {arccosh}}(\sqrt{\beta }) \mp \sqrt{\beta (\beta -1)}\) with sign \({{\,\mathrm{sgn}\,}}(h_{\pm })=\mp 1\) and thus \(\varphi _{\pm }= \pm \sqrt{\frac{\beta -1}{\beta }}.\) In particular, in the subcritical regime \(\beta >1\) all global minima \(\varphi _{*}\) have sign \({{\,\mathrm{sgn}\,}}(\varphi _{*})={{\,\mathrm{sgn}\,}}(h)\), such that the renormalized potential satisfies \(V_1''(\varphi _{*})>0.\) Moreover, for \(\beta =1\) and \(h \ne 0\) there are no points at which both the first and second derivative vanish. The third derivative at this point however is always non-zero and given by
Proposition 4.2
(Ising model, strong field). Let \(\beta \ge 1\) and \(h> h_c(\beta )\), i.e. \(V_1\) is a single well potential. We obtain for the Ising model a SGI\((\gamma )\)
where \(\frac{1}{\gamma }\) is uniformly bounded in N.
Proof
Since the renormalized Schrödinger operator and renormalized generator are unitarily equivalent up to a factor, see (3.9), the semiclassical eigenvalue distribution stated in [Sim83, Theo. 1.1] implies the statement of the Proposition:
It follows immediately from the renormalized Schrödinger operator (3.9)
that the low-lying eigenfunction of \(\Delta _{\text {ren}}\) accumulate at the unique non-degenerate (the second derivative is non-zero) potential well and the spectral gap of the renormalized measure grows linearly in N. The result then follows from Prop. 3.5. \(\quad \square \)
4.4 Critical magnetic fields in \(n=1\)
Proposition 4.3
Let \(h=h_{\pm }\) and \(\beta > 1.\) The spectral gap of the radial renormalized Schrödinger operator grows as \(\Theta ( N^{2/3})\) and in particular, the spectral gap of the full measure does not close faster than \(\Theta ( N^{-1/3}).\)
Proof
Let \(\lambda := N/2\) and consider the Schrödinger operator, defined in (3.9),
for the renormalized potential and auxiliary Schrödinger operators, which are obtained as the Taylor expansion of (4.16)
on \(L^2({{\mathbb {R}}})\) localized to the two critical points, the inflection point \(\varphi _{\pm }\) and the global minimum \(\varphi _{*}.\) We then define \(j \in C_c^{\infty }((-2,2);[0,1])\) such that \(j(x)=1\) for \(\left|x\right|\le 1\) and from this functions
Invoking then unitary maps \(U_{\varphi _{*} }, U_{\varphi _{\pm }} \in {\mathcal {L}}(L^2({\mathbb {R}}))\) defined as
shows that the two Schrödinger operators in (4.17) are in fact unitarily equivalent, up to multiplication by powers of \(\lambda \), to the \(\lambda \)-independent Schrödinger operators
respectively. Both operators have discrete spectrum and that \(\inf ({{\,\mathrm{Spec}\,}}(S_{\varphi _{\pm }}))>0\) is shown in Section C. We illustrate the behaviour of the smallest eigenvalues of \(S_{\varphi _{\pm }}\) in Figure 4. More precisely, we have that
Taylor expansion of the potential at the respective critical point and the estimate on the gradient (4.18) imply that
Let \(0=e_1<e_2\le ..\) be the eigenvalues (counting multiplicities) of \(S_{\varphi _{*}}\) and \(0<f_1\le f_2\le ...\) the ones of \(S_{\varphi _{\pm }}\) and choose \(\tau \) such that \(\lambda e_{n+1}>\tau >\lambda e_n\) and \(\lambda ^{2/3} f_{m+1}>\tau >\lambda ^{2/3} f_m\) with \(P_i\) being the projection onto the eigenspace to all eigenvalues of \(S_i\) below \(\tau .\)
The IMS formula, see [CFKS87, (11.37)] for a version on manifolds, implies that
On the other hand, it follows that
and also
In particular, we find
and
This implies for large \(\lambda \) that
From (4.23) we then conclude that for some \(C>0\)
This implies the claim of the Proposition, since
More precisely, for the eigenvalues \(E_1(\lambda )\le E_2(\lambda )\le ..\) of \({\mathcal {H}}\) we have shown that
In particular, the lowest possible eigenvalue \(e_1=0\) of the renormalized Schrödinger operator is of course attained as the nullspace of the renormalized Schrödinger operator \(H_{\varphi _{*}}\) is non-trivial. This shows that the spectral gap of the renormalized Schrödinger operator grows at least proportional to \(\lambda ^{2/3}.\) \(\quad \square \)
5 Multi-component \({\mathcal {O}}(n)\)-Models
5.1 \(n\ge 2\): Zero magnetic field, \(h=0\)
Let \(h=0\) then the renormalized potential for \(n \ge 2\) is radially symmetric and possesses a critical point at \(\varphi =0\). In the supercritical case, i.e. \(\beta >n,\) the renormalized potential possesses another critical radius \(r=\Vert \varphi \Vert \in (0,1),\) see Fig. 6. To see this, we differentiate the renormalized potential
It is now obvious that \(r=0\) is a critical point of the renormalized potential at which
where we used that \(\beta >n\) is supercritical. To conclude the existence of precisely one other critical radius \(r_{\text {min}}\) at which the renormalized potential attains its global minimum it suffices therefore to show that \(\tfrac{I_{n/2}(\beta r)}{r I_{n/2-1}(\beta r)}\) decays monotonically to zero. We prove this in Lemma B.2 in the appendix. This implies that also the factor \(\left( 1- \tfrac{I_{n/2}(\beta r)}{r I_{n/2-1}(\beta r)} \right) \) has precisely one root, i.e. the second critical radius.
In the next proposition we show that the radial part of the measure \(d\nu _N(\varphi )\) which we denote by \(dr_N:=\nu _N^{(n)} r^{n-1} e^{-NV_n(r)} \ dr\) in the sequel satisfies a SGI with a constant that is uniformly bounded in the number of spins.
5.2 Zero magnetic field—a lower bound on the spectral gap
When \(h=0\) and \(n \ge 2\), then the renormalized Schrödinger operator (3.9) for \(\lambda :=N/2\) is the self-adjoint operator
This operator is also rotationally symmetric such that by separating (spherical coordinates) the angular part from the radial part, the remaining radial component \(\Delta ^{\text {rad},\ell }_{\text {ren}}\) of the renormalized Schrödinger operator on \(L^2((0,\infty ),r^{n-1} dr )\) for \(\ell \in {\mathbb {N}}_0\) reads
Here, the term \(\ell (\ell +n-2)\) accounts for the eigenvalues of the angular part of the Laplacian. The renormalized potential possesses, when \(h=0\) and \(n \ge 2\), exactly two critical radii at which \(\left|\partial _r V_n(r) \right|^2=0.\) The radii are \(r=0\) and \(r=r_{\text {min}},\) see the beginning of this Section 5.1. However, \(V_n(r)\) is strictly concave at 0, i.e. \( \partial _r^2 V_n(0)<0,\) and by Lemma B.2 strictly convex at \(r_{\text {min}}\) such that \( \partial _r^2 V_n(r_{\text {min}})>0\). This follows from
see the beginning of Section 5.
By the tensorization principle we already know that the rotational invariance of the renormalized measure implies that the spectral gap inequality for the renormalized measure is at least uniform in N. In our next Proposition we therefore study the low-lying spectrum of the radial component, \(\Delta _{\text {ren}}^{\text {rad},0}\), as \(\lambda \rightarrow \infty \).
Proposition 5.1
Let \(h=0\), \(n \ge 2\) and \(\beta >n.\) The spectral gap of the radial renormalized Schrödinger operator \(\Delta _{\text {ren}}^{\text {rad},0}\) grows linearly in N.
Proof
To study the low-lying spectrum of the radial component of the renormalized Schrödinger operator, let \(\lambda := N/2\) and consider Schrödinger operators
where we use the variable x rather than r to emphasize that the last operator is defined on \(L^2({\mathbb {R}})\), unlike the first one which is an operator on \(L^2((0,\infty ),r^{n-1} \ dr).\) Observe that in (5.3) we replaced the gradient term of the Schrödinger operator by its Taylor approximation at the critical point. This explains the occurrence of the second derivative at the critical point in (5.3). Invoking the unitary maps \(U_0 \in {\mathcal {L}}( L^2((0,\infty ),r^{n-1} \ dr))\) and \(U_{r_{\text {min}}} \in {\mathcal {L}}(L^2({\mathbb {R}}))\) defined as
shows that the two Schrödinger operators in (5.3) are in fact unitarily equivalent, up to multiplication by \(\lambda \), to the \(\lambda \)-independent Schrödinger operators
respectively. More precisely, we have that
Since the bottom of the spectrum of the operator \(S^0_{\text {osc}}\) is strictly positive \(S^0_{\text {osc}}\ge -\partial _r^2 V_n(0)>0,\) we conclude from (5.6) that the bottom of the spectrum of \(H^{0}_{\text {osc}}(\lambda )\) increases linearly to infinity as \(\lambda \rightarrow \infty .\)
To connect the low-energy spectrum of the renormalized Schrödinger operator with the above auxiliary operators, take \(j \in C_c^{\infty }(-\infty ,2)\) such that \(j(x)=1\) for \(\left|x \right|\le 1.\) Then, we define
for \(i \in \left\{ 0,r_{\text {min}} \right\} \) and \(J := \sqrt{1-J_{r_{\text {min}}}^2-J_0^2}.\)
Without loss of generality we can assume that \(\lambda \) is large enough such that \(J_0\) and \(J_{r_{\text {min}}}\) are disjoint.
Taylor expansion of the potential at 0 and \(r_{\text {min}}\) respectively and the estimate on the gradient (5.7) imply that
Let \(0=e_1<e_2\le ..\) be the eigenvalues (counting multiplicities) of \(S^{0}_{\text {osc}} \oplus S^{r}_{\text {osc}}\) and choose \(\tau \) such that \(e_{n+1}>\tau >e_n\) with \(P_i\) being the projection onto the eigenspace to all eigenvalues of \(H^{i}_{\text {osc}}\) below \(\tau \lambda .\) The IMS (Ismagilov, Morgan, and Simon/Sigal) formula, see [CFKS87, (11.37)] for a version on manifolds, implies that
such that
On the other hand, it follows that
By construction, since \(\nabla V_n\) vanishes linearly on the support of \(J_i,\) we have
Since \(\Delta V_n\) is globally bounded anyway, this implies for large \(\lambda \) that
From (5.8) we then conclude that for some \(C>0\)
This implies the claim of the Proposition, since
More precisely, for the eigenvalues \(E_1(\lambda )\le E_2(\lambda )\le ..\) of \(\Delta ^{\text {rad},0}_{\text {ren}}\) we have shown that
In particular, the lowest possible eigenvalue \(e_1=0\) of the renormalized Schrödinger operator is of course attained as the nullspace of the renormalized Schrödinger operator is non-trivial. This shows that the spectral gap of the renormalized Schrödinger operator grows at least linearly in \(\lambda \) in the angular sector \(\ell =0\). \(\quad \square \)
Corollary 5.2
Let \(h=0\), \(n \ge 2\) and \(\beta >n\). The spectral gap of the full Gibbs measure \(\rho \) does not close faster than \(\Theta (1/N).\) In particular, for radial functions, i.e. f only depends on \(\vert {\bar{\sigma }} \vert ,\) the spectral gap remains open.
Proof
Since the spectral gap of the radial component of the renormalized measure grows linearly in N and the spectral gap of the angular component is uniform in N, the tensorization principle implies that the full renormalized measure satisfies a SGI that is uniform in N. Due to Proposition 3.5, the spectral gap of the full measure does therefore not close faster than of order 1/N.
For radial functions f, the \({{\mathbb {R}}}^n \ni \varphi \mapsto E_{\mu _{\varphi }}(f)\) maps also into radial functions and therefore the spectral gap of the renormalized measure is only determined by the radial renormalized Schrödinger operator in Prop. 5.1. Using Proposition 3.5 and (3.14), this implies that for radial functions, the gap remains open. \(\quad \square \)
In the next Proposition we show that the rate \(N^{-1}\) in this case is in fact optimal:
Proposition 5.3
Let \(h=0\), \(n \ge 2\) and \(\beta >n\). The spectral gap of the full measure \(\rho \) of the dynamics decays at least as fast as \(N^{-1}\).
Proof
We consider the mean-spin \({\bar{\sigma }}:({\mathbb {S}}^n)^N \rightarrow {{\mathbb {R}}}^{n+1}\) defined by
In analogy to the spherical harmonics which in cartesian coordinates reads \(x_1/\Vert x \Vert \), we consider the function:
where \(\eta \in C^{\infty }(\mathbb {R};[0,1])\) is a cut-off function such that for fixed \(1>\delta >0\):
As we want to compute the covariant derivative \(\nabla _{\sigma _1} t(\sigma ), \) we consider the parametrisation \(\gamma _1(t)\) so that \(\gamma _1(0)= \sigma _1\). Then we define \(\gamma (t):=(\gamma _1(t), \sigma _2, \dots , \sigma _N)\) and \(s(t):= {\bar{\sigma }}(\gamma (t))\). It is then clear that for \(v:=\gamma _1'(0)\) we have \(s'(0)=v/N\), the first coordinate of which is \(s_1'(0)=\langle e_1, v \rangle /N\). We define then
Thus, since \(f(\gamma (t))=\frac{s_1(t)}{\Vert s(t) \Vert },\) we find for the derivative
Therefore, we see that in terms of
the derivative is just
The cut-off function \(\eta \) ensures that \(\vert {\bar{\sigma }} (\sigma ) \vert \) is not small. Therefore we can bound \(| Z(\sigma )| ={\mathcal {O}}(1)\) which implies that \( \mathbb {E}_{\rho }(| \nabla _{\sigma _1}{\bar{\sigma }}(\sigma )|^2) \lesssim 1/N^2\) or that
By rotational symmetry we also know that \({\mathbb {E}}_{\rho }(f)=0\). For the second moment \({\mathbb {E}}_{\rho }(f(\sigma )^2)\), we have by rotational invariance again
where \(\mathcal {R}_N\) is the error
Our aim is now to argue that \( \mathcal {R}_N\) is small as N is large.
For \(\beta >n\) we know that the renormalized potential attains its minimum at hyperspheres \(\partial B_{{{\mathbb {R}}}^n}(0,r_{\text {min}}).\) This implies that the renormalized measure concentrates at such \(\varphi \in \partial B(0,r_{\text {min}})\) with exponential tail bounds, i.e. the probability of \(\varphi \) away from \(\partial B(0,r_{\text {min}})\) is exponentially small in N. The fluctuation measure then enforces that also the mean spin \({\bar{\sigma }} \) has to be outside of a ball of radius \(\delta >0\) with high probability. To see this recall that the fluctuation measure can be rewritten as
Here, the radial normalizing function
is a strictly monotonically increasing function of \(\vert \varphi \vert \) that satisfies \({\mathcal {N}}(\varphi ) \ge 1\) and \({\mathcal {N}}(\varphi )=1\) if and only if \(\varphi =0\). This follows directly from the Taylor series of the modified Bessel function.
Hence, we can pick \(\delta \) such that \(e^{\beta \langle \varphi , {\bar{\sigma }} \rangle } < (1+{\mathcal {N}}(\varphi ))/2\) for all \(\varphi \in \partial B(0,r_{\text {min}})\) and \(\vert {\bar{\sigma }} \vert \le \delta .\) Hence, we see that for such \(\varphi \)
This shows that \( {\mathbb {E}}_{\rho }(\mathbb {1}_{\vert {\bar{\sigma }} \vert \le \delta }) = {\mathcal {O}}\left( \left( \frac{1}{2{\mathcal {N}}(\varphi )}+\frac{1}{2} \right) ^N \right) \) and hence that \({\mathcal {R}}_N\) tends exponentially fast to zero as well, as N tends to infinity, under the condition that \(\beta >n.\) \(\quad \square \)
5.3 Nonzero magnetic fields for \(n\ge 2\)
The situation \(h\ne 0\) and \(n \ge 2\) cannot be reduced to a one-dimensional model due to lack of symmetries. Yet, the renormalized Schrödinger operator provides a very elegant tool to show that the spectral gap of the full generator of the Ginzburg–Landau dynamics dynamics remains open as \(N \rightarrow \infty .\)
In fact, whereas the global minimum for \(h=0\) of the renormalized potential is attained on a hypersphere, the global minimum for \(h \ne 0\) is attained at a single point, only. This allows us to identify the asymptotic of the low-energy spectrum of the renormalized Schrödinger operator directly with the spectrum of a quantum harmonic oscillator.
Let \(\varphi _{\text {c}} \in {\mathbb {R}}^n\) be a critical point of the renormalized potential (3.2). We define the set
where \(\lambda _1,...,\lambda _n\) comprise the entire spectrum of \(D^2V_n(\varphi _{\text {c}})\).
Let \(e_k\) be the k-th smallest element counting multiplicity in \(\Sigma \) we then have the following Proposition:
Proposition 5.4
Let \(h \ne 0\), \(\beta \ge n\), and \(n \ge 2\). Let \(E_k(\lambda )\) denote the k-th lowest eigenvalue of the renormalized generator then this eigenvalue satisfies the asymptotic law \(\lim _{\lambda \rightarrow \infty } \frac{E_k(\lambda )}{\lambda } = e_{k}.\) In particular, the ground state of the renormalized generator in the limit as \(\lambda \rightarrow \infty \) is unique and the spectral gap of the renormalized Schrödinger operator remains open and linearly in \(\lambda \).
Proof
When \(h \ne 0\) then the renormalized potential has a unique non-degenerate minimum. To see this recall that the renormalized potential reads
Introducing the new variable \(\zeta :=\beta \varphi + h\) implies that
Computing the gradient of that expression yields
where we introduced the auxiliary function \(g_{\beta }(r):= \left( \frac{r}{\beta } - \frac{I_{n/2} (r)}{I_{n/2-1}( r)}\right) \). Thus for the gradient to vanish the vectors h and \(\zeta \) have to be linearly dependent.
Assuming thus that \({\widehat{e}}_h = \pm {\widehat{e}}_{\zeta }\) we obtain from setting the gradient to zero the following equation
Thus, when h and \(\zeta \) are aligned, there is precisely one solution, the global minimum of the renormalized potential, satisfying
with \(g_{\beta }(\Vert \zeta \Vert )= \beta ^{-1}\Vert h \Vert >0.\) That the aligned scenario corresponds to the global minimum is evident from the expression of the renormalized potential (5.17).
The simplicity of the solution follows since the left hand side \(\tfrac{ \beta I_{n/2} (\left\Vert \zeta \right\Vert ) }{ I_{n/2-1}( \left\Vert \zeta \right\Vert )}\) is a concave, monotonically increasing function from 0 to \(\beta \) as \(\left\Vert \zeta \right\Vert \rightarrow \infty .\)
When h and \(\zeta \) point in opposite directions, there can, by concavity of the left-hand side, be between zero and two solutions to the equation
with \(g_{\beta }(\Vert \zeta \Vert )= -\beta ^{-1}\Vert h \Vert <0.\) In particular, for sufficiently low temperatures there exists a local maximum and a saddle point of the renormalized potential as shown in Figure 7.
From differentiating (5.18), the Hessian is given by
We note that the Hessian has full rank unless at critical points unless \(g_{\beta }'(\Vert \zeta \Vert )+g_{\beta }(\Vert \zeta \Vert )(\Vert \zeta \Vert - \Vert \zeta \Vert ^{-1})=0,\) since \(g_{\beta }(\Vert \zeta \Vert )\ne 0\) by (5.18) for non-zero magnetic fields.
In addition, there can be only a saddle point which can only happen at one fixed temperature depending on n.
Finally, if the temperature is sufficiently high, yet still such that \(\beta >n\), there may be no critical point if h and \(\zeta \) point in opposite directions. This is in particular the case when \(\beta =n\) and \(h \ne 0\): Taylor expansion at zero yields
where for \(\beta =n\) we find \(\frac{n \Gamma (n/2)}{2\Gamma (1+n/2)}=1\) and concavity of the function \(\Vert \zeta \Vert \mapsto \frac{ \beta I_{n/2} (\left\Vert \zeta \right\Vert ) }{ I_{n/2-1}( \left\Vert \zeta \right\Vert )} \) show.
Thus \(\Vert \nabla V_n \Vert ^2\) vanishes at not more than three critical points \(\varphi _{\text {c}}\) on the span of h. In particular, all eigenvalues of \(D^2V_n\) are non-negative only at the global minimum of \(V_n\) by (5.19), since we already established that \(g'(\Vert \zeta \Vert )<0\) at the other two. To see that they are strictly positive there, it suffices to analyze for \(r=\Vert \zeta \Vert \)
Hence, we find that
In particular, this expression is strictly positive at the global minimum, since \(g_{\beta }(\Vert \zeta \Vert ) >0\) and \({\mathcal {I}}'(\Vert \zeta \Vert )>0\) by general principles, see Lemma B.2.
The asymptotic behaviour of the spectrum of the renormalized Schrödinger operator has been computed in [Sim83] and our above representation of \(\Sigma \) follows by noticing that \(\tfrac{1}{2} D^2 \left|\nabla V_n \right|^2(\varphi _{\text {c}}) = \left( D^2V_n(\varphi _{\text {c}})\right) ^2>0.\)
Since the renormalized Schrödinger operator and renormalized generator are unitarily equivalent up to a factor, the semiclassical eigenvalue distribution stated in [Sim83, Theorem 1.1] implies the statement of the Proposition. \(\quad \square \)
6 The Critical Regime, Proof of Theo. 3
We conclude our analysis by investigating the critical case \(\beta =n\) and prove Theorem 3. As before, we distinguish between \(n=1\) and multi-component systems \(n \ge 2\):
6.1 Critical Ising model
It follows from (4.1), which always vanishes for all \(x>0\), that the spectral gap, at the critical point \(\beta =n=1\), does not close exponentially fast in the number of spins. We want to show in this subsection that it closes at least polynomially, though. For a refined analysis in dimension \(n=1\), we recall some basic ideas from discrete Fourier analysis:
Let \(f: \left\{ \pm 1 \right\} ^N \rightarrow {\mathbb {C}}\) be an arbitrary function on the hypercube. The \(L^2(\left\{ \pm 1\right\} ^N,2^{-N}d\mu _{\text {count}})\) inner product on the hypercube is defined as
The characteristic function \(\chi _S\) for \(S \subset [N]\) is defined as \(\chi _S(x):= \prod _{i \in S} \sigma _i\) and the family \((\chi _S)_{S \subset [N]}\) forms an orthonormal basis of \(L^2(\left\{ \pm 1\right\} ^N).\) In particular, \(\chi _{\emptyset }=1.\) We also define indicator vectors \(\mathbb {1}_{S} \in {\mathbb {R}}^N\) such that \(\mathbb {1}_{S}(x)=1\) if \(x \in S\) and 0 otherwise.
Every function \(f \in L^2(\left\{ \pm 1\right\} ^N)\) admits a unique Fourier decomposition
where \({\widehat{f}}(S) := \langle f, \chi _S \rangle .\) The variance of the stationary measure is given as the sum of
Since the first term on the right-hand side of this equation is always uniformly bounded by the Dirichlet form, as shown in the proof of Proposition 3.5, it suffices to study the behaviour of the second term. Thus, applying the expectation with respect to the fluctuation measure yields by the Fourier decomposition (6.1)
In particular, using the explicit form of \(V_1(\phi )\), a direct computation yields for all \(x \in [N]\)
Using that \(\mu _{\varphi }\) is a product measure, this implies that the full expression for (6.3) is given by
Hence, we find for the variance
For the Dirichlet form, we find, with \(S_1 \triangle S_2\) denoting the symmetric difference of sets \(S_1\) and \(S_2\),
Proposition 6.1
For zero magnetic fields, i.e. \(h=0\), and \(\beta \ge 1\),all functions with Fourier support on sets of fixed cardinality \(k \in {\mathbb {N}}\), i.e. for f given as
satisfy the inequality \({\text {Var}}_{\nu _{N}}({\mathbb {E}}_{\mu _{\varphi }}(f)) \le \tfrac{N}{4k} \sum _{x \in [N]} \left|\nabla _{{\mathbb {S}}^{n-1}}^{(x)}f \right|^2_{L^2(d\rho )}.\)
In particular, for the magnetization
we obtain an inequality
Moreover, the spectral gap for critical \(\beta =1\) closes at least like \({\mathcal {O}}(N^{-1/2}).\)
Proof
When \(h=0\), it suffices to estimate the variance by Jensen’s inequality as
Using (6.6) we then obtain the spectral gap inequality
Turning to the magnetization (6.7), we can write the variance of the magnetization M in terms of the expectation value \({\mathbb {E}}_{\nu _N} \left( \tanh ( \beta \varphi )^{2}\right) \)
We now recall that \(\tanh (\beta \varphi )^2 = \beta ^2 \varphi ^2 +{\mathcal {O}}(\varphi ^4)\) and for \(\beta =1\)
by Taylor expanding around 0. It therefore follows from Laplace’s principle [Won01, Ch. II,Theorem 1] that
On the other hand, we can compute the Dirichlet form of the magnetization using (6.6)
Thus, comparing (6.10) with (6.12) implies the claim together with the asymptotic (6.11). \(\quad \square \)
While Proposition 6.1 shows that the magnetization leads for critical \(\beta =1\) to a spectral gap that closes at least like \(\sim N^{-1/2}\), when \(h=0\), the next Proposition shows that the magnetization does not imply a vanishing spectral gap when \(h > 0.\)
Proposition 6.2
Let \(h>0\), \(\beta \ge 1\), and f a function with Fourier transform supported on sets of cardinality \(\le k\) for some fixed \(k \in {\mathbb {N}}_0\) independent of N, i.e.
Then such functions satisfy an improved inequality with \(\varphi _{\text {min}}={\text {argmin}}_{\varphi } V_1(\varphi )\)
with a constant \(\frac{ \beta ^2 {\text {csch}}^2(2(\beta \varphi _{\text {min}}+h))}{2V''_1(\varphi _{\text {min}})} (1+o(1))\) that strictly bounded away from zero in the limit \(N \rightarrow \infty .\) In particular, \(V_1''(\varphi _{\text {min}}) >0\) by the discussion in the beginning of Section 4.3.
Proof
Using (D.2), which applies since \(V''_1(\varphi _{\text {min}})>0\) by the discussion in Subsection 4.3, we conclude that
implies since
that
where we used (D.2) in the first line, \(\vert S \vert =\langle \mathbb {1}_{S},\mathbb {1}_{[N]} \rangle \) in the second line, Cauchy–Schwarz and \({\text {csch}}(x)^4\tanh (x)^2=4{\text {csch}}(2x)^2\) in the third line, (D.1) and (6.14) in the fourth line, Jensen’s inequality in the fifth line and finally (6.6) in the last line. \(\quad \square \)
6.2 Critical multi-component systems
In this subsection, we prove the multi-component part of Theorem 3:
Proof of Theorem 3
The magnetization \(M =N^{-1/2} \sum _{x \in [N]} \sigma (x)\) has in the multi-component case always unit Dirichlet norm
On the other hand, we can explicitly calculate using the derivative of the modified Bessel function of the first kind, \(\partial _z I_{\nu }(z) = \frac{\nu }{z} I_{\nu }(z)+I_{\nu +1}(z)\), and (3.2), the expectation value \({\mathbb {E}}_{\mu _{\varphi }}(\sigma (x))\) that is independent of \(x \in [N]\) for \(\varphi \ne 0\)
Taylor expansion at zero then yields
For the renormalized potential we find by Taylor expansion, which we shall already specialize to critical temperatures \(\beta =n\), at zero
For the magnetization M (6.7), we can write
We then have by radial symmetry of both the renormalized potential and the integrand that at critical temperatures \(\beta =n\)
Applying Laplace’s principle, cf. [Won01, Ch. II,Theorem 1], with constants \(\mu =4\) and \(\alpha =3+(n-1)\) implies that
Combining this asymptotic behavior with (6.16) and (6.18) then yields the multi-component claim of Theorem 3, i.e. the rate \(N^{1/2}\) is caught for the trial (mean spin) function M and thus the spectral gap is decaying at least with speed \(N^{-1/2}\). \(\quad \square \)
The following Proposition shows that the upper bound \(N^{-1/2}\) on the spectral gap in the critical regime \(\beta =n\) for all dimensions \(n\ge 1\), is in fact sharp:
Proposition 6.3
Let \(h=0\) and \(\beta =n \ge 1.\) The spectral gap of the radial renormalized Schrödinger operator grows as \(\Theta (N^{1/2})\) and in particular, the spectral gap of the full measure does not close faster than \(\Theta ( N^{-1/2}).\)
Proof
Let \(\lambda := N/2\), we then consider the equivalent Schrödinger operators to the renormalized generator
where we used that by rotational symmetry of the renormalized potential, for \(n \ge 2\), we can decompose the Schrödinger operator into individual angular sectors parametrized by \(\ell \in {\mathbb {N}}_0\). We then introduce auxiliary Schrödinger operators
on \(L^2({{\mathbb {R}}})\) and \(L^2((0,\infty ), r^{n-1} \ dr)\), respectively. The five first eigenvalues of \(H_1\) are shown in Fig. 10.
We then define \(j \in C_c^{\infty }(-2,2)\) such that \(j(x)=1\) for \(\left|x \right|\le 1\) and from this
Invoking the unitary maps \(U_{1} \in {\mathcal {L}}(L^2({\mathbb {R}}))\) and \(U_n \in {\mathcal {L}}( L^2((0,\infty ),r^{n-1} \ dr))\) defined as
shows that the two Schrödinger operators in (6.20) are in fact unitarily equivalent, up to multiplication by \(\sqrt{\lambda }\), to the \(\lambda \)-independent Schrödinger operators
respectively. That \(\inf ({{\,\mathrm{Spec}\,}}(S_n^0))=0\) is shown in Section C. Since \(\tfrac{\ell (\ell +n-2)}{r^2}>0\) we have consequently that for \(\ell >0\) by monotonicity \(\inf ({{\,\mathrm{Spec}\,}}(S_n^{\ell }))\ge \inf ({{\,\mathrm{Spec}\,}}(S_n^{1}))>0.\) More precisely, we have that
More precisely, since \((U_{n}f)(x) := \lambda ^{-n/8}f(\lambda ^{-1/4}x),\) it follows that
Then, applying \((U_n^{-1}f)(r) = \lambda ^{n/8} f(\lambda ^{1/4}r)\) shows that
Taylor expansion of the potential at 0 and the estimate on the gradient (6.21) imply that
Let \(0=e_1<e_2\le ..\) be the eigenvalues (counting multiplicities) of \(S_n\) (over all angular sectors \(\ell \)) and choose \(\tau \) such that \(e_{n+1}>\tau >e_n\) with P being the projection onto the eigenspace to all eigenvalues of H below \(\tau \sqrt{\lambda }.\) The IMS formula, see [CFKS87, (11.37)] for a version on manifolds, implies that
such that
On the other hand, it follows that
By construction, since \(\nabla V_n\) vanishes to third order on the support of \(J_0,\) we have
Since \(\Delta V_n\) vanishes to second order
This implies for large \(\lambda \) that
From (6.27) we then conclude that for some \(C>0\)
This implies the claim of the Proposition, since
More precisely, for the eigenvalues \(E_1(\lambda )\le E_2(\lambda )\le ..\) of \({\mathcal {H}}_n\) we have shown that
In particular, the lowest possible eigenvalue \(e_1=0\) of the renormalized Schrödinger operator is of course attained as the nullspace of the renormalized Schrödinger operator is non-trivial. This shows that the spectral gap of the renormalized Schrödinger operator grows at least proportional to \(\sqrt{\lambda }.\) \(\quad \square \)
Notes
If the magnetic field is zero, i.e. \(h=0,\) both wells are of equal size.
References
Ané, C., Blachère, S., Chafaï, D., Fougères, P., Gentil, I., Malrieu, F., Roberto, C., Scheffer, G.: Sur les inégalités de Sobolev logarithmiques, volume 10 of Panoramas et Synthèses [Panoramas and Syntheses]. Société Mathématique de France, Paris, (2000). With a preface by Dominique Bakry and Michel Ledoux
Bauerschmidt, R., Bodineau, T.: Spectral gap critical exponent for glauber dynamics of hierarchical spin models. arXiv:1809.02075
Bauerschmidt, R., Bodineau, T.: A very simple proof of the LSI for high temperature spin systems. J. Funct. Anal. 276(8), 2582–2588 (2019)
Bauerschmidt, R., Bodineau, T.: Log-sobolev inequality for the continuum sine-gordon model. Commun. Pure Appl. Math. (2020)
Bauerschmidt, R., Brydges, D., Slade, G.: Introduction to a Renormalisation Group Method. Lecture Notes in Mathematics, vol. 2242. Springer, Singapore (2019)
Bakry, D., Émery, M.: Diffusions hypercontractives. In: Séminaire de probabilités, XIX, 1983/84. Lecture Notes in Mathematics, vol 1123, pp. 177–206. Springer, Berlin (1985)
Bobkov, S.G., Götze, F.: Exponential integrability and transportation cost related to logarithmic Sobolev inequalities. J. Funct. Anal. 163(1), 1–28 (1999)
Bakry, D., Gentil, I., Ledoux, M.: Analysis and geometry of Markov diffusion operators. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 348. Springer, Cham (2014)
Cycon, H.L., Froese, R.G., Kirsch, W., Simon, B.: Schrödinger Operators with Application to Quantum Mechanics. Texts and Monographs in Physics and Global Geometry, study edn. Springer, Berlin (1987)
Ding, J., Lubetzky, E., Peres, Y.: The mixing time evolution of Glauber dynamics for the mean-field Ising model. Commun. Math. Phys. 289(2), 725–764 (2009)
Ding, J., Lubetzky, E., Peres, Y.: Censored glauber dynamics for the mean field ising model. J. Stat. Phys. 137(3), 407–458 (2009)
Ellis, R.S.: Entropy, Large Deviations, and Statistical Mechanics. Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. Springer, Berlin (1985)
Gentil, I., Roberto, C.: Spectral gaps for spin systems: some non-convex phase examples. J. Funct. Anal. 180(1), 66–84 (2001)
Gross, L.: Logarithmic Sobolev inequalities and contractivity properties of semigroups. In: Dell’Antonio, G., Mosco, U. (eds.) Dirichlet forms (Varenna, 1992). Lecture Notes in Mathematics, vol. 1563, pp. 54–88. Springer, Berlin (1993)
Guionnet, A., Zegarlinski, B.: Lectures on logarithmic Sobolev inequalities. In: Séminaire de Probabilités, XXXVI, Lecture Notes in Mathematics, vol. 1801, pp. 1–134. Springer, Berlin (2003)
Helffer, B., Sjöstrand, J.: Effet tunnel pour l’opérateur de schrödinger semi-classique. i. Journées équations aux dérivées partielles, (2) (1985)
Helffer, B., Sjöstrand, J.: Puits multiples en mécanique semi-classique vi. (cas des puits sous-variétés). Annales de l’I.H.P. Physique théorique 46(4), 353–372 (1987)
Ledoux, M.: Concentration of measure and logarithmic Sobolev inequalities. In: Azéma, J., Émery, M., Ledoux, M., Yor, M. (eds.) Séminaire de Probabilités, XXXIII. Lecture Notes in Mathematics, vol. 1709, pp. 120–216. Springer, Berlin (1999)
Ledoux, M.: The Concentration of Measure Phenomenon. Mathematical Surveys and Monographs, vol. 89. American Mathematical Society, Providence, RI (2001)
Levin, D.A., Luczak, M.J., Peres, Y.: Glauber dynamics for the mean-field Ising model: cut-off, critical power law, and metastability. Probab. Theory Relat. Fields 146(1–2), 223–265 (2010)
Lu, S.L., Yau, H.-T.: Spectral gap and logarithmic Sobolev inequality for Kawasaki and Glauber dynamics. Commun. Math. Phys. 156(2), 399–433 (1993)
Menz, G., Otto, F.: Uniform logarithmic sobolev inequalities for conservative spin systems with super-quadratic single-site potential. Ann. Probab. 41(3B), 2182–2224 (2013)
Muckenhoupt, B.: Hardy’s inequality with weights. Studia Math., 44, 31–38 (1972). Collection of articles honoring the completion by Antoni Zygmund of 50 years of scientific activity, I
Nier, F., Helffer, B.: Hypoelliptic Estimates and Spectral Theory for Fokker–Planck Operators and Witten Laplacians, Lecture Notes in Mathematics. Springer, Berlin (2005)
Saloff-Coste, L.: Lectures on finite Markov chains. In: Bernard, P. (ed.) Lectures on Probability Theory and Statistics (Saint-Flour, 1996). Lecture Notes in Mathematics, vol. 1665, pp. 301–413. Springer, Berlin (1997)
Simon, B.: Semiclassical analysis of low lying eigenvalues. i. non-degenerate minima: asymptotic expansions. Annales de l’I.H.P. Physique théorique 38(3), 295–308 (1983)
Stroock, D., Zegarliński, B.: The equivalence of the logarithmic Sobolev inequality and the Dobrushin–Shlosman mixing condition. Commun. Math. Phys. 144(2), 303–323 (1992)
Stroock, D., Zegarliński, B.: The logarithmic Sobolev inequality for continuous spin systems on a lattice. J. Funct. Anal. 104(2), 299–326 (1992)
Stroock, D., Zegarliński, B.: The logarithmic Sobolev inequality for discrete spin systems on a lattice. Commun. Math. Phys. 149(1), 175–193 (1992)
Wong, R.: Asymptotic Approximations of Integrals, Classics in Applied Mathematics, vol. 34. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2001). Corrected preprint of the 1989 original
Zhang, Z., Qian, B., Ma, Y.: Uniform logarithmic Sobolev inequality for Boltzmann measures with exterior magnetic field over spheres. Acta Appl. Math. 116(3), 305–315 (2011)
Acknowledgements
Both authors were supported by the EPSRC grant EP/L016516/1 for the University of Cambridge CDT, the CCA. The authors are grateful to Roland Bauerschmidt for many useful discussions and bringing this problem to our attention.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H. Spohn
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Numerical results
Recall that the eigenfunctions of the operator
are given for \(n \in {\mathbb {N}}_0\) by
Then, it follows that
and
Using the annihilation operator \(a=2^{-1/2}(\partial _q+q)\) where \(q=\sqrt{\frac{\mu \omega }{\hbar }} x\) and its adjoint we can explicitly compute the matrix elements of all \((\langle \psi _n, x^n \psi _m \rangle )\) by writing \(q^n=\sqrt{2}(a+a^*)^n\) and using the well-known action of the annihilation operator on eigenstates of (A.1). Using a finite-basis truncation of the above matrices allowed us then to obtain Figs. 4 and 10.
Appendix B. Asymptotic properties of the Ising model
Lemma B.1
Let \(\beta >1\) and \(h \in [0,h_{\text {c}}).\) The three critical points of \(\eta _{N,h}:(-1,1)\rightarrow {\mathbb {R}}\)
are given by  where \(\gamma (\beta )\) satisfies the critical equation for the continuous renormalized potential
where \(\gamma (\beta )\) satisfies the critical equation for the continuous renormalized potential
Let us order the solutions \(\gamma (\beta )\) to that equation by \(\gamma _1(\beta )<\gamma _2(\beta )<\gamma _3(\beta ).\) For \(h=0\) the function \(\eta _{N,0}\) attains (in the limit \(N \rightarrow \infty \)) its maximum at \(\gamma _1(\beta )=-\gamma _3(\beta )<0\) and minimum at \(\gamma _2(\beta )=0\).
Let \(h>0\), then the function \(\eta _{N,h}\) attains (in the limit \(N \rightarrow \infty \)) its unique global maximum at \(\gamma _3(\beta )>0\) whereas both \(\gamma _1(\beta ),\gamma _2(\beta )<0\) and \( \gamma _1(\beta ),\gamma _2(\beta )\) are local maxima and minima respectively.
The logarithmic derivative \(\zeta _{N,h}(s) = \partial _s \log (\eta _{N,h}(s))\) satisfies

Proof
For \(h=0\) we note that \(\eta _{N,0}\) is even and for \(h>0\) the global maxima of \(\eta _{N,h}\) must be attained at some \(s \ge 0.\) Direct computations show by the logarithmic scaling of the digamma function \(\psi _2(s) = \log (\Gamma )'(s)= \log (s)+ {\mathcal {O}}(1/s)\) that the logarithmic derivative \(\zeta _{N,h}(s) = \partial _s \log (\eta _{N,h}(s))\) is given by (B.1). Thus, for all critical values \(s_N^{\text {c}}\) of \(\eta _{N,h}\), i.e. those values that satisfy \(\zeta _{N,h}(s_N^{\text {c}})=0,\) there exists \(\gamma (\beta ) \in [-1,1]\) such that \(\gamma (\beta ):= \lim _{N \rightarrow \infty }s_N^{\text {c}}\) and \(\gamma (\beta )\) is any solution to \( \gamma (\beta ) = {\text {tanh}}(\gamma (\beta ) \beta + h).\)
We then obtain (B.1) directly by differentiating \(\log (\eta _{N,h})\) and using the identity

Moreover, we read off from (B.1) that
In particular, \(\gamma (\beta )\) solves the implicit equation \(\gamma (\beta ) = \tanh (\beta \gamma (\beta )+h).\) For the second derivative of \(\zeta _{N,h}\) which is h-independent, we find the closed-form expression using the derivative of the trigamma function \(\psi _3\)
This implies that \(\zeta _N\) is strictly convex on \([-1,0)\) and strictly concave on (0, 1]. Using the asymptotic of the trigamma function \(\psi _3(s)= 1/s + 1/(2s^2)+ {\mathcal {O}}(1/s^3)\) we find that \(\zeta _{N,h}\) is strictly monotone increasing at zero, independent of h,

since \(\beta >1.\) \(\quad \square \)
Lemma B.2
The function \({\mathcal {I}}(r):= r \frac{I_{n/2-1}(r)}{I_{n}(r)}\) is strictly monotonically increasing on \((0,\infty ).\) In particular \({\mathcal {I}}'(r)>0\).
Proof
By differentiating and using that \(I_{\nu }'(r) = \frac{\nu }{r} I_{\nu }(r) + I_{\nu +1}(r)\) we find
Thus, it suffices to record that the product of Bessel functions satisfies \(I_{n/2}(z)^2 > (I_{n/2-1}I_{n/2+1})(z):\)
Hence, the identity follows from
which follows itself from logarithmic convexity of the gamma function. \(\quad \square \)
Appendix C. SUSY Quantum Mechanics
We use ideas from supersymmetric quantum mechanics, to show positivity and analyze the ground state of several Schrödinger operators appearing in this article:
In one dimension, we recall that using operators
with real-valued and smooth superpotential W, we can write
In particular, \(W(x):=\sqrt{\beta (\beta -1)}\beta x^2\) yields operator \(S_{\varphi _{\pm }}\) defined in (4.20).
However, solving \(A\psi =0\) or \(A^*\psi = 0 \) shows that \(\psi =C e^{\pm \sqrt{\beta (\beta -1)}\beta x^3}\notin L^2({{\mathbb {R}}}).\) This shows that \(\inf ({{\,\mathrm{Spec}\,}}(AA^*)),\inf ({{\,\mathrm{Spec}\,}}(A^*A))>0.\)
We now analyze operators in (6.23). Choosing \(W(x):=\frac{x^3}{3}\), yields \(A^*A=S_1\) in (6.23), and we find by solving \(A\psi (x)=0\) that \(\psi (x)\propto e^{-x^4/12}\) which implies that \(\inf ({{\,\mathrm{Spec}\,}}(A^*A))=0.\)
For radial operators on \(L^2((0,\infty ),r^{n-1} \ dr)\), a similar argument applies:
We define operators
Choosing then \(W(r):=\frac{n^3}{(2+n)}r^3,\) such that \(A^*A =S_n\) with \(S_n\) in (6.23), we find by solving
Appendix D. Asymptotic properties
Lemma D.1
[BBS19, Theo 1.4.10]. Let \(V: {\mathbb {R}} \rightarrow {\mathbb {R}}\) be smooth with unique global minimum at \(\varphi _{\text {min}} \in {\mathbb {R}}\) and \(V''(\varphi _{\text {min}})>0.\) Assume that \(\int _{{\mathbb {R}}} e^{-V(\varphi )} \ d\varphi \) is finite and that \(\left\{ \varphi \in {\mathbb {R}}; V(\varphi ) \le V(\varphi _{\text {min}})+1 \right\} \) is compact. We also define the probability measure \(d\zeta _N(\varphi ) = e^{-N V(\varphi )} \ d\varphi / \int _{{\mathbb {R}}}e^{-N V(\varphi )} d \varphi .\) Then for any bounded smooth function \(g: {\mathbb {R}} \rightarrow {\mathbb {R}}\)
and for the variance
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Becker, S., Menegaki, A. Spectral Gap in Mean-Field \({\mathcal {O}}(n)\)-Model. Commun. Math. Phys. 380, 1361–1400 (2020). https://doi.org/10.1007/s00220-020-03908-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03908-9



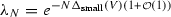 . In particular, for magnetic fields
. In particular, for magnetic fields 








