Introduction

Floquet systems have a periodic Hamiltonian in time: H(t + T) = H(t). Recently, together with the possibility for many-body time crystals1,2, Floquet systems attracted wide interest in the field of condensed matter physics, photonic crystals, and ultra-cold atomic physics. Especially, Floquet-Bloch band structures have been widely investigated3,4 due to potential topological properties5,6. Floquet systems are usually realized by a strong coherent external driving force (e.g., an optical electric field, or microwave oscillation)7,8. Here, the word “coherent” means a regular monotonic perturbation with long dephasing time, rather than a random noisy perturbation. Electron-phonon coupling has also been discussed as a path for Floquet states, especially if a given phonon mode can be selectively excited by other external perturbations. The Floquet electron sidebands can also appear in photoelectron spectroscopy as a phonon dressed electronic structure9. It will be interesting if the Floquet states can be realized automatically by a strong intrinsic electron–phonon coupling under thermodynamic equilibrium condition. Traditionally, the electron–phonon coupling effects at thermodynamics equilibrium are often described by random phase perturbation theory, for example, to normalize the electron quasi-particle band gap10, to introduce a finite quasi-particle lifetime11, or to produce side peaks in electron transition spectra12. In order to form the Floquet states, however, the phonon perturbation must be coherent, which is often considered not possible under the thermodynamic equilibrium condition. In this work, we report a surprising finding: a Floquet state induced by a natural electron–phonon coupling in a wire-like crystal under the thermodynamic equilibrium condition. It is found that, in a quasi 1D wire crystal, there is a selective giant electron–phonon interaction, where one particular phonon mode can be responsible for influencing the band gap of the electronic structure, causing the Dirac cone band gap to close and open at the frequency of that phonon mode. Such oscillation has a coherent time equal to the life time of that particular phonon mode (which typically could be tens of picoseconds or longer). During this time period, it is adequate to describe the electronic structure of the system by the Floquet band structure. We have carefully investigated the cause of this Floquet oscillation and the related phonon dynamics, and found the system is indeed in the thermodynamic equilibrium state. This natural formation of the Floquet states in thermal equilibrium without artificial external drive/perturbation can provide a different view to understand the electron–phonon coupling in some authentic materials, beyond the traditional perturbation theory. It might also provide ways for future electronic devices (e.g., a natural cyclic switch). The sensitivity of the band gap to the phonon mode can provide a way to probe the phonon dynamics through the THz electric measurement directly. We note that, without external perturbation, the whole system’s Hamiltonian will still have a continuous time translational symmetry. When the electronic Hamiltonian is coupled to a phonon mode, the electronic structure part of the Hamiltonian will lose its continuous time translation symmetry, resulting in the Floquet oscillation.

Results and discussion

Electronic structure and dynamics simulated by TDDFT

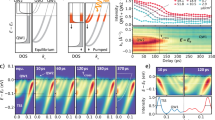
The classes of the system we studied are M(MoS)3 and M(MoSe)3, where M = Li, Na, K, Rb, Tl, In, I13, although in the following, we will use Rb(MoS)3 as our main example. All materials have a symmetry group of P63/m and a similar structure to Rb(MoS)3 as shown in Fig. 1a. Mo and S atoms form an atomic wire. Within one unit cell, the six Mo atoms in the wires reside in two cross sections (A and B), and each cross section holds a C3 symmetry, and the two cross sections are connected by screw-rotation symmetry, which is a product of π-rotation around the z-axis and a shift by a half-unit cell in the z-direction (see the illustration in Fig. 1b). Rb atoms are located at the interstitial points between the wires, donating its electrons to the wires without forming strong bonds with the wires. The calculated band structure is shown in Fig. 1c. The energy disperses only in the kz direction near the Fermi level, and bands are flat in the kx-ky plane due to small couplings between the wires. In deeper occupied bands and higher unoccupied bands, the energy disperses in all directions. The valence band and conduction band cross each other in the plane of kz = π/c (with c being the z-direction lattice constant), resulting in a two-fold degeneracy at kz = π/c with half occupation for each band. The linearly dispersed bands predominately consist of Mo-dyz and Mo-dxz orbitals. The calculated eigenstates are shown in Fig. 1d. Eigenstates have C3 symmetry. The two degenerated eigenstates near the Fermi level can be approximated as

$$\begin{array}{l}\left| {u_{\mathrm{A}}} \right\rangle = d_{xz}^1 - \frac{1}{2}d_{xz}^2 + \frac{{\sqrt 3 }}{2}d_{yz}^2 - \frac{1}{2}d_{xz}^3 - \frac{{\sqrt 3 }}{2}d_{yz}^3\,{\mathrm{and}}\\ \left| {u_{\mathrm{B}}} \right\rangle = \frac{1}{2}d_{xz}^4 + \frac{{\sqrt 3 }}{2}d_{yz}^4 - d_{xz}^5 + \frac{1}{2}d_{xz}^6 - \frac{{\sqrt 3 }}{2}d_{yz}^6\end{array}$$
(1)

where the superscript denotes the Mo atom index 1–3 belong to cross section A, while 4–6 belong to cross section B). The full band structure is shown in Fig. 2a, and the corresponding high symmetric k-point path is shown in Fig. 2g. The comparison between the band structures of bulk and a single wire reveals that the main energy dispersion is caused by coupling within the wires of MoS. If screw-rotation symmetry is broken, a band gap would be opened14,15. For example, if we artificially shift different atoms in different directions by 0.1 Å, the band gap will be opened with different magnitude (see Fig. 2b). The shift of Mo atom in z-direction leads to the largest band gap. For example, the band splitting near the Fermi level is 8 (7) meV, if one of the S atoms shift by 0.1 Å in the z (x) direction. On the other hand, the band splitting is 102 (3) meV if one Mo atom shifts by 0.1 Å in the z (x) direction. Similarly, the other modes of atomic displacements have small effects on the band gap.

Fig. 1: Structure and symmetry of Rb(MoS)3.
figure 1

a Atomic structure of Rb(MoS)3 in the top (upper) and side (lower) views. b Illustration of screw-rotation symmetry. The half circle represents a rotation of π, and vertical arrow represents the translation of a half cell in the z-direction. Numbers index the Mo atoms in a unit cell. Dash arrows indicate how atoms are mapped under screw-rotation symmetry operation R. Dash horizontal lines indicate the unit cell. c Valence and conduction bands. d Calculated charge density near the Fermi level.

Full size image
Fig. 2: Electronic structure and phonon information.
figure 2

a Band structures of bulk Rb(MoS)3 (left) and single quantum wire of MoS (right). b Bandgap as a function of atomic perturbation in different directions. c Transmission eigenvalue as a function of energy in gapless (blue) and gapped (red) states. d Partial phonon density of states projected on different atoms. Dash line implies the particular phonon mode. e Relative-motion phonon mode of Mo atoms in the z-direction. f Phonon spectrum. Highlight color represents the weight of relative-motion (Wm(q)). g Brillouin Zone in the blue frame and high-symmetric k-path in red.

Full size image

It is useful to characterize the electronic behavior of the system by its z-direction quantum transport conductance. For such a wire-like system, the calculated conductance is a constant in the unit of 2e2h−1 in the energy window of [−1.0, 0.4] eV (see Fig. 2c), where e and h are the electron charge and Planck constant, respectively. On the other hand, if the screw-rotation symmetry is broken by a phonon mode, a gap will be opened and the conductance is 0 near the Fermi level. Quantum ballistic conductivity is common in one-dimensional materials, e.g., in carbon nanotubes. However, synthesized quantum wires are difficult to be stacked parallel in the same direction without interference. The wires here are embedded inside a bulk, but with relatively independent behavior like a nanowire, providing potential usages as ballistic conduction materials in future device applications (e.g., used as interconnect without x–y direction scattering).

To study the effect of phonon on the gap opening of the system, we have performed real-time time-dependent density functional theory (rt-TDDFT) simulation. The reason to use rt-TDDFT, instead of Born-Oppenheimer ab initio molecular dynamics (AIMD) will be explained later. Figure 3a shows the simulated results of the instantaneous band energy dynamics at the temperature of about 100 K. The NVE ensemble, where the atomic number, volume, and energy in the system are constant, is used. Here the instantaneous band structure (also called adiabatic band structure) is defined as the band structure obtained from diagonalizing electronic Hamiltonian H(t) at time t. The instantaneous band edges as functions of time can be approximated by sine/cosine curves. A surprise is that such oscillation can be represented predominately by a single sine oscillation with a small mixture with other frequencies. By Fourier transformation of the energy difference of the two bands near the chemical potential, the period is determined to be ~124 fs (see Supplementary Fig. 1), and the corresponding phonon energy is at 33.4 meV. Such oscillation drives the band gap to close and open periodically, and the largest opening can reach about 0.14 eV. This regular oscillation caused by the thermodynamic fluctuation of the phonon modes is rather surprising. Usually, random white noise fluctuations are expected by the thermal equilibrium movement. Such regular oscillation also constitutes a natural occurrence of Floquet states with its electronic structure, and Hamiltonian exhibiting periodicity16. Dynamics of electron and atoms is simulated for 1200 fs by rt-TDDFT. We expect the regular oscillation will continue for a much longer time. In other words, the decoherence time can be much longer than 1200 fs. Indeed, such a Floquet state will not likely last for an infinitely long time, but just like in the pulse laser induced Floquet states in the experiment17,18. We believe the oscillation is long enough to justify the use of the Floquet band structure to analyze its electronic property. This presents a way to analyze the electron–phonon coupling phenomena in this special case beyond the traditional perturbation theory.

Fig. 3: Oscillation of electronic structure.
figure 3

a Energy at A point as a function of time. Bottom of the conduction band and top of valence band are colored by pink and blue, respectively. b Occupation as a function of time (upper) and its corresponding energy. c Energy evolution at A point simulated by AIMD. d Energy evolution obtained in the analytical method. e Velocity coherence as a function of time. f Current as a function of time J(t) under a constant biased voltage.

Full size image

The band gap oscillation magnitude increases with the increasing temperature. (see Supplementary Fig. 2) However the frequency itself is rigid and keeps the same even at different temperatures below a critical value of ~600 K. Thus, the oscillation is robust against environmental perturbation if the temperature is below 600 K. However, above 600 K, the particular band structures of the system, namely the crossing of the valence band and the conduction band, will be mixed with the other part of the electronic structure, and the phenomena of oscillation will disappear.

Selective electron–phonon coupling

To test whether such regular oscillation is coincidental, we have carried out the rt-TDDFT with different initial atomic positions and movements, similar phenomena are observed. To analyze this further, we have calculated the whole phonon spectrum of the system, and generated the initial atomic displacements and velocities from the thermal equilibrium average energies for each phonon mode. The same regular oscillation of the band gap is also observed under these initial conditions. Thus, this behavior is a thermal equilibrium behavior, not caused by any nonequilibrium phonon condition. Note that, due to the use of rt-TDDFT simulation, the electron can be pumped to the state above the band gap, as shown in Fig. 3b, creating an oscillating electron-hole excited state, which can potentially be probed by optical experiments. This is a behavior beyond the Born-Oppenheimer equilibrium ground state approximation. Such behavior cannot be described by AIMD, where only the states below the band gap will be occupied. To test the effect of this occupation on the nuclear movement, we have recalculated the system with AIMD under the same initial condition. The band gap oscillation is shown in Fig. 3c. As one can see, the oscillation is less regular, indicating that the redistribution of the electron charge to different states during AIMD might damp the regular oscillations (Supplementary Fig. 3). This might not be surprising, because in AIMD, the lower energy state will be occupied. But in a band gap close-open oscillating dynamics, where two states crossing each other in time, always occupying the lower energy state means redistribution of the electron to different electron states during the dynamics, which usually corresponds to dissipative dumping behavior.

To check whether this is a common phenomenon besides Rb(MoS)3, other materials M(MoS)3 and M(MoSe)3 are also simulated in the same way. Similar results are obtained, even if Rb atoms are replaced by Tl or are removed (see Supplementary Figs. 3b, c and 4). These results are in good accordance with the phonon density of state calculated using the dynamic matrix method19. Figure 2d shows that the band gap oscillation frequency corresponds to a phonon mode with large Mo, S amplitude, which corresponds to a peak in phonon density of states. The contribution of Rb is almost zero at this energy. Density of states projected on Rb is mainly in the range from 6 to 12 meV in Supplementary Fig. 5b.

One peculiar possibility is that the whole dynamics is controlled by some nonlinear effect, which can guide the kinetic energy into some special nonlinear modes, which leads to long time correlation in this mode. To test this possibility, we have calculated the velocity-velocity time correlation function as follows:

$$f(\tau ) = {\int} {dt_1} \frac{{\mathop {\sum}\limits_n {{\mathbf{v}}_n(t_1) \cdot {\mathbf{v}}_n(t_1 + \tau )} }}{{(\mathop {\sum}\limits_n {{\mathbf{v}}_n} (t_1) \cdot {\mathbf{v}}_n(t_1))^{\frac{1}{2}}(\mathop {\sum}\limits_n {{\mathbf{v}}_n} (t_1 + \tau ) \cdot {\mathbf{v}}_n(t_1 + \tau ))^{\frac{1}{2}}}}$$
(2)

In above, the n-index denotes the atoms. Velocity \({\mathbf{v}}_n = \frac{{\partial {\mathbf{R}}_n}}{{\partial t}}\) is obtained by TDDFT or AIMD calculation. If the dynamics is correlated, the f(τ) can oscillate regularly without decay. If f(τ) decays quickly, the dynamics as a whole is not correlated. The result is shown in Fig. 3e. We see that the curve f(τ) decays quickly to a value close to zero in about 150 fs. This time length is much shorter than the time duration of regular oscillation of the band gap. This means the overall dynamics is indeed random as expected from a thermal equilibrium system. Indeed, the potential function fitting as shown in Supplementary Fig. 6 also indicates the anharmonic effect is extremely small, and thus can be neglected (see Supplementary Note 1).

To fully understand the dynamics, we have used the independent movements of phonon modes to reproduce the molecular dynamics results. In a pure harmonic phonon mode picture, the atomic displacement ΔR from its equibrium position can be calculated as:

$${\Delta} {\mathbf{R}} = \frac{1}{{\sqrt {M_RN} }}\mathop {\sum}\limits_{{\mathbf{q}} \in BZ,m} {{\mathbf{u}}_m(q)Q_m^\prime ({\mathbf{q}},t)e^{i{\mathbf{R}} \cdot {\mathbf{q}}}}$$
(3)

where MR is the mass of atom located at R, and N is the number of primary cell in a supercell, considered, q is the phonon momentum, and m is the phonon mode index, \(Q_m^\prime ({\mathbf{q}},t) = Q_{m,{\mathbf{q}}}e^{ - i\omega _{m,{\mathbf{q}}}t}\) is the amplitude, ωm,q is the phonon frequency, um(q) is the phonon eigen state. Both um(q) and ωm,q are obtained from the dynamic matrix phonon calculations19. Qm,q is estimated based on equilibrium condition:\(\frac{1}{2}Q_{m,{\mathbf{q}}}^2\omega _{m,{\mathbf{q}}}^2 = \frac{1}{2}k_BT\). The initial phase of \(Q_m^\prime ({\mathbf{q}},t)\) is randomly sampled at t = 0, and it has been proved unimportant to the main dynamics. The calculated atomic movement using Eq. (3) is in good accordance to the rt-TDDFT simulation, especially the vibronic frequency of different atoms (see Supplementary Fig. 7). This proves again that the molecular dynamics can be well described by the independent phonon modes without special nonlinear effects, and the phonon degree of freedom is indeed in its thermal equilibrium. Since all phonon modes have nonzero Qm,q according to the \(\frac{{k_BT}}{2}\) energy, the puzzle is: why the band gap oscillation exhibits a single phonon mode behavior, instead of an incoherent random noise?

To understand this, we have estimated the contribution to band gap opening of different phonon modes. Since the band gap opening is related to the breaking of the screw-rotation symmetry, we like to measure such symmetry breaking by different phonon modes. Under a screw-rotation operation, an atom “a” in cross-section A (e.g., atom 2 in Fig. 1b) will be transformed to atom “b” in cross-section B (e.g., atom 5 in Fig. 1b). If we use R to denote this screw-rotation operation, we can write R(a) = b for indexing. Furthermore, a phonon mode displacement vector uma(q) on atom a will be transformed into a different displacement vector R[uma(q)]. Thus, we can measure the symmetry violation (especially for the z-component displacement) as:

$$W_m({\mathbf{q}}) = \mathop {\sum}\limits_{a \propto A} {|R[{\mathbf{u}}_m^a({\mathbf{q}})] - {\mathbf{u}}_m^{R(a)}({\mathbf{q}})|_z}$$
(4)

where a runs over all atoms in cross section A, and Wm(q) measures the symmetry breaking by the (m,q) phonon mode. One of the most important modes is a short-wave optical mode illustrated in Fig. 2e. We can see that only a few phonon bands have a strong Wm(q) in the phonon bands shown in Fig. 2f, and these bands have similar frequencies. A particularly important band is the one around the energy of 33.4 meV, which has band width as small as 0.058 meV in qx-qy plane, while the dispersion is in the qz direction is about 4 meV (zoom in of Fig. 2f is shown in Supplementary Fig. 5a). Based on Fig. 2b, the contribution of a phonon mode to the band gap opening is roughly proportional to Wm(q). Among the phonon modes with large Wm(q), the strongest mode frequency corresponds well with the phonon energy of 33.4 meV. Thus, the regular oscillation of the band gap is caused by a selective giant coupling of one phonon mode (shown in Fig. 2e) to the band edge states, thus the band gap oscillation reflects the oscillation of this single phonon mode. This is rather unusual. As far as we know, there are no other systems exhibiting such behavior. The duration of such Floquet oscillation thus corresponds to the coherence life time of that particular phonon mode.

Hamiltonian and oscillating current

To study such oscillations analytically, we have constructed a tight-binding Hamiltonian using the atomic basis set from Eq. (1):

$$\begin{array}{l}H = \mathop {\sum}\limits_j {\varepsilon _{jA}c_{jA}^\dagger c_{jA}}+ \mathop {\sum}\limits_j {(\xi _j + g({\Delta} {\mathbf{R}}_{jA} - {\Delta} {\mathbf{R}}_{jB}))c_{jB}^\dagger c_{jA}} \\ \qquad\;+ (\xi _j + g({\Delta} {\mathbf{R}}_{j + 1A} - {\Delta} {\mathbf{R}}_{jB}))c_{jB}^\dagger c_{j + 1A} + (A \leftrightarrow B)\end{array}$$
(5)

where εj is the onsite potential on each atom, ξj is nearest-neighbor hopping integration. g is the electron–phonon coupling constant of the hopping term. \(c_{jA/B}^\dagger\) (\(c_{jA/B}\)) is creation (annihilation) operator of \(\left| {u_{jA}} \right\rangle\) or \(\left| {u_{jB}} \right\rangle\) at the jth primary cell. Note, due to symmetry, the first order onsite potential oscillation is zero, thus its change with time has been neglected. Figure 2b also shown that the intra-site electron–phonon coupling can be ten times smaller than inter-site electron–phonon coupling. To get the instantaneous band structure, the Fourier transformation of \(c_{jA/B}^\dagger = \frac{1}{{\sqrt N }}\mathop {\sum}\limits_{\Im {\mathbf{k}}} {c_{A/B{\mathbf{k}}}^\dagger e^{i{\mathbf{k}} \cdot {\mathbf{R}}_{jA/B}}}\) is used with electron k-point k. ΔRjA/B in Eq. (4) including the phonon modes from 26.4 to 36.9 meV with a large weigh in Fig. 2f are substituted into Eq. (5). A 1 × 1 × 80 supercell is used to include the long-wave phonons. The analytical result of instantaneous bandgap oscillation is shown in Fig. 4a, which is in good agreement with the direct rt-TDDFT results.

Fig. 4: Time-dependent band structure and Fouquet band structure.
figure 4

a Instantaneous energy surfaces in the space of momentum and time. b Floquet band structure under a drive of ħω = 33.4 meV. The color and line width represent the weight of projection on the original valence states without including phonons.

Full size image

To further simplify the analysis, we include only the single strongest coupling optical phonon mode in Eq. (3), substitute that in Eq. (5), and obtained a k-resolved Hamiltonian Hk for the Bloch state wave function is:

$$H_{\mathbf{k}} = {\mathrm{2}}\xi \cos (\frac{1}{2}ck_z)\sigma _x{\mathrm{ + 2}}\delta \xi \cos (\omega t)\sigma _y\sin (\frac{1}{2}ck_z)$$
(6)

here δξ = gΔR is electron–phonon interaction and is determined by fitting band gap opening. The parameters ξ = 1.2 eV is obtained from fitting the DFT calculation. While the instantaneous band structure can be obtained from diagonalizing Eq. (6) at a given time t (e.g., Fig. 4a), a more interesting property is the Floquet band structure of Eq. (6). For Hamiltonian H(r,t) periodic in both space and time, Floquet theorem implies a state in the form of \(u_{m,{\mathbf{k}}}({\mathbf{r}},t)e^{(i{\mathbf{k}} \cdot {\mathbf{r}} - i\tilde \varepsilon t)}\) satisfying the time-dependent Schrodinger Equation, leading to the following equation (details seen in Supplementary Note 2)20,21

$$(H_{\mathbf{k}}(t) - i\hbar \frac{\partial }{{\partial t}})u_{m,{\mathbf{k}}}({\mathbf{r}},t) = \tilde \varepsilon _{m,{\mathbf{k}}}u_{m,{\mathbf{k}}}({\mathbf{r}},t)$$
(7)

where \(u_{m,{\mathbf{k}}}({\mathbf{r}} + c,t) = u_{m,{\mathbf{k}}}({\mathbf{r}},t)\), \(u_{m,{\mathbf{k}}}({\mathbf{r}},t + T) = u_{m,{\mathbf{k}}}({\mathbf{r}},t)\) (T is the period in time). m is band index. Equation (7) is diagonalized using Eq. (6) with \(\left| {u_{jA}} \right\rangle\), \(\left| {u_{jB}} \right\rangle\) as the basis set in spatial space, and e(−inωt) in time space. The resulting Floquet band structure is shown in Fig. 4. The original bands are duplicated into a series of subbands separated by ω. Essentially, there are two parameters controlling this Floquet band structure, one is ω, determining the band duplication, another is the electron–phonon coupling constant, determining the inter-band coupling strength. In Rb(MoS)3, the inter-band coupling constant is much larger than the energy of the phonon (Fig. 4b).

Floquet band structure is itself a quantity that can be compared with ARPES experiment9. The role of Floquet band structure in Floquet systems is similar to the role of Bloch band structure in normal crystals. Each Floquet band state satisfies the time-dependent Schrodinger’s equation, thus can be used as the basis to analyze time-dependent properties of the system4. The occupation of the Floquet band state can be approximated by a “sudden approximation” as proposed by Oka and Aoki22. This is to project (overlapping) each Floquet state with the original time independent Bloch state (without the phonon mode) and time averaged over the oscillating time period. Multiplying each projection with the occupation of the original Bloch states, and sum over all the Bloch state, we get the occupation of the Floquet state. The amplitude of such Floquet occupation is indicated by the white color in Fig. 4b. Most electrons still reside on the original bands, whose wave function is time independent, while a small part of electrons are excited to high-energy bands. To amplify the effect, in Supplementary Fig. 8, we increase the phonon frequency to 334 meV, just to demonstrate the effect of high-frequency oscillations. We see a very different band structure in that case compared to Fig. 4b.

It is interesting to investigate the time-resolved electron transport in a Floquet system. One approach is to occupy the Eigen states in an instantaneous band structure at time t = 0, then following the time-dependent Schrodinger’s equation to study their dynamics. The time-dependent wave function can be solved using \(\left| {\psi _{\mathbf{k}}(t)} \right\rangle = e^{ - \frac{i}{\hbar }{\int} {H_{\mathbf{k}}d} t}\left| {\psi _0} \right\rangle \approx \prod e^{ - \frac{i}{\hbar }H_{\mathbf{k}}{\Delta} t}\left| {\psi _0} \right\rangle\)23. Under the atomic basis\(\left| {\varphi _{A{\mathbf{k}}}} \right\rangle = u_A({\mathbf{r}})e^{i{\mathbf{k}} \cdot {\mathbf{R}}_A}\)and \(\left| {\varphi _{B{\mathbf{k}}}} \right\rangle = u_{B{\mathbf{k}}}({\mathbf{r}})e^{i{\mathbf{k}} \cdot {\mathbf{R}}_B}\), we have

$$\left| {\psi _{\mathbf{k}}(t)} \right\rangle = \left( {\begin{array}{*{20}{c}} {c_{11}({\mathbf{k}},t)} & {c_{12}({\mathbf{k}},t)} \\ {c_{21}({\mathbf{k}},t)} & {c_{22}({\mathbf{k}},t)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\left| {\varphi _{A{\mathbf{k}}}} \right\rangle } \\ {\left| {\varphi _{B{\mathbf{k}}}} \right\rangle } \end{array}} \right)$$
(8)

Then the coefficients cij(t) can be solved using Hamiltonian of Eq. (6). We have used the instantaneous eigenstates at t = 0 as the initial states of Eq. (8). When solving Eqs. (6)–(8), only z-direction is important, and k is reduced to kz due to anisotropy. The current is calculated as:

$$J_{k_z}(t) = \frac{{2e}}{{m_e}}{\mathrm{real}}(\left\langle {\psi _{k_z}(t)} \right| - i\hbar \nabla \left| {\psi _{k_z}(t)} \right\rangle )$$
(9)

The total current J(t) is calculated by integrating over all the occupied states at different k-points (in Supplementary Note 3). In the absence of an electric field, occupied states are balanced in −k and k, resulting in a pair of Fermi wave vector kF and −kF with same amplitude but opposite signs. Thus, the electric current is zero in normal materials. When a constant electric field is applied, the Fermi wave vector will shift by δk (δk ~ electric field), leading to a pair of Fermi wave vector by kF + δk and by −kF + δk. The integration of Jkz is nonzero, resulting in a constant current in normal crystals. In the Floquet system, if the two initial states are not equally occupied, there will be a an oscillating current24. The current is divided into two parts, J(t) = J0 + Jdc(t). The first part is a constant similar to that in common crystals, and the second term is an oscillating current. Note, the oscillating current depends on the initial state occupation or excitation. If the initial states at t = 0 are the states where low-energy states below Fermi level are occupied and high-energy states above Fermi level are unoccupied, an oscillating current is shown in Fig. 3f. The ultrafast oscillation of momentum and energy has been observed experimentally in other driven systems using femtosecond techniques25,26. Here we show that it can also appear automatically in such an intrinsic Floquet state due to internal electron–phonon coupling. Similar technology can be used to observe the proposed phenomenon.

Another approach to study the current oscillation under the Bloch state occupation of Supplementary Fig. 9a is to use the Floquet state (see Supplementary Note 5). Using the sudden approximation, we can calculate the corresponding occupations of the Floquet state, the results are shown in Supplementary Fig. 8. Note, the Floquet band states are time dependent. Thus, each of them has a time-dependent current. Sum over the time-dependent current of those occupied Floquet states, we yield a time-dependent current of the whole system, as shown in Supplementary Fig. 9b which is similar to that of Fig. 3f using direct time integration. To understand the current oscillation in another angle, we have also estimated from another angle, using a Landau-Zener tunneling, as shown in Supplementary Eqs. (23)–(25) in Supplementary Note 4. This rough estimation yields an oscillation amplitude in the same order of amplitudes as the methods discussed above, but is less accurate than the above methods.

In summary, we have studied the electronic structure and dynamics of M(MoS)3 and M(MoSe)3 with different metals M using rt-TDDFT. Such crystals have an embedded quasi-1D chain consisted of Mo atoms. The static band structure of the ground state shows a Dirac cone at Fermi energy in the wire z-direction at kz = π/c. We found that there is a giant electron–phonon coupling with one particular optical phonon mode, which causes a regular oscillation of closing and opening of the band gap, as well as an oscillating electron-hole excitation state. This constitutes a rare case of natural Floquet states due to intrinsic electron–phonon coupling in thermodynamic equilibrium. Such coupling induces a coherent electronic structure behavior, is beyond the traditional electron–phonon perturbation theory. This demonstrates a coherent phenomenon for electron-hole coupling, and the Floquet band structure provides a view to analyze such electron–phonon coupling effect. Such a phenomenon can also be used to detect the phonon dynamics through optical or electric conductivity measurements. It might also provide an opportunity for future device design. We believed our theoretical prediction could be tested in the future by experimental measurements for such systems. The Floquet band structures with duplication and splitting can be observed by ARPES, and oscillating current can be detected by ultrafast technology.

Methods

Calculation details

The numerical calculation is performed using the code package of PWmat27 in the projector augmented wave basis set. Perdew-Burke-Ernzerhof exchange-correlation functional and SG15 norm-conserving pseudopotentials are applied. The energy cutoff is 50 and 200 Ry for plane-wave basis set and charge density, respectively. The rt-TDDFT uses an algorithm developed previously, which expands the time-dependent wave function using the instantaneous state as the basis set28,29. This effectively reduces the dimension of the system into a small matrix, allowing fast time integration using very small time steps (10−4 fs). A larger time step (0.1 fs) is used to calculate the instantaneous states, with a linear interpolation scheme to yield the reduced dimension Hamiltonian for the time between the 0.1 fs interval. A leapfrog algorithm is used to reach self-consistency for the instantaneous state calculations at the 0.1 fs time steps. In the rt-TDDFT calculation, no external field is applied, but the phonons dynamics is described via the Ehrenfest dynamics. The equilibrium state of the molecular dynamic simulation at 100 K is used as the initial structure. A k-mesh of 1 × 1 × 3 is used based on the convergence tests. Since the rt-TDDFT calculation is expensive, we cannot use a very large supercell in rt-TDDF. Different supercells are tested (see Supplementary Fig. 10), and a supercell of 1 × 1 × 3 (with 42 atoms) is found to be enough and thus used in all rt-TDDFT simulation.