Economic fish production inventory model for perishable fish items with the detoriation rate and the added value under pentagonal fuzzy number

Abstract

In marine fishing, a considerable planning is required for developing socio-economic value of fishermen. This research explores the discussion in optimal fish manufacturing quantity for perishable fish items in the vessel during yachting. The rate of deterioration is treated as a Pentagonal Fuzzy Number (PFN) to obtain the optimal total cost. The convexity of the model is proved by satisfying the constraint equation in a fuzzy environment. An efficient procedure is applied to find the annual fish production quantity and the production in a single period to avoid the faulty measurement in the demand for fish items and the supply to the retailers. In addition, a few sensitivity analyses are carried out for the repair cost and the added value cost to indicate the existence of the total cost in the least possible range. Some managerial discrimination is also included.

Introduction

High financial investment plays a vital role in Marine fishing industry. A large number of fishing vessels are required for marine fishing. Very high financial setup is needed for one production plane which includes groceries, diesel, ice, medical things etc. The cost of the new medium-range vessel for nearly 70 lakhs and the cost of the second-hand vessel nearly 40 lakhs are used by the fishermen in Kasimedu (North Chennai, Tamil Nadu).

It is possible to carry 4000 kg of fish items in one production cycle for a new vessel and 2000 kg of fish items in one production cycle for the second-hand vessel. In the fishing industry, lack of market infrastructure, the imbalance between the fish demand and the supply of fish to the retailer’s knowledge in the quality of the fish are the main consequences faced by the fishermen. In this paper, the importance of finding the fish production quantity techniques is used for maximizing the profit of the fishermen. For making the high profit in the fishing industry, the high financial investments and the perfect plan to supply the fish products are required to the buyer in an optimal time.

Chidambaram and Debhi [1] published the book in which, they examined the coastal areas mainly in Gujarat and they collected the risk factors that were influencing the fish marketing. The cost spent on handling the fish products and the cost function of fresh fish handled and dry fish handled per year are discussed.

Sugapriya and Jeyaraman [2] discussed the production cycle for the EPQ model for the decaying items allowing price discount for the product. They discussed the two cases for suppliers by giving credit period to minimize the total cost. Ganesh Kumar et al. [3] derived the concept of total marketing costs in all aspects like vendor, buyer, retailer and customer. Finally, they derived the uniform marketing for the fish and operations for regulating fish marketing.

Yazdani et al. [4] investigated the markets of various types of fishes with seasonal root and non-seasonal root for long-run process of wholesale and retail prices. Taleizadeh et al. [5] explained a hybrid method of fuzzy simulation and the genetic algorithm is proposed to solve the problem. They demonstrated the model in non-linear programming type with fuzzy demand.

Taleizadeh et al. [6] developed an inventory control model to construct the optimal order and the shortage quantities of decayed items when the supplier offers a special sale. Taleizadeh et al. [7] described an economic production quantity model with random defective items. The aim of this research is to derive the optimal production quantity, the optimal cycle length and the optimal back ordered quantity to minimize the optimal total cost. Karteek and Jyoti [8] explained the different kinds of inventory model with the solution procedure to minimize the overall holding cost of the finished products. He mainly compared the deterministic and the probabilistic model to prove his result.

Aswathy et al. [9] discussed the fish marketing at Ernakulam district in Kerala and they briefly analyzed the marketing channels in different places. They analyzed the annual income for commission agents, retailers and women vendors of different areas. Kumar and Rajput [10] described the fuzzy inventory model with full back-ordered situation and for defuzzification they compared the centroid method and the signed distance method, and finally they proved that centroid method is more profitable. Zhivit Skaya and Safranava [11] approaches the linguistic fuzzy variables not as a numerical crisp case and they optimize the uncertainty at the time of making the decisions using fuzzy logic.

Babalola et al. [12] showed the potential of fish marketing education, instability in the purchase price, the major constrains that affect fish marketing and price stability. Castillo et al. [13] present a comparative study of type-2 fuzzy logic systems with type-1 and type-2 fuzzy logic controllers for designing the complex non-linear plants. This result is verified with four benchmark problems. Payva et al. [14] discussed the production and the marketing of fish products they investigate for the production, fish species, maintenance cost, sources of raw fish, selling price of dry fish, the cost functions involved in selling and the production of fish products. Finally, they concluded that the dry fish is more profitable than the fresh fish products in the West Bengal coast. Ganesh et al. [15] dealt with the vendor buyer inventory model with the coordination situation for vendor and non-coordination situation for buyers to reduce the total cost for both the vendor and the buyer. Comparison between coordination and non-coordination system is explained clearly in this paper with numerical examples. Chen and Wang [16] used a quantum particle swam optimization (QPSO) algorithm are used to optimize all the proposed GT2 FLS methods compared with their type-1(T1) and interval type-2 (T2) methods for forecasting. Servakula and Verma [17] explained the fuzzy support vector machine by treating all samples of a class with a single MFC (membership function) and compared the results with 15—real-world benchmark datasets.

Aswathy et al. [18] dealt with the net profit of the fisheries management and the total earnings of the fishermen societies including the cost and revenue of fishing. In this paper, the perishable rate of the crisp case is compared with the fuzzy environment using Pentagonal Fuzzy Number (PFN). For defuzzification, graded mean difference method is used. Sugapriya [19] formulated an EPQ model for deteriorating items with exponential distribution in an infinite planning horizon which provides also price discount for the deteriorating items. Xu and Gou [20] characterize the uncertain information more sufficiently and accurately. They provide an overview of interval-valued intuionistic fuzzy information techniques. Nobil and Sedigh [21] explained the fuzzy inventory model for decaying items considering machinery uptime in the linear programming problem and it was solved by trapezoidal fuzzy number to get the optimal total cost. Jana et al. [22] present a new approach to mamdani interval type 2 fuzzy logic inference systems. Sensitivity analysis is performed using fuzzy C- means clustering to the models. Punt [23] analysis outlines some of the key decisions that need to be made when conducting a spatial stock assessment. Reasons for including special structure in stock assessments explain how to select the stocks fleets and areas included in the stock assessment. Taleizadeh and Moshtagh [24] explained the concept of multi-level closed-loop supply chain (CLSC) for a supplier, a producer, a retailer and collector with higher acceptance quality of return. Also they considered the situation in which remanufactured items are perceived different from the newly produced items by customers. Debnath et al. [25] developed with type-1 and type-2 fuzzy parameters under trade credit policy. Type-1 is not sufficient to formulate the model. They exhibit the model in the type-2 fuzzy model to obtain the optimal total cost depending upon the positions of trade credit and retailer with respect to the time period. Ontiverous-Robles et al. [26] presented a comparison in the robustness of interval type-2 and generalized type-2 fuzzy logic controllers. Sanjai and Periyasamy [27] discussed the imperfect system with rework, he derived the EPQ with a backorder and without back order to minimize the total cost of the system. Sang et al. [28] proposed a interval type-2 fuzzy numbers have advantages in modeling uncertainty. This application has been performed in stock selection of real estate industry in china.

Kuppulakshmi and Sugapriya [29] explained the paper for deteriorating products with the penalty maintenance cost. This paper focused on the demand function with three different cases and finally, the optimum cycle time, the optimum ordered quantity and the total cost are derived for n number of cycles. Dorfeshan and Mousavi [30] analyze a comparison method for determining the critical path of production projects under group decision— making process. A new relative preference relation and interval type-2 fuzzy sets are performed for air craft maintenance planning.

In this paper, the yachting time is treated as pentagonal fuzzy number to prove the convexity. The repair cost and the labor cost are treated as fuzzy numbers to show various fluctuations in the total cost of the production cycle. The main aim is to find the annual fish production quantity and the fish quantity in one cycle to avoid the false assumption in demand for various seasons. In 1965, Zadeh launched the notations of a fuzzy set. Definitions are given below:

Definition 1.1

A fuzzy set $\tilde{\Delta }$ in X is represented as a set of ordered pairs as given below.

$$ \tilde{\Delta } = \left\{ {(N,\mu_{{\tilde{A}}} \left( N \right) :N \in X} \right\}\;{\text{where}} $$

$$ \mu_{{\tilde{\Delta } }} :X \to \left[ {0,1} \right]. $$

If X is a finite set then $\tilde{\Delta }$ is presented as $\mathop \sum \limits_{N \in X} \frac{{\mu_{{\tilde{\Delta }}} \left( N \right)}}{N}$.

If X is a countable set then $\tilde{\Delta }$ is presented as $\mathop \sum \limits_{i = 0}^{\infty } \frac{{{\upmu }_{{\tilde{\Delta }}} \left( {{\text{N}}_{{\text{i}}} } \right)}}{{{\text{N}}_{{\text{i}}} }}$.

If X is a continuous case, then $\tilde{\Delta }$ is presented as integral $\mathop \smallint \limits_{X}^{{}} \mu_{{\tilde{\Delta }}} \left( N \right) {\text{d}}N$.

Definition 1.2

A fuzzy set $\tilde{\Delta } = \left\{ {(X,\mu_{{\tilde{\Delta }}} \left( X \right)} \right\}\underline { \subset }$ is convex fuzzy set if all $\tilde{\Delta }_{x}$ are convex set that is for each element $u \in \Delta_{ \propto }$ and $v \in \Delta_{ \propto }$ for every $\propto \in \left[ {0,1} \right]$. uλ + (1 − λ)$v, \forall {\uplambda } \in \left[ {0,1} \right]$. On the other hand fuzzy set is called non-convex fuzzy set.

Definition 1.3

A fuzzy set [$u_{ \propto } , v_{ \propto } ]$ where 0 ≤ $\propto$ ≤ 1 and a < b determined on R is termed as the fuzzy interval when its membership function is given by.

$$ \mu_{{\left[ {a_{ \propto } , b_{ \propto } } \right]}} = \left\{ { 0 ,\begin{array}{*{20}c} { \propto , u \le x \le v} \\ {\text{or else}} \\ { } \\ \end{array} } \right\}. $$

Definition 1.4

A fuzzy number (FN) $\tilde{\Delta }$ = (u, v, w) where u < v < w and determined on R is termed as a triangular fuzzy number when the function of membership is.

$$ \mu_{{\tilde{\Delta }}} \left( X \right) = \left\{ {\begin{array}{*{20}c} {\frac{x - u}{{v - u}} , u \le x \le v} \\ {\frac{w - x}{{w - v}} , v \le x \le w} \\ {0 , {\text{otherwise }} } \\ \end{array} } \right\}. $$

When u = v = w, we have fuzzy points (w, w, w) = w the group of all triangular fuzzy numbers on R is determined as,

$$ F_{N} \left\{ {\left( {u,v, w} \right):u < v < w \forall u,v,w \in R } \right\}. $$

The $\propto$-cut of $\tilde{\Delta } = \left( {u,v,w} \right) \in F_{N}$, 0 ≤ $\propto$ ≤ 1, is $(\Delta \propto ) = \left[ {\Delta_{L} \left( \propto \right),\Delta_{R} \left( \propto \right)} \right].$

Where $\Delta_{L} \left( \propto \right) = u + \left( {v - u} \right) \propto$ and $\Delta_{R} \left( \propto \right) = w - \left( {w - v} \right) \propto$ are the left and the right end points of $\Delta ( \propto )$.

Definition 1.5

A pentagonal fuzzy number $\tilde{\Delta }$ = (a, b, c, d, e,) is indicated with the performance of membership $\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }}$.

$$ \mu_{{\tilde{\Delta }}} = \left\{ \begin{gathered} L_{1} \left( x \right) = \frac{1}{2} \left( {\frac{x - a}{{b - a}}} \right), a \le x \le b \hfill \\ L_{2} \left( x \right) = \left( {\frac{x - b}{{c - d}}} \right), b \le x \le c \hfill \\ R_{1} \left( x \right) = \left( {\frac{d - x}{{d - c}}} \right), c \le x \le d \hfill \\ R_{2} \left( x \right) = \left( {\frac{e - x}{{e - d}}} \right), d \le x \le e \hfill \\ 0, {\text{ otherwise}} \hfill \\ \end{gathered} \right\}. $$

The $\propto$-cut on $\tilde{\Delta }$ = (a, b, c, d, e,), 0 ≤ $\propto$ ≤ 1 is $\Delta$ ($\propto$) = $\left[ {\Delta_{L} \left( \propto \right),\Delta_{R} \left( \propto \right)} \right].$

where

$$ \Delta_{{L_{1} }} \left( \propto \right) = a + \left( {b - a} \right) \propto = L_{1}^{ - 1} \left( \propto \right) $$

$$ \Delta_{{L_{2} }} \left( \propto \right) = b + \left( {c - b} \right) \propto = L_{2}^{ - 1} \left( \propto \right) $$

$$ \Delta_{{R_{1} }} \left( \propto \right) = d - \left( {d - c} \right) \propto = R_{1}^{ - 1} \left( \propto \right) $$

$$ \Delta_{{R_{2} }} \left( \propto \right) = e - \left( {e - d} \right) \propto = R_{2}^{ - 1} \left( \propto \right). $$

Hence,

$$ L^{ - 1} \left( \propto \right) = \frac{{L_{1}^{ - 1} \left( \propto \right) + L_{2}^{ - 1} \left( \propto \right)}}{2} = \frac{{a + b + \left( {c - a} \right) \propto }}{2} $$

$$ R^{ - 1} \left( \propto \right) = \frac{{R_{1}^{ - 1} \left( \propto \right) + R_{2}^{ - 1} \left( \propto \right)}}{2} = \frac{{d + e - \left( {e - c} \right) \propto }}{2}. $$

Definition 1.6

If $\tilde{\Delta }$ = (u, v, w, x, y) is a pentagonal fuzzy number, Grated Mean Representation Method (GMRM) of $\tilde{\Delta }$ is derived as.

$$ P(\tilde{\Delta }) = \frac{1}{12}\left[ {u + 3v + 4w + 3x + y} \right]. $$

Assumptions

• 1. The yachting time is less than or equal to the total production run time.

• 2. Back orders are not allowed.

• 3. The yachting time is treated as a pentagonal fuzzy number $\tilde{y} = \left( {0,0,0.07,0.08,0.09} \right)$.

• 4. Shipment cost, added value cost are treated as constant.

• 5. Setup cost, unexpected maintenance cost and labor cost are treated as a logarithmic function.

• 6. The yachting time is more than the maintenance and setup time of the vessel.

Notations

$I_{\max }$: Maximum inventory level of fish products during yachting.

$\omega$: The rate of deteriorated fish items in the vessel.

$F_{{\text{p}}}$: Annual fish production rate/tonnes.

$F_{{\text{d}}}$: Annual fish demand rate /tonnes.

$F_{{\text{Q}}}$: Production quantity of fish products during yachting.

$\tau_{{\text{p}}}$: Fish yachting time during the production period.

$\tau_{{\text{d}}}$: Vessel downtime during production.

$A$: Set up cost for the vessel/per setup.

$h$: Holding cost of fish products/unit/per period.

$S_{0}$: Setup cost before any production starts /$

$S$: Setup cost per cycle/$

$L_{0}$: Advance for the labor who works in the yacht/$

$L$: Labor cost per cycle/$

$R_{{\text{c}}}$: Repair cost per cycle/$

$P_{r}$: Percentage value of overall production rate/per period.

$U_{0}$: Initial amount spent for the maintenance of the yacht/$

$U$: Amount spent for unexpected maintenance per cycle/$

V: Added value cost of the fish product/$

$F_{{\text{S}}}$: Constant setup time during yachting /period.

$F_{{\text{M}}}$: Constant setup time during yachting /period.

T: Total duration of the fish production.

Problem formulation

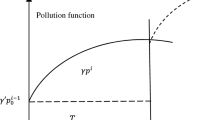
Based on Fig. 1, the following equations are formed

$$ I_{\max } = \left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]\frac{{F_{{\text{Q}}} }}{{F_{{\text{p}}} }} $$

(1)

$$ \tau_{{\text{p}}} = \frac{{I_{\max } }}{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}} = \frac{{F_{{\text{Q}}} }}{{F_{{\text{p}}} }} $$

(2)

$$ \tau_{{\text{d}}} = \frac{{I_{\max } }}{{F_{{\text{d}}} }} = \frac{{F_{{\text{Q}}} }}{{F_{{\text{p}}} F_{{\text{d}}} }}\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right] $$

(3)

$$ T = \tau_{{\text{p}}} + \tau_{{\text{d}}} = \frac{{\left( {1 - \omega } \right)F_{{\text{Q}}} }}{{F_{{\text{d}}} }}. $$

(4)

Fig. 1

The inventory level of the vessel during yachting time and shipment time

$I_{\max }$ is the inventory level respective to the fish production time $\tau_{{\text{p}}} {\text{and}} \tau_{{\text{d}}}$.

The total annual cost $({\text{TC}}_{F} )$ of fish products includes the setup cost for the vessel (SC), annual repair cost of the vessel (RC), labor cost (LC), annual disposal cost (FDC), annual maintenance cost (MC), shipment cost (SP) added value cost $({\text{AV}}_{c} )$

$$ {\text{TC}}_{F} = {\text{SC}} + {\text{RC}} + {\text{LC}} + {\text{FDC}} + {\text{UMC}} + {\text{SP}} + {\text{AV}}_{c} . $$

(5)

Setup cost

Each vessel has a setup cost to prepare for the yachting during different seasons (φ), they spent a different amount for the vessel. In this paper, the setup cost is considered as the average of all the seasons

$$ {\text{SC}} = nA = \frac{A}{T} $$

(6)

$$ {\text{SC}} = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} . $$

(7)

Repair cost

Due to the vessel depreciation, the vessel needs to be repaired during the April–May lockdown period every year. The cost which is used to repair the vessel is called repair cost. This cost is common for both the new or pre-owned vessels which include mainly the spare parts of the vessel.

$$ {\text{RC}} = {\text{n}}R_{{\text{c}}} = \frac{{R_{{\text{c}}} }}{T} $$

(8)

$$ {\text{RC}} = \frac{{R_{{\text{c}}} F_{{\text{d}}} }}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} . $$

(9)

Labor cost

For each yachting period, some labors are allotted for shipping. The cost providing to the labor plays a vital role. The percentage value of the overall production rate is allotted for labors.

$$ {\text{LC}} = \frac{{P_{{\text{r}}} log\left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} {\text{and}} P_{{\text{r}}} = F_{{\text{p}}} \delta $$

(10)

Holding cost

Holding cost of fish products in the vessel include ice, water, coolant cans which are used during yachting etc., the cost function is given below,

$$ {\text{HC}} = nh\frac{{I_{\max } T}}{2} $$

(11)

$$ {\text{HC}} = h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}} . $$

(12)

Unexpected maintenance cost

Due to some natural calamities, some cost is allotted for the maintenance of the yacht; this cost is unexpected for the fishermen.

$$ {\text{LC}} = \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} . $$

(13)

Shipment cost

The cost is used for loading the goods for the yachting and unloading the fish products from the boat after completing the yachting which is given under shipment cost.

$$ {\text{SC}} = \frac{{AF_{{\text{d}}} }}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }}. $$

(14)

Added value cost

Due to the yachting time, fishes caught on the first day are spoiled and they are ready to degrade. So, fishermen planned to sell instead of disposing. They sell this kind of fish in a discounted rate to get profit for them. So, it is reduced from the total cost.

$$ AVC = \frac{{F_{d} V\omega }}{{\left( {1 - \omega } \right)}} $$

(15)

The annual total cost of the yachting period is given by the Eqs. (7), (9), (10), (12), (13), (14) and (15) is given as,

$$ \begin{aligned} {\text{TC}}_{F} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} + \frac{{R_{{\text{c}}} F_{{\text{d}}} }}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} \\ &\quad + h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}} + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} \\ &\quad + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \omega } \right)F_{{\text{Q}}} }} - \frac{{F_{{\text{d}}} V\omega }}{{\left( {1 - \omega } \right)}} \\ \end{aligned} $$

(16)

$$ {\text{TC}}_{F} = \gamma_{1} F_{{\text{Q}}} + \frac{{\gamma_{2} }}{{F_{{\text{Q}}} }} - \gamma_{3} $$

(17)

$$ \gamma_{1} = h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }} $$

(18)

$$ \begin{aligned} \gamma_{2} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \omega } \right)}} + \frac{{R_{{\text{c}}} F_{{\text{d}}} }}{{\left( {1 - \omega } \right)}} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \omega } \right)}} \\ &\quad + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \omega } \right)}} + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \omega } \right)}} \end{aligned} $$

(19)

$$ \gamma_{3} = \frac{{F_{d} V\omega }}{{\left( {1 - \omega } \right)}} $$

(20)

To find the optimal solution for $F_{{\text{Q}}}$ differentiate Eq. (17) with respect to $F_{{\text{Q}}}$ and equal to zero is given as,

$$ \frac{{\partial {\text{TC}}_{F} }}{{\partial F_{{\text{Q}}} }} = \gamma_{1} - \frac{{\gamma_{2} }}{{F_{{\text{Q}}}^{2} }} $$

(21)

$$ \gamma_{1} - \frac{{\gamma_{2} }}{{F_{{\text{Q}}}^{2} }} = 0 $$

(22)

$$ F_{{\text{Q}}} = \sqrt {\frac{{\gamma_{2} }}{{\gamma_{1} }}} . $$

(23)

Substitute $F_{{\text{Q}}}$ in Eq. (16), we get the total cost of the one fish production in one cycle.

Subjective constraints

The yachting time and the production quantity of fish are associated with the constraints equation. The total production time is always greater than or equal to the production time, setup time for yachting and the maintenance time is given as,

$$ \left( {\text{i}} \right) F_{{\text{Q}}} \ge 0 $$

(24)

$$ \left( {{\text{ii}}} \right)\tau_{{\text{p}}} + F_{{\text{S}}} + F_{{\text{M}}} \le T $$

(25)

From the Eqs. (2) and (4) we have

$$ \left( {{\text{iii}}} \right) F_{{\text{Q}}} \ge \frac{{\left( {F_{{\text{S}}} + F_{{\text{M}}} } \right)F_{{{\text{d}}F_{{\text{p}}} }} }}{{F_{{\text{p}}} \left( {1 - \omega } \right) - F_{{\text{d}}} }} = F_{{\text{Q}}}^{{\max}} . $$

(26)

Fuzzy model

The production or the yachting time $\tilde{y} = \left( {0,0,0.07,0.08,0.09} \right)$ is treated as the trapezoidal fuzzy number to check the fuzzy constrains so as to obtain ${\text{TC}}_{F}$ is minimum which is graphically explained in Fig. 2. The production time is always less than its permitting time.

$$ \left( {\text{i}} \right)\tau_{{\text{p}}} \le \widetilde{y } $$

(27)

$$ \left( {{\text{ii}}} \right)\frac{{F_{{\text{Q}}} }}{{F_{{\text{p}}} }} \le \tilde{y} $$

(28)

Fig. 2

Membership function of uptime duration of yachting (Pentagonal fuzzy number)

Then

$$ \min {\text{TC}}_{F} = \gamma_{1} F_{{\text{Q}}} + \frac{{\gamma_{2} }}{{F_{{\text{Q}}} }} - \gamma_{3} $$

(29)

Subject to:

$$ F_{{\text{Q}}} \ge F_{{\text{Q}}} ^{\max } $$

(30)

$$ \frac{{F_{{\text{Q}}} }}{{F_{{\text{p}}} }} \le \tilde{y} $$

(31)

$$ F_{{\text{Q}}} \ge 0 $$

(32)

To check the convexity of the function, the above Eqs. (30) to (32) are verified using matlab2014.

Using Fig. 2 the total production cost in pentagonal fuzzy number is given below:

$$ \widetilde{{{\text{TC}}_{F} }} = \left( {\widetilde{{{\text{TC}}_{{F_{1} }} }}, \widetilde{{{\text{TC}}_{{F_{2} }} }},\widetilde{{{\text{TC}}_{{F_{3} }} }},\widetilde{{{\text{TC}}_{{F_{4} }} }},\widetilde{{{\text{TC}}_{{F_{5} }} }}} \right) $$

(33)

The rate of deteriorated fish items in a vessel, added value cost of fish product and repair cost are treated as a pentagonal fuzzy number, according to that, the following total cost function is also obtained as a pentagonal fuzzy number which is given by Eqs. (34)–(38)

$$ \begin{aligned} \widetilde{{{\text{TC}}_{{F_{1} }} }} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{\widetilde{{R_{{\text{c}}} }}F_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ &\quad + h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}}^{*} + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ &\quad + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} - \frac{{F_{{\text{d}}} \tilde{V}\omega }}{{\left( {1 - \tilde{\omega }} \right)}} \\ \end{aligned} $$

(34)

$$ \begin{aligned} \widetilde{{{\text{TC}}_{{F_{2} }} }} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{\widetilde{{R_{{\text{c}}} }}F_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ & \quad + h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}}^{*} + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ &\quad + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} - \frac{{F_{{\text{d}}} \tilde{V}\omega }}{{\left( {1 - \tilde{\omega }} \right)}} \\ \end{aligned} $$

(35)

$$ \begin{aligned} \widetilde{{{\text{TC}}_{{F_{3} }} }} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{\widetilde{{R_{{\text{c}}} }}F_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ & \quad + h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}}^{*} + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ &\quad + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} - \frac{{F_{{\text{d}}} \tilde{V}\omega }}{{\left( {1 - \tilde{\omega }} \right)}} \\ \end{aligned} $$

(36)

$$ \begin{aligned} \widetilde{{{\text{TC}}_{{F_{4} }} }} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{\widetilde{{R_{{\text{c}}} }}F_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ & \quad + h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}}^{*} + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ &\quad + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} - \frac{{F_{{\text{d}}} \tilde{V}\omega }}{{\left( {1 - \tilde{\omega }} \right)}} \\ \end{aligned} $$

(37)

$$ \begin{aligned} \widetilde{{{\text{TC}}_{{F_{5} }} }} & = \frac{{F_{{\text{d}}} \log \left( {\frac{{S_{0} }}{S}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{\widetilde{{R_{{\text{c}}} }}F_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} + \frac{{P_{{\text{r}}} \log \left( {\frac{{L_{0} }}{L}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} \\ & \quad + h\frac{{\left[ {\left( {1 - \omega } \right)F_{{\text{p}}} - F_{{\text{d}}} } \right]}}{{2F_{{\text{p}}} }}F_{{\text{Q}}}^{*} + \frac{{F_{{\text{d}}} \log \left( {\frac{{U_{0} }}{U}} \right)}}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }}\\ &\quad + \frac{{AF_{{\text{d}}} }}{{\left( {1 - \tilde{\omega }} \right)F_{{\text{Q}}}^{*} }} - \frac{{F_{{\text{d}}} \tilde{V}\omega }}{{\left( {1 - \tilde{\omega }} \right)}} \\ \end{aligned} $$

(38)

Similarly, the defuzzification of the total cost function and the decision variables using GMRM are given by

$$ \widetilde{{TC_{F} }} = \frac{1}{12}\left[ {\widetilde{{{\text{TC}}_{{F_{1} }} }} + 3\widetilde{{{\text{TC}}_{{F_{2} }} }} + 4\widetilde{{{\text{TC}}_{{F_{3} }} }} + 3\widetilde{{{\text{TC}}_{{F_{4} }} }} + \widetilde{{{\text{TC}}_{{F_{5} }} }}} \right] $$

(39)

$$ \tilde{V} = \frac{1}{12}\left[ {\widetilde{{V_{1} }} + 3\widetilde{{V_{2} }} + 4\widetilde{{V_{3} }} + 3\widetilde{{V_{4} }} + \widetilde{{V_{5} }}} \right] $$

(40)

$$ \tilde{\omega } = \frac{1}{12}\left[ {\widetilde{{\omega_{1} }} + 3\widetilde{{\omega_{2} }} + 4\widetilde{{\omega_{3} }} + 3\widetilde{{\omega_{4} }} + \widetilde{{\omega_{5} }}} \right] $$

(41)

$$ \widetilde{{R_{{\text{c}}} }} = \frac{1}{12}\left[ {\widetilde{{R_{{{\text{c}}_{1} }} }} + 3\widetilde{{R_{{{\text{c}}_{2} }} }} + 4\widetilde{{R_{{{\text{c}}_{3} }} }} + 3\widetilde{{R_{{{\text{c}}_{4} }} }} + \widetilde{{R_{{{\text{c}}_{5} }} }}} \right] $$

(42)

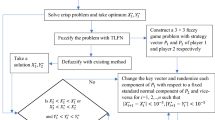
Algorithm to find the optimal solution

• Step 1. Calculate the values of $\gamma_{1} ,\gamma_{2} {\text{and}} \gamma_{3}$ by the Eqs. (18), (19), (20).

• Step 2. If $F_{{\text{p}}} \left( {1 - \omega } \right) \ge F_{{\text{d}}}$, then feasible solution exists then go to step: 3, otherwise the problem is infeasible go to step: 9

• Step 3. Calculate $F_{{\text{Q}}}^{{\max}} = \frac{{\left( {F_{{\text{S}}} + F_{{\text{M}}} } \right)F_{{{\text{d}}F_{{\text{p}}} }} }}{{F_{{\text{p}}} \left( {1 - \omega } \right) - F_{{\text{d}}} }}$ go to step: 4.

• Step 4. Find $F_{{\text{Q}}} = \sqrt {\frac{{\gamma_{2} }}{{\gamma_{1} }}}$ go to step: 5.

• Step 5. Check $F_{{\text{Q}}} \ge 0$ then go to step: 6 otherwise the problem is infeasible go to step: 9.

• Step 6. Check $F_{{\text{Q}}} \ge F_{{\text{Q}}}^{\max }$ then go to step: 7 otherwise the problem is infeasible go to step: 9.

• Step 7. Check $\frac{{F_{{\text{Q}}} }}{{F_{{\text{p}}} }} \le \tilde{y}$ then go to step: 8 otherwise the problem is infeasible go to step: 9.

• Step 8. Solve Eq. (16) which gives the minimum total cost of the fish production time.

• Step 9. End and show the problem is infeasible.

This algorithm is explained in Fig. 3 as a flow chart.

Fig. 3

Flow chart for the solution algorithm

Numerical solution

To illustrate the numerical calculations for the proposed model, some values of the parameters are adopted from Taleizadeh et al. [5]. Data for this research are collected from the coastal area of Kasimedu, Tamilnadu, India in the year 2019 during the month of December. We collected the data from 20 to 30 vessel owners and the average values are assigned in the numerical example. Then, these values are considered as pentagonal fuzzy number. The production plane data are considered as the predicted value and the model output as the observed value and from these values are defined from statistical parameters. These statistical parameters are compared with Taleizadeh et al. [5] by changing the predicted value in the fuzzy logic we get outcome result as a feasible solution. In Taleizadeh et al. [5] crisp set, the negative values and the non-feasible solutions are occurred for the optimal total time and the optimal total cost of the production plan.

Crisp model

To exhibit the cost effectiveness of the proposed model and the performance of the solution process, effective numerical examples are performed in this section. Highly degradation nature of the fish leads to fluctuations in the price of the fish products. Assuming $\omega = 0.2$,$F_{{\text{p}}} = 1000$,$F_{{\text{d}}} = 400$,$L = 10$,$L_{0} = 3$,$\delta = 2\%$, h = 10, A = 5,$F_{{\text{M}}} = 0.005$, $F_{{\text{S}}} = 0.008$, v = 5, $R_{{\text{c}}} = 10$, $U_{0} = 1$,$U = 0.8$,$S_{0} = 1$,$S = 0.5$,

The solution of the crisp model is

$$ \begin{gathered} {\text{TC}}_{F} = 29427,F_{{\text{Q}}} = 55.8998,F_{{\text{Q}}}^{{\max}} = 13,T \, = \, 0.1263, \hfill \\ \tau_{{\text{p}}} = 0.0631,I_{{\max}} = 25.2510. \hfill \\ \end{gathered} $$

Fuzzy model

Suppose

$\tilde{\omega }$ = (0.1 0.15 0.2 0.25 0.3), ${\tilde{\text{V}}}$ = (4 4.5 5 5.5 6) and $\widetilde{{R_{{\text{c}}} }}$ = (8 9 10 11 12) are pentagonal fuzzy numbers, the fuzzy total cost for the fish production, fuzzy annual production quantity, fuzzy production quantity, fuzzy total run time, fuzzy yachting time and the fuzzy inventory level during the run time are given as,

$$ \begin{gathered} \widetilde{{{\text{TC}}_{F}^{*} }} = 30340,\widetilde{{F_{{\text{Q}}}^{*} }} = 63.95,\widetilde{{F_{{\text{Q}}}^{\max *} }} = 13.25, \hfill \\ T = \, 0.1269,\widetilde{{\tau_{{\text{p}}}^{*} }} = 0.0640,\;{\text{and}}\;\widetilde{{I_{\max }^{*} }} = 25.1339 \hfill \\ \end{gathered} $$

Optimal results of the fuzzy model are defuzzified by GMDM.

Sensitivity analysis

Table 1 shows that the total cost for the fish production $({\text{TC}}_{F}$) is increased when the setup cost and the demand rate of the fish product increase from − 30 to + 30%. The total cost for the fish production $({\text{TC}}_{F}$) is decreased when the holding cost and the production rate of the fish product increase from − 30 to + 30%. The parameter change in setup cost, holding cost, demand rate and production rate are shown in Fig. 4.

Table 1 The outcomes of parameter change in percentage

Fig. 4

Parameter change in setup cost (A), holding cost (h), demand rate $(F_{{\text{d}}}$) and production rate $\left( {F_{{\text{p}}} } \right)$, (Vs) Total cost

From Table 2, the fuzzy parameter $\tilde{\omega }$ for different values are analyzed, and from this the fuzzy total cost.

Table 2 The outcomes of fuzzy Parameter change in deteriorated fish product rate

($\widetilde{{{\text{TC}}_{F}^{*} }}$) is increased when the fuzzy total run time (T) and fuzzy uptime are increased which are shown in Fig. 5a.

Fig. 5

Sensitivity analysis of fuzzy Parameter change in deteriorated fish items

In Fig. 5b, the deteriorated fish items in the vessel are compared with the annual production quantity and the fish quantity per cycle. Annual production quantity and production quantity per cycle also increased when the deterioration rate increased. In Fig. 5c, it is shown that, when the deterioration rate increased, the total cost for the fish production is also increased. While increasing the value of the rate of deteriorated fish items in a vessel $\widetilde{(\omega })$, fuzzy inventory level during the run time and the fuzzy total cost for the fish production is also increased which is shown in Fig. 5d.

From Table 3, the total cost for the fish production is decreased when repair cost of the vessel is discussed under different fuzzy parameter. Figure 6 graphically shows the total cost for the fish production is increased when added value cost of the fish items is discussed under different fuzzy parameters.

Table 3 The outcomes of fuzzy Parameter change in the repair cost of fish product and added value cost of fish product

Fig. 6

Sensitivity analysis of fuzzy Parameter change in repair cost and added value cost

Conclusion

The result of this analysis gives a better solution in the fish production process and it results in good marketing infrastructure by obtaining the minimum total cost of the fish production. By calculating the unexpected maintenance cost and the annual production quantity, the fishermen will be able to balance the demand and the supply of fish to avoid faulty measurement in fish marketing. This conclusion holds for total cost value but incorporating the cost of fishing can change discrimination on fuzzy parameters. This vast and more appropriate view can change the fishing strategies discern as optimal in supply chain fisheries resulting in the increased cooperation and ultimately they turn more profitable and viable fisheries for all users.

Highly deteriorating nature of fish gives fluctuations in the price of fish and it is assumed in a fuzzy environment to get the optimal total cost of the fish production. GMIR method is used for the defuzzification. This research can be extended to fuzzy shortage level, lockdown situations, Fish ban period, multi buyer with a single vendor and stochastic nature. The higher advantage of this model is that it will reduce the cost of production. Some time indicator may not help to achieve determining the deterioration rate of the fish products due to the variation in yachting time. To avoid this advance interference in fuzzy logic like linguistic [21], Fuzzy artificial neural network, interpretative structural modeling method and Simulink are used to assess the scale of effectiveness of this current study. In future research, we will utilize the other fuzzy methods like mamdani interval type -2 fuzzy logic to control the deterioration rate during the production period.