Supervisor synthesis and throughput optimization of partially-controllable manufacturing systems

Abstract

One of the challenges in the design of supervisors with optimal throughput for manufacturing systems is the presence of behavior outside the control of the supervisor. Uncontrollable behavior is typically encountered in the presence of (user) inputs, external disturbances, and exceptional behavior. This paper introduces an approach for the modeling and synthesis of a throughput-optimal supervisor for manufacturing systems with partially-controllable behavior on two abstraction levels. Extended finite automata are used to model the high abstraction level in terms of system activities, where uncontrollability is modeled by the presence of uncontrollable activities. In the lower abstraction level, activities are modeled as directed acyclic graphs that define the constituent actions and dependencies between them. System feedback from the lower abstraction level, including timing, is captured using variables in the extended finite automata of the higher abstraction level. For throughput optimization, game-theoretic methods are employed on the state space of the synthesized supervisor to determine a guarantee to the lower-bound system performance. This result is also used in a new method to automatically compute a throughput-optimal controller that is robust to the uncontrollable behavior.

1 Introduction

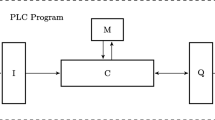
Over the past decades, increasing complexity of manufacturing systems has driven the development of model-based systems engineering (MBSE) and supervisory control methods to aid in the design process (Estefan 2008; Steimer et al. 2017). Executable models created by these methods allow engineers to test and adjust the system before it is built. This increases design flexibility and reduces time-to-market, and has the potential to improve system performance. In controller design, the developed models can be used for automatic generation of supervisory controllers using controller synthesis techniques (Baeten et al. 2016). These controllers must ensure functional correctness with respect to the specifications, and provide optimal control decisions in terms of relevant performance criteria. A challenge in the construction and analysis of models in these methods is the inclusion of system behavior outside the influence of the controller. For example, products may enter the manufacturing system with varying time intervals, or actions on a different control layer may require a response from the supervisor. In the design phase, it is useful to assess functional correctness and achievable performance under the influence of such behavior, while it is desirable for a controller to make correct and optimal control decisions when these activities occur.

This paper introduces an approach, shown in Fig. 1, for synthesizing throughput-optimal supervisors for manufacturing systems with partially-controllable behavior. It is based on the recently developed Activity modeling formalism (van der Sanden et al. 2016), which enables the compositional modeling of functionality and timing of manufacturing systems. Functionality in the Activity modeling formalism is specified on two abstraction levels: high-level activities, and low-level actions. An activity expresses some deterministic functionality, such as picking up and moving a product, in terms of the individual actions and dependencies between the actions. Resources provide the services to execute actions; an activity consisting of multiple actions may require more than one resource for its execution. Functional design is carried out on the level of activities by the use of finite automata (FAs), called plants and specifications. Plants describe the activity sequences that are available in the system, and specifications describe the order in which activities should be executed. The key benefit of this abstraction is a much smaller state-space for controller design, when compared to the case where all actions are modeled explicitly (van der Sanden et al. 2016). The internal structure of activities allows timing, expressed on the level of actions, to be collected into a (max,+) timing characterization of each activity. By orthogonally adding timing characterizations to the state space, a (max,+) state space can be constructed for performance analysis. Existing optimal cycle ratio algorithms (Dasdan 2004) can be used to find a throughput-optimal controller, which dispatches activities in an optimal ordering. The Activity modeling formalism is already in use within ASML,¹ the world-leading manufacturer of lithography machines for the semiconductor industry, to formalize the description of the product handling part of their machines. It acts as the semantic underpinning of a domain-specific language (DSL) that allows domain engineers to model a complete system. In the available tool chain, CIF (van Beek et al. 2014) is used for synthesizing a supervisor, and throughput-optimization techniques of (van der Sanden 2018) are used.

Fig. 1

Overview of the modeling approach for supervisor synthesis and throughput optimization of a partially-controllable manufacturing system

Our modeling approach expands on the Activity modeling formalism in two fundamental ways. First, it defines uncontrollable system behavior explicitly by partitioning activities into controllable and uncontrollable (to the supervisor) activities. This is a common concept from supervisory control theory (Ramadge and Wonham 1987; Cassandras and Lafortune 2008). As uncontrollable activities may influence the performance that can be achieved, performance can no longer be guaranteed by looking at the controller alone. To overcome this, we use game-theoretic methods (van der Sanden 2018) to determine the optimal strategy for the supervisor. From this result a guarantee on the lower bound system performance in the presence of uncontrollable behavior can be achieved. Further, we use the optimal strategy in a new method to automatically compute a throughput-optimal controller that is robust to the uncontrollable behavior. One of the main challenges here is how to deal with situations where both uncontrollable and controllable behaviour is enabled at the same time.

The second fundamental change of our approach is the inclusion of (uncontrollable) feedback from lower abstraction levels into the level of the supervisor. We do this by augmenting a finite automaton with variables, obtaining an extended finite automaton (EFA) (Chen and Lin 2000; Sköldstam et al. 2007). Timing from the Activity modeling formalism, captured by resource time stamps and their change upon the execution of an activity, can be naturally expressed as variables and update functions in the EFA. This approach enables the description of functionality based on information induced by the actions, including the availability times of resources. It also provides for concise and unified description of functionality and timing in a single model.

The remainder of the paper is structured as follows. We start by introducing a motivating example system, the Dice Factory, in Section 2, which presents several challenges with regard to uncontrollability. In Section 3 we introduce the Activity modeling formalism in more detail and outline several concepts and definitions that are used in our modeling approach. That approach is described in Section 4, where we present the methods that can be used to express and model uncontrollability. We subsequently turn to optimization of a partially-controllable system in Section 5, where we describe methods to determine guarantees for system performance and to automatically compute an optimal controller that is robust to the uncontrollable behavior. All introduced modeling and optimization methods are put to use in Section 6, where we model and optimize the example Dice Factory system. We discuss the similarities and differences between our work and related works in Section 7. Section 8 concludes the paper and describes future extensions that may be investigated.

2 Motivating case study: Dice Factory

As a motivating example for investigating partial controllability in manufacturing processes, consider the fictional Dice Factory, shown in Fig. 2. In the Dice Factory, high-grade game dice are produced in two stages. During the Mill stage, holes are milled in a side of the unfinished die in a pattern corresponding to the value of that side. During the Paint stage, the milled holes are filled with a colored paint. Transporting the dice is the job of two carts, which carry a die from an input position, through the two production steps, onto an output position. Because there are two carts and two production stages, while one die is processed on the Mill stage, another die can be simultaneously processed on the Paint stage. This system is a simplification of the product processing within an ASML TWINSCAN machine, modeled using similar resources and constraints.

Fig. 2

Top-down view of the Dice Factory manufacturing system with two carts (CR1 and CR2), two production stages (MIL and PNT) and a load robot (LR). The names of positions with a dashed outline are shown below or above the position

Each die is processed in the system by following a similar life cycle. An unfinished die is put on either cart 1 (CR1) or cart 2 (CR2) by the load robot (LR). We assume no preference to which cart picks up a die. The cart then transports the die to the mill station (MIL) where it is milled. Upon finishing, the cart moves onto an exchange disc, which it may choose to do either directly, or via one of two wait positions. The exchange disc transports the cart to the opposite side. To avoid collisions between carts, the cart exchange always moves the two carts simultaneously; the cart on the mill side is moved to the paint side, while the cart on the paint side is moved to the mill side. The cart that was transported to the paint side of the factory subsequently moves to the paint station (PNT), where the die is painted. After the paint operation finishes, the cart once again moves onto the exchange disc, directly or via a wait position, and the reverse exchange operation is executed. Finally, the cart transports the finished die to the In/Out position where it is offloaded by the load robot.

In Section 6, we will show how the full system can be modeled using our approach.

For now, let us zoom in on the aspects of desired system behavior that present a challenge to our modeling efforts. First, we assume that the choice of the pattern that must be produced on the die (1–6) is unknown to the supervisor until a mill or paint operation is executed, for instance because it is determined by a different controller. The supervisor may thus request a mill or paint operation, but has no control over which mill or paint operation is executed. This introduces uncertainty about the duration of the operation, as different patterns have different execution times. Second, there is a choice between moving directly, or via a wait position, onto the exchange disc from the Mill and Paint stages. The purpose of a wait position is to avoid unnecessary load on the exchange disc, when one cart rests on it while the other cart is not yet available. As the exchange disc is sensitive to unbalanced loads, it contains an emergency procedure that limits its speed of operation if it was loaded off-balance. This can be avoided by the use of a wait position, which adds a delay so the exchange disc entry procedure is better synchronized. There are two wait positions on either side of the exchange disc: a low and a high wait position. As the position of a cart on the stage depends on the pattern that was milled or painted, a cart may move to the wait position to which it is closest. This depends only on its coordinate in y-direction in this example. Figure 3 illustrates the available moves for a cart after a paint operation. Here, arrows 1a and 1b highlight the moves to the low and high wait positions, and arrow 2 highlights a direct move onto the exchange disc.

Fig. 3

Detail of the Dice factory showing the Paint stage. Arrows 1a and 1b show the choice of a cart to move to a wait position before moving onto the exchange disc, while arrow 2 shows a direct move onto the exchange disc

Consider two scenarios shown in Fig. 4, which shows possible schedules of cart 2 at the paint station leading up to a cart exchange. If the mill operation has already finished before the paint operation ends, desired cart behavior on the Paint side is usually a direct move onto the exchange disc, as the other cart is also available to move onto the exchange disc (Fig. 4a). If the mill operation is still in progress when painting ends, the cart on the Paint side may chose to move to a wait position so as to avoid the exchange disc emergency procedure when the cart on the Mill side is not yet available (Fig. 4b). We will later show how these scenarios can be accounted for without the need to specify each case individually. For now, it suffices to recognize that description of behavior based on resource timing presents a challenge to our modeling efforts.

Fig. 4

Gantt charts of two possible schedules of cart 2 at the paint station leading up to a cart exchange. The finish time of the parallel activities of cart 1 and the mill station, which are not shown here, is indicated by the dashed line labeled MILL. Figure a shows a scenario where milling activities have finished when the paint activities end, and cart 2 makes a direct move onto the exchange disc. Figure b shows a case where milling has not yet finished when the paint activities end, and cart 2 decides to first move to a wait position, before moving onto the exchange disc

In what follows, we will use the Dice Factory system as a running example to illustrate the concepts that are introduced, and how our approach can be used to account for the presented modeling challenges.

3 Preliminaries

In this section, several of the concepts and definitions that are used in our modeling approach are introduced. We start by outlining the concepts of the Activity language (van der Sanden et al. 2016), to the extent that is relevant for its application in the modeling approach presented in the next section.

3.1 Activity modeling formalism

The Activity modeling formalism views a system as a set $\mathcal {P}$ of peripherals that can execute actions from a set $\mathcal {A}$. Peripherals are aggregated into resources in a set $\mathcal {R}$, which can be claimed or released for the execution of some task. Given these semantics, activities are used to describe a deterministic procedure of co-ordinated actions, essentially aggregating them to describe a common functional operation. Activities are modeled as directed acyclic graphs that define the actions involved and the dependencies between them.

Definition 1 (Activity 2016)

An activity is a directed acyclic graph $(N,\rightarrow )$, consisting of a set N of nodes and a set $\rightarrow {} \subseteq N \times N$ of dependencies. The mapping function $M : N \to (\mathcal {A} \times \mathcal {P}) \cup (\mathcal {R} \times \lbrace cl,rl \rbrace )$ associates a node to either a pair (a,p) referring to an action $a \in \mathcal {A}$ executed on a peripheral $p \in \mathcal {P}$, or to a pair (r,v) with v ∈{cl,rl}, referring to the claim or release of a resource $r \in \mathcal {R}$.

Example 1

As an example, consider the Paint_1 activity on cart 2 of the Dice Factory system, which is shown in Fig. 5. This activity paints pattern “1” on a die using two resources (CR2 and PNT), which are first claimed and later released, and several action nodes that execute actions on either of the resources. In the activity, peripheral XY of cart CR2 moves the cart in XY-direction. For paint resource PNT, peripheral PNT.Z is used to move the paint nozzle up and down, and peripheral PNT.NZ is used to turn the paint nozzle on and off. See Section 6.1 for the full system description of all resources and peripherals.

Fig. 5

Activity Paint_1_CR2, showing nodes and dependencies. Resource claims and releases are represented by a clear circle, while action nodes are shaded. An incoming arrow represents a dependency on the source node of the arrow. The number in an action node gives the execution time of the action

A number of constraints exist on the activity structure to ensure proper resource claiming, such as that each resource is claimed and released no more than once, and that each action on a resource is preceded by the claim of that resource and succeeded by the release of it.

For the purpose of performance analysis, timing is added to the static semantics. The execution time of a node is given by the mapping function $T : N \to \mathbb {R}_{\geq 0}$. For the execution time of a node n with M(n) = (a,p) for some $a \in \mathcal {A}, p \in \mathcal {P}$, a fixed execution time T(n) = T_a is assumed. The execution time of a node corresponding to the claim or release of a resource is 0.

Given the execution time of nodes, the dynamic semantics of an activity are concisely captured using (max,+) algebra. (max,+) algebra uses two operators, max and addition, which correspond conveniently to two essential characteristics of the execution of an activity: synchronization while a node waits for all its dependencies to finish, and delay as the node takes an amount of time to execute. Since activities are executed by system resources, the timed state of the system can be expressed by a set of clocks indicating the availability time of resources. These clock values are collected in resource availability vector $\gamma _{R} : \mathcal {R} \to \mathbb {R}^{-\infty }$, whose elements express when each resource $r \in \mathcal {R}$ is available and can thus be claimed for the execution of an activity. Here, we use $\mathbb {R}^{-\infty } = \mathbb {R} \cup \lbrace -\infty \rbrace$. Operations max and + are defined as usually in algebra, with the additional convention that $-\infty$ is the unit element of max: $max(-\infty ,x)=max(x,-\infty )=x$, and the zero element of $+: -\infty + x = x + -\infty = -\infty$. We use $-\infty$ for resources that are not used by an activity, such that there is no impact on the synchronization when taking the max over all resources.

Given a vector γ_R this allows the start and completion times of the nodes of an activity to be uniquely defined.

Definition 2 (Start/completion time 2016)

Given activity Act = (N,→) and resource availability vector γ_R, the start time start(n) and completion time end(n) for each node n ∈ N are given by

$$ \begin{array}{@{}rcl@{}} start(n) &=& \left\{\begin{array}{ll} \gamma_{R}(r), & \text{if}~M(n) = (r,cl) \\ &\text{for some}~ r \in \mathcal{R}, \\ \max\limits_{n_{\mathit{in}} \in Pred(n)} end(n_{\mathit{in}}), & \text{otherwise}, \end{array}\right. \\ end(n) &=& start(n) + T(n), \end{array} $$

where $Pred(n) = \left \lbrace n_{in} \in N \mid (n_{in}, n) \in \to \right \rbrace$ is the set of predecessor nodes of node n.

As the dynamic semantics of an activity Act = (N,→) are uniquely defined by N, →, and timing function T, the change of resource availability vector γ_R when an activity is executed can be defined.

Definition 3 (Activity execution 2016)

Given activity Act = (N,→), timing function T, and resource availability vector γ_R, the new resource availability vector after execution of Act is given by $\gamma ^{\prime }_{R}$, whose elements are given by

$$ \begin{array}{@{}rcl@{}} \gamma^{\prime}_{R}(r) &= \left\{\begin{array}{ll} \begin{array}{ll} \gamma_{R}(r), & \text{if}~ r \notin R(Act), \\ end(n) , & \text{if}~ r \in R(Act) \land M(n) = (r,rl) \text{ for some}~ n \in N, \end{array} \end{array}\right. \end{array} $$

where $R(Act) = \left \lbrace r \in \mathcal {R} \mid (\exists n \in N \mid M(n) = (r,cl)) \right \rbrace$ is the set of resources used by Act. Each resource that is used by an activity is first claimed and subsequently released. From this it follows that if r ∈ R(Act), there also exists a node n in the activity with M(n) = (r,rl).

The dynamics of an activity can be equivalently expressed using a (max,+) matrix multiplication of vector γ_R with an activity matrix M_Act, called the (max,+) characterization of activity Act. An algorithm for the automatic computation of (max,+) characterizations can be found in (Geilen 2010). Each entry M_Act[i,j] captures the longest path in terms of total execution time from the claim of resource j to the release of resource i.

Since (max,+) algebra is a linear algebra, it can be extended to matrices and vectors in the usual way. Given m × p matrix A and p × n matrix B, the elements of the result of (max,+) matrix multiplication A ⊗B are determined by: $\left [ A \otimes B \right ]_{ij} = \displaystyle \max \limits _{k=1}^{p} ([A]_{ik} + [B]_{kj})$. The new resource availability vector after execution of an activity is computed by (max,+) matrix multiplication $\gamma ^{\prime }_{R} = \mathbf {M}_{Act} \otimes \gamma _{R}$. Here, $\max \limits _{k=1}^{m} \left (M_{ik} + \gamma _{k} \right )$ is the new value of the i-th element of γ_R after the update, where m is the size of γ_R. The dynamics of the execution of a sequence of activities is then given by repeated matrix multiplication.

Example 2

Figure 6 shows the Gantt chart of activity Paint_1_CR2, of Example 1, given the starting resource availability vector $\gamma _{R} = \left [ 1, 0 \right ]^{\intercal }$. Vector $\gamma _{R}^{\prime }$ after execution of the activity can be computed using matrix multiplication of the starting vector with (max,+) characterization M_Act of the activity. The (1,2) element of M_Act, for example, is determined by summing the execution times of actions on the path from the claim of resource PNT to the release of resource CR2, 2 + 2 + 1 = 5. After repeating this procedure for the other entries of M_Act, vector $\gamma _{R}^{\prime }$ can then be computed by

$$ \begin{array}{@{}rcl@{}} \gamma^{\prime}_{R} = \begin{bmatrix} 5 & 5\\6 & 6 \end{bmatrix} \otimes \begin{bmatrix} 1\\0 \end{bmatrix} = \begin{bmatrix} 6\\7 \end{bmatrix}. \end{array} $$

Fig. 6

Gantt chart of activity Paint_1_CR2 given starting vector $\gamma _{R} = \left [ 1, 0 \right ]^{\intercal }$

Functional specifications of the system are expressed in terms of the order in which activities can be executed, modeled as finite automata in which transitions are labeled with activities. Supervisory control synthesis (Ramadge and Wonham 1987) can be used to obtain an Activity-FA, which contains all allowed activity sequences. As the supervisor is not aware of the inner structure of an activity, it may influence the order in which activities are executed, but not the order of the actions within an activity.

Definition 4 (Activity-FA 2016)

An Activity-FA on $\mathcal {A}ct$ is a tuple $\left \langle L, \mathcal {A}ct, \delta , l_{0} \right \rangle$ where L is a finite, nonempty set of locations, $\mathcal {A}ct$ is a nonempty set of activities, $\delta \subseteq L \times \mathcal {A}ct \times L$ is the transition relation, and l₀ ∈ L is the initial location. Let $l \overset {{Act}}{\to } l^{\prime }$ be a shorthand for $(l,Act,l^{\prime }) \in \delta$.

From the Activity-FA, a (max,+) state space can be constructed that records the different timed configurations of the system. The (max,+) state space can be used for performance analysis of the system. In principle, the (max,+) state space is infinite, which jeopardizes performance analysis. To counter this, and because future behavior is affected only by the relative timing differences of resources, and not by their absolute offset from the initial configuration, the resource availability vector is normalized in each configuration. This effectively collapses states that are equivalent in their timing differences, resulting in the normalized (max,+) state space. Using $\| \gamma \| = \max \limits _{i} \gamma _{i}$ to denote the maximum element of a vector γ, the normalized resource availability vector is given by $\gamma _{R}^{norm} = \gamma _{R} - \| \gamma _{R} \|$. We use 0 to denote a vector with all zero-valued entries. In addition to the name of the activity, transitions in the normalized (max,+) state space are labeled with the total execution time (or transit time) ∥M_Act ⊗ γ_R∥, which is the time added by activity Act to the complete schedule given starting vector γ_R. We need to store the total execution time on the transition, because configurations only capture the normalized availability times. After normalization, the additional execution time that is added to the schedule cannot be retrieved without explicitly storing this information, and precisely these execution times of activities are needed to determine the throughput of the system.

Definition 5 (Normalized (m a x,+) state space 2016)

Given Activity-FA $\left \langle L, \mathcal {A}ct, \delta , l_{0} \right \rangle$, resource set $\mathcal {R}$, and a (max,+) matrix M_Act for each $Act \in \mathcal {A}ct$, the normalized (max,+) state space is defined as a 3-tuple

$$ \begin{array}{@{}rcl@{}} \left\langle C, c_{0}, {\varDelta} \right\rangle, \end{array} $$

where:

• $C = L \times \mathbb {R}^{-\infty ^{|\mathcal {R}|}}$ is a set of configurations consisting of a location and a normalized resource availability vector,

• c₀ = 〈l₀,0〉 is the initial configuration,

• ${\varDelta } \subseteq C \times \mathbb {R} \times \mathcal {A}ct \times C$ is the labeled transition relation consisting of the transitions in the set

  $$ \lbrace \langle \langle l,\gamma_{R} \rangle, \| \gamma^{\prime}_{R} \|, Act, \langle l^{\prime},\gamma_{R}^{\prime norm} \rangle \rangle \mid l \overset{{Act}}{\to} l^{\prime} \land \gamma_{R}^{\prime} = \mathbf{M}_{Act} \otimes \gamma_{R} \rbrace. $$

3.2 Ratio games

Ratio games have been proposed for the computation of robust controllers in supervisory control problems (Bloem et al. 2009; van der Sanden 2018). We will use these to compute a robust optimal supervisor that is throughput-optimal given a partially-controllable system.

A ratio game is a two-player infinite game, played on a finite double-weighted directed graph, where each edge has two associated non-negative weights w₁(e) and w₂(e). Each turn of the game constitutes a move by one of the players of a unique pebble on a vertex in the game over an edge to an adjacent vertex. The pebble indicates the current state of the system. The two players have opposite goals: one player wants to maximize the ratio of the sum of weights w₁ and w₂ in the limit of an infinite play, whereas the other player wants to minimize it.

Definition 6 (Ratio game graph 2018)

A ratio game graph Γ is a 5-tuple 〈V,E,w₁,w₂,〈V₀,V₁〉〉, where G^Γ = 〈V,E,w₁,w₂〉 is a (double) weighted directed graph and 〈V₀,V₁〉 partitions V into a set V₀, belonging to player 0, and V₁, belonging to player 1. Weighted graph G^Γ consists of a finite set V of vertices, a set $E \subseteq V \times V$ of edges, and weight functions $w_{1},w_{2} : E \to \mathbb {R}_{\geq 0}$ that assign two nonnegative real weights to edges.

G^Γ is assumed to be total, meaning that for all v ∈ V, there exists a $v^{\prime } \in V$ such that $(v,v^{\prime }) \in E$. Note that although V is partitioned into disjoint subsets V₀ and V₁ for players 0 and 1, the game graph does not need to be bipartite. This means that a player may sometimes make multiple consecutive moves, i.e., there may exist $(v,v^{\prime }) \in E$ with both v and $v^{\prime }$ in either V₀ or V₁.

In an infinite game, two players move a pebble along the edges of the graph for infinitely many rounds. Taking V^ω as the set of infinite sequences over V, a playπ = v₀v₁... ∈ V^ω is an infinite sequence of vertices such that (v_i,v_i+ 1) ∈ E for all i ≥ 0. A ratio game (Bloem et al. 2009) is an infinite game played on a ratio game graph. The ratio of a play π is defined as

$$ \begin{array}{@{}rcl@{}} Ratio(\pi) = \lim\limits_{m \to \infty} \liminf\limits_{l \to \infty} \frac{{\sum}_{i=m}^{l} w_{1}(v_{i},v_{i+1})}{1 + {\sum}_{i=m}^{l} w_{2}(v_{i},v_{i+1})}. \end{array} $$

A memoryless strategy σ_i for player i is a function σ_i : V_i → V that defines a unique successor σ_i(v) for every vertex v ∈ V_i such that (v,σ_i(v)) ∈ E. A play is consistent with memoryless strategy σ_i of player i if v_j+ 1 = σ_i(v_j) for all j ≥ 0 and v_j ∈ V_i. Strategy σ_i of player i is considered optimal if it achieves for all v ∈ V the highest (lowest) ratio of a play starting in v that is consistent with σ_i given the worst-case strategy by the opponent player. It is shown in van der Sanden (2018) that in a ratio game there exist strategies σ₀ for player 0 and σ₁ for player 1 for which the ratios of consistent plays are equal and optimal. The optimal (maximum) ratio that player 0 can achieve is thus equal to the optimal (minimum) ratio that player 1 can achieve.

4 Modeling for uncontrollability

In this section, the concepts that we use to express uncontrollability in the Activity modeling formalism are addressed. First, we show how the occurrence of activities outside the influence of the controller can be expressed. We then introduce the Activity-EFA, which extends an Activity-FA with variables, that is used to model functionality based on resource availability times and system feedback. We highlight the application of the introduced concepts on the Dice Factory system.

4.1 Controllability of activities

In supervisory control theory, a transition is typically labeled with an event from a nonempty alphabet (Cassandras and Lafortune 2008; Ramadge and Wonham 1987). To express events whose occurrence the supervisor cannot influence, but can observe and may wish to respond to, the alphabet is in these theories partitioned into a set of controllable events, and a set of uncontrollable events.

In the Activity-FA, each transition is labeled with an activity. We express uncontrollability in the same way as in supervisory control theory. The nonempty set $\mathcal {A}ct$ of activities is partitioned into a set $\mathcal {A}ct_{c}$ of controllable activities, and a set $\mathcal {A}ct_{u}$ of uncontrollable activities. We consider uncontrollability only at the level of activities, so that we retain the deterministic nature of an activity. Variations within an activity can be translated to a set of corresponding deterministic activities that together capture all possibilities; hence, we are not concerned with partitioning the set of actions into controllable and uncontrollable actions.

Example 3

In the Dice Factory, the choice of a paint pattern (1–6) is considered uncontrollable to the supervisor. Using uncontrollable activities, this can be modeled as shown in Fig. 7. Here, the controllable Paint activity can contain shared system behavior that precedes the paint activity of any pattern, or can be an empty activity acting only as a command followed by the painting of a pattern.

Fig. 7

Automaton of a paint sequence where controllable activity Paint is followed by uncontrollable paint activities 1–6, which paint the patterns corresponding to their numbers

A supervisory controller is said to be controllable with respect to the system it acts on, if it does not attempt to disable the occurrence of any uncontrollable activity that is otherwise admissible in the system (see Cassandras and Lafortune 2008 for a formal definition). It may, however, disable a controllable activity leading up to the uncontrollable activity, effectively preventing the uncontrollable activity from becoming admissible in the system.

4.2 Activity-EFA

In previous work (van der Sanden et al. 2016), plants and specifications were modeled using Activity-FAs. In this paper we wish to benefit from the use of variables to capture system feedback from the lower abstraction level. This gives rise to the notion of an Activity-EFA, which we formally introduce below. An extended finite automaton (EFA) (Sköldstam et al. 2007) is a finite automaton augmented with variables. Guard expressions and update functions can be added, which restrict behavior depending on the variable values, and update the variable values during a transition, respectively. An Activity-EFA is an EFA in which transitions are labeled by activities.

Definition 7 (Activity-EFA)

An Activity-EFA can be viewed as a 7-tuple,

$$ \begin{array}{@{}rcl@{}} \langle L, \mathcal{A}ct, \delta, V, G, U, \langle l_{0},v_{0} \rangle \rangle, \end{array} $$

where L is the location set, $\mathcal {A}ct$ is the alphabet (of activities), $\delta \subseteq L \times G \times \mathcal {A}ct \times U \times L$ is the transition relation, V is a set of variables, G is a collection of Boolean expressions over the variables, U is a collection of value assignments to the variables of the form x := e, where x is a variable and e is an expression over the variables, and 〈l₀,v₀〉 are the initial location and valuation. We denote the collection of all valuations by Val(V ). As shorthand for a transition in the Activity-EFA, we write $l \overset {Act}{\to }_{g/u} l^{\prime }$, where $l,l^{\prime } \in L$, $Act \in \mathcal {A}ct$, $g \in \mathcal {G}$ and $u \in \mathcal {U}$.

The meaning of an update x := e on a transition that is executed is that the new value of the variable x is the value of the expression e evaluated with the values of the variables prior to the execution of the transition. In literature such updates are also denoted $x^{\prime } = e$.

For convenience, and to keep the size of the plant model manageable, typically a collection, or network, of Activity-EFAs is used. Formally, the network of Activity-EFAs represents a single Activity-EFA, which can be obtained by computing the full synchronous composition (see Sköldstam et al. 2007) of the contained Activity-EFAs. Intuitively, in full synchronous composition the automata synchronize on shared activities. If, in such a synchronization, a variable is updated in both transitions, then these updates have to result in the same value for the transition to take place (and the value of the variable is updated to that value). If the variable is only updated by one of the transitions, then the variable changes value according to that transition. Finally, if the variable is not updated by either transition, then its value is not changed.

Variables can now also be used to capture feedback from lower abstraction levels, and to represent resource availability times. In the timing analysis of the Activity modeling formalism, the timed state of a system is expressed in terms of resource availability time stamps in a vector γ_R. For each resource $r \in \mathcal {R}$, we now assume a variable τ_r representing the availability time of that resource, which we do not normalize for now. This enables the description of functionality based on the timing information that they provide. As (max,+) algebra is used for the computation of availability times, all τ_r are defined on the domain $\mathbb {R}^{-\infty }$. When it is convenient to refer to these variables in vector form, we will continue to denote this by γ_R.

Timing variables are special for two reasons: we get their updates for free from the timing characterization of an activity, and we wish to normalize their values after each update in the performance analysis methods.

Example 4

In the time dependency problem of the Dice Factory (Fig. 4), two resources are shown: cart 2 and the paint station. For each resource we assume an availability time stamp variable, which we denote by τ_CR2 and τ_PNT, respectively. Let us assume, as we will later show, that the indicated finish time of the parallel activities on the Mill side is reflected by the availability time stamp of a third resource, the mill station. We denote its variable by τ_MIL.

The values of resource time stamps are updated by (max,+) multiplication. For any transition in the Activity-EFA, multiplication matrix M is given by (max,+) characterization M_Act of the corresponding activity. These can be automatically computed from the structure of the activity and timing function T on the nodes of the activity, as pointed out in Section 3.1. Note that the number of rows and columns in the matrix is equal to the number of resources in the system. If some resource is not used, value $-\infty$ is used for the corresponding rows and columns, except on the diagonal of the matrix where value 0 is added. Timing updates thus require no additional effort from the modeler. Given a vector γ_R of timing variables and some matrix M_Act, a timing update is written as γ_R := M_Act ⊗ γ_R.

Example 5

Given a vector of resource time variables $\gamma _{R} = \left [ \tau _{{CR2}}, \tau _{{PNT}}, \tau _{{MIL}} \right ]^{\intercal }$, the timing characterization of activity Paint_1_CR2, shown in Fig. 5, is given by

$$ \begin{array}{@{}rcl@{}} \mathbf{M}_{\text{Paint\_1\_CR2}} = \begin{bmatrix} 5 & 5 & -\infty \\ 6 & 6 & -\infty \\ -\infty & -\infty & 0 \end{bmatrix}. \end{array} $$

The corresponding update of these timing variables for activity Paint_1_CR2 is then shown in Fig. 8. Going forward, we will hide the updates of timing variables in our models and assume they are all automatically determined this way.

Fig. 8

Update of timing variables $\gamma _{R} = \left [ \tau _{{CR2}}, \tau _{{PNT}}, \tau _{{MIL}} \right ]^{\intercal }$ for activity Paint_1_CR2 in the Dice Factory system

Note that we do not normalize the resource availability time stamps at this point. Normalization discards the absolute time offset between consecutive transitions, which denotes the duration of an activity during performance analysis. It is therefore necessary to preserve this information until a state space for performance analysis is constructed. We must, however, account for normalization if we wish to ensure that the meaning of a guard on timing variables does not change when these variables are normalized. A meaningful guard involving timing variables is therefore an expression over the difference between two of these variables, as the difference between timing variables is not altered by normalization.

Example 6

The time dependency problem of the Dice Factory (Fig. 4) relates to the timing difference between the end of the Mill and Paint operations. This is expressed as guards using the difference between timing variables τ_MIL and τ_PNT in Fig. 9. Note that this is a simplified example; the application of a guard for this problem in a practical setting is further discussed in Section 6.

Fig. 9

Example of a guard on the difference of timing variables

4.3 Synthesis

Given these building blocks, our method to construct the Supervisor Activity-EFA, which contains all allowed activity sequences including time-dependent and feedback-dependent behavior, is shown in Fig. 10. As the domain of the non-normalized variables representing the resource availability times is potentially infinite, we choose a two-step approach to construct the supervisor. In the first step, the timing variables are stripped from the Plant and Specification Activity-EFAs. In case timing variables have been used in relation to other variables, these must also be removed. Note that other variables may be maintained, so long as they are supported by the used synthesis method. On the resulting Untimed Activity-EFAs, we apply supervisory controller synthesis of EFAs (Ouedraogo et al. 2011) to compute an Untimed Activity-EFA, which contains activity sequences in which the omitted timing variables are neglected. This Untimed Activity-EFA acts as an intermediary and is augmented in the second step with the omitted variables and their guards and updates to form the Supervisor Activity-EFA. We can add these variables by computing the full synchronous composition (Sköldstam et al. 2007) of the Untimed Activity-EFA and the original Plant and Specification Activity-EFAs.

Fig. 10

Overview of the method to construct the Supervisor Activity-EFA

The removal of some variables before the application of synthesis, and the addition of them in the resulting supervisor, potentially has an effect on the controllability and nonblockingness properties achieved by synthesis. If we only remove variables with guards on transitions with controllable activities in specifications, controllability of the supervisor with respect to the original plant and specification Activity-EFAs is guaranteed.

Nonblockingness of the supervisor, however, cannot be guaranteed. Methods found in the literature (Voronov and Åkesson 2009; Mohajerani et al. 2016) can be used to verify nonblockingness of the supervisor.

In the proposed approach the modelling of the behaviour of the system is split into two levels. Synthesis is only applied to the models of the higher abstraction level as these are relatively small. In literature there are methods for synthesizing supervisory controllers that utilize abstractions and decompositions such as hierarchical (Zhong and Wonham 1990), decentralized (Feng and Wonham 2008), and multilevel supervisory control synthesis (Komenda et al. 2016). A clear difference with our approach is that in our approach the activities of the higher abstraction level are defined in terms of the lower-level actions, whereas in the other approaches there is no such notion of activity refinement.

4.4 Configuration space

As before, we construct a state space in terms of the system configurations, this time starting from the Supervisor Activity-EFA. The constructed configuration space can be used for performance analysis.

Definition 8 (Configuration space)

Given an Activity-EFA $\langle L, \mathcal {A}ct, \delta , V,$ G,U,〈l₀,v₀〉〉, the configuration space is defined as a 3-tuple

$$ \begin{array}{@{}rcl@{}} \left\langle C, c_{0}, {\varDelta} \right\rangle, \end{array} $$

(1)

where:

• C = L ×Val(V ) is the (possibly infinite) set of configurations consisting of a location and a valuation of variables;

• c₀ = 〈l₀,v₀〉 is the initial configuration;

• ${\varDelta } \subseteq C \times \mathbb {R} \times \mathcal {A}ct \times C$ is the transition relation consisting of the transitions in the set

  $$ \begin{array}{@{}rcl@{}} \lbrace (\langle l,v \rangle, \theta, Act,\langle l^{\prime},v^{\prime} \rangle) \mid (\exists l \overset{Act}{\to}_{g/u} l^{\prime} & \in & \delta \mid \\ g(v) & \land & v^{\prime} = u(v) \land \theta = \|\gamma_{R}^{\prime}\| - \|\gamma_{R}\| ) \rbrace, \end{array} $$

  in which γ_R is a vector of the timing values in v, before the transition, and $\gamma _{R}^{\prime }$ is the corresponding vector in $v^{\prime }$, after the transition.

A configuration refers to both a location in the EFA and a valuation of the variables. When a transition is taken, the variable values in the new configuration are updated according to the specified update function. As before, the timing variables are used to determine the transit time𝜃 of a transition, which expresses by how much the largest resource availability time has shifted by the execution of an activity. The transit time is used in performance analysis to determine the duration of an activity sequence.

Variables in V may be defined on a possibly infinite domain, potentially leading to an infinite configuration space L ×Val(V ). For example, consider a counter variable that is incremented for each finished product in a cyclic production process. Many performance analysis and optimization algorithms, including the ratio games we wish to employ, require a finite solution space to terminate (Brim et al. 2011; van der Sanden 2018). By instead defining variables on a finite domain, we can ensure a finite configuration space for performance analysis. This does not restrict our modeling efforts in many practical situations. An infinite counter variable may be replaced by a counter that can only go up to a feasible number of products in a shift. Even values from sensors can normally be expressed on a finite domain, as sensors have a finite precision and their values are typically discretized. From now on, we assume that all non-timing variables are defined on a finite domain.

Normalization of the timing variables, as used in the construction of the normalized (max,+) state space (Definition 5), serves the same purpose. Using normalization, it has been shown that the normalized (max,+) state space remains finite under the condition that each cycle contains a dependency on each of the resources at least once, i.e., no part of the system evolves completely independently of another part (Geilen and Stuijk 2010). We denote normalization of the timing variables in a valuation v by v^norm.

Normalization affects the evaluation of guards on timing variables, as the meaning of their absolute values is no longer clear. It is easily shown that the relative difference between timing variables is invariant under normalization. Suppose we take the difference between the values v_τ,1 and v_τ,2 of two timing variables in the same valuation v, and apply normalization using a value ∥γ∥, then

$$ \begin{array}{@{}rcl@{}} v_{\tau,1}^{norm} - v_{\tau,2}^{norm} &=& (v_{\tau,1} - \|\gamma\|) - (v_{\tau,2} - \|\gamma\|) \\ &=& v_{\tau,1} - v_{\tau,2}. \end{array} $$

A finite state space can now be constructed for performance analysis of the system.

Definition 9 (Normalized configuration space)

Given an Activity-EFA $\langle L, \mathcal {A}ct, \delta , V, G, U, \langle l_{0},v_{0} \rangle \rangle$, the normalized configuration space is defined as a triple

$$ \begin{array}{@{}rcl@{}} \langle C, c_{0}, {\varDelta} \rangle, \end{array} $$

(2)

where:

• C = L ×Val(V ) is the finite set of configurations consisting of a location and a valuation;

• c₀ = 〈l₀,v₀〉 is the initial configuration;

• ${\varDelta } \subseteq C \times \mathbb {R} \times \mathcal {A}ct \times C$ is the transition relation consisting of the transitions in the set

  $$ \begin{array}{@{}rcl@{}} \lbrace (\langle l,v \rangle, \theta, Act,\langle l^{\prime},w^{norm} \rangle) \mid (\exists~ l \overset{Act}{\to}_{g/u} l^{\prime} \in \delta \mid & \\ & g(v) \land w = u(v) \land \theta = \|\gamma_{R}^{\prime}\| ) \rbrace, \end{array} $$

  in which $\gamma ^{\prime }_{R}$ is the non-normalized vector of timing values in w, and $\theta = \|\gamma _{R}^{\prime }\|$.

Notice that the Activity-FA and timing characterization of the original formalism are embedded in the definition of an Activity-EFA. To see this, given an Activity-FA $\left \langle L,\mathcal {A}ct,\delta ,l_{0} \right \rangle$, resource set $\mathcal {R}$, and (max,+) matrices M_Act for each $Act \in \mathcal {A}ct$, construct the Activity-EFA by introducing a timing variable for each resource $r \in \mathcal {R}$, and adding an update γ_R := M_Act ⊗ γ_R for each edge labeled by activity Act. Any Activity-FA may thus equivalently be expressed as an Activity-EFA and gain the ability to express functionality based on timing or other variables.

5 Robust optimal supervisor design

A reachable cycle in the configuration space relates to the periodic execution of the system. Each transition in the configuration space is equipped with a transit time that describes the time that is added by executing the activity on the resources (see Definitions 8 and 9). The value can also be 0, if the activity does not add time to the total execution of the activity sequence. To illustrate, consider a system with two resources R1 and R2 that are initially available in state s₀. First, we execute an activity with one action on resource R1 that takes 5 time units and go to state s₁. This activity will have a transit time of 5. Then, we execute another activity with one action on resource R2 that takes 4 time units. This activity will have a transit time of 0 from s₁, since no additional time is added to the total execution. However, if we would execute the activity from s₀, the transit time will be 4, since 4 time units are added to the schedule.

A second value is assigned to each transition, which we call the reward of the transition. The reward can be used to describe progress. For instance, we can assign a reward to each activity that delivers a finished product. In the synthesis step marked states have been used for modelling the progress of the system. This role is taken over by the rewards on transitions. It is expected (and confirmed in the case study) that transitions with (higher/positive) rewards and marked states are closely connected. The transit time of a cycle equals the sum of the transit times of the transitions of the cycle, and the reward of a cycle equals the sum of the rewards. We define the cycle ratio as its reward divided by its transit time.²

Optimal cycle ratio algorithms (Dasdan 2004; Geilen and Stuijk 2010) can be used to find cycles in the system with the highest value, or the lowest value for the cycle ratio. These cycles relate to best-case, or worst-case system performance.

The partitioning of activities into controllable and uncontrollable activities allows us to consider new scenarios. It is likely that we wish to design a controller that attains the highest achievable performance by directing system execution to an optimal cycle. It may do so by dictating the choice of controllable activities. Uncontrollable activities act as a disturbance, which may aid system performance if they lead to a higher cycle ratio, or hurt performance if they lead to a lower cycle ratio. Viewed this way, the highest cycle ratio that can be achieved by the controller, given worst-case uncontrollable disturbances, determines a guarantee to the lower bound of periodic system performance. In this paper we call such a controller a robust throughput-optimal controller.

The challenge is now to find a controller that makes optimal choices. We are interested in two results: i) a guarantee to the achievable lower-bound system performance, and ii) an optimal controller that is robust to uncontrollable behavior, i.e., it makes optimal choices regardless of the occurrence of uncontrollable disturbances. The structure of this challenge corresponds well to the ratio games that were introduced in Section 3.2. Recall that the result of a ratio game are optimal strategies for player 1 and player 2, given that one player aims to achieve the highest ratio, and the other player aims to achieve the lowest ratio. In our challenge, player 1 is the controller, who controls the moves on edges with a controllable activity, and whose aim is to achieve the highest cycle ratio. Player 2 is the environment, who controls the moves on edges with an uncontrollable activity and aims to achieve the lowest cycle ratio. Optimal strategies then relate to the the best achievable controller performance given worst-case disturbances. We give some examples to illustrate the expected results.

Example 7

Consider the system represented given in Fig. 11 with only activity c uncontrollable. Consider the situation that all activities have a reward of 1. Furthermore activity b has a transit time of 1, activity c has a transit time of 3, and activity e has a transit time of 2. All other transit times are 0. Although the cycle with the highest ratio between reward and transit times is ab (with ratio 2/1), this is not the cycle with the highest guaranteed ratio since in state 2 the environment can decide to execute activity c which brings the ratio down to 2/3. The cycle with activities d and e has a ratio of 2/2 (and the environment cannot do anything to negatively influence this). Therefore, as we are pursuing the highest guaranteed ratio, the controller should enable d in state 1 (thereby effectively preventing to reach state 2 where possibly uncontrollable activity c could have its detrimental effect on the achieved ratio).

Fig. 11

System where the throughput-optimal behaviour does not constitute the cycle with the highest ratio. The rewards of the activities are indicated by a superscript and the transit times as a subscript

Example 8

If we now consider the same system but with b uncontrollable and c controllable (see Fig. 12), the situation arises where the highest ratio cycle containing a and b requires co-operation of the environment by actually executing the uncontrollable event. We do not want to rely on this and therefore our approach should in such cases, a state with both controllable and uncontrollable activities, always select a controllable activity (for the case that the environment decides not to execute the uncontrollable activity).

Fig. 12

System where the cycle with the highest ratio involves a choice for an uncontrollable activity. The cycle that has highest ratio involves an uncontrollable activity from a location that also allows controllable activities

A ratio game requires a graph whose vertices are partitioned into vertices controlled by player 1, and vertices controlled by player 2. The graph structure of the configuration space is typically not partitioned in this way, as from any state there may exist both controllable and uncontrollable transitions to another location (see state 2 in Fig. 11 for example). We must therefore introduce a partitioning. Given that a characteristic property of uncontrollable behavior is that it may not be blocked by a controller, we assume a priority of uncontrollable behavior over controllable behavior. In our game setting, this can be interpreted as the rule that at each turn in which both players can make a move, the player who commands the uncontrollable moves may make a move first. This player may equally choose to pass its turn to the other player, at which point the player in charge of the controllable moves may make a move.

We introduce a new uncontrollable activity $\tau \notin \mathcal {A}ct$ which is the ‘pass a turn’ activity. No variables are updated by execution of this activity and hence variable values do not change when it is executed. In the game graph, the reward and transit time of τ are both 0. For a location q in which both a controllable and an uncontrollable transition are possible, we introduce a new location $\hat {q}$ and a transition $(q, \tau , \hat {q})$ so that location $\hat {q}$ can be reached via the ‘pass a turn’ move. Transitions from location q labeled with a controllable activity are removed from location q and added to location $\hat {q}$.

Example 9

Consider the example system of Fig. 13a, where from state q there are two controllable transitions a and b, and one uncontrollable transition c. To partition the system, a transition $(q,\tau ,\hat {q})$ is added and transitions (q,a,1) and (q,b,2) are replaced by transitions $(\hat {q}, a, 1)$ and $(\hat {q}, b, 2)$. The uncontrollable transition is maintained at the original location. We end up with the partitioned system shown in Fig. 13b.

Fig. 13

Partitioning of a transition system with competing controllable and uncontrollable players. Figure a shows the system before partitioning. Figure b shows the system after partitioning with the thick arrow indicating the optimal controller choice. Figure c shows the resulting robust optimal controller

Ratio game algorithms (van der Sanden 2018) can be applied to the partitioned configuration space where rewards and transit times are assigned as weights w₁ and w₂ to the transitions. A guarantee to the achievable periodic system performance is given by the ratio of a reachable cycle consistent with the computed optimal strategies of both players. The chosen values of reward and transit time for τ ensure that its introduction does not affect the computed ratio.

A play consistent with the strategies of both players gives us one periodic sequence of activities. For our controller, we are interested in all activity sequences in which the controller follows an optimal strategy for any behaviour of the uncontrollable environment. To compute this controller, we start with the partitioned configuration space S and optimal controller strategy σ_c. Recall that σ_c defines a unique successor $c^{\prime } = \sigma _{c}(c)$ for each c ∈ C^ctb, where C^ctb contains the configurations under the control of the controller. From each such configuration, we remove the outgoing controllable transitions that are not consistent with optimal controller strategy σ_c, such that $c^{\prime } = \sigma _{c}(c)$ for every remaining transition $(c,\theta ,Act,c^{\prime }) \in {\varDelta }$ of S where c ∈ C^ctb. All uncontrollable transitions are retained since we want to keep all possible uncontrollable behavior. As we do not observe the artificial activity τ in our original system, we use the natural projection (Cassandras and Lafortune 2008) $P : \mathcal {A}ct^{\tau } \to \mathcal {A}ct$, where $\mathcal {A}ct^{\tau } = \mathcal {A}ct \cup \lbrace \tau \rbrace$, to project out τ from the configuration space. This effectively erases all transitions labeled with τ and maps back the remaining transitions of each artificially introduced location $q^{\prime }$ to their original location q. Finally, we can compute the reachable subautomaton (Cassandras and Lafortune 2008) to obtain the supervisory controller that is minimal (i.e., prohibits all but one controllable enabled activity in each state), controllable, and throughput-optimal in the presence of uncontrollable behavior. We call this the robust throughput-optimal controller, as it determines throughput-optimal controller choices while respecting the occurrence of uncontrollable behavior.

Example 10

The optimal controller strategy of the partitioned system in Fig. 13b chooses $(\hat {q},a,1)$, as indicated by the thick arrow. To compute the robust throughput-optimal controller, $(\hat {q},b,2)$ is removed as it is not consistent with the optimal controller strategy. Both uncontrollable transitions from location q are kept. The natural projection $P : \mathcal {A}ct^{\tau } \to \mathcal {A}ct$ removes τ and maps $\hat {q}$ onto q. As location 2 is no longer reachable after $(\hat {q},b,2)$ was removed, it is not present when we compute the reachable subautomaton. The result of these steps is the robust optimal controller of Fig. 13c.

In locations that have both outgoing transitions labelled with controllable and uncontrollable events, always at least one controllable event is maintained, even though “selection” of the uncontrollable event may correspond with the optimal throughput. This choice is justified by the observation that uncontrollable events (such as a failure) may as well not occur at all, in which case there is no progress anymore.

Note that even in cases where the supervisory controller obtained from synthesis is nonblocking, the resulting optimal controller is not necessarily nonblocking. As mentioned previously, it is assumed that the rewards of transitions are such that progress is achieved in the optimal controller.

6 Case study: Dice Factory

In this section we show how our approach is used for the synthesis of a throughput-optimal supervisor for a partially-controllable manufacturing system. We do this by systematically describing the components of our modeling method (Fig. 1) and applying the performance analysis methods of Section 5. As a case study we take the Dice Factory system that was introduced in Section 2, which we now look at in more detail. Figure 14 shows the system with all components.

Fig. 14

Top-down view of the Dice Factory manufacturing system with two carts (CR1 and CR2), two production stages (MIL and PNT) and a load robot (LR). Resource names are shown in shaded circles, peripherals are indicated by arrows and rounded rectangles with their names, and dashed outlines indicate logical positions which are labeled below or above the position

6.1 System description

The Dice Factory contains five resources. Two carts (CR1 and CR2) transport dice in the system. A load robot (LR) is used to put an unfinished die from the input buffer onto a waiting cart, and to pick a processed die from a cart and put it in the output buffer. The other two resources are the processing stations: the mill station (MIL), which mills holes in a side of a die, and the paint station (PNT), which fills the holes with a colored substance.

The two functionally equivalent carts have a single peripheral: an undercarriage (XY), which moves the cart to a position in the XY-plane. The load robot has two peripherals: an arm (X), which moves to and from a waiting cart, and a clamp, which grips the die when the arm is moving. The mill station has two peripherals, an R-motor (R), which rotates the mill cutter, and a Z-motor (Z), which moves the mill cutter up and down. The paint station has a nozzle (NZ), which turns on and off to release paint, and a Z-motor, which moves the nozzle to and from the die. Note that the mill and paint stations are fixed in the XY-plane and the carts move during processing to correctly position the die for a mill or paint operation.

6.2 Activities

There are twelve production activities: six milling activities, one for each possible value of a side of a die, and six corresponding painting activities. We denote the milling and painting activities by Mill_N and Paint_N, where N = {1,2,...,6} corresponds to the value that is milled or painted. Two additional activities, Paint and Mill, are used to control the execution of the respective production activities, which we shall consider later.

The production activities operate on either cart 1 or cart 2. The CartExchange activity works on both carts as they are moved simultaneously. Finally, there are several Move_ activities by cart 1 and cart 2 that move the respective cart from one position to another. The labeled positions are shown in Fig. 14 as dashed cart outlines.

Since the two carts are modeled as separate resources, we define individual activities for each cart. As they are functionally equivalent, we define their activities once and use the following notation to refer to the activity executed by cart 1 or cart 2. Given a cart activity Act, the set Act_⋆ = {Act_CR1,Act_CR2} contains activity Act executed by cart 1 and by cart 2.

All activities are defined by denoting the resources, actions, and dependencies between actions, as outlined in Section 3. As an example, recall activity Paint_1_CR1 for cart 1, shown in Fig. 5, which paints a die on cart 1. The full set of activities is listed in Table 1; activity structures of individual activities are available in (van Putten 2018).

Table 1 Activities of the Dice Factory system

6.3 Plants and specifications

For the description of allowed activity sequences, we model the system as a set of automata of which transitions are labeled with the activities. We first define a set of plant automata that define all admissible, if not necessarily desired, behavior. These are complemented with specifications that enforce the functional specification of our system. As mentioned before, full synchronous composition is used for composing the automata in the set so that execution of shared activities is synchronous.

6.3.1 Plants

The possible behavior of carts 1 and 2 is modeled by two similar plant automata, that differ only in their initial locations. Cart 1 is initially on the Mill stage at location atMill, while cart 2 starts on the Paint stage at location atPaint. The automaton of a cart is shown in Fig. 15, where the initial locations of carts 1 and 2 have been marked.

Fig. 15

Plant automaton of cart i, where i can be 1 or 2. The initial locations of carts 1 and 2 are marked by shaded circles labeled 1 and 2, respectively

In addition to the cart models, the plant contains two automata that model the Mill and Paint stations, as introduced in Section 2. These station plants, shown in Fig. 16a and b, respectively, allow for different patterns to be milled and painted. As before, we assume the choice of a pattern is uncontrollable. Taking the Paint station as an example, controllable activity Paint_i starts the operation and is followed by one of six uncontrollable activities, Paint_N_i, which finish the operation. This way, the controller may choose when to start a paint operation, but has no control over which paint operation is subsequently executed. To reflect this, activity Paint_i contains no actions so that it does not affect the resource availability times. Activities Paint_N_i contain the actions that constitute the paint operation (see for example Paint_1_CR1 in Fig. 5). In our example we assume that a larger value for N results in a larger transit time for the activity, as more holes are milled or painted.

Fig. 16

Plant automata of the Mill station (a) and Paint station (b), which allow for six patterns to be milled and painted

Because the system contains five resources, there are five (max,+) variables available with timed information. We denote these by τ_MIL, τ_PNT, τ_CR1, τ_CR2 and τ_LR according to the respective resource identifiers. The update of (max,+) variables during a transition is given by the (max,+) matrix of the corresponding activity, as explained in Section 4.2.

We add two additional variables to represent the real-valued y-coordinates of cart 1 and cart 2, which we denote by y₁ and y₂. As the system is modeled using a finite number of positions for the carts, these variables can take on a finite number of values. For their update functions, we consider the milling and painting production activities, as these affect the y-coordinate of a cart. Since the new y-coordinate is determined solely by the execution of an activity, we apply the corresponding value as a fixed assignment to each transition labeled with the activity. Because we use full synchronous composition, this is easily achieved using the automata shown in Fig. 17.

Fig. 17

Updates of variable y_i in the Dice Factory plant

6.3.2 Specifications

The plant model is complemented by specifications that enforce the correct sequence of activities in a production cycle, and the activity orderings based on timing information of the resources and position information of the carts. These specifications are shown in Figs. 18, 19 and 20. The specifications in Fig. 18a and b ensure that a die is processed by one mill or paint operation before it is moved along. The specifications in Fig. 18c and d ensure that the carts are not exchanged before a mill and paint operation have taken place. The specification in Fig. 18e avoids product collisions by enforcing that a die must be put on the output buffer before a new die can be picked up for processing. The specification in Fig. 18f ensures that the cart exchange cannot take place before both carts are ready to be exchanged.

Fig. 18

Specification automata that enforce the production life cycle

Fig. 19

Specification that enforces an emergency limp mode on the cart exchange procedure by conditionally disabling the regular CartExchange activity, which is disabled when the time difference between the moments at which both carts have entered the exchange disc exceeds a threshold of 2.0 [s]

Fig. 20

Specification for the choice of a wait position based on cart position y_i

As discussed in Section 2, the exchange disc is sensitive to unbalanced loading and contains an emergency “limp” mode, which slows down its operation to protect sensitive parts if it has been subjected to an unbalanced load. We now assume that this mode is activated when the two carts enter the exchange disc more than two seconds apart. This is modeled in the specification of Fig. 19 by adding a guard that compares the availability times of the two cart resources. Note that according to the cart plants of Fig. 15, a cart exchange is only allowed after both carts have entered the exchange disc. Clock values τ_CR1 and τ_CR2 therefore always refer to the time of arrival of the two carts at any point that the guard is evaluated, namely when a CartExchange activity is enabled. Notice that the system, when modeled this way, allows some freedom to influence the values of τ_CR1 and τ_CR2 to avoid the “limp” mode, by the appropriate choice of a (faster) direct move onto the exchange disc, or via a wait position. We will see in Section 6.5 how this is automatically achieved for different combinations of occurrence of the uncontrollable Mill_N_⋆ and Paint_N_⋆ activities, using the presented throughput optimization methods.

In the presented case study, we have modeled the plants conveniently, such that the state of the resources is clear when the guard is evaluated. We may therefore access their clocks and receive the time at which their operation finished. In general, the meaning of a clock value for use in a guard can be ambiguous. For example, the cart resources are used in several activities, and the meaning of the value of their clocks for use in specifications can depend on which of these activities is last executed. In these cases, it is useful to introduce a new resource, which we call a virtual resource. We can synchronize the clock of this virtual resource with some other resource by defining a dependency on it at the point of interest in an activity. As the clock of the virtual resource is decoupled from the original resource, we can access its value at a later time, even if the clock of the original resource changes with subsequent activities. This allows for concise and meaningful descriptions using clock values.

To capture the choice between the high and low wait positions, as introduced in Section 2, we use the specification shown in Fig. 20. This specification ensures that a cart moves to the correct wait position depending on the value of its y-coordinate. It describes only which wait position is allowed; it does not denote if a move to a wait position is at all enabled. As the move to a wait position is only available immediately after a mill or paint operation, the value of the y-coordinate is determined by the end position of the Mill and Paint activities. For the values of y given earlier, this means, for example, that a cart may only move to the lower waiting position after activity Paint_6, whereas it may move to either wait position after activity Paint_1.

6.4 Constructing the supervisor activity-EFA

Given the model components specified in the previous sections, we construct the supervisor using the approach shown in Fig. 10. First, we strip the guards and updates associated with timing variables τ_r, of each resource $r \in \mathcal {R}$, from the plants and specifications of Figs. 15–20. Supervisory controller synthesis on these stripped plants and specifications gives the intermediary Untimed Activity-EFA. This EFA is more permissive compared to the modeled specifications, as the guards of the EFAs in Figs. 19 and 20 have been disregarded. We add back these guards, as well as the updates of timing variables τ_r, by computing the full synchronous composition of the Untimed Activity-EFA and the original plants and specifications. This gives us the Supervisor Activity-EFA, which contains the allowed system behavior including timing and state feedback dependency. As the stripped guards only occurred in relation to controllable activities, as mentioned in Section 4.3, the resulting supervisor is controllable.

The synthesis step is performed on Activity-EFAs that only consider the activity level, abstracting from all the interleavings of constituent actions. This has a big impact in terms of scalability of the approach, since an EFA at action level is often too big to fit in memory (van der Sanden et al. 2016). Moreover, the timing is at this point not yet relevant, and also abstracted from.

6.5 Performance analysis

The normalized configuration space is computed by eliminating variables from the constructed supervisor, and the methods of Section 5 are used to obtain the robust throughput-optimal controller. This controller and the configuration space are too large to be shown. Therefore, for the purpose of illustration, Fig. 21 shows the activity sequences of the controller for a system in which the choice of patterns is limited to either 1 or 6. Note that the activity sequences of the controller can always be traced back to the Supervisor Activity-EFA, which we have chosen to do here for the purpose of visibility. Activity sequences of the Supervisor Activity-EFA that are rejected by the computed controller are shown in the background to provide some reference.

Fig. 21

Activity sequences of the computed robust throughput-optimal controller, in case the choice of paint or mill patterns is reduced to either 1 or 6. For the purpose of visibility, the sequences in this illustration have been traced back to transitions of the Supervisor Activity-EFA, and guards and updates are omitted. The faded background represents the activity sequences of the Supervisor Activity-EFA that are rejected by the computed optimal controller

7 Related work

Timed Petri nets are a commonly encountered modeling mechanism for manufacturing systems, which also allow for uncontrollable transitions (Wang 1998). Performance analysis of timed Petri nets can be achieved by associating delay bounds with each place in the net (Hulgaard and Burns 1995). Petri nets are generally well suited for the design and analysis of systems operating on multiple resources, as they can naturally express concurrent execution of system behavior. Studies that consider uncontrollable transitions generally focus on finding minimally-restrictive controllers (Moody and Antsaklis 2000) or deadlock-avoidance (Aybar and Iftar 2008), rather than timed performance. Recently, an effort was made in Lefebvre (2017) to incrementally compute an optimal control sequence using timed Petri nets, with knowledge of the probability of occurrence of some uncontrollable events. This makes it suitable for a real-time control solution of a known system, but not as much for performance analysis in the design phase. An alternative approach that considers both uncontrollability and timed performance is proposed in Basile et al. (2002). Here, uncontrollability is replaced by a control cost of an event, and optimization aims to minimize control cost and cycle time of the closed loop net simultaneously. In Pena et al. (2016) also a setting with both controllable and uncontrollable events is considered, where the objective is to minimize the makespan for the production of a batch of products. The optimization is done using a heuristic optimization method. Related is also the optimal directed control problem introduced by Huang and Kumar (2008), where the goal is to accomplish a pending task in a minimal cost. Again, the objective is towards makespan-related optimization objectives rather than throughput. Another difference between our work and that reported in Huang and Kumar (2008) is that we treat states with both controllable and uncontrollable activities differently.

Su et al. (2012) look at the synthesis problem to find a maximally permissive supervisor with minimum makespan for a fixed batch of products. First, the maximally-permissive supervisor is generated, and then a tree automaton is constructed that encodes all the possible strings and their completion times. From this tree automaton, a permissive supervisory controller is obtained by removing all paths with a non-optimal makespan while preserving nonblockingness and controllability with respect to the system. This approach is not scalable for larger problems, because the tree automaton grows exponentially in size in the worst-case. The (max,+) state space is typically much smaller, since possible redundancy in substrings with the same timing information can be encoded more efficiently.

In Raman et al. (2015) an approach is provided for synthesis of reactive controllers for systems satisfying signal temporal logic specifications. Using a cost-function over infinite runs of the system, optimality of the resulting control is achieved. The approach is based on reactive synthesis (Kupferman and Vardi 2000) instead of supervisory control theory as used in this paper. In Ehlers et al. (2017) the (formal) relationship and inherent differences between supervisory control theory and reactive synthesis approaches are clearly and precisely described. The work presented in Ehlers et al. (2017) does not offer a layered approach towards the specification of the supervisory control problem reducing the state space as offered in this paper.

Other approaches for modeling or performance analysis of partially-controllable systems include the use of probabilistic automata and stochastic scheduling. In Kobetski et al. (2007), probabilistic automata are combined with extended finite automata to find uncontrollable alternative working sequences with corresponding occurrence probabilities. A version of the A^* search algorithm (Hart et al. 1968) is used to find the shortest cycle time. Stochastic scheduling (Niño-Mora 2008) considers uncertainty only in the duration of activities by assuming stochastic operation times. Controller synthesis methods can be found (Kempf et al. 2013) to compute a controller with an expected optimal performance. What these methods have in common is the assumption of a priori knowledge of the probabilities of duration or occurrence of uncontrollable system behavior. Instead, our approach is based on worst-case execution times and can thus be used to guarantee a certain level of performance.

Scenario-Aware Data Flow (SADF) (Geilen and Stuijk 2010) is a related modeling approach that has a similar separation of concerns with respect to functionality and timing. This formalism uses the same model of computation, (max,+) algebra, to perform throughput analysis. The throughput analysis considered in SADF is restricted to fully-controllable systems. In this setting, an approach has been presented in Skelin and Geilen (2018) where also guards can be added on transitions in an FA on explicit values of time stamps of events. There is no distinction between controllable and uncontrollable events, and no synthesis step. Similar to our approach, the guards are evaluated only when constructing the (max,+) state space.

Game theory applied to timed automata (Behrmann et al. 2007) has been used for the synthesis of a controller that ensures safe behavior, as well as reachability of a final (goal) state. Timed automata have also been used in Abdeddaïm et al. (2006) to solve a scheduling problem using shortest path algorithms. Using timed automata poses challenges with respect to scaling for large systems, as timing of individual actions must be considered during analysis. This is avoided by the use of (max,+) timing characterizations of activities.

8 Conclusions

This paper introduces a new approach to model partial controllability of functionality in manufacturing systems on two abstraction levels. It is based on the recently developed Activity modeling formalism (van der Sanden et al. 2016) with associated tools, which is used to model the functionality and timing of manufacturing systems at a high level of abstraction using deterministic activities. The Activity modeling formalism allows for the scheduling of desirable sequences of activities on multiple resources by means of (max,+) algebra. Our approach extends the modeling by the introduction of uncontrollability at the level of activities, as commonly found in a supervisory control context (Cassandras and Lafortune 2008). Moreover, functional dependency at activity level on feedback from lower abstraction levels is captured using variables in Activity-EFAs. The Activity-EFAs contain the allowed activity sequences, along with guard expressions that limit behavior depending on the values of the variables. We introduce a new performance analysis method that employs game-theoretic methods to provide a guarantee to system performance, and to automatically compute a robust, throughput-optimal controller given a partially-controllable system. The methods are illustrated on an example manufacturing system.

There are a number of directions in which our approach can be extended. First, there are various other performance analysis and optimization techniques that can be investigated that cope with uncontrollability in different ways. For batch production systems, the use of finite two-player games and different performance metrics, such as makespan, could be investigated. When the probability of occurrence of uncontrollable behavior is known, stochastic scheduling methods (Niño-Mora 2008) can be employed, which may further optimize performance. Another aspect that is currently not present is the extension with strategies for bringing the system out of the maximum-throughput strategy. This could be useful in cases that the operator wants to shut the machine down when production is finished, or maintenance is needed. Finally, we want to investigate the application of our approach on an industrial-size case. The approach we present can easily be adopted in a domain-specific language that already uses the semantics of the Activity modeling formalism.