Skip to main content
SpringerLink
Log in

Analytical Study on the Generalized Fifth-Order Kaup–Kupershmidt Equation from the Shallow Water Wave

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

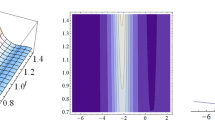
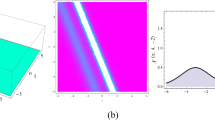
In this paper, the generalized fifth-order Kaup–Kupershmidt (KK) equation from the shallow water wave, have been investigated. With the help of bilinear method and auxiliary function, the multi-soliton solutions of the generalized fifth-order KK equation have been obtained, and those solutions have not been given before. From the analytical view, the interactions of the solitons have been presented. Through the discussion, we have found that the velocity of the soliton is related to the sign of the physical parameters \(b\) and \({{c}_{j}}\). Also, the (bright or dark-like) types of the soliton interaction are related to the physical parameters \(a\). Hence, the velocities and bright-dark types of the soliton interactions could be controlled by adjusting the physical parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.

Similar content being viewed by others

REFERENCES

  1. X. Q. Zhao, D. B. Tang, and L. M. Wang, “New soliton-like solutions for KdV equation with variable coefficient,” Phys. Lett. A 346, 288–291 (2005).

    Article  MathSciNet  Google Scholar 

  2. H. Motschmann, W. Forner, and J. Ladik, “Influence of heat bath and disorder in the sequence of amino acid masses on Davydov solitons,” J. Phys. Condens. Matt. 31, 5083–5093 (1989).

    Article  Google Scholar 

  3. N. A. Nevskaya and Y. N. Chirgadze, “Infrared spectra and resonance interactions of amide-I and II vibrations of \(\alpha \)-helix,” Biopolymers 15, 637–648 (1976).

    Article  Google Scholar 

  4. A. S. Davydov and N. I. Kislukha, “Solitary excitons in one-dimensional molecular chains,” Phys. Stat. Sol. 59, 465–470 (2006).

    Article  Google Scholar 

  5. N. H. Seong and D. Y. Kim, “Experimental observation of stable bound solitons in a figure-eight fiber laser,” Opt. Lett. 27, 1321–1323 (2002).

    Article  Google Scholar 

  6. W. S. Kim and H. T. Moon, “Soliton-kink interactions in a generalized nonlinear Schrödinger equation,” Phys. Lett. A 266, 364–369 (2000).

    Article  MathSciNet  Google Scholar 

  7. D. W. Zuo, Y. T. Gao, G. Q. Meng, Y. J. Shen, and X. Yu, “Multi-soliton solutions for the three-coupled KdV equations engendered by the Neumann system,” Nonlinear Dyn. 75, 701–708 (2014).

    Article  MathSciNet  Google Scholar 

  8. R. Radhakrishnan, A. Kundu, and M. Lakshmanan, “Coupled nonlinear Schrödinger equations with cubic-quintic nonlinearity: Integrability and soliton interaction in non-Kerr media,” Phys. Rev. E 60, 3314–3323 (1999).

    Article  Google Scholar 

  9. M. Daniel and M. M. Latha, “A generalized Davydov soliton model for energy transfer in alpha helical proteins,” Phys. A 298, 351–370 (2001).

    Article  Google Scholar 

  10. M. Karlsson, D. J. Kaup, and B. A. Malomed, “Interactions between polarized soliton pulses in optical fibers: Exact solutions,” Phys. Rev. E 54, 5802–5808 (1996).

    Article  Google Scholar 

  11. C. Chin, T. Kraemer, M. Mark, J. Herbig, P. Waldburger, H.-C. Ngerl, and R. Grimm, “Observation of Feshbach-like resonances in collisions between ultracold molecules,” Phys. Rev. Lett. 94, 123201–123204 (2005).

    Article  Google Scholar 

  12. F. K. Abdullaev, A. Gammal, L. Tomio, and T. Frederico, “Stability of trapped Bose–Einstein condensates,” Phys. Rev. A 63, 043604–043614 (2001).

    Article  Google Scholar 

  13. L. Wang, C. Geng, L. L. Zhang, and Y. C. Zhao, “Characteristics of the nonautonomous breathers and rogue waves in a generalized Lenells–Fokas equation,” Europhys. Lett. 108 (1–5), 50009 (2014).

  14. L. Wang, X. Li, F. H. Qi, and L. L. Zhang, “Breather interactions and higher-order nonautonomous rogue waves for the inhomogeneous nonlinear Schrödinger Maxwell–Bloch equations,” Ann. Phys. 359, 97–114 (2015).

    Article  Google Scholar 

  15. A. H. Salas, “Solving the generalized Kaup–Kupershmidt equation,” Adv. Stud. Theor. Phys. 6, 879–885 (2012).

    MathSciNet  MATH  Google Scholar 

  16. S. Sanaydin, S. T. Mohyud-Din, and A. Yildirim, “Numerical soliton solution of the Kaup–Kupershmidt equation,” Int. J. Numer. Methods Heat Fluid Flow 21, 272–281 (2011).

    Article  MathSciNet  Google Scholar 

  17. C. Verhoeven and M. Musette, “Extended soliton solutions for the Kaup–Kupershmidt equation,” J. Phys. A 34, 2515–2523 (2001).

    Article  MathSciNet  Google Scholar 

  18. S. Lou, J. Yu, J. Weng, and X. Qian, “Soliton solutions of the Kaup–Kupershmidt and Sawada–Kotera equations,” Stud. Math. Sci. 43, 38–44 (2010).

    Google Scholar 

  19. A. R. Adem and C. M. Khalique, “Exact solutions and conservation laws of a two-dimensional integrable generalization of the Kaup–Kupershmidt equation,” J. Appl. Math. 11, 924–970 (2012).

    Google Scholar 

  20. A. Parker, “On soliton solutions of the Kaup–Kupershmidt equation. II: ‘Anomalous’ \(N\)-soliton solutions,” Physica D 137, 34–48 (2000).

    Article  MathSciNet  Google Scholar 

  21. D. J. Kaup, “On the inverse scattering problem for cubic eigenvalue problems of the class \({{\psi }_{{xxx}}} + 6q{{\psi }_{x}} + 6r\psi = \lambda \psi \),” Stud. Appl. Math. 62, 189–216 (1980).

    Article  MathSciNet  Google Scholar 

  22. J. B. Li and Z. J. Qiao, “Explicit soliton solutions of the Kaup–Kupershmidt equation through the dynamical system approach,” J. Appl. Anal. Comput. 1, 243–250 (2011).

    MathSciNet  MATH  Google Scholar 

  23. R. Hirota and Y. Ohta, “Hierarchies of coupled soliton equations I,” J. Phys. Soc. Jpn. 60, 798–809 (1991).

    Article  MathSciNet  Google Scholar 

  24. R. Hirota, “Exact solution of the Korteweg–de Vries equation for multiple collisions of solitons,” Phys. Rev. Lett. 27, 1192–1194 (1971).

    Article  Google Scholar 

Download references

Funding

This work has been supported by the National Natural Science Foundation of China under grant nos. 11426041 and 11605011.

Author information

Authors and Affiliations

  1. Sports Business School, Beijing Sport University, no.48, 100084, Beijing, China

    Pan Wang, Jian-Rong Yang & Li Chen

  2. School of Management, Beijing Sport University, no.48, 100084, Beijing, China

    Sheng-Xin Li

  3. School of Information, Beijing Wuzi University, 101149, Beijing, China

    Feng-Hua Qi

Authors
  1. Pan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian-Rong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sheng-Xin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Feng-Hua Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pan Wang.

APPENDIX

APPENDIX

The related parameters for the three-soliton solution are as follows:

$$\begin{gathered} g = {{P}_{1}}{{e}^{{{{\theta }_{1}}}}} + {{P}_{2}}{{e}^{{{{\theta }_{2}}}}} + {{P}_{3}}{{e}^{{{{\theta }_{3}}}}} + {{P}_{7}}{{e}^{{{{\theta }_{1}} + {{\theta }_{2}}}}} + {{P}_{8}}{{e}^{{{{\theta }_{1}} + {{\theta }_{3}}}}} + {{P}_{9}}{{e}^{{{{\theta }_{2}} + {{\theta }_{3}}}}} + {{P}_{{10}}}{{e}^{{{{\theta }_{1}} + 2{{\theta }_{2}}}}} + {{P}_{{11}}}{{e}^{{2{{\theta }_{1}} + {{\theta }_{2}}}}} \\ + \;{{P}_{{12}}}{{e}^{{{{\theta }_{1}} + 2{{\theta }_{3}}}}} + {{P}_{{13}}}{{e}^{{2{{\theta }_{1}} + {{\theta }_{3}}}}} + {{P}_{{14}}}{{e}^{{{{\theta }_{2}} + 2{{\theta }_{3}}}}} + {{P}_{{15}}}{{e}^{{2{{\theta }_{2}} + {{\theta }_{3}}}}} + {{P}_{{16}}}{{e}^{{{{\theta }_{1}} + {{\theta }_{2}} + {{\theta }_{3}}}}} + {{P}_{{20}}}{{e}^{{{{\theta }_{1}} + {{\theta }_{2}} + 2{{\theta }_{3}}}}} \\ + \;{{P}_{{21}}}{{e}^{{{{\theta }_{1}} + 2{{\theta }_{2}} + {{\theta }_{3}}}}} + {{P}_{{22}}}{{e}^{{2{{\theta }_{1}} + {{\theta }_{2}} + {{\theta }_{3}}}}} + {{P}_{{23}}}{{e}^{{2{{\theta }_{1}} + 2{{\theta }_{2}} + {{\theta }_{3}}}}} + {{P}_{{24}}}{{e}^{{2{{\theta }_{1}} + {{\theta }_{2}} + 2{{\theta }_{3}}}}} + {{P}_{{25}}}{{e}^{{{{\theta }_{1}} + 2{{\theta }_{2}} + 2{{\theta }_{3}}}}}, \\ \end{gathered} $$
$${{P}_{7}} = \tfrac{{15a{{{({{c}_{1}} - {{c}_{2}})}}^{2}}(2c_{1}^{4} + 3c_{1}^{2}c_{2}^{2} + 2c_{2}^{4})}}{{(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})}},\quad {{P}_{8}} = \tfrac{{15a{{{({{c}_{1}} - {{c}_{3}})}}^{2}}(2c_{1}^{4} + 3c_{1}^{2}c_{3}^{2} + 2c_{3}^{4})}}{{(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})}},$$
$${{P}_{9}} = \tfrac{{15a{{{({{c}_{2}} - {{c}_{3}})}}^{2}}(2c_{2}^{4} + 3c_{2}^{2}c_{3}^{2} + 2c_{3}^{4})}}{{(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})}},\quad {{P}_{{10}}} = \tfrac{{15ac_{1}^{4}{{{({{c}_{1}} - {{c}_{2}})}}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2})}}{{8{{{({{c}_{1}} + {{c}_{2}})}}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})}},$$
$${{P}_{{11}}} = \tfrac{{15ac_{2}^{4}{{{({{c}_{1}} - {{c}_{2}})}}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2})}}{{8{{{({{c}_{1}} + {{c}_{2}})}}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})}},\quad {{P}_{{12}}} = \tfrac{{15ac_{1}^{4}{{{({{c}_{1}} - {{c}_{3}})}}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2})}}{{8{{{({{c}_{1}} + {{c}_{3}})}}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})}},$$
$${{P}_{{13}}} = \tfrac{{15ac_{3}^{4}{{{({{c}_{1}} - {{c}_{3}})}}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2})}}{{8{{{({{c}_{1}} + {{c}_{3}})}}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})}},\quad {{P}_{{14}}} = \tfrac{{15ac_{2}^{4}{{{({{c}_{2}} - {{c}_{3}})}}^{2}}(c_{2}^{2} - {{c}_{2}}{{c}_{3}} + c_{3}^{2})}}{{8{{{({{c}_{2}} + {{c}_{3}})}}^{2}}(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})}},$$
$$\begin{gathered} {{P}_{{16}}} = \{ 15a[2c_{2}^{4}c_{3}^{4}{{(c_{2}^{2} - c_{3}^{2})}^{2}}(2c_{2}^{4} + 3c_{2}^{2}c_{3}^{2} + 2c_{3}^{4}) + c_{1}^{{12}}(4c_{2}^{4} - 2c_{2}^{2}c_{3}^{2} + 4c_{3}^{4}) - c_{1}^{8}{{(c_{2}^{2} - c_{3}^{2})}^{2}}(4c_{2}^{4} + 5c_{2}^{2}c_{3}^{2} + 4c_{3}^{4}) \\ - \;c_{1}^{8}{{(c_{2}^{2} - c_{3}^{2})}^{2}}(4c_{2}^{4} + 5c_{2}^{2}c_{3}^{2} + 4c_{3}^{4}) - c_{1}^{{10}}(2c_{2}^{6} + c_{2}^{4}c_{3}^{2} + c_{2}^{2}c_{3}^{4} + 2c_{3}^{6}) - c_{1}^{2}c_{2}^{2}c_{3}^{2}{{(c_{2}^{2} - c_{3}^{2})}^{2}}(2c_{2}^{6} + 5c_{2}^{4}c_{3}^{2} + 5c_{2}^{2}c_{3}^{4} + 2c_{3}^{6}) \\ \end{gathered} $$
$$\begin{gathered} - \;c_{1}^{6}(2c_{2}^{{10}} - 3c_{2}^{8}c_{3}^{2} + 4c_{2}^{6}c_{3}^{4} + 4c_{2}^{4}c_{3}^{6} - 3c_{2}^{2}c_{3}^{8} + 2c_{3}^{{10}}) + c_{1}^{4}(4c_{2}^{{12}} - c_{2}^{{10}}c_{3}^{2} + 2c_{2}^{8}c_{3}^{4} - 4c_{2}^{6}c_{3}^{6} + 2c_{2}^{4}c_{3}^{8} - c_{2}^{2}c_{3}^{{10}} + 4c_{3}^{{12}})]\} \\ \times \;{{[2{{({{c}_{1}} + {{c}_{2}})}^{2}}{{({{c}_{1}} + {{c}_{3}})}^{2}}{{({{c}_{2}} + {{c}_{3}})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})]}^{{ - 1}}}, \\ \end{gathered} $$
$$\begin{gathered} {{P}_{{20}}} = 15a{{({{c}_{1}} - {{c}_{2}})}^{2}}{{({{c}_{1}} - {{c}_{3}})}^{2}}{{({{c}_{2}} - {{c}_{3}})}^{2}}(2c_{1}^{4} + 3c_{1}^{2}c_{2}^{2} + 2c_{2}^{4})(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2})(c_{2}^{2} - {{c}_{2}}{{c}_{3}} + c_{3}^{2}) \\ \times \;{{[16{{({{c}_{1}} + {{c}_{3}})}^{2}}{{({{c}_{2}} + {{c}_{3}})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})]}^{{ - 1}}}, \\ \end{gathered} $$
$$\begin{gathered} {{P}_{{21}}} = 15a{{({{c}_{1}} - {{c}_{2}})}^{2}}{{({{c}_{1}} - {{c}_{3}})}^{2}}{{({{c}_{2}} - {{c}_{3}})}^{2}}(2c_{1}^{4} + 3c_{1}^{2}c_{3}^{2} + 2c_{3}^{4})(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{2}^{2} - {{c}_{2}}{{c}_{3}} + c_{3}^{2}) \\ \times \;{{[16{{({{c}_{1}} + {{c}_{2}})}^{2}}{{({{c}_{2}} + {{c}_{3}})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})]}^{{ - 1}}}, \\ \end{gathered} $$
$$\begin{gathered} {{P}_{{22}}} = 15a{{({{c}_{1}} - {{c}_{2}})}^{2}}{{({{c}_{1}} - {{c}_{3}})}^{2}}{{({{c}_{2}} - {{c}_{3}})}^{2}}(2c_{2}^{4} + 3c_{2}^{2}c_{3}^{2} + 2c_{3}^{4})(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2}) \\ \times \;{{[16{{({{c}_{1}} + {{c}_{2}})}^{2}}{{({{c}_{1}} + {{c}_{3}})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2}) \times (c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})]}^{{ - 1}}}, \\ \end{gathered} $$
$$\begin{gathered} {{P}_{{23}}} = 15ac_{3}^{4}{{({{c}_{1}} - {{c}_{2}})}^{4}}{{({{c}_{1}} - {{c}_{3}})}^{2}}{{({{c}_{2}} - {{c}_{3}})}^{2}}{{(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2})}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2})(c_{2}^{2} - {{c}_{2}}{{c}_{3}} + c_{3}^{2}) \\ \times \;{{[128{{({{c}_{1}} + {{c}_{2}})}^{4}}{{({{c}_{1}} + {{c}_{3}})}^{2}}{{({{c}_{2}} + {{c}_{3}})}^{2}}{{(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})]}^{{ - 1}}}, \\ \end{gathered} $$
$$\begin{gathered} {{P}_{{24}}} = 15ac_{2}^{4}{{({{c}_{1}} - {{c}_{3}})}^{4}}{{({{c}_{1}} - {{c}_{2}})}^{2}}{{({{c}_{2}} - {{c}_{3}})}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2}){{(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2})}^{2}}(c_{2}^{2} - {{c}_{2}}{{c}_{3}} + c_{3}^{2}) \\ \times \;{{[128{{({{c}_{1}} + {{c}_{3}})}^{4}}{{({{c}_{1}} + {{c}_{2}})}^{2}}{{({{c}_{2}} + {{c}_{3}})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2}){{(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2})}^{2}}(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})]}^{{ - 1}}}, \\ \end{gathered} $$
$$\begin{gathered} {{P}_{{25}}} = 15ac_{1}^{4}{{({{c}_{2}} - {{c}_{3}})}^{4}}{{({{c}_{1}} - {{c}_{2}})}^{2}}{{({{c}_{1}} - {{c}_{3}})}^{2}}(c_{1}^{2} - {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} - {{c}_{1}}{{c}_{3}} + c_{3}^{2}){{(c_{2}^{2} - {{c}_{2}}{{c}_{3}} + c_{3}^{2})}^{2}} \\ \times \;{{[128{{({{c}_{2}} + {{c}_{3}})}^{4}}{{({{c}_{1}} + {{c}_{2}})}^{2}}{{({{c}_{1}} + {{c}_{3}})}^{2}}(c_{1}^{2} + {{c}_{1}}{{c}_{2}} + c_{2}^{2})(c_{1}^{2} + {{c}_{1}}{{c}_{3}} + c_{3}^{2}){{(c_{2}^{2} + {{c}_{2}}{{c}_{3}} + c_{3}^{2})}^{2}}]}^{{ - 1}}}. \\ \end{gathered} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, P., Yang, JR., Chen, L. et al. Analytical Study on the Generalized Fifth-Order Kaup–Kupershmidt Equation from the Shallow Water Wave. Comput. Math. and Math. Phys. 60, 1480–1487 (2020). https://doi.org/10.1134/S0965542520090158

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542520090158

Keywords:

Search

Navigation