1 Introduction

Stationary inflow–outflow problems in fluid mechanics are well-modeled by the (steady state) Navier–Stokes equations describing the motion of the fluid and by nonhomogeneous boundary conditions prescribing how a given fluid enters or exits the considered bounded domain \(\Omega \) (either in \({\mathbb {R}}^2\) or in \({\mathbb {R}}^3\)):

$$\begin{aligned} -\eta \Delta u+(u\cdot \nabla )u+\nabla p=0,\ \quad \nabla \cdot u=0 \ \text{ in } \ \Omega ,\quad u=h \ \text{ on } \ \partial \Omega \,. \end{aligned}$$
(1.1)

In (1.1), u is the velocity vector field, p is the scalar pressure and \(\eta >0\) is the kinematic viscosity, while the datum h contains both the inflow–outflow conditions and the behavior on the remaining part of the boundary. The theory developed so far in order to manage Navier–Stokes equations under nonhomogeneous Dirichlet conditions (see e.g. [17]) suggests to reduce the problem to homogeneous conditions through a suitable solenoidal extension of the boundary data. Namely, one needs to find a vector field \(v_0\) satisfying

$$\begin{aligned} \nabla \cdot v_0=0 \ \text { in } \ \Omega ,\quad v_0=h \ \text { on } \ \partial \Omega \, . \end{aligned}$$
(1.2)

This problem, whose interest and applicability go far beyond fluid mechanics, has a long history, starting from the pioneering works of Sobolev [34], Cattabriga [7] and Ladyzhenskaya-Solonnikov [29, 30]; see also the book by Galdi [17, Section III.3]. If the boundary conditions are themselves of solenoidal type such as constants, Poiseuille or Couette flows (see [31] for other models), the extension is found by a fairly standard procedure, see [26, 35, 36] for bounded domains and [8, 9] for a special class of unbounded domains. The classical way to solve (1.2) relies in the use of a proper extension of the data h as a curl, together with a Hopf’s-type cutoff function, see [29, p.130] and also [17, Section IX.4]. However, if the inflow–outflow datum h does not have a straightforward solenoidal extension, the problem becomes significantly more difficult. This is the case, for instance, when the considered domain contains an obstacle where, due to the effects of viscosity, the flow satisfies no-slip conditions. Then, even if the inflow–outflow datum has a simple solenoidal extension, one can still use cutoff functions in order to meet the homogeneous boundary conditions on the obstacle. Nevertheless, it turns out that, in real life, the obstacle perturbs the fluid flow, creating some vortices behind itself even for low-Reynolds-numbers. Recent experimental and numerical evidence [6, 37, 38] shows that, at a sufficiently large distance behind the obstacle, the perturbed flow concentrates its turbulent motion mostly in the wake of the body, see Fig. 1 for a wind tunnel experiment and [6, 13] for some experimental data.

Fig. 1
figure 1

Vortices around a plate obtained in wind tunnel experiments at Politecnico di Milano

Full size image

It is then clear that different boundary conditions should be imposed on the outlet, see [22, 23, 28]. Overall, in presence of an obstacle, the most realistic physical boundary conditions are different (nonhomogeneous) inflow and outflow conditions, combined with homogenous conditions on the obstacle. In this situation, the construction of a solenoidal extension appears possible only in two steps. First, to find an extension, not necessarily solenoidal, of the inflow–outflow data, thereby “inverting” the trace operator for vector fields; this problem has been systematically studied since the works of Miranda [32], Prodi [33] and Gagliardo [16], giving a full characterization of the trace operator and providing an explicit extension for any locally Lipschitz domain and any boundary datum. Second, to solve the Bogovskii problem [3, 4] with the resulting divergence: the celebrated Bogovskii formula, dating back to 1979, yields a class of solutions by means of the Calderón–Zygmund theory of singular integrals. Durán [14] proposed in 2012 an alternative approach based on the Fourier transform. Incidentally, let us also mention that the Bogovskii problem is strictly related to several inequalities arising both in fluid mechanics and elasticity; see [1, 2, 10, 15, 24, 27].

Fig. 2
figure 2

The obstacle K in the box Q, in 2d (left) and in 3d (right)

Full size image

As a consequence of the vortex shedding, the fluid exerts forces on the obstacle and, if one is interested in the stability of the obstacle itself, the most relevant one is the lift force. With the final purpose of analyzing the stability of a suspension bridge under the action of the wind [18], a simplified geometric framework where to analyze the appearance a of lift force was first suggested in [21] and subsequently discussed in [5, 20, 22]. The setting can be simply described as follows: the container Q is given by an open square in \({\mathbb {R}}^2\) or an open cube in \({\mathbb {R}}^3\), while the obstacle is represented as a compact, connected, and simply connected domain K with Lipschitz boundary contained into Q, see Fig. 2. In this geometric setting, the main purpose of this paper is the construction of estimable solenoidal extensions of quite general boundary data to \(\Omega =Q {\setminus } K\). Precisely, in dimension \(d=2\) or \(d=3\), given a vector field h satisfying suitable assumptions, we determine a solution \(v_0\) to the boundary value problem (1.2), along with some upper bound on the Dirichlet norm of \(v_0\) in \(\Omega \). The goal is not simply to show the existence of some solenoidal extension, but also to obtain an explicit form of it, in order to derive explicit bounds on its norm. The reason is that we are mainly interested in applications to fluid mechanics, such as finding bounds on the inflow velocity guaranteeing the unique solvability of the Navier–Stokes equations (1.1). In turn, in view of the results contained in [20], in a symmetric framework, unique solvability implies that the lift applied over K is zero.

The paper is organized as follows. Section 2 serves as a guideline, where the outline of our strategy is presented, together with our main result (Theorem 2.1) and its application to Navier–Stokes equations. The steps of this strategy are carried over in the remaining sections of the article. In Sect. 3 we formulate an extension result, see Theorem 3.1, that not only allows to invert the trace operator in our geometric framework, but also to study two new inflow–outflow models that are suggested. Then, in Sect. 4 we explicitly solve a variational problem involving the infinity-Laplacian, yielding a sharp bound on the \(W^{1,\infty }\)-norm of a class of scalar cutoff functions. Through a delicate combination of the results contained in [3, 4, 14, 17], an upper bound for the Bogovskii constant of the domain \(\Omega \) is found in Sect. 5, see Theorem 5.1; this requires the estimation of the norms of certain mollifiers given in Sect. 6. By using these results we finally give the proof of Theorem 2.1 in Sect. 7.

2 The paper at a glance

2.1 Assumptions and outline of the strategy

We let \(Q=(-L,L)^{d}\) and \(K \subset Q \subset {\mathbb {R}}^ d\) (\(d = 2\) or \(d= 3\)) be as described above, see again Fig. 2. We fix here the assumptions on the boundary datum h in problem (1.2): we view h as the compound of four fields \(h_{i}\) defined on the four sides \(\Sigma _i\)’s of Q in dimension 2, and of six fields \(h_{i}\) defined on the six faces \(\Sigma _i\)’s of Q in dimension 3. We denote by \(\hat{n}\) the outward unit normal to (the sides/faces of) Q and by \({\mathcal {V}}\) the family of vertices of Q:

$$\begin{aligned} h \in {\mathcal {C}} (\partial Q)\, , \quad h _i \in H ^ 1 (\Sigma _i) \, , \quad \int _{\partial Q} h \cdot \hat{n} = 0\, , \quad h{ \big | _{\mathcal {V}} } = 0 \ \ \text { if } \ \ d = 3\,. \end{aligned}$$
(2.1)

Note that the vanishing condition for h at the vertices of Q is assumed only for \(d = 3\), while it is not needed for the validity of our results in dimension \(d = 2\). We fix real numbers a, b, c so that

$$\begin{aligned}&L> a \ge b \ge c >0 \quad \text { and } \quad K \subset P \subset Q \, , \quad \nonumber \\&\quad \text { with } \ {\left\{ \begin{array}{ll} P=(-a,a)\times (-b,b) &{} \ \text { if }d=2 \\ P=(-a,a)\times (-b,b) \times (-c, c) &{} \ \text { if }d=3 \, , \end{array}\right. } \end{aligned}$$
(2.2)

so that the obstacle K is enclosed by the parallelepiped P. Throughout the paper we set

$$\begin{aligned} \Omega _{0} \doteq Q{\setminus } {\overline{P}}\,. \end{aligned}$$
(2.3)

Working on the set \(\Omega _{0}\) allows us to obtain explicit bounds; with our approach, it is clear that the best possible bounds are found by taking P as the smallest parallelepiped enclosing K. We shall proceed in four steps:

Step 1 We determine a vector field

$$\begin{aligned} A_1 \in H^{1}(Q) \cap \mathcal {C}(\overline{Q}) \quad \text{ with } \quad A_1=h \ \ \text{ on } \ \ \partial Q\, , \end{aligned}$$

such that the \(H ^ 1\)-norm of \(A _1\) on Q can be explicitly computed in terms of the \(H ^ 1\)-norms of the fields \(h _ i\) on \(\Sigma _i\). The expression of this (not necessarily solenoidal) field is given in Theorem 3.1.

Step 2 We construct a scalar function \(\phi \in W^{1,\infty }(Q)\) such that

$$\begin{aligned} \phi = 1 \ \ \text {on} \ \ \partial Q, \quad \phi = 0 \ \ \text {in} \ \ {\overline{P}}\, , \end{aligned}$$

in such a way that the \(W ^{1, \infty }\)-norm of \(\phi \) in \(\Omega _{0}\) is explicitly computable and as small as possible. This function \(\phi \) is defined in Sect. 4, and its minimizing property (which is obtained by using the variational properties of infinity-harmonic functions) is stated in Theorem 4.1; incidentally, we point out that this bound is sharp. Then the vector field \(A_{2} \doteq \phi A_{1}\) satisfies

$$\begin{aligned} A_{2}=h \ \ \text{ on } \ \ \partial Q \, , \quad A_2 = 0 \ \ \text { in } \ \ {\overline{P}}\,. \end{aligned}$$

By using the \(H ^1\)-bounds on \(A_2\) and the \(W ^ {1, \infty }\)-bounds on \(\phi \), we can control the \(H ^1\)-norm of \(A_2\) on Q.

Step 3 We construct a vector field

$$\begin{aligned} A_3\in H^1_0(\Omega _{0}) \ \ \text {satisfying} \ \ \nabla \cdot A_3=-\nabla \cdot A_2 \ \ \text{ in } \ \ \Omega _{0}\, , \end{aligned}$$

such that the \(L ^ 2\)-norm of \(\nabla A _ 3\) is estimated in terms of the \(L ^2\)-norm of \(\nabla \cdot A_2\). To this aim, we provide an upper bound for the Bogovskii constant of \(\Omega _{0}\) (and, hence, of \(\Omega \)), defined as

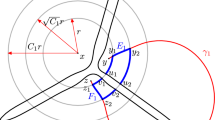
$$\begin{aligned} C_B (\Omega _{0}) \doteq \sup _ {g \in L ^ 2 _0 (\Omega _{0}) {\setminus } \{ 0 \} } \inf \left\{ \frac{ \Vert \nabla v\Vert _{L^2(\Omega _{0})} }{ \Vert g\Vert _{L^2(\Omega _{0})}} \ \Bigg | \ v \in H ^ 1 _ 0 (\Omega _{0}) \, , \ \nabla \cdot v=g \ \text { in } \ \Omega _{0} \right\} \, , \end{aligned}$$
(2.4)

where \(L ^ 2 _0 (\Omega _{0})\) denotes the subspace of functions in \(L ^ 2 (\Omega _{0} )\) having zero mean value. This upper bound is stated Theorem 5.1 and has its own independent interest. The proof is based on the following idea: first we derive a quantitative version of a result by Durán [14], allowing to estimate the Bogovskii constant of a domain which is star-shaped with respect to a ball (see Proposition 5.1), and then we apply such result after decomposing \(\Omega _{0} \) as the union of two domains \(\Omega _{1}\) and \(\Omega _{2}\) that are star-shaped with respect to a ball placed in a corner: these sets are the regions “illuminated” by spherical lamps placed in two opposite corners (namely, each one tangent to the sides of Q intersecting at the corner), see Sect. 5 for the analytic description. In Fig. 3 we illustrate the intersection \(\Omega _1 \cap \Omega _2\) as the colored region “doubly-illuminated” by both lamps.

Fig. 3
figure 3

The (colored) “doubly-illuminated” region \(\Omega _1 \cap \Omega _2\), in 2d (left) and in 3d (right)

Full size image

Step 4—Conclusion Finally, we observe that the field \(v_0\) defined by \(v_0 \doteq A_2+A_3\) in \(\Omega _{0}\), and extended by zero on \(P {\setminus } K\), is a solution to problem (1.2) in \(\Omega \); moreover, by making use of the preceding steps we are in position to find an explicit bound for the \(L ^2\)-norm of \(\nabla v_0\), see (2.5)–(2.6).

2.2 Main result and applications to the Navier–Stokes equations

Putting together all the previously described steps, we now state our main result.

Theorem 2.1

Under assumptions (2.1)–(2.2), there exists a vector field \(v_0\in H^{1}(\Omega )\) satisfying (1.2) such that

$$\begin{aligned} \Vert \nabla v_{0} \Vert _{L^{2}(\Omega )} \le \Gamma \, , \end{aligned}$$
(2.5)

where \(\Gamma \) is a positive constant depending only on L, a, b, c and the norms in \(H ^ 1 (\Sigma _i)\) of the functions \(h _i\). Specifically, the value of \(\Gamma \) is given by

$$\begin{aligned} \Gamma = \frac{1 + M}{L-a} \, \Vert A_{1} \Vert _{L^{2}( Q)} + \Vert \nabla A_{1} \Vert _{L^{2}(Q)} + M \, \Vert \nabla \cdot A_{1} \Vert _{L^{2}(Q)} \,, \end{aligned}$$
(2.6)

where \(A_1\) is the extension of h found in Step 1, and M is the upper bound for the Bogovskii constant of \(\Omega _{0}\) found in Step 3.

Remark 2.1

Concerning the value of the constant \(\Gamma \) given in (2.6), we further precise that:

  • It is explicitly computable, relying on the explicit expressions of the field \(A_1\) and of the constant M; to simplify the presentation, such expressions are postponed to Theorems 3.1 and 5.1.

  • It is far from being optimal. In particular, it might be improved by refining the estimates in Steps 1 and 3 (whereas the estimate for the function \(\phi \) in Step 2 is sharp).

Thanks to Theorem 2.1 we can give necessary conditions for the appearance of lift forces over an obstacle exerted by Navier–Stokes flows. Let us consider Eq. (1.1) with the boundary datum h satisfying (2.1) and a no-slip condition on the obstacle

$$\begin{aligned} h=0 \ \text { on } \ \partial K. \end{aligned}$$
(2.7)

Since \(h\ne 0\) on \(\partial Q\), we need to deal with both the Sobolev space \(H_{0}^{1}(\Omega )\) and the space of functions vanishing only on \(\partial K\), which is a proper connected part of \(\partial \Omega \):

$$\begin{aligned} H^1_*(\Omega )=\{v\in H^1(\Omega ) \ | \ v=0 \ \ \text{ on } \ \ \partial K\}\, . \end{aligned}$$

This space is the closure of the space \(\mathcal {C}^\infty _c(\overline{Q}{\setminus }\overline{K})\) with respect to the Dirichlet norm. We also need the two functional spaces of vector fields

$$\begin{aligned} \mathcal {V}_{*}(\Omega ) = \{ v \in H^1_*(\Omega ) \ | \ \nabla \cdot v = 0 \ \ \text {in} \ \Omega \} \ \ \ \text {and} \ \ \ \mathcal {V}(\Omega ) = \{ v \in H^{1}_{0}(\Omega ) \ | \ \nabla \cdot v = 0 \ \ \text {in} \ \Omega \}. \end{aligned}$$

Assuming (2.1), we say that a vector field \(u \in \mathcal {V}_{*}(\Omega )\) is a weak solution of (1.1)–(2.7) if u verifies the boundary conditions in the trace sense and

$$\begin{aligned} \eta \int _{\Omega } (\nabla u \cdot \nabla \varphi ) \, dx + \int _{\Omega } (u\cdot \nabla )u \cdot \varphi \, dx = 0 \ \ \ \ \ \ \forall \varphi \in \mathcal {V}(\Omega ). \end{aligned}$$
(2.8)

It is well-known [17, Section IX.4] that a solution always exists and that it is unique provided that \(\Vert h\Vert _{H^{1/2}(\partial Q)}\) is sufficiently small, see also [20, Section 3] for the particular case of a domain with obstacle. The flow of the fluid exerts a force \(F_{K}\) over the obstacle, which can be computed through the stress tensor \(\mathbb {T}(u,p)\) of the fluid [31, Chapter 2] and, in a weak sense, is defined as

$$\begin{aligned} F_{K}(u,p)= - \langle \mathbb {T}(u,p) \cdot \hat{n} , 1 \rangle _{\partial K} \, . \end{aligned}$$
(2.9)

Here \(\langle \cdot , \cdot \rangle _{\partial K}\) denotes the duality pairing between \(W^{-\frac{2}{3}, \frac{3}{2}}(\partial K)\) and \(W^{\frac{2}{3}, 3}(\partial K)\), while the minus sign is due to the fact that the outward unit normal \(\hat{n}\) to \(\Omega \) is directed towards the interior of K. In the case of suspension bridges, the boundary conditions should model an horizontal inflow on the (2d or 3d) face \(x=-L\) of Q, as in conditions (3.2) and (3.4), see also [19]. Then, the most relevant component of the force (2.9), leading to structural instability, is the lift force \(\mathcal {L}_{K}(u,p)\) which is oriented vertically and, in our generalized context, can be computed as

$$\begin{aligned} \mathcal {L}_{K}(u,p) = F_{K}(u,p) \cdot \mathbf{v }, \end{aligned}$$

where \(\mathbf{v} \) is the unit vector in the y-direction in the 2d space and in the z-direction of z in the 3d space. The connection between the unique solvability of (1.1), the existence of symmetric solutions and the appearance of a lift force over K is expressed in the following result:

Proposition 2.1

Assume (2.2). For any \(h\in H^{1/2}(\partial \Omega )\cap \mathcal {C}(\partial Q)\) satisfying (2.1)–(2.7), there exists a weak solution of (1.1). Moreover, there exists \(\chi >0\) such that, if \(\Vert h\Vert _{H^{1/2}(\partial Q)} <\chi \), then the weak solution is unique. Furthermore, if the obstacle K is symmetric with respect to the y-direction (2d case) or to the z-direction (3d case) and the boundary datum satisfies \(\Vert h\Vert _{H^{1/2}(\partial Q)} <\chi \) and

$$\begin{aligned} h(x,-y)=h(x,y) \quad \text {(2d case)} \quad \text {or} \quad h(x,y,-z)=h(x,y,z) \quad \text {(3d case)} \quad \text {on} \ \ \partial Q, \end{aligned}$$

then the fluid exerts no lift force on the obstacle, that is, \(\mathcal {L}_{K}(u,p)=0\).

Note that the symmetry assumption on the inflow is satisfied by a Poiseuille flow but not by a Couette flow, see (3.4) and (3.2) below. Proposition 2.1 is equally valid if we drop the continuity assumption on h; this assumption is put only for compatibility with the remaining parts of the paper. From [20] we know that the constant \(\chi \) in Proposition 2.1 depends on:

  • the viscosity \(\eta \), with \(\eta \mapsto \chi (\eta )\) being increasing;

  • the geometric measures L, a, b, that modify the embedding constants for \(H_{*}^{1}(\Omega ),H_{0}^{1}(\Omega )\subset L^{4}(\Omega )\);

  • the constant \(\Gamma \) describing the size of the solenoidal extension, see Theorem 2.1.

In [20] the Authors merely considered constant inflows and gave explicit bounds on \(\chi \). The main novelty of the present paper is that we also handle more general inflow–outflow problems and still ensure that no lift force is exerted on the obstacle, as in Proposition 2.1.

3 An extension result and two new inflow–outflow models

We decompose \(\partial Q\) as the union of its \((d-1)\)-dimensional faces, that we name in dimension \(d=2\) by

$$\begin{aligned} \Sigma _{1}= & {} \partial Q \cap \{x=L\} , \ \quad \Sigma _{2} = \partial Q \cap \{y =L\}, \ \quad \Sigma _{3} = \partial Q \cap \{x=-L\}, \ \quad \\ \Sigma _{4}= & {} \partial Q \cap \{y= -L\}, \end{aligned}$$

and in dimension \(d= 3\) by

$$\begin{aligned} \begin{array}{lll} \Sigma _{1} = \partial Q \cap \{x=L\} , \quad &{} \Sigma _{2} =\partial Q \cap \{y =L\}, \quad &{} \Sigma _{3} = \partial Q \cap \{x=-L\}, \\ \Sigma _{4} = \partial Q \cap \{y= -L\}, \quad &{} \Sigma _{5} = \partial Q \cap \{z=L\}, \quad &{} \Sigma _{6} = \partial Q \cap \{z=-L\}. \end{array} \end{aligned}$$

We point out that, while in the 2d case we numbered the faces of \(\partial Q\) counterclockwise, in the 3d case we kept this ordering and simply added the two extra faces in the z-direction. Then, denoting by \(h _i \) the restriction of h to \(\Sigma _i\), the continuity of h at the vertices of Q in dimension 2 and at the edges of Q in dimension 3 reads

$$\begin{aligned} h _ i = h _ j \quad \text { on } \ \Sigma _i \cap \Sigma _j \,, \quad \forall i ,j \in \{1,\dots ,d\} \,. \end{aligned}$$
(3.1)

Aim of this section is to construct a vector field \(A_1\) as in Step 1 of the outline, namely, a vector field \(A_{1} \in H^{1}(Q)\cap \mathcal {C}(\overline{Q})\) such that \(A_{1} |_{\partial Q} =h\). We point out that, if the boundary datum is not solenoidal, then the construction of a solenoidal extension to \(\Omega _{0}\) cannot be performed merely by the use of cutoff functions and it is therefore necessary to extend it first to \(\overline{Q}\). In view of the special choice of the geometry, such extension can be explicitly found by taking the convex combination of the boundary datum on opposite faces of \(\partial Q\).

Theorem 3.1

Let h satisfy assumptions (2.1).

  • For \(d= 2\), the function \(A_{1} \in H^{1}(Q)\cap \mathcal {C}(\overline{Q})\) defined on \( \overline{Q}\) by

    $$\begin{aligned} \begin{aligned} A_{1}(x,y)&= \dfrac{L+x}{2L} h_{1}(y) + \dfrac{L-x}{2L} h_{3}(y) \\&\quad + \dfrac{L+y}{2L} \left[ h_{2}(x) - \dfrac{L+x}{2L} h_{2}(L) - \dfrac{L-x}{2L} h_{2}(-L) \right] \\&\quad + \dfrac{L-y}{2L} \left[ h_{4}(x) - \dfrac{L+x}{2L} h_{4}(L) - \dfrac{L-x}{2L} h_{4}(-L) \right] \end{aligned} \end{aligned}$$

    is an extension of h to \({\overline{Q}}\), whose \(H ^1\)-norm on Q can be explicitly computed in terms of the \(H ^1\)-norm of the functions \(h _i\) on \(\Sigma _i\), for \(i = 1, \dots , 4\).

  • For \(d = 3\), assuming in addition that h vanishes at the vertices of Q, the function \(A_{1}\in H^{1}(Q)\cap \mathcal {C}(\overline{Q})\) defined on \(\overline{Q}\) by

    $$\begin{aligned} \begin{aligned} A_{1}(x,y)&= \dfrac{L+x}{2L} h_{1}(y,z) + \dfrac{L-x}{2L} h_{3}(y,z) \\&\quad + \dfrac{L+y}{2L} \left[ h_{2}(x,z) - \dfrac{L+x}{2L} h_{2}(L,z) - \dfrac{L-x}{2L} h_{2}(-L,z) \right]&\quad \\&\quad + \dfrac{L-y}{2L} \left[ h_{4}(x,z) - \dfrac{L+x}{2L} h_{4}(L,z) - \dfrac{L-x}{2L} h_{4}(-L,z) \right] \\&\quad + \dfrac{L+z}{2L} \left[ h_{5}(x,y) - \dfrac{L+x}{2L} h_{5}(L,y) - \dfrac{L-x}{2L} h_{5}(-L,y) \right. \\&\quad \left. - \dfrac{L+y}{2L} h_{5}(x,L) - \dfrac{L-y}{2L} h_{5}(x,-L) \right] \\&\quad + \dfrac{L-z}{2L} \left[ h_{6}(x,y) - \dfrac{L+x}{2L} h_{6}(L,y) - \dfrac{L-x}{2L} h_{6}(-L,y) \right. \\&\quad \left. - \dfrac{L+y}{2L} h_{6}(x,L) - \dfrac{L-y}{2L} h_{6}(x,-L) \right] \end{aligned} \end{aligned}$$

    is an extension of h to \({\overline{Q}}\), whose \(H ^1\)-norm on Q can be explicitly computed in terms of the \(H ^1\)-norm of the functions \(h _i\) on \(\Sigma _i\), for \(i = 1, \dots , 6\).

Proof

The proof follows by computing \(A_1\) on \(\partial Q\), taking into account conditions (3.1) . \(\square \)

In order to highlight the relevance of Theorem 3.1, we introduce here two new inflow–outflow models in which the boundary velocity is not solenoidal. In the 2d case we suggest a model for a turbulent flow, whereas in the 3d case we suggest a model for an “almost laminar” flow. We emphasize that these models should not be interpreted as a precise description of turbulent or laminar flows in a channel. They merely serve as possible boundary data to be prescribed in inflow–outflow problems, showing a new level of complexity that can be treated by the methods presented in this article.

A 2d-model for a turbulent flow. In the planar domain \(\Omega _{0}\), we consider an inflow of Couette type and an outflow of “modified Couette” type. More precisely, for some \(\lambda \gg 1\) and \(\alpha , \tau > 0\), we take the boundary datum \(h : \partial \Omega _{0} \longrightarrow {\mathbb {R}}^2\) as

$$\begin{aligned} h= & {} 0 \ \text { on } \Sigma _ 4 \cup \partial K \, ; \quad h(x,L)= \left( \begin{array}{c} 2\lambda L\\ 0 \end{array}\right) \ \ \forall |x|\le L\, ; \quad \nonumber \\ h(-L,y)= & {} \left( \begin{array}{c} \lambda (y+L)\\ 0 \end{array}\right) \ \ \forall |y|\le L; \nonumber \\ h(L,y)= & {} \left( \begin{array}{c} \lambda (y+L)\\ g(y) \end{array}\right) \ \ \ \forall |y|\le L, \quad \text{ where } \quad g(y)=\left\{ \begin{array}{ll} 0 &{} \text{ if } |y|>b\\ \tau |y|^{\alpha } \sin \left( \dfrac{\pi b}{\sqrt{|y|}} \right) &{} \text{ if } |y|<b\, . \end{array}\right. \nonumber \\ \end{aligned}$$
(3.2)

Conditions (3.2) aim to model the behavior of the wind on the deck of a bridge, with no-slip condition on the boundary of the bridge and on the floor, see (3.2)\(_1\). Indeed, it is well-known that there is no wind at the ground level (at \(y=-L\)) and the velocity of the wind increases with altitude, reaching a maximum strength at \(y=L\), see (3.2)\(_2\)–(3.2)\(_3\). Moreover, this law is linear and, at high altitude, the wind is very strong (large \(\lambda \)). The datum is assumed to be regular on the inflow edge \(x = - L\), then the flow becomes turbulent after bypassing the obstacle K (see Fig. 1 for the illustration of an experiment), and it regularizes only partially on the outflow edge \(x = L\), as in (3.2)\(_4\): in the wake of the obstacle, the flow oscillates as \(y\rightarrow 0\), more quickly but with decreasing amplitude towards the center of the outflow edge. The intensity of the turbulent motion is measured by the positive parameter \(\tau \).

The boundary datum h defined in (3.2) satisfies the assumptions in (2.1), and hence it admits a solenoidal extension. The intermediate (non-solenoidal) extension given by Theorem 3.1 reads

$$\begin{aligned} A_1(x,y)=\left( \begin{array}{c} \lambda (y+L)\\ \dfrac{L+x}{2L}\, g(y) \end{array}\right) \quad \forall (x,y)\in \overline{Q}\, . \end{aligned}$$
(3.3)

The vector and stream plots of the field \(A_1\) on \(\overline{Q}\) (without the obstacle) are displayed in Fig. 4, for \(L=1\), \(a=0.7\), \(b=0.5\), \(\lambda =3\), \(\alpha =0.1\) and \(\tau =10\).

Fig. 4
figure 4

Vector plot (left) and stream plot (right) of the field \(A_{1}\) defined in (3.3)

Full size image

A 3d-model for an “almost-laminar” flow. In the 3d domain \(\Omega _{0}\), we consider an inflow of Poiseuille type and an outflow of “modified Poiseuille” type, namely we take the datum \(h : \partial \Omega _{0} \longrightarrow {\mathbb {R}}^3\) as

$$\begin{aligned} h= & {} 0 \ \ \text{ on } \ \ \Sigma _{2} \cup \Sigma _{4} \cup \Sigma _{5} \cup \Sigma _{6} \cup \partial K \, ; \quad \nonumber \\ h(-L,y,z)= & {} \left( \begin{matrix} 2L^2 - y^2 - z^2 \\ 0\\ 0 \end{matrix}\right) \quad \forall (y,z) \in [-L,L]^2\,;\nonumber \\ h(L,y,z)= & {} \left( \begin{matrix} 2L^2-y^2-z^2\\ \dfrac{y(y^2-L^2)(z^2-L^2)}{L^4}\\ \dfrac{z(y^2-L^2)(z^2-L^2)}{L^4} \end{matrix}\right) \quad \forall (y,z) \in [-L,L]^2\,. \end{aligned}$$
(3.4)

Condition (3.4)\(_2\) aims at representing a regular inflow, which is expected to slightly modify after by-passing the obstacle, but then tends to recompose at the outflow face, as in (3.4)\(_3\) (see [6] for experimental evidence). In fact, in a wind tunnel, the inflow is generated by a turbine (see the left picture in Fig. 5), which usually reproduces a Poiseuille flow, which is faster at the midpoint of the inflow face and vanishes on its edges as modeled by (3.4)\(_2\).

If the inflow is sufficiently small, the motion of the fluid remains almost laminar. It is then reasonable to consider an outflow which tends to redistribute regularly also in the wake of the obstacle: this is the reason why in (3.4)\(_3\) the flow is oriented towards the center of the outlet (see Fig. 5 on the right). The vector field h given by (3.4)\(_2\)–(3.4)\(_3\) is also represented in 3d in the left picture of Fig. 6. Finally, on the four remaining faces of the cube (the wind tunnel walls) and on the obstacle, the velocity is zero due to the viscosity, as in (3.4)\(_1\).

Fig. 5
figure 5

2d view of the inflow–outflow faces of the cube in the 3d model

Full size image
Fig. 6
figure 6

Left: 3d view of the inflow–outflow faces of the cube in the 3d model, for \(L=1\). Right: vector plot of the field \(A_{1}\) defined in (3.5) for \(L=1\)

Full size image

The boundary datum h defined in (3.4) satisfies the assumptions in (2.1), and hence it admits a solenoidal extension. Notice also that h vanishes at the vertices of the cube Q, as requested in (2.1). The (non-solenoidal) extension (3.4), given by Theorem, 3.1 reads

$$\begin{aligned} A_1 (x,y,z)=\left( \begin{matrix} 2L^2-y^2-z^2\\ \dfrac{x+L}{2L}\, \dfrac{y(y^2-L^2)(z^2-L^2)}{L^4}\\ \dfrac{x+L}{2L}\, \dfrac{z(y^2-L^2)(z^2-L^2)}{L^4} \end{matrix}\right) \quad \forall (x,y,z) \in \overline{Q}\,. \end{aligned}$$
(3.5)

The vector plot of the field \(A_1\) on Q is displayed in Fig. 6 right, for \(L=1\).

4 A Lipschitz function with gradient of minimal \(L^\infty \)-norm

Aim of this section is to construct a scalar function \(\phi \) as in Step 2 of the outline.

  • For \(d = 2\), we denote by \(Q_+\) the intersection of Q with the first quadrant. Setting

    $$\begin{aligned} \gamma (x, y): = (L-a) y + (b-L) x + L ( a-b) \quad \forall (x,y) \in \mathbb {R}^2, \end{aligned}$$

    we decompose \(Q_+\) as \(Q _+ = {\mathcal {Q}}_0 \cup {\mathcal {Q}} _1 \cup {\mathcal {Q}} _2\), where

    $$\begin{aligned} {\mathcal {Q}} _0 := Q _+ \cap \overline{P},\quad {\mathcal {Q}} _1 := ( Q _+ {\setminus } \overline{P}) \cap \big \{\gamma \le 0 \},\quad {\mathcal {Q}} _2 := ( Q _+ {\setminus } \overline{P}) \cap \big \{ \gamma \ge 0 \big \}, \end{aligned}$$

    see Fig. 7 on the left. Then we define \(\phi \) on Q as the function given on \(Q_+\) by

    $$\begin{aligned} \phi (x, y) = {\left\{ \begin{array}{ll} 0 &{} \text{ if } (x, y) \in {\mathcal {Q}} _0 \\ 1-\frac{L-x}{L-a} &{} \text { if } (x, y) \in {\mathcal {Q}}_1 \\ 1-\frac{L-y}{L-b} &{} \text{ if } (x, y) \in {\mathcal {Q}} _2\,. \end{array}\right. } \end{aligned}$$
    (4.1)

    and extended by even reflection to the other quadrants. We have

    $$\begin{aligned} \Vert \phi \Vert _{L ^ \infty (Q)} = 1 \quad \text { and } \quad \Vert \nabla \phi \Vert _{L ^ \infty (Q)} = \max \Big \{ \frac{1}{L-a}, \frac{1}{L-b} \Big \} = \frac{1}{L-a} \,. \end{aligned}$$
    (4.2)

  • For \(d = 3\), we denote by \(Q_+\) the intersection of Q with the first octant. Setting

    $$\begin{aligned} \displaystyle \gamma _ 1 ( y, z):= & {} (L-c) y + ( b-L) z + L (c-b), \quad \\ \displaystyle \gamma _ 2 (x, z):= & {} (L-a) z + (c-L) x + L ( a-c),\\ \displaystyle \gamma _ 3 (x, y):= & {} (L-b) x + (a-L) y + L (b-a) \quad \forall (x,y,z) \in \mathbb {R}^3 \, , \end{aligned}$$

    we decompose \(Q_+\) as \(Q _+ = {\mathcal {Q}}_0 \cup {\mathcal {Q}} _1 \cup {\mathcal {Q}} _2 \cup {\mathcal {Q}} _ 3\), where (see Fig. 7 on the right)

    $$\begin{aligned} \begin{array}{ll} \displaystyle {\mathcal {Q}} _0 := Q _+ \cap {\overline{P}} \quad &{} \displaystyle {\mathcal {Q}} _1 := (Q _+ {\setminus } \overline{P}) \cap \big \{ \gamma _2 \le 0 \big \} \cap \big \{ \gamma _3 \ge 0 \big \} \\ \displaystyle {\mathcal {Q}} _2 := (Q _+ {\setminus } \overline{P}) \cap \big \{\gamma _1 \ge 0 \big \} \cap \big \{ \gamma _3 \le 0 \big \} \quad &{} \displaystyle {\mathcal {Q}} _3 := (Q _+ {\setminus } \overline{P}) \cap \big \{ \gamma _2 \ge 0 \big \} \cap \big \{ \gamma _1 \le 0 \big \} \, . \end{array} \end{aligned}$$

    Then we define \(\phi \) on Q as the function given on \(Q_+\) by

    $$\begin{aligned} \phi (x, y, z) := {\left\{ \begin{array}{ll} 0 &{} \text { if } (x, y, z) \in {\mathcal {Q}} _0 \\ 1- \frac{L-x}{L-a} &{} \text { if } (x, y, z) \in {\mathcal {Q}} _1 \\ 1 - \frac{L-y}{L-b} &{} \text{ if } (x, y, z) \in {\mathcal {Q}} _2 \\ 1 - \frac{L-z}{L-c} &{} \text{ if } (x, y, z) \in {\mathcal {Q}} _3 \end{array}\right. } \end{aligned}$$
    (4.3)

    and extended by even reflection to the other octants. We have

    $$\begin{aligned} \Vert \phi \Vert _{L ^ \infty (Q)} = 1 \quad \text { and } \quad \Vert \nabla \phi \Vert _{L ^ \infty (Q)} = \max \left\{ \frac{1}{L-a}, \frac{1}{L-b} , \frac{1}{L-c} \right\} = \frac{1}{L-a}.\nonumber \\ \end{aligned}$$
    (4.4)
Fig. 7
figure 7

Decomposition of \(Q_+\) into the regions \({\mathcal {Q}}_i\), in 2d (left) and in 3d (right)

Full size image

The next result shows that the norm of the function \(\phi \) in \(W ^ {1, \infty } (Q)\) is minimal in the class of functions in \(W ^ {1, \infty } (Q)\) which are equal to 1 on \(\partial Q\) and vanish on \({\overline{P}}\).

Theorem 4.1

The function \(\phi \) defined for \(d= 2\) by (4.1) and for \(d=3\) by (4.3) solves the variational problem

$$\begin{aligned} \min \Big \{ \Vert \nabla u \Vert _{ L ^\infty (\Omega _{0} ) } \ : \ u \in W ^ {1, \infty } ( \Omega _{0} ) \,, \ u = 1 \ \text { on } \ \partial Q \, ,\ u = 0 \ \text { on } \ \partial P \Big \} \,. \end{aligned}$$

Proof

Let w be the infinity-harmonic potential of \({\overline{P}}\) relative to Q, namely the unique viscosity solution to the boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _\infty w = 0, &{} \text {in}\ \Omega _{0},\\ w = 1, &{}\text {on}\ \partial Q,\\ w = 0, &{}\text {on}\ \partial P \, , \end{array}\right. } \end{aligned}$$
(4.5)

where \(\Delta _\infty \) denotes the infinity-Laplacian operator, defined for smooth functions u by

$$\begin{aligned} \Delta _\infty u\doteq D ^ 2 u \cdot \nabla u \cdot \nabla u \, . \end{aligned}$$

The existence and uniqueness of a viscosity solution to problem (4.5) is due to Jensen (see [25, Section 3]), who also proved that w has the following variational property (usually referred to as AML, i.e. absolutely minimizing Lipschitz extension): for every open bounded set \(A \subset \Omega _{0} \), and for every function \(v \in \mathcal {C} ({\overline{A}})\) such that \( v = w \) on \(\partial A\), it holds \(\Vert \nabla w \Vert _{L ^\infty (A)} \le \Vert \nabla v \Vert _{ L ^\infty (A)}\) (see also [11]). Then the statement of the theorem is equivalent to assert that

$$\begin{aligned} \Vert \nabla w \Vert _ {L ^\infty (\Omega _{0} ) } = \Vert \nabla \phi \Vert _ {L ^\infty (\Omega _{0} ) } \,. \end{aligned}$$
(4.6)

Since \(\phi = w\) on \(\partial \Omega _{0} \), the inequality \(\Vert \nabla w \Vert _ {L ^\infty (\Omega _{0} ) } \le \Vert \nabla \phi \Vert _ {L ^\infty (\Omega _{0} ) } \) follows directly from the AML property of w. To prove the converse inequality, we recall from [12, Proposition 9] that, if \(q\in \partial Q \) and \(p\in \partial P \) are two points such that \(|q-p| = \mathrm{dist}({\overline{P}}, \partial Q)\), then w is affine on the segment [q, p], and hence it agrees with the function \(\phi \) defined in (4.1)–(4.3). Therefore,

$$\begin{aligned} \Vert \nabla w \Vert _ {L ^\infty (\Omega _{0} )} \displaystyle\ge & {} \sup \left\{ \frac{|w (q) - w (p)| }{|q-p| } \ :\ q \in \partial Q , \ p \in \partial P\, , \ |q-p| = \mathrm{dist}({\overline{P}}, \partial Q) \right\} \\ \displaystyle= & {} \sup \left\{ \frac{|\phi (q) - \phi (p)| }{|q-p| } \ :\ q \in \partial Q , \ p \in \partial P\, , \ |q-p| = \mathrm{dist}({\overline{P}}, \partial Q) \right\} \\= & {} \Vert \nabla \phi \Vert _ {L ^\infty (\Omega _{0} ) } \,. \end{aligned}$$

This shows that \(\phi \) solves the variational problem and completes the proof. \(\square \)

5 An upper bound for the Bogovskii constant

Aim of this section is to construct a vector field \(A_3\) as in Step 3 of the outline. To that purpose, let us recall that the Bogovskii problem in \(\Omega _{0}\) consists in finding a positive constant C, depending only on \(\Omega _{0}\), such that

$$\begin{aligned} \forall g \in L ^ 2 _0 (\Omega _{0})\, , \ \exists v \in H_{0}^{1}(\Omega _{0}) \quad :\quad \nabla \cdot v=g \ \ \text {in} \ \ \Omega _{0} \quad \text { and } \quad \Vert \nabla v\Vert _{L^2(\Omega _{0})} \le C \Vert g\Vert _{L^2(\Omega _{0})}\, .\nonumber \\ \end{aligned}$$
(5.1)

The smallest among such positive constants C, that we denote by \(C_B (\Omega _{0})\), is the Bogovskii constant of \(\Omega _{0}\), see (2.4). We now provide an explicit upper bound for \(C _B (\Omega _{0})\). Notice that proving an inequality of the form \(C _B (\Omega _{0}) \le M\) is equivalent to proving that the claim in (5.1) holds true with \(C = M\). Let us introduce the following notation:

  • for \(d= 2\), we set

    $$\begin{aligned} \sigma _{2}= & {} \dfrac{(L-a)^2}{16 a(L+a)} \left[ (L+3a)(L+a-2b) - (L-a) \sqrt{(L+a-2b)^{2} + 8a(L+a)} \right] \nonumber \\&+\,3 L^2 - (a + b) L -a b , \nonumber \\ \gamma _{2}= & {} \dfrac{(L-a)^2}{8a(L+a)} \left[ (L+3a)(L+a-2b) - (L-a) \sqrt{(L+a-2b)^{2} + 8a(L+a)} \right] \nonumber \\&+\, 2L ^ 2 - 2(a+b) L + 2ab \,; \end{aligned}$$
    (5.2)

  • for \(d = 3\), we set

    $$\begin{aligned} \sigma _{3}= & {} 7 L^3 - (a + b + c) L^2 - (a b +a c + b c) L -a b c , \nonumber \\ \gamma _{3}= & {} 6 L^3- 2 (a + b + c) L^2 - 2 (a b + a c + b c) L+6 a b c \,. \end{aligned}$$
    (5.3)

We point out that \(\sigma _{d}= |\Omega _1| = |\Omega _2| \) and \(\gamma _{d} = |\Omega _1 \cap \Omega _2|\), where \(\Omega _1\) and \(\Omega _2\) are the two domains in which we subdivide \(\Omega _{0}\) in order to obtain Theorem 5.1 below, as outlined in Step 3 of Sect. 2.1. Note also that, while (5.3) is symmetric in a, b, c, this is not the case for (5.2): the reason is the different decomposition we performed in 2d and 3d (see Fig. 3). This will become fully clear after reading the proof given hereafter.

Theorem 5.1

There holds \(C _B (\Omega _{0}) \le M\), where the explicit value of the constant M is given below:

\(\bullet \) for \(d=2\), letting \(\sigma _{2}\) and \(\gamma _{2}\) be defined in (5.2),

$$\begin{aligned} M\doteq & {} 2 \sqrt{ 2 \left( 1 + \dfrac{8}{\gamma _{2}} (L^2 - ab) \right) } \Bigg [ 129.35 + \dfrac{143.86 \sqrt{\sigma _{2}}}{L-a} + \dfrac{45.36\sigma _{2}}{(L-a)^2} \\&+\, \dfrac{64L^{2}}{(L-a)^2} \left( 13.79 + \dfrac{7.28 \sqrt{\sigma _{2}}}{L-a} \right) ^{2} \Bigg ]^{1/2} \, ; \end{aligned}$$

  • for \(d = 3\), letting \(\sigma _{3}\) and \(\gamma _{3}\) be defined in (5.3),

    $$\begin{aligned} M\doteq & {} \sqrt{ 12 \left( 1 + \dfrac{16}{\gamma _{3}} (L^3 - abc) \right) } \Bigg [ 327.23 + \dfrac{445.17 \sqrt{\sigma _{3}}}{(L-a)^{3/2}} + \dfrac{153.85 \sigma _{3}}{(L-a)^3}\\&+\, \dfrac{144 L^{2}}{(L-a)^2} \left( 22.4 + \dfrac{15.79 \sqrt{\sigma _{3}}}{(L-a)^{3/2}} \right) ^{2} \Bigg ]^{1/2} . \end{aligned}$$

In order to prove Theorem 5.1, we need as a preliminary result the following estimate for the Bogovskii constant of a domain which is star-shaped with respect to a ball.

Proposition 5.1

Let \(\mathcal {O}\subset \mathbb {R}^d\) be a bounded domain which is star-shaped with respect to a ball \(\mathcal {B}\subset \mathcal {O}\) of radius \(r>0\). Then the following upper bound for the Bogovskii constant \(C_B ({\mathcal {O}})\) holds:

$$\begin{aligned} \left\{ \begin{aligned}&C_B ({\mathcal {O}}) \le 2 \Bigg [ 129.35 + \dfrac{71.93}{r} \sqrt{| \mathcal {O} |} + \dfrac{11.34}{r^2} | \mathcal {O} | + 2 \dfrac{\delta (\mathcal {O})^2}{r^2}\left( 13.79 + \dfrac{3.64}{r} \sqrt{| \mathcal {O} |} \right) ^{2} \Bigg ]^{1/2} \qquad \text {if} \ \ \ d=2, \\&C_B ({\mathcal {O}}) \le \sqrt{6} \Bigg [ 327.23 + \dfrac{157.92}{r^{3/2}} \sqrt{| \mathcal {O} |} + \dfrac{19.23}{r^3} | \mathcal {O} | + 3 \dfrac{\delta (\mathcal {O})^2}{r^2}\left( 22.4 + \dfrac{5.58}{r^{3/2}} \sqrt{| \mathcal {O} |} \right) ^{2} \Bigg ]^{1/2} \quad \text {if} \ \ \ d=3, \end{aligned} \right. \end{aligned}$$

where \(|{\mathcal {O}}|\) and \(\delta (\mathcal {O})\) denote, respectively, the Lebesgue measure and the diameter of \(\mathcal {O}\).

Proof

After a translation we may assume that the ball \(\mathcal {B}\) is centered at the origin of \(\mathbb {R}^d\). Let \(\omega _{d} \in \mathcal {C}^{\infty }_{0}(\mathbb {R}^{d})\) be the standard radial mollifier whose support coincides with \(\mathcal {B}\), that is,

$$\begin{aligned} \omega _{2}(x,y) = \left\{ \begin{aligned}&\dfrac{\ell _2}{r^{2}} \exp \left( \dfrac{r^2}{x^2 + y^2 - r^2} \right) \, \, \, \,&\text {if} \ \ x^2 + y^2 < r^2, \\&0&\text {if} \, \, x^2 + y^2 \ge r^2, \end{aligned} \right. \end{aligned}$$
(5.4)

and

$$\begin{aligned} \omega _{3}(x,y,z) = \left\{ \begin{aligned}&\dfrac{\ell _3}{r^{3}} \exp \left( \dfrac{r^2}{x^2 + y^2 + z^2 - r^2} \right) \, \, \, \,&\text {if} \ \ x^2 + y^2 + z^2 < r^2, \\&0&\text {if} \ \ x^2 + y^2 + z^2 \ge r^2. \end{aligned} \right. \end{aligned}$$
(5.5)

In (5.4)–(5.5), \(\ell _{d} > 0\) is the normalization constant such that \(\Vert \omega _{d}\Vert _{L^1(\mathcal {B})} = 1\); hence,

$$\begin{aligned} \ell _{2}= & {} \left( 2\pi \int _0^1 t \, e^{1/(t^2-1)}dt\right) ^{-1}\approx 2.14357, \quad \nonumber \\ \ell _{3}= & {} \left( 4\pi \int _0^1 t^{2} e^{1/(t^2-1)}dt\right) ^{-1}\approx 2.26712. \end{aligned}$$
(5.6)

Given \(g \in L^{2}_0(\mathcal {O})\), Bogovskii [3] showed that a solution \(W \in H_{0}^{1}(\mathcal {O})\) of the problem \(\nabla \cdot W = g\) can be written as

$$\begin{aligned} W(\xi ) = \int \limits _{\mathcal {O}} \int \limits _{0}^{1} \dfrac{\xi - \xi '}{t^{3}}\, \omega _{d} \left( \xi ' + \dfrac{\xi - \xi '}{t} \right) g(\xi ') \ dt\,d\xi ' \ \ \ \ \ \forall \xi \in \mathbb {R}^{d}. \end{aligned}$$
(5.7)

Following [14], we differentiate (5.7) under the integral sign, and we interpret the partial derivatives of the field \(W= ( W ^ 1, \dots , W ^ d)\) as operators acting on the function g. In other words, for \(k,j \in \{1,\ldots ,d\}\),

$$\begin{aligned} \dfrac{\partial W^{k}}{\partial \xi _{j}}(\xi ) = T_{kj,1}(g)(\xi ) - T_{kj,2}(g)(\xi )\ \ \ \ \ \forall \xi \in \mathbb {R}^{d}\, , \end{aligned}$$
(5.8)

where, if g is extended by zero outside \(\mathcal {O}\),

$$\begin{aligned} \left\{ \begin{aligned}&T_{kj,1}(g)(\xi ) = \lim \limits _{\varepsilon \rightarrow 0} \int \limits _{\varepsilon }^{1} \int \limits _{\mathbb {R}^{d}} \dfrac{1}{t^{2}} \dfrac{\partial }{\partial \xi _{j}} \left[ \left( \xi '_{k} + \dfrac{\xi _{k} - \xi '_{k}}{t} \right) \omega _{d} \left( \xi ' + \dfrac{\xi - \xi '}{t} \right) \right] g(\xi ') \ dt\,d\xi ', \\&T_{kj,2}(g)(\xi ) = \lim \limits _{\varepsilon \rightarrow 0} \int \limits _{\varepsilon }^{1} \int \limits _{\mathbb {R}^{d}} \dfrac{\xi '_{k}}{t^{2}} \dfrac{\partial }{\partial \xi _{j}} \left[ \omega _{d} \left( \xi ' + \dfrac{\xi - \xi '}{t} \right) \right] g(\xi ') \ dt\,d\xi '\,. \end{aligned} \right. \end{aligned}$$

In view of (5.8), by applying Young’s inequality, we get

$$\begin{aligned} \Vert \nabla W \Vert ^{2}_{L^{2}(\mathcal {O})} \le 2 \left( \sum _{k,j=1}^{d} \left\| T_{kj,1}(g) \right\| ^{2}_{L^{2}(\mathcal {O})} + \sum _{k,j=1}^{d} \left\| T_{kj,2}(g) \right\| ^{2}_{L^{2}(\mathcal {O})} \right) . \end{aligned}$$
(5.9)

In order to estimate the right hand side of (5.9) we recall from [14, Theorem 3.1] that, for \(k,j \in \{1,...,d\}\),

$$\begin{aligned} \left\{ \begin{aligned}&\Vert T_{kj,1}(g) \Vert _{L^{2}(\mathcal {O})} \le \left( 2^{\frac{d-1}{2}} A_{kj} + 2^{\frac{d}{2}} \widetilde{A}_{kj} \sqrt{ | \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})}, \\&\Vert T_{kj,2}(g) \Vert _{L^{2}(\mathcal {O})} \le \delta (\mathcal {O}) \left( 2^{\frac{d-1}{2}} B_{kj} + 2^{\frac{d}{2}} \widetilde{B}_{kj} \sqrt{ | \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})} \,, \end{aligned} \right. \end{aligned}$$
(5.10)

where the constants \(A_{kj}\), \(\widetilde{A}_{kj}\), \(B_{kj}\) and \(\widetilde{B}_{kj}\) are explicitly given by

$$\begin{aligned} \left\{ \begin{aligned}&A_{kj} = \dfrac{1}{r} \Vert \xi _{k} \, \omega _{d} \Vert _{L^{1}(\mathcal {B})} + r \left\| \dfrac{\partial ^{2}}{\partial \xi ^{2}_{j}} (\xi _{k} \, \omega _{d}) \right\| _{L^{1}(\mathcal {B})} \ \ \ \ \widetilde{A}_{kj} = \left\| \dfrac{\partial }{\partial \xi _{j}} (\xi _{k} \, \omega _{d}) \right\| ^{\frac{1}{2}}_{L^{1}(\mathcal {B})} \left\| \dfrac{\partial }{\partial \xi _{j}} (\xi _{k} \, \omega _{d}) \right\| ^{\frac{1}{2}}_ {L^{\infty }(\mathcal {B})}, \\&B_{kj} = \dfrac{1}{r} \Vert \omega _{d} \Vert _{L^{1}(\mathcal {B})} + r \left\| \dfrac{\partial ^{2} \omega _{d}}{\partial \xi ^{2}_{j}} \right\| _{L^{1}(\mathcal {B})} \ \ \ \ \ \ \ \widetilde{B}_{kj} = \left\| \dfrac{\partial \omega _{d}}{\partial \xi _{j}} \right\| ^{\frac{1}{2}}_{L^{1}(\mathcal {B})} \left\| \dfrac{\partial \omega _{d}}{\partial \xi _{j}} \right\| ^{\frac{1}{2}}_ {L^{\infty }(\mathcal {B})}. \end{aligned}\right. \nonumber \\ \end{aligned}$$
(5.11)

At this point we distinguish between the cases \(d=2\) and \(d=3\):

  • For \(d=2\), the constants in (5.11) admit the following upper bounds (see Sect. 6.1):

    $$\begin{aligned} A_{11}= & {} A_{22}< 7.29, \ \ \ \ \ \ A_{12} = A_{21}< 3.39, \ \ \ \ \ \ \widetilde{A}_{11} = \widetilde{A}_{22}< \dfrac{1.19}{r}, \ \ \ \ \ \ \\ \widetilde{A}_{12}= & {} \widetilde{A}_{21}< \dfrac{0.66}{r},\nonumber \\ B_{11}= & {} B_{12} = B_{21} = B_{22}< \dfrac{9.75}{r}, \ \ \ \ \ \ \ \widetilde{B}_{11} = \widetilde{B}_{12} = \widetilde{B}_{21} = \widetilde{B}_{22} < \dfrac{1.82}{r^{2}}. \end{aligned}$$

    By inserting these values into (5.10) we obtain:

    $$\begin{aligned} \left\{ \begin{aligned}&\Vert T_{11,1}(g) \Vert _{L^{2}(\mathcal {O})} = \Vert T_{22,1}(g) \Vert _{L^{2}(\mathcal {O})} \le \left( 10.31 + \dfrac{2.38}{r} \sqrt{| \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})}, \\&\Vert T_{12,1}(g) \Vert _{L^{2}(\mathcal {O})} = \Vert T_{21,1}(g) \Vert _{L^{2}(\mathcal {O})} \le \left( 4.8 + \dfrac{2.38}{r} \sqrt{| \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})}, \\&\Vert T_{kj,2}(g) \Vert _{L^{2}(\mathcal {O})} \le \dfrac{\delta (\mathcal {O})}{r} \left( 13.79 + \dfrac{3.64}{r} \sqrt{| \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})} \ \ \ \ \ \ \text {for every} \ k,j \in \{1,2\}. \end{aligned} \right. \end{aligned}$$
    (5.12)

  • For \(d=3\), the constants in (5.11) admit the following upper bounds (see Sect. 6.2):

    $$\begin{aligned} \begin{aligned}&A_{11} = A_{22} = A_{33}< 7.57, \quad A_{12} = A_{13} = A_{21} = A_{23} = A_{31} = A_{32}< 3.5, \\&\widetilde{A}_{11} = \widetilde{A}_{22} = \widetilde{A}_{33}< \dfrac{1.21}{r^{3/2}}, \quad \widetilde{A}_{12} = \widetilde{A}_{13} = \widetilde{A}_{21} = \widetilde{A}_{23} = \widetilde{A}_{31} = \widetilde{A}_{32}< \dfrac{0.68}{r^{3/2}},\\&B_{11} = B_{21} = B_{31} = B_{12} = B_{22} = B_{32} = B_{13} = B_{23} = B_{33}< \dfrac{11.2}{r},\\&\widetilde{B}_{11} = \widetilde{B}_{21} = \widetilde{B}_{31} = \widetilde{B}_{12} = \widetilde{B}_{22} = \widetilde{B}_{32} = \widetilde{B}_{13} = \widetilde{B}_{23} = \widetilde{B}_{33} < \dfrac{1.97}{r^{5/2}}. \end{aligned} \end{aligned}$$

By inserting these values into (5.10) we obtain:

$$\begin{aligned} \left\{ \begin{aligned}&\Vert T_{11,1}(g) \Vert _{L^{2}(\mathcal {O})} = \Vert T_{22,1}(g) \Vert _{L^{2}(\mathcal {O})} = \Vert T_{33,1}(g) \Vert _{L^{2}(\mathcal {O})} \le \left( 15.14 + \dfrac{3.43}{r^{3/2}} \sqrt{| \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})}, \\&\Vert T_{kj,1}(g) \Vert _{L^{2}(\mathcal {O})} \le \left( 7 + \dfrac{1.93}{r^{3/2}} \sqrt{| \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})} \quad \text {for every} \ k,j \in \{1,2,3\}, \ k \ne j, \\&\Vert T_{kj,2}(g) \Vert _{L^{2}(\mathcal {O})} \le \dfrac{\delta (\mathcal {O})}{r} \left( 22.4 + \dfrac{5.58}{r^{3/2}} \sqrt{| \mathcal {O} |} \right) \Vert g \Vert _{L^{2}(\mathcal {O})} \ \ \ \ \ \ \text {for every} \ k,j \in \{1,2,3\}. \end{aligned} \right. \end{aligned}$$
(5.13)

Finally, the conclusion is obtained by inserting the estimates (5.12)–(5.13) into (5.9). \(\square \)

We are now in a position to give the

Proof of Theorem 5.1

We have to show that the claim in (5.1) is fulfilled if one takes C equal to the constant M defined in the statement. Thus, for a given \(g \in L ^ 2 _ 0 (\Omega _{0})\), we are going to construct a vector field \(v \in H ^ 1_0 (\Omega _{0})\) such that \(\nabla \cdot v = g\) in \(\Omega _{0} \), and \(\Vert \nabla v \Vert _{ L ^ 2 (\Omega _{0}) } \le M \Vert g \Vert _{L ^ 2 (\Omega _{0})}\). For the sake of clearness, we divide the procedure into four steps.

(1) Domain decomposition We write \(\Omega _{0} = \Omega _1 \cup \Omega _2\), where \(\Omega _1\) and \(\Omega _2\) are star-shaped with respect to some ball. Essentially, \(\Omega _{1}\) is the region lying above P which is “illuminated” by a ball placed in an upper corner of Q, while \(\Omega _{2}\) is the region lying below P which is “illuminated” by a ball placed in the opposite corner. To give a precise analytic description of these sets, we need to distinguish the cases \(d = 2\) and \(d = 3\), having in mind Fig. 3.

  • For \(d=2\), we denote by \(T(P_{1}; P_{2}; P_{3}) \subset \mathbb {R}^{2}\) the triangle with vertices \(P_{1}\), \(P_{2}\) and \(P_{3}\). We set

    \(\triangleright \):

    \(\Omega _ {1} \doteq [(-L,-a) \times (-L,L)] \cup [(-a,L) \times (b,L)] \cup T ((a,b); (L,b); (L, b - \alpha _{*}) )\). This domain is star-shaped with respect to the disk \(\left( x + \frac{L+a}{2} \right) ^2 + \left( y - \frac{L+a}{2} \right) ^2 < \left( \frac{L-a}{2} \right) ^2\), provided the point \((L, b - \alpha _{*})\) is defined as the intersection between the tangent line to such a disk through the vertex (a, b) and the line \(\{ x = L\}\). Some lengthy computations show that

    $$\begin{aligned} \alpha _{*} {=} \frac{L-a}{8a(L{+}a)} \left[ (L+3a)(L{+}a-2b) {-} (L-a) \sqrt{(L+a-2b)^{2} + 8a(L+a)} \right] \,. \end{aligned}$$

    Note in particular that \(\alpha _* \ge 0\) since \(a \ge b\).

    \(\triangleright \):

    \(\Omega _ {2} {\doteq } [(a,L) {\times } (-L,L)] {\cup } [(-L,a) {\times } (-L,-b)] {\cup } T ((-a,-b); (-L,-b); (-L, \alpha _{*}-b ))\), with \(\alpha _*\) defined as above. The domain \(\Omega _ {2}\) is star-shaped with respect to the disk \(\left( x - \frac{L+a}{2} \right) ^2 + \left( y + \frac{L+a}{2} \right) ^2 < \left( \frac{L-a}{2} \right) ^2\).

    Some tedious computations give

    $$\begin{aligned} | \Omega _{1} | = | \Omega _{2} |=\sigma _{2} \, , \quad | \Omega _{1} \cap \Omega _{2} | = \gamma _{2} \,, \end{aligned}$$
    (5.14)

    with \(\sigma _{2}\) and \(\gamma _{2}\) defined as in (5.2).

  • For \(d= 3\), in order to avoid too lengthy computations, we opt for a simpler decomposition: we set

    \(\triangleright \):

    \(\Omega _ {1} \doteq [(-L,L) \times (-L,L) \times (c,L)] \cup [(a,L) \times (-L,L) \times (-L,c)] \cup [(-L,a) \times (b,L) \times (-L,c)]\). This domain is star-shaped with respect to the ball

    $$\begin{aligned} \left( x - \dfrac{L+a}{2} \right) ^2 + \left( y - \dfrac{L+b}{2} \right) ^2 + \left( z - \dfrac{L+c}{2} \right) ^2 < \left( \dfrac{L-a}{2} \right) ^2. \end{aligned}$$
    \(\triangleright \):

    \(\Omega _ {2} \doteq [(-L,L) \times (-L,L) \times (-L,-c)] \cup [(-L,-a) \times (-L,L) \times (-c,L)] \cup [(-a,L) \times (-L,-b) \times (-c,L)]\). The domain \(\Omega _2\) is star-shaped with respect to the ball

    $$\begin{aligned} \left( x + \dfrac{L+a}{2} \right) ^2 + \left( y + \dfrac{L+b}{2} \right) ^2 + \left( z + \dfrac{L+c}{2} \right) ^2 < \left( \dfrac{L-a}{2} \right) ^2. \end{aligned}$$

    In this case, again via direct computations, we obtain

    $$\begin{aligned} | \Omega _{1} | = | \Omega _{2} |=\sigma _{3} \, , \quad | \Omega _{1} \cap \Omega _{2} | = \gamma _{3} \,. \end{aligned}$$
    (5.15)

    with \(\sigma _3\) and \(\gamma _3\) as in (5.3).

(2) Decomposition of the datum g We argue as in [4], see also [17, Lemma III.3.2 and Theorem III.3.1], and we decompose g as

$$\begin{aligned} g = g_1 + g_2 \ \ \text {in} \ \ \Omega _{0}, \ \ \ \ g_{1} \in L_{0}^{2}(\Omega _{1}) \ \text {s.t.} \ \text {supp}(g_{1}) \subset \overline{\Omega _{1}}, \ \ \ \ g_{2} \in L_{0}^{2}(\Omega _{2}) \ \text {s.t.} \ \text {supp}(g_{2}) \subset \overline{\Omega _{2}}. \end{aligned}$$

The functions \(g_{1}, g_ {2} : \Omega _{0} \longrightarrow \mathbb {R}\) are explicitly defined by

$$\begin{aligned} g_{1}(\xi )= & {} \left\{ \begin{array}{ll} g(\xi ) - \dfrac{\chi ^{*}(\xi )}{| \Omega _{1} \cap \Omega _{2} |} \displaystyle \int _{\Omega _{1}} g(\xi ') \,d\xi ' \ \ &{} \text {if} \ \xi \in \Omega _{1}, \\ 0 \ \ &{} \text {if} \ \xi \in \Omega _{2} {\setminus } \Omega _{1}, \end{array} \right. \\ g_{2}(\xi )= & {} \left\{ \begin{array}{ll} [1 - \chi ^{*}(\xi )]g(\xi ) - \dfrac{\chi ^{*}(\xi )}{| \Omega _{1} \cap \Omega _{2} |} \displaystyle \int _{\Omega _{2} {\setminus } \Omega _{1}} g(\xi ') \,d\xi ' \ \ &{} \text {if} \ \xi \in \Omega _{2}, \\ 0 \ \ &{} \text {if} \ \xi \in \Omega _{1} {\setminus } \Omega _{2}, \end{array} \right. \end{aligned}$$

where \(\chi ^{*}\) is the characteristic function of the set \(\Omega _{1} \cap \Omega _{2}\). We have

$$\begin{aligned} \Vert g_{1} \Vert _{L^{2}(\Omega _{0})} = \alpha _g\, ,\quad \Vert g_{2} \Vert _{L^{2}(\Omega _{0})} = \beta _g\, , \end{aligned}$$
(5.16)

where

$$\begin{aligned} \begin{aligned}&\alpha _{g} \doteq \left\{ \Vert g \Vert ^{2}_{L^{2}(\Omega _{1})} + \dfrac{1}{| \Omega _{1} \cap \Omega _{2} |} \left( \int _{\Omega _{1}} g(\xi )\,d\xi \right) \left[ \int _{\Omega _{1}} g(\xi )\,d\xi - 2 \int _{\Omega _{1} \cap \Omega _{2}} g(\xi )\,d\xi \right] \right\} ^{1/2} , \\&\beta _{g} \doteq \left\{ \Vert g \Vert ^{2}_{L^{2}(\Omega _{2} {\setminus } \Omega _{1})} + \dfrac{1}{| \Omega _{1} \cap \Omega _{2} |} \left( \int _{\Omega _{2} {\setminus } \Omega _{1}} g(\xi )\,d\xi \right) ^{2} \right\} ^{1/2}. \end{aligned} \end{aligned}$$
(5.17)

Notice that for every \(g \in L_{0}^{2}(\Omega _{0})\), we have

$$\begin{aligned} \int _{\Omega _{1}} g(\xi )\,d\xi + \int _{\Omega _{2} {\setminus } \Omega _{1}} g(\xi )\,d\xi = 0. \end{aligned}$$
(5.18)

In view of (5.18), and applying Jensen inequality, we get

$$\begin{aligned} \begin{aligned} \alpha _{g}^{2} + \beta _{g}^{2}&= \Vert g \Vert ^{2}_{L^{2}(\Omega _{0})} + \dfrac{2}{\gamma _{d}} \left( \int _{\Omega _{1}} g(\xi )\,d\xi \right) \left( \int _{\Omega _{1} {\setminus } \Omega _{2}} g(\xi )\,d\xi \right) \\&\le \Vert g \Vert ^{2}_{L^{2}(\Omega _{0})} + \dfrac{2}{\gamma _d} \left( \int _{\Omega _{0}} |g(\xi )| \,d\xi \right) ^2 \\&\le \left( 1 + \dfrac{2}{\gamma _{d}} |\Omega _{0}| \right) \, \Vert g \Vert ^{2}_{L^{2}(\Omega _{0})} \, , \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} \alpha _{g} + \beta _{g} \le \sqrt{ 2 \left( \alpha _ g ^ 2 + \beta _g ^ 2 \right) } \le \sqrt{2 \left( 1 + \dfrac{2}{\gamma _{d}} |\Omega _{0}| \right) } \, \Vert g \Vert _{L^{2}(\Omega _{0})}. \end{aligned}$$
(5.19)

(3) Solving two distinct Bogovskii problems We deal with the Bogovskii problem on each of the two domains \(\Omega _1\) and \(\Omega _2\).

  • For \(d=2\), we have \(r=\frac{L-a}{2}\) and \( \delta (\Omega _{1})=\delta (\Omega _{2})=2\sqrt{2}\, L\). By Proposition 5.1, there exist two vector fields \(v_{1} \in H_{0}^{1}(\Omega _{1})\) and \(v_{2} \in H_{0}^{1}(\Omega _{2})\) verifying, for \(k = 1, 2\),

    $$\begin{aligned}&\nabla \cdot v_{k} = g_{k} \quad \text {in} \quad \Omega _{k} \, , \\&\Vert \nabla v_{k} \Vert _{L^{2}(\Omega _{k})} \le 2 \Bigg [ 129.35 + \dfrac{143.86 \sqrt{\sigma _{2}}}{L-a} + \dfrac{45.36\sigma _{2}}{(L-a)^2} \\&\qquad \quad ~~~~~~~~~~~~~~~~+ \dfrac{64L^{2}}{(L-a)^2} \left( 13.79 + \dfrac{7.28 \sqrt{\sigma _{2}}}{L-a} \right) ^{2} \Bigg ]^{1/2} \Vert g_{k} \Vert _{L^{2}(\Omega _{k})}\,. \end{aligned}$$

  • For \(d= 3\), we have \(r=\frac{L-a}{2}\) and \( \delta (\Omega _{1})=\delta (\Omega _{2})= 2\sqrt{3}\, L \,.\) By Proposition 5.1, there exist two vector fields \(v_{1} \in H_{0}^{1}(\Omega _{1})\) and \(v_{2} \in H_{0}^{1}(\Omega _{2})\) verifying, for \(k = 1, 2\),

    $$\begin{aligned} \nabla \cdot v_{k} = g_{k} \quad \text {in} \quad \Omega _{k} \, , \end{aligned}$$

(4) Glueing and conclusion After extending both the fields \(v_{1}\) and \(v_{2}\) defined in Step 3 to zero, respectively outside \(\Omega _{1}\) and \(\Omega _{2}\), we infer that the vector field \(v_0\doteq v_1+v_2\in H_{0}^{1}(\Omega _{0})\), satisfies \(\nabla \cdot v _0 = g\) in \(\Omega _{0}\), along with the following bounds

  • For \(d= 2\),

    $$\begin{aligned} \Vert \nabla v_0 \Vert _{L^{2}(\Omega _{0})}\le & {} 2 \Bigg [ 129.35 + \dfrac{143.86 \sqrt{\sigma _{2}}}{L-a} + \dfrac{45.36\sigma _{2}}{(L-a)^2} \nonumber \\&+ \dfrac{64L^{2}}{(L-a)^2} \left( 13.79 + \dfrac{7.28 \sqrt{\sigma _{2}}}{L-a} \right) ^{2} \Bigg ]^{1/2} (\alpha _{g} + \beta _{g}). \end{aligned}$$
    (5.20)

  • For \(d = 3\),

    $$\begin{aligned} \Vert \nabla v_{0} \Vert _{L^{2}(\Omega _{0})}\le & {} \sqrt{6} \Bigg [ 327.23 + \dfrac{445.17 \sqrt{\sigma _{3}}}{(L-a)^{3/2}} + \dfrac{153.85 \sigma _{3}}{(L-a)^3} \nonumber \\&+ \dfrac{144 L^{2}}{(L-a)^2} \left( 22.4 + \dfrac{15.79 \sqrt{\sigma _{3}}}{(L-a)^{3/2}} \right) ^{2} \Bigg ]^{1/2} (\alpha _{g} + \beta _{g}). \end{aligned}$$
    (5.21)

The conclusion then follows by inserting (5.19) into (5.20) and (5.21). \(\square \)

6 Estimates for the norms of mollifiers

In this section we provide the computations leading to the estimates of the norms appearing in (5.11), that we have used in the proof of Proposition 5.1. We observe that the radial mollifier introduced in (5.4)–(5.5) can be rewritten as

$$\begin{aligned} \omega _{d}(\xi ) = \dfrac{\ell _{d}}{r^{d}} \, \omega _{0}\left( \dfrac{\xi }{r} \right) \quad \forall \xi \in \mathbb {R}^d, \end{aligned}$$

where \(\ell _{d} > 0\) is the normalization constant in (5.6), and \(\omega _{0} \in \mathcal {C}^{\infty }_{0}(\mathbb {R}^d)\) is the standard radial mollifier supported in the unit ball \(B_{0}\) of \(\mathbb {R}^d\), namely

$$\begin{aligned} \omega _{0}(\xi ) = \left\{ \begin{aligned}&\exp \left( \dfrac{1}{| \xi |^{2} - 1} \right) \, \, \,&\text {if} \ \ | \xi | < 1, \\&0&\text {if} \ \ | \xi | \ge 1. \end{aligned} \right. \end{aligned}$$

Thus, in order to compute all the norms appearing in (5.11), after writing the corresponding integrals over \(B(0,r) \subset \mathbb {R}^d\), via the change of variables \( \zeta = \xi / r \) we reduce ourselves to integrals over the unit ball \(B_{0} \subset \mathbb {R}^d\). These integrals are independent of r, and they can be easily computed numerically, yielding the following bounds.

6.1 2d case

Let \(\omega _{2}\) be the mollifier defined in (5.4), with \(\ell _{2} \approx 2.14357\).

  • Bounds for the norms of zeroth-order derivatives:

    $$\begin{aligned} \begin{aligned}&\Vert \omega _{2} \Vert _{L^{1}(\mathcal {B})} = 1; \ \ \ \ \ \Vert x\, \omega _{2} \Vert _{L^{1}(\mathcal {B})} = \Vert y\, \omega _{2} \Vert _{L^{1}(\mathcal {B})} = r \ell _{2} \Vert x\, \omega _{0} \Vert _{L^{1}(B_{0})} < 0.31r. \end{aligned} \end{aligned}$$

  • Bounds for the norms of first-order derivatives:

    $$\begin{aligned} \begin{aligned}&\left\| \dfrac{\partial \omega _{2}}{\partial x} \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial \omega _{2}}{\partial y} \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{2}}{r} \left\| \dfrac{\partial \omega _{0}}{\partial x} \right\| _{L^{1}(B_{0})}< \dfrac{1.91}{r};\\&\left\| \dfrac{\partial \omega _{2}}{\partial x} \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial \omega _{2}}{\partial y} \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{2}}{r^3} \left\| \dfrac{\partial \omega _{0}}{\partial x} \right\| _{L^{\infty }(B_0)}< \dfrac{1.72}{r^3}; \\&\left\| \dfrac{\partial }{\partial x} (x \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (y \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \ell _{2} \left\| \dfrac{\partial }{\partial x} (x \omega _{0}) \right\| _{L^{1}(B_{0})}< 1.18; \\&\left\| \dfrac{\partial }{\partial x} (x \omega _{2}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (y \omega _{2}) \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{2}}{r^2} \left\| \dfrac{\partial }{\partial x} (x \omega _{0}) \right\| _{L^{\infty }(B_{0})}< \dfrac{1.19}{r^2};\\&\left\| \dfrac{\partial }{\partial x} (y \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (x \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \ell _{2} \left\| \dfrac{\partial }{\partial x} (y \omega _{0}) \right\| _{L^{1}(B_{0})}< 0.64;\\&\left\| \dfrac{\partial }{\partial x} (y \omega _{2}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (x \omega _{2}) \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{2}}{r^{2}} \left\| \dfrac{\partial }{\partial x} (y \omega _{0}) \right\| _{L^{\infty }(B_{0})} < \dfrac{0.67}{r^2}. \end{aligned} \end{aligned}$$

  • Bounds for the norms of second-order derivatives:

    $$\begin{aligned}&\left\| \dfrac{\partial ^2 \omega _{2}}{\partial x^2} \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^2 \omega _{2}}{\partial y^2} \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{2}}{r^2} \left\| \dfrac{\partial ^2 \omega _{0}}{\partial x^2} \right\| _{L^{1}(B_{0})}< \dfrac{8.75}{r^2};\\&\left\| \dfrac{\partial ^{2} }{\partial x^{2}}(x \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial y^{2}}(y \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{2}}{r} \left\| \dfrac{\partial ^{2} }{\partial x^{2}}(x \omega _{0}) \right\| _{L^{1}(B_{0})}< \dfrac{6.98}{r};\\&\left\| \dfrac{\partial ^{2} }{\partial x^{2}}(y \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial y^{2}}(x \omega _{2}) \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{2}}{r} \left\| \dfrac{\partial ^{2} }{\partial x^{2}}(y \omega _{0}) \right\| _{L^{1}(B_{0})} < \dfrac{3.08}{r}. \end{aligned}$$

6.2 3d case

Let \(\omega _3\) be the mollifier defined in (5.5), with \(\ell _{3} \approx 2.26712\).

  • Bounds for the norms of zeroth-order derivatives:

    $$\begin{aligned} \Vert \omega _{3} \Vert _{L^{1}(\mathcal {B})} {=} 1; \ \ \ \ \ \Vert x\, \omega _{3} \Vert _{L^{1}(\mathcal {B})} = \Vert y\, \omega _{3} \Vert _{L^{1}(\mathcal {B})} = \Vert z\, \omega _{3} \Vert _{L^{1}(\mathcal {B})}= r \ell _{3} \Vert x\, \omega _{0} \Vert _{L^{1}(B_{0})} < 0.28r. \end{aligned}$$

  • Bounds for the norms of first-order derivatives:

    $$\begin{aligned}&\left\| \dfrac{\partial \omega _{3}}{\partial x} \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial \omega _{3}}{\partial y} \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial \omega _{3}}{\partial z} \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{3}}{r} \left\| \dfrac{\partial \omega _{0}}{\partial x} \right\| _{L^{1}(B_{0})}< \dfrac{2.12}{r};\\&\left\| \dfrac{\partial \omega _{3}}{\partial x} \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial \omega _{3}}{\partial y} \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial \omega _{3}}{\partial z} \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{3}}{r^4} \left\| \dfrac{\partial \omega _{0}}{\partial x} \right\| _{L^{\infty }(B_0)}< \dfrac{1.82}{r^4};\\&\left\| \dfrac{\partial }{\partial x} (x \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (y \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial z} (z \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \ell _{3} \left\| \dfrac{\partial }{\partial x} (x \omega _{0}) \right\| _{L^{1}(B_{0})}\\&\qquad \qquad \quad ~~~~~~~~~~~~~~~~~< 1.16;\\&\left\| \dfrac{\partial }{\partial x} (x \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (y \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial z} (z \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{3}}{r^3} \left\| \dfrac{\partial }{\partial x} (x \omega _{0}) \right\| _{L^{\infty }(B_{0})} \\&\qquad \qquad \quad ~~~~~~~~~~~~~ ~~~~~< \dfrac{1.26}{r^3};\\&\left\| \dfrac{\partial }{\partial x} (y \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial x} (z \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (x \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \ell _{3} \left\| \dfrac{\partial }{\partial x} (y \omega _{0}) \right\| _{L^{1}(B_{0})}\\&\qquad \qquad \quad ~~~~~~~~~~~~~~~~< 0.64;\\&\left\| \dfrac{\partial }{\partial y} (z \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial z} (x \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial }{\partial z} (y \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \ell _{3} \left\| \dfrac{\partial }{\partial x} (y \omega _{0}) \right\| _{L^{1}(B_{0})}\\&\qquad \qquad \quad ~~~~~~~~~~~~~~~~~< 0.64;\\&\left\| \dfrac{\partial }{\partial x} (y \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial x} (z \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial y} (x \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{3}}{r^{3}} \left\| \dfrac{\partial }{\partial x} (y \omega _{0}) \right\| _{L^{\infty }(B_{0})} \\&\qquad \qquad \quad ~~~~~~~~~~~~~~~~~< \dfrac{0.71}{r^{3}};\\&\left\| \dfrac{\partial }{\partial y} (z \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial z} (x \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \left\| \dfrac{\partial }{\partial z} (y \omega _{3}) \right\| _{L^{\infty }(\mathcal {B})} = \dfrac{\ell _{3}}{r^{3}} \left\| \dfrac{\partial }{\partial x} (y \omega _{0}) \right\| _{L^{\infty }(B_{0})} \\&\qquad \qquad \quad ~~~~~~~~~~~~~~~~~~ < \dfrac{0.71}{r^{3}};\\ \end{aligned}$$

  • Bounds for the norms of second-order derivatives:

    $$\begin{aligned} \begin{aligned}&\left\| \dfrac{\partial ^2 \omega _{3}}{\partial x^2} \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^2 \omega _{3}}{\partial y^2} \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^2 \omega _{3}}{\partial z^2} \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{3}}{r^2} \left\| \dfrac{\partial ^2 \omega _{0}}{\partial x^2} \right\| _{L^{1}(B_{0})}\\&\quad ~~~~~~~~~~~~~~~~~~~~~~~~< \dfrac{10.22}{r^2};\\&\left\| \dfrac{\partial ^{2} }{\partial x^{2}}(x \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial y^{2}}(y \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial z^{2}}(z \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{3}}{r} \left\| \dfrac{\partial ^{2} }{\partial x^{2}}(x \omega _{0}) \right\| _{L^{1}(B_{0})} \\&\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~< \dfrac{7.29}{r};\\&\left\| \dfrac{\partial ^{2} }{\partial x^{2}}(y \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial x^{2}}(z \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial y^{2}}(x \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{3}}{r} \left\| \dfrac{\partial ^{2} }{\partial x^{2}}(y \omega _{0}) \right\| _{L^{1}(B_{0})} \\&\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~< \dfrac{3.22}{r}; \\&\left\| \dfrac{\partial ^{2} }{\partial y^{2}}(z \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial z^{2}}(x \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \left\| \dfrac{\partial ^{2} }{\partial z^{2}}(y \omega _{3}) \right\| _{L^{1}(\mathcal {B})} = \dfrac{\ell _{3}}{r} \left\| \dfrac{\partial ^{2} }{\partial x^{2}}(y \omega _{0}) \right\| _{L^{1}(B_{0})} \\&\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~< \dfrac{3.22}{r}. \end{aligned} \end{aligned}$$

7 Proof of Theorem 2.1

We proceed as outlined in Sect. 2.1. Firstly we denote by \(A_1 \in H^{1}(Q) \cap \mathcal {C}(\overline{Q})\) the extension of h to Q given by Theorem 3.1, so that the norm of \(A_1\) in \(H ^ 1 (Q)\) can be explicitly computed in terms of the restrictions of h to the \((d-1)\)-dimensional faces of Q. Secondly, we take the function \(\phi \in W^{1,\infty }(Q)\) defined as in Sect. 4 (by (4.1)–(4.3)), which satisfies in particular \(\phi = 1\) on \(\partial Q\) and \(\phi = 0\) in \({\overline{P}}\). Recall from (4.2) and (4.4) that, both for \(d=2\) and \(d= 3\),

$$\begin{aligned} \Vert \phi \Vert _{L ^ \infty (Q)} = 1 \quad \text { and } \quad \Vert \nabla \phi \Vert _{L ^ \infty (Q)} = \frac{1}{L-a} \,. \end{aligned}$$
(7.1)

The vector field \(A_{2} \doteq \phi A_{1}\), satisfies \(A_{2}=h\) on \(\partial Q\) and \(A_2 = 0\) in \({\overline{P}}\). Moreover, \(\nabla \cdot A_ 2 \in L^ 2_0 (\Omega _0)\), since (2.1) implies

$$\begin{aligned} \int _{\Omega _0} \nabla \cdot A_ 2 = \int _{\partial \Omega _0} A_2 \cdot {\hat{n}} = \int _{\partial Q} h \cdot {\hat{n}} = 0\,. \end{aligned}$$

Thirdly, let \(A_3 \in H_{0}^{1}(\Omega _{0})\) be the solution to Bogovskii’s problem with right-hand side given by \(-\nabla \cdot A_2\):

$$\begin{aligned} \nabla \cdot A_{3} = - \nabla \cdot A_2 \quad \text {and} \quad \Vert \nabla A_{3} \Vert _{L^{2}(\Omega _{0})} \le M \, \Vert \nabla \cdot A _2 \Vert _{L^{2}(\Omega _{0})}, \end{aligned}$$
(7.2)

where M is given by Proposition 5.1. Since

$$\begin{aligned} \nabla \cdot A _ 2 = \nabla \cdot (\phi A _1) = \phi (\nabla \cdot A_{1}) + \nabla \phi \cdot A_{1} \quad \text {in} \quad \Omega _{0}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} \Vert \nabla \cdot A_2 \Vert _{L^{2}(\Omega _{0})}&\le \Vert \phi (\nabla \cdot A_{1}) \Vert _{L^{2}(\Omega _{0})} + \Vert \nabla \phi \cdot A_{1} \Vert _{L^{2}(\Omega _{0})} \\&\le \Vert \phi \Vert _{L^{\infty }(\Omega _{0})} \, \Vert \nabla \cdot A_{1} \Vert _{L^{2}(Q)} + \Vert \nabla \phi \Vert _{L^{\infty }(\Omega _{0})} \, \Vert A_{1} \Vert _{L^{2}(Q)} \\ (\hbox {by}\,(7.1))&=\Vert \nabla \cdot A_{1} \Vert _{L^{2}(Q)} + \frac{1}{L-a} \, \Vert A_{1} \Vert _{L^{2}(Q)}\,. \end{aligned} \end{aligned}$$
(7.3)

We point out that the function \( \phi \) in (4.1) or (4.3) minimizes the second line in (7.3) and, in this respect, the choice of \(\phi \) is optimal thanks to Theorem 4.1. By construction, the function \(v_0 \doteq A_2 + A_3\) satisfies

$$\begin{aligned} v_0= & {} h \ \text { on } \partial Q\,, \quad v= 0 \ \text { on } \partial P \,, \quad \nabla \cdot v _0 = 0 \ \text { in } \Omega _0\, , \quad \\ \nabla v_{0}= & {} \nabla \phi \otimes A_1 + \phi \nabla A_1 + \nabla A_3 \ \text { in } \Omega _{0} \, . \end{aligned}$$

From (7.2) and (7.3) we derive the estimate

$$\begin{aligned} \begin{aligned} \Vert \nabla v_{0} \Vert _{L^{2}(\Omega _{0})}&\le \Vert \nabla \phi \otimes A_1 \Vert _{L^{2}(\Omega _{0})} + \Vert \phi \nabla A_1 \Vert _{L^{2}(\Omega _{0})} + \Vert \nabla A_3 \Vert _{L^{2}(\Omega _{0})} \\&\le \frac{1}{L-a} \, \Vert A_{1} \Vert _{L^{2}(Q)} + \Vert \nabla A_{1} \Vert _{L^{2}(Q)} \\&\quad + M \Big ( \Vert \nabla \cdot A_{1} \Vert _{L^{2}(Q)} + \frac{1}{L-a} \, \Vert A_{1} \Vert _{L^{2}(Q)} \Big ). \end{aligned} \end{aligned}$$
(7.4)

After extending it to zero to \(P {\setminus } \overline{K}\), \(v_0\) becomes a solution to problem (1.2). Indeed, it is clear that it matches the boundary condition \(v_0= h\) on \(\partial \Omega \), and that it is divergence free separately in \(\Omega {\setminus } P\) and in \(P {\setminus } K\). It is also readily checked that the equation \(\nabla \cdot v_0 = 0\) is satisfied in distributional sense in \(\Omega \) since, for every test function \(\psi \in {\mathcal {C}} ^ \infty _0 (\Omega )\), we have

$$\begin{aligned} \int _\Omega v _0 \cdot \nabla \psi= & {} \int _{Q {\setminus } P} v _0 \cdot \nabla \psi + \int _{P {\setminus } K} v _0 \cdot \nabla \psi = \int _{Q {\setminus } P} v _0 \cdot \nabla \psi \\= & {} - \int _{Q {\setminus } P} \psi (\nabla \cdot v _0 ) + \int _{\partial (Q {\setminus } P)} \psi ( v_0 \cdot \hat{n} ) = 0\,. \end{aligned}$$

Finally, we observe that the inequality (7.4) can be re-written as:

$$\begin{aligned} \Vert \nabla v_{0} \Vert _{L^{2}(\Omega )} = \Vert \nabla v_{0} \Vert _{L^{2}(\Omega _{0})} \le \frac{1 + M}{L-a} \, \Vert A_{1} \Vert _{L^{2}( Q)} + \Vert \nabla A_{1} \Vert _{L^{2}(Q)} + M \, \Vert \nabla \cdot A_{1} \Vert _{L^{2}(Q)} .\nonumber \\ \end{aligned}$$
(7.5)

By inserting (4.2)–(4.4) into (7.5), Theorem 2.1 is proved. \(\square \)