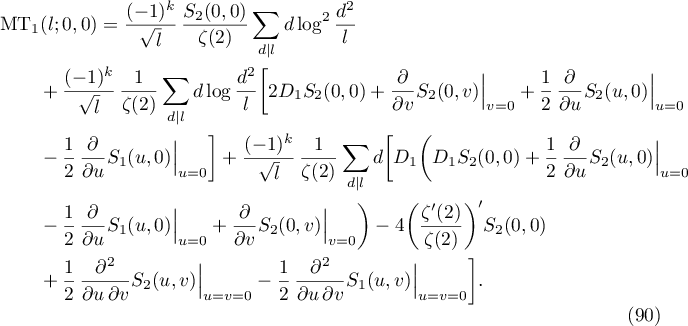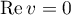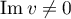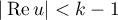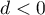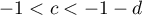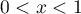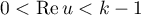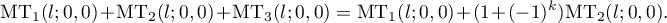Abstract
We investigate the exact formula for the second moment of central  -values associated to primitive cusp forms of level one and weight
-values associated to primitive cusp forms of level one and weight 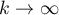 ,
,  , which was proved by Kuznetsov in 1994. Nondiagonal terms in this formula are expressed in terms of several convolution sums of divisor functions. We investigate the main terms of the convolution sums and show that they cancel out.
, which was proved by Kuznetsov in 1994. Nondiagonal terms in this formula are expressed in terms of several convolution sums of divisor functions. We investigate the main terms of the convolution sums and show that they cancel out.
Bibliography: 8 titles.
Export citation and abstract BibTeX RIS
| This research was carried out at Pacific National University and supported by the Russian Science Foundation under grant no. 18-41-05001. |
§ 1. Introduction
Let 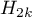 be the normalized Hecke basis of the space of holomorphic cusp forms of level one and weight
be the normalized Hecke basis of the space of holomorphic cusp forms of level one and weight  . For every function
. For every function  we can use the Fourier expansion
we can use the Fourier expansion
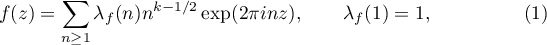
in order to define the associated  -function
-function
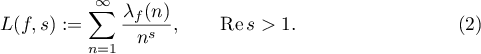
It is possible to construct an analytic continuation of 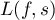 to the whole complex plane. The so-called completed
to the whole complex plane. The so-called completed  -function
-function
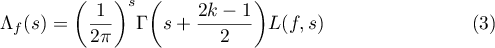
satisfies the functional equation
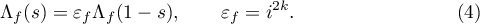
One of the central problems in the theory of  -functions is to determine the proportion of nonvanishing central
-functions is to determine the proportion of nonvanishing central  -values. Note that the functional equation (4) implies that
-values. Note that the functional equation (4) implies that  for all odd
for all odd  . Therefore, it is interesting to consider only even
. Therefore, it is interesting to consider only even  .
.
Nonvanishing results for central values of  -functions are not only of theoretical interest but also have important applications (see [1] for references). One of the most interesting examples of such applications (discovered by Iwaniec and Sarnak [5]) is the nonexistence of Landau-Siegel zeros for Dirichlet
-functions are not only of theoretical interest but also have important applications (see [1] for references). One of the most interesting examples of such applications (discovered by Iwaniec and Sarnak [5]) is the nonexistence of Landau-Siegel zeros for Dirichlet  -functions of real primitive characters.
-functions of real primitive characters.
The most common approach to nonvanishing problems is the method of moments. In particular, the given technique was used in [1] to prove that  of the
of the  -functions associated to holomorphic cusp forms of weight
-functions associated to holomorphic cusp forms of weight  and level one have nonzero central values. The proof is based on the following exact formula for the twisted second moment, which was first obtained by Kuznetsov (preprint 1994, see also [1], Theorem 4.2 for the proof) and independently proved by Iwaniec and Sarnak (see [5], Theorem 17).
and level one have nonzero central values. The proof is based on the following exact formula for the twisted second moment, which was first obtained by Kuznetsov (preprint 1994, see also [1], Theorem 4.2 for the proof) and independently proved by Iwaniec and Sarnak (see [5], Theorem 17).
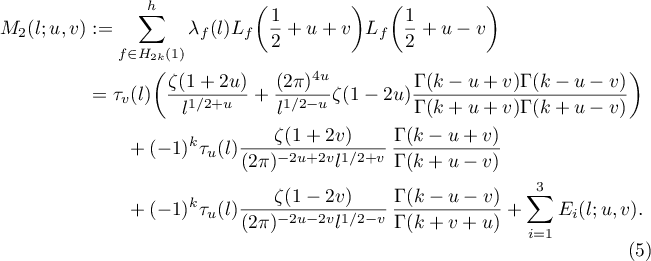
Each summand  can be expressed in terms of hypergeometric functions:
can be expressed in terms of hypergeometric functions:
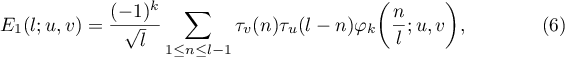
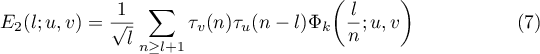
and
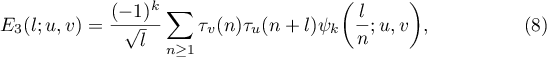
where
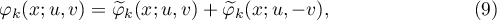
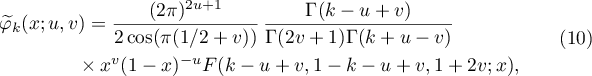
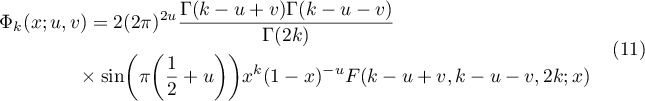
and
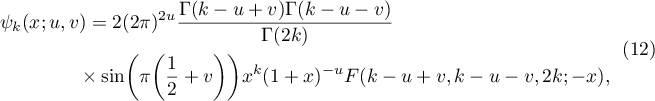
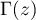 is the Gamma function,
is the Gamma function, 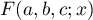 is the Gauss hypergeometric function ( definitions and properties of these functions can be found in [7], Chs. 5 and 15) and
is the Gauss hypergeometric function ( definitions and properties of these functions can be found in [7], Chs. 5 and 15) and
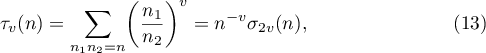
where 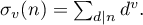
For simplicity, let 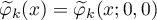 and
and  . Using the asymptotic expansions for
. Using the asymptotic expansions for 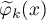 and
and 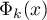 obtained in [1], §5, and then estimating the absolute values of everything in the error terms
obtained in [1], §5, and then estimating the absolute values of everything in the error terms 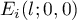 , the following formula was proved in [1], Theorem 6.4:
, the following formula was proved in [1], Theorem 6.4:
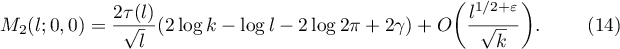
This is nontrivial for  . We observe that taking an additional smooth average over weight
. We observe that taking an additional smooth average over weight  , it is possible to obtain a nontrivial asymptotic formula for
, it is possible to obtain a nontrivial asymptotic formula for 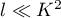 (see [1], Theorem 7.4, for details). Iwaniec and Sarnak [5] showed that a possible approach to demonstrate the nonexistence of Landau-Siegel zeros is to prove an asymptotic formula for the averaged twisted moment for
(see [1], Theorem 7.4, for details). Iwaniec and Sarnak [5] showed that a possible approach to demonstrate the nonexistence of Landau-Siegel zeros is to prove an asymptotic formula for the averaged twisted moment for  . In this sense,
. In this sense,  is a natural barrier caused by the behaviour of the corresponding special functions. Indeed, if
is a natural barrier caused by the behaviour of the corresponding special functions. Indeed, if 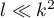 , then according to [1], Lemma 6.2, we have
, then according to [1], Lemma 6.2, we have
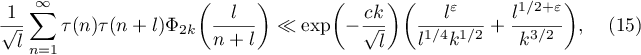
and thus the term  is negligibly small. For
is negligibly small. For  this term is no longer negligible. This is because for large
this term is no longer negligible. This is because for large  the function
the function  decays exponentially, but for
decays exponentially, but for 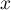 very close to 1 it does not (see [1], §5.3)! As a result, for
very close to 1 it does not (see [1], §5.3)! As a result, for  the left-hand side of (15) will not be negligible. Since
the left-hand side of (15) will not be negligible. Since  does not have oscillatory behaviour, even averaging over
does not have oscillatory behaviour, even averaging over  will not make
will not make  smaller. We show below that
smaller. We show below that
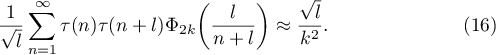
So it is reasonable to conjecture that there is a second main term in (14) for  . The problem is that this second main term is larger than the main term in (14). It might seem that this strange phenomenon makes it impossible to improve the
. The problem is that this second main term is larger than the main term in (14). It might seem that this strange phenomenon makes it impossible to improve the 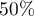 nonvanishing result due to Iwaniec and Sarnak, since, as it is shown in [3], the first moment does not change its behaviour for
nonvanishing result due to Iwaniec and Sarnak, since, as it is shown in [3], the first moment does not change its behaviour for  (note that when proving results on nonvanishing the twist in the second moment should grow as the square of the twist in the first moment). However, it is widely believed that the percentage of nonvanishing should be
(note that when proving results on nonvanishing the twist in the second moment should grow as the square of the twist in the first moment). However, it is widely believed that the percentage of nonvanishing should be 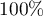 , and therefore it is reasonable to investigate the second main terms further.
, and therefore it is reasonable to investigate the second main terms further.
According to (5), there are three convolution sums (6)–(8). Each of them has the following form of a binary additive divisor problem:
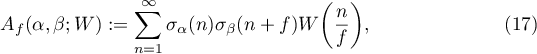
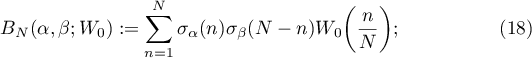
see [6], pp. 531 and 533. This problem has a long history and is very well studied (for references see [2]). An exact formula with a precise form of both the main term and the error term was discovered by Kuznetsov. In this paper we are interested only in the shape of the main terms. In the notation of [6], (4.9) and (4.29), we have
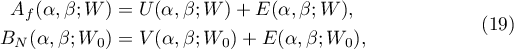
where 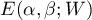 and
and 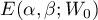 are error terms and
are error terms and
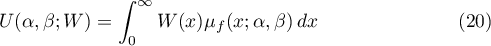
and
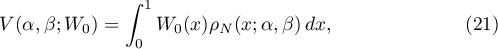
where
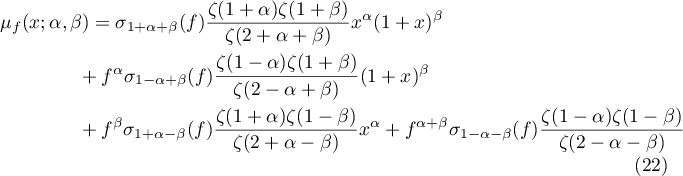
and
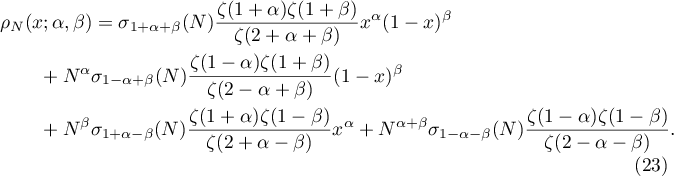
We conjecture that one can apply this result to each 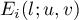 . For
. For  let
let
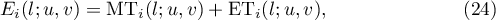
where 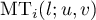 is the main term.
is the main term.
Conjecture 1.2. The main term 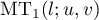 of the summand
of the summand 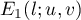 can be evaluated using (21). For
can be evaluated using (21). For 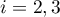 the main term
the main term 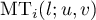 of
of 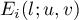 can be evaluated using (20).
can be evaluated using (20).
Assuming that this conjecture holds, it is possible to evaluate the predicted main term 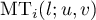 of each
of each 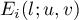 . Using the results of [6], it is also possible to evaluate the error terms, but we have not been successful in obtaining any reasonably good estimates for them. This is because the application of the results of [6] unfortunately leads to a dead loop by which we recover back the initial value of the second moment.
. Using the results of [6], it is also possible to evaluate the error terms, but we have not been successful in obtaining any reasonably good estimates for them. This is because the application of the results of [6] unfortunately leads to a dead loop by which we recover back the initial value of the second moment.
The main result of this paper is the following.
Theorem 1.3. Assuming Conjecture 1.2 we have
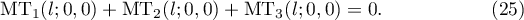
This theorem asserts that for large  there is no second main term in (14).
there is no second main term in (14).
§ 2. Special functions
For the convenience of the reader we first recall the definitions and some properties of the Gamma function and the Gauss hypergeometric function. These facts, among others, can be found in [7], Chs. 5 and 15, for example.
For  the Gamma function
the Gamma function 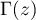 is defined by means of the Euler integral
is defined by means of the Euler integral
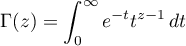
([7], 5.2.1). The Gamma function is a meromorphic function with simple poles at negative integers 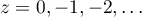 . This function satisfies the following functional equations:
. This function satisfies the following functional equations:
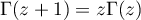
([7], 5.5.1) and
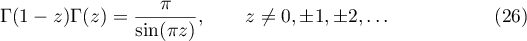
([7], 5.5.3). For  one can define the psi-function
one can define the psi-function 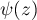
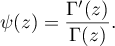
This is a meromorphic function with simple poles at the nonpositive integers 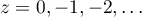 . The psi-function satisfies the following functional equation:
. The psi-function satisfies the following functional equation:

(see [7], 5.5.2). For 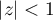 the Gauss hypergeometric function is defined by the absolutely convergent series
the Gauss hypergeometric function is defined by the absolutely convergent series
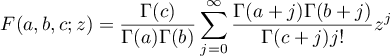
(see [7], 15.2.1). This function can be continued analytically to the whole complex plane. In the case of 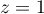 and
and 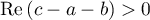 the Gauss hypergeometric function can be evaluated in terms of Gamma functions:
the Gauss hypergeometric function can be evaluated in terms of Gamma functions:
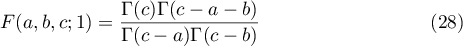
(see [7], 15.4.20).
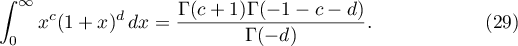
For  the following identity holds:
the following identity holds:
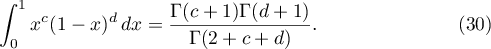
Equation (29) follows from [7], 5.12.3. To prove (30) we apply [7], 5.12.1.
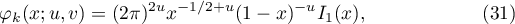
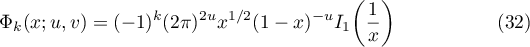
and
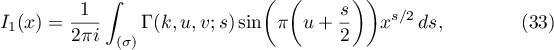
where 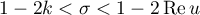 and
and
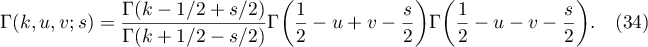
Proof. It follows from [1], (4.15), that

where
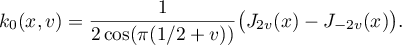
In the same way, we obtain
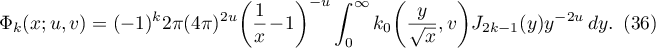
Using [4], Lemma 5.7, to transform the right-hand sides of (35) and (36), we show that
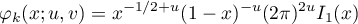
and
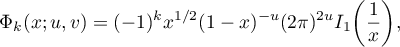
where  is defined in [4], §5, and coincides with (33). The lemma is proved.
is defined in [4], §5, and coincides with (33). The lemma is proved.
§ 3. Evaluating the main term of 
Replacing the function 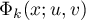 in (7) by (32) and using (13) we obtain
in (7) by (32) and using (13) we obtain
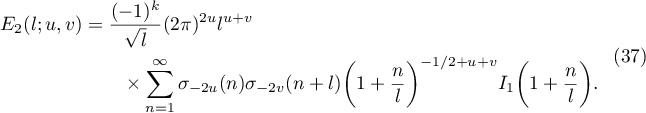
Assuming Conjecture 1.2, the main term 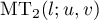 of (37) is given by
of (37) is given by
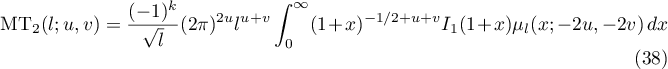
(see (17), (19) and (20)). Let
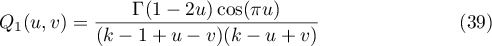
and
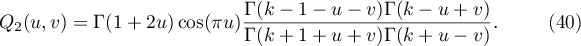
Lemma 3.1. The following identity holds:
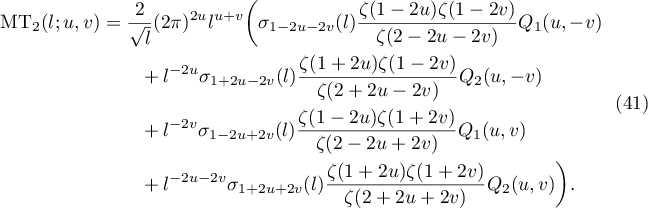
Proof. To prove the lemma we substitute (33) and (22) into (38). In doing so we obtain four similar terms: each of them can be evaluated in the same way. We consider the first and second terms. The first term is given by
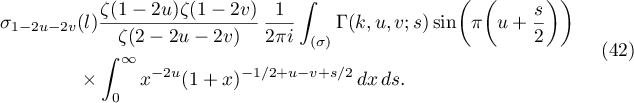
To evaluate the integral with respect to  we apply (29), getting
we apply (29), getting
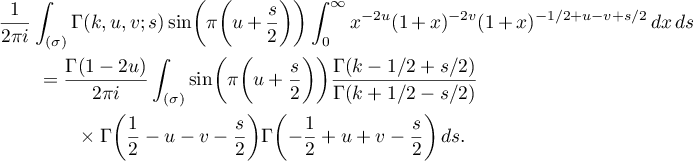
Moving the line of integration to the left and evaluating the residues at 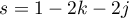 for
for 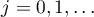 , we infer
, we infer
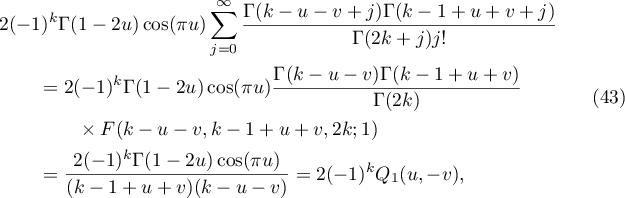
where (28) was used to evaluate the hypergeometric function. Substituting (43) into (42), we obtain the first term in (41).
Let us briefly describe how the second term in (41) can be obtained. In this case, we need to compute
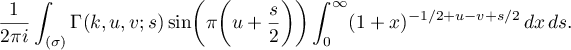
To evaluate the integral with respect to 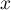 we apply (29). Consequently,
we apply (29). Consequently,
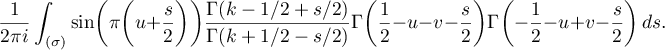
Moving the line of integration to the left and evaluating the residues at 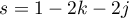 for
for 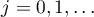 , we show that
, we show that
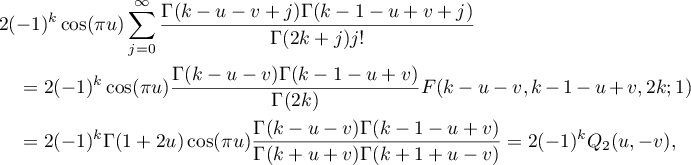
where (28) was used to compute the hypergeometric function. The lemma is proved.
Our next goal is to evaluate 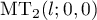 using (41). To this end, we need to study the properties of
using (41). To this end, we need to study the properties of 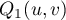 and
and 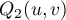 .
.
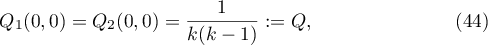
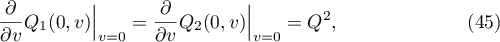
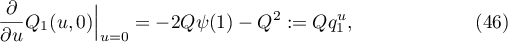
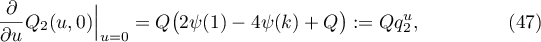
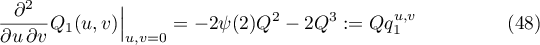
and
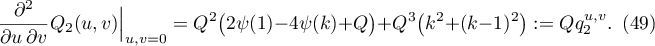
Proof. It follows from (39) that
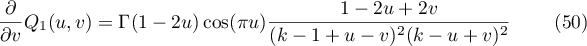
and
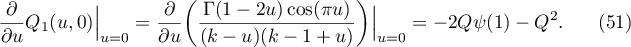
Thus (46) and a part of (45) are proved. Computing the derivative of (50) with respect to  , we prove (48).
, we prove (48).
Formula
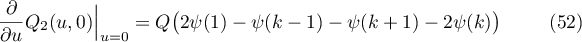
follows immediately from (40). Since 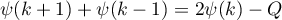 (see (27)), we prove (47).
(see (27)), we prove (47).
Also as a consequence of (40) we have

Letting 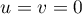 on the right-hand side of (53), we show that
on the right-hand side of (53), we show that
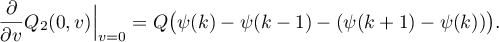
Since 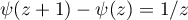 (see (27)), we complete the proof of (45). Letting
(see (27)), we complete the proof of (45). Letting  in (53) and then computing the derivative of (53) with respect to
in (53) and then computing the derivative of (53) with respect to  , we obtain
, we obtain
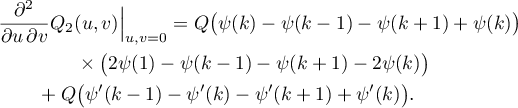
Since 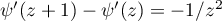 , we finally prove (49). The lemma is proved.
, we finally prove (49). The lemma is proved.
Let
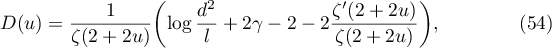

and
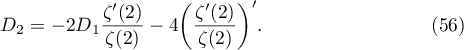
Then
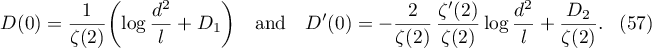
Now we are ready to evaluate  using (41).
using (41).
Theorem 3.3. The following formula holds:
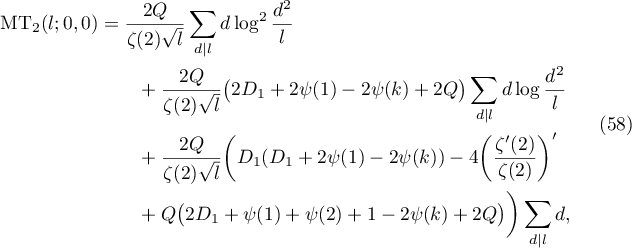
where 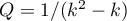 and
and 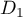 is defined in (55).
is defined in (55).
Proof. First, we continue (41) analytically to a region containing  . To do this, we rewrite (41) in the following form
. To do this, we rewrite (41) in the following form
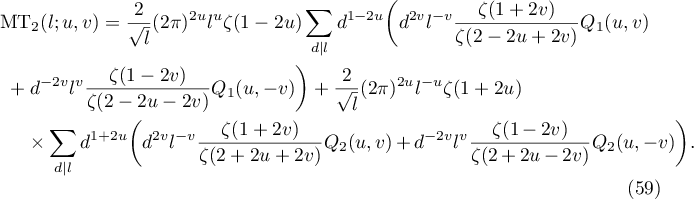
The next step is to evaluate the limits of two brackets in (59) as 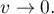 To this end, we use the Laurent expansion of the Riemann zeta-function
To this end, we use the Laurent expansion of the Riemann zeta-function
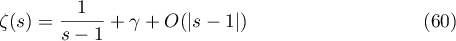
(see [7], 25.2.4). We compute the limit of the first bracket in (59). Using (60), we obtain that it is equal to
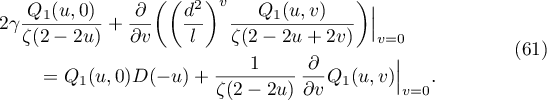
Using (59) and (61), we show that
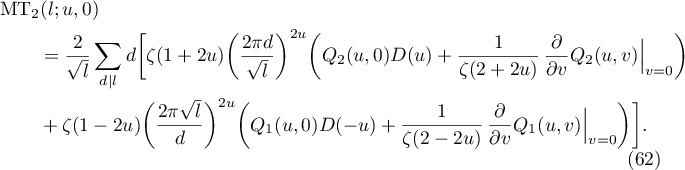
We need to verify that the right-hand side of (62) is holomorphic at  . For this goal, it is enough to check that
. For this goal, it is enough to check that
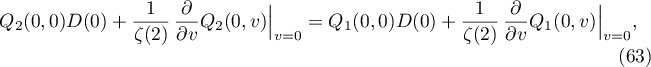
which follows from (44) and (45). Applying L'Hôpital's rule and (60), we compute the limit of the right-hand side of (62) at  :
:

Evaluating the derivative, using (63) and making some transformations, we obtain
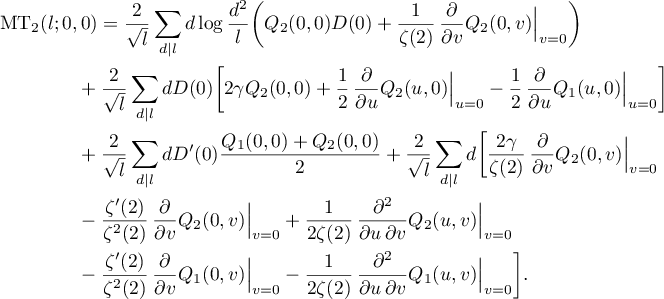
Substituting (57) and using (44) and (45), we conclude that
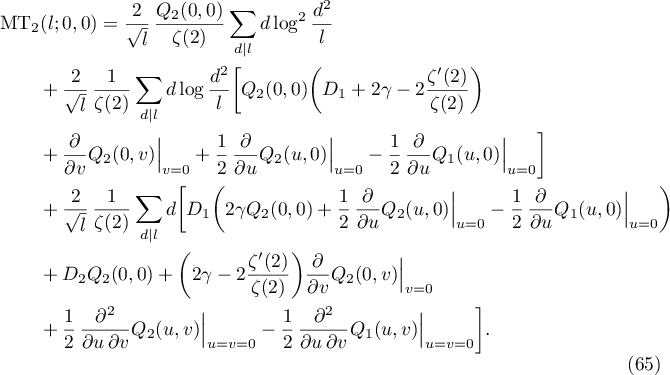
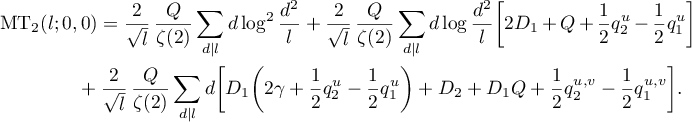
Substituting (55), (56) and (46)–(49), we finally prove (58). Theorem 3.3 is proved.
§ 4. Evaluating the main term of 
Substituting (31) into (6) and using (13), we have
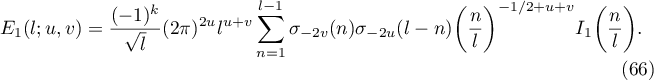
Assuming Conjecture 1.2, the main term 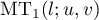 of (66) is given by
of (66) is given by

(see (18), (19) and (21)). Let
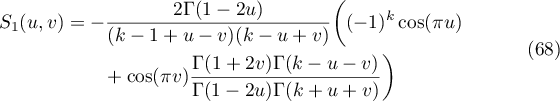
and

Lemma 4.1. The following identity holds
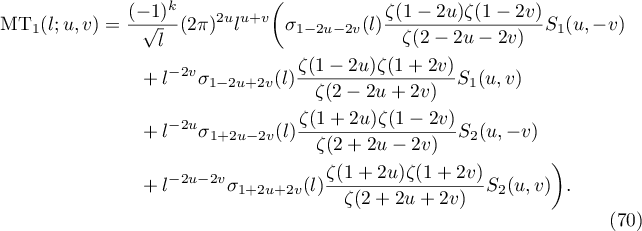
Proof. The proof is similar to that of Lemma 3.1. We substitute (33) and (23) into (67). In this way we obtain four terms that can be evaluated in the same way. We consider the first and fourth terms. The first term is given by
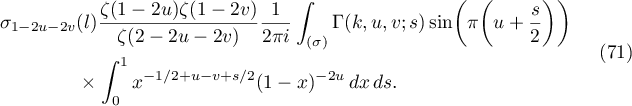
To evaluate the integral with respect to 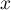 we apply (30). In doing so, we obtain
we apply (30). In doing so, we obtain
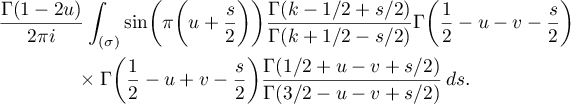
Moving the line of integration to the left and evaluating the residues at 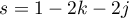 ,
, 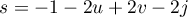 for
for 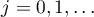 , we show that
, we show that
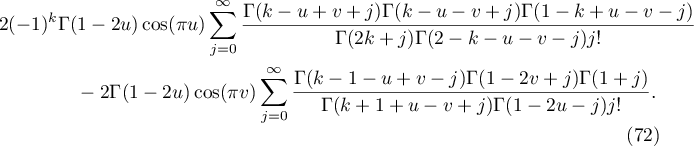
Consider the first sum in (72). Applying (26) twice, we prove that it is equal to
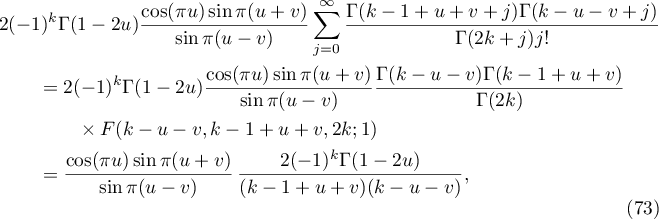
where we have used (28) to evaluate the hypergeometric function.
Consider the second sum in (72). Applying (26) twice, we show that it is equal to
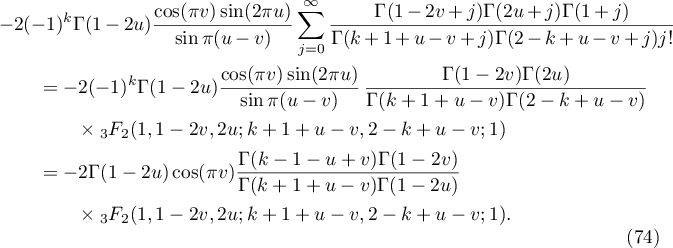
Applying [8], §7.4.4, formula 27 (for  ), we obtain
), we obtain
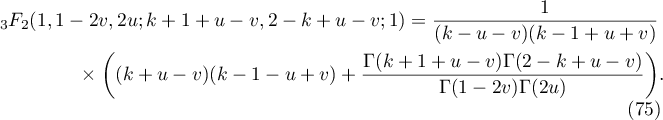
Substituting (75) into (74) and using (26) twice, we prove that the second sum in (72) is equal to
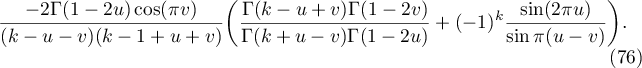
Summing (73) and (76), we conclude that the integral in (71) is equal to
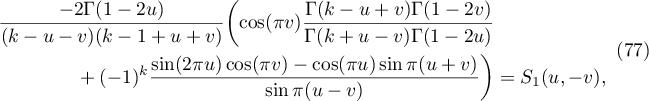
and therefore we recover the first summand in (70).
Let us briefly describe how we can obtain the fourth term in (70). In this case, we must compute
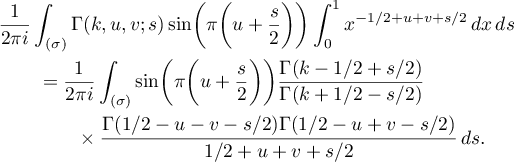
Moving the line of integration to the left and evaluating the residues at 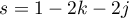 for
for 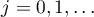 and
and 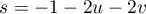 , we have
, we have
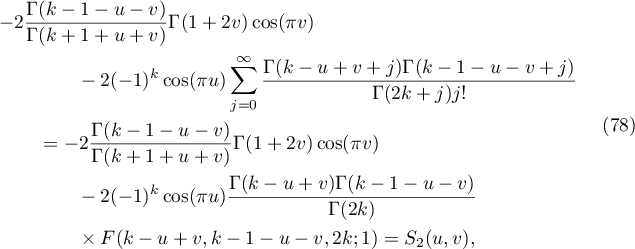
where we have applied (28) to evaluate the hypergeometric function. Lemma 4.1 is proved.
Next, we compute 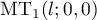 using (70). For this goal, we study the properties of
using (70). For this goal, we study the properties of 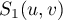 and
and 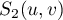 .
.
Lemma 4.2. The following identities hold:
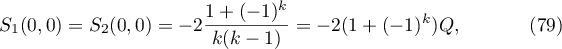
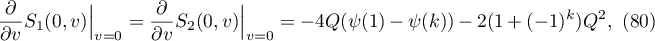
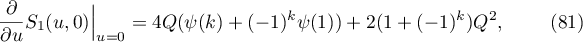
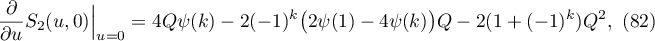
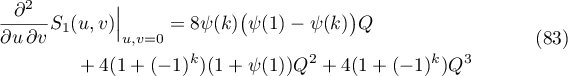
and
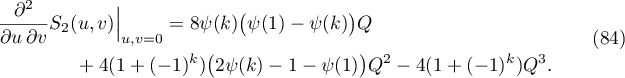
Proof. Equality (79) is a direct consequence of (68) and (69). Furthermore, it follows from (68) and (69) that

and
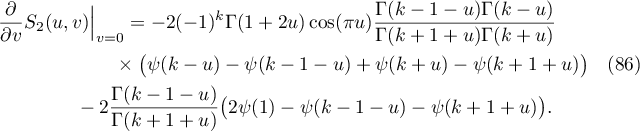
Substituting  in (85) and (86) we obtain (80) by applying the relation
in (85) and (86) we obtain (80) by applying the relation
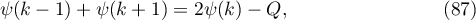
which follows from (27), in the case of (86).
Applying (87), the proof of (81) and (82) follows directly from (68) and (69), respectively. Moreover, we prove (83) by computing the derivative of (85). To show that (84) holds, we compute the derivative of (86) and obtain
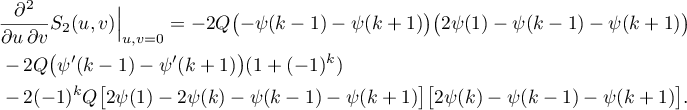
Using (87) and the relation
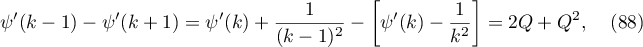
we finally prove (84). The lemma is proved.
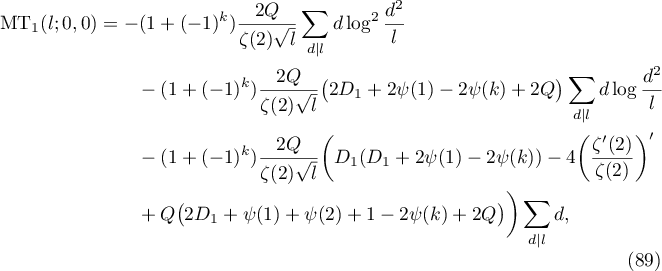
where 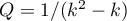 and
and 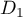 is defined in (55).
is defined in (55).
Proof. Identity (89) is a consequence of (70). More precisely, we proceed similarly to the proof of Theorem 3.3 by starting from (41) and repeating all the steps required to derive (58). Note that in order to prove analytic continuation to the point  in Theorem 3.3 we require that (63) holds. Now we need the analogue of this equation:
in Theorem 3.3 we require that (63) holds. Now we need the analogue of this equation:

which is a consequence of (79) and (80). Finally, applying (56), we derive the analogue of (65):