Abstract
It was recently proposed (P A Brandão and S B Cavalcanti 2019 Phys. Rev. A 100 043822) that two small (Dirac) scatterers, one having gain and the other having loss, drastically modifies the spectral density of the scattered radiation field. Here, we extend this previous work by studying the scattering of stochastic radiation by two finite spheres having gain and loss, satisfying the parity-time symmetry condition, and verifying the spectral changes in frequency domain, i.e. the non-Hermitian Wolf effect. Under the Born approximation, we analytically found the specific frequencies where the spectral density of the scattered field vanishes and show that they depend on the gain and loss parameter γ of each material. This is evidence of a non-Hermitian Wolf effect, meaning that the spectrum can be tuned by the gain/loss properties of the system. We have also shown that there is a π/2 phase shift when 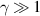 compared to the Hermitian configuration (γ = 0).
compared to the Hermitian configuration (γ = 0).
Export citation and abstract BibTeX RIS
1. Introduction
The concept of parity-time (PT) symmetry introduced by Bender and Boettcher in 1998 has become a very powerful tool in which many branches of science have used to explore new effects not present in its Hermitian configurations [1–7]. However, given a Hamiltonian H that commutes with PT, where P and T are the parity and time-reversal operators, respectively, does not guarantee a real spectra. The antilinear property of T spoils this conjecture since it is not true that two operator share a common set of eigenvectors if one or both are antilinear. Thus, PT symmetry is neither necessary nor sufficient for all-real spectra. The necessary and sufficient conditions for a real spectrum were exposed by Mostafazadeh in a series of interesting papers that led to the notion of pseudo-Hermitian Hamiltonians where PT symmetry is a special case [8]. Nevertheless, if H commutes with PT
and if they share a common set of eigenvectors, then a complete formulation of non-relativistic quantum mechanics can be constructed through the identification of a new symmetry operation C and a new definition for the inner product on the Hilbert space [7]. Allowing Hermitian physical systems to be extended into the complex plane can be of great value. To give one example, consider the one-dimensional upside-down potential 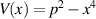 , where p and x are the momentum and position operators, respectively [9]. A classical particle described by this Hamiltonian is apparently under an unstable force that pushes the particle away from the origin. However, once we extend this analysis to the complex plane, it becomes clear that the particle is actually performing periodic stable motion and, if one invokes the quantization condition of closed orbits, the eigenvalues of this quantum system must be real, positive and discrete. This is in fact the case as shown by a more quantitative analysis [1, 9]. Thus, in this way, one gains a very deep insight into the problem which was not possible by inspection on the real axis only.
, where p and x are the momentum and position operators, respectively [9]. A classical particle described by this Hamiltonian is apparently under an unstable force that pushes the particle away from the origin. However, once we extend this analysis to the complex plane, it becomes clear that the particle is actually performing periodic stable motion and, if one invokes the quantization condition of closed orbits, the eigenvalues of this quantum system must be real, positive and discrete. This is in fact the case as shown by a more quantitative analysis [1, 9]. Thus, in this way, one gains a very deep insight into the problem which was not possible by inspection on the real axis only.
Probably the area of physics that most took advantage of the concepts of PT symmetry was optics and photonics [10, 11]. Due to the analogy existent between the paraxial wave equation of optical beams and the time-dependent Schrödinger equation, a host of quantum phenomena could be simulated in laboratory conditions in a pure classical realm [12]. The very first paper published on physical optics discussing a non-Hermitian material having PT symmetry seems to be that of Moayedi and Rostami [13], although the work of Ruschhaupt, Delgado and Muga [14] attracted much more attention over the years. Nevertheless, they both attempted to design a system consisting of a material medium with gain and loss satisfying the PT symmetry requirements. If we denote the parity and time-reversal operators by P and T, respectively, then a one-dimensional inhomogeneous refractive index n(x) is said to be PT-symmetric if it remains invariant under the simultaneous operation of PT: (PT)−1
n(x)(PT) = n(x). If the parity operator is defined as the reflection through the origin x = 0, then 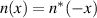 must be obeyed by the potential function. In this way, periodic materials having PT symmetry have received much attention as they provide many interesting effects, such as power oscillations and double refraction [15], optical solitons [16, 17], unidirectional invisibility [18, 19], photonic Bloch oscillations [20] and Bragg scattering [21–23] to cite a few.
must be obeyed by the potential function. In this way, periodic materials having PT symmetry have received much attention as they provide many interesting effects, such as power oscillations and double refraction [15], optical solitons [16, 17], unidirectional invisibility [18, 19], photonic Bloch oscillations [20] and Bragg scattering [21–23] to cite a few.
It is well known that real optical wavefields are intrinsically statistical in nature [24–28]. Optical effects directly linked to the coherence properties of the wavefield are numerous and involve applications in determining the size of stellar objects [29], ghost imaging [30, 31], propagation of light through turbulent media [32] and tomography [33]. A very nice and important book chapter exposing the applications of optical coherence theory has been published recently [34]. Scattering of stochastic radiation by deterministic Hermitian materials [35] and non-Hermitian materials having balanced gain and loss, satisfying the condition of PT symmetry, have also been considered [36–38]. It was demonstrated that the loss and gain properties of the material, along with the correlations present in the incident field, strongly affect the statistical properties of the scattered radiation. It was shown that the spatial coherence properties of the incident field can inhibit the asymmetrical character of the scattered radiation [37] and that the frequency spectrum of the scattered radiation can be dynamically modified depending on the loss and gain properties of the material without changing its geometry [36, 38]. However, the authors of [37] considered only two point (Dirac) scatterers and did not explore the spectral changes in frequency of the scattered radiation. We formulate here an extension of this theory, by considering finite materials, and show that several interesting effects in frequency analysis are present in this system.
2. Scattering theory for stochastic radiation
The theory of partially coherent radiation scattered by deterministic materials is well documented [25]. The purpose of this section is to fix notation and to define the dynamical variables of interest. To this end, consider an incident stochastic scalar radiation field described by the ensemble 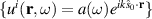 , where a(ω) is a random function of angular frequency ω,
, where a(ω) is a random function of angular frequency ω, 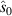 is a unit vector (
is a unit vector (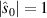 ) representing a fixed incident direction and k = ω/c with c being the speed of light in vacuum. Here, we are taking advantage of the frequency-space formulation of second order coherence theory. The spectral density of the incident radiation is therefore
) representing a fixed incident direction and k = ω/c with c being the speed of light in vacuum. Here, we are taking advantage of the frequency-space formulation of second order coherence theory. The spectral density of the incident radiation is therefore 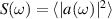 , independent of position. That is, we are dealing with a polychromatic incident plane wave. The total field
, independent of position. That is, we are dealing with a polychromatic incident plane wave. The total field  present in the scattering system satisfies the inhomogeneous Helmholtz equation
present in the scattering system satisfies the inhomogeneous Helmholtz equation
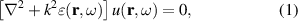
whose solution, using the first Born approximation and considering points far away from the scatterers (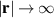 ), is given by
), is given by
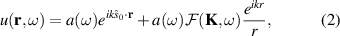
where
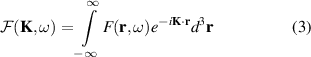
is the three-dimensional spatial Fourier transform of the the function  evaluated at
evaluated at 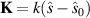 with
with 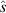 being a unit vector in the direction of observation
being a unit vector in the direction of observation 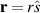 . The potential function
. The potential function 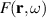 represents the material under which the incident radiation interacts. It is related to the inhomogeneous (relative) dielectric permittivity
represents the material under which the incident radiation interacts. It is related to the inhomogeneous (relative) dielectric permittivity 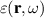 by the formula
by the formula
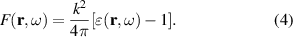
The scattered radiation is represented by the second term on the right hand side of equation (2),
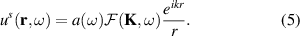
From (5) the cross-spectral density 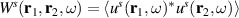 can be calculated and, consequently, the spectral density
can be calculated and, consequently, the spectral density  which is given by
which is given by

We are interested here in devising a scattering material which is a generalization of the model discussed in [37]. There, two point scatterers (described by Dirac delta functions) was considered rendering useless the size of the material. Our objective is to determine what effect the size of the two scatterers have on the scattered spectrum. Also, the authors of [37] did not consider the changes in the frequency of the radiation. One possible generalization of the cited model is to consider the following material
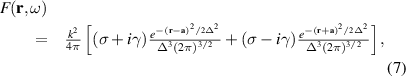
where σ and γ are the real and non-Hermitian parameters of the material, which control the real and imaginary parts of the permittivity, Δ is the size of each individual scatterer and the vector 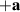 (-
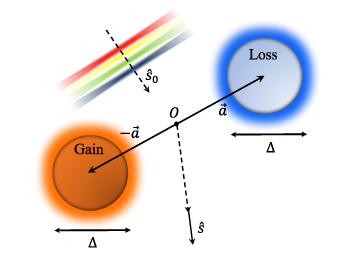
(- ) points to the center of the material that has loss (gain). All the geometrical parameters defined in this section along with a pictorial representation of the scatterers and the incident polychromatic plane wave can be viewed in figure 1. The model considered in [37] can be obtained from equation (7) in the limit
) points to the center of the material that has loss (gain). All the geometrical parameters defined in this section along with a pictorial representation of the scatterers and the incident polychromatic plane wave can be viewed in figure 1. The model considered in [37] can be obtained from equation (7) in the limit 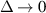 .
.
Figure 1. A polychromatic plane wave propagating in the direction represented by the unit vector  is incident upon two scatterers located at positions
is incident upon two scatterers located at positions 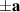 .
.
Download figure:
Standard image High-resolution imageBefore we discuss the properties of the spectral density of the scattered field, a word about the material dispersion (7) in PT-symmetric systems is in order here. It was demonstrated that the Kramers–Kroning relations between the real and imaginary parts of the dielectric permitivitty are not satisfied for a PT-symmetric material in a finite domain of frequencies [39]. However, inhomogeneous broadening can be implemented in a physical material by doping the host medium with active impurities such that PT symmetry is almost satisfied for a finite range of frequencies [40]. This quasi-PT-symmetry concept has enabled the study of the propagation of broadband optical pulses through active periodic structures in the Laue and Bragg geometries [40, 41]. The main idea behind the quasi-PT-symmetry concept is that if the inhomogeneous relaxation time 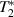 is much less than the homogeneous relaxation time T2, which in turn is much less than the pulse duration
is much less than the homogeneous relaxation time T2, which in turn is much less than the pulse duration 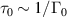 , where Γ0 is the spectral bandwith of the pulse, then the dielectric permittivity is approximately PT symmetric. To see the connection between the formalism presented here with that of [40], we write the permittivity as
, where Γ0 is the spectral bandwith of the pulse, then the dielectric permittivity is approximately PT symmetric. To see the connection between the formalism presented here with that of [40], we write the permittivity as 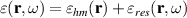 where
where 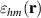 is the frequency-independent permittivity of the host medium and
is the frequency-independent permittivity of the host medium and 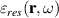 is the permittivity of the resonant medium describing the role of the active impurities giving gain and loss to the material. If we write the resonant part as
is the permittivity of the resonant medium describing the role of the active impurities giving gain and loss to the material. If we write the resonant part as 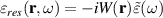 then it can be shown that
then it can be shown that 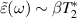 as
as 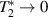 , where β is a constant proportional to the concentration of resonant atoms. Then, if we also assume that
, where β is a constant proportional to the concentration of resonant atoms. Then, if we also assume that  , the total permittivity
, the total permittivity 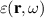 is quasi-PT-symmetric. For the model considered in this paper, one can easily verify that
is quasi-PT-symmetric. For the model considered in this paper, one can easily verify that

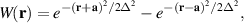
and  . Thus, although we use normalized physical quantities in the next sections, we assume that the approximations discussed here remain valid in the domain of interest.
. Thus, although we use normalized physical quantities in the next sections, we assume that the approximations discussed here remain valid in the domain of interest.
3. Results and discussion
To obtain the spectral density 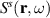 of the scattered radiation, one needs to calculate the Fourier transform of equation (7). Since we are dealing with Gaussian functions, this is simple to perform. The result is
of the scattered radiation, one needs to calculate the Fourier transform of equation (7). Since we are dealing with Gaussian functions, this is simple to perform. The result is
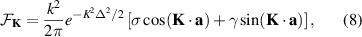
where 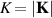 . By inspecting equation (8) one concludes that the effect of the size of the materials, represented by the parameter Δ, is present in the equation. The fact that
. By inspecting equation (8) one concludes that the effect of the size of the materials, represented by the parameter Δ, is present in the equation. The fact that 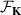 is a real function of
is a real function of 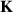 is a reflection of the PT symmetry of the system. Thus, by considering Dirac point scatterers, the authors of [37] may have overlooked some effects related to the finite size of the scatterers. We will proceed judiciously to see just what has been ignored. The spectral density of the scattered field can now be written as
is a reflection of the PT symmetry of the system. Thus, by considering Dirac point scatterers, the authors of [37] may have overlooked some effects related to the finite size of the scatterers. We will proceed judiciously to see just what has been ignored. The spectral density of the scattered field can now be written as
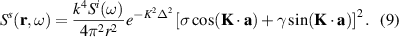
We now choose the incident wavefield direction as the z direction (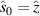 ) and assume that the two scatterers are located in the x axis such that
) and assume that the two scatterers are located in the x axis such that 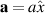 , where a is a positive constant. Suppose the incident spectral density has a Gaussian form
, where a is a positive constant. Suppose the incident spectral density has a Gaussian form
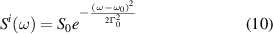
where S0 is a constant, ω0 the center frequency and Γ0 the linewidth. By making the normalizations  ,
, 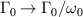 ,
, 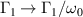 ,
, 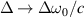 and
and 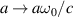 , the radiant intensity
, the radiant intensity 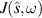 , defined by
, defined by 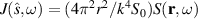 can be written as a product of three terms,
can be written as a product of three terms,
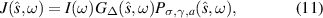
where

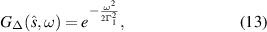
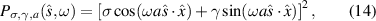
with the linewidth Γ1 of 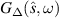 given by
given by

where θ ∈ [0, π] is the angle between  and the z axis. To illuminate the physics behind equation (11), observe that the product between equations (12) and (13) can be written as
and the z axis. To illuminate the physics behind equation (11), observe that the product between equations (12) and (13) can be written as
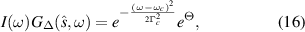
where
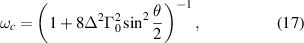
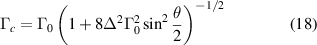
and
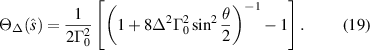
Since  does not depend on the frequency ω, it will not influence the shape of the radiant intensity for fixed
does not depend on the frequency ω, it will not influence the shape of the radiant intensity for fixed  and we will ignore this term in what follows since it only contributes with an overall amplitude factor. Figure 2 shows the plot of the center frequency (17) of the product
and we will ignore this term in what follows since it only contributes with an overall amplitude factor. Figure 2 shows the plot of the center frequency (17) of the product  as a function of the scattered angle
as a function of the scattered angle 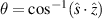 . Viewed as a function of frequency ω, the product
. Viewed as a function of frequency ω, the product 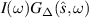 describes a Gaussian profile centered at ωc
. Thus, regarding the frequency distribution of this product, it is always centered at ωc
with the overall amplitude varying with the direction of observation. It is clear from figure 2 that the major influence of this factor is in the backward direction θ = π.
describes a Gaussian profile centered at ωc
. Thus, regarding the frequency distribution of this product, it is always centered at ωc
with the overall amplitude varying with the direction of observation. It is clear from figure 2 that the major influence of this factor is in the backward direction θ = π.
Figure 2. Center frequency of the product 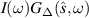 as a function of θ (the angle between
as a function of θ (the angle between  and
and 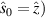 for three nonzero values of Δ. Parameters used: Γ0 = 0.01.
for three nonzero values of Δ. Parameters used: Γ0 = 0.01.
Download figure:
Standard image High-resolution image3.1. Hermitian spectral changes
Now that we have put the radiant intensity in a convenient mathematical form, let us consider the overall effect of multiplying 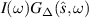 by the periodic function
by the periodic function 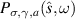 in order to finally grasp the physics behind the scattering process. To this end, let us write the radiant intensity as
in order to finally grasp the physics behind the scattering process. To this end, let us write the radiant intensity as
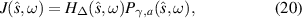
where
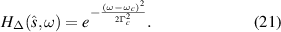
Also, without loss of generality, we assume that σ = 1. In this way, the subscript σ has been dropped from the notation. We are mainly interested in the dependence of 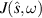 on ω for a fixed direction
on ω for a fixed direction 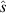 . Let us fix the distance between scatterers at 2a = 68π (which represents a physical distance of 34λ0) and consider scattering angles (in spherical coordinates where sx
= sinθcosφ) fixed at θ = π/4 (polar angle) and φ = π/4 (azimuthal angle). Figure 3 illustrates the behavior of
. Let us fix the distance between scatterers at 2a = 68π (which represents a physical distance of 34λ0) and consider scattering angles (in spherical coordinates where sx
= sinθcosφ) fixed at θ = π/4 (polar angle) and φ = π/4 (azimuthal angle). Figure 3 illustrates the behavior of 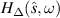 ,
, 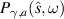 and
and 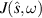 for the Hermitian case where γ = 0, i.e, the materials have no loss or gain. Part (a) of figure 3 shows the plots of
for the Hermitian case where γ = 0, i.e, the materials have no loss or gain. Part (a) of figure 3 shows the plots of  (continuous lines) along with the periodic term
(continuous lines) along with the periodic term  (dashed line) for the sizes Δ = 3π, 5π and 7π. One sees that, as Δ varies, the function
(dashed line) for the sizes Δ = 3π, 5π and 7π. One sees that, as Δ varies, the function 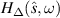 experiences an overall red shift in such a way that it passes through a zero of the
experiences an overall red shift in such a way that it passes through a zero of the 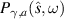 function, which is Δ-independent. The result of this effect is shown in part (b) of the same figure where the radiant intensity (continuous lines) is compared with the incident spectrum (dashed line). Thus, a splitting in the spectrum of the scattered radiation takes place as the size of both scatterers materials increases. This correlation-induced red shift in frequency is named the Wolf effect or, in this case, the Hermitian–Wolf effect since the material has no gain or loss. It appears as a consequence of a change in the geometry of the system. This behavior could be explored to exclude a particular frequency inside the scattered spectrum by realizing that the zeros (
function, which is Δ-independent. The result of this effect is shown in part (b) of the same figure where the radiant intensity (continuous lines) is compared with the incident spectrum (dashed line). Thus, a splitting in the spectrum of the scattered radiation takes place as the size of both scatterers materials increases. This correlation-induced red shift in frequency is named the Wolf effect or, in this case, the Hermitian–Wolf effect since the material has no gain or loss. It appears as a consequence of a change in the geometry of the system. This behavior could be explored to exclude a particular frequency inside the scattered spectrum by realizing that the zeros (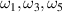 , ...) of
, ...) of 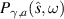 are located at
are located at 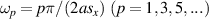 so that the condition
so that the condition 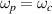 could be satisfied for some choice of the geometrical parameters. The zeros of
could be satisfied for some choice of the geometrical parameters. The zeros of 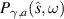 present in the plot of figure 3 are ω31, ω33 and ω35.
present in the plot of figure 3 are ω31, ω33 and ω35.
Figure 3. Correlation-induced spectral changes in the Hermitian configuration. (a) Periodic function 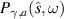 (dashed black line) and
(dashed black line) and  (continuous line) for Δ = 3π (blue), Δ = 5π (orange) and Δ = 7π (green) as a function of ω. (b) Plots of the the incident spectrum Si
(ω) (dashed black line) and the radiant intensities
(continuous line) for Δ = 3π (blue), Δ = 5π (orange) and Δ = 7π (green) as a function of ω. (b) Plots of the the incident spectrum Si
(ω) (dashed black line) and the radiant intensities 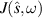 (continuous lines) for Δ = 3π (blue), Δ = 5π (orange) and Δ = 7π (green). Parameters used: Γ0 = 0.01,
(continuous lines) for Δ = 3π (blue), Δ = 5π (orange) and Δ = 7π (green). Parameters used: Γ0 = 0.01,  , a = 34π and γ = 0.
, a = 34π and γ = 0.
Download figure:
Standard image High-resolution imageIt is clear from the above analysis that by increasing the distance between the two scatterers, the period of the 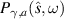 function decreases and strong variations start to appear inside the frequency range where
function decreases and strong variations start to appear inside the frequency range where 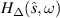 is nonzero. As a result of this, the spectrum appears oscillatory in character where the zeros of the profile are determined by the zeros of the periodic function
is nonzero. As a result of this, the spectrum appears oscillatory in character where the zeros of the profile are determined by the zeros of the periodic function 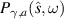 described above. Figure 4 illustrates this effect by considering a distance 2a = 400π between the two scatterers with fixed Δ = 5π. Thus, the spectrum passes through a transition between Gaussian-like (with possible splitting and distortion) and oscillatory character when the geometry (size and distance) of the scatterers is changed.
described above. Figure 4 illustrates this effect by considering a distance 2a = 400π between the two scatterers with fixed Δ = 5π. Thus, the spectrum passes through a transition between Gaussian-like (with possible splitting and distortion) and oscillatory character when the geometry (size and distance) of the scatterers is changed.
Figure 4. This plot illustrates the oscillatory effect on the spectrum of the scattered radiation when a = 200π (continuous orange line) along with the incident spectrum (dashed line). The zeros inside the spectrum are the roots of  . Parameters used: Γ0 = 0.01,
. Parameters used: Γ0 = 0.01, 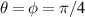 , Δ = 5π and γ = 0.
, Δ = 5π and γ = 0.
Download figure:
Standard image High-resolution image3.2. Non-Hermitian spectral changes
Let us now consider the influence of the gain and loss parameter γ on the frequency distribution of the radiant intensity 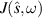 . Such influence can only appear through the presence of the term
. Such influence can only appear through the presence of the term 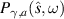 , since this is the only term that depends on γ. The first important aspect in this non-Hermitian configuration is that the zeros
, since this is the only term that depends on γ. The first important aspect in this non-Hermitian configuration is that the zeros 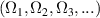 of the periodic function
of the periodic function 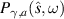 are now γ-dependent and located at
are now γ-dependent and located at
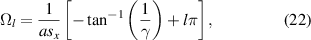
where p is a positive integer. It is easy to demonstrate that as  we obtain
we obtain 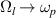 (with p = 2l − 1) in a continuous manner. Therefore, by allowing the complex extension of this scattering system, we do not observe any abrupt change in the physical properties of the scattered radiation. To see the effect of γ on the zeros of
(with p = 2l − 1) in a continuous manner. Therefore, by allowing the complex extension of this scattering system, we do not observe any abrupt change in the physical properties of the scattered radiation. To see the effect of γ on the zeros of 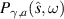 more explicitly, consider again figure 3 with the zeros ω31, ω33 and ω35. These correspond to Ω16, Ω17 and Ω18, respectively, according to the relation p = 2l − 1. Figure 5 illustrates the behavior of Ωl
for l = (16, 17, 18) as a function of γ. What this plot indicates is the existence of a non-Hermitian correlation-induced Wolf effect that occurs irrespective of the geometrical changes of the system. That is, one can control the frequency spectrum of the scattered radiation by a judicious choice of the gain and loss parameters of the materials without changing the geometry of the system. It is also suggested by the inspection of figure 5 and equation (22) that this shift has a maximum value as
more explicitly, consider again figure 3 with the zeros ω31, ω33 and ω35. These correspond to Ω16, Ω17 and Ω18, respectively, according to the relation p = 2l − 1. Figure 5 illustrates the behavior of Ωl
for l = (16, 17, 18) as a function of γ. What this plot indicates is the existence of a non-Hermitian correlation-induced Wolf effect that occurs irrespective of the geometrical changes of the system. That is, one can control the frequency spectrum of the scattered radiation by a judicious choice of the gain and loss parameters of the materials without changing the geometry of the system. It is also suggested by the inspection of figure 5 and equation (22) that this shift has a maximum value as 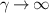 given by
given by  for sx
≠ 0. Thus, there is a saturation process involved in this non-Hermitian Wolf shift linked to the gain and loss properties of the material as they increase. To the best of our knowledge, the fundamental origin of the non-Hermitian Wolf effect (that is, the exact influence of loss and gain on the correlation properties of the wavefield) remains unexplored until now and is not being considered in the present article. Perhaps some atomic investigation following the lines of [42] could bring some light into the discussion. Such an atomic approach to non-Hermitian optical coherence remains, however, unexplored.
for sx
≠ 0. Thus, there is a saturation process involved in this non-Hermitian Wolf shift linked to the gain and loss properties of the material as they increase. To the best of our knowledge, the fundamental origin of the non-Hermitian Wolf effect (that is, the exact influence of loss and gain on the correlation properties of the wavefield) remains unexplored until now and is not being considered in the present article. Perhaps some atomic investigation following the lines of [42] could bring some light into the discussion. Such an atomic approach to non-Hermitian optical coherence remains, however, unexplored.
Figure 5. This plot illustrates the behavior of the zeros Ωl
of the function 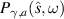 as γ varies. The values
as γ varies. The values 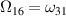 ,
, 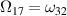 and
and 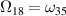 shown here are to be compared with the zeros of the Hermitian configuration of figure 3.
shown here are to be compared with the zeros of the Hermitian configuration of figure 3.
Download figure:
Standard image High-resolution imageOccurring together with the shifts in the zeros of 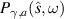 is a change in the overall amplitude. This implies that the scattered spectrum could be amplified by tuning the gain and loss properties of the scatterers. Both effects, the shifts in the zeros and the changes in amplitude, occur together and depend on γ. When compared to the Hermitian configuration, an interesting π/2 phase shift appears if
is a change in the overall amplitude. This implies that the scattered spectrum could be amplified by tuning the gain and loss properties of the scatterers. Both effects, the shifts in the zeros and the changes in amplitude, occur together and depend on γ. When compared to the Hermitian configuration, an interesting π/2 phase shift appears if  , as can be verified from equation (14):
, as can be verified from equation (14):
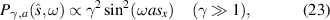
whose zeros are located at 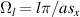 , as discussed before. Figure 6 illustrates this effect by considering the scattering of polychromatic light from two scatterers with γ = 10. It is easy to see the exchange of maxima and minima of the radiant intensities as the non-Hermitian parameter γ increases. Thus, equation (13) could be used, along with its appropriate limits, to design a specific scattering system with tunable frequency properties without changing the geometry (size or distance) of the scatterers, which should be an advantage from the experimental point of view.
, as discussed before. Figure 6 illustrates this effect by considering the scattering of polychromatic light from two scatterers with γ = 10. It is easy to see the exchange of maxima and minima of the radiant intensities as the non-Hermitian parameter γ increases. Thus, equation (13) could be used, along with its appropriate limits, to design a specific scattering system with tunable frequency properties without changing the geometry (size or distance) of the scatterers, which should be an advantage from the experimental point of view.
Figure 6. This plot illustrates the π/2 phase shift that occurs in the scattered spectrum when 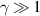 . The continuous orange line represents the radiant intensity in the Hermitian configuration where γ = 0 multiplied by a factor of 50 to aid the visualization. The continuous blue line is the radiant intensity for γ = 10 and the dashed black line is the incident spectrum. The parameters used are the same as in figure 4.
. The continuous orange line represents the radiant intensity in the Hermitian configuration where γ = 0 multiplied by a factor of 50 to aid the visualization. The continuous blue line is the radiant intensity for γ = 10 and the dashed black line is the incident spectrum. The parameters used are the same as in figure 4.
Download figure:
Standard image High-resolution imageIt is important to note that scattering experiments with partially coherent light have been performed for many years in different contexts [43–45]. Therefore, we believe that the introduction of gain and loss into the system will not present any real difficulty from the experimental point of view since, as discussed at the end of section 2, one can fabricate doped materials with large inhomogeneous broadening [39–41]. It should also be mentioned that the theory presented here is more adequate to describe systems with field noise (which are intrinsic in every real laboratory) since this feature is included into the model from the start.
4. Conclusions
We have considered the scattering of polychromatic radiation by two finite spheres, one having gain and the other having loss, satisfying the condition of PT symmetry. Under the Born approximation our results suggest that the frequency spectrum of the scattered radiation strongly depends on the size and distance of the scatterers as well as on their gain and loss properties. Conditions are derived such that the frequency distribution of the scattered radiation in the far field has a particular frequency excluded from the spectrum without changing the geometry of the system.
Acknowledgments
The author R A Vieira would like to thank the financial support of FAPEAL (Fundação de Amparo à Pesquisa do Estado de Alagoas).