Introduction

Quantum entanglement1,2, as one of the most important phenomena in quantum information, has been proven to play a central role in many applications: fault-tolerant quantum computation3, device-independent quantum communication4 and quantum precision measurements5. In recent years, the research on quantum entanglement mainly focused on multipartite qubit systems6,7, or two-partite high-dimensional systems8,9. For example, in optical systems, the preparation of quantum entanglement mainly develops in two directions: one is to increase the number of qubits of entanglement, such as 12-photon entanglement6, 18 qubit entanglement7, the other is to increase the dimensionality of two photons, such as entanglement of 100 × 100 orbital angular momentum (OAM) degrees of freedom10. Since the higher-dimensional entanglement is naturally present in downconversion processes, it would be desirable to harness this high-dimensionality for multi-photon experiments. Unfortunately, there are few experimental studies on multipartite high-dimensional entangled quantum states. The main reason is that the preparation of such entangled states requires very delicate manipulation for high-dimensional quantum systems.

In the field of quantum information, the most commonly used high-dimensional degrees of freedom (DoFs) in photonic systems are as follows: OAM11, time bin12, path13,14,15,16,17. The high-dimensional DoFs of these photons have their advantages and disadvantages in the application of quantum information. For example, using OAM is easier to expand the dimension18, but the fidelity of the preparation and operation is lower19 and the long-distance distribution is more difficult20. The advantage of time bin DoF is that it is more suitable for long-distance distribution21, however, it is difficult to implement arbitrary unitary operations on time bins. The path DoF has a very high fidelity and is easy to manipulate22,23, and its dimension scalability16 and long-distance distribution were also demonstrated24. Until now, multipartite high-dimensional quantum entangled states have been successfully prepared only on OAM DoF. If classified according to Schmidt number vector25, (3, 3, 2) state (\(1/\sqrt{3}(\left|000\right\rangle +\left|111\right\rangle +\left|221\right\rangle )\))26, (3, 3, 3) state (\(1/\sqrt{3}(\left|000\right\rangle +\left|111\right\rangle +\left|222\right\rangle )\))27 and high-dimensional Dicke states28 have been successfully prepared on OAM (See Fig. 1). Due to the difficulties of state preparation, the largest dimension encoded in each photon is 3, and the observed fidelities are a bit low compared to other multi-photon experiments.

Fig. 1: Schematic representation of a few sets of states with a given Schmidt number vector25.
figure 1

Multipartite states can be classified by calculating Schmidt number vectors of each particle in a multipartite state. After years of development, the preparation of (2, 2, 2), (3, 3, 2)26 and (3, 3, 3)27 quantum states has been completed. Here we have completed the preparation of (4, 4, 2) quantum state.

Full size image

Results

(4, 4, 2) Multi-photon high-dimensional layered quantum states

For potential application in quantum key distribution, ref. 25,29 proposed to use a multipartite high-dimensional quantum state, that has so far not been created in any experiment:

$$\left|{\Psi }_{442}\right\rangle =\frac{1}{2}(\left|000\right\rangle +\left|111\right\rangle +\left|220\right\rangle +\left|331\right\rangle ).$$
(1)

Notice that the first two photons, A and B, live in a four-dimensional space, whereas the third photon, C, lives in a two-dimensional space. The state’s dimensionality is given by a vector of three numbers (4, 4, 2), which are the ordered ranks of the single particle reductions of the state density operator:

$${\rm{rank}}\left({\rho }_{\rm{A}}\right)=4,\ {\rm{rank}}\left({\rho }_{\rm{B}}\right)=4,\ {\rm{rank}}\left({\rho }_{\rm{C}}\right)=2,$$
(2)

where \({\rho }_{i}={{\rm{Tr}}}_{\overline{i}}{\left|\Psi \right\rangle }_{442}\left\langle {\left.\Psi \right|}_{442}\right.\). This quantum state is obviously different from the general GHZ state (\(\left|{\Psi }_{333}\right\rangle\)), and it contains quantum state \(\left|{\Psi }_{332}\right\rangle\), see Fig. 1.

This quantum state exhibits different properties from other multipartite entangled states. If we observe the two-dimensional subspaces of this quantum state, we find that there is a perfect correlation between particle A, B, and C in \(\{\left|0\right\rangle ,\left|1\right\rangle \}\) space (\(\{\left|000\right\rangle ,\left|111\right\rangle \}\)), simultaneously there is also a perfect correlation between A, B, and C in \(\{\left|2\right\rangle ,\left|3\right\rangle \}\) space and C in \(\{\left|0\right\rangle ,\left|1\right\rangle \}\) space (\(\{\left|220\right\rangle ,\left|331\right\rangle \}\)). So there is always a perfect GHZ correlation between A, B, and C if we observe the quantum state in a specific subspace. On the other hand, if C is detected in mode \(\left|0\right\rangle\), then A, B are perfectly correlated in modes \(\left|0\right\rangle\) and \(\left|2\right\rangle\); if C is detected in mode \(\left|1\right\rangle\), then A, B are perfectly correlated in modes \(\left|1\right\rangle\) and \(\left|3\right\rangle\). This property is quite different from all the previous states26,27,28, and enables a layered quantum network and exhibits the advantage of high-dimensional systems. For this reason this quantum state has been called layered quantum state. In this letter, we use the path and polarization DoFs of photons to build four-dimensional systems, demonstrate the creation and verification of one such entangled state with a fidelity of 0.854, which is higher than previous experiments26,27,28. Owing to the highest fidelity, we demonstrate its application in a highly efficient layered quantum communication protocol in principle. This technique can be applied to construct complex quantum networks in the future.

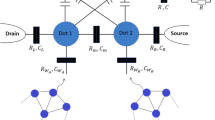
Because the polarization DoF of photons has only two levels, it is impossible to construct high-dimensional quantum states only by using polarization DoF in a single photon30,31. So we use a beam displacer (BD) to additionally use the path DoF and combine it with the polarization DoF to complete hybrid high-dimensional coding. The experiment setup is shown in Fig. 2, experimental details are presented in the “Methods” section.

Fig. 2: Experimental setup.
figure 2

The blue region shows the process of preparing quantum states. The ultraviolet pulse laser (390 nm) from the doubler sequentially pumps nonlinear crystals to generate two entanglement source \((\left|HH\right\rangle +\left|VV\right\rangle )/\sqrt{2}\) at 780 nm. One of the photons serves as a trigger, the other three photons are prepared on a three-photon GHZ state \((\left|HHH\right\rangle +\left|VVV\right\rangle )/\sqrt{2}\)37. Finally, the particle 3 is directly measured in the polarization basis, the other two photons are incident into the high-dimensional post-selection device, which is used to post-select the two-dimensional polarization entangled state \((\left|HH\right\rangle +\left|VV\right\rangle )/\sqrt{2}\) into the polarization-path hybrid entangled state \((\left|{H}_{u}{H}_{u}\right\rangle +\left|{V}_{u}{V}_{u}\right\rangle +\left|{H}_{l}{H}_{l}\right\rangle +\left|{V}_{l}{V}_{l}\right\rangle )/2\). If we encode \(\left|{H}_{u}\right\rangle \to \left|0\right\rangle\), \(\left|{V}_{u}\right\rangle \to \left|2\right\rangle\), \(\left|{H}_{l}\right\rangle \to \left|1\right\rangle\), and \(\left|{V}_{l}\right\rangle \to \left|3\right\rangle\), we will get three-partite layered entangled state \((\left|000\right\rangle +\left|111\right\rangle +\left|220\right\rangle +\left|331\right\rangle )/2\). The pink part shows the measurement device for three-photon states. Among them, particle 1 and 2 are encoded on 4-dimensional space, and particle 3 is encoded on 2-dimensional space.

Full size image

Experiment result

We have witnessed the fidelity Fexp of the ideal quantum state \(\left|{\Psi }_{442}\right\rangle\) with the state ρexp. One can conclude that the multipartite entangled state is genuinely (4, 4, 2) entangled from the obtained fidelity Fexp. This method relies on proving that the measured (4, 4, 2) state cannot be decomposed into entangled states of a smaller dimensionality structure (4, 3, 2). We found the best achievable overlap of a \(\left|{\Psi }_{432}\right\rangle\) state with an ideal \(\left|{\Psi }_{442}\right\rangle\) state to be Fmax = 0.750 (see Supplementary Note 2). If Fexp > Fmax, our state is certified to be entangled in 4 × 4 × 2 dimensions. To calculate Fexp, it is sufficient to measure the 32 diagonal and 6 unique real parts of off-diagonal elements of ρexp as shown in Fig. 3 (see Supplementary Note 3 for details). The coincidence efficiencies of 2–8 nm and 3–2 nm entangled sources are 19% and 13%, the total success probability of the post-selection is 25%. Our four-photon counting rate is 0.66 per second, and the integration time of each measurement setting is 1800 s. From the experimental data, Fexp is calculated to be 0.854 ± 0.007, which is above the bound of Fmax = 0.750 by 14 standard deviations. This certifies that the three-photon state is indeed entangled in 4 × 4 × 2 dimensions.

Fig. 3: Experimental results.
figure 3

a The 32 diagonal elements and 6 unique real parts of off-diagonal elements of ρexp (elements which were not measured in the experiment are left gray). From these values, we can calculate Fexp = 0.854 ± 0.007. The fidelity exceeds the upper bound 0.75 with 14 standard deviations, which proves that we have successfully prepared (4, 4, 2) entangled state. The red column represents the experimental value and the transparent column represents the theoretical value of an ideal state. The difference is due to imperfect interferences and multi-photon noise. b–g Diagonal and real parts of unique off-diagonal elements of GHZ state in two-dimensional subspaces. From these values, we can get the fidelities of these states. b \(F((\left|000\right\rangle +\left|111\right\rangle )/\sqrt{2})=0.910\pm 0.029\), c \(F((\left|000\right\rangle +\left|331\right\rangle )/\sqrt{2})=0.906\pm 0.030\), d \(F((\left|111\right\rangle +\left|220\right\rangle )/\sqrt{2})=0.914\pm 0.030\), e \(F((\left|220\right\rangle +\left|331\right\rangle )/\sqrt{2})=0.922\pm 0.028\), f \(F((\left|000\right\rangle +\left|220\right\rangle )/\sqrt{2})=0.933\pm 0.030\), g \(F((\left|111\right\rangle +\left|331\right\rangle )/\sqrt{2})=0.941\pm 0.031\). The fidelities of these states are far beyond the lower bound of genuine multipartite entanglement (F = 0.5).

Full size image

In order to prove the layered property of (4, 4, 2) state, we calculate the fidelity of the two-dimensional subspace GHZ state. There are six maximally entangled states in two-dimensional subspaces. Four of them are maximally entangled states of three photons (A, B, C), and two of them are maximally entangled states of two photons (A, B). We still use the fidelity witness to certify the correlation of those subspaces. As shown in Fig. 3b–g, we measure all diagonal and unique off-diagonal elements of the density matrix. Through them, we can calculate the fidelity of each state and the maximally entangled state. The fidelity of these entangled states are F = 0.910 ± 0.029, 0.906 ± 0.030, 0.914 ± 0.030, 0.922 ± 0.028, 0.933 ± 0.030, 0.941 ± 0.031 (F > 0.5 is the bound for genuinely multipartite entangled states). The results proved that the (4, 4, 2) entangled state we prepared has good correlations in different subspaces.

Our method can be easily extended to generate more-partite high-dimensional layered entangled states. Compared with the OAM DoF in photons, the path DoF is easier to manipulate. According to the method in ref. 32, arbitrary multipartite high-dimensional GHZ quantum states can also be realized by our experimental scheme.

The layered quantum communication network

As shown in Fig. 4(a), if there is a banking system including central bank, branches, and ATMs, which have different communication security levels, a layered quantum communication network will be formed. There are many ways to complete this network, such as establishing QKD between two bodies many times or GHZ state29. However, in order to maximize the average key bits per photon, multi-photon high-dimensional quantum states can be used to implement layered quantum key distribution protocol29. The state \(\left|{\Psi }_{442}\right\rangle\) we prepared can complete the simplest layered quantum communication network (central bank, branch1, and ATM1). Due to the dimensionality of four, one can share secret keys among all the three parties, and share secret keys among A (central bank) and B (branch1) simultaneously independent of the measurement results of C (ATM1)29 as shown in Fig. 4(b). We take the simplest layered quantum communication network as an example.

Fig. 4: A layered quantum communication network.
figure 4

a The central bank, branches and ATM share a common secret key, while central bank shares a key with each of branches. We show the minimum network including central bank (A), branch1 (B), and ATM1 (C). b A, B, and C share a quantum state \(\left|{\Psi }_{442}\right\rangle\), three-party quantum communication or AB two-party quantum communication can be accomplished by using different two-dimensional subspaces.

Full size image

As shown in Fig. 4b, consider the quantum states \(\left|{\Psi }_{442}\right\rangle\) we prepared. Each of the four possible outcome combinations {000, 111, 220, 331} is distributed uniformly to A, B, and C. Moreover, the outcomes of A, B {00, 11, 22, 33} are perfectly correlated and partially independent of the outcomes of C. Between A, B, and C, the following measurements can be used to complete the tripartite quantum communication kABC.

$${k}_{\rm{ABC}}=\left\{\begin{array}{ll}0&{\rm{for}}\ {\rm{outcomes}}\ 0\ {\rm{and}}\ 2\\ 1&{\rm{otherwise}}.\end{array}\right.$$
(3)

At the same time, A and B can communicate with each other in the following way kAB.

$${k}_{\rm{AB}}=\left\{\begin{array}{ll}0&{\rm{for}}\ {\rm{outcomes}}\ 0\ {\rm{and}}\ 1\\ 1&{\rm{otherwise}}.\end{array}\right.$$
(4)

kABC is completely correlated with C’s measurement results; therefore, it constitutes a random string shared by the three users. On the other hand, string kAB is completely independent of C’s data conditioned on either of C’s two measurement outcomes, the value of kAB is 0 or 1, each with probability 1/2. So the simplest layered quantum communication can be achieved by the above method. Of course, we can use the high-dimensional GHZ state or (3, 3, 2) state to complete the same quantum communication protocol, but it is proved that the communication efficiency is lower29.

In order to assess usefulness of the produced (4, 4, 2) state for quantum key distribution, we calculate asymptotic key rates R for each layer. We use a method developed in ref. 33, which considers security against adversaries using coherent attacks. More precisely we use their equation (23), which uses parameters QBERZ, QBERX, QBERZ(AB), and QBERZ(AC). These are in order: quantum bit error rate between all three parties in Z and X basis, and quantum bit error rate in Z basis between pairs of users A, B and A, C. All of these parameters can be obtained directly from experimental data. We present values of these experimental parameters for all four layers in Table 1. Plugging the highest values from these intervals into equation (23) of ref. 33 yields a lower bound for the asymptotic key rate (bits per round), which also listed in the table.

Table 1 Security analysis for QKD in different subspaces.
Full size table

Discussion

We have created a (4, 4, 2) quantum state using photons’ path and polarization DoFs. This state exhibits different correlations from all the previously reported state26,27,28 because we have promoted the dimension from 3 to 4. The post-selection scheme we employed to increase the dimension allows a heralded generation of the (4, 4, 2) state, with an overhead of 1/2 compared to the canonical (2, 2, 2) generation. We have also experimentally demonstrated, as a proof-of-principle, that this quantum state can complete an efficient layered quantum communication network. Compared with OAM DoF or time bin DoF, the path DoF has higher fidelity and more controllability, so many physical phenomena15,17,23 and quantum information tasks22,34,35 are realized in the path DoF. Our experimental method can be effectively extended to produce more kinds of multipartite high-dimensional entanglement32,36, and to construct more complex high-dimensional quantum networks.

The biggest remaining challenge is the efficiency of promoting bipartite sources of downconversion into multipartite states. Correlated single-photon sources would provide an obvious route toward more efficient production and would also be compatible with our post-selection scheme.

Methods

Experiment setup

First, we prepare a standard three-photon qubit GHZ state, as shown in Fig. 2. The ultraviolet pulse laser (390 nm) from the doubler sequentially pumps two entanglement source (780 nm). Then, the two entanglement sources, both are prepared in the state \((\left|HH\right\rangle +\left|VV\right\rangle )/\sqrt{2}\). Afterward, the output photon 2 and 3 are directed to a polarizing beam splitter (PBS1). Here, all the PBSs are set to transmit horizontal polarization (H) and reflect vertical polarization (V). If there is one and only one photon in each output of the four-photon source part, the state \((\left|HHH\right\rangle +\left|VVV\right\rangle )/\sqrt{2}\) is generated (one of the photons acts as a trigger)37.

Then, one photon is directly measured in the polarization basis (particle 3), and the other two photons incident to a post-selection setup consisting of BD1, 2, PBS2 and half-wave plates (HWPs) set at 22.5∘. At this time, we define the polarization DoF of particle 1 and particle 2 in the upper path as \(\left|H\right\rangle \longrightarrow \left|0\right\rangle\), \(\left|V\right\rangle \longrightarrow \left|2\right\rangle\), and lower path \(\left|H\right\rangle \longrightarrow \left|1\right\rangle\) and \(\left|V\right\rangle \longrightarrow \left|3\right\rangle\). The function of this device is to post-select the two-dimensional entangled state \((\left|HH\right\rangle +\left|VV\right\rangle )/\sqrt{2}\) into the four-dimensional entangled state \((\left|00\right\rangle +\left|11\right\rangle +\left|22\right\rangle +\left|33\right\rangle )/2\)13,38,39 (see Supplementary Note 1).

After this post-selection, the quantum state becomes:

$$\begin{array}{ll}\left|{\Psi }_{442}\right\rangle\, =\,\frac{1}{2}(\left|00\right\rangle +\left|22\right\rangle )\left|0\right\rangle +\frac{1}{2}(\left|11\right\rangle +\left|33\right\rangle )\left|1\right\rangle \\ \,=\,\frac{1}{2}(\left|000\right\rangle +\left|111\right\rangle +\left|220\right\rangle +\left|331\right\rangle ).\end{array}$$
(5)

Since the witness of quantum states and layered quantum communication protocols only needs two-dimensional subspace projection measurements, we only perform the measurement in two-dimensional subspaces. The measurement device consists of HWPs, QWPs, BDs, and PBSs. These setup can also be used to construct measurement setups of any dimension40.