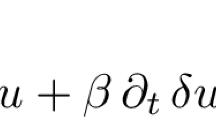Abstract
We prove the existence of almost-periodic solutions for quasi-linear perturbations of the Airy equation. This is the first result about the existence of this type of solutions for a quasi-linear PDE. The solutions turn out to be analytic in time and space. To prove our result we use a Craig–Wayne approach combined with a KAM reducibility scheme and pseudo-differential calculus on \(\mathbb {T}^\infty \).
Similar content being viewed by others
1 Introduction
In this paper we study response solutions for almost-periodically forced quasilinear PDEs close to an elliptic fixed point.
The problem of response solutions for PDEs has been widely studied in many contexts, starting from the papers [24, 25], where the Author considers a periodically forced PDE with dissipation. In the presence of dissipation, of course there is no small divisors problem. However as soon as the dissipation is removed, small divisors appear even in the easiest possible case of a periodic forcing when the spacial variable is one dimensional.
The first results of this type in absence of dissipation were obtained by means of a KAM approach [16,17,18,19, 22, 28]. However, a more functional approach, via a combination of a Ljapunov-Schmidt reduction and a Newton scheme, in the spirit of [24, 25], was proposed by Craig–Wayne [14], and then generalized in many ways by Bourgain; see for instance [5,6,7] to mention a few. All the results mentioned above concern semi-linear PDEs and the forcing is quasi-periodic.
In more recent times, the Craig–Wayne–Bourgain approach has been fruitfully used and generalized in order to cover quasi-linear and fully nonlinear PDEs, again in the quasi-periodic case; see for instance [1, 2, 12, 15].
Regarding the almost-periodic case, most of the classical results are obtained via a KAM-like approach; see for instance [9, 10, 23]. A notable exception is [8], where the Craig–Wayne–Bourgain method is used. More recently there have been results such as [20, 26, 27], which use a KAM approach. We mention also [3, 4, 11, 29] which however are tailored for an autonomous PDE.
All the aforementioned results, concern semi-linear PDEs, with no derivative in the nonlinearity. Moreover they require a very strong analyticity condition on the forcing term. Indeed the difficulty of proving the existence of almost-periodic response solution is strongly related to the regularity of the forcing, since one can see an almost periodic function as the limit of quasi-periodic ones with an increasing number of frequencies. If such limit is reached sufficiently fast, the most direct strategy would be to iteratively find approximate quasi-periodic response solutions and then take the limit. This is the overall strategy of [23] and [20, 26, 27]. However this procedure works if one considers a sufficiently regular forcing term and a bounded nonlinearity, but becomes very delicate in the case of unbounded nonlinearities.
In the present paper we study the existence of almost-periodic response solutions, for a quasi-linear PDE on \(\mathbb {T}\). To the best of our knowledge this is the first result of this type.
Specifically we consider a quasi-linear Airy equation
where Q is a Hamiltonian, quadratic nonlinearity and \({{\mathfrak {f}}}\) is an analytic forcing term with zero average w.r.t. x. We assume \({{\mathfrak {f}}}\) to be “almost-periodic” with frequency \(\omega \in \ell ^{\infty }\), in the sense of Definition 1.1.
We mention that in the context of reducibility of linear PDEs a problem of this kind has been solved in [21]. Our aim is to provide a link between the linear techniques of [21] and the nonlinear Craig–Wayne–Bourgain method. Note that such a link is nontrivial, and requires a delicate handling; see below.
The overall setting we use is the one of [1]. However their strategy is taylored for Sobolev regularity; the quasi-periodic analytic case has been covered in [13]. Unfortunately the ideas of [13] cannot be directly applied in the almost-periodic case. Roughly, it is well known that the regularity and the small-divisor problem conflict. Thus, in the almost-periodic case one expect this issue to be even more dramatic. Specifically, we were not able to define a “Sobolev” norm for almost-periodic functions, satisfying the interpolation estimates needed in the Nash-Moser scheme; this is why we cannot use the theorem of [13].
Let us now present our main result in a more detailed way.
First of all we note that (1.1) is an Hamiltonian PDE whose Hamiltonian is given by
where \(G(u, u_x)\) is a cubic Hamiltonian density of the form
and the symplectic structure is given by \(J=\partial _x\). The Hamiltonian nonlinearity \(Q(u, \ldots , u_{xxx})\) is therefore given by
and the Hamilton equations are
We look for an almost-periodic solution to (1.1) with frequency \(\omega \) in the sense below.
For \(\eta >0\), define the set of infinite integer vectors with finite support as
Note that \(\ell _i \ne 0\) only for finitely many indices \(i \in {\mathbb {N}}\). In particular \(\mathbb {Z}^\infty _*\) does not depend on \(\eta \).
Definition 1.1
Given \(\omega \in [1,2]^{\mathbb {N}}\) with rationally independent componentsFootnote 1 and a Banach space \((X,|\cdot |_X)\), we say that \(F(t):{\mathbb {R}}\rightarrow X\) is almost-periodic in time with frequency \(\omega \) and analytic in the strip \(\sigma >0\) if we may write it in totally convergent Fourier series
We shall be particularly interested in almost-periodic functions where \(X={{\mathcal {H}}}_0({\mathbb {T}}_\sigma )\)
is the space of analytic, real on real functions \({\mathbb {T}}_s\rightarrow {\mathbb {C}}\) with zero-average, where \({\mathbb {T}}_s := \{ \varphi \in {\mathbb {C}}: {\mathrm{Re}}(\varphi ) \in {\mathbb {T}}, \ |{\mathrm{Im}}(\varphi )| \le s \}\) is the thickened torus. We recall that a function \(u : {\mathbb {T}}_s \rightarrow {\mathbb {C}}\) is real on real if for any \(x \in {\mathbb {T}}\), \(u(x) \in {\mathbb {R}}\).
Of course we need some kind of Diophantine condition on \(\omega \). We give the following, taken from [9, 21].
Definition 1.2
Given \(\gamma \in (0, 1)\), we denote by \({\mathtt {D}_\gamma }\) the set of Diophantine frequencies
We are now ready to state our main result.
Theorem 1.3
(Main Theorem) Fix \(\overline{\gamma }\). Assume that \({{\mathfrak {f}}}\) in (1.1) is almost-periodic in time and analytic in a strip S (both in time and space). Fix \(\overline{s}<S\). If \({{\mathfrak {f}}}\) has an appropriately small norm depending on \(S-\overline{s}\), namely
then there is a Cantor-like set \({{\mathcal {O}}}^{(\infty )}\subseteq {\mathtt {D}_{\overline{\gamma }}}\) with positive Lebesgue measure, and for all \(\omega \in {{\mathcal {O}}}^{(\infty )}\) a solution to (1.1) which is almost-periodic in time with frequency \(\omega \) and analytic in a strip \(\overline{s}\) (both in time and space).
Remark 1.4
Of course the same result holds verbatim if we replace the quadratic polynomial Q by a polinomial of arbitrary degree. We could also assume that the coefficients \({\mathtt {c}}_j\) appearing in (1.4) depend on x and \(\omega t\). In that case Theorem 1.3 holds provided we further require a condition of the type \( \sup _{j} |\partial _x^2 {\mathtt {c}}_j|_S \le C\). Actually one could also take Q to be an analytic function with a zero of order two. However this leads to a number of long and non particularly enlightening calculations.
To prove Theorem 1.3 we proceed as follows. First of all we regard (1.1) as a functional Implicit Function Problem on some appropriate space of functions defined on an infinite dimensional torus; see Definition 2.1 below. Then in Sect. 3 we prove an iterative “Nash-Moser-KAM” scheme to produce the solution of such Implicit Function Problem. It is well known that an iterative rapidly converging scheme heavily relies on a careful control on the invertibility of the linearized operator at any approximate solution. Of course, in the case of a quasi-linear PDE this amounts to study an unbounded non-constant coefficients operator. To deal with this problem, at each step we introduce a change of variables \(T_n\) which diagonalizes the highest order terms of the linearized operator. An interesting feature is that \(T_n\) preserves the PDE structure. As in [13] and differently from the classical papers, at each step we apply the change of variables \(T_n\) to the whole nonlinear operator. This is not a merely technical issue. Indeed, the norms we use are strongly coordinate-depending, and the change of variable \(T_n\) that we need to apply are not close-to-identity, in the sense that \(T_n - \mathtt { Id}\) is not a bounded operator small in size.
In Sect. 4 we show how to construct the change of variables \(T_n\) satisfying the properties above. Then in order to prove the invertibility of the linearized operator after the change of variables \(T_n\) is applied, one needs to perform a reducibility scheme: this is done in Sect. 5. For a more detailed description of the technical aspects see Remark 3.2.
2 Functional Setting
As it is habitual in the theory of quasi-periodic functions we shall study almost periodic functions in the context of analytic functions on an infinite dimensional torus. To this purpose, for \(\eta ,s>0\), we define the thickened infinite dimensional torus \({\mathbb {T}}^\infty _s\) as
Given a Banach space \((X, | \cdot |_X )\) we consider the space \({{\mathcal {F}}}\) of pointwise absolutely convergent formal Fourier series \({\mathbb {T}}^\infty _s \rightarrow X\)
and define the analytic functions as follows.
Definition 2.1
Given a Banach space \((X, | \cdot |_X )\) and \(s > 0\), we define the space of analytic functions \({\mathbb {T}}^\infty _s \rightarrow X\) as the subspace
We denote by \({{\mathcal {H}}}_s\) the subspace of \({{\mathcal {H}}}({\mathbb {T}}^\infty _s, {{\mathcal {H}}}_0({\mathbb {T}}_s))\) of the functions which are real on real. Moreover, we denote by \( {{\mathcal {H}}}({\mathbb {T}}^\infty _{s}\times \mathbb {T}_s)\), the space of analytic functions \({\mathbb {T}}^\infty _s \times {\mathbb {T}}_s \rightarrow {\mathbb {C}}\) which are real on real. The space \({{\mathcal {H}}}_s\) can be identified with the subspace of zero-average functions of \( {{\mathcal {H}}}({\mathbb {T}}^\infty _{s}\times \mathbb {T}_s)\). Indeed if \(u \in {{\mathcal {H}}}_s\), then
For any \(u\in {{\mathcal {H}}}({\mathbb {T}}^\infty _{s}\times \mathbb {T}_s)\) let us denote
Throughout the algorithm we shall need to control the Lipschitz variation w.r.t. \(\omega \) of functions in some \({{\mathcal {H}}}({\mathbb {T}}^\infty _s,X)\), which are defined for \(\omega \) in some Cantor set. Thus, for \({{\mathcal {O}}}\subset {{\mathcal {O}}}^{(0)}\) we introduce the following norm.
Parameter dependence. Let Y be a Banach space and \(\gamma \in (0, 1)\). If \(f : \Omega \rightarrow Y\), \(\Omega \subseteq [1, 2]^{\mathbb {N}}\) is a Lipschitz function we define
If \(Y = {{\mathcal {H}}}_s\) we simply write \(| \cdot |_\sigma ^{{\mathrm{sup}}}\), \(| \cdot |_\sigma ^{{\mathrm{lip}}}\), \(| \cdot |_\sigma ^{\Omega }\). If Y is a finite dimensional space, we write \(| \cdot |^{{\mathrm{sup}}}\), \(| \cdot |^{{\mathrm{lip}}}\), \(| \cdot |^{\Omega }\).
Linear operators. For any \(\sigma > 0\), \(m \in {\mathbb {R}}\) we define the class of linear operators of order m (densely defined on \(L^2({\mathbb {T}})\)) \({{\mathcal {B}}}^{\sigma , m}\) as
and for \({{\mathcal {T}}}\in {{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma , {{\mathcal {B}}}^{\sigma , m})\) we set
In particular we shall denote by \(\Vert \cdot \Vert _{{\sigma , m}}^{\Omega }\) the corresponding Lipshitz norm. Moreover if \(m=0\) we shall drop it, and write simply \(\Vert \cdot \Vert _{{\sigma }}\) or \(\Vert \cdot \Vert _{{\sigma }}^{\Omega }\).
3 The Iterative Scheme
Let us rewrite (1.1) as
where
where we \({{\mathfrak {f}}}(t,x)=f(\omega t,x)\) and, as custumary the unknown u is a function of \((\varphi ,x)\in \mathbb {T}^\infty \times \mathbb {T}\).
We introduce the (Taylor) notation
so that (3.1) reads
Note that \(Q_0\) is of the form
with the coefficients \(q^{(0)}_{i,j} \) satisfying
where the constant C depends clearly on \(|{\mathtt {c}}_0|, \ldots , |{\mathtt {c}}_3|\). In particular, this implies that for all \(u\in {{\mathcal {H}}}_s\) one has the following.
-
Q1.
\(|Q_0(u)|_{s-\sigma } \lesssim \sigma ^{-4}|u|_s^2\)
-
Q2.
\(|Q_0'(u)[h]|_{s-\sigma }\lesssim \sigma ^{-4}|u|_s |h|_s\)
We now fix the constants
where \(\varepsilon _0\) is such that
Introduce
We also set \({{\mathcal {O}}}^{(-1)}:= {\mathtt {D}}_{\overline{\gamma }}\) and
Proposition 3.1
There exists \(\tau ,\tau _1,\tau _2,\tau _3, {\mathtt {C}},\epsilon _0\) (pure numbers) such that for
for all \(n\ge 1\) the following hold.
-
1.
There exist a sequence of Cantor sets \({{\mathcal {O}}}^{(n)}\subseteq {{\mathcal {O}}}^{(n-1)}\), \(n\ge 1\) such that
$$\begin{aligned} {{\mathbb {P}}} ({{\mathcal {O}}}^{(n-1)}\setminus {{\mathcal {O}}}^{(n)}) \lesssim \frac{\gamma _0}{n^2}. \end{aligned}$$(3.11) -
2.
For \(n\ge 1\), there exists a sequence of linear, invertible, bounded and symplectic changes of variables defined for \(\omega \in {{\mathcal {O}}}^{(n-1)}\), of the form
$$\begin{aligned} T_{n} v(\varphi ,x)= (1+\xi ^{(n)}_x)v( \varphi +\omega \beta ^{(n)}(\varphi ), x+ \xi ^{(n)}(\varphi ,x) + p^{(n)}(\varphi ))\, \end{aligned}$$(3.12)satisfying
$$\begin{aligned} | \xi ^{(n)}|_{s_{n-1}- \sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}},|\beta ^{(n)}|_{s_{n-1}- \sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}}, |p^{(n)}|_{s_{n-1}- \sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}} \lesssim \sigma _{n-1}^{-\tau _1} \varepsilon _{n-1} e ^{C \sigma _{n-1}^{-\mu }}, \end{aligned}$$(3.13)for some constant \(C>0\).
-
3.
For \(n\ge 0\), there exists a sequence of functionals \(F_n(u) \equiv F_n(\omega , u(\omega ))\), defined for \(\omega \in {{\mathcal {O}}}^{(n-1)}\), of the form
$$\begin{aligned} F_n(u)=f_n + L_n u +Q_n(u), \end{aligned}$$(3.14)such that
-
(a)
\(L_n\) is invertible for \(\omega \in {{\mathcal {O}}}^{(n)}\) and setting
$$\begin{aligned} h_n:=-L_n^{-1}f_n, \end{aligned}$$(3.15)there exists \({{\mathtt {r}}}_n ={{\mathtt {r}}}_{n}(\varphi )\in {{\mathcal {H}}}({\mathbb {T}}^\infty _{s_{n-1}-3\sigma _{n-1}})\) such that
$$\begin{aligned} \begin{aligned}&F_{n}(u) = {{\mathtt {r}}}_nT_{n}^{-1}F_{n-1}(h_{n-1}+T_k u),\qquad n\ge 1, \\&|{{\mathtt {r}}}_n-1|_{s_{n-1}-3\sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}} \le \sigma _{n-1}^{-\tau _2} e^{C\sigma _{n-1}^{-\mu }}\varepsilon _{n-1} \end{aligned} \end{aligned}$$(3.16) -
(b)
\(f_n=f_n(\varphi ,x)\) is a given function satisfying
$$\begin{aligned} |f_n|_{s_{n-1}-2\sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}}\lesssim \sigma _{n-1}^{-4} \varepsilon _{n-1}^2,\qquad n\ge 1 \end{aligned}$$(3.17) -
(c)
\(L_n\) is a linear operator of the form
$$\begin{aligned} L_n = \omega \cdot \partial _\varphi + (1+A_n)\partial _{xxx} + B_n(\varphi ,x)\partial _x + C_n(\varphi ,x) \end{aligned}$$(3.18)such that
$$\begin{aligned} \frac{1}{2\pi }\int _\mathbb {T}B_n(\varphi ,x) dx = \overline{b}_n \end{aligned}$$(3.19)and for \(n\ge 1\)
$$\begin{aligned} \begin{aligned} |A_n-A_{n-1}|^{{{\mathcal {O}}}^{(n-1)}}&\le \sigma _{n-1}^{-\tau _2} e^{C\sigma _{n-1}^{-\mu }}\varepsilon _{n-1},\\ |B_{n}-B_{n-1}|_{s_{n-1}-3\sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}}&\lesssim \sigma _{n-1}^{-\tau _2} e^{C\sigma _{n-1}^{- \mu }}\varepsilon _{n-1} \\ |C_{n}-C_{n-1}|_{s_{n-1}-3\sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}}&\lesssim \sigma _{n-1}^{-\tau _2} e^{C\sigma _{n-1}^{- \mu }}\varepsilon _{n-1} . \end{aligned} \end{aligned}$$(3.20) -
(d)
\(Q_n\) is of the form
$$\begin{aligned} Q_n(u)= \sum _{\begin{array}{c} 0\le i\le 2,\,0\le j\le 3 \\ 0\le i+j\le 4 \end{array}} q^{(n)}_{i,j} (\varphi ,x) (\partial _x^i u)(\partial _x^j u) \end{aligned}$$(3.21)with the coefficients \(q^{(n)}_{i,j} (\varphi ,x) \) satisfying (3.5) for \(n=0\), while for \(n\ge 1\)
$$\begin{aligned} \begin{aligned}&\sum _{\begin{array}{c} 0\le i\le 2,\,0\le j\le 3 \\ 0\le i+j\le 4 \end{array}} |q^{(n)}_{i,j}|_{s_{n-1}-3\sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}}\le C\sum _{l=1}^{n}2^{-l}, \\&|q^{(n)}_{i,j}-q^{(n-1)}_{i,j}|_{s_{n-1}-3\sigma _{n-1}}^{{{\mathcal {O}}}^{(n-1)}}\lesssim \sigma _{n-1}^{-\tau _3} e^{C\sigma _{n-1}^{- \mu }}\varepsilon _{n-1}. \end{aligned} \end{aligned}$$(3.22)
-
(a)
-
4.
Finally one has
$$\begin{aligned} |h_n|_{s_n}^{{{\mathcal {O}}}^{(n)}}\le \varepsilon _n \end{aligned}$$(3.23)
Moreover, setting
and
then
is well defined for \(\omega \in {{\mathcal {O}}}^{(\infty )}\), belongs to \({{\mathcal {H}}}_{\overline{s}}\), and solves \(F(u_\infty )=0\). Finally the \({{\mathcal {O}}}^{(\infty )}\) has positive measure; precisely
From Proposition 3.1 our main result Theorem 1.3 follows immediately by noting that (3.7) and (3.10) follow from (1.7) for an appropriate choice \(\varepsilon (S-\overline{s})\).
Remark 3.2
Let us spend few words on the strategy of the algorithm. At each step we apply an affine change of variables translating the approximate solution to zero; the translation is not particularly relevant and we perform it only to simplify the notation. On the other hand the linear change of variables is crucial.
In (3.14) we denote by \(f_n\) the “constant term”, by \(L_n\) is the “linearized” term and by \(Q_n\) the “quadratic” part. In this way the approximate solution at the n-th step is \(h_n=-L_n^{-1}f_n\).
In a classical KAM algorithm, in order to invert \(L_n\) one typically applies a linear change of variables that diagonalizes \(L_n\); this, together with the translation by \(h_n\) is the affine change of variables mentioned above, at least in the classical KAM scheme.
Unfortunately, in the case of unbounded nonlinearities this cannot be done. Indeed in order to diagonalize \(L_n\) in the unbounded case, one needs it to be a pseudo-differential operator. On the other hand, after the diagonalization is performed, one loses the pseudo-differential structure for the subsequent step. Thus we chose the operators \(T_n\) in (3.12) in such a way that we preserve the PDE structure and at the same time we diagonalize the highest order terms.
In the [1]-like algorithm the Authors do not apply any change of variables, but they use the reducibility of \(L_n\) only in order to deduce the estimates. However such a procedure works only in Sobolev class. Indeed in the analytic case, at each iterative step one needs to lose some analyticity, due to the small divisors. Since we are studying almost-periodic solutions, we need the analytic setting to deal with the small divisors. As usual, the problem is that the loss of the analyticity is related to the size of the perturbation; in the present case, at each step \(L_n\) is a diagonal term plus a perturbation \(O(\varepsilon _0)\) with the same \(\varepsilon _0\) for all n.
A more refined approach is to consider \(L_n\) as a small variation of \(L_{n-1}\); however the problem is that such small variation is unbounded. As a consequence, the operators \(T_n\) are not “close-to-identity”. However, since \(F_n\) is a differential operator, then the effect of applying \(T_n\) is simply a slight modification of the coefficients; see (3.20) and (3.22). Hence there is a strong motivation for applying the operators \(T_n\). In principle we could have also diagonalized the terms up to order \(-k\) for any \(k\ge 0\); however the latter change of variables are close to the identity and they introduce pseudo-differential terms.
3.1 The Zero-th Step
Item 1., 2. are trivial for \(n=0\) while item 3.(b), (c), (d) amount to the definition of \(F_0\), see (3.2), (3.3), (3.4). Regarding item 3.(a) the invertibility of \(L_0\) follows from the definition of \({{\mathcal {O}}}^{(0)}\). Indeed, consider the equation
with
we have the following result.
Lemma 3.3
(Homological equation) Let \(s > 0\), \(0<\sigma <1\), \(f_0 \in {{\mathcal {H}}}_{s+\sigma }\), \(\omega \in {{\mathcal {O}}}^{(0)}\) (see (1.6)). Then there exists a unique solution \(h_0 \in {{\mathcal {H}}}_s\) of (3.27) . Moreover one has
for some constant \(\tau =\tau (\eta ) > 0\).
Remark 3.4
Note that from Lemma 3.3 above it follows that there is \({\mathtt {C}}_0\) such that a solution \(h_0\) of (3.27) actually satisfies
where we recall that by (3.6), \(\mu > \max \{ 1, \frac{1}{\eta }\}\). Of course the constant \({\mathtt {C}}_0\) is correlated with the correction to the exponent \(\frac{1}{\eta }\).
From Lemma 3.3 and (3.27) it follows that \(h_0\) is analytic in a strip \(s_0\) (where \(S=s_0+\sigma _{-1}\) is the analyticity of f, to be chosen). Moreover, by Lemma 3.3 the size of \(h_0\) is
proving item 4. for \(|f_0|_S\) small enough, which is true by (3.7).
3.2 The \( n+1\)-th Step
Assume now that we iterated the procedure above up to \(n\ge 0\) times. This means that we arrived at a quadratic equation
Defined on \({{\mathcal {O}}}^{(n-1)}\) (recall that \({{\mathcal {O}}}^{(-1)}={\mathtt {D}_\gamma }\)).
By the inductive hypothesis (3.22) we deduce that for all \(0<s-\sigma < s_{n-1}- 3\sigma _{n-1}\) one has
Moreover, again by the inductive hypothesis, we can invert \(L_n\) and define \(h_n\) by (3.15). Now we set
where
and \(r_{n+1}\) are to be chosen in order to ensure that \(L_{n+1}:= F'_{n+1}(0)\) has the form (3.18) with \(n\rightsquigarrow n+1\).
Of course by Taylor expansion we can identify
Remark 3.5
Note that the last equality in (3.34) follows from the fact that the nonlinearity Q in (1.1) is quadratic. In the general case, the last term is controlled by the second derivative, and thus one has to assume a bound of the type (3.31) for \(Q''\).
In Sect. 4 we prove the following
Proposition 3.6
Assuming that
for some \(C>0\), there exist \(\xi ^{(n+1)}\), \(\beta ^{(n+1)}\), \(p^{(n+1)}\) and \( {{\mathtt {r}}}_{n+1}\in {{\mathcal {H}}}({\mathbb {T}}^\infty _{s_n - \sigma _n} \times {\mathbb {T}}_{s_n - \sigma _n})\), defined for all \(\omega \in {{{\mathcal {O}}}^{(n)}}\) and satisfying
such that (3.33) is well defined and symplectic as well as its inverse, and moreover
and (3.19) and (3.20) hold with \(n\rightsquigarrow n+1\).
The assumption (3.35) follows from (3.10), provided that we choose the constants \(\tau ,{\mathtt {C}}\) and \(\epsilon _0\) appropriately.
We now prove (3.21) and (3.22) for \(n\rightsquigarrow n+1\), namely the following result.
Lemma 3.7
One has
with the coefficients \(q^{(n+1)}_{i,j} (\varphi ,x) \) satisfying
Proof
By construction
Now we first note that
where
Hence the terms \(\partial _x^i T_{n+1}v\) are of the form
Inserting (3.41) into (3.40) we get
so that
In order to obtain the bound (3.43) we used the first line of (3.22) to control the sums appearing in (3.42).
Finally, since
the bound follows. \(\square \)
Now, by (3.31a) and (3.34) \(f_{n+1}=f_{n+1}(\varphi ,x)\) satisfies
In Sect. 5 we prove the existence of a Cantor set \({{\mathcal {O}}}^{(n+1)}\) where item 3.(a) of the iterative lemma holds with \(n\rightsquigarrow n+1\).
Proposition 3.8
Assume that
with \(\tau \ge \tau _2\). Setting \(\lambda _3^{(n+1)}:=1+A_{n+1}\), there exist Lipschitz functions
satisfying
such that setting
for \(\omega \in {{\mathcal {E}}}^{(n+1)}\) there exists an invertible and bounded linear operator \(M^{(n+1)}\)
such that
The assumption (3.45) follows from (3.10), provided that we choose the constants \(\tau ,{\mathtt {C}}\) and \(\epsilon _0\) appropriately.
Remark 3.9
Note that in the context of [13] Proposition 3.8 is much simpler to prove, because in order to diagonalize the linearized operator one uses tame estimates coming from the Sobolev regularity on the boundary of the domain. Then the smallness conditions are much simpler to handle. Here we have to strongly rely on the fact that \(L_{n+1}\) is a “small” unbounded perturbation of \(L_n\) in order to show that the operators \(M^{(n)}\) and \(M^{(n+1)}\) are close to each other. This is a very delicate issue; see Lemma 5.2 and Sect. 5.3, which are probably the more technical parts of this paper.
Lemma 3.10
(Homological equation) Set
For \(\omega \in {{\mathcal {O}}}^{(n+1)}:= {{\mathcal {U}}}^{(n+1)}\cap {{\mathcal {E}}}^{(n+1)}\) one has
and one has
Proof
The result follows simply by using the definition of \({{\mathcal {O}}}^{(n+1)}\) and applying Lemma A.7. \(\square \)
Of course from Lemma 3.10 it follows that,
Now we want to show inductively that
for \(\varepsilon _0\) small enough.
By the definition of \(\varepsilon _n\) in (3.6), (3.54) is equivalent to
Since the r.h.s. of (3.55) admits a positive minimum, we can regard it as a smallness condition on \(\varepsilon _0\), which is precisely (3.10).
We now prove (3.11) with \(n\rightsquigarrow n+1\). We only prove the bound for the set \({{\mathcal {E}}}^{(n)} \setminus {{\mathcal {E}}}^{(n+1)}\). The other one can be proved by similar arguments (it is actually even easier). Let us start by writing
Lemma 3.11
Denote \(|\ell |_1\) as in (1.5) with \(\eta \rightsquigarrow 1\). For any \((\ell , j, j') \ne (0, j, j)\) such that \(|\ell |_1 \le n^{2}\), one has that \({{\mathcal {R}}}(\ell , j , j') = \emptyset \).
Proof
Let \((\ell , j, j') \in {\mathbb {Z}}^\infty _* \times ({\mathbb {Z}}\setminus \{ 0 \})\times ({\mathbb {Z}}\setminus \{ 0 \})\), \((\ell , j, j') \ne (0, j, j)\), \(|\ell |_1 \le n^{2}\). If \(j = j'\), clearly \(\ell \ne 0\) and \({{\mathcal {R}}}(\ell , 0, 0) = \emptyset \) because \(\omega \in {\mathtt {D}_{\overline{\gamma }}}\) with \(\overline{\gamma }>2 \gamma _{n+1}\); recall (3.6). Hence we are left to analyze the case \(j \ne j'\).
By (3.47), for any \(j, j' \in {\mathbb {Z}}\setminus \{ 0 \}\), \(j \ne j'\)
Therefore, for any \(\omega \in {{\mathcal {E}}}^{(n)}\)
where in the last inequality we used (3.6) and the fact that, by (A.4) one has
The estimate (3.58) clearly implies that \({{\mathcal {R}}}(\ell , j, j') = \emptyset \) for \(|\ell |_1 \le n^2\). \(\square \)
Lemma 3.12
Let \({{\mathcal {R}}}(\ell , j, j') \ne \emptyset \). Then \(\ell \ne 0\), \(|j^3 - j'^3| \lesssim \Vert \ell \Vert _1\) and \({{\mathbb {P}}}\Big ({{\mathcal {R}}}(\ell , j, j')\Big ) \lesssim \frac{\gamma _{n+1}}{{\mathtt {d}}(\ell )}\)
Proof
The proof is identical to the one for Lemma 6.2 in [21], simply replacing \(j^2\) with \(j^3\). \(\square \)
By (3.56) and collecting Lemmata 3.11, 3.12, one obtains that
where in the last inequality we used Lemma A.8. Thus (3.11) follows.
We now study the convergence of the scheme. Precisely we show that the series (3.25) converges totally in \({{\mathcal {H}}}_{\overline{s}}\) . Note that
Thus, using (3.60) into (3.25) we get
Now since
we deduce that \(u_\infty \in {{\mathcal {H}}}_{\overline{s}}\). Finally by continuity
so the assertion follows since (recall \(\overline{s}:= s_\infty - \sum _{n\ge 1} \sigma _n\) and (3.62))
We finally conclude the proof of Proposition 3.1 by showing that (3.26) holds.
First of all, reasoning as in Lemma 3.12 and using Lemma A.8, we see that
Then
4 Proof of Proposition 3.6
In order to prove Proposition 3.6, we start by dropping the index n, i.e. we set \({{\mathcal {L}}} \equiv L_n\) (see (3.18)) and \({{\mathcal {Q}}} \equiv Q'_n(h_n)\) (see (3.34)).
More generally, we consider a Hamiltonian operator of the form
defined for all \(\omega \in \Omega \subseteq {\mathtt {D}_\gamma }\) and \(\lambda _3\), \(a_0, a_1, d_0 \ldots , d_3\) satisfy the following properties.
-
1.
There is \(\delta _0\) small enough such that
$$\begin{aligned} |\lambda _3 -1|^{\Omega } \le \delta _0 \end{aligned}$$(4.2) -
2.
There is \(\rho >0\) such that \(a_i\in {{\mathcal {H}}}({\mathbb {T}}^\infty _\rho \times {\mathbb {T}}_\rho )\) and
$$\begin{aligned} | a_i |_{\rho }^{\Omega } \le \delta _0,\qquad i=0,1 \end{aligned}$$(4.3)and moreover
$$\begin{aligned} \lambda _1 := \frac{1}{2 \pi } \int _{\mathbb {T}}a_1(\varphi , x)\, d x \end{aligned}$$(4.4)i.e. it does not depend on \(\varphi \).
-
3.
\(d_0 \ldots , d_3 \in {{\mathcal {H}}}({\mathbb {T}}^\infty _\rho \times {\mathbb {T}}_\rho )\) (note that by the Hamiltonian structure \(d_2 = \partial _x d_3\)) and they satisfy the estimate
$$\begin{aligned} | d_i |_{\rho }^{\Omega } \lesssim \delta , \end{aligned}$$(4.5)for some \(\delta \ll \min \{\delta _0,\rho \}\).
Let us now choose \(\zeta \) such that \(0<\zeta \ll \rho \) and
for some \(\tau '>0\). We shall conjugate \({{\mathcal {L}}}^{(0)}\) to a new operator \(\frac{1}{{\mathtt {r}}}{{\mathcal {L}}}_+\) with \({{\mathtt {r}}}={{\mathtt {r}}}(\varphi )\) an explicit function with
with the coefficients satisfying
and
This will allow us to conclude the proof of Proposition 3.6.
4.1 Elimination of the x-Dependence from the Highest Order Term
Consider an analytic function \(\alpha (\varphi , x)\) (to be determined) and let
We choose \(\alpha (\varphi , x)\) and \(m_3(\varphi )\) in such a way that
which implies
By (4.2), (4.5) and Lemma A.5 one has
Note that for any \(0<\zeta \ll \rho \) such that \(\delta \zeta ^{-1} \ll 1\), by Lemma A.1, \(x \mapsto x + \alpha (\varphi , x)\) is invertible and the inverse is given by \(y \mapsto y + {{\widetilde{\alpha }}}(\varphi , y)\) with
A direct calculations shows that
and the following conjugation rules hold:
Clearly one can get similar conjugation formulae for higher order derivatives, having expression similar to (3.41). In conclusion
for some (explicitly computable) coefficients \(b_i\), where in the last equality we used (4.10) and the fact that \({{\mathcal {T}}}_1\) is symplectic, so that \(b_2(\varphi , x) = 2 \partial _x m_3(\varphi ) = 0\).
Furthermore, the estimates (4.2), (4.3), (4.12), (4.13), Corollary A.2 and Lemmata A.3, A.4 imply that for \(0 < \zeta \ll \rho \)
4.2 Elimination of the \(\varphi \)-Dependence from the Highest Order Term
We now consider a quasi periodic reparametrization of time of the form
where \(\beta : {\mathbb {T}}^\infty _{\rho -\zeta } \rightarrow {\mathbb {R}}\) is an analytic function to be determined. Precisely we choose \(\lambda _3^+ \in {\mathbb {R}}\) and \(\beta (\varphi )\) in such a way that
obtaining thus
where we recall the definition A.3. By the estimates (4.12) and by Lemma 3.3, one obtains that for \(0 < \zeta \ll \rho \)
By Lemma A.1 and (4.6) we see that \(\varphi \mapsto \varphi + \omega \beta (\varphi )\) is invertible and the inverse is given by \(\vartheta \mapsto \vartheta + \omega {{\widetilde{\beta }}}(\vartheta )\) with
The inverse of the operator \({{\mathcal {T}}}_2\) is then given by
so that
where
Therefore by the estimates (4.12), (4.21), (4.22) and by applying Corollary A.2, Lemma A.5, and (4.6), one gets
4.3 Time Dependent Traslation of the Space Variable
Let \(p : {\mathbb {T}}^\infty _{\rho -2\zeta } \rightarrow {\mathbb {R}}\) be an analytic function to be determined and let
Computing explicitly
and by (4.4) one has
We want to choose \(p(\varphi )\) in such a way that the x-average of \(d_1\) is constant. To this purpose we define
where for any \(a : {\mathbb {T}}^\infty _\sigma \times {\mathbb {T}}_\sigma \rightarrow {\mathbb {C}}\), \(\langle a \rangle _{\varphi , x}\) is defined by
(recall the definition A.3). By (4.26) and Lemma 3.3 one gets
Moreover
Finally using (4.26), (A.2) (with \(\Phi _\alpha = {{\mathcal {T}}}_3^{- 1}\)), (4.31), one gets
for some \(\tau '>0\).
4.4 Conclusion of the Proof
We start by noting that \({{\mathcal {T}}}:={{\mathcal {T}}}_3\circ {{\mathcal {T}}}_2\circ {{\mathcal {T}}}_1\) has the form (3.33) with \(p^{(n+1)}=p\), \(\beta ^{(n+1)}=\beta \) and \(\xi ^{(n+1)}(\varphi ,x) = \alpha (\varphi +\omega \beta (\varphi ),x+p(\varphi ))\). Hence, setting \( {{\mathtt {r}}}:={{\mathtt {r}}}_{n+1}\), \(\rho := s_n-\sigma _n\), \(\delta := \sigma _n^{-4}\varepsilon _n\), \(\delta _0:=2\varepsilon _0\) and \(\zeta := \sigma _n\) we denote
and thus Proposition 3.6 follows. \(\square \)
5 Proof of Proposition 3.8
In order to prove Proposition 3.8, we start by considering a linear Hamiltonian operator defined for \(\omega \in {{\mathcal {O}}} \subseteq {\mathtt {D}}_\gamma \) of the form
We want to show that, for any choice of the coefficients \(\lambda _3,a_1,a_0\) satisfying some hypotheses (see below), it is possible to reduce \({{\mathcal {L}}}\) to constant coefficients. Moreover we want to show that such reduction is “Lipshitz” w.r.t. the parameters \(\lambda _3,a_1,a_0\), in a sense that will be clarified below.
Regarding the coefficients, we need to require that
for some \(0<\ldots<\rho _m< \ldots < \rho _0\) and \(0<\ldots \ll \delta _m \ll \ldots \ll \delta _0\ll 1\) so that there is a third sequence \(\zeta _i\) such that \(0< \zeta _i < \rho _i\) and
for some \(\tau ,C>0\).
5.1 Reduction of the First Order Term
We consider an operator \({{\mathcal {L}}}\) of the form (5.1) satisfying the hypotheses above. We start by showing that it is possible to reduce it to constant coefficients up to a bounded reminder, and that such reduction is “Lipshitz” w.r.t. the parameters \(\lambda _3,a_1,a_0\).
Lemma 5.1
There exists a symplectic invertible operator \({{\mathcal {M}}} = {\mathrm{exp}}({{\mathcal {G}}})\), with \({{\mathcal {G}}} \equiv {{\mathcal {G}}}(\lambda _3, a_1)\) and an operator \({{\mathcal {R}}}_0 \equiv {{\mathcal {R}}}_0(\lambda _3, a_1, a_0)\) satisfying
for some \(C , \tau \gg 1\), such that
Proof
We look for \({{\mathcal {G}}}\) of the form
and we choose the function \(g (\varphi , x)\) where \(g = g(\lambda _3, a_1)\) in order to solve
By (5.2), one obtains that
and therefore
Of course we can also write the operator \({{\mathcal {G}}} := \pi _0^\bot g(\varphi , x) \partial _x^{- 1} = \sum _{i = 0}^{m } {{\mathcal {G}}}_i\) where \({{\mathcal {G}}}_i := \pi _0^\bot g_i(\varphi , x) \partial _x^{- 1}\) and one has
Again by (5.2), defining \({{\mathcal {P}}} := a_1 \partial _x + a_0\), one has that \({{\mathcal {P}}} = \sum _{i = 0}^{m} {{\mathcal {P}}}_i\), where \({{\mathcal {P}}}_i := a_1^{(i)} \partial _x + a_0^{(i)}\) satisfies
Therefore
where
Then (5.3), (5.9), (5.10) guarantee that the hypotheses of Lemmata A.10-A.11 are verified. Hence, we apply Lemma A.10-(ii) to expand the operator \(e^{-{{\mathcal {G}}}} {{\mathcal {P}}} e^{{\mathcal {G}}} - {{\mathcal {P}}}\), Lemma A.11-(ii) to expand \(e^{- {{\mathcal {G}}}} \partial _x^3 e^{{\mathcal {G}}} - \partial _x^3 - 3 g_x \partial _x\) and Lemma A.11-(iii) to expand \(e^{- {{\mathcal {G}}}} \omega \cdot \partial _\varphi e^{{\mathcal {G}}} - \omega \cdot \partial _\varphi \). The expansion of the multiplication operator \(a_0\) is already provided by (5.2). Hence, one obtains that there exist \(C, \tau \gg 1\) such that (5.4) is satisfied. \(\square \)
We now consider a “small modification” of the operator \({{\mathcal {L}}}\) in the following sense. We consider an operator
with
Of course we can apply Lemma 5.1 and conjugate \({{\mathcal {L}}}^+\) to
with \({{\mathcal {R}}}_0^+\) a bounded operator. We want to show that \({{\mathcal {L}}}_0^+\) is “close” to \({{\mathcal {L}}}_0\), namely the following result.
Lemma 5.2
One has
Proof
The first bound follows trivially from (5.14). Regarding the second bound one can reason as follows. As in Lemma 5.1, er can define \({{\mathcal {G}}}^+ := \pi _0^\bot g^+(\varphi , x) \partial _x^{- 1}\) with
so that
Defining \({{\mathcal {P}}}^+ := a_1^+ \partial _x + a_0^+\) and recalling that \({{\mathcal {P}}} := a_1 \partial _x + a_0\), by (5.14), one gets
The estimate on \({{\mathcal {R}}}_0^+ - {{\mathcal {R}}}_0\) follows by applying Lemmata A.13, A.14, and by the estimates (5.14), (5.19), (5.18). \(\square \)
5.2 Reducibility
We now consider an operator \({{\mathcal {L}}}_0\) of the form
with \({{\mathcal {P}}}_0\) a bounded operator and
and we show that, under some smallness conditions specified below it is possible to reduce it to constant coefficients, and that the reduction is “Lipschitz” w.r.t. the parameters \(\lambda _1, \lambda _3, {{\mathcal {P}}}_0\).
In order to do so, we introduce three sequences \( 0<\ldots< \rho _{m }< \ldots < \rho _0\), \(0<\ldots \ll \delta _{m } \ll \ldots \ll \delta _0\) and \(1\ll N_0 \ll N_1 \ll \cdots \) and we assume that setting \(\Delta _i=\rho _i-\rho _{i+1}\) one has
and
for some \(\tau ,C>0\).
We have the following result.
Lemma 5.3
Fix \(\gamma \in [\gamma _0/2,2\gamma _0]\). For \(k=0,\ldots ,m\) there is a sequence of sets \({{\mathcal {E}}}_k\subseteq {{\mathcal {E}}}_{k-1}\) and a sequence of symplectic maps \(\Phi _k\) defined for \(\omega \in {{\mathcal {E}}}_{k+1}\) such that setting \({{\mathcal {L}}}_0\) as in (5.20) and for \(k\ge 1\),
one has the following.
-
1.
\({{\mathcal {L}}}_k\) is of the form
$$\begin{aligned} {{\mathcal {L}}}_k := \omega \cdot \partial _\varphi + {{\mathcal {D}}}_k + {{\mathcal {P}}}_k \end{aligned}$$(5.27)where
-
The operator \({{\mathcal {D}}}_k\) is of the form
$$\begin{aligned} \begin{aligned} {{\mathcal {D}}}_k := {\mathrm{diag}}_{j \in {\mathbb {Z}}\setminus \{ 0 \}} \Omega _k(j), \quad \Omega _k(j) = \Omega _0 (j) + r_k(j) \end{aligned} \end{aligned}$$(5.28)with \(r_0(j)=0\) and for \(k\ge 1\), \(r_k(j)\) is defined for \(\omega \in {{{\mathcal {E}}}}_0={{\mathcal {O}}}\) and satisfies
$$\begin{aligned} \begin{aligned} \sup _{j \in {\mathbb {Z}}\setminus \{ 0 \}}|r_k(j) - r_{k - 1}(j)|^{{\mathcal {O}}} \le \delta _{k - 1} \sum _{i=1}^{k - 1}2^{-i} . \end{aligned} \end{aligned}$$(5.29) -
The operator \({{\mathcal {P}}}_k\) is such that
$$\begin{aligned} \begin{aligned}&\text {for} \quad 0 \le k \le m, \quad {{\mathcal {P}}}_k = \sum _{i = k}^{m} {{\mathcal {P}}}_k^{(i)},\quad \Vert {{\mathcal {P}}}_k^{(i)}\Vert _{\rho _i}^{{{{\mathcal {E}}}}_k} \le \delta _i \sum _{j=1}^{k} 2^{-j}, \quad \forall i = k, \ldots , m. \\ \end{aligned}\nonumber \\ \end{aligned}$$(5.30)
-
-
2.
One has \(\Phi _{k - 1} := {\mathrm{exp}}(\Psi _{k - 1})\), such that
$$\begin{aligned} \begin{aligned} \Vert \Psi _{k - 1} \Vert _{\rho _k}^{{{{\mathcal {E}}}}_k} \lesssim e^{C \Delta _{k-1}^{- \mu }} \Vert {{\mathcal {P}}}_{k - 1}^{(k - 1)}\Vert _{\rho _{k - 1}}^{{{{\mathcal {E}}}}_{k - 1}} \lesssim e^{C \Delta _{k-1}^{- \mu }} \delta _{k - 1} \end{aligned} \end{aligned}$$(5.31) -
3.
The sets \({{\mathcal {E}}}_k\) are defined as
$$\begin{aligned} \begin{aligned} {{{\mathcal {E}}}}_k&:= \Big \{\omega \in {{{\mathcal {E}}}}_{k - 1} \ : \ |\omega \cdot \ell + \Omega _{k - 1}(j) - \Omega _{ k - 1}(j')| \ge \frac{\gamma |j^3 - j'^3|}{{\mathtt {d}}(\ell )}, \\&\qquad \forall (\ell , j, j') \ne (0, j, j), \quad |\ell |_\eta \le N_{k - 1} \Big \}. \end{aligned} \end{aligned}$$(5.32)
Proof
The statement is trivial for \(k=0\) so we assume it to hold up to \(k<m\) and let us prove it for \(k + 1\). For any \(\Phi _k := {\mathrm{exp}}(\Psi _k)\) one has
where the operator \({{\mathcal {P}}}_{k + 1}\) is defined by
Then we choose \(\Psi _k\) in such a way that
namely for \(\omega \in {{{\mathcal {E}}}}_{k + 1}\) we set
Therefore,
and by applying Lemma A.6, using the induction estimate (5.30), one obtains
for any \(\zeta <\rho _k\).
We now define the diagonal part \({{\mathcal {D}}}_{k + 1}\).
For any \(j \in {\mathbb {Z}}\setminus \{ 0 \}\) and any \(\omega \in {{{\mathcal {E}}}}_k\) one has \(|({{\mathcal {P}}}_k^{(k)})_j^j(0)| \lesssim \Vert {{\mathcal {P}}}_k^{(k)}\Vert _{\rho _k}^{{{{\mathcal {E}}}}_{k} } {\mathop {\le }\limits ^{(5.30)}} \delta _k \). The Hamiltonian structure guarantees that \({{\mathcal {P}}}_k^{(k)}(0)_j^j\) is purely imaginary and by the Kiszbraun Theorem there exists a Lipschitz extension \(\omega \in {{\mathcal {O}}} \rightarrow {{\mathrm{i}}}z_k(j)\) (with \(z_k(j)\) real) of this function satisfying the bound \(|z_k(j)|^{{\mathcal {O}}}\lesssim \delta _k\). Then, we define
and one has
which is the estimate (5.29) at the step \(k + 1\).
We now estimate the remainder \({{\mathcal {P}}}_{k + 1}\) in (5.34). Using (5.35) we see that
Denote
Estimate of \({{\mathcal {P}}}_{k + 1}^{(i)}\), \(i = k + 2, \ldots , m\). By the induction estimate, one has
Estimate of \({{\mathcal {P}}}_{k + 1}^{(k + 1)}\). We estimate separately the four terms in the definition of \({{\mathcal {P}}}_{k + 1}^{(k + 1)}\) in (5.42). By Lemma A.9-(ii), one has
By applying (A.7) and the estimate of Lemma A.9-(iii), one obtains
and similarly
In conclusion we obtained
where \(C'\) is an appropriate constant and the last summand is a bound for the term \(e^{- \Psi _k} {{\mathcal {P}}}^{(k + 1)}_{k } e^{\Psi _k}\), which can be obtained reasoning as in (5.43). Thus we obtain
provided
which is of course follows from (5.23). \(\square \)
Now that we reduced \({{\mathcal {L}}}_0\) to the form \({{\mathcal {L}}}_m = \omega \cdot \partial _\varphi + {{\mathcal {D}}}_m + {{\mathcal {P}}}_m\) we can apply a “standard” KAM scheme to complete the diagonalization. This is a super-exponentially convergent iterative scheme based on iterating the following KAM step.
Lemma 5.4
(The \((m+1)\)-th step) Following the notation of Lemma 5.3 we define
and fix any \(\zeta \) such that
Then there exists a change of variables \(\Phi _{m} := {\mathrm{exp}}(\Psi _{m})\), such that
which conjugates \({{\mathcal {L}}}_m\) to the operator
The operator \({{\mathcal {D}}}_{m+1}\) is of the form (5.28) and satisfies (5.29), with \(k\rightsquigarrow m+1\), while the operator \({{\mathcal {P}}}_{m+1}\) is such that
Proof
We reason similarly to Lemma 5.3 i.e. we fix \(\Psi _{m}\) in such a way that
so that we obtains
for any \(\zeta <\rho _m\).
Now, for any \(j \in {\mathbb {Z}}\setminus \{ 0 \}\) and any \(\omega \in {{{\mathcal {E}}}}_{m}\) one has \(|({{\mathcal {P}}}_m)_j^j(0)| \lesssim \Vert {{\mathcal {P}}}_m\Vert _{\rho _m}^{{{{\mathcal {E}}}}_{m} } {\le } 2\delta _m \). The Hamiltonian structure guarantees that \({{\mathcal {P}}}_m(0)_j^j\) is purely imaginary and by the Kiszbraun Theorem there exists a Lipschitz extension \(\omega \in {{\mathcal {O}}} \rightarrow {{\mathrm{i}}}z_m(j)\) (with \(z_m(j)\) real) of this function satisfying the bound \(|z_m(j)|^{{\mathcal {O}}}\lesssim \delta _m\). Then, we define
and (5.29), with \(k\rightsquigarrow m+1\).
In order to obtain the bound 5.51 we start by recalling that
so that reasoning as in (5.47) we obtain
and by (5.49) the assertion follows. \(\square \)
We now iterate the step of Lemma 5.4, using at each step a smaller loss of analyticity, namely at the p-th step we take \(\zeta _p\) with
so that we obtain the following standard reducibility result; for a complete proof see [21].
Proposition 5.5
For any \(j \in {\mathbb {Z}}\setminus \{ 0 \}\), the sequence \(\Omega _k(j) = \Omega _0(j) + r_k(j)\), \(k \ge 1\) provided in Lemmata 5.3, 5.4, and defined for any \(\omega \in {{\mathcal {O}}}\) converges to \(\Omega _\infty (j) = \Omega _0(j) + r_\infty (j)\) with \(|r_\infty (j) - r_k(j)|^{{\mathcal {O}}} \lesssim \delta _k\). Defining the Cantor set
and
one has \({{{\mathcal {E}}}}_\infty \subseteq \cap _{k \ge 0} {{{\mathcal {E}}}}_k\).
Defining also
the sequence \({{\widetilde{\Phi }}}_k\) converges for any \(\omega \in {{{\mathcal {E}}}}_\infty \) to a symplectic, invertible map \(\Phi _\infty \) w.r.t. the norm \(\Vert \cdot \Vert _{\rho _m - 2\zeta }^{{{{\mathcal {E}}}}_\infty }\) and \(\Vert \Phi _\infty ^{\pm 1} - {\mathrm{Id}} \Vert _{\rho _m - 2\zeta }^{{{{\mathcal {E}}}}_\infty } \lesssim \delta _0 \). Moreover for any \(\omega \in {{{\mathcal {E}}}}_\infty \), one has that \(\Phi _\infty ^{- 1} {{\mathcal {L}}}_0 \Phi _\infty = {{\mathcal {L}}}_\infty \).
5.3 Variations
We now consider an operator
such that
where \({{\mathcal {L}}}\), \(\lambda _1\), \(\lambda _3\), \({{\mathcal {P}}}_0\) are given in (5.21) and \({{{\mathcal {O}}}^+}\subseteq {{\mathcal {O}}}\). In other words, \({{\mathcal {L}}}_0^+\) is a small variation of \({{\mathcal {L}}}_0\) in (5.20) with also \(m\rightsquigarrow m+1\).
Of course we can apply Proposition 5.5 to \({{\mathcal {L}}}_0^+\); our aim is to compare the “final frequencies” of \({{\mathcal {L}}}_\infty ^+\) with those of \({{\mathcal {L}}}_\infty \).
To this aim, we first apply Lemma 5.3 with \({{\mathcal {L}}}_0\rightsquigarrow {{\mathcal {L}}}_0^+\) and \(\gamma \rightsquigarrow \gamma _+<\gamma \). In this way we obtain a sequence of sets \({{\mathcal {E}}}_k^+\subseteq {{\mathcal {E}}}_{k-1}^+\) and a sequence of symplectic maps \(\Phi _k^+\) defined for \(\omega \in {{\mathcal {E}}}_{k+1}^+\) such that setting \({{\mathcal {L}}}_0^+\) as in (5.60) and
one has
where
The sets \({{\mathcal {E}}}_k^+\) are defined as \({{\mathcal {E}}}_0^+ := {{\mathcal {O}}^+}\) and for \(k \ge 1\)
Moreover one has \(\Phi _{k - 1}^+ := {\mathrm{exp}}(\Psi _{k - 1}^+)\), with
The following lemma holds.
Lemma 5.6
For all \(k = 1, \ldots , m+1\) one has
and
Proof
We procede differently for \(k=1,\ldots ,m\) and \(k=m+1\).
For the first case we argue by induction. Assume the statement to hold up to some \(k<m\). We want to prove
By Lemma 5.3, one has for \(\omega \in {{\mathcal {E}}}_{k + 1}^+\)
and direct calculation shows that for \(\omega \in {{\mathcal {E}}}_{k + 1} \cap {{\mathcal {E}}}_{k + 1}^+\), one has
and hence
Therefore, reasoning as in (5.37)–(5.38), one uses Lemma A.6, the smallness condition (5.23) and the induction estimate (5.67a) so that (5.69) follows.
Now, from the definition of \(r_{k+1}\) in (5.39) it follows
and by Kiszbraun Theorem applied to \(r_{k+1}^+(j) - r_{k+1}(j)\), (5.67b) holds.
The estimate of \({{\mathcal {P}}}_{k + 1}^+ - {{\mathcal {P}}}_{k + 1}\) follows by explicit computation the difference by using the expressions provided in (5.41), using the induction estimates (5.30), (5.67a), the estimate (5.69) and by applying Lemma A.12.
For \(k=m+1\) the proof can be repeated word by word, the only difference being that \(\Psi _m\) is defined in (5.52) while \(\Psi _m^+\) is defined in (5.36) with \(k=m\). \(\square \)
5.4 Conclusion of the Proof
To conclude the proof of Proposition 3.8 we start by noting that, setting \({{\mathcal {O}}}\) appearing in (5.2) as \({{\mathcal {O}}}^{(n)}\) appearing in (3.11), the operator \(L_{n+1}\) appearing in (3.18) with of course \(n\rightsquigarrow n+1\) is of the form (5.1) with
Moreover from (3.20) we have
where \(s_k\), \(\sigma _k\) and \(\varepsilon _k\) are defined in (3.6), so that \(L_{n+1}\) satisfies (5.2) with \(m=n\). Thus, fixing
the smallness conditions (5.3) follows by definition. Hence we can apply Lemma 5.1 to \(L_{n+1}\) obtaining an operator of the form (5.5). In particular the conjugating operator \({{\mathcal {M}}}\) satisfies
We are now in the setting of Sect. 5.2 with
for some \(\tau _3>0\). A direct calculation shows that the smallness conditions (5.22), (5.23), (5.24), (5.49) are satisfied provided we choose \(N_k\) appropriately, so that we can apply Proposition 5.5.
In conclusion we obtain an operator \(M_{n+1} ={{\mathcal {M}}}\circ \Phi _\infty \) (recall that \({{\mathcal {M}}}\) is constructed in Lemma 5.1) satisfying (3.49), (3.50), where \(\Omega ^{(n+1)}(j) := \Omega _{\infty }(j)\) and \({{\mathcal {E}}}^{(n+1)} ={{\mathcal {E}}}_{\infty }\). Note that in particular the functions \(\Omega ^{(n+1)}(j)\) turn out to be of the form (3.46).
Finally (3.47) follows from Lemmata 5.2 and 5.6 where \({{\mathcal {L}}}_+\) has the role of \(L_{n+1}\) while \({{\mathcal {L}}}\) has the role of \(L_n\). This means that here we are taking \(m\rightsquigarrow n-1\).
Notes
We say that \(\omega \) has rationally independent components if for any \(N>0\) and any \(k\in \mathbb {Z}^N\) one has \(\sum _{i=1}^N \omega _i k_i \ne 0\).
References
Baldi, P., Berti, M., Montalto, R.: KAM for quasi-linear and fully nonlinear forced KdV. Math. Ann. 359, 471–536 (2014)
Baldi, P., Berti, M., Haus, E., Montalto, R.: Time quasi-periodic gravity water waves in finite depth. Inventiones Math. 214(2), 739–911 (2018)
Biasco, L., Massetti, J.E., Procesi, M.: An abstract Birkhoff Normal Form Theorem and exponential type stability of the 1d NLS
Biasco, L., Massetti, J.E., Procesi, M.: Almost periodic solutions for the 1d NLS, 2019. Preprint
Bourgain, J.: Construction of quasi-periodic solutions for Hamiltonian perturbations of linear equations and applications to nonlinear PDE. Int. Math. Res. Not. (1994)
Bourgain, J.: Quasi-periodic solutions of Hamiltonian perturbations of 2D linear Schrödinger equations. Ann. Math. 148, 1 (1998)
Bourgain, J.: Green’s function estimates for lattice Schrödinger operators and applications. Princeton University Press, Princeton (2005)
Bourgain, J.: Construction of approximative and almost periodic solutions of perturbed linear Schrödinger and wave equations. Geom. Funct. Anal. 6(2), 201–230 (1996)
Bourgain, J.: On invariant tori of full dimension for 1D periodic NLS. J. Funct. Anal. 229(1), 62–94 (2005)
Chierchia, L., Perfetti, P.: Second order Hamiltonian equations on f \({\mathbb{T}}^\infty \) and almost-periodic solutions. J. Differ. Equ. 116, 1 (1995)
Cong, H., Liu, J., Shi, Y., Yuan, X.: The stability of full dimensional KAM tori for nonlinear Schrödinger equation. J. Differ. Equ. 264(7), 1 (2018)
Corsi, L., Montalto, R.: Quasi-periodic solutions for the forced Kirchhoff equation on \({\mathbb{T}}^d\). Nonlinearity 31(11), 5075–5109 (2018)
Corsi, L., Feola, R., Procesi, M.: Finite dimensional invariant KAM tori for tame vector fields. Trans. AMS 372(3), 1913–1983 (2019)
Craig, W., Wayne, C.E.: Newton’s method and periodic solutions of nonlinear wave equation. Commun. Pure Appl. Math. 46, 1409–1498 (1993)
Feola, R., Procesi, M.: KAM for Quasi-Linear Autonomous NLS, preprint (2017)
Kuksin, S.: Hamiltonian perturbations of infinite-dimensional linear systems with imaginary spectrum. Funktsional Anal. i Prilozhen. 21, 22–37 (1987). 95
Kuksin, S.: Perturbations of quasiperiodic solutions of infinite-dimensional Hamiltonian systems. Math. USSR Izvestiya 32, 39–62 (1989)
Kuksin, S.: The perturbation theory for the quasiperiodic solutions of infinite-dimensional Hamiltonian systems and its applications to the Korteweg de Vries equation. Math. USSR Sbornik 64, 397–413 (1989)
Kuksin, S., Pöschel, J.: Invariant Cantor manifolds of quasi-periodic oscillations for a nonlinear Schrödinger equation. Ann. Math. (2) 143(1), 149–179 (1996)
Liu, S.: The existence of almost-periodic solutions for 1-dimensional nonlinear Schrödinger equation with quasi-periodic forcing. J. Math. Phys. 61, 031502 (2020)
Montalto, R., Procesi, M.: Linear Schrödinger equation with an almost periodic potential (2019). Preprint arXiv:1910.12300
Pöschel, J.: A KAM-Theorem for some nonlinear PDEs. Ann. Sci. Norm. Pisa 23, 119–148 (1996)
Pöschel, J.: On the construction of almost periodic solutions for a nonlinear Schrödinger equation. Ergod. Theory Dyn. Syst. 22(5), 1537–1549 (2002)
Rabinowitz, P.H.: Periodic solutions of nonlinear hyperbolic partial differential equations. Commun. Pure Appl. Math. 20, 145–205 (1967)
Rabinowitz, P.H.: Periodic solutions of nonlinear hyperbolic partial differential equations II. Commun. Pure Appl. Math. 22, 15–39 (1968)
Rui, J., Liu, B., Zhang, J.: Almost periodic solutions for a class of linear Schrödinger equations with almost periodic forcing. J. Math. Phys. 57(092702), 18 (2016)
Rui, J., Liu, B.: Almost-periodic solutions of an almost-periodically forced wave equation. J. Math. Anal. Appl. 451(2), 629–658 (2017)
Wayne, C.E.: Periodic and quasi-periodic solutions of nonlinear wave equations via KAM theory. Commun. Math. Phys. 127, 479–528 (1990)
Xu, X., Geng, J.: Almost periodic solutions of one dimensional Schrödinger equation with the external parameters. J. Dyn. Differ. Equ. 25, 435–450 (2013)
Acknowledgements
Riccardo Montalto is supported by INDAM-GNFM.
Funding
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Technical Lemmata
Technical Lemmata
We start by recalling few results proved in [21]. Of course, as already noted in [21]-Remark 2.2, all the properties holding for \({{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \rho }, \ell ^\infty )\) hold verbatim for \({{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \rho }\times \mathbb {T}_{\sigma +\rho }, \ell ^\infty )\). In particular, all the estimates below hold also for the Lipschitz norms \(|\cdot |_\sigma ^\Omega \) and \(\Vert \cdot \Vert _{\sigma }^\Omega \). Given two Banach spaces X, Y we denote by \({{\mathcal {B}}}(X,Y)\) the space of bounded linear operators from X to Y.
Proposition A.1
(Torus diffeomorphism) Let \(\alpha \in {{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \rho }, \ell ^\infty )\) be real on real. Then there exists a constant \(\delta \in (0, 1)\) such that if \( \rho ^{- 1}| \alpha |_{\sigma + \rho } \le \delta \), then the map \( \varphi \mapsto \varphi + \alpha (\varphi )\) is an invertible diffeomorphism of \({\mathbb {T}}^\infty _\sigma \) (w.r.t. the \(\ell ^\infty \)-topology) and its inverse is of the form \(\vartheta \mapsto \vartheta + {{\widetilde{\alpha }}}(\vartheta )\), where \({{\widetilde{\alpha }}} \in {{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma +\frac{\rho }{2}}, \ell ^\infty )\) is real on real and satisfies the estimate \(| {{\widetilde{\alpha }}} |_{\sigma +\frac{\rho }{2}} \lesssim | \alpha |_{\sigma + \rho }\).
Corollary A.2
Given \(\alpha \in {{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \rho }, \ell ^\infty )\) as in Proposition A.1, the operators
are bounded, satisfy
and for any \(\varphi \in {\mathbb {T}}^\infty _\sigma \), \(u\in {{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \rho }, X), v\in {{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \frac{\rho }{2}}, X)\) one has
Moreover \(\Phi \) is close to the identity in the sense that
Given a function \(u \in {{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma , X)\), we define its average on the infinite dimensional torus as
By Lemma 2.6 in [21], this definition is well posed and
where u(0) is the zero-th Fourier coefficient of u.
Lemma A.3
(Algebra) One has \(| u v |_\sigma \le | u |_\sigma | v |_\sigma \) for \(u,v\in {{\mathcal {H}}}(\mathbb {T}^\infty _\sigma \times \mathbb {T}_\sigma )\).
Lemma A.4
(Cauchy estimates) Let \(u \in {{\mathcal {H}}}(\mathbb {T}^\infty _{\sigma + \rho }\times \mathbb {T}_{\sigma + \rho })\). Then \(| \partial ^k u |_{\sigma } \lesssim _k \rho ^{- k} | u |_{\sigma + \rho }\).
Lemma A.5
(Moser composition lemma) Let \(f : B_R(0) \rightarrow { \mathbb {C}}\) be an holomorphic function defined in a neighbourhood of the origin \(B_R(0)\) of the complex plane \({ \mathbb {C}}\). Then the composition operator \(F (u) := f \circ u\) is a well defined non linear map \({{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma \times {\mathbb {T}}_\sigma ) \rightarrow {{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma \times {\mathbb {T}}_\sigma )\) and if \(| u |_\sigma \le r < R\), one has the estimate \(| F(u) |_\sigma \lesssim 1 + | u |_\sigma \). If f has a zero of order k at 0, then for any \(| u |_\sigma \le r < R\), one gets the estimate \(| F(u) |_\sigma \lesssim | u |_\sigma ^k\).
For any function \(u \in {{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma , X)\), given \(N > 0\), we define the projector \(\Pi _N u\) as
Lemma A.6
- (i):
-
Let \(\rho >0\). Then
$$\begin{aligned} \sup _{\begin{array}{c} \ell \in {\mathbb {Z}}^\infty _* \\ |\ell |_\eta < \infty \end{array}} \prod _{i}( 1+ \langle i \rangle ^{5} | \ell _i|^{5}) e^{- \rho |\ell |_\eta } \le e^{{\tau } \ln \Big (\frac{\tau }{\rho } \Big ) \rho ^{-\frac{1}{\eta }}} \end{aligned}$$for some constant \(\tau = \tau (\eta ) > 0\).
- (ii):
-
Let \(\rho > 0\). Then
$$\begin{aligned} \sum _{\ell \in {\mathbb {Z}}^\infty _*} e^{- \rho |\ell |_\eta } \lesssim e^{{\tau } \ln \Big (\frac{\tau }{\rho } \Big ) \rho ^{-\frac{1}{\eta }}}, \end{aligned}$$for some constant \(\tau = \tau (\eta ) > 0\).
- (iii):
-
Let \(\alpha > 0\). For \(N\gg 1\) one has
$$\begin{aligned} \sup _{\ell \in {\mathbb {Z}}^\infty _*:\; |\ell |_{\alpha }<N} \prod _{i}(1+\langle i \rangle ^{5} |\ell _i|^{5}) \le (1+N)^{C(\alpha )N^{\frac{1}{1+\alpha }}} \end{aligned}$$(A.4)for some constant \(C(\alpha )>0\) such that \(C(\alpha )\rightarrow \infty \) as \(\alpha \rightarrow 0\).
Lemma A.7
Given \(u\in {{\mathcal {H}}}(\mathbb {T}^\infty _\sigma ,X)\) for X some Banach space, let g be a pointwise absolutely convergent Formal Fourier series such that
for some \(\tau '>0\). Then for any \(0<\rho <\sigma \), then \(g\in {{\mathcal {H}}}(\mathbb {T}^\infty _{\sigma -\rho },X)\) and satisfies
Proof
Follows directly from Lemma A.6 and Definition 2.1. \(\square \)
Lemma A.8
Recalling (3.8) and the definition of \(|\ell |_1\) in (1.5), one has
Proof
First of all note that for all \(\ell \in \mathbb {Z}^*_{\infty }\) one has
which implies
Then we recall that (see [9])
which implies (A.5). \(\square \)
Lemma A.9
Let \(N,\sigma , \rho > 0\), \(m, m' \in {\mathbb {R}}\), \({{\mathcal {R}}} \in {{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma , {{\mathcal {B}}}^{\sigma , m})\), \({{\mathcal {Q}}} \in {{\mathcal {H}}}({\mathbb {T}}^\infty _{\sigma + \rho }, {{\mathcal {B}}}^{\sigma + \rho , m'})\).
- (i):
-
The product operator \({{\mathcal {R}}} {{\mathcal {Q}}} \in {{\mathcal {H}}}({\mathbb {T}}^\infty _\sigma , {{\mathcal {B}}}^{\sigma , m + m'})\) with \(\Vert {{\mathcal {R}}} {{\mathcal {Q}}}\Vert _{\sigma , m + m'} \lesssim _m \rho ^{- |m|} \Vert {{\mathcal {R}}}\Vert _{\sigma , m} \Vert {{\mathcal {Q}}}\Vert _{\sigma + \rho , m'}\). If \({{\mathcal {R}}}(\omega ), {{\mathcal {Q}}}(\omega )\) depend on a parameter \(\omega \in \Omega \subseteq {\mathtt {D}_\gamma }\), then \(\Vert {{\mathcal {R}}}{{\mathcal {Q}}}\Vert _{\sigma , m + m'}^\Omega \lesssim _m \rho ^{- (|m| + 2)} \Vert {{\mathcal {R}}}\Vert _{ \sigma , m}^\Omega \Vert {{\mathcal {Q}}}\Vert _{\sigma + \rho , m'}^\Omega \). If \(m = m' = 0\), one has \(\Vert {{\mathcal {R}}}{{\mathcal {Q}}}\Vert _\sigma ^\Omega \lesssim \Vert {{\mathcal {R}}}\Vert _\sigma ^\Omega \Vert {{\mathcal {Q}}}\Vert _\sigma ^\Omega \).
- (ii):
-
The projected operator \(\Vert \Pi _N^\bot {{\mathcal {R}}}\Vert _{\sigma , m} \le e^{- \rho N} \Vert {{\mathcal {R}}}\Vert _{\sigma + \rho , m}\).
Given two linear operators \({{\mathcal {A}}}, {{\mathcal {B}}}\), we define for any \(n \ge 0\), the operator \({\mathrm{Ad}}_{{{\mathcal {A}}}}^n({{\mathcal {B}}})\) as
where
By iterating the estimate (i) of Lemma A.9, one has that for any \(n \ge 1\)
for some constant \(C > 0\).
Lemma A.10
Let \(0< \ldots< \rho _n< \ldots < \rho _0\) and \(0 < \ldots \ll \delta _n \ll \ldots \ll \delta _0\). Assume that \(\sum _{i \ge 0} \delta _i < \infty \), choose any \(n\ge 0\) and let \({{\mathcal {A}}}\) and \({{\mathcal {B}}}\) be linear operators such that
Then for any \(0< \zeta _i < \rho _i\) the following holds.
- (i):
-
For any \(k \ge 1\), one has
$$\begin{aligned}&{\mathrm{Ad}}_{{\mathcal {A}}}^k({{\mathcal {B}}}) = \sum _{i = 0}^n {{\mathcal {R}}}_i^{(k)} \quad \text{ with } \quad \\&\quad \Vert {{\mathcal {R}}}_i^{(k)}\Vert _{\rho _i - \zeta _i} \le C_0^k \zeta _i^{- 1} \delta _i\, \quad \forall i = 0, \ldots , n \end{aligned}$$ - (ii):
-
Let \({{\mathcal {R}}} := e^{- {{\mathcal {A}}}} {{\mathcal {B}}} e^{ {{\mathcal {A}}}} - {{\mathcal {B}}}\). Then
$$\begin{aligned} {{\mathcal {R}}} = \sum _{i = 0}^n {{\mathcal {R}}}_i\quad \text{ with } \quad \Vert {{\mathcal {R}}}_i\Vert _{\rho _i - \zeta _i} \lesssim \zeta _i^{- 1} \delta _i\, \quad \forall i = 0, \ldots , n \end{aligned}$$
Proof of item (i). We prove the statement by induction on k. For \(k = 1\), one has that
Since for \(j < i\) one has that \( \rho _j > \rho _i\) and so all the terms in the above sum are analytic at least in the strip of width \(\rho _i\). By applying Lemma A.9-(i) one has for any \(0< \zeta _i < \rho _i\)
for \(i = 0, \ldots , n\). Now we argue by induction. Assume that for some \(k \ge 1\), \({{\mathcal {R}}}^{(k)} := {\mathrm{Ad}}_{{\mathcal {A}}}^k({{\mathcal {B}}}) = \sum _{i = 0}^{n} {{\mathcal {R}}}_i^{(k)}\), with
for any \(0< \zeta _i < \rho _i\). Of course this implies that for all \(j<i\) one has
By definition
Hence by applying Lemma A.9-(i) and using the induction hypothesis, one obtains
Proof of (ii). One has
so that
Therefore the assertion follows. \(\square \)
Lemma A.11
Let \(\{\rho _n\}_{n\ge 0}\) and \(\{\delta _n\}_{n\ge 0}\) as in Lemma A.10. Choose any \(n>0\) and consider
Then the following holds.
- (i):
-
Consider the commutator \( [\partial _x^3, {{\mathcal {G}}}]\) where \({{\mathcal {G}}} := \pi _0^\bot g(\varphi , x) \partial _x^{- 1} \). Then, one has
$$\begin{aligned} {[}\partial _x^3, {{\mathcal {G}}}]= 3 g_x \partial _x + {{\mathcal {R}}}, \quad {{\mathcal {R}}} := \sum _{k = 0}^n {{\mathcal {R}}}_i, \qquad \text{ where } \quad \Vert {{\mathcal {R}}}_i\Vert _{\rho _i - \zeta _i} \lesssim \zeta _i^{- 3}\delta _i,\quad \text{ for } \ 0< \zeta _i < \rho _i. \end{aligned}$$ - (ii):
-
Let \(\zeta _0, \zeta _1, \ldots , \zeta _n\) satisfying \(0< 2 \zeta _i < \rho _i\), \(0< \rho _n - \zeta _n< \rho _{n - 1} - \zeta _{n - 1}< \ldots < \rho _0 - \zeta _0\) and assume that \(\sum _{i \ge 0} \zeta _i^{- 3} \delta _i < \infty \). Then, one has
$$\begin{aligned} e^{- {{\mathcal {G}}}} \partial _x^3 e^{{\mathcal {G}}} = \partial _x^3 + 3 g_x \partial _x + {{\mathcal {R}}} , \qquad {{\mathcal {R}}} = \sum _{i = 0}^n {{\mathcal {R}}}_i ,\quad \Vert {{\mathcal {R}}}_i\Vert _{\rho _i - 2 \zeta _i } \lesssim \zeta _i^{- 4} \delta _i , \quad i = 0, \ldots , n. \end{aligned}$$ - (iii):
-
Let \(\zeta _0, \zeta _1, \ldots , \zeta _n\) satisfying \(0< \zeta _i < \rho _i\), \(0< \rho _n - \zeta _n< \rho _{n - 1} - \zeta _{n - 1}< \ldots < \rho _0 - \zeta _0\) and assume that \(\sum _{i \ge 0} \zeta _i^{- 1} \delta _i < \infty \). Then
$$\begin{aligned} e^{- {{\mathcal {G}}}} (\omega \cdot \partial _\varphi ) e^{{\mathcal {G}}} = \omega \cdot \partial _\varphi + {{\mathcal {R}}}, \qquad {{\mathcal {R}}} = \sum _{i = 0}^n {{\mathcal {R}}}_i,\quad \Vert {{\mathcal {R}}}_i\Vert _{\rho _i - \zeta _i } \lesssim \zeta _i^{- 1} \delta _i, \quad i = 0, \ldots , n. \end{aligned}$$
Proof
Proof of (i). One has
Therefore
Proof of (ii). In view of the item (i), it is enough to estimate
Let
One has
For any \(k \ge 2\) one has
hence, we can apply Lemma A.10 (replacing \(\rho _i\) with \(\rho _i - \zeta _i\) and \(\delta _i\) with \( \zeta _i^{- 3}\delta _i\)) obtaining
where \({{\mathcal {R}}}_i^{(k)}\) satisfies
and hence by setting
item (ii) follows.
Proof of item (iii). The proof can be done arguing as in the item (ii), using that
\(\square \)
Lemma A.12
Let \({{\mathcal {A}}}, {{\mathcal {A}}}_+, {{\mathcal {B}}}, {{\mathcal {B}}}_+\) be bounded operators w.r.t. a norm \(\Vert \cdot \Vert _\sigma \), and define
Then the following holds.
- (i):
-
For any \(k \ge 0\), one has
$$\begin{aligned} \Vert {\mathrm{Ad}}_{{{\mathcal {A}}}_+}^k({{\mathcal {B}}}_+) - {\mathrm{Ad}}_{{{\mathcal {A}}}}^k({{\mathcal {B}}}) \Vert _{\sigma } \le C_*^k M_{{\mathcal {A}}}^k M_{{\mathcal {B}}} \big (\Vert {{\mathcal {A}}}_+ - {{\mathcal {A}}}\Vert _\sigma + \Vert {{\mathcal {B}}}_+ - {{\mathcal {B}}}\Vert _\sigma \big ) \end{aligned}$$for some constant \(C_* > 0\).
- (ii):
-
$$\begin{aligned} \Vert e^{- {{\mathcal {A}}}_+} {{\mathcal {B}}}_+ e^{{{\mathcal {A}}}_+} - e^{- {{\mathcal {A}}}} {{\mathcal {B}}} e^{{{\mathcal {A}}}}\Vert _\sigma \lesssim \Vert {{\mathcal {A}}}_+ - {{\mathcal {A}}}\Vert _\sigma + \Vert {{\mathcal {B}}}_+ - {{\mathcal {B}}}\Vert _\sigma . \end{aligned}$$
Proof
Proof of (i). We argue by induction. Of course the result is trivial for \(k=0\). Assume that the estimate holds for some \(k \ge 1\). Then
Hence, by the induction hypothesis, using (A.11), (A.7) and Lemma A.9-(i), one obtains that
for some \(C_* > 0\) large enough.
Proof of (ii). It follows by item (i), using that
\(\square \)
Lemma A.13
Let \({{\mathcal {A}}}, {{\mathcal {A}}}^+ , {{\mathcal {B}}}, {{\mathcal {B}}}^+\) be linear operators satisfying
Then the following holds.
- (i):
-
For any \(k \ge 1\),
$$\begin{aligned} \Vert {\mathrm{Ad}}_{{{\mathcal {A}}}_+}^k({{\mathcal {B}}}_+) - {\mathrm{Ad}}_{{{\mathcal {A}}}}^k({{\mathcal {B}}})\Vert _{\rho - \zeta } \le C^k \zeta ^{- 1} \big (\Vert {{\mathcal {A}}}_+ - {{\mathcal {A}}}\Vert _{\rho , - 1} + \Vert {{\mathcal {B}}}_+ - {{\mathcal {B}}}\Vert _{\rho , 1} \big ) \end{aligned}$$for some constant \(C > 0\) depending on \(C_0\).
- (ii):
-
Setting \({{\mathcal {R}}} := e^{- {{\mathcal {A}}}} {{\mathcal {B}}} e^{{\mathcal {A}}} - {{\mathcal {B}}}\), and \({{\mathcal {R}}}_+ := e^{- {{\mathcal {A}}}_+} {{\mathcal {B}}}_+ e^{{{\mathcal {A}}}_+} - {{\mathcal {B}}}_+\), one has
$$\begin{aligned} \Vert {{\mathcal {R}}} - {{\mathcal {R}}}_+\Vert _{\rho - \zeta } \lesssim \zeta ^{- 1} \big ( \Vert {{\mathcal {A}}} - {{\mathcal {A}}}_+\Vert _{\rho , - 1} + \Vert {{\mathcal {B}}} - {{\mathcal {B}}}_+\Vert _{\rho , 1}\big ). \end{aligned}$$
Proof
Proof of (i). We first estimate \({\mathrm{Ad}}_{{{\mathcal {A}}}_+}({{\mathcal {B}}}_+) - {\mathrm{Ad}}_{{{\mathcal {A}}}}({{\mathcal {B}}})\). One has
By Lemma A.9-(i), one has
and
In order to estimate \({\mathrm{Ad}}^{k }_{{{\mathcal {A}}}_+}({{\mathcal {B}}}_+) - {\mathrm{Ad}}^{k }_{{{\mathcal {A}}}}({{\mathcal {B}}}) = {\mathrm{Ad}}^{k - 1}_{{{\mathcal {A}}}_+}{\mathrm{Ad}}_{{{\mathcal {A}}}_+}({{\mathcal {B}}}_+) - {\mathrm{Ad}}^{k - 1}_{{{\mathcal {A}}}}{\mathrm{Ad}}_{{\mathcal {A}}}({{\mathcal {B}}})\) for any \(k \ge 2\), we apply Lemma A.12-(i) where we replace \({{\mathcal {B}}}_+\) with \({\mathrm{Ad}}_{{{\mathcal {A}}}_+}({{\mathcal {B}}}_+)\) and \({{\mathcal {B}}}\) with \({\mathrm{Ad}}_{{{\mathcal {A}}}}({{\mathcal {B}}})\), together with the estimates (A.12), (A.13).
Proof of (ii). It follows by (i) using that \({{\mathcal {R}}}_+ - {{\mathcal {R}}} = \sum _{k \ge 1} \frac{{\mathrm{Ad}}^k_{{{\mathcal {A}}}_+}({{\mathcal {B}}}_+) - {\mathrm{Ad}}^k_{{{\mathcal {A}}}}({{\mathcal {B}}})}{k!}\). \(\square \)
Lemma A.14
Let \(g_+, g \in {{\mathcal {H}}}_\rho \), \({{\mathcal {G}}} := \pi _0^\bot g(\varphi , x) \partial _x^{- 1}\), \({{\mathcal {G}}}_+ := \pi _0^\bot g_+(\varphi , x) \partial _x^{- 1}\). Then the following holds.
- (i):
-
The operators \({{\mathcal {R}}} := e^{-{{\mathcal {G}}}} \partial _x^3 e^{{\mathcal {G}}} - \partial _x^3 - 3 g_x \partial _x \), \({{\mathcal {R}}}_+ := e^{-{{\mathcal {G}}}_+} \partial _x^3 e^{{{\mathcal {G}}}_+} - \partial _x^3 - 3 (g_+)_x \partial _x \) satisfy \(\Vert {{\mathcal {R}}}_+ - {{\mathcal {R}}}\Vert _{\rho - \zeta } \lesssim \zeta ^{- \tau } | g_+ - g |_\rho \) for some constant \(\tau > 0\).
- (ii):
-
The operators \({{\mathcal {R}}} := e^{-{{\mathcal {G}}}} \omega \cdot \partial _\varphi e^{{\mathcal {G}}} - \omega \cdot \partial _\varphi \) and \({{\mathcal {R}}}_+ := e^{-{{\mathcal {G}}}_+} \omega \cdot \partial _\varphi e^{{{\mathcal {G}}}_+} - \omega \cdot \partial _\varphi \) satisfy the estimate \(\Vert {{\mathcal {R}}}_+ - {{\mathcal {R}}}\Vert _{\rho - \zeta } \lesssim \zeta ^{- \tau } | g_+ - g |_\rho \), for some constant \(\tau > 0\).
Proof
We only prove the item (i). The item (ii) can be proved by similar arguments. We compute
Hence
By a direct calculation one can show the estimates
The latter estimates, together with Lemma A.13-(i) allow to deduce
for some constant \(\tau > 0\). Thus (A.15)-(A.17) imply the desired bound. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Corsi, L., Montalto, R. & Procesi, M. Almost-Periodic Response Solutions for a Forced Quasi-Linear Airy Equation. J Dyn Diff Equat 33, 1231–1267 (2021). https://doi.org/10.1007/s10884-020-09906-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-020-09906-8