Nuclear Embeddings in Weighted Function Spaces

Abstract

We study nuclear embeddings for weighted spaces of Besov and Triebel–Lizorkin type where the weight belongs to some Muckenhoupt class and is essentially of polynomial type. Here we can extend our previous results concerning the compactness of corresponding embeddings. The concept of nuclearity was introduced by A. Grothendieck in 1955. Recently there is a refreshed interest to study such questions. This led us to the investigation in the weighted setting. We obtain complete characterisations for the nuclearity of the corresponding embedding. Essential tools are a discretisation in terms of wavelet bases, operator ideal techniques, as well as a very useful result of Tong about the nuclearity of diagonal operators acting in $\ell _p$ spaces. In that way we can further contribute to the characterisation of nuclear embeddings of function spaces on domains.

1 Introduction

Grothendieck introduced the concept of nuclearity in [14] more than 60 years ago. It paved the way to many famous developments in functional analysis later one, like the theories of nuclear locally convex spaces, operator ideals, eigenvalue distributions, and traces and determinants in Banach spaces. Enflo used nuclearity in his famous solution [10] of the approximation problem, a long-standing problem of Banach from the Scottish Book. We refer to [29, 31], and, in particular, to [32] for further historic details.

Let X, Y be Banach spaces, $T\in {\mathcal {L}}(X,Y)$ a linear and bounded operator. Then T is called nuclear, denoted by $T\in {\mathcal {N}}(X,Y)$, if there exist elements $a_j\in X'$, the dual space of X, and $y_j\in Y$, $j\in {\mathbb {N}}$, such that $\sum _{j=1}^\infty \Vert a_j\Vert _{X'} \Vert y_j\Vert _Y < \infty$ and a nuclear representation $Tx=\sum _{j=1}^\infty a_j(x) y_j$ for any $x\in X$. Together with the nuclear norm

$$\begin{aligned} \nu (T)=\inf \Big \{ \sum _{j=1}^\infty \Vert a_j\Vert _{X'} \Vert y_j\Vert _Y:\ T =\sum _{j=1}^\infty a_j(\cdot ) y_j\Big \}, \end{aligned}$$

where the infimum is taken over all nuclear representations of T, the space ${\mathcal {N}}(X,Y)$ becomes a Banach space. It is obvious that nuclear operators are, in particular, compact.

Already in the early years there was a strong interest to study examples of nuclear operators beyond diagonal operators in $\ell _p$ sequence spaces, where a complete answer was obtained in [43] (with some partial forerunner in [29]). Concentrating on embedding operators in spaces of Sobolev type, first results can be found, for instance, in [28, 33, 34].

Though the topic was always studied to a certain extent, we realised an increased interest in the last years. Concentrating on the Sobolev embedding for spaces on a bounded domain, some of the recently published papers we have in mind are [5,6,7,8, 49] using quite different techniques however.

We observed several directions and reasons for this. For example, the problem to describe a compact operator outside the Hilbert space setting is a partly open and very important one. It is well known from the remarkable Enflo result [10] that there are compact operators between Banach spaces which cannot be approximated by finite-rank operators. This led to a number of—meanwhile well-established and famous—methods to circumvent this difficulty and find alternative ways to ‘measure’ the compactness or ‘degree’ of compactness of an operator. It can be described by the asymptotic behaviour of its approximation or entropy numbers, which are basic tools for many different problems nowadays, e.g. eigenvalue distribution of compact operators in Banach spaces, optimal approximation of Sobolev-type embeddings, but also for numerical questions. In all these problems, the decomposition of a given compact operator into a series is an essential proof technique. It turns out that in many of the recent papers [5, 6, 49] studying nuclearity, a key tool in the arguments are new decomposition techniques as well, adapted to the different spaces. So we intend to follow this strategy, too.

Concerning weighted spaces of Besov and Sobolev type, we are in some sense devoted to the program proposed by Edmunds and Triebel [9] to investigate the spectral properties of certain pseudo-differential operators based on the asymptotic behaviour of entropy and approximation numbers, together with Carl’s inequality and the Birman–Schwinger principle. Similar questions in the context of weighted function spaces of this type were studied by the first named author and Triebel, cf. [15], and were continued and extended by Kühn, Leopold, Sickel and the second author in the series of papers [21,22,23]. Here the considered weights are always assumed to be ‘admissible’: These are smooth weights with no singular points, with $w(x)=(1+|x|^2)^{\gamma /2}$, $\gamma \in {\mathbb {R}}$, $x\in {{\mathbb {R}}}^{{d}}$, as a prominent example.

We started in [17] a different approach and considered weights from the Muckenhoupt class ${\mathcal {A}}_\infty$ which—unlike ‘admissible’ weights—may have local singularities, that can influence embedding properties of such function spaces. Weighted Besov and Triebel–Lizorkin spaces with Muckenhoupt weights are well known concepts, cf. [1,2,3,4, 12, 16, 35]. In [17] we dealt with general transformation methods from function to appropriate sequence spaces provided by a wavelet decomposition; we essentially concentrated on the example weight

$$\begin{aligned} w_{\alpha ,\beta }(x) \sim {\left\{ \begin{array}{ll}|x|^\alpha &{} \text {if} \quad |x|\le 1\, ,\\ |x|^\beta &{} \text {if} \quad |x|> 1\, ,\end{array}\right. } \qquad \text {with}\quad \alpha>-{d},\quad \beta >0, \end{aligned}$$

of purely polynomial growth both near the origin and for $|x|\rightarrow \infty$. In the general setting for $w\in {\mathcal {A}}_\infty$ we obtained sharp criteria for the compactness of embeddings of type

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _{\alpha ,\beta } : A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{\alpha ,\beta }) \hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}), \end{aligned}$$

where $s_2\le s_1$, $0<p_1, p_2<\infty$, $0<q_1,q_2\le \infty$, and $A^s_{p,q}$ stands for either Besov spaces $B^s_{p,q}$ or Triebel–Lizorkin spaces $F^s_{p,q}$. More precisely, we proved in [17] that $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ is compact if, and only if,

$$\begin{aligned} \frac{\beta }{p_1}>{d}\max \left( \frac{1}{p_2}-\frac{1}{p_1},0\right) \end{aligned}$$

and      

$$\begin{aligned} s_1-\frac{{d}}{p_1}- s_2+\frac{{d}}{p_2} > \max \left( {d}\max \left( \frac{1}{p_2}-\frac{1}{p_1},0\right) ,\frac{\alpha }{p_1}\right) . \end{aligned}$$

In the same paper [17] we determined the exact asymptotic behaviour of corresponding entropy and approximation numbers of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ in the compactness case. Now we can refine this characterisation by our new result about the nuclearity of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$. One of our main results in the present paper, Theorem 3.12 below, states that $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ is nuclear if, and only if,

$$\begin{aligned} \frac{\beta }{p_1}>{d}- {d}\max \left( \frac{1}{p_1}-\frac{1}{p_2},0\right) \end{aligned}$$

and      

$$\begin{aligned} s_1-\frac{{d}}{p_1}- s_2+\frac{{d}}{p_2} > \max \left( {d}-{d}\max \left( \frac{1}{p_1}-\frac{1}{p_2},0\right) ,\frac{\alpha }{p_1}\right) , \end{aligned}$$

where $1\le p_1<\infty$ and $1\le p_2, q_1, q_2\le \infty$.

In [19] we studied the weight

$$\begin{aligned} w_{({\varvec{\alpha }},{\varvec{\beta }})}(x)\, = \ {\left\{ \begin{array}{ll} |x|^{\alpha _1} (1-\log |x|)^{\alpha _2}, &{} \text {if} \quad |x|\le 1\, ,\\ |x|^{\beta _1} (1+\log |x|)^{\beta _2},&{} \text {if} \quad |x|> 1\,, \end{array}\right. } \end{aligned}$$

where ${\varvec{\alpha }} = (\alpha _1,\alpha _2)$, $\alpha _1> -{d}$, $\alpha _2\in {\mathbb {R}}$, ${\varvec{\beta }} = (\beta _1,\beta _2)$, $\beta _1>-{d}$, $\beta _2\in {\mathbb {R}}$. Again we obtained the complete characterisation of the compactness of

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})} : B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w_{({\varvec{\alpha }},{\varvec{\beta }})}) \hookrightarrow B^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}), \end{aligned}$$

as well as asymptotic results for the corresponding entropy numbers. The intention was not only to generalise the weight function, but also to cover some limiting cases in that way. Our second main result, Theorem 3.22 below, completely answers the question of the nuclearity of $\mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}$, where now even the fine parameters $q_1, q_2$ are involved in the criterion.

While proving our result we benefit from Tong’s observation [43] (and the fine paper [5] which has drawn our attention to it), and the available wavelet decomposition and operator ideal techniques used in our previous papers [17, 19] already. Moreover, we used and slightly extended Triebel’s result [49] (with forerunners in [33, 34]) on the nuclearity of the embedding operator

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _\Omega : A^{s_1}_{p_1,q_1}(\Omega ) \rightarrow A^{s_2}_{p_2,q_2}(\Omega ), \end{aligned}$$

where $\Omega \subset {{\mathbb {R}}}^{{d}}$ is assumed to be a bounded Lipschitz domain and the spaces $A^s_{p,q}(\Omega )$ are defined by restriction. In [5] some further limiting cases were studied and we may now add a little more to this limiting question.

Beside embeddings of appropriately weighted spaces and embeddings of spaces on bounded domains, we also consider embeddings of radial spaces which may admit compactness,

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _R: RA^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\rightarrow RA^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}), \end{aligned}$$

for definitions we refer to Sect. 3.3 below. This has been studied in detail in [38, 39]. In particular, we can now gain from the close connection between radial spaces and appropriately weighted spaces established in [38, 39]. In that way we are able to prove a criterion of nuclearity of the embedding $\mathop {\mathrm {id}}\nolimits _R$ in Theorem 3.27 below.

The paper is organised as follows. In Sect. 2 we recall basic facts about weight classes and weighted function spaces needed later on. Section 3 is devoted to our main findings about the nuclearity of embeddings: we start with a collection of known results in Sect. 3.1 which we shall need later; in Sect. 3.2 we present our new results for the weighted embeddings described above, while in Sect. 3.3 we turn our attention to radial spaces and nuclearity of embeddings.

2 Weighted Function Spaces

First of all we need to fix some notation. By ${{\mathbb {N}}}$ we denote the set of natural numbers, by ${{\mathbb {N}}}_{0}$ the set ${{\mathbb {N}}}\cup \{ 0\}$, and by ${\mathbb {Z}}^{{d}}$ the set of all lattice points in ${{\mathbb {R}}}^{{d}}$ having integer components.

The positive part of a real function f is given by $f_{+}(x)=\max (f(x),0)$. For two positive real sequences $\{a_k\}_{k\in {{\mathbb {N}}}}$ and $\{b_k\}_{k\in {{\mathbb {N}}}}$ we mean by $a_k\sim b_k$ that there exist constants $c_1,c_2>0$ such that $c_1\ a_k\le b_k\le c_2 \ a_k$ for all $k\in {{\mathbb {N}}}$; similarly for positive functions.

Given two (quasi-) Banach spaces X and Y, we write $X\hookrightarrow Y$ if $X\subset Y$ and the natural embedding of X in Y is continuous.

All unimportant positive constants will be denoted by c, occasionally with subscripts. For convenience, let both $\;\mathrm {d}x$ and $|\cdot |$ stand for the (${d}$-dimensional) Lebesgue measure in the sequel.

2.1 Weight Functions

We shall essentially deal with weight functions of polynomial type. Here we use our preceding results in [17,18,19] which partly rely on general features of Muckenhoupt weights. For that reason we first recall some fundamentals on this special class of weights. By a weight w we shall always mean a locally integrable function $w\in L_1^{\mathrm {loc}}({{\mathbb {R}}}^{{d}})$, positive a.e. in the sequel. Let M stand for the Hardy-Littlewood maximal operator given by

$$\begin{aligned} Mf(x)= \sup _{B(x,r) \in {\mathcal {B}}} \ \frac{1}{|B(x,r)|}\int _{B(x,r)} |f(y)| \;\mathrm {d}y, \quad x\in {{\mathbb {R}}}^{{d}}, \end{aligned}$$

(2.1)

where ${\mathcal {B}}$ is the collection of all open balls $B(x,r)=\Big \{y\in {{\mathbb {R}}}^{{d}}:\;\; |y-x|<r \Big \}$, $r>0$.

Definition 2.1

Let w be a weight function on ${{\mathbb {R}}}^{{d}}$.

(i):

Let $1<p<\infty$. Then w belongs to the Muckenhoupt class ${\mathcal {A}}_p$, if there exists a constant $0<A<\infty$ such that for all balls B the following inequality holds

$$\begin{aligned} \left( \frac{1}{|B|}\int _{B}w(x) \;\mathrm {d}x\right) ^{1/p} \left( \frac{1}{|B|}\int _{B}w(x)^{-p'/p} \;\mathrm {d}x \right) ^{1/p'} \le A , \end{aligned}$$

(2.2)

where $p'$ is the dual exponent to p given by $1/p'+ 1/p=1$ and |B| stands for the Lebesgue measure of the ball B.

(ii):

Let $p=1$. Then w belongs to the Muckenhoupt class ${\mathcal {A}}_1$ if there exists a constant $0<A<\infty$ such that the inequality

$$\begin{aligned} Mw(x)\le A w(x) \end{aligned}$$

holds for almost all $x\in {{\mathbb {R}}}^{{d}}$.

(iii):

The Muckenhoupt class ${\mathcal {A}}_{\infty }$ is given by $\quad \displaystyle {\mathcal {A}}_{\infty }=\bigcup \nolimits _{p> 1} {\mathcal {A}}_p$.

Since the pioneering work of Muckenhoupt [25,26,27], these classes of weight functions have been studied in great detail, we refer, in particular, to the monographs [13, 42, 44, Ch. IX], and [41, Ch. V] for a complete account on the theory of Muckenhoupt weights. As usual, we use the abbreviation

$$\begin{aligned} w(\Omega )=\int _{\Omega }w(x) \;\mathrm {d}x, \end{aligned}$$

(2.3)

where $\Omega \subset {{\mathbb {R}}}^{{d}}$ is some bounded, measurable set.

Examples 2.2

(i):

One of the most prominent examples of a Muckenhoupt weight $w\in {\mathcal {A}}_r$, $1\le r<\infty$, is given by $\ w_\alpha (x) = |x|^\alpha$, where $w_\alpha \in {\mathcal {A}}_r$ if, and only if, $-{d}<\alpha <{d}(r-1)$ for $1<r<\infty$, and $-{d}<\alpha \le 0$ for $r=1$. We modified this example in [17] by

$$\begin{aligned} w_{\alpha ,\beta }(x) = {\left\{ \begin{array}{ll} |x|^\alpha ,&{} |x|<1, \\ |x|^\beta ,&{} |x|\ge 1,\end{array}\right. } \end{aligned}$$

(2.4)

where $\alpha , \beta >-{d}$. Straightforward calculation shows that for $1<r<\infty$, $w_{\alpha ,\beta }\in {\mathcal {A}}_r \quad \text {if, and only if,}\quad -{d}<\alpha ,\beta <{d}(r-1)$.

(ii):

We also need the example considered in [19],

$$\begin{aligned} w_{({\varvec{\alpha }},{\varvec{\beta }})}(x)\, = \ {\left\{ \begin{array}{ll} |x|^{\alpha _1} (1-\log |x|)^{\alpha _2}, &{} \text {if} \quad |x|\le 1\, ,\\ |x|^{\beta _1} (1+\log |x|)^{\beta _2},&{} \text {if} \quad |x|> 1\,, \end{array}\right. } \end{aligned}$$

(2.5)

where

$$\begin{aligned} {\varvec{\alpha }} \!=\! (\alpha _1,\alpha _2), \ \alpha _1> -{d},\ \alpha _2\in {\mathbb {R}}, \quad {\varvec{\beta }} \!=\! (\beta _1,\beta _2), \ \beta _1>\!-\!{d}, \ \beta _2\in {\mathbb {R}}. \end{aligned}$$

(2.6)

Straightforward calculation shows that $w_{({\varvec{\alpha }},{\varvec{\beta }})}\in {\mathcal {A}}_r$ if $\max \{\alpha _1,\beta _1\}<{d}(r-1)$. A special case here is the ‘purely logarithmic’ weight

$$\begin{aligned} w^{\log }_{{\varvec{\gamma }}}(x) = {\left\{ \begin{array}{ll} (1-\log |x|)^{\gamma _1}, &{} \text {if} \quad |x|\le 1\, ,\\ (1+\log |x|)^{\gamma _2},&{} \text {if} \quad |x|> 1\,, \end{array}\right. } \end{aligned}$$

(2.7)

where ${\varvec{\gamma }}=(\gamma _1,\gamma _2)\in {\mathbb {R}}^2$. Then $w^{\log }_{{\varvec{\gamma }}} \in {\mathcal {A}}_1$ for $\gamma _2\le 0\le \gamma _1$.

For further examples we refer to [11, 17, 18].

We need some refined study of the singularity behaviour of Muckenhoupt ${\mathcal {A}}_\infty$ weights. Let for $m\in {\mathbb {Z}}^{{d}}$ and $j \in {{\mathbb {N}}}_{0}$, $Q_{j, m}$ denote the ${d}$-dimensional cube with sides parallel to the axes of coordinates, centered at $2^{-j}m$ and with side length $2^{-j}$. In [18] we introduced the following notion of their set of singularities ${\mathbf {S}}_{\mathrm {sing}}(w)$.

Definition 2.3

For $w\in {\mathcal {A}}_\infty$ we define the set of singularities ${\mathbf {S}}_{\mathrm {sing}}(w)$ by

$$\begin{aligned} {\mathbf {S}}_{\mathrm {sing}}(w)&= \ \left\{ x_0\in {{\mathbb {R}}}^{{d}}: \ \inf _{Q_{j,m}\ni x_0} \ \frac{w(Q_{j,m})}{|Q_{j,m}|} = 0 \right\} \\&\ \cup \ \left\{ x_0\in {{\mathbb {R}}}^{{d}}: \ \sup _{Q_{j,m}\ni x_0} \ \frac{w(Q_{j,m})}{|Q_{j,m}|} = \infty \right\} . \end{aligned}$$

Recall the following result.

Proposition 2.4

[20, Prop. 2.6] If $w\in {\mathcal {A}}_\infty$, then $|{\overline{{\mathbf {S}}_{\mathrm {sing}}(w)}}|=0$.

Remark 2.5

${\mathbf {S}}_{\mathrm {sing}}(w)$ is a special case of ${\mathbf {S}}_{\mathrm {sing}}(w_1,w_2)$ defined in [18] with $w_2\equiv 1$, $w_1\equiv w$. There we also proved some forerunner of Proposition 2.4. Let us explicitly recall a very useful consequence of the above result, cf. [20, Cor. 2.7]. We call a cube (or ball) $Q\subset {{\mathbb {R}}}^{{d}}$ regularity cube (or regularity ball) of a given weight w, if the weight is regular there, that is, if there exist positive constants $c_1, c_2$ such that for all $x\in Q$ it holds $c_1\le w(x)\le c_2$, i.e., $w\sim 1$ on Q. Hence the above proposition implies that for any $w\in {\mathcal {A}}_\infty$ any cube or ball $Q\subset {{\mathbb {R}}}^{{d}}$ contains a regularity cube or ball ${\widetilde{Q}}\subset Q$.

Remark 2.6

In [15] we studied so-called ‘admissible’ weights. These are smooth weights with no singular points. One can take

$$\begin{aligned} w(x)=\langle x\rangle ^\gamma = (1+|x|^2)^{\gamma /2}, \quad \gamma \in {\mathbb {R}},\quad x\in {{\mathbb {R}}}^{{d}}, \end{aligned}$$

as a prominent example. For the precise definition we refer to [15] and the references given therein.

2.2 Weighted Function Spaces of Type $B^s_{p,q}({{\mathbb {R}}}^{{d}},w)$ and $F^s_{p,q}({{\mathbb {R}}}^{{d}},w)$

Let $w\in {\mathcal {A}}_{\infty }$ be a Muckenhoupt weight, and $\ 0<p< \infty$. Then the weighted Lebesgue space $L_p({{\mathbb {R}}}^{{d}}, w)$ contains all measurable functions such that

$$\begin{aligned} \Vert f\;|L_p({{\mathbb {R}}}^{{d}},w)\Vert = \left( \int _{{{\mathbb {R}}}^{{d}}}|f(x)|^p w(x) \;\mathrm {d}x\right) ^{1/p} \end{aligned}$$

(2.8)

is finite. Note that for $p=\infty$ one obtains the classical (unweighted) Lebesgue space,

$$\begin{aligned} L_\infty ({{\mathbb {R}}}^{{d}}, w) = L_\infty ({{\mathbb {R}}}^{{d}}),\quad w\in {\mathcal {A}}_\infty . \end{aligned}$$

(2.9)

Thus we mainly restrict ourselves to $\ p<\infty$ in what follows.

The Schwartz space $\ {\mathcal {S}}({{\mathbb {R}}}^{{d}})\$ and its dual $\ {\mathcal {S}}'({{\mathbb {R}}}^{{d}})\$ of all complex-valued tempered distributions have their usual meaning here. Let $\ \varphi _0=\varphi \in {\mathcal {S}}({{\mathbb {R}}}^{{d}})\$ be such that

$$\begin{aligned} \mathop {\mathrm {supp}}\nolimits \varphi \subset \left\{ y\in {{\mathbb {R}}}^{{d}}:|y|<2\right\} \quad \text{ and }\quad \varphi (x)=1\quad \text{ if }\quad |x|\le 1\;, \end{aligned}$$

and for each $\ j\in {{\mathbb {N}}}\;$ let $\ \varphi _j(x)= \varphi (2^{-j}x)-\varphi (2^{-j+1}x)$. Then $\ \{\varphi _j\}_{j=0}^\infty$ forms a smooth dyadic resolution of unity. Given any $\ f\in {\mathcal {S}}'({{\mathbb {R}}}^{{d}})$, we denote by ${\mathcal {F}}f$ and ${\mathcal {F}}^{-1}f$ its Fourier transform and its inverse Fourier transform, respectively.

Definition 2.7

Let $0 <q\le \infty$, $\ 0<p<\infty$, $\ s\in {\mathbb {R}}$ and $\ \left\{ \varphi _j\right\} _j$ a smooth dyadic resolution of unity. Assume $\ w\in {\mathcal {A}}_\infty$.

(i):

The weighted Besov space $B^s_{p,q}({{\mathbb {R}}}^{{d}},w)$ is the set of all distributions $f\in {\mathcal {S}}'({{\mathbb {R}}}^{{d}})$ such that

$$\begin{aligned} \big \Vert f\;| B^s_{p,q}({{\mathbb {R}}}^{{d}},w)\big \Vert = \left\| \left\{ 2^{js}\big \Vert {\mathcal {F}}^{-1}(\varphi _j{\mathcal {F}}f)| L_p({{\mathbb {R}}}^{{d}},w)\big \Vert \right\} _{j\in {{\mathbb {N}}}_{0}} | \ell _q\right\| \end{aligned}$$

(2.10)

is finite.

(ii):

The weighted Triebel - Lizorkin space $F^s_{p,q}({{\mathbb {R}}}^{{d}},w)$ is the set of all distributions $f\in {\mathcal {S}}'({{\mathbb {R}}}^{{d}})$ such that

$$\begin{aligned} \big \Vert f |F^s_{p,q}({{\mathbb {R}}}^{{d}},w)\big \Vert =\left\| \big \Vert \left\{ 2^{js}| {\mathcal {F}}^{-1}(\varphi _j{\mathcal {F}}f)(\cdot )|\right\} _{j\in {{\mathbb {N}}}_{0}} | \ell _q\big \Vert ~ |L_p({{\mathbb {R}}}^{{d}},w)\right\| \end{aligned}$$

(2.11)

is finite.

Remark 2.8

The spaces $B^s_{p,q}({{\mathbb {R}}}^{{d}},w)$ and $F^s_{p,q}({{\mathbb {R}}}^{{d}},w)$ are independent of the particular choice of the smooth dyadic resolution of unity $\left\{ \varphi _j\right\} _j$ appearing in their definitions. They are quasi-Banach spaces (Banach spaces for $p,q\ge 1$), and $\ {\mathcal {S}}({{\mathbb {R}}}^{{d}})\hookrightarrow B^s_{p,q}({{\mathbb {R}}}^{{d}}, w)\hookrightarrow {\mathcal {S}}'({{\mathbb {R}}}^{{d}})$, similarly for the F-case, where the first embedding is dense if $q<\infty$; cf. [3]. Moreover, for $\ w_0\equiv 1 \in {\mathcal {A}}_\infty$ we obtain the usual (unweighted) Besov and Triebel–Lizorkin spaces; we refer, in particular, to the series of monographs by Triebel [45,46,47,48] for a comprehensive treatment of the unweighted spaces.

The above spaces with weights of type $\ w\in {\mathcal {A}}_\infty$ have been studied systematically by Bui first in [3, 4]. It turned out that many of the results from the unweighted situation have weighted counterparts: e.g., we have $F^0_{p,2}({{\mathbb {R}}}^{{d}},w) = h_p({{\mathbb {R}}}^{{d}},w)$, $\ 0<p<\infty$, where the latter are Hardy spaces, see [3, Thm. 1.4], and, in particular, $h_p({{\mathbb {R}}}^{{d}}, w) = L_p({{\mathbb {R}}}^{{d}}, w) = F^0_{p,2}({{\mathbb {R}}}^{{d}},w)$, $\ 1<p<\infty$, $\ w\in {\mathcal {A}}_p$, see [42, Ch. VI, Thm. 1]. Concerning (classical) Sobolev spaces $W^k_p({{\mathbb {R}}}^{{d}}, w)$ built upon $L_p({{\mathbb {R}}}^{{d}}, w)$ in the usual way, it holds

$$\begin{aligned} W^k_p({{\mathbb {R}}}^{{d}}, w) = F^k_{p,2}({{\mathbb {R}}}^{{d}}, w), \quad k\in {{\mathbb {N}}}_{0}, \quad 1<p<\infty , \quad w\in {\mathcal {A}}_p, \end{aligned}$$

(2.12)

cf. [3, Thm. 2.8]. In [37] the above class of weights was extended to the class $\ {\mathcal {A}}_p^{\mathrm {loc}}$. We partly rely on our approaches [16,17,18].

Convention. We adopt the nowadays usual custom to write $A^s_{p,q}$ instead of $B^s_{p,q}$ or $F^s_{p,q}$, respectively, when both scales of spaces are meant simultaneously in some context (but always with the understanding of the same choice within one and the same embedding, if not otherwise stated explicitly).

Remark 2.9

Occasionally we use the following embeddings which are natural extensions from the unweighted case. If $0<q\le \infty$, $0<q_0\le q_1\le \infty$, $\ 0<p<\infty$, $\ s, s_0,s_1\in {\mathbb {R}}$ with $s_1\le s_0$, and $\ w\in {\mathcal {A}}_\infty$, then $A^{s_0}_{p,q}({{\mathbb {R}}}^{{d}}, w) \hookrightarrow A^{s_1}_{p,q}({{\mathbb {R}}}^{{d}},w)$ and $A^{s}_{p,q_0}({{\mathbb {R}}}^{{d}}, w) \hookrightarrow A^{s}_{p,q_1}({{\mathbb {R}}}^{{d}}, w)$, and

$$\begin{aligned} B^s_{p, \min (p,q)}({{\mathbb {R}}}^{{d}}, w) \hookrightarrow F^s_{p,q}({{\mathbb {R}}}^{{d}}, w) \hookrightarrow B^s_{p, \max (p,q)}({{\mathbb {R}}}^{{d}}, w). \end{aligned}$$

(2.13)

For the unweighted case $w\equiv 1$ see [45, Prop. 2.3.2/2, Thm. 2.7.1] and [40, Thm. 3.2.1]. The above result essentially coincides with [3, Thm. 2.6] and can be found in [17, Prop. 1.8].

Finally, we briefly describe the wavelet characterisations of Besov spaces with ${{\mathcal {A}}}_\infty$ weights proved in [17]. Let for $m\in {\mathbb {Z}}^{{d}}$ and $j \in {{\mathbb {N}}}_{0}$ the cubes $Q_{j, m}$ be as above. Apart from function spaces with weights we introduce sequence spaces with weights: for $0<p<\infty$, $0<q \le \infty$, $\sigma \in {\mathbb {R}}$, and $w\in {\mathcal {A}}_\infty$, let

$$\begin{aligned} b^\sigma _{p,q}(w) :=&\ \Bigg \{ \lambda = \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, m\in {\mathbb {Z}}^{{d}}} : \ \lambda _{j,m} \in {{\mathbb {C}}}\, , \\&\Vert \lambda |b^\sigma _{p,q}(w)\Vert \sim \Big \Vert \Big \{2^{j \sigma } \Big (\sum _{m \in {\mathbb {Z}}^{{d}}} |\lambda _{j,m}|^p\ 2^{j {d}}\ w(Q_{j,m})\Big )^{\frac{1}{p}} \Big \}_{j\in {{\mathbb {N}}}_{0}} | \ell _q\Big \Vert < \infty \Bigg \}\, \end{aligned}$$

and

$$\begin{aligned} \ell _p(w) :=&\ \Bigg \{ \lambda = \{\lambda _m\}_{m\in {\mathbb {Z}}^{{d}}} : \lambda _{m} \in {{\mathbb {C}}}, \\&\Vert \lambda |\ell _p(w)\Vert \sim \Big (\sum _{m \in {\mathbb {Z}}^{{d}}} |\lambda _{m}|^p \ 2^{j {d}}\ w(Q_{0,m})\Big )^{\frac{1}{p}} < \infty \Bigg \}\, . \end{aligned}$$

If $w\equiv 1$ we write $b^\sigma _{p,q}$ instead of $b^\sigma _{p,q}(w)$.

Let ${\widetilde{\phi }}\in C^{N_1}({\mathbb {R}})$ be a scaling function on ${\mathbb {R}}$ with $\mathop {\mathrm {supp}}\nolimits {\widetilde{\phi }}\subset [-N_2,\, N_2]$ for certain natural numbers $N_1$ and $N_2$, and ${\widetilde{\psi }}$ an associated wavelet. Then the tensor-product ansatz yields a scaling function $\phi$ and associated wavelets $\psi _1, \ldots , \psi _{2^{{d}}-1}$, all defined now on ${{\mathbb {R}}}^{{d}}$. This implies

$$\begin{aligned} \phi , \, \psi _i \in C^{N_1}({{\mathbb {R}}}^{{d}}) \quad \text {and} \quad \mathop {\mathrm {supp}}\nolimits \phi ,\, \mathop {\mathrm {supp}}\nolimits \psi _i \subset [-N_3,\, N_3]^{{d}} \, , \quad i=1, \ldots \, , 2^{{d}}-1 \, . \end{aligned}$$

(2.14)

Using the standard abbreviations

$$\begin{aligned} \phi _{j,m}(x) = 2^{j {d}/2} \phi (2^j x-m)\quad \text {and}\quad \psi _{i,j,m}(x) = 2^{j {d}/2} \psi _i(2^j x-m) \end{aligned}$$

we proved in [17] the following wavelet decomposition result.

Theorem 2.10

[17, Thm. 1.13] Let $0 < p,q \le \infty$ and let $s\in {\mathbb {R}}$. Let $\phi$ be a scaling function and let $\psi _i$, $i=1, \ldots ,2^{{d}}-1$, be the corresponding wavelets satisfying (2.14). We assume that $|s|<N_1$. Then a distribution $f \in {\mathcal {S}}'({{\mathbb {R}}}^{{d}})$ belongs to $B^s_{p,q}({{\mathbb {R}}}^{{d}},w)$, if, and only if,

$$\begin{aligned} \Vert \, f \, |B^s_{p,q}({{\mathbb {R}}}^{{d}}, w)\Vert ^\star&= \Big \Vert \left\{ \langle f,\phi _{0,m}\rangle \right\} _{m\in {\mathbb {Z}}^{{d}}} | \ell _p(w)\Big \Vert \\&\quad + \sum _{i=1}^{2^{{d}}-1} \Big \Vert \left\{ \langle f,\psi _{i,j,m}\rangle \right\} _{j\in {{\mathbb {N}}}_{0}, m\in {\mathbb {Z}}^{{d}}} | b^\sigma _{p,q}(w)\Big \Vert \end{aligned}$$

is finite, where $\sigma =s+\frac{{d}}{2} - \frac{{d}}{p}$. Furthermore, $\Vert \, f \, |B^s_{p,q}({{\mathbb {R}}}^{{d}}, w) \Vert ^\star$ may be used as an equivalent (quasi-) norm in $B^s_{p,q}({{\mathbb {R}}}^{{d}}, w)$.

2.3 Compact Embeddings

We collect some compact embedding results for weighted spaces of the above type that will be used later. For that purpose, let us introduce the following notation: for $s_i\in {\mathbb {R}}$, $0<p_i,q_i\le \infty$, $i=1,2$, we call

$$\begin{aligned} \delta :=s_1 - \frac{{d}}{p_1}-s_2 + \frac{{d}}{p_2}, \quad \end{aligned}$$

(2.15)

and

$$\begin{aligned} \frac{1}{p^*} = \max \left( \frac{1}{p_2} - \frac{1}{p_1},0\right) , \quad \frac{1}{q^*} = \max \left( \frac{1}{q_2} - \frac{1}{q_1},0\right) \end{aligned}$$

(2.16)

(with the understanding that $p^*=\infty$ when $p_1\le p_2$, $q^*=\infty$ when $q_1\le q_2$).

We restrict ourselves to the situation when only the source space is weighted, and the target space unweighted,

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _w:A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w)\hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}), \end{aligned}$$

(2.17)

where $w\in {\mathcal {A}}_\infty$. The identity operator $\mathop {\mathrm {id}}\nolimits _w$ is a bounded linear operator if the parameters s, p and q defining the function spaces and the weight w satisfy certain natural conditions. We refer to our earlier papers [17,18,19] for a detailed description. Here we consider the weights $w_{\alpha ,\beta }$ given by (2.4), or $w_{({\varvec{\alpha }},{\varvec{\beta }})}$ given by (2.5) (with the special case $w^{\log }_{{\varvec{\gamma }}}$ as in (2.7)) and the compact embeddings $\mathop {\mathrm {id}}\nolimits _w$. The corresponding conditions for the compactness are formulated in Proposition 2.11 and Proposition 2.14 below. To indicate the weight we work with, we will write $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ or $\mathop {\mathrm {id}}\nolimits _{(\alpha ,\beta )}$ instead of $\mathop {\mathrm {id}}\nolimits _w$. Moreover, we shall assume in the sequel that $p_1<\infty$ for convenience, as otherwise we have $B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w)=B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})$, recall (2.9), and we arrive at the unweighted situation in (2.17) which is well-known already. We first recall the result for Example 2.2(i).

Proposition 2.11

[17, Prop. 2.6] Let $\alpha >-{d}$, $\beta >-{d}$, $w_{\alpha ,\beta }$ be given by (2.4) and

$$\begin{aligned} -\infty< s_2\le s_1<\infty , \ 0<p_1<\infty ,\ 0<p_2\le \infty , \ 0<q_1, q_2\le \infty . \end{aligned}$$

(2.18)

Then the embedding

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }: A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{\alpha ,\beta })\hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

is compact if, and only if,

$$\begin{aligned} \frac{\beta }{p_1}>\frac{{d}}{p^*} \qquad \text {and}\qquad \delta >\max \left( \frac{{d}}{p^*},\frac{\alpha }{p_1}\right) . \end{aligned}$$

(2.19)

Remark 2.12

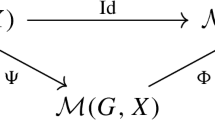
Let us briefly point out the main argument in [17,18,19] concerning compactness assertions as we shall follow a similar idea when dealing with nuclearity below. The argument justifies also why we can restrict ourselves to the case when the target space is unweighted, and it shows how the double-weighted case follows from the one-weighted one. We rely on a reduction of the function space embeddings to corresponding sequence space embeddings based on the wavelet decomposition Theorem 2.10: we make use of the commutative diagram

with appropriate isomorphisms S and T. Similarly, with an appropriate isomorphism A it is sufficient to investigate the embedding of a weighted sequence space into an unweighted one, using

This will be our starting point below.

Remark 2.13

In the special case $\alpha =0$ the weight $w_{0,\beta }$ can be regarded as a so-called admissible weight, $w_{0,\beta }(x) \sim \langle x\rangle ^\beta =:w^\beta (x)$, recall Remark 2.6. For such weights compact embeddings were studied in many papers, see for instance [15, 21]. The well-known counterpart of Proposition 2.11 reads as

$$\begin{aligned}&\mathop {\mathrm {id}}\nolimits ^\beta : A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w^\beta )\hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})\quad \text {compact}\quad \nonumber \\&\quad \iff \quad \frac{\beta }{p_1}>\frac{{d}}{p^*} \qquad \text {and}\qquad \delta > \frac{{d}}{p^*}. \end{aligned}$$

(2.20)

Now we turn our attention to Example 2.2(ii) and the model weight $w_{({\varvec{\alpha }},{\varvec{\beta }})}$. The compactness result reads as follows.

Proposition 2.14

[19, Prop. 3.9] Let $w_{({\varvec{\alpha }},{\varvec{\beta }})}$ be given by (2.5), (2.6). The embedding

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _{(\alpha ,\beta )} : B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w_{({\varvec{\alpha }},{\varvec{\beta }})}) \hookrightarrow B^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

(2.21)

is compact if, and only if,

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {either}&{} \frac{\beta _1}{p_1} \> \ \frac{{d}}{p^*},\quad \beta _2\in {\mathbb {R}}, \\ \text {or} &{} \frac{\beta _1}{p_1} \ = \ \frac{{d}}{p^*}, \quad \frac{\beta _2}{p_1} > \frac{1}{p^*},\end{array}\right. } \end{aligned}$$

(2.22)

and

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{either}&{}{} \delta>\max \left( \frac{\alpha _1}{p_1}, \frac{{d}}{p^*}\right) ,\quad \alpha _2\in {\mathbb {R}}, \\ \mathrm{or} &{}{} \delta =\frac{\alpha _1}{p_1}> \frac{{d}}{p^*}, \quad \frac{\alpha _2}{p_1}>\frac{1}{q^*}. \end{array}\right. \end{aligned}$$

(2.23)

Remark 2.15

In case of F-spaces there is an almost complete characterisation in [19, Cor. 3.15]. For the ‘purely logarithmic’ weight $w^{\log }_{{\varvec{\gamma }}}$ given by (2.7) the above result, cf. [19, Prop. 3.9] reads as follows:

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _{\log }: B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w^{\log }_{{\varvec{\gamma }}}) \hookrightarrow B^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})\quad&\text {is compact}\\ \iff \quad&p_1\le p_2, \quad \delta>0,\quad \gamma _1\in {\mathbb {R}}, \quad \gamma _2>0. \end{aligned}$$

Remark 2.16

Let $\Omega \subset {{\mathbb {R}}}^{{d}}$ be a bounded Lipschitz domain and $0<p,q\le \infty$ (with $p<\infty$ in the F-case), $s\in {\mathbb {R}}$. Let the spaces $B^s_{p,q}(\Omega )$ and $F^s_{p,q}(\Omega )$ be defined by restriction. It is well known that

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _\Omega : A^{s_1}_{p_1,q_1}(\Omega ) \rightarrow A^{s_2}_{p_2,q_2}(\Omega ) \end{aligned}$$

(2.24)

is compact, if, and only if,

$$\begin{aligned} s_1-s_2 > {d}\left( \frac{1}{p_1}-\frac{1}{p_2}\right) _+, \end{aligned}$$

(2.25)

where $s_i\in {\mathbb {R}}$, $0<p_i,q_i\le \infty$ ($p_i<\infty$ if A=F), $i=1,2$.

3 Nuclear Embeddings

Our main goal in this paper is to study nuclear embeddings between the weighted spaces introduced above. So we first recall some fundamentals of the concept and important results we rely on in the sequel.

3.1 The Concept and Recent Results

Let X, Y be Banach spaces, $T\in {\mathcal {L}}(X,Y)$ a linear and bounded operator. Then T is called nuclear, denoted by $T\in {\mathcal {N}}(X,Y)$, if there exist elements $a_j\in X'$, the dual space of X, and $y_j\in Y$, $j\in {\mathbb {N}}$, such that $\sum _{j=1}^\infty \Vert a_j\Vert _{X'} \Vert y_j\Vert _Y < \infty$ and a nuclear representation $Tx=\sum _{j=1}^\infty a_j(x) y_j$ for any $x\in X$. Together with the nuclear norm

$$\begin{aligned} \nu ( T)=\inf \Big \{ \sum _{j=1}^\infty \Vert a_j\Vert _{X'} \Vert y_j\Vert _Y:\ T =\sum _{j=1}^\infty a_j(\cdot ) y_j\Big \}, \end{aligned}$$

where the infimum is taken over all nuclear representations of T, the space ${\mathcal {N}}(X,Y)$ becomes a Banach space. It is obvious that any nuclear operator can be approximated by finite rank operators, hence nuclear operators are, in particular, compact.

Remark 3.1

This concept has been introduced by Grothendieck [14] and was intensively studied afterwards, cf. [29,30,31] and also [32] for some history. At that time applications were intended to better understand, for instance, nuclear locally convex spaces, operator ideals, eigenvalues of compact operators in Banach spaces. There exist extensions of the concept to r-nuclear operators, $0<r<\infty$, where $r=1$ refers to the nuclearity. It is well-known that ${\mathcal {N}}(X,Y)$ possesses the ideal property. In Hilbert spaces $H_1,H_2$, the nuclear operators ${\mathcal {N}}(H_1,H_2)$ coincide with the trace class $S_1(H_1,H_2)$, consisting of those T with singular numbers $(s_n(T))_n \in \ell _1$.

We collect some more or less well-known facts needed in the sequel.

Proposition 3.2

(i):

If X is an n-dimensional Banach space, then

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits :X\rightarrow X)= n. \end{aligned}$$

(ii):

For any Banach space X and any bounded linear operator $T:\ell ^n_\infty \rightarrow X$ we have

$$\begin{aligned} \nu ( T) = \sum _{i=1}^n \Vert Te_i\Vert . \end{aligned}$$

(iii):

If $T\in {\mathcal {L}}(X,Y)$ is a nuclear operator and $S\in {\mathcal {L}}(X_0,X)$ and $R\in {\mathcal {L}}(Y,Y_0)$, then STR is a nuclear operator and

$$\begin{aligned} \nu ( STR) \le \Vert S\Vert \Vert R\Vert \nu ( T) . \end{aligned}$$

Already in the early years there was a strong interest to find further examples of nuclear operators beyond diagonal operators in $\ell _p$ spaces, where a complete answer was obtained in [43]. Let $\tau =(\tau _j)_{j\in {{\mathbb {N}}}}$ be a scalar sequence and denote by $D_\tau$ the corresponding diagonal operator, $D_\tau : x=(x_j)_j \mapsto (\tau _j x_j)_j$, acting between $\ell _p$ spaces. Let us introduce the following notation: for numbers $r_1,r_2\in [1,\infty ]$, let $\mathbf {t}(r_1,r_2)$ be given by

$$\begin{aligned} \frac{1}{\mathbf {t}(r_1,r_2)} = {\left\{ \begin{array}{ll} 1, &{} \text {if}\ 1\le r_2\le r_1\le \infty , \\ 1-\frac{1}{r_1}+\frac{1}{r_2}, &{} \text {if}\ 1\le r_1\le r_2\le \infty . \end{array}\right. } \end{aligned}$$

(3.1)

Hence $1\le \mathbf {t}(r_1,r_2)\le \infty$, and

$$\begin{aligned} \frac{1}{\mathbf {t}(r_1,r_2)}= 1-\left( \frac{1}{r_1}-\frac{1}{r_2}\right) _+ \ge \frac{1}{r^*}= \left( \frac{1}{r_2}-\frac{1}{r_1}\right) _+\, \end{aligned}$$

with $\mathbf {t}(r_1,r_2)=r^*$ if, and only if, $\{r_1,r_2\}=\{1,\infty \}$.

Recall that $c_0$ denotes the subspace of $\ell _\infty$ containing the null sequences.

Proposition 3.3

[43, Thms. 4.3, 4.4] Let $1\le r_1,r_2\le \infty$ and $D_\tau$ be the above diagonal operator.

(i):

Then $D_\tau$ is nuclear if, and only if, $\tau =(\tau _j)_j \in \ell _{\mathbf {t}(r_1,r_2)}$, with $\ell _{\mathbf {t}(r_1,r_2)}= c_0$ if $\mathbf {t}(r_1,r_2)=\infty$. Moreover,

$$\begin{aligned} \nu ( D_\tau :\ell _{r_1}\rightarrow \ell _{r_2}) = \Vert \tau |{\ell _{\mathbf {t}(r_1,r_2)}}\Vert . \end{aligned}$$

(ii):

Let $n\in {{\mathbb {N}}}$ and $D^n_\tau : \ell ^n_{r_1}\rightarrow \ell ^n_{r_2}$ be the corresponding diagonal operator $D_\tau ^n: x=(x_j)_{j=1}^n \mapsto (\tau _j x_j)_{j=1}^n$. Then

$$\begin{aligned} \nu ( D_\tau ^n:\ell _{r_1}^n\rightarrow \ell ^n_{r_2}) = \left\| (\tau _j)_{j=1}^n | {\ell _{\mathbf {t}(r_1,r_2)}^n} \right\| . \end{aligned}$$

(3.2)

Example 3.4

In the special case of $\tau \equiv 1$, i.e., $D_\tau =\mathop {\mathrm {id}}\nolimits$, (i) is not applicable and (ii) reads as

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits :\ell _{r_1}^n\rightarrow \ell ^n_{r_2}) = {\left\{ \begin{array}{ll} n &{} \text {if}\qquad 1\le r_2\le r_1\le \infty ,\\ n^{1-\frac{1}{r_1}+\frac{1}{r_2}} &{} \text {if}\qquad 1\le r_1\le r_2\le \infty . \end{array}\right. } \end{aligned}$$

In particular, $\nu ( \mathop {\mathrm {id}}\nolimits :\ell _1^n\rightarrow \ell ^n_\infty )=1$.

Remark 3.5

The remarkable result (ii) can be found in [43], see also [29] for the case $p=1$, $q=\infty$.

We return to the situation of compact embeddings of spaces on domains, as described in Remark 2.16. Recently Triebel proved in [49] the following counterpart for its nuclearity.

Proposition 3.6

[49] Let $\Omega \subset {{\mathbb {R}}}^{{d}}$ be a bounded Lipschitz domain, $1<p_i,q_i<\infty$, $s_i\in {\mathbb {R}}$. Then the embedding $\mathop {\mathrm {id}}\nolimits _\Omega$ given by (2.24) is nuclear if, and only if,

$$\begin{aligned} s_1-s_2 > {d}-{d}\left( \frac{1}{p_2}-\frac{1}{p_1}\right) _+. \end{aligned}$$

(3.3)

Remark 3.7

The proposition is stated in [49] for the B-case only, but due to the independence of (3.3) of the fine parameters $q_i$, $i=1,2$, and in view of (the corresponding counterpart of) (2.13) it can be extended immediately to F-spaces. The if-part of the above result is essentially covered by [33] (with a forerunner in [34]). Also part of the necessity of (3.3) for the nuclearity of $\mathop {\mathrm {id}}\nolimits _\Omega$ was proved by Pietsch in [33] such that only the limiting case $s_1-s_2 = {d}-{d}(\frac{1}{p_2}-\frac{1}{p_1})_+$ was open for many decades. Only recently Edmunds, Gurka and Lang in [7] (with a forerunner in [8]) obtained some answer in the limiting case which was then completely solved in [49]. In [5] the authors dealt with the nuclearity of the embedding $B^{s_1,\alpha _1}_{p_1,q_1}(\Omega )\rightarrow B^{s_2,\alpha _2}_{p_2,q_2}(\Omega )$ where the indices $\alpha _i$ represent some additional logarithmic smoothness. They obtained a characterisation for almost all possible settings of the parameters. Note that in [33] some endpoint cases (with $p_i,q_i\in \{1,\infty \}$) were already discussed for embeddings of Sobolev and certain Besov spaces (with $p=q$) into Lebesgue spaces. We are able to further extend Proposition 3.6 in Corollary 3.17 below.

Remark 3.8

In [6] some further limiting endpoint situations of nuclear embeddings like $\mathop {\mathrm {id}}\nolimits :B^{{d}}_{p,q}(\Omega )\rightarrow L_p(\log L)_a(\Omega )$ are studied. For some weighted results see also [28].

Remark 3.9

For later comparison we may reformulate the compactness and nuclearity characterisations of $\mathop {\mathrm {id}}\nolimits _\Omega$ in (2.25) and (3.3) as follows, involving the number $\mathbf {t}(p_1,p_2)$ defined in (3.1). Let $1<p_i,q_i<\infty$, $s_i\in {\mathbb {R}}$. Then

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _\Omega : A^{s_1}_{p_1,q_1}(\Omega ) \rightarrow A^{s_2}_{p_2,q_2}(\Omega ) \quad \text {is compact}\quad&\iff \quad \delta> \frac{{d}}{p^*}\qquad \text {and}\\ \mathop {\mathrm {id}}\nolimits _\Omega : A^{s_1}_{p_1,q_1}(\Omega ) \rightarrow A^{s_2}_{p_2,q_2}(\Omega ) \quad \text {is nuclear}\quad&\iff \quad \delta > \frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

Hence apart from the extremal cases $\{p_1,p_2\}=\{1,\infty \}$ (not admitted in Proposition 3.6) nuclearity is indeed stronger than compactness also in this setting, i.e.,

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _\Omega : A^{s_1}_{p_1,q_1}(\Omega ) \rightarrow A^{s_2}_{p_2,q_2}(\Omega ) \quad&\text {is compact, but not nuclear}\\&\qquad \iff \quad \frac{{d}}{p^*} < \delta \le \frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

We shall observe similar phenomena in the weighted setting later.

3.2 Weighted Spaces

We begin with some general implication from Proposition 3.6 for Muckenhoupt weights $w\in {\mathcal {A}}_\infty$. Here we benefit from the regularity result Proposition 2.4, in particular, the observation recalled in Remark 2.5.

Corollary 3.10

Let $1<p_i,q_i<\infty$, $s_i\in {\mathbb {R}}$, $w\in {\mathcal {A}}_\infty$. If the embedding

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _w: A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w) \rightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

is nuclear, then

$$\begin{aligned} s_1-s_2>{d}-{d}\left( \frac{1}{p_2}-\frac{1}{p_1}\right) _+,\qquad \text {i.e.,}\quad \delta > \frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

(3.4)

Proof

Assume that $\mathop {\mathrm {id}}\nolimits _w$ is nuclear and $\Omega$ is a regularity ball for w which always exists according to Remark 2.5. Consider now the spaces $A^{s_1}_{p_1,q_1}(\Omega )$ and $A^{s_2}_{p_2,q_2}(\Omega )$ defined by restriction (and equipped with the equivalent norm induced by the regularity ball), together with the corresponding linear and bounded extension operator, cf. [36]. Then Proposition 3.2(iii) implies the nuclearity of $\mathop {\mathrm {id}}\nolimits _\Omega :A^{s_1}_{p_1,q_1}(\Omega )\rightarrow A^{s_2}_{p_2,q_2}(\Omega )$ which leads to (3.4) by Proposition 3.6. $\square$

Remark 3.11

Later we can slightly extend the above result and incorporate limiting cases $p_i,q_i\in \{1,\infty \}$, see Corollary 3.19 below. Note, that the above result is in general a necessary condition for nuclearity only, as the simple example $w\equiv 1\in {\mathcal {A}}_\infty$ shows: in that case the unweighted embedding $\mathop {\mathrm {id}}\nolimits : A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\rightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is known to be never compact (let alone nuclear), no matter what the other parameters $s_i, p_i, q_i$ are.

We return to the weight function $w_{\alpha ,\beta }$ in Example 2.2(i) and give the counterpart of Proposition 2.11.

Theorem 3.12

Let $\alpha >-{d}$, $\beta >-{d}$, $w_{\alpha ,\beta }$ be given by (2.4). Assume that $1\le p_1< \infty$, $1\le p_2\le \infty$ ($p_2<\infty$ in the F-case), and $1\le q_i\le \infty$, $s_i\in {\mathbb {R}}$, $i=1,2$. Then the embedding $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }: A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{\alpha ,\beta })\hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear if, and only if,

$$\begin{aligned} \frac{\beta }{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)} \qquad \text {and}\qquad \delta >\max \left( \frac{{d}}{\mathbf {t}(p_1,p_2)},\frac{\alpha }{p_1}\right) . \end{aligned}$$

(3.5)

Remark 3.13

Note that dealing with the weighted setting we have the same phenomenon in Theorem 3.12 compared with the compactness result Proposition 2.11, as described in Remark  for the situation of spaces on bounded domains: the stronger nuclearity condition (3.5) is exactly achieved when $p^*$ is replaced by $\mathbf {t}(p_1,p_2)$.

Proof

First note that in view of (2.13) and the independence of (3.5) from the fine parameters $q_i$, $i=1,2$, together with Proposition 3.2(iii), it is sufficient to consider the case $A=B$, i.e., the Besov spaces.

Step 1.   We first deal with the sufficiency of (3.5) for the nuclearity. We return to Remark 2.12 where we explained our general strategy. Thus, to show the nuclearity of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ it is equivalent to proving the nuclearity of

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits : b^{\sigma _1}_{p_1,q_1}(w_{\alpha ,\beta }) \hookrightarrow b^{\sigma _2}_{p_2,q_2} \quad \text {with}\quad \sigma _i=s_i-\frac{{d}}{2}-\frac{{d}}{p_i}\ ,\quad i=1,2, \end{aligned}$$

which is obviously equivalent to the nuclearity of

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits : b^{\sigma _1-\sigma _2}_{p_1,q_1}(w_{\alpha ,\beta }) \hookrightarrow b^0_{p_2,q_2}, \end{aligned}$$

which in view of $\sigma _1-\sigma _2=\delta$ can be written as

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits : b^\delta _{p_1,q_1} (w_{\alpha ,\beta }) \hookrightarrow \ell _{q_2}(\ell _{p_2}). \end{aligned}$$

(3.6)

Note that

$$\begin{aligned} w_{\alpha ,\beta }(Q_{j, m}) \ \sim \ 2^{-j {d}} \left\{ \begin{array}{llr} 2^{-j\alpha } &{}\text {if} &{} m=0, \\ \left| 2^{-j} m\right| ^{\alpha } &{}\text {if} &{} 1\le |m| < 2^j, \\ \left| 2^{-j} m\right| ^{\beta } &{}\text {if} &{} |m| \ge 2^j. \end{array}\right. \end{aligned}$$

(3.7)

The operator $\mathop {\mathrm {id}}\nolimits$ is compact if the conditions (3.5) are satisfied, cf. [17]. We split $\ \mathop {\mathrm {id}}\nolimits : b^\delta _{p_1,q_1} (w_{\alpha ,\beta }) \hookrightarrow \ell _{q_2}(\ell _{p_2})\$ into

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits = \mathop {\mathrm {id}}\nolimits _1+\mathop {\mathrm {id}}\nolimits _2\quad \text {with}\quad \mathop {\mathrm {id}}\nolimits _r: b^\delta _{p_1,q_1} (w_{\alpha ,\beta }) \hookrightarrow \ell _{q_2}(\ell _{p_2}), \ r=1,2. \end{aligned}$$

The operator $\mathop {\mathrm {id}}\nolimits _1$ is defined as a composition of $\mathop {\mathrm {id}}\nolimits$ with the projection

$$\begin{aligned} \ell _{q_2}(\ell _{p_2})\ni (\lambda _{j,m})_{j,m} \mapsto ({\tilde{\lambda }}_{j,m})_{j,m}\in \ell _{q_2}(\ell _{p_2}), \quad {\tilde{\lambda }}_{j,m}={\left\{ \begin{array}{ll} \lambda _{j,m}&{} \text {if}\ |m|<2^j,\\ 0, &{} \text {if}\ |m|\ge 2^j.\end{array}\right. } \end{aligned}$$

In a slight abuse of notation we can understand $\mathop {\mathrm {id}}\nolimits _1$ as

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _1 : \ell _{q_1}\left( 2^{j(\delta -\frac{\alpha }{p_1})} \ell _{p_1}^{2^{j {d}}}(|m|^\alpha )\right) \hookrightarrow \ell _{q_2}(\ell _{p_2}), \end{aligned}$$

with

$$\begin{aligned} \left\| \lambda | \ell _{q_1}\left( 2^{j(\delta -\frac{\alpha }{p_1})} \ell _{p_1}^{2^{j {d}}}(|m|^\alpha )\right) \right\| = \Big \Vert \Big \{2^{j(\delta -\frac{\alpha }{p_1})} \Big (\sum _{|m|<2^j} |\lambda _{j,m}|^{p_1}\ |m|^\alpha \Big )^{\frac{1}{p_1}} \Big \}_{j\in {{\mathbb {N}}}_{0}} | \ell _{q_1}\Big \Vert . \end{aligned}$$

A simple argument that justifies this identification is left to the reader.

Now we study the nuclearity of $\mathop {\mathrm {id}}\nolimits _1$ and $\mathop {\mathrm {id}}\nolimits _2$. We further decompose $\mathop {\mathrm {id}}\nolimits _1$ into

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _1 = \sum _{j=0}^\infty \mathop {\mathrm {id}}\nolimits _{1,j}\quad \text {with}\quad \mathop {\mathrm {id}}\nolimits _{1,j}= Q_j \circ \mathop {\mathrm {id}}\nolimits ^j\circ P_j, \end{aligned}$$

(3.8)

where $P_j$ is the projection onto $\ell _{p_1}^{2^{j {d}}}(|m|^\alpha )$, hence

$$\begin{aligned} \left\| P_j : \ell _{q_1}\left( 2^{j(\delta -\frac{\alpha }{p_1})} \ell _{p_1}^{2^{j {d}}}(|m|^\alpha )\right) \rightarrow \ell _{p_1}^{2^{j {d}}}(|m|^\alpha )\right\| = 2^{-j(\delta -\frac{\alpha }{p_1})}, \end{aligned}$$

$\mathop {\mathrm {id}}\nolimits ^j: \ell _{p_1}^{2^{j {d}}}(|m|^\alpha ) \rightarrow \ell _{p_2}$ is the embedding on level j, and $Q_j$ is the embedding of $\ell _{p_2}$ into $\ell _{q_2}(\ell _{p_2})$ with $\Vert Q_j: \ell _{p_2} \rightarrow \ell _{q_2}(\ell _{p_2})\Vert =1$. Thus Proposition 3.2(iii) yields

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _{1,j}) \le \nu ( \mathop {\mathrm {id}}\nolimits ^j) 2^{-j(\delta -\frac{\alpha }{p_1})},\quad j\in {{\mathbb {N}}}_{0}. \end{aligned}$$

(3.9)

Consequently, (3.8) and (3.9) lead to

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1) \le \sum _{j=0}^\infty 2^{-j(\delta -\frac{\alpha }{p_1})} \nu ( \mathop {\mathrm {id}}\nolimits ^j). \end{aligned}$$

(3.10)

Next we decompose $\mathop {\mathrm {id}}\nolimits ^j$ into certain diagonal operators and the natural embedding,

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits ^j = \left( \mathop {\mathrm {id}}\nolimits : \ell _{p_2}^{2^{j d}} \hookrightarrow \ell _{p_2}\right) \circ D_{-\alpha } \circ D_\alpha \end{aligned}$$

with

$$\begin{aligned} \begin{array}{ll} D_\alpha : \ell _{p_1}^{2^{j {d}}}(|m|^\alpha ) \rightarrow \ell _{p_1}^{2^{j {d}}}, &{} D_\alpha : \{\lambda _{j,m}\}_{|m|<2^j} \mapsto \{\lambda _{j,m} |m|^{\frac{\alpha }{p_1}}\}_{|m|<2^j},\\ &{} \left\| D_\alpha : \ell _{p_1}^{2^{j {d}}}(|m|^\alpha ) \rightarrow \ell _{p_1}^{2^{j {d}}}\right\| = 1, \\ D_{-\alpha } : \ell _{p_1}^{2^{j {d}}} \rightarrow \ell _{p_2}^{2^{j {d}}}, \quad &{} D_{-\alpha }: \{\mu _{j,m}\}_{|m|<2^j} \mapsto \{\mu _{j,m} |m|^{-\frac{\alpha }{p_1}}\}_{|m|<2^j},\\ &{} \nu ( D_{-\alpha }) = \left\| \left\{ |m|^{-\frac{\alpha }{p_1}}\right\} _{|m|<2^j}| {\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| , \\ \mathop {\mathrm {id}}\nolimits : \ell _{p_2}^{2^{j {d}}} \hookrightarrow \ell _{p_2}, &{} \mathop {\mathrm {id}}\nolimits : \{\lambda _{j,m}\}_{|m|<2^j}\mapsto \{{\tilde{\lambda }}_{j,m}\}_{m\in {\mathbb {Z}}^{{d}}}, \\ &{} {\tilde{\lambda }}_{j,m}={\left\{ \begin{array}{ll}\lambda _{j,m}, &{} |m|<2^j, \\ 0, &{} |m|\ge 2^j, \end{array}\right. } \quad \Vert \mathop {\mathrm {id}}\nolimits : \ell _{p_2}^{2^{j {d}}} \hookrightarrow \ell _{p_2}\Vert =1, \end{array} \end{aligned}$$

where we applied Proposition 3.3, in particular (3.2). Thus

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^j) \le \left\| \left\{ |m|^{-\frac{\alpha }{p_1}}\right\} _{|m|<2^j}| {\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| . \end{aligned}$$

(3.11)

It remains to calculate the latter norm. First assume that $\mathbf {t}(p_1,p_2)<\infty$. In this case,

$$\begin{aligned}&{ \left\| \left\{ |m|^{-\frac{\alpha }{p_1}}\right\} _{|m|<2^j}|{\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}} \right\| ^{\mathbf {t}(p_1,p_2)}}\nonumber \\&\quad = \sum _{|m|<2^j} |m|^{-\frac{\alpha }{p_1} \mathbf {t}(p_1,p_2)} \ = \ \sum _{k=0}^j \sum _{|m|\sim 2^k} |m|^{-\frac{\alpha }{p_1} \mathbf {t}(p_1,p_2)} \nonumber \\&\quad \sim \sum _{k=0}^j 2^{-k\frac{\alpha }{p_1} \mathbf {t}(p_1,p_2)} 2^{k{d}} \ = \ \sum _{k=0}^j 2^{k({d}-\frac{\alpha }{p_1} \mathbf {t}(p_1,p_2))} \nonumber \\&\quad \sim \ {\left\{ \begin{array}{ll} 2^{j({d}-\frac{\alpha }{p_1} \mathbf {t}(p_1,p_2))}, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} > \frac{\alpha }{p_1}, \\ j, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} = \frac{\alpha }{p_1}, \\ 1, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} < \frac{\alpha }{p_1}.\end{array}\right. } \end{aligned}$$

(3.12)

Thus (3.10), (3.11) and (3.12) result in

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1)&\le \sum _{j=0}^\infty 2^{-j(\delta -\frac{\alpha }{p_1})} {\left\{ \begin{array}{ll} 2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)} -\frac{\alpha }{p_1} )}, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)}> \frac{\alpha }{p_1}, \\ j^{\frac{1}{\mathbf {t}(p_1,p_2)}}, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} = \frac{\alpha }{p_1}, \\ 1, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)}< \frac{\alpha }{p_1},\end{array}\right. } \\&\sim {\left\{ \begin{array}{ll} \displaystyle \sum _{j=0}^\infty 2^{-j(\delta -\frac{{d}}{\mathbf {t}(p_1,p_2)})}, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} > \frac{\alpha }{p_1}, \\ \displaystyle \sum _{j=0}^\infty 2^{-j(\delta -\frac{\alpha }{p_1})} j^{\frac{1}{\mathbf {t}(p_1,p_2)}}, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} = \frac{\alpha }{p_1}, \\ \displaystyle \sum _{j=0}^\infty 2^{-j(\delta -\frac{\alpha }{p_1})}, &{} \frac{{d}}{\mathbf {t}(p_1,p_2)} < \frac{\alpha }{p_1}.\end{array}\right. } \end{aligned}$$

Hence $\nu ( \mathop {\mathrm {id}}\nolimits _1)\le c<\infty$ if $\delta > \max (\frac{{d}}{\mathbf {t}(p_1,p_2)}, \frac{\alpha }{p_1})$ as assumed by (3.5).

If $t(p_1,p_2)=\infty$, i.e., if $p_1=1$ and $p_2=\infty$, then $\nu ( \mathop {\mathrm {id}}\nolimits ^j) { \le }1$ if $\alpha \ge 0$ and $\nu ( \mathop {\mathrm {id}}\nolimits ^j) { \le } 2^{-j\alpha }$ if $\alpha < 0$. In consequence,

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1)\le \sum _{j=0}^\infty 2^{-j(\delta - \max (\alpha ,0))}<\infty \qquad \text {if}\qquad \delta >\max (\alpha ,0). \end{aligned}$$

Next we deal with

$$\begin{aligned}&\mathop {\mathrm {id}}\nolimits _2: b^\delta _{p_1,q_1} (w_{\alpha ,\beta }) \hookrightarrow \ell _{q_2}(\ell _{p_2}), \end{aligned}$$

which is a composition of the identity map $\mathop {\mathrm {id}}\nolimits$ with the projection

$$\begin{aligned}&\ell _{q_2}(\ell _{p_2})\ni (\lambda _{j,m})_{j,m} \mapsto ({\tilde{\lambda }}_{j,m})_{j,m} \in \ell _{q_2}(\ell _{p_2}), \quad {\tilde{\lambda }}_{j,m}={\left\{ \begin{array}{ll} \lambda _{j,m}&{} \text {if}\ |m|\ge 2^j,\\ 0 &{} \text {if}\ |m|< 2^j,\end{array}\right. } \end{aligned}$$

such that (in a slight abuse of notation) we can understand $\mathop {\mathrm {id}}\nolimits _2$ as

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _2 : \ell _{q_1}\left( 2^{j(\delta -\frac{\beta }{p_1})} \ell _{p_1}(|m|^\beta )\right) \hookrightarrow \ell _{q_2}(\ell _{p_2}), \end{aligned}$$

with

$$\begin{aligned} \left\| \lambda | \ell _{q_1}\left( 2^{j(\delta -\frac{\beta }{p_1})} \ell _{p_1}(|m|^\beta )\right) \right\| = \Big \Vert \Big \{2^{j(\delta -\frac{\beta }{p_1})} \Big (\sum _{|m|\ge 2^j} |\lambda _{j,m}|^{p_1}\ |m|^\beta \Big )^{\frac{1}{p_1}} \Big \}_{j\in {{\mathbb {N}}}_{0}} | \ell _{q_1}\Big \Vert . \end{aligned}$$

Again we decompose

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _2 = \sum _{j=0}^\infty \mathop {\mathrm {id}}\nolimits _{2,j}\quad \text {with}\quad \mathop {\mathrm {id}}\nolimits _{2,j}= {\widetilde{Q}}_j \circ {\widetilde{\mathop {\mathrm {id}}\nolimits }}^j\circ {\widetilde{P}}_j, \end{aligned}$$

(3.13)

where ${\widetilde{P}}_j$ is the projection onto $\ell _{p_1}(|m|^\beta )$, hence

$$\begin{aligned} \left\| {\widetilde{P}}_j : \ell _{q_1}\left( 2^{j(\delta -\frac{\beta }{p_1})} \ell _{p_1}(|m|^\beta )\right) \rightarrow \ell _{p_1}(|m|^\beta )\right\| = 2^{-j(\delta -\frac{\beta }{p_1})}, \end{aligned}$$

${\widetilde{\mathop {\mathrm {id}}\nolimits }}^j: \ell _{p_1}(|m|^\beta ) \rightarrow \ell _{p_2}$ is the embedding on level j, and ${\widetilde{Q}}_j$ is the embedding of $\ell _{p_2}$ into $\ell _{q_2}(\ell _{p_2})$ with $\Vert {\widetilde{Q}}_j: \ell _{p_2} \rightarrow \ell _{q_2}(\ell _{p_2})\Vert =1$. Proposition 3.2(iii) together with (3.13) yield

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _2) \le \sum _{j=0}^\infty 2^{-j(\delta -\frac{\beta }{p_1})} \nu ( {\widetilde{\mathop {\mathrm {id}}\nolimits }}^j) \end{aligned}$$

(3.14)

if ${\widetilde{\mathop {\mathrm {id}}\nolimits }}^j$ is a nuclear map. So we proceed similar as above,

$$\begin{aligned} {\widetilde{\mathop {\mathrm {id}}\nolimits }}^j = \left( {\widetilde{\mathop {\mathrm {id}}\nolimits }} : \ell _{p_2}\hookrightarrow \ell _{p_2}\right) \circ D_{-\beta } \circ D_\beta \end{aligned}$$

with

$$\begin{aligned}\begin{array}{ll} D_\beta : \ell _{p_1}(|m|^\beta ) \rightarrow \ell _{p_1}, \quad &{} D_\beta : \{\lambda _{j,m}\}_{|m|\ge 2^j} \mapsto \{\lambda _{j,m} |m|^{\frac{\beta }{p_1}}\}_{|m|\ge 2^j},\\ &{} \left\| D_\beta : \ell _{p_1}(|m|^\beta ) \rightarrow \ell _{p_1}\right\| = 1, \\ D_{-\beta } : \ell _{p_1} \rightarrow \ell _{p_2}, \quad &{} D_{-\beta }: \{\mu _{j,m}\}_{|m|\ge 2^j} \mapsto \{\mu _{j,m} |m|^{-\frac{\beta }{p_1}}\}_{|m|\ge 2^j},\\ &{}\nu ( D_{-\beta }) = \left\| \left\{ |m|^{-\frac{\beta }{p_1}}\right\} _{|m|\ge 2^j}|{\ell _{\mathbf {t}(p_1,p_2)}}\right\| , \\ {\widetilde{\mathop {\mathrm {id}}\nolimits }} : \ell _{p_2} \hookrightarrow \ell _{p_2}, \quad &{}{\widetilde{\mathop {\mathrm {id}}\nolimits }}: \{\lambda _{j,m}\}_{|m|\ge 2^j}\mapsto \{{\tilde{\lambda }}_{j,m}\}_{m\in {\mathbb {Z}}^{{d}}}, \\ &{}{\tilde{\lambda }}_{j,m}={\left\{ \begin{array}{ll}\lambda _{j,m}, &{} |m| \ge 2^j, \\ 0, &{} |m|< 2^j, \end{array}\right. }\quad \Vert {\widetilde{\mathop {\mathrm {id}}\nolimits }} : \ell _{p_2} \hookrightarrow \ell _{p_2}\Vert =1,\end{array} \end{aligned}$$

where we applied Proposition 3.3(i). Hence

$$\begin{aligned} \nu ( {\widetilde{\mathop {\mathrm {id}}\nolimits }}^j) \le \left\| \left\{ |m|^{-\frac{\beta }{p_1}}\right\} _{|m|\ge 2^j}|{\ell _{\mathbf {t}(p_1,p_2)}}\right\| . \end{aligned}$$

(3.15)

It remains to calculate that norm. If $t(p_1,p_2)<\infty$, then

$$\begin{aligned}&{\left\| \left\{ |m|^{-\frac{\beta }{p_1}}\right\} _{|m|\ge 2^j}|{\ell _{\mathbf {t}(p_1,p_2)}}\right\| ^{\mathbf {t}(p_1,p_2)}}\nonumber \\&\quad = \sum _{|m|\ge 2^j} |m|^{-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2)} \ = \ \sum _{k=j}^\infty \sum _{|m|\sim 2^k} |m|^{-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2)} \nonumber \\&\quad \sim \sum _{k=j}^\infty 2^{-k\frac{\beta }{p_1} \mathbf {t}(p_1,p_2)} 2^{k{d}} \ = \ \sum _{k=j}^\infty 2^{k({d}-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2))} \ \sim \ 2^{j({d}-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2))}\qquad \qquad \end{aligned}$$

(3.16)

using our assumption (3.5), i.e., $\frac{{d}}{\mathbf {t}(p_1,p_2)} < \frac{\beta }{p_1}$. Thus (3.14), (3.15) and (3.16) result in

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _2) \&\le \sum _{j=0}^\infty 2^{-j(\delta -\frac{\beta }{p_1})} 2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)} -\frac{\beta }{p_1} )} \ = \ \sum _{j=0}^\infty 2^{-j(\delta -\frac{{d}}{\mathbf {t}(p_1,p_2)})} \ \le \ c<\infty \end{aligned}$$

in view of (the second part of) (3.5) again.

If $t(p_1,p_2)=\infty$, that is, $p_1=1$ and $p_2=\infty$, then ${\widetilde{\mathop {\mathrm {id}}\nolimits }}^j$ is nuclear if $\{|m|^{-\beta }\}_{|m|\ge 2^j} \in c_0\subset \ell _\infty$, recall Proposition 3.3(i). This requires $\beta >0$ and leads to

$\nu ( {\widetilde{\mathop {\mathrm {id}}\nolimits }}^j) \le 2^{-j\beta }$. So

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _2) \le \sum _{j=0}^\infty 2^{-j\delta }<\infty \qquad \text {if}\qquad \delta >0. \end{aligned}$$

This concludes the argument for the sufficiency part.

Step 2.   Now we show the necessity of (3.5) for the nuclearity of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ and begin with the global behaviour of the weight and have to prove that the nuclearity of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ implies $\frac{\beta }{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)}$. So assume $\frac{\beta }{p_1}\le \frac{{d}}{\mathbf {t}(p_1,p_2)}$. We return to our above construction. Let $k\in {{\mathbb {N}}}$ and consider the following commutative diagram

where

$$\begin{aligned} P_k: \{\mu _m\}_{|m|\le 2^k} \mapsto \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, |m|\ge 2^j}, \quad \lambda _{j,m}={\left\{ \begin{array}{ll} \mu _m, &{} j=0,\quad 1\le |m|\le 2^k, \\ 0, &{} \text {otherwise},\end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} Q_k: \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, |m|\ge 2^j} \ \mapsto \{\mu _m\}_{|m|\le 2^k}, \quad \mu _m = {\left\{ \begin{array}{ll} \lambda _{0,m}, &{} 1\le |m|\le 2^k, \\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

such that $\Vert P_k\Vert = \Vert Q_k\Vert =1$, $k\in {{\mathbb {N}}}$. Thus

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^k) \le \nu ( \mathop {\mathrm {id}}\nolimits _2),\quad k\in {{\mathbb {N}}}. \end{aligned}$$

Similar as above, let

$$\begin{aligned}\begin{array}{ll} {D}_\beta : \ell _{p_1}^{2^{k {d}}} \rightarrow \ell _{p_1}^{2^{k {d}}}(|m|^\beta ), \quad &{} {D}_\beta : \{\mu _m\}_{|m|\le 2^k} \mapsto \{\mu _m |m|^{-\frac{\beta }{p_1}}\}_{|m|\le 2^k},\\ &{} \left\| {D}_\beta : \ell _{p_1}^{2^{k {d}}} \rightarrow \ell _{p_1}^{2^{k {d}}}(|m|^\beta )\right\| = 1, \\ D_{-\beta } : \ell _{p_1}^{2^{k {d}}} \rightarrow \ell _{p_2}^{2^{k {d}}}, \quad &{} D_{-\beta }: \{\mu _m\}_{|m|\le 2^k} \mapsto \{\mu _m |m|^{-\frac{\beta }{p_1}}\}_{|m|\le 2^k},\\ &{}\nu ( D_{-\beta }) = \left\| \left\{ |m|^{-\frac{\beta }{p_1}}\right\} _{|m|\le 2^k}|{\ell ^{2^{k{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| \end{array} \end{aligned}$$

where we applied Proposition 3.3, in particular (3.2). Then

$$\begin{aligned}&\left\| \left\{ |m|^{-\frac{\beta }{p_1}}\right\} _{|m|\le 2^k}|{\ell ^{2^{k{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| = \nu ( D_{-\beta }) = \nu ( \mathop {\mathrm {id}}\nolimits ^k\circ {D}_\beta ) \nonumber \\&\quad \le \Vert {D}_\beta \Vert \ \nu ( \mathop {\mathrm {id}}\nolimits ^k) \le \nu ( \mathop {\mathrm {id}}\nolimits _2), \quad k\in {{\mathbb {N}}}. \end{aligned}$$

(3.17)

On the other hand, parallel to (3.12),

$$\begin{aligned}&{ \left\| \left\{ |m|^{-\frac{\beta }{p_1}}\right\} _{|m|\le 2^k}|{\ell ^{2^{k{d}}}_{\mathbf {t}(p_1,p_2)}}|\right\| ^{\mathbf {t}(p_1,p_2)}}\nonumber \\&\quad = \sum _{|m|\le 2^k} |m|^{-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2)} = \ \sum _{l=0}^k \sum _{|m|\sim 2^l} |m|^{-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2)} \nonumber \\&\quad \sim \sum _{l=0}^k 2^{-l\frac{\beta }{p_1} \mathbf {t}(p_1,p_2)} 2^{l{d}} \ = \ \sum _{l=0}^k 2^{l({d}-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2))}\nonumber \\&\quad \sim \ {\left\{ \begin{array}{llll} 2^{k({d}-\frac{\beta }{p_1} \mathbf {t}(p_1,p_2))}, &{}{}\quad \frac{{d}}{\mathbf {t}(p_1,p_2)} > \frac{\beta }{p_1}, \\ k, &{}{}\quad \frac{{d}}{\mathbf {t}(p_1,p_2)} = \frac{\beta }{p_1}, \end{array}\right. } \end{aligned}$$

(3.18)

for arbitrary $k\in {{\mathbb {N}}}$. But this leads to a contradiction in (3.17) for $\nu ( \mathop {\mathrm {id}}\nolimits _2)<\infty$ in the considered cases. Thus $\frac{\beta }{p_1}> \frac{{d}}{\mathbf {t}(p_1,p_2)}$.

We are left to deal with the local part of the weight which is related to the second condition in (3.5). Since any nuclear map is compact, the nuclearity of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ implies its compactness which by Proposition 2.11 leads to $\delta >\frac{\alpha }{p_1}$. It remains to show $\delta >\frac{{d}}{\mathbf {t}(p_1,p_2)}$ in all admitted cases of the parameters. If $1<p_i,q_i<\infty$, $i=1,2$, this is an immediate consequence of Corollary 3.10. If $\mathbf {t}(p_1,p_2)=\infty$, i.e., $p_1=1$ and $p_2=\infty$, then ${\mathbf {t}(p_1,p_2)} = {p^*}$ and the statement follows from Proposition 2.11 again. We are left to deal with the limiting cases of $p_i$ and $q_i$, $i=1,2$, in case of $\mathbf {t}(p_1,p_2)<\infty$.

Assume that $\mathop {\mathrm {id}}\nolimits$ is a nuclear operator. Then $\mathop {\mathrm {id}}\nolimits _1$ is also a nuclear operator and $\nu ( \mathop {\mathrm {id}}\nolimits _1)\le \nu ( \mathop {\mathrm {id}}\nolimits )$. For a fixed $k\in {{\mathbb {N}}}$, let $\pi _k:\{1,\ldots , 2^{k{d}}\}\rightarrow \{m\in {\mathbb {Z}}^{{d}}: 2^{k}\le |m|\le 2^{k+1}\}$ be a bijection. For simplicity we assume that $\# \{m\in {\mathbb {Z}}^{{d}}: 2^{k}\le |m|\le 2^{k+1}\} = 2^{k{d}}$, neglecting constants.

First, let us consider the following commutative diagram

(3.19)

where

$$\begin{aligned} \Pi _k: \{\mu _i\}_{i=1,\ldots , 2^{k{d}}} \mapsto \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, |m| \le 2^j}, \quad \lambda _{j,m}={\left\{ \begin{array}{ll} \mu _i, &{} j=k+1,\ m=\pi _k(i), \\ 0, &{} \text {otherwise},\end{array}\right. }\nonumber \\ \end{aligned}$$

(3.20)

and

$$\begin{aligned} Q_k: \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, |m|\le 2^j} \ \mapsto \{\mu _i\}_{i=1,\ldots , 2^{k{d}}}, \quad \mu _i = \lambda _{k+1,m} \quad \text {if}\quad i=\pi _k^{-1}(m). \end{aligned}$$

Both operators $Q_k$ and $\Pi _k$ are bounded. Moreover

$$\begin{aligned} \left\| Q_k: \ell _{q_2}\left( \ell ^{2^{j{d}}}_{p_2}\right) \rightarrow \ell _{p_2}^{2^{k{d}}}\right\| =1, \quad k\in {{\mathbb {N}}}, \end{aligned}$$

and

$$\begin{aligned} \left\| \Pi _k: \ell _{q_1}\left( 2^{j(\delta -\frac{\alpha }{p_1})} \ell ^{2^{j{d}}}_{p_1}(|m|^{\alpha })\right) \rightarrow \ell _{p_1}^{2^{k{d}}}\right\| =2^{(k+1)\delta }, \quad k\in {{\mathbb {N}}}, \end{aligned}$$

since $|m|^\alpha \sim 2^{k\alpha }$ if $m\in \pi _k(\{1,\ldots 2^{k{d}}\})$. Thus

$$\begin{aligned} 2^{\frac{k{d}}{\mathbf {t}(p_1,p_2)}}=\nu ( \mathop {\mathrm {id}}\nolimits ^k) \le c 2^{k\delta }\nu ( \mathop {\mathrm {id}}\nolimits ),\quad k\in {{\mathbb {N}}}. \end{aligned}$$

(3.21)

Hence, letting $k\rightarrow \infty$, we obtain $\delta \ge \frac{{d}}{\mathbf {t}(p_1,p_2)}$.

It remains to exclude the case $\delta = \frac{{d}}{\mathbf {t}(p_1,p_2)}>0$. The operator $\mathop {\mathrm {id}}\nolimits _1$ is nuclear, so there exist $f_i\in (\ell _{q_1}(2^{j(\delta {-\frac{\alpha }{p_1}})}\ell _{p_1}^{2^{j{d}}}(|m|^\alpha )))'$ and $g_i\in \ell _{q_2}(\ell _{p_2}^{2^{j{d}}})$ such that

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _1(\lambda )= \sum _{i=1}^\infty f_i(\lambda )g_i \end{aligned}$$

with

$$\begin{aligned} \sum _{i=1}^\infty \left\| f_i | (\ell _{q_1}(2^{j(\delta {-\frac{\alpha }{p_1}})}\ell _{p_1}^{2^{j{d}}}(|m|^\alpha )))' \right\| \,\left\| g_i|\ell _{q_2}(\ell _{p_2}^{2^{j{d}}}) \right\| <\infty . \end{aligned}$$

We choose $0<\varepsilon <1$ and take $i_o$ such that

$$\begin{aligned} \sum _{i=i_o+1}^\infty \left\| f_i | (\ell _{q_1}(2^{j(\delta {-\frac{\alpha }{p_1}})}\ell _{p_1}^{2^{j{d}}}(|m|^\alpha )))' \right\| \,\left\| g_i|\ell _{q_2}(\ell _{p_2}^{2^{j{d}}}) \right\| <\varepsilon . \end{aligned}$$

Let $X_\varepsilon =\bigcap _{i=1}^{i_o} \ker f_i$ and $\mathop {\mathrm {id}}\nolimits _\varepsilon (\lambda )= \sum _{i=i_o+1}^\infty f_i(\lambda )g_i$. The operator $\mathop {\mathrm {id}}\nolimits _\varepsilon$ is nuclear and $\nu ( \mathop {\mathrm {id}}\nolimits _\varepsilon )<\varepsilon$. Moreover, if $\lambda \in X_\varepsilon$, then $\lambda =\mathop {\mathrm {id}}\nolimits _1(\lambda )=\mathop {\mathrm {id}}\nolimits _\varepsilon (\lambda )$. We consider the subspaces $X_k= \Pi _k(\ell _{p_1}^{2^{k{d}}} )$, $k\in {{\mathbb {N}}}$, cf. (3.20). If k is such that $2^{{d}k}>i_o$, then $\dim \left( X_\varepsilon \cap X_k\right) \ge 2^{{d}k}-i_o$, since $\mathrm {codim}\,X_\varepsilon \le i_o$. Now we can repeat the argument used in the diagram (3.19) for the operator $\mathop {\mathrm {id}}\nolimits _\varepsilon$. More precisely, if $k_\varepsilon = \dim \left( X_\varepsilon \cap X_k\right)$, then we have the following commutative diagram

(3.22)

with $\Pi _{k,\varepsilon }$ and $Q_{k,\varepsilon }$ defined in a similar way as above, i.e., $\Pi _{k,\varepsilon }$ is the restriction of $\Pi _{k}$ to $\ell _{p_1}^{k_\varepsilon }$. Note that $\Pi _{k,\varepsilon }$ is a linear bijection of $\ell _{p_1}^{k_\varepsilon }$ onto $X_\varepsilon \cap X_k$, and $\mathop {\mathrm {id}}\nolimits _1 = \mathop {\mathrm {id}}\nolimits _\varepsilon$ on $X_k\ \cap X_\varepsilon$. Thus

$$\begin{aligned}&{ \nu ( \mathop {\mathrm {id}}\nolimits ^{k_\varepsilon }: \ell _{p_1}^{k_\varepsilon }\rightarrow \ell _{p_2}^{k_\varepsilon } )} \nonumber \\&\quad = \nu ( \Pi _{k,\varepsilon } \circ \mathop {\mathrm {id}}\nolimits _\varepsilon \circ Q_{k,\varepsilon })\nonumber \\&\quad \le \left\| \Pi _{k,\varepsilon }: \ell _{p_1}^{k_\varepsilon }\rightarrow \ell _{q_1} \left( 2^{j(\delta -\frac{\alpha }{p_1})} \ell ^{2^{j{d}}}_{p_1}(|m|^{\alpha })\right) \right\| \nu ( \mathop {\mathrm {id}}\nolimits _\varepsilon ) \left\| Q_{k,\varepsilon }: \ell _{q_2}\left( \ell ^{2^{j{d}}}_{p_2}\right) \rightarrow \ell _{p_2}^{k_\varepsilon }\right\| \nonumber \\&\quad \le c\ 2^{k \delta } \ \nu ( \mathop {\mathrm {id}}\nolimits _\varepsilon ) < c\ 2^{k \delta } \varepsilon . \end{aligned}$$

(3.23)

On the other hand, in view of (3.2),

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^{k_\varepsilon }: \ell _{p_1}^{k_\varepsilon }\rightarrow \ell _{p_2}^{k_\varepsilon } ) = \dim \left( X_k\cap X_\varepsilon \right) ^{\frac{1}{\mathbf {t}(p_1,p_2)}} = k_\varepsilon ^{\frac{1}{\mathbf {t}(p_1,p_2)}} \ge \ \left( 2^{{d}k}-i_o\right) ^{\frac{1}{\mathbf {t}(p_1,p_2)}}. \end{aligned}$$

Together with (3.23) and in view of our assumption $\delta = \frac{{d}}{\mathbf {t}(p_1,p_2)}$ we thus arrive at

$$\begin{aligned} (2^{k{d}}-i_o)^{\frac{1}{\mathbf {t}(p_1,p_2)}}< c'\ \varepsilon \ 2^{k\delta },\quad \text {that is,}\quad (1 -i_o2^{-k {{d}}})^{\frac{1}{\mathbf {t}(p_1,p_2)}}< c'\ \varepsilon ,\quad k\in {{\mathbb {N}}}.\nonumber \\ \end{aligned}$$

(3.24)

Taking $k\rightarrow \infty$ with fixed $\varepsilon$ and $i_o$ we get the contradiction. $\square$

Remark 3.14

We briefly want to discuss the above result and compare it with the compactness criterion as recalled in Proposition 2.11.

In view of the parameters (2.18) we now naturally have to assume the Banach case situation, i.e., $p_i,q_i\ge 1$, $i=1,2$, when studying nuclearity. Moreover, as an easy observation shows, it might well happen that for certain parameter settings the compact embedding $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ can never be nuclear, independent of the target space. This is, for instance, the case when $\frac{1}{p_1}+\frac{\beta }{p_1 {d}}<1$, as then (3.5) for $\beta$ is never satisfied. Moreover, this excludes, in particular, an application of Theorem 3.12 to the situation of Sobolev spaces, $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }^W: W^{k_1}_{p_1}({{\mathbb {R}}}^{{d}},w_{\alpha ,\beta })\hookrightarrow W^{k_2}_{p_2}({{\mathbb {R}}}^{{d}})$, $1< p_i< \infty$, and $k_i\in {{\mathbb {N}}}_{0}$, $i=1,2$, based on (2.12) and Theorem 3.12 with $A=F$. Here we would need $w_{\alpha ,\beta }\in {\mathcal {A}}_{p_1}$ which, by Example 2.2(i), reads as $-{d}<\alpha ,\beta <{d}(p_1-1)$. But, as just observed, this contradicts (3.5) for $\beta$. So it very much depends on the source space, including the weight parameters, whether or not in some compactness case the embedding $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ is even nuclear.

To illustrate the difference between compactness and nuclearity of $\mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }$ in the area of parameters in the usual $(\frac{1}{p},s)$ diagram above, where any space $A^s_{p,q}$ is indicated by its smoothness and integrability (neglecting the fine index q), we have chosen the situation when

$$\begin{aligned} \frac{\beta }{{d}p_1}>1>\frac{\alpha }{{d}p_1} >1-\frac{1}{p_1}\ge 0. \end{aligned}$$

In the sense of Remark 2.13 we can immediately conclude the nuclearity result for embeddings of spaces with admissible weights.

Corollary 3.15

Let $\beta \ge 0$, $w^\beta (x)=\langle x\rangle ^\beta$. Assume that $1\le p_1< \infty$, $1\le p_2\le \infty$ ($p_2<\infty$ in the F-case), and $1\le q_i\le \infty$, $s_i\in {\mathbb {R}}$, $i=1,2$. Then the embedding $\ \mathop {\mathrm {id}}\nolimits ^\beta : A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w^\beta )\hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear if, and only if,

$$\begin{aligned} \frac{\beta }{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)} \qquad \text {and}\qquad \delta > \frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

(3.25)

In view of (2.20) we observe the phenomenon again that the nuclearity characterisation is distinct from the compactness one by replacing $p^*$ by $\mathbf {t}(p_1,p_2)$ only. In particular, when $\mathbf {t}(p_1,p_2)=p^*$, that is, when $p_1=1$ and $p_2=\infty$ (recall that we always assume $p_1<\infty$), thus $A=B$, then nuclearity and compactness conditions coincide. In that case $\mathbf {t}(p_1,p_2)=p^*=\infty$ and Theorem 3.12 together with Proposition 2.11 imply the following result.

Corollary 3.16

Let $\alpha >-{d}$, $\beta >-{d}$, $w_{\alpha ,\beta }$ be given by (2.4). Assume that $1\le q_i\le \infty$, $s_i\in {\mathbb {R}}$, $i=1,2$. The following conditions are equivalent

(i):

the operator $\ \mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }: B_{1,q_1}^{s_1}({{\mathbb {R}}}^{{d}},w_{\alpha ,\beta })\hookrightarrow B_{\infty ,q_2}^{s_2}({{\mathbb {R}}}^{{d}})$ is nuclear,

(ii):

the operator $\ \mathop {\mathrm {id}}\nolimits _{\alpha ,\beta }: B_{1,q_1}^{s_1}({{\mathbb {R}}}^{{d}},w_{\alpha ,\beta })\hookrightarrow B_{\infty ,q_2}^{s_2}({{\mathbb {R}}}^{{d}})$ is compact,

(iii):

$\beta >0$ and $\delta > \max (0,\alpha )$.

We can also extend Proposition 3.6 to limiting cases $p_1$, $p_2$, $q_1$, $q_2$ equal to 1 or $\infty$. The generalisation follows easily from Theorem 3.12 for domains with the extension property, in particular for bounded Lipschitz domains. The sufficiency part has already been obtained in [5, Thm. 4.2], we may now complete the argument for the necessity part and thus partly extend [5, Cor. 4.6], i.e., when $\alpha _1=\alpha _2=0$ in the notation used in [5].

Corollary 3.17

Let $\Omega \subset {{\mathbb {R}}}^{{d}}$ be a bounded Lipschitz domain, $s_i\in {\mathbb {R}}$, $1\le p_i,q_i\le \infty$ ($p_i<\infty$ in the F-case) . Then

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _\Omega : A^{s_1}_{p_1,q_1}(\Omega ) \rightarrow A^{s_2}_{p_2,q_2}(\Omega ) \quad \text {is nuclear if, and only if,}\quad \delta > \frac{{d}}{\mathbf {t}(p_1,p_2)}.\nonumber \\ \end{aligned}$$

(3.26)

Proof

Since the q-parameters play no role it is sufficient to prove the corollary for Besov spaces. The corresponding statement for the F-spaces follows then by elementary embeddings.

For the sufficiency part we benefit from the result [5, Thm. 4.2] (with $\alpha _1=\alpha _2=0$ in their notation). The necessity can be proved in a way similar to the local part in the Step 2 of the proof of Theorem 3.12. Using the standard wavelet basis argument with Daubechies wavelets we can factorise the embedding $\ell _{q_1}(2^{j\delta } \ell ^{2^{j{d}}}_{p_1}) \hookrightarrow \ell _{q_2}( \ell ^{2^{j{d}}}_{p_2})$ through the embedding $\mathop {\mathrm {id}}\nolimits _\Omega : B^{s_1}_{p_1,q_1} (\Omega ) \hookrightarrow B^{s_2}_{p_2,q_2}(\Omega )$. Then we can argue in the same way as in Step 2, (3.19)-(3.24) of the proof of the last theorem. $\square$

Remark 3.18

Parallel to Corollary 3.16 we can thus state that for arbitrary $q_1,q_2\in [1,\infty ]$,

$$\begin{aligned} B^{s_1}_{1,q_1}(\Omega ) \hookrightarrow B^{s_2}_{\infty ,q_2}(\Omega )\quad \text{ compact } \iff \quad&B^{s_1}_{1,q_1}(\Omega ) \hookrightarrow B^{s_2}_{\infty ,q_2}(\Omega ) \quad \text{ nuclear }\\ \iff \quad&s_1-s_2>d, \end{aligned}$$

and

$$\begin{aligned} B^{s_1}_{\infty ,q_1}(\Omega ) \hookrightarrow B^{s_2}_{1,q_2}(\Omega )\quad \text{ compact } \iff \quad&B^{s_1}_{\infty ,q_1}(\Omega ) \hookrightarrow B^{s_2}_{1,q_2}(\Omega )\quad \text{ nuclear }\\ \iff \quad&s_1>s_2, \end{aligned}$$

recall Remark 2.16. Hence in the extremal cases $\{p_1,p_2\}=\{1,\infty \}$ compactness and nuclearity coincide. In the usual $(\frac{1}{p},s)$-diagram below, where any space $A^s_{p,q}(\Omega )$ is characterised by its parameters s and p (neglecting q), we indicated the parameter areas for $(\frac{1}{p_2}, s_2)$ (in dependence on a given original space $A^{s_1}_{p_1,q_1}(\Omega )$ with $(\frac{1}{p_1},s_1)$) such that the corresponding embedding $\mathop {\mathrm {id}}\nolimits _\Omega :A^{s_1}_{p_1,q_1}(\Omega )\rightarrow A^{s_2}_{p_2,q_2}(\Omega )$ is compact or even nuclear.

Corollary 3.17 leads immediately to an extended version of Corollary 3.10.

Corollary 3.19

Let $1\le p_1<\infty$, $1\le p_2,q_i\le \infty$ ($p_i<\infty$ in the F-case), $s_i\in {\mathbb {R}}$, $i=1,2$, $w\in {\mathcal {A}}_\infty$. If the embedding

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _w: A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w) \rightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

is nuclear, then

$$\begin{aligned} s_1-s_2>{d}-{d}\left( \frac{1}{p_2}-\frac{1}{p_1}\right) _+,\qquad \text {i.e.,}\quad \delta > \frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

Proof

One can copy the proof of Corollary 3.10 and benefit from the extension of Proposition 3.6 (used there) to the above Corollary 3.17. $\square$

Remark 3.20

In the sense of Remark 3.11 we can add a further simple argument now, showing that the above criterion is a necessary one for nuclearity only: when $p_1=\infty$ and $w\in {\mathcal {A}}_\infty$ (arbitrary), then in view of (2.9) the above embedding $\mathop {\mathrm {id}}\nolimits _w$ is an unweighted one which is never compact (let alone nuclear).

Now we study the counterpart of Theorem 3.12 for the weight function $w_{({\varvec{\alpha }},{\varvec{\beta }})}$ in Example 2.2(ii). For convenience we recall the following well-known fact, which can also be found in [19, Lemma 3.8].

Lemma 3.21

Let $\gamma \in {\mathbb {R}}$, $\varkappa \in {\mathbb {R}}$, $j\in {{\mathbb {N}}}$. Then

$$\begin{aligned} \sum _{k=1}^j 2^{k\gamma } k^\varkappa \ \sim \ {\left\{ \begin{array}{ll} 2^{j\gamma } j^\varkappa , &{} \text {if}\quad \gamma >0, \\ 1, &{} \text {if}\quad \gamma <0,\end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \sum _{k=1}^j k^\varkappa \ \sim \ {\left\{ \begin{array}{ll} 1,&{} \text {if}\quad \varkappa <-1,\\ j^{1+\varkappa },&{} \text {if}\quad \varkappa >-1,\\ \log (1+j),&{} \text {if}\quad \varkappa =-1,\end{array}\right. } \end{aligned}$$

always with equivalence constants independent of j.

Now we can give the counterpart of the compactness result Proposition 2.14.

Theorem 3.22

Let $w_{({\varvec{\alpha }},{\varvec{\beta }})}$ be given by (2.5) with $\alpha _1>-{d}$, $\alpha _2\in {\mathbb {R}}$, $\beta _1>-{d}$, $\beta _2\in {\mathbb {R}}$. Assume that $1\le p_1,q_1<\infty$, $1\le p_2,q_2\le \infty$, $s_i\in {\mathbb {R}}$, $i=1,2$. Then the embedding $\mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}: B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{({\varvec{\alpha }},{\varvec{\beta }})})\hookrightarrow B^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear if, and only if,

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {either}&{} \frac{\beta _1}{p_1} \> \ \frac{{d}}{\mathbf {t}(p_1,p_2)},\quad \beta _2\in {\mathbb {R}}, \\ \text {or} &{} \frac{\beta _1}{p_1} \ = \ \frac{{d}}{\mathbf {t}(p_1,p_2)}, \quad \frac{\beta _2}{p_1} > \frac{1}{\mathbf {t}(p_1,p_2)},\end{array}\right. } \end{aligned}$$

(3.27)

and

$$\begin{aligned}&{\left\{ \begin{array}{ll} \text {either}&{} \delta>\max \left( \frac{\alpha _1}{p_1}, \frac{{d}}{\mathbf {t}(p_1,p_2)}\right) ,\quad \alpha _2\in {\mathbb {R}}, \\ \text {or} &{} \delta =\frac{\alpha _1}{p_1}> \frac{{d}}{\mathbf {t}(p_1,p_2)}, \quad \frac{\alpha _2}{p_1}> \frac{1}{\mathbf {t}(q_1,q_2)}. \end{array}\right. }\qquad \end{aligned}$$

(3.28)

Proof

Step 1.    We proceed essentially parallel to the arguments presented in the proof of Theorem 3.12. So again we may restrict ourselves to the study of the corresponding sequence spaces where the counterparts of (3.6) and (3.7) now read as

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits : b^\delta _{p_1,q_1} (w_{({\varvec{\alpha }},{\varvec{\beta }})}) \hookrightarrow \ell _{q_2}(\ell _{p_2}) \end{aligned}$$

(3.29)

and

$$\begin{aligned} w_{({\varvec{\alpha }},{\varvec{\beta }})}(Q_{j, m}) {\sim } \ 2^{-j {d}} \left\{ \begin{array}{llr} 2^{-j\alpha _1} (1+j)^{\alpha _2} &{}\text {if} &{} m=0, \\ \left| 2^{-j} m\right| ^{\alpha _1} \left( 1 - \log \left| 2^{-j} m\right| \right) ^{\alpha _2} &{}\text {if} &{} 1\le |m| < 2^j, \\ \left| 2^{-j} m\right| ^{\beta _1} \left( 1 + \log \left| 2^{-j} m\right| \right) ^{\beta _2} &{}\text {if} &{} |m| \ge 2^j. \end{array}\right. \qquad \end{aligned}$$

(3.30)

We split $\mathop {\mathrm {id}}\nolimits =\mathop {\mathrm {id}}\nolimits _1+\mathop {\mathrm {id}}\nolimits _2$ as above, where only the weight $w_{\alpha ,\beta }$ has to be replaced by $w_{({\varvec{\alpha }},{\varvec{\beta }})}$. First we consider the non-limiting case $\delta >\max (\frac{\alpha _1}{p_1}, \frac{{d}}{\mathbf {t}(p_1,p_2)})$. By the same arguments as in the proof of Theorem 3.12 we arrive at the following counterpart of (3.10),

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1) \le \sum _{j=0}^\infty 2^{-j(\delta -\frac{\alpha _1}{p_1})} \nu ( \mathop {\mathrm {id}}\nolimits ^j). \end{aligned}$$

(3.31)

The counterpart of (3.11) is

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^j) \le \left\| \left\{ |m|^{-\frac{\alpha _1}{p_1}}(1- \log \left| 2^{-j} m\right| )^{-\frac{\alpha _2}{p_1}}\right\} _{|m|<2^j} | {\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| . \end{aligned}$$

(3.32)

We calculate the norm. First we assume that $\mathbf {t}(p_1,p_2)<\infty$. Thus

$$\begin{aligned}&{ \left\| \left\{ |m|^{-\frac{\alpha _1}{p_1}} (1- \log \left| 2^{-j} m\right| )^{-\frac{\alpha _2}{p_1}}\right\} _{|m|<2^j} | {\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| ^{\mathbf {t}(p_1,p_2)}}\nonumber \\&\quad = \sum _{|m|<2^j} |m|^{-\frac{\alpha _1}{p_1} \mathbf {t}(p_1,p_2)} (1- \log \left| 2^{-j} m\right| )^{-\frac{\alpha _2}{p_1} \mathbf {t}(p_1,p_2)} \nonumber \\&\quad = \ \sum _{k=0}^j \sum _{|m|\sim 2^k} |m|^{-\frac{\alpha _1}{p_1} \mathbf {t}(p_1,p_2)}(1- \log \left| 2^{-j} m\right| )^{-\frac{\alpha _2}{p_1} \mathbf {t}(p_1,p_2)} \nonumber \\&\quad \sim \sum _{k=0}^j \ 2^{k{d}} 2^{-k\frac{\alpha _1}{p_1}\mathbf {t}(p_1,p_2)} \left( 1 + j-k\right) ^{-\frac{\alpha _2}{p_1} \mathbf {t}(p_1,p_2)} \nonumber \\&\quad \sim \ 2^{j({d}-\frac{\alpha _1}{p_1}\mathbf {t}(p_1,p_2))} \ \sum _{k=1}^{j+1} \ 2^{k(\frac{\alpha _1}{p_1}-\frac{{d}}{\mathbf {t}(p_1,p_2)})\mathbf {t}(p_1,p_2)} k^{-\frac{\alpha _2}{p_1} \mathbf {t}(p_1,p_2)}, \end{aligned}$$

(3.33)

such that (3.32) and Lemma 3.21 imply

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^j)\le & {} (1+j)^{-\frac{\alpha _2}{p_1}} \qquad \text {if}\quad \displaystyle \frac{\alpha _1}{p_1} > \frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \alpha _2\in {\mathbb {R}}, \end{aligned}$$

(3.34)

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^j)&\le \&2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)}-\frac{\alpha _1}{p_1})} \qquad \begin{array}[t]{l}\displaystyle \text {if}\quad \frac{\alpha _1}{p_1} < \frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \alpha _2\in {\mathbb {R}}, \\ \text {or}\quad \displaystyle \frac{\alpha _1}{p_1} = \frac{{d}}{\mathbf {t}(p_1,p_2)},\ \frac{\alpha _2}{p_1}>\frac{1}{\mathbf {t}(p_1,p_2)},\end{array}\end{aligned}$$

(3.35)

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^j)&\le \&(1+j)^{\frac{1}{\mathbf {t}(p_1,p_2)}-\frac{\alpha _2}{p_1}} \qquad \text {if}\quad \frac{\alpha _1}{p_1} = \frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \frac{\alpha _2}{p_1}<\frac{1}{\mathbf {t}(p_1,p_2)}, \end{aligned}$$

(3.36)

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits ^j)&\le \&\log ^{\frac{1}{\mathbf {t}(p_1,p_2)}}(1+j) \qquad \text {if}\quad \frac{\alpha _1}{p_1} = \frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \frac{\alpha _2}{p_1}=\frac{1}{\mathbf {t}(p_1,p_2)}. \qquad \quad \end{aligned}$$

(3.37)

We study the different cases to estimate $\nu ( \mathop {\mathrm {id}}\nolimits _1)$ by (3.31). In case of (3.34) we obtain that

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1) \le \sum _{j=0}^\infty 2^{-j (\delta -\frac{\alpha _1}{p_1})} (1+j)^{-\frac{\alpha _2}{p_1}} \le c<\infty \end{aligned}$$

if   

$$\begin{aligned} \frac{\alpha _1}{p_1}> \frac{{d}}{\mathbf {t}(p_1,p_2)}, \quad {\delta >\frac{\alpha _1}{p_1}\quad \text {and}\quad \alpha _2\in {\mathbb {R}}.} \end{aligned}$$

In all other cases (3.35)–(3.37), we obtain that

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1) \le c<\infty \qquad \text {if}\quad \delta >\frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

Hence our assumption (3.28) ensures the nuclearity of $\mathop {\mathrm {id}}\nolimits _1$.

Now let $\mathbf {t}(p_1,p_2)=\infty$, i.e., $p_1=1$ and $p_2=\infty$. Thus in a parallel way as above,

$$\begin{aligned}&{\left\| \left\{ |m|^{-{{\alpha _1}}}(1- \log \left| 2^{-j} m\right| )^{-{{\alpha _2}}} \right\} _{|m|<2^j}| {\ell ^{2^{j{d}}}_{{\infty }}}\right\| }\\&\quad \le \ C \ {\left\{ \begin{array}{ll} 2^{-j\alpha _1} &{} \text {if}\quad \alpha _1<0,\\ (1+j)^{-\alpha _2} &{} \text {if}\quad \alpha _1=0\quad \text {and}\quad \alpha _2<0,\\ 1 &{} \text {if}\quad \alpha _1>0\quad \text {or}\quad \alpha _1=0\quad \text {and} \quad {\alpha _2 \ge 0}. \end{array}\right. } \end{aligned}$$

So

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1) \le \sum _{j=0}^\infty 2^{-j(\delta -\alpha _1)} \nu ( \mathop {\mathrm {id}}\nolimits ^j)< \infty \qquad \text {if}\quad \delta > {\max (\alpha _1,0)}. \end{aligned}$$

We deal with $\mathop {\mathrm {id}}\nolimits _2$ and again follow and adapt the arguments in the proof of Theorem 3.12. The counterparts of (3.14) and (3.15) lead to

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _2)\le & {} \sum _{j=0}^\infty 2^{-j(\delta -\frac{\beta _1}{p_1})} \nu ( {\widetilde{\mathop {\mathrm {id}}\nolimits }}^j)\nonumber \\\le & {} \sum _{j=0}^\infty 2^{-j(\delta -\frac{\beta _1}{p_1})} \left\| \left\{ |m|^{-\frac{\beta _1}{p_1}}\left( 1 + \log \left| 2^{-j} m\right| \right) ^{-\frac{\beta _2}{p_1}}\right\} _{|m|\ge 2^j}| {\ell _{\mathbf {t}(p_1,p_2)}}\right\| . \nonumber \\ \end{aligned}$$

(3.38)

Now, if $\mathbf {t}(p_1,p_2)<\infty$, then

$$\begin{aligned}&{\left\| \left\{ |m|^{-\frac{\beta _1}{p_1}}\left( 1 + \log \left| 2^{-j} m\right| \right) ^{-\frac{\beta _2}{p_1}}\right\} _{|m|\ge 2^j}| {\ell _{\mathbf {t}(p_1,p_2)}}\right\| ^{\mathbf {t}(p_1,p_2)}}\\&\quad \sim \sum _{|m|\ge 2^j} \left| m\right| ^{-\frac{\beta _1}{p_1}\mathbf {t}(p_1,p_2)} \left( 1 + \log \left| 2^{-j} m\right| \right) ^{-\frac{\beta _2}{p_1} \mathbf {t}(p_1,p_2)} \\&\quad \sim \sum _{l=j}^\infty \ \sum _{|m|\sim 2^l} \left| m\right| ^{-\frac{\beta _1}{p_1}\mathbf {t}(p_1,p_2)} \left( 1 + \log \left| 2^{-j} m\right| \right) ^{-\frac{\beta _2}{p_1}\mathbf {t}(p_1,p_2)} \\&\quad \sim \sum _{l=j}^\infty \ 2^{l({d}-\frac{\beta _1}{p_1}\mathbf {t}(p_1,p_2))} \left( 1 + l-j\right) ^{-\frac{\beta _2}{p_1}\mathbf {t}(p_1,p_2)} \end{aligned}$$

which by Lemma 3.21 is finite if, and only if,

$$\begin{aligned} \text {either}\quad \frac{\beta _1}{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \beta _2\in {\mathbb {R}}, \quad \text {or}\quad \frac{\beta _1}{p_1}=\frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \frac{\beta _2}{p_1} > \frac{1}{\mathbf {t}(p_1,p_2)},\nonumber \\ \end{aligned}$$

(3.39)

assumed by (3.27). If $\mathbf {t}(p_1,p_2)=\infty$, that is, $p_1=1$ and $p_2=\infty$, then for the nuclearity we first have to ensure that $\{|m|^{-\beta _1} (1+ \log \left| 2^{-j} m\right| )^{-{\beta _2}}\}_{|m|\ge 2^j} \in c_0\subset \ell _\infty$, recall Proposition 3.3(i). So we benefit from our assumption (3.27) which reads in this case as $\beta _1>0$ or $\beta _1=0$ and $\beta _2>0$. Furthermore, we conclude that

$$\begin{aligned} \left\| \left\{ |m|^{-{\beta _1}}(1+ \log \left| 2^{-j} m\right| )^{-{\beta _2}}\right\} _{|m|\ge 2^j}| {\ell _{{\infty }}}\right\| \le C {\left\{ \begin{array}{ll} 2^{-j\beta _1} &{} \text {if}\; \beta _1>0,\\ 1&{} \text {if}\; \beta _1=0\; \text {and}\; \beta _2>0. \end{array}\right. } \end{aligned}$$

In other words, in both cases we arrive at

$$\begin{aligned}&\left\| \left\{ |m|^{-\frac{\beta _1}{p_1}}\left( 1 + \log \left| 2^{-j} m \right| \right) ^{-\frac{\beta _2}{p_1}}\right\} _{|m|\ge 2^j}| {\ell _{\mathbf {t}(p_1,p_2)}} \right\| \\&\sim { {\left\{ \begin{array}{ll}\displaystyle 2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)}-\frac{\beta _1}{p_1})} , &{}\text {if}\ \frac{\beta _1}{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \beta _2\in {\mathbb {R}}, \\ \displaystyle 1, &{} \text {if}\ \frac{\beta _1}{p_1}=\frac{{d}}{\mathbf {t}(p_1,p_2)}, \ \frac{\beta _2}{p_1} > \frac{1}{\mathbf {t}(p_1,p_2)}, \end{array}\right. }} \end{aligned}$$

and (3.38) results in $\nu ( \mathop {\mathrm {id}}\nolimits _2)\le c<\infty$ since $\delta >\frac{{d}}{\mathbf {t}(p_1,p_2)}$ by (3.28). This completes the proof of the sufficiency in the non-limiting case.

Step 2. Next we consider the limiting situation $\delta =\frac{\alpha _1}{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)}$ and $\frac{\alpha _2}{p_1}>\frac{1}{\mathbf {t}(q_1,q_2)}$. We deal with the case $\max \{\mathbf {t}(p_1,p_2), \mathbf {t}(q_1,q_2)\}<\infty$ and the case $\max \{\mathbf {t}(p_1,p_2),\mathbf {t}(q_1,q_2)\}=\infty$ simultaneously. Now

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _1 : \ell _{q_1}\left( \ell _{p_1}^{2^{j {d}}}\big (|m|^{\alpha _1} (1-\log |2^{-j}m|)^{\alpha _2}\big )\right) \hookrightarrow \ell _{q_2}(\ell _{p_2}), \end{aligned}$$

with

$$\begin{aligned}&{\left\| \lambda | \ell _{q_1}\left( \ell _{p_1}^{2^{j {d}}}\big (|m|^{\alpha _1} (1-\log |2^{-j}m|)^{\alpha _2}\big )\right) \right\| }\\&\quad = \Big \Vert \Big \{ \Big (\sum _{|m|<2^j} |\lambda _{j,m}|^{p_1}\ |m|^{\alpha _1} (1-\log |2^{-j}m|)^{\alpha _2}\Big )^{\frac{1}{p_1}} \Big \}_{j\in {{\mathbb {N}}}_{0}} | \ell _{q_1}\Big \Vert . \end{aligned}$$

Let $I_j=\{m\in {\mathbb {Z}}^{{d}}:\; 2^{j-1}\le |m|< 2^j\}$ if $j\in {{\mathbb {N}}}$ and $I_0=\{0\}$. We decompose $\mathop {\mathrm {id}}\nolimits _1$ in the following way,

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _1 = \sum _{j=0}^\infty {\widetilde{\mathop {\mathrm {id}}\nolimits }}_{1,j} \end{aligned}$$

where

$$\begin{aligned} \left\{ {\widetilde{\mathop {\mathrm {id}}\nolimits }}_{1,j} \lambda \right\} _{k,m} = {\left\{ \begin{array}{ll} \lambda _{k,m} &{} \text {if} \; k\ge j \;\text {and}\;m\in I_j,\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

First we show that the operators ${\widetilde{\mathop {\mathrm {id}}\nolimits }}_{1,j}$ are nuclear and that

$$\begin{aligned} \nu ({\widetilde{\mathop {\mathrm {id}}\nolimits }}_{1,j})\le c 2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)}- \frac{\alpha _1}{p_1})} \left\| \left\{ k^{-\frac{\alpha _2}{p_1}}\right\} _{k\ge j}|\ell _{\mathbf {t}(q_1,q_2)}\right\| . \end{aligned}$$

In a similar way as above we factorise the operator ${\widetilde{\mathop {\mathrm {id}}\nolimits }}_{1,j}$ through the diagonal operator. Now j is fixed and $m\in I_j$, i.e., $|m|\sim 2^{j}$. So we can take the operator $D_{j}:\widetilde{\ell _{q_1}(\ell _{p_1}^{2^{j{d}}})}\rightarrow \widetilde{\ell _{q_2}(\ell _{p_1}^{2^{j{d}}})}$ defined on the mixed norm space

$$\begin{aligned} \widetilde{\ell _{q_1}(\ell _{p_1}^{2^{j{d}}})} =\Big \{\lambda =\{\lambda _{\ell ,m}\}_{\ell \in {{\mathbb {N}}}_0, \ m\in I_j} \&:\\ \quad \Vert \lambda |\widetilde{\ell _{q_1}(\ell _{p_1}^{2^{j{d}}})}\Vert =&\Big (\sum _{\ell =0}^\infty \Big (\sum _{m\in I_j} |\lambda _{\ell ,m}|^{p_1}\Big )^{\frac{q_1}{p_1}}\Big )^{\frac{1}{q_1}}<\infty \Big \} \end{aligned}$$

by

$$\begin{aligned} D_{j}: \{\lambda _{\ell ,m}\} \mapsto \{ \lambda _{\ell ,m} |m|^{-\frac{\alpha _1}{p_1}} (\ell +1)^{-\frac{\alpha _2}{p_1}}\}, \qquad \ell \in {{\mathbb {N}}}_0,\quad m\in I_j. \end{aligned}$$

Similarly we define the target space $\widetilde{\ell _{q_2}(\ell _{p_2}^{2^{j{d}}})}$. Then

where

$$\begin{aligned} T_j:&\{\lambda _{k,m}\} \mapsto \{ \lambda _{\ell ,m} = \lambda _{k,m} |m|^{\frac{\alpha _1}{p_1}} (\ell +1)^{\frac{\alpha _2}{p_1}}\}_{\ell ,m} \quad \text {if}\ \ell =k-j\in {{\mathbb {N}}}_0 \ \text {and}\ m\in I_j, \end{aligned}$$

and

$$\begin{aligned} P_j:&\{\lambda _{\ell ,m}\} \mapsto \{ \lambda _{j+\ell ,m}\}, \qquad \ell \in {{\mathbb {N}}}_0 \quad \text {and}\quad m\in I_j. \end{aligned}$$

Moreover $\Vert P_j\Vert =1$ and the norm $\Vert T_j\Vert$ is uniformly bounded in $j\in {{\mathbb {N}}}_{0}$.

The operators

$$\begin{aligned} D_{1}:\ell _{q_1}\rightarrow \ell _{q_2}, \qquad D_1: \{\gamma _{\ell }\}_{\ell \in {{\mathbb {N}}}_{0}} \mapsto \{ (\ell +1)^{-\frac{\alpha _2}{p_1}}\gamma _{\ell } \}_{\ell \in {{\mathbb {N}}}_{0}} \end{aligned}$$

and

$$\begin{aligned} D_{2}:\ell _{p_1}^{2^{j{d}}}\rightarrow \ell _{p_2}^{2^{j{d}}}, \qquad D_{2}: \{\mu _{m}\}_{m\in I_j} \mapsto \{ |m|^{-\frac{\alpha _1}{p_1} }\mu _{m} \}_{m\in I_j} \end{aligned}$$

are nuclear and

$$\begin{aligned} \nu (D_1) = \left\| \left\{ (\ell +1)^{-\frac{\alpha _2}{p_1}}\right\} _{\ell \in {{\mathbb {N}}}_{0}} |\ell _{\mathbf {t}(q_1,q_2)}\right\| , \quad \nu (D_2) = \left\| \left\{ |m|^{-\frac{\alpha _1}{p_1}}\right\} _{m\in I_j} |\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}\right\| .\nonumber \\ \end{aligned}$$

(3.40)

Let

$$\begin{aligned} D_1(\gamma )=\sum _{k=0}^\infty a_k(\gamma ) y_k,\qquad a_k\in (\ell _{q_1})'= \ell _{q'_1} \quad \text {and}\quad y_k\in \ell _{q_2} \end{aligned}$$

and

$$\begin{aligned} D_2(\mu )=\sum _{\ell =0}^\infty b_\ell (\mu ) x_\ell ,\qquad b_\ell \in (\ell ^{2^{j{d}}}_{p_1})'= \ell ^{2^{j{d}}}_{p'_1} \quad \text {and}\quad x_\ell \in \ell ^{2^{j{d}}}_{p_2} \end{aligned}$$

be the corresponding nuclear decompositions. We define the following (double) sequences,

$$\begin{aligned} c_{k,\ell }=\{a_{k,i}b_{\ell , n}\}_{i\in {{\mathbb {N}}}, n\in I_j},\qquad k,\ell \in {{\mathbb {N}}}_{0}, \end{aligned}$$

and

$$\begin{aligned} z_{k,\ell }= \{y_{k,i}z_{\ell , n}\}_{i\in {{\mathbb {N}}}, n\in I_j},\qquad k,\ell \in {{\mathbb {N}}}_{0}. \end{aligned}$$

One can easily check that, for each $k,\ell \in {{\mathbb {N}}}_{0}$,

$$\begin{aligned} c_{k,\ell } \in \ell _{q'_1}\left( \ell _{p'_1}^{2^{{d}j}}\right) = \Big ( \ell _{q_1}(\ell _{p_1}^{2^{j{d}}})\Big )', \quad \left\| c_{k,\ell } |\ell _{q'_1}(\ell _{p'_1}^{2^{j{d}}}) \right\| = \left\| a_{k} |\ell _{q'_1}\right\| \left\| b_{\ell } |\ell _{p'_1}^{2^{j{d}}} \right\| , \end{aligned}$$

and

$$\begin{aligned} z_{k,\ell } \in \ell _{q_2}\left( \ell _{p_2}^{2^{j{d}}}\right) , \quad \left\| z_{k,\ell } |\ell _{q_2}(\ell _{p_2}^{2^{j{d}}}) \right\| = \left\| y_{k} |\ell _{q_2} \right\| \left\| x_{\ell } |\ell _{p_2}^{2^{j{d}}} \right\| . \end{aligned}$$

Moreover,

$$\begin{aligned}&{\sum _{k,\ell } \left\| c_{k,\ell } |\ell _{q'_1}(\ell _{p'_1}^{2^{j{d}}}) \right\| \left\| z_{k,\ell } |\ell _{q_2}(\ell _{p_2}^{2^{j{d}}}) \right\| }\nonumber \\&\quad = \sum _k \left\| a_{k} |\ell _{q'_1} \right\| \left\| y_{k} |\ell _{q_2} \right\| \sum _\ell \left\| x_{\ell } |\ell _{p_2}^{2^{j{d}}} \right\| \left\| b_{\ell } |\ell _{p'_1}^{2^{j{d}}} \right\| <\infty . \end{aligned}$$

(3.41)

Direct calculations show that (appropriately interpreted)

$$\begin{aligned} D_j(\lambda ) = D_1\left( \left\{ D_2\left( \left\{ \lambda _{\ell ,m}\right\} _{m\in I_j}\right) \right\} _{\ell \in {{\mathbb {N}}}_{0}}\right) = \sum _{k,\ell } c_{k,\ell }(\lambda ) z_{k,\ell } . \end{aligned}$$

So $D_j$ is a nuclear operator. Taking the infimum over all possible nuclear representations of $D_1$ and $D_2$ we get

$$\begin{aligned} \nu (D_j)\le&\ \nu (D_1)\nu (D_2) \\ \le&\left\| \left\{ (\ell +1)^{-\frac{\alpha _2}{p_1}}\right\} _{\ell \in {{\mathbb {N}}}_{0}} |\ell _{\mathbf {t}(q_1,q_2)}\right\| \ \left\| \left\{ |m|^{-\frac{\alpha _1}{p_1}}\right\} _{m\in I_j} |\ell ^{2^{j{d}}}_{\mathbf {t}(p_1,p_2)}\right\| \\ \le&\ 2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)}-\frac{\alpha _1}{p_1})}\left\| \left\{ (\ell +1)^{-\frac{\alpha _2}{p_1}}\right\} _{\ell \in {{\mathbb {N}}}_{0}} |\ell _{\mathbf {t}(q_1,q_2)}\right\| , \end{aligned}$$

cf. (3.40) and (3.41). In consequence,

$$\begin{aligned} \nu (\mathop {\mathrm {id}}\nolimits _1)\le \sum _{j=0}^\infty \nu ({\widetilde{\mathop {\mathrm {id}}\nolimits }}_{1,j}) \le \sum _{j=0}^\infty 2^{j(\frac{{d}}{\mathbf {t}(p_1,p_2)}-\frac{\alpha _1}{p_1})}\left\| \left\{ k^{-\frac{\alpha _2}{p_1}}\right\} _{k\ge j} | {\ell _{\mathbf {t}(q_1,q_2)}} \right\| <\infty \end{aligned}$$

since $\frac{{d}}{\mathbf {t}(p_1,p_2)}<\frac{\alpha _1}{p_1}$ and $\frac{\alpha _2}{p_1}>\frac{1}{\mathbf {t}(q_1,q_2)}$. This completes the proof of the sufficiency.

Step 3.   It remains to show the necessity of (3.27), (3.28) when $\mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}: B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{({\varvec{\alpha }},{\varvec{\beta }})})\hookrightarrow B^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear. First we collect what is immediately clear by Corollary 3.10 and Proposition 2.14, in the same spirit as in the beginning of Step 2 of the proof of Theorem 3.12. Thus the nuclearity of $\mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}$ implies

$$\begin{aligned} \delta>\frac{{d}}{\mathbf {t}(p_1,p_2)}, \quad \text {and}\quad \delta>\frac{\alpha _1}{p_1}\quad \text {or}\quad \delta =\frac{\alpha _1}{p_1}\quad \text {and}\ \frac{\alpha _2}{p_1} > \frac{1}{q^*}. \end{aligned}$$

Moreover, in the limiting cases $\mathbf {t}(p_1,p_2)=\infty$ or $\mathbf {t}(q_1,q_2)=\infty$ the sufficient conditions coincide with the conditions for compactness, therefore they are necessary.

Let $\mathbf {t}(p_1,p_2)<\infty$ and $\mathbf {t}(q_1,q_2)<\infty$. Using [19, Cor. 3.11] we get $B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w_{{\tilde{\alpha }},{\tilde{\beta }}}) \hookrightarrow B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{({\varvec{\alpha }},{\varvec{\beta }})})$ where ${\tilde{\alpha }}<\alpha _1$ or ${\tilde{\alpha }}=\alpha _1$ and $\alpha _2\le 0$, and ${\tilde{\beta }}>\beta _1$, or ${\tilde{\beta }}=\beta _1$ and $\beta _2\le 0$. Thus the nuclearity of $\mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}$ implies the nuclearity of $\mathop {\mathrm {id}}\nolimits _{{\tilde{\alpha }},{\tilde{\beta }}}$ which by Theorem 3.12 leads, in particular, to

$$\begin{aligned} \frac{{\tilde{\beta }}}{p_1}> \frac{{d}}{\mathbf {t}(p_1,p_2)}, \end{aligned}$$

hence $\frac{\beta _1}{p_1}\ge \frac{{d}}{\mathbf {t}(p_1,p_2)}$, $\beta _2\in {\mathbb {R}}$, or $\frac{\beta _1}{p_1}> \frac{{d}}{\mathbf {t}(p_1,p_2)}$ and $\beta _2\le 0$. So we are left to deal with the limiting cases in (3.27), (3.28), that is, when

$$\begin{aligned} \frac{\beta _1}{p_1} = \frac{{d}}{\mathbf {t}(p_1,p_2)}\qquad \text {and}\qquad \delta =\frac{\alpha _1}{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)}. \end{aligned}$$

We prove it by contradiction and assume first $\frac{\beta _1}{p_1} = \frac{{d}}{\mathbf {t}(p_1,p_2)}$, but $\frac{\beta _2}{p_1}\le \frac{1}{\mathbf {t}(p_1,p_2)}$. We follow essentially the same argument as in Step 2 of the proof of Theorem 3.12. The counterpart of (3.17) reads now as

$$\begin{aligned} \left\| \left\{ |m|^{-\frac{\beta _1}{p_1}}(1- \log \left| 2^{-k} m\right| )^{-\frac{\beta _2}{p_1}}\right\} _{|m|\le 2^k} | {\ell ^{2^{k{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| \le \nu ( \mathop {\mathrm {id}}\nolimits _2), \quad k\in {{\mathbb {N}}}.\nonumber \\ \end{aligned}$$

(3.42)

On the other hand, similar to (3.33),

$$\begin{aligned}&{ \left\| \left\{ |m|^{-\frac{\beta _1}{p_1}}(1- \log \left| 2^{-k} m\right| )^{-\frac{\beta _2}{p_1}}\right\} _{|m|\le 2^k}| {\ell ^{2^{k{d}}}_{\mathbf {t}(p_1,p_2)}}\right\| ^{\mathbf {t}(p_1,p_2)} }\\&\quad = \sum _{|m|\le 2^k} |m|^{-\frac{\beta _1}{p_1} \mathbf {t}(p_1,p_2)}(1- \log \left| 2^{-k} m\right| )^{-\frac{\beta _2}{p_1} \mathbf {t}(p_1,p_2)} \\&\quad = \ \sum _{l=0}^k \sum _{|m|\sim 2^l} |m|^{-\frac{\beta _1}{p_1} \mathbf {t}(p_1,p_2)}(1- \log \left| 2^{-k} m \right| )^{-\frac{\beta _2}{p_1} \mathbf {t}(p_1,p_2)} \\&\quad \sim \sum _{l=0}^k \ 2^{l{d}} 2^{-l\frac{\beta _1}{p_1}\mathbf {t}(p_1,p_2)} \left( 1 + k-l\right) ^{-\frac{\beta _2}{p_1} \mathbf {t}(p_1,p_2)} \ \sim \ \sum _{l=1}^{k+1} \ l^{-\frac{\beta _2}{p_1} \mathbf {t}(p_1,p_2)}, \end{aligned}$$

such that

$$\begin{aligned}&{ \left\| \left\{ |m|^{-\frac{\beta _1}{p_1}}(1- \log \left| 2^{-k} m\right| )^{-\frac{\beta _2}{p_1}}\right\} _{|m|\le 2^k} | {\ell ^{2^{k{d}}}_{\mathbf {t}(p_1,p_2)}} \right\| }\\&\quad \sim {\left\{ \begin{array}{ll} (1+k)^{\frac{1}{\mathbf {t}(p_1,p_2)}-\frac{\beta _2}{p_1}}, &{} \text {if}\quad \frac{\beta _2}{p_1}<\frac{1}{\mathbf {t}(p_1,p_2)},\\ \log ^{\frac{1}{\mathbf {t}(p_1,p_2)}}(1+k), &{} \text {if}\quad \frac{\beta _2}{p_1} =\frac{1}{\mathbf {t}(p_1,p_2)}\end{array}\right. } \end{aligned}$$

which again leads to a contradiction in (3.42) if $k\rightarrow \infty$ since $\nu ( \mathop {\mathrm {id}}\nolimits _2)<\infty$.

We finally deal with the case $\delta =\frac{\alpha _1}{p_1}>\frac{{d}}{\mathbf {t}(p_1,p_2)}$, $\frac{1}{q^*}< \frac{\alpha _2}{p_1}\le \frac{ 1}{\mathbf {t}(q_1,q_2)}$. Consider the commutative diagram

where

$$\begin{aligned} P_\ell : \{\mu _k\}_{0\le k< 2^{\ell }} \mapsto \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, |m|< 2^j}, \quad \lambda _{j,m}= {\left\{ \begin{array}{ll} \mu _k, &{} j=k,\quad m=0, \\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} Q_\ell : \{\lambda _{j,m}\}_{j\in {{\mathbb {N}}}_{0}, |m|< 2^j} \ \mapsto \{\mu _k\}_{0\le k<2^\ell }, \quad \mu _k = {\left\{ \begin{array}{ll} \lambda _{j,0}, &{} k=j, \\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

such that $\Vert P_\ell \Vert = \Vert Q_\ell \Vert =1$, $k\in {{\mathbb {N}}}_{0}$. Thus

$$\begin{aligned} \nu ( \mathop {\mathrm {id}}\nolimits _1)\ge \nu ( \mathop {\mathrm {id}}\nolimits ^\ell ) = \left\| \left\{ (1+k)^{-\frac{\alpha _2}{p_1}}\right\} _{k<2^\ell } |\ell _{\mathbf {t}(q_1,q_2)}^{2^\ell } \right\| . \end{aligned}$$

But $\Vert \{(1+k)^{-\frac{\alpha _2}{p_1}}\}_{k<2^\ell } |\ell _{\mathbf {t}(q_1,q_2)}^{2^\ell } \Vert \rightarrow \infty$ when $\ell \rightarrow \infty$ if $\frac{\alpha _2}{p_1}\le \frac{ 1}{\mathbf {t}(q_1,q_2)}$. This again leads to a contradiction since $\nu ( \mathop {\mathrm {id}}\nolimits _1)<\infty$.

Remark 3.23

If $\delta >\max (\frac{\alpha _1}{p_1}, \frac{{d}}{\mathbf {t}(p_1,p_2)})$ and $\alpha _2\in {\mathbb {R}}$, then the condition (3.27) implies the nuclearity of the embedding $\ \mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}: B^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{({\varvec{\alpha }},{\varvec{\beta }})})\hookrightarrow B^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})\$ for $1\le p_1<\infty$, $1\le p_2\le \infty$ and $1\le q_1,q_2 \le \infty$. This can be easily seen rewriting the sufficiency part of the above proof literally. Moreover, by elementary embeddings this statement holds also for $\mathop {\mathrm {id}}\nolimits _{({\varvec{\alpha }},{\varvec{\beta }})}: F^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}},w_{({\varvec{\alpha }},{\varvec{\beta }})})\hookrightarrow F^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$.

The next statement is a direct consequence of Proposition 2.14, in particular, Remark 2.15, Theorem 3.22 and Remark 3.23.

Corollary 3.24

Let ${\varvec{\gamma }}=(\gamma _1,\gamma _2)\in {\mathbb {R}}^2$ and $w^{\log }_{{\varvec{\gamma }}}$ be given by (2.7). Assume that $1\le p_1<\infty$, $1\le p_2\le \infty$ ($p_2<\infty$ in the F-case), $1\le q_i\le \infty$, $s_i\in {\mathbb {R}}$, $i=1,2$. Then

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _{\log }: A^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}}, w^{\log }_{{\varvec{\gamma }}}) \hookrightarrow A^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

is compact if, and only if, $\delta >0$, $p_1\le p_2$ and $\gamma _2>0$.

The embedding is nuclear if, and only if, $\delta >0$, $\gamma _2>0$ , $p_1=1$ and $p_2=\infty$.

Proof

Recall our Remark 2.15 for the compactness. As for nuclearity, we apply Theorem 3.22 with $\alpha _1=\beta _1=0$ and observe, that (3.27) is never satisfied unless $\mathbf {t}(p_1,p_2)=\infty$. $\square$

3.3 Radial Spaces

So far we considered embeddings within the scale of spaces $A^s_{p,q}$ which are compact—and studied the question whether they are even nuclear. In case of spaces on bounded domains $\Omega$ or weighted spaces on ${{\mathbb {R}}}^{{d}}$ it is well-known that compactness can appear, unlike in case of unweighted spaces on ${{\mathbb {R}}}^{{d}}$. Furthermore, such Sobolev-type embeddings can also be compact in presence of symmetries, i.e., if we restrict our attention to subspaces consisting of distributions that satisfy certain symmetry conditions, in particular, if they are radial. We want to consider this setting now. Here the sufficient and necessary conditions for the nuclearity of the compact embeddings can be easily proved due to the relation between subspaces of radial distributions and appropriately weighted spaces. Indeed the conditions follow from Theorem 3.12. We start with recalling the definition of radial subspaces of Besov and Triebel–Lizorkin spaces.

Let $\Phi$ be an isometry of ${{\mathbb {R}}}^{{d}}$. For $g \in {\mathcal {S}}({{\mathbb {R}}}^{{d}})$ we put $g^\Phi (x)=g(\Phi x)$. If $f\in {\mathcal {S}}'({{\mathbb {R}}}^{{d}})$, then $f^\Phi$ is a tempered distribution defined by

$$\begin{aligned} f^\Phi (g)=f(g^{\Phi ^{-1}})\;, \quad g\in {\mathcal {S}}({{\mathbb {R}}}^{{d}}), \end{aligned}$$

where $\Phi ^{-1}$ denotes the isometry inverse to $\Phi$.

Definition 3.25

Let $SO({{\mathbb {R}}}^{{d}})$ be the group of rotations around the origin in ${{\mathbb {R}}}^{{d}}$. We say that the tempered distribution f is invariant with respect to $SO({{\mathbb {R}}}^{{d}})$ if $f^\Phi =f$ for any $\Phi \in SO({{\mathbb {R}}}^{{d}})$. For any possible s, p, q we put

$$\begin{aligned} RA^s_{p,q}({{\mathbb {R}}}^{{d}})= & {} \{f\in A^s_{p,q}({{\mathbb {R}}}^{{d}}): f\;\text {is invariant with respect to}\;SO({{\mathbb {R}}}^{{d}})\}\, . \end{aligned}$$

Remark 3.26

The space $RA^s_{p,q}({{\mathbb {R}}}^{{d}})$ is a closed subspace of $A^s_{p,q}({{\mathbb {R}}}^{{d}})$. Thus, it is a Banach space with respect to the induced norm if $p,q\ge 1$.

Let $w_{{d}-1}$ denote the weight defined by (2.4) with $\alpha =\beta ={d}-1$, ${d}\ge 2$. If $p,q\ge 1$ and $s>0$, then the space $RA^s_{p,q}({{\mathbb {R}}}^{{d}})$ is isomorphic to the space $RA^s_{p,q}({\mathbb {R}},w_{{d}-1})$ that consists of even functions belonging to $A^s_{p,q}({\mathbb {R}}, w_{{d}-1})$, cf. [39, Thms. 3 and 9].

We recall that the embedding

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _R: RA^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\hookrightarrow RA^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

is compact if, and only if,

$$\begin{aligned} s_1-s_2>{d}\left( \frac{1}{p_1}-\frac{1}{p_2}\right)>0 \qquad \text {and} \qquad {d}>1 , \end{aligned}$$

(3.43)

cf. [38]. Further properties of spaces of radial functions, in particular Strauss type inequalities as well as the description of traces on real lines through the origin, can be found in [38, 39].

Theorem 3.27

Let $1\le p_i,q_i\le \infty$, $s_i\in {\mathbb {R}}$, $i=1,2$ ($p_i< \infty$ in the case of $F_{p,q}^s$ spaces). Then the embedding

$$\begin{aligned} \mathop {\mathrm {id}}\nolimits _R : RA^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\hookrightarrow RA^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}}) \end{aligned}$$

is nuclear if, and only if,

$$\begin{aligned} s_1-s_2>{d}\left( \frac{1}{p_1}-\frac{1}{p_2}\right) >1. \end{aligned}$$

Proof

It is sufficient to prove the theorem for Besov spaces and large values of $s_1$ and $s_2$. The rest follows by the elementary embeddings between Besov and Triebel–Lizorkin spaces in the sense of (2.13) and the lift property for the scale of Besov spaces. So we assume that $s_1\ge s_2> 0$. It was proved in [39] that the space $RB^{s_i}_{p_i,q_i}({\mathbb {R}}^{{d}})$ is isomorphic to the weighted space $RB^{s_i}_{p_i,q_i}({\mathbb {R}}, w_{{d}-1})$, cf. Theorem 3 and Theorem 9 ibidem. So the embedding $RB^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\hookrightarrow RB^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear if, and only if, $RB^{s_1}_{p_1,q_1}({\mathbb {R}}, w_{{d}-1})\hookrightarrow RB^{s_2}_{p_2,q_2}({\mathbb {R}}, w_{{d}-1})$ is nuclear. But the double-weighted situation can be reduced to the one-side weighted case, i.e., the last embedding is nuclear if, and only if, the embedding $RB^{s_1}_{p_1,q_1}({\mathbb {R}}, w_{\alpha })\hookrightarrow RB^{s_2}_{p_2,q_2}({\mathbb {R}})$ with $\alpha = ({d}-1)(1-\frac{p_1}{p_2})$ is nuclear. Now Theorem 3.12 (one-dimensional with $\beta =\alpha$) implies that the embedding is nuclear if $s_1-s_2>{d}(\frac{1}{p_1}-\frac{1}{p_2})>1$.

Conversely, if the embedding $\mathop {\mathrm {id}}\nolimits _R: RB^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\hookrightarrow RB^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear, then it is compact. This implies $s_1-s_2>{d}(\frac{1}{p_1}-\frac{1}{p_2})>0$, see (3.43), in particular, $p_1<p_2$. Moreover the nuclearity of $\mathop {\mathrm {id}}\nolimits _R: RB^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\hookrightarrow RB^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is equivalent to the nuclearity of $RB^{s_1}_{p_1,q_1}({\mathbb {R}}, w_{\alpha })\hookrightarrow RB^{s_2}_{p_2,q_2}({\mathbb {R}})$.

Furthermore, the space

$$\begin{aligned} RB^{s}_{p,q}({{\mathbb {R}}}^{{d}}, (t,\infty ))=\left\{ f\in RB^s_{p,q}({{\mathbb {R}}}^{{d}}): \mathop {\mathrm {supp}}\nolimits f \subset \{x\in {{\mathbb {R}}}^{{d}}: |x|\ge t\}\right\} , \end{aligned}$$

is isomorphic to the space

$$\begin{aligned} B^{s}_{p,q}({\mathbb {R}}, w_{{d}-1},(t,\infty ))=\left\{ f\in B^s_{p,q}({\mathbb {R}},w_{{d}-1}): \mathop {\mathrm {supp}}\nolimits f\subset [t,\infty )\right\} , \end{aligned}$$

cf. [24]. So if the embedding $\mathop {\mathrm {id}}\nolimits _R: RB^{s_1}_{p_1,q_1}({{\mathbb {R}}}^{{d}})\hookrightarrow RB^{s_2}_{p_2,q_2}({{\mathbb {R}}}^{{d}})$ is nuclear, then the embedding $\mathop {\mathrm {id}}\nolimits : B^{s_1}_{p_1,q_1}({\mathbb {R}}, w_{{d}-1},(t,\infty ))\hookrightarrow B^{s_2}_{p_2,q_2}({\mathbb {R}}, w_{{d}-1},(t,\infty ))$ is nuclear, too. But now we can use the wavelet expansions and arguments similar to that ones that were used for the global behaviour of the purely polynomial weight in Step 2 of the proof of Theorem 3.12. Thus, the one-dimensional version of Theorem 3.12, in particular (3.5) with $\alpha =\beta =({d}-1)(1-\frac{p_1}{p_2})$, lead to

$$\begin{aligned} \frac{\beta }{p_1}=\frac{{d}-1}{p_1}\left( 1-\frac{p_1}{p_2}\right) > \frac{1}{\mathbf {t}(p_1,p_2)} = 1-\left( \frac{1}{p_1}-\frac{1}{p_2}\right) \end{aligned}$$

in view of (3.1) and $p_1<p_2$, and

$$\begin{aligned} \delta =s_1-s_2-\frac{1}{p_1}+\frac{1}{p_2}> \frac{\alpha }{p_1}=\frac{{d}-1}{p_1}\left( 1-\frac{p_1}{p_2}\right) . \end{aligned}$$

This finally results in $s_1-s_2>{d}(\frac{1}{p_1}-\frac{1}{p_2})>1$, as desired. $\square$