Introduction

With the exception of the Russian GLONASS, all current satellite navigation systems such as GPS, Galileo, BeiDou, and QZSS make use of the code division multiple access (CDMA) scheme to separate the signals from different satellites at the user receiver. Since with CDMA the carrier-phase measurements from all satellites share common wavelengths, the resulting double-difference (DD) ambiguities are directly estimable as integers.

The GLONASS legacy signals are based on frequency division multiple access (FDMA), where different satellites transmit on slightly different carrier frequencies. Differencing the carrier phases between two satellites, therefore, involves measurements with different wavelengths, so that the conventional DD ambiguities are no longer integer estimable. In Teunissen (2019), a new FDMA model was introduced, in which a new set of integer ambiguity parameters is defined, that enables integer ambiguity resolution also for GLONASS. The performance of this model with GLONASS and GPS data was first demonstrated for short baseline positioning and direction finding in Teunissen and Khodabandeh (2019), and for short to long baseline positioning in Hou et al. (2020). As shown in Teunissen and Khodabandeh (2019), the FDMA model is much weaker than the CDMA model in terms of the ambiguity resolution performance so that, for instance, GLONASS only reliable single-epoch ambiguity resolution is often not possible on short baselines with dual-frequency observations as for CDMA systems.

Teunissen (2019) and Teunissen and Khodabandeh (2019) pointed out the importance of partial ambiguity resolution (PAR) when using GLONASS data. They showed that even with the geometry-fixed model, which is the strongest possible model that assumes the relative receiver satellite geometry known, PAR is required for a high ambiguity resolution reliability, thus implying the necessity of PAR for any other model. As demonstrated in Odijk et al. (2014), Brack (2016), and Nardo et al. (2016) with simulations and in Parkins (2011) and Brack (2017a, b) with real GNSS data, PAR techniques can greatly enhance the positioning performance.

We focus on combined multi-GNSS solutions and give a detailed analysis of the capabilities of this new FDMA model for single baseline real-time kinematic (RTK) positioning for combinations of up to five systems. Short, medium, and long baselines are considered and analyzed formally, through simulations, and with real data from four permanent GNSS stations in the area of Perth, Australia. Generally, combining systems strongly improves the RTK positioning capabilities, as was demonstrated for GPS and Galileo (Tiberius et al. 2002; Julien et al. 2003; Odijk et al. 2012), GPS and BeiDou (Deng et al. 2014; He et al. 2014; Teunissen et al. 2014; Zhao et al. 2014; Odolinski et al. 2015b), and four-system GPS, Galileo, BeiDou, and QZSS (Odolinski et al. 2015a). Such improvement can also occur when including GLONASS FDMA data (Teunissen and Khodabandeh 2019; Hou et al. 2020), but it is shown that the ambiguity resolution performance can also be clearly reduced compared to the case without GLONASS.

Given the above weakness, it is discussed whether it is actually useful to include GLONASS FDMA data when already up to four CDMA systems are employed, and how they should be included. We show that, with a difference test (DT)-based PAR method, including GLONASS data is beneficial in all considered cases. This implies a higher availability of centimeter-level solutions for instantaneous solutions on short and medium baselines, faster solutions for long baselines, and improved positioning precision.

Single baseline observation model

The single-system CDMA and FDMA DD observation models are introduced. For the combined system analysis presented later, all systems are essentially treated separately with only the receiver coordinates and the tropospheric zenith delay as common parameters. That is, differencing between systems with common frequencies after a possible calibration of inter-system biases is not considered (Odijk and Teunissen 2013; Paziewski and Wielgosz 2015).

Let \(S\) denote the number of satellites that are tracked by both receivers on \(F\) frequencies. The single-epoch system of linearized observation equations can be written in the form

$$\left[\begin{array}{c}\varvec{p}\\ \boldsymbol{\varphi }\end{array}\right]=\left[\begin{array}{cc}{{\varvec{e}}}_{F}\otimes {\varvec{G}}& {\varvec{q}}\otimes {{\varvec{I}}}_{S-1}\\ {{\varvec{e}}}_{F}\otimes {\varvec{G}}& -{\varvec{q}}\otimes {{\varvec{I}}}_{S-1}\end{array}\right]\left[\begin{array}{c}{\varvec{b}}\\{\varvec{\iota}}\end{array}\right]+\left[\begin{array}{c}\boldsymbol{0}\\ \boldsymbol{\Lambda }\otimes {\varvec{L}}\end{array}\right]{\varvec{a}}+{\varvec{\eta}}$$
(1)

where \({\varvec{p}}\in {\mathbb{R}}^{\left(S-1\right)F}\) and \(\boldsymbol{\varphi }\in {\mathbb{R}}^{\left(S-1\right)F}\) contain the DD code and carrier-phase observations, \({\varvec{b}}\in {\mathbb{R}}^{3/4}\) the three receiver coordinates and optionally the residual between receiver differential tropospheric zenith delay, \({\varvec{\iota}}\in {\mathbb{R}}^{S-1}\) the DD ionospheric delays on the reference frequency, and \({\varvec{a}}\in {\mathbb{Z}}^{\left(S-1\right)F}\) the carrier-phase integer ambiguities. The geometry matrix is \({\varvec{G}}\in {\mathbb{R}}^{\left(S-1\right)\times 3/4}\), \({{\varvec{e}}}_{F}\) is an \(F\) vector of ones, and \(\otimes\) denotes the Kronecker product. The vector \({\varvec{q}}\in {\mathbb{R}}^{F}\) contains the coefficients of the first-order ionospheric delays, \({{\varvec{I}}}_{S-1}\) is the unit matrix of dimension \(S-1\), and \(\boldsymbol{\Lambda }\in {\mathbb{R}}^{F\times F}\) is a diagonal matrix with the wavelengths as defined by the center frequencies of the signal bands.

With CDMA, the matrix \({\varvec{L}}\in {\mathbb{R}}^{(S-1)\times (S-1)}\) is simply a unit matrix and \({\varvec{a}}\) are the DD ambiguities. For GLONASS L1 and L2 FDMA data, the wavelengths are proportional to \(1/(2848+{\kappa }^{s})\), with the satellite-specific channel numbers \({\kappa }^{s}\in \left[-7,\dots ,6\right]\), so that it is not possible to simply set up a separate integer ambiguity parameter for each carrier-phase DD observation with a common wavelength as a coefficient. A lower triangular matrix \({\varvec{L}}\) defining a set of integer estimable ambiguity combinations was proposed in Teunissen (2019). As the ratio between the L1 and L2 frequencies is identical for all GLONASS satellites, the ionospheric parameterization is still valid.

The additive noise \({\varvec{\eta}}\in {\mathbb{R}}^{2\left(S-1\right)F}\) is assumed as zero-mean Gaussian with covariance matrix

$${\varvec{Q}}=2\cdot \mathrm{blkdiag} ({{\varvec{Q}}}_{{\varvec{p}}},{{\varvec{Q}}}_{\boldsymbol{\varphi }})$$
(2)

where \({{\varvec{Q}}}_{{\varvec{p}}}=\mathrm{diag}\left({\sigma }_{p,1}^{2},\dots ,{\sigma }_{p,F}^{2}\right)\otimes {\varvec{D}}{\varvec{W}}{{\varvec{D}}}^{\mathrm{T}}\), with \({\sigma }_{p,f}\) the frequency specific zenith referenced standard deviations of the undifferenced code observations, \({\varvec{D}}\in {\mathbb{Z}}^{\left(S-1\right)\times S}\) the between satellite differencing operator, and \({\varvec{W}}\in {\mathbb{R}}^{S\times S}\) a diagonal matrix with elevation-dependent exponential noise amplification factors from Euler and Goad (1991). The carrier-phase covariance matrix \({{\varvec{Q}}}_{\boldsymbol{\varphi }}\) is defined accordingly with the standard deviations \({\sigma }_{\varphi ,f}\).

The FDMA-based observations may further be affected by inter-channel biases caused by different carrier frequencies. GLONASS inter-channel phase biases are negligible and are therefore not considered (Sleewaegen et al. 2012). Inter-channel code biases are assumed absent in this contribution, e.g., through the use of similar hardware for both receivers or a priori calibration (Yamada et al. 2010; Reussner and Wanninger 2011; Al-Shaery et al. 2013; Chuang et al. 2013).

The expected ambiguity resolution performance of the FDMA model can be understood by analyzing the covariance matrix \({{\varvec{Q}}}_{\widehat{{\varvec{a}}}}\) of the estimated float ambiguities \(\widehat{{\varvec{a}}}\). Figure 1 shows the LAMBDA (Teunissen 1995) decorrelated conditional ambiguity standard deviations of the FDMA model and the corresponding CDMA model, cf. Teunissen and Khodabandeh (2019). As discussed in Teunissen (2019) and Teunissen and Khodabandeh (2019), the decorrelated FDMA ambiguity spectrum is not flat like the CDMA spectrum, but the first \(F\) values, which are the last ones to be considered, are much larger, which is caused by the structure of the \({\varvec{L}}\) matrix in (1). As is shown later, it is virtually impossible to quickly and reliably resolve these ambiguities. Teunissen (2019) and Teunissen and Khodabandeh (2019) proposed a PAR method as a remedy, where these \(F\) elements are excluded from ambiguity fixing, the impact of which is discussed later. Further, we can already see that the values of FDMA are increased compared to the CDMA spectrum, so that we can expect a weaker ambiguity resolution performance.

Fig. 1
figure 1

Conditional ambiguity standard deviations of the FDMA and CDMA models for a single- (top) and dual-frequency (bottom) example

Full size image

The different magnitude of the elements of \({\varvec{L}}\) that causes this behavior might also lead to numerical problems when implementing the FDMA model, in particular when using a filtered solution. A mathematical equivalent implementation is given by replacing \({\varvec{a}}\in {\mathbb{Z}}^{n}\) by the non-integer

$$\tilde{{\varvec{a}}}=\left({{\varvec{I}}}_{F}\otimes {\varvec{L}}\right){\varvec{a}},\quad \mathrm{ with }\tilde{{\varvec{a}}}\in {\mathbb{R}}^{n}$$
(3)

when computing float estimates, so that in fact the CDMA model is used. By applying the inverse transformation to the resulting float solution \(\widehat{{\varvec{a}}}=\left({{\varvec{I}}}_{F}\otimes {{\varvec{L}}}^{-1}\right)\widehat{{\tilde{\varvec{a}}}}\) and its covariance matrix, the integer estimable ambiguity vector is restored for the subsequent integer fixing. This formulation also allows for a simpler and more intuitive reparameterization for rising and setting satellites in a recursive estimation scheme. A similar strategy was proposed in Hou et al. (2020).

In the following, short baselines refer to the case where all differential atmospheric delays are negligible and can be removed from the model. The differential tropospheric delay is estimated for medium baselines, whereas the ionospheric delays are modeled as zero-mean additive noise, referred to as the ionosphere weighted model (Schaffrin and Bock 1988; Teunissen 1998b; Odijk 2000). For long baselines, both the tropospheric delay and the ionospheric delays in (1) are estimated.

Ambiguity resolution methods

We compare three methods for reliable ambiguity resolution that can be formulated such as to meet a user-defined constraint on the maximum tolerable ambiguity failure rate \({P}_{\mathrm{f}}\) and the best integer equivariant estimator.

Two methods are used for full ambiguity resolution (FAR), both of which use integer least-squares (ILS) ambiguity estimation in combination with an acceptance criterion. The first criterion is the integer bootstrapping (IB) failure rate (Teunissen 1998a) as an upper bound of the ILS failure rate (IB FAR). As a second criterion, we use the DT (Tiberius and De Jonge 1995) with a fixed failure rate critical value (DT FAR), so that a maximum failure rate of \({P}_{\mathrm{f}}\) can also be guaranteed (Verhagen and Teunissen 2013). With DT FAR, reliable ambiguity fixing can still be possible even if the IB failure rate, as defined by the system model, is too large.

The concept of the DT was extended to PAR in Brack and Günther (2014) by means of a per-element DT, in which each scalar entry of the ILS ambiguity solution is tested for acceptance (DT PAR). A maximum failure rate is again guaranteed through a proper choice of the critical value, for which the conservative functional approximation in Brack (2015) is used.

The concept of the best integer equivariant (BIE) estimator (Teunissen 2003) is to not fix the ambiguities to integers but to form a weighted sum of integers. The resulting estimates of the geometry parameters \({\varvec{b}}\) are the minimum variance unbiased estimates within the integer equivariant estimators class, which also contains the float solution and all admissible fixed or partially fixed solutions. Therefore, the variances of the BIE estimates can serve as benchmark results for analyzing the best possible performance of any given model.

Experimental setup

The RTK positioning performance of single and combined system GPS (G), Galileo (E), BeiDou-2 (C), QZSS (J), and GLONASS (R) is analyzed for different baselines. The data with a sampling interval of \(30 \,\mathrm{s}\) were collected at the stations CUT0, CUTA, PERT (all Trimble NetR9), and NNOR (Septentrio PolaRx5TR) in the area of Perth, Australia, during May 15, 2020. The number of visible satellites with an elevation angle greater than \({10}^{\circ }\) is shown in Fig. 2. We can see that the number of GLONASS satellites is mostly smaller than for the other global systems, which we have to keep in mind when interpreting the positioning performance. The estimated zenith referenced code standard deviations of the considered signals are given in Table 1. They are derived from a different day of DD code data in a least-squares sense following Teunissen and Amiri-Simkooei (2008) with a priori fixed coordinates. For CUT0-CUTA, differential atmospheric delays are neglected, whereas for PERT-NNOR the ionosphere weighted model is applied, cf. Section "Medium baselines," and residual tropospheric delays are ignored. The quality of the GLONASS signals is comparable to the other systems. The ambiguity failure rate constraint is set to \({P}_{\mathrm{f}}=0.1\%\).

Fig. 2
figure 2

Number of visible GNSS satellites in Perth, Australia, during May 15, 2020

Full size image
Table 1 Estimated zenith referenced standard deviations \({\sigma }_{p,f}\) of the code observables in \((\mathrm{cm})\) for GPS L1/L2, Galileo E1/E5a, BeiDou-2 B1/B2, QZSS L1/L2, and GLONASS L1/L2 for two different baselines. The carrier-phase standard deviations are assumed as \({\sigma }_{\varphi ,f}=2\, \mathrm{mm}\)
Full size table

Short baselines

Instantaneous single- and dual-frequency positioning on the \(8.4 \,\mathrm{m}\) baseline between CUT0 and CUTA is considered. Differential atmospheric delays are assumed absent.

Formal and simulation analysis

The average ambiguity float and fixed single-epoch positioning precision for the east, north, and up component is given in Table 2 for different systems. The ambiguity-fixed precision values are derived from the conditional coordinate covariance matrices and do not reflect whether it is possible to reliably resolve the ambiguities. For the GLONASS only cases, only epochs with six or more visible satellites are included. As mentioned above, the \(F\) least precise LAMBDA-transformed ambiguities are removed for GLONASS. The single-system GLONASS results are worse compared to single-system GPS, which can be attributed to fewer visible satellites. However, sub-centimeter-level horizontal positioning results should also be possible already with single-frequency GLONASS data. The gain of combined system GPS + Galileo and GPS + GLONASS compared to GPS only is on a similar level, in particular when considering the lower number of GLONASS satellites. Even for the already very strong four-system GPS + Galileo + BeiDou-2 + QZSS case, adding GLONASS data still improves the precision.

Table 2 Average formal ambiguity float and fixed positioning standard deviations for the east/north/up components with single- and dual-frequency observations
Full size table

The ambiguity-fixed precision values are only meaningful, given that it is actually possible to reliably resolve the ambiguities. To formally analyze the different models' ambiguity resolution capabilities, we consider the IB success rate and the ambiguity dilution of precision (ADOP, Teunissen 1997), a measure for the strength of the model for successful ambiguity resolution. It was found that an \(\mathrm{ADOP}\le 0.12\) generally allows for reliable ILS ambiguity resolution with a failure rate of less than \(0.1\%\) (Odijk and Teunissen 2008). The average IB success rates in Fig. 3 show that the single-system, single-frequency model is too weak to support reliable ambiguity resolution, whereas the dual-frequency GPS or single-frequency GPS + Galileo model is strong enough. For GLONASS, we consider three cases, where R reduced (red.) stands for the above case of removing the \(F\) least precise ambiguities, R full means that all ambiguities are included, and R CDMA means that GLONASS is simulated as if it was a CDMA system, i.e., all channel numbers \({\kappa }^{s}\) are assumed as zero. The dual-frequency results clearly show that we cannot expect to resolve all GLONASS ambiguities. Even when removing the two least precise elements, the IB success rates are still considerably lower than for the CDMA model, whose results are comparable to GPS. Reliable dual-frequency GLONASS ambiguity resolution only becomes possible, starting from about eight satellites. The IB success rates of the single-frequency combined GPS + GLONASS model are also lower than the ones of the GPS + Galileo counterpart. The average ADOP values confirm these findings in Fig. 4, where the black line indicates an ADOP of 0.12 cycles.

Fig. 3
figure 3

Average IB success rates versus the number of satellites for single- (top) and dual-frequency (bottom) observations

Full size image
Fig. 4
figure 4

Average ADOP versus the number of satellites for single- (top) and dual-frequency (bottom) observations. The black line marks 0.12 cycles

Full size image

We cannot expect to reliably resolve the \(F\) least precise ambiguities for GLONASS, so the question is whether they are actually relevant for positioning, and if so, can we make use of them? The formal ambiguity-fixed precision for the GPS + GLONASS case in Table 3 indeed shows a slight penalty in the average standard deviations when ignoring those ambiguities, although on the sub-millimeter level. The BIE estimator leads to the highest possible precision values that can actually be obtained so that applying the BIE to the full GLONASS ambiguity set shows the model's capability. Comparing these BIE results to those of the reduced case, in which the integer property of \(F\) ambiguities is ignored, shows the potential loss of the reduced scenario. For the single-frequency case, there is a slight advantage when including also those \(F\) ambiguities. More interesting, for the stronger dual-frequency case where on average sub-centimeter positioning is possible, the BIE results of the reduced and full set are identical, and they are also identical to the fixed precision with the reduced set. Therefore, the strategy to remove those F least precise ambiguities is very reasonable, since even when they are included optimally, they do not noticeably contribute to the positioning precision. For a reliable integer fixing of the GLONASS ambiguities, excluding those \(F\) elements is essential (Teunissen 2019; Teunissen and Khodabandeh 2019). From now on, we only consider this reduced case for GLONASS, so that the IB success rates and ADOP values refer to this case, and the two FAR methods and DT PAR are applied to the reduced ambiguity set. That is, with GLONASS data, all considered methods are, in fact, partial ambiguity resolution methods.

Table 3 Average formal ambiguity-fixed and simulated BIE positioning precision for the east/north/up components with single- and dual-frequency observations
Full size table

Although the above-presented IB success rate and ADOP are very useful measures for the models' ambiguity resolution capabilities, high-precision positioning might still be possible even for seemingly weak models when using the DT-based methods for FAR and PAR. The simulated average availability of coordinate estimates with a formal precision of 3 cm or better for the horizontal components and 15 cm for the up component is given in Table 4, where the DT FAR and DT PAR results are computed by Monte Carlo integration. As expected, the single-frequency GPS model is too weak for reliable ambiguity resolution, but the dual-frequency counterpart is sufficiently strong. Adding GLONASS data improves significantly the single-frequency results, where the DT-based methods are again clearly superior to the IB FAR scheme. For the dual-frequency case, however, we can see that adding GLONASS may even worsen the ambiguity resolution performance, especially for IB FAR, whereas with DT PAR, one can expect full availability. The same is observed for the by itself very strong four-system model, where adding GLONASS data when attempting FAR decreases the availability, whereas DT PAR can again guarantee full availability.

Table 4 Simulated availability of precise coordinate estimates with a formal precision of 3 cm for the horizontal components and 15 cm for the up component in %
Full size table

Real data analysis

For the real data analysis, the conventional IB FAR method and DT PAR are considered. Standalone GLONASS was shown to be too weak for instantaneous positioning with reliable ambiguity resolution. Figure 5 shows the dual-frequency IB FAR results when combining three consecutive epochs. When the model is sufficiently strong so that an integer solution can be accepted, centimeter-level results are possible.

Fig. 5
figure 5

Dual-frequency GLONASS only positioning errors for CUT0-CUTA using three consecutive measurement epochs with IB FAR. Blue and gray indicate accepted and rejected integer solutions

Full size image

The benefit of integrating GLONASS FDMA data in a multi-GNSS solution is shown in Fig. 6 for single-frequency GPS + GLONASS positioning. With IB FAR, reliable ambiguity resolution for GPS only is not possible, and DT PAR only allows for centimeter-level results for a very limited number of epochs. In the combined model, as predicted by the simulations, the acceptance rate of IB FAR is clearly improved, although still limited, and DT PAR further increases the availability of precise results.

Fig. 6
figure 6

Single-frequency GPS + GLONASS single-epoch positioning errors for CUT0-CUTA with IB FAR and DT PAR. Blue and gray indicate all ambiguities fixed and no ambiguities fixed; for PAR all shades in between are possible

Full size image

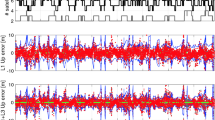
The single-frequency four-/five-system results with GPS, Galileo, BeiDou-2, QZSS, and GLONASS are shown in Fig. 7. Without GLONASS, single-epoch FAR is already possible with IB FAR at every epoch. Adding GLONASS reduces the system model's ambiguity resolution strength, which results in some gaps in which an integer solution cannot be accepted with IB FAR and we obtain errors at the meter level. These gaps can, however, be avoided with DT PAR. The root mean square (RMS) positioning errors without GLONASS and IB FAR are 1.6, 1.4, and 3.7 mm for the east, north, and up components. They are slightly reduced to 1.5, 1.4, and 3.5 mm with GLONASS and DT PAR, so that the positioning capabilities still benefit from adding GLONASS, although not always the full set of ambiguities is resolved.

Fig. 7
figure 7

Single-frequency GPS + Galileo + BeiDou-2 + QZSS + GLONASS single-epoch positioning errors for CUT0-CUTA with IB FAR and DT PAR. Blue and gray indicate all ambiguities fixed and no ambiguities fixed; for PAR all shades in between are possible

Full size image

Almost identical results are obtained for the dual-frequency case with GPS and GLONASS in Fig. 8, where GLONASS reduces the RMS errors from 2.1, 2.2, and 5.3 mm to 1.7, 1.8, and 4.3 mm. The problem of rejected integer ambiguity solutions with integrated GLONASS data and IB FAR also remains when adding further constellations to this dual-frequency case, even with five systems (not shown here).

Fig. 8
figure 8

Dual-frequency GPS + GLONASS single-epoch positioning errors for CUT0-CUTA with IB FAR and DT PAR. Blue and gray indicate all ambiguities fixed and no ambiguities fixed; for PAR all shades in between are possible

Full size image

Medium baselines

Instantaneous dual-frequency positioning on the \(22.4\, \mathrm{km}\) baseline between CUT0 and PERT and the \(88.5 \,\mathrm{km}\) baseline between PERT and NNOR is considered. The measurements are a priori corrected for the tropospheric delays with the blind MOPS tropospheric model (MOPS 1999) and the global mapping function (Böhm et al. 2006). Residual zenith wet tropospheric delays are estimated. The ionospheric delays are treated as additional noise, where the uncertainty \({\sigma }_{\iota }\) of the between receiver differenced ionospheric delays is modeled depending on the length of the baseline as

$${\sigma }_{\iota }=\sqrt{2}\cdot 0.4\frac{\mathrm{mm}}{\mathrm{km}}$$
(4)

to which the elevation-dependent weighting of Euler and Goad (1991) is applied. Since the GLONASS only model is already too weak for single-epoch positioning on short baselines, this case is not considered, and the focus is on integrating GLONASS FDMA data with data from CDMA systems.

Formal and simulation analysis

The average single-epoch ambiguity float and fixed positioning precision is shown for the east component in Fig. 9 for different systems depending on the length of the baseline. The increasing uncertainty of the differential ionospheric delays with increasing baseline length transforms into less precise positioning results. Adding GLONASS to the GPS only case improves the positioning precision both for the ambiguity float and fixed cases by roughly \(20\%\), which is slightly less but comparable to adding Galileo. Further improvements are observed by adding more systems, where adding GLONASS is still beneficial when already four systems are combined.

Fig. 9
figure 9

Average dual-frequency formal ambiguity float (top) and ambiguity-fixed (bottom) positioning precision versus the length of the baseline for the east component

Full size image

We now look at the ambiguity resolution capabilities of the model with different systems included. The average values of the IB success rate and ADOP are shown in Fig. 10. The IB success rate of GPS quickly drops when the length of the baseline exceeds a few kilometers, and the ADOP increases to above \(0.12 \,\mathrm{cycles}\). Adding Galileo clearly improves this situation. Based on the ADOP values, a range of about \(20\, \mathrm{km}\) for instantaneous positioning should be possible sometimes when using \(0.12\, \mathrm{cycles}\) as threshold. The impact of adding GLONASS to GPS is not so obvious. Although the IB success rate is worse than for GPS only, the ADOP values are slightly improved. For the four-/five-system case without and with GLONASS, including GLONASS significantly reduces the IB success rate, but only leads to slightly increased ADOP values.

Fig. 10
figure 10

Average dual-frequency IB success rates (top) and ADOP (bottom) versus the length of the baseline. The black line marks \(0.12\, \mathrm{cycles}\)

Full size image

The simulated average availability of precise coordinate estimates with IB FAR, DT FAR, and DT PAR is shown in Fig. 11. As expected, IB FAR is only helpful for very short baselines. Applying the DT for FAR can slightly extend the range for instantaneous positioning, but DT PAR leads to a significant improvement, especially for the four and five-system cases, where instantaneous results should be possible for baselines of up to almost \(100 \,\mathrm{km}\). The above concern about the ambiguity resolution performance with GLONASS data is confirmed. With the two FAR methods, which imply that the \(F\) least precise ambiguities are removed, adding GLONASS mostly decreases the positioning performance, more notably for the four-/five-system cases. Adding Galileo to GPS, on the other hand, leads to improved results. With DT PAR, the availability with GLONASS data is increased.

Fig. 11
figure 11

Simulated availability of dual-frequency single-epoch precise coordinate estimates with a formal precision of \(3 \,\mathrm{cm}\) for the horizontal components and \(15\, \mathrm{cm}\) for the up component. In the second subfigure, the dashed lines mark G + E

Full size image

Real data analysis

Considering the baseline lengths of \(22.4 \,\mathrm{km}\) and \(88.5\, \mathrm{km}\), the only method that can provide instantaneous centimeter-level positioning is DT PAR. GPS and GPS + GLONASS results for CUT0-PERT are shown in Fig. 12. Adding GLONASS clearly improves the availability of the GPS only solution. For the four- and five-system cases, the more challenging PERT-NNOR baseline is employed. Continuous single-epoch centimeter-level positioning results with reliable ambiguity resolution are indeed feasible, see Fig. 13. The RMS east, north, and up positioning errors of the ambiguity float solution are \(12.3\), \(14.9\), and \(102.6 \,\mathrm{cm}\) without and \(11.7\), \(14.0\), and \(91.6\, \mathrm{cm}\) with GLONASS. The corresponding partially fixed RMS errors are \(4.4\), \(5.4\), and \(63.4\, \mathrm{mm}\) versus \(4.3\), \(5.3\), and \(60.1\, \mathrm{mm}\). Including GLONASS data into an already strong four-system model is therefore still beneficial. As mentioned above, nonzero inter-channel code biases can be present in a mixed receiver setup like PERT-NNOR. From the results, they appear small enough to not visibly affect the positioning performance, but one has to be very careful when ignoring these biases for inhomogeneous receivers.

Fig. 12
figure 12

Dual-frequency GPS + GLONASS single-epoch positioning errors for CUT0-PERT with DT PAR. Blue and gray indicate all ambiguities fixed and no ambiguities fixed, where all shades in between are possible

Full size image
Fig. 13
figure 13

Dual-frequency GPS + Galileo + BeiDou-2 + QZSS + GLONASS single-epoch positioning errors for PERT-NNOR. The DT PAR results are shown in blue and the ambiguity float results in light gray

Full size image

Long baselines

Both the residual zenith wet tropospheric delay and the double-difference ionospheric delays are estimated. Reliable ambiguity resolution now requires the use of multiple measurement epochs with time constant ambiguity parameters. The following analysis is based on dual-frequency observations from the \(88.5 \,\mathrm{km}\) baseline between PERT and NNOR. Rising satellites are immediately included in the processing. The coordinates and ionospheric delays are assumed completely unlinked in time, and the zenith tropospheric delay is modeled as a random walk with a process noise of \(2\, \mathrm{mm}/\sqrt{\mathrm{h}}\).

Formal and simulation analysis

The average ambiguity float and fixed precision over the number of epochs is shown in Fig. 14 for the east component. Similar conclusions as for short and medium baselines can be drawn, i.e., adding more systems visibly improves both the float and fixed precision. This is more pronounced for the ambiguity float case, in which the decimeter level can be reached much faster for a combined approach than for GPS only.

Fig. 14
figure 14

Average dual-frequency formal ambiguity float (top) and ambiguity-fixed (bottom) positioning precision against the number of epochs for the east component

Full size image

The strength of the models with regard to ambiguity resolution as demonstrated with the IB success rate and ADOP in Fig. 15 shows that in the present setup adding GLONASS to GPS clearly improves the situation, whereas adding GLONASS to the four-system case leads to slightly inferior results so that, for instance, the IB success rate of the GPS + Galileo model is higher than the one of the five-system model. This again shows the importance of choosing a suitable ambiguity resolution strategy when dealing with the weaker GLONASS FDMA model. The average number of epochs required to reach an IB success rate of less than \(0.1\%\) is shown in Table 5. Adding a second system clearly shortens the convergence time, but between the dual-system GPS + Galileo case and the four-system case, including also BeiDou-2 and QZSS there is almost no difference. This can be attributed to more frequently rising satellites with more systems. Such problems can be avoided with DT PAR as is demonstrated below. Adding GLONASS to the four-system case clearly prolongs the convergence time.

Fig. 15
figure 15

Average dual-frequency IB success rates (top) and ADOP (bottom) versus the number of epochs. The black line marks \(0.12 \,\mathrm{cycles}\)

Full size image
Table 5 Average convergence times of IB FAR in terms of the number of epochs required to reach an IB success rate of less than \(0.1\%\). One epoch corresponds to \(30\, \mathrm{s}\)
Full size table

The simulated average availability of precise solutions with IB FAR, DT FAR, and DT PAR is presented in Fig. 16. For GPS only, we cannot expect fast results with any of the three methods, and DT PAR shows almost no advantage over DT FAR. Adding a second system already leads to significant improvements, and the benefit of PAR becomes evident. Although GLONASS helps to enhance the performance of GPS only, it is clearly inferior to combined GPS and Galileo, for which we can expect continuous solutions within about \(15\) epochs. For the four- and five-system cases, the improvements with both FAR methods are minor, but with DT PAR we should be able to reach precise solutions within only a few epochs. We can also see that the problems of reduced availability with FAR when adding GLONASS to the four-system case disappear with DT PAR. The combination of all available systems with PAR can, therefore, be considered the key to fast positioning when atmospheric delays have to be estimated, keeping in mind that with the conventional IB FAR method and standalone GPS the average convergence time is \(52.1\) epochs.

Fig. 16
figure 16

Simulated availability of dual-frequency precise coordinate estimates on a long baseline with a formal precision of \(3 \,\mathrm{cm}\) for the horizontal components and \(15\, \mathrm{cm}\) for the up component. In the second subfigure, the dashed lines mark G + E

Full size image

Real data analysis

It is now verified whether it is actually possible to reach the centimeter level on long baselines within only a few epochs. We focus on the four- and five-system cases with DT PAR. The strategy is to continuously add measurement epochs until the formal precision value of the partially fixed solution reaches \(3\, \mathrm{cm}\) for the horizontal components and \(15\, \mathrm{cm}\) for the up component. The computation of this solution is started at every epoch.

The positioning results for the \(88.5 \,\mathrm{km}\) baseline PERT-NNOR with the long baseline model are shown in Fig. 17 for the five-system case. The last row shows the number of epochs that were used to obtain the solutions. The distribution on the right shows that although single-epoch positioning is not possible, mostly only two to four epochs are required. The average number of employed epochs is \(3.27\) with GLONASS and \(3.38\) without GLONASS, showing the advantage of including GLONASS again. It also means that almost instantaneous results can actually be obtained when making use of all available systems and applying DT PAR. Similar results are obtained for the \(109.6\, \mathrm{km}\) baseline CUT0-NNOR with \(4.03\) and \(4.09\) epochs with and without GLONASS.

Fig. 17
figure 17

Dual-frequency GPS + Galileo + BeiDou-2 + QZSS + GLONASS positioning errors for PERT-NNOR. The DT PAR results are shown in blue; the ambiguity float results in light gray. The number of measurement epochs that are used at each time instance is shown in the last row together with their distribution

Full size image

Conclusions

The performance of the GLONASS FDMA model for single- and dual-frequency single baseline RTK positioning was analyzed. The main conclusions can be summarized as follows.

While the formal positioning precision of the FDMA model was shown to be comparable to the CDMA model, its ambiguity resolution capabilities are clearly inferior. Removing the least precise LAMBDA-transformed ambiguity on each frequency as suggested in Teunissen (2019) and Teunissen and Khodabandeh (2019) strongly enhanced the situation, but the CDMA performance could still not be reached. Importantly, the achievable positioning precision was not visibly impaired by this, as was demonstrated with the BIE estimator.

As a result, centimeter-level single-epoch GLONASS FDMA only positioning was usually not possible. Integrating GLONASS FDMA data with GPS CDMA data improved the availability of ambiguity resolved results only in a limited number of cases, namely for short baselines with a single frequency and for long baselines with two frequencies. For short baselines with two frequencies, medium baselines, or when further CDMA systems were added, using the FDMA data reduced the availability compared to the cases without it.

To cope with the comparably weaker FDMA model, we proposed a PAR approach based on the per-element DT. This was demonstrated to lead to higher availability of centimeter-level solutions with better precision when integrating GLONASS data in all considered cases.

With the combined GPS, Galileo, BeiDou-2, QZSS, and GLONASS model and DT PAR, instantaneous centimeter-level positioning on an \(88.5\, \mathrm{km}\) baseline was shown to be possible with the ionosphere weighted model. An average of only \(3.27\) measurement epochs was shown to be sufficient with the ionosphere float model. This is particularly promising since the single baseline ionosphere float model is comparable to single receiver ambiguity resolution-enabled precise point positioning (PPP-RTK) without atmospheric corrections, so that almost instantaneous solutions can also be expected with this method.