The averaging of numerosities: A psychometric investigation of the mental line

Abstract

Humans and animals are capable of estimating and discriminating nonsymbolic numerosities via mental representation of magnitudes—the approximate number system (ANS). There are two models of the ANS system, which are similar in their prediction in numerosity discrimination tasks. The log-Gaussian model, which assumes numerosities are represented on a compressed logarithmic scale, and the scalar variability model, which assumes numerosities are represented on a linear scale. In the first experiment of this paper, we contrasted these models using averaging of numerosities. We examined whether participants generate a compressed mean (i.e., geometric mean) or a linear mean when averaging two numerosities. Our results demonstrated that half of the participants are linear and half are compressed; however, in general, the compression is milder than a logarithmic compression. In Experiments 2 and 3, we examined averaging of numerosities in sequences larger than two. We found that averaging precision increases with sequence length. These results are in line with previous findings, suggesting a mechanism in which the estimate is generated by population averaging of the responses each stimulus generates on the numerosity representation.

Research over the past two decades has converged on the idea that humans (including infants) and animals have at their disposal a set of analog numerosity (or magnitude) representations, which allows them to estimate and discriminate the numerosity of large sets of items (e.g., dots in a visual display or rapid sequences of sound clicks) without counting (Barth, Kanwisher, & Spelke, 2003; Dehaene, Dehaene-Lambertz, & Cohen, 1998; Feigenson, Dehaene, & Spelke, 2004; Gallistel & Gelman, 2000; Katzin, Salti, & Henik, 2018; Leibovich & Henik, 2014; Nieder, Freedman, & Miller, 2002; Nieder & Miller, 2003; Piazza, Pinel, Le Bihan, & Dehaene, 2007; Whalen, Gallistel, & Gelman, 1999). These numerosity representations, also labeled as the approximate number system (ANS), are akin to a “number line,” which is thought to be mediated by broadly tuned numerosity detectors in the parietal cortex (Nieder et al., 2002; Nieder & Miller, 2003). The ANS representations account for data showing that humans (including infants) and animals are characterized by a Weber fraction in numerosity discrimination and estimation tasks (Barth et al., 2003; Cordes, Gelman, Gallistel, & Whalen, 2001; Whalen et al., 1999). Moreover, it has been suggested that the ANS representations are, at least partially, involved in the processing of symbolic numbers, as indicated by well-known distance and magnitude effects (Dehaene, Dupoux, & Mehler, 1990; Moyer & Landauer, 1967).

There are at present two versions of the ANS systems, which are roughly equivalent in terms of their prediction in numerosity discrimination tasks. The first is the log-Gaussian model, which assumes that the location of the number representation on the mental-line continuum is logarithmically compressed with a fixed variability (Dehaene, 2007; Feigenson et al., 2004). The second is the scalar variability model, which assumes that the representation of numerosities is linear (noncompressed) on the mental line, with regards to both its mean and its variability (Gallistel & Gelman, 2000), resulting in similar Weber-type predictions (Dehaene, 2007). Some extra support for the log-Gaussian model comes from the mapping of numbers onto space (or a number line), which typically indicate compression (10 and 20 are more separated than 80 and 90 on the number line), especially for young children (Booth & Siegler, 2006; Siegler & Booth, 2004; Siegler & Opfer, 2003) or for adults under attentional load (Anobile, Cicchini, & Burr, 2012). However, the scalar variability model can also account for this compression under the assumption that participants rely on the central tendency principle (a type of regression to the mean), which affects larger numbers more than small numbers due to their increased encoding variability (Anobile et al., 2012).

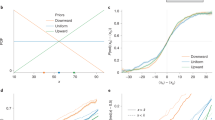
While most of the numerosity research has relied on estimation, discrimination, or comparison (same–different) tasks, some research has also targeted arithmetic operations, like addition and subtraction (Barth et al., 2006; Barth, La Mont, Lipton, & Spelke, 2005; Cordes, Gallistel, Gelman, & Latham, 2007; McCrink, Dehaene, & Dehaene-Lambertz, 2007; Pica, Lemer, Izard, & Dehaene, 2004). One area that was less explored within the ANS domain, however, is averaging. While, analytically, averaging can be viewed as being equivalent to addition (followed by division by the number of terms), there are reasons to believe that this is not the way that participants estimate the average of rapid sequences of (symbolic) numbers (Brezis, Bronfman, & Usher, 2015, 2018; Malmi & Samson, 1983; Mitrani-Rosenbaum, Glickman, & Usher, 2020), as they can provide accurate and rapid estimations of the average, even when they do not know the number of elements, or when elements in a specific range are to be discarded after the sequence presentation (Malmi & Samson, 1983). Rather, the evidence indicates that the estimation mechanism corresponds to a frequency-based estimation (the estimation of the center of mass of a noisy frequency distribution of the numbers), which is somewhat similar to the one suggested by the ANS representation system (see Brezis, Bronfman, Jacoby, Lavidor, & Usher, 2016; Brezis et al., 2015, 2018). In particular, Brezis et al. (2015, 2018) have proposed an ANS type of population code model, which accounts for a characteristic signature of the population code: Precision improves with the length of the sequence (see Fig. 1, blue line). While this is a straightforward prediction of population averaging (encoding noise in the representation of each number is averaged out), it contradicts the predictions of an analytical (and working-memory capacity limited) model, which computes via a sequential rule-based algorithm, predicting a decreasing precision with the number of terms (see Fig. 1, red line; Brezis et al., 2015). The latter is illustrated by the red line, which shows the prediction of the analytical model, which symbolically computes the average based on three random samples from a sequence of n numbers (the larger the n, the less the samples can approximate the true average).

Fig. 1

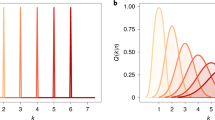
The population code model of numerical averaging. Upper panels show the ANS-based averaging that operates on a set of analog broadly tuned numerosity detectors (a). Each stimulus generates a noise response on this representation (b), illustrated here for a sequence with three stimuli (20, 50, and 80). The responses are summed (c). The average is the center of mass of the distribution (see Brezis et al., 2015, for an explicit mechanism), resulting in a precision that improves with sequence length (blue line in lower panel). An alternative symbolic-based computation results in precision that decreases with sequence length (red line). Reproduced with permission from Brezis et al. (2015). (Color figure online)

The aim of this study is to probe the estimation of sequence-average with numerosity stimuli—sets of dots. This is important for several reasons. First the estimation of the average is critical for common life activities, like decision-making, in which one has to estimate the utility of alternatives that vary across time or attributes (Betsch, Kaufmann, Lindow, Plessner, & Hoffmann, 2006; Brusovansky, Glickman, & Usher, 2018; Brusovansky, Vanunu, & Usher, 2017; Pleskac, Yu, Hopwood, & Liu, 2019; Roe, Busemeyer, & Townsend, 2001; Spitzer, Waschke, & Summerfield, 2017; Tsetsos, Chater, & Usher, 2012; Usher & McClelland, 2004; Vanunu, Pachur, & Usher, 2018; Zeigenfuse, Pleskac, & Liu, 2014). Second, recent research has indicated an impressive ability of human subjects in estimating summary statistics (in particular the average) of perceptual properties of sets of elements, such as size, orientation, and even emotional expression (Ariely, 2001; Chong & Treisman, 2005; Dakin, 2001; Haberman, Harp & Whitney, 2009; Haberman & Whitney, 2011; Khayat & Hochstein, 2018; Parkes, Lund, Angelucci, Solomon, & Morgan, 2001; Robitaille & Harris, 2011). To our knowledge, there is less research on the averaging of (nonsymbolic) numerosities. While there is research on averaging of numerical (symbolic) numbers (Brezis et al., 2015, 2018; Spitzer et al., 2017; Vandormael, Castañón, Balaguer, Li, & Summerfield, 2017), testing averaging of nonsymbolic numbers has the added bonus of excluding symbolic computations, and thus exclusively targeting the ANS system.

In testing the averaging of numerosities, we wish to focus on two central questions: (i) Can we find evidence for systematic biases, which would confirm/disconfirm the presence of a compression mechanism in the number-line representation? (i.e., will some participants show a bias towards a geometric mean, as possibly suggested by a log-Gaussian model; see next section). (ii) Does the precision of the estimate increase (decrease) with the length of the sequence? An increased precision with sequence length would indicate that the ANS system can operate not only for single (or pairs of) stimuli but also for multiple ones, and that it can contribute to the mechanism for the formation of preferences over sequences of numerical values or payoffs (Brusovansky et al., 2018; Vanunu et al., 2018; Zeigenfuse et al., 2014).

Towards this aim, we carried out three experiments. The first experiment examined the averaging of pairs of numerosity stimuli. Here, we wanted to establish whether people can perform the task, by indication their estimate on a continuous mental line, and we examined potential compressive biases (in all the experiments, we quantified individual differences). In our second and third experiments, we examined sequences that vary in length from two to eight stimuli, and we focused on the estimation precision as a function of sequence length. The two experiments vary regarding the manipulation of the sequence length (randomized in Experiment 2 and blocked in Experiment 3), and regarding the response mode (on a continuous scale in Experiment 2, and based on comparison with a probe in Experiment 3). To anticipate our results, we find that whereas almost all participants were able to make good estimations, there are compressive biases in about half of them, but (except in one participant) those were milder than logarithmic. Critically, we find that precision improves with the length of the sequence, as predicted by the population code mechanism operating on ANS representations.

Experiment 1

Computational predictions and design motivation

Whereas the log-Gaussian and the scalar-variability models make similar predictions in discrimination tasks, they can potentially be distinguished in averaging. Figure 2 illustrates how this can happen. The left panels illustrate two extreme models (linear scalar variability vs. logarithmic compression; see also Feigenson et al., 2004), and the right panels show the responses following a pair of 10–70 numerosity stimuli. If the average is estimated by a population averaging over the same numerosity representation, one may expect, for the logarithmic (but not the linear model), an underestimation of the average that increases with the difference between them (see values pointed by the arrows in the right panel), which is analogous to the way risk aversion is generated as a result of a compressive utility function (see Figs. 1–2 in Birnbaum, 2008). This is illustrated in Fig. 2a–b, with a simple sequence of two numerosities: 10, 70. By computing the center of mass (on the same ANS representation), we obtain the arithmetic mean (40) if the numbers are represented according to the scalar variability model, and the geometric mean (26.4) if the numbers are encoded based on the log-Gaussian model (see Fig. 2c, black and red lines, respectively, for an illustration over the range of 10–90). Interestingly, an intermediate degree of compression is obtained if the averaging in the scalar variability model is weighted by the variance of the number representation, as suggested by a combination of the scalar-variability model with a Bayesian framework that includes a prior (Anobile et al., 2012; see Appendix for computational details).

Fig. 2

a–b The left panels illustrate the representation assumptions of two ANS models: (a) the scalar varaibility model and (b) the log-gaussian model. . In both cases, we plot the neural response for a sequence of numbers 10–90 (in steps of 10); the red–blue continuum corresponds to the number magnitude. The right panels illustrate the averaging of numerosities 10 and 70 in each of the models. In both models, the average is the midpoint on the ANS, in the linear model it is the arithmetic average (40), and in the log-Gaussian model it is the geometric average (26.4). c Averaging estimation for pairs of values (x-axis) that are symmetric around the midrange (50), for the scalar-variability model in which the average is the center of mass (black line), the log-Gaussian model (red line). The blue lines correspond to a Bayesian version of the scalar-variability model, in which each value is weighted in inverse proportion to its standard deviation, and a prior for the estimate is assumed to be a Gaussian centered at the middle of the range (50) with standard deviation labeled by a (see legend). (Color figure online)

To test the sensitivity of the average estimate to the difference between the numerosities, we designed the stimuli to systematically manipulate the difference between the pairs of stimuli. This is illustrated in Fig. 3a, which illustrates the predictions for extreme ANS representation models (linear [black] and a logarithmic [red]; in the latter, we assumed that the estimation would correspond to the geometric mean) for pairs of numbers in the range 5–85 (each bin has a width of 10). As one can see, the difference is small close to the diagonal (when the numbers are similar), but increases with the difference of the pair (larger difference for bins 1–8; bottom left corner). In Fig. 3b, we illustrate how the difference between the linear and the geometric average depends on the relative difference.

Fig. 3

a The linear (black) and geometric (red) average of the various numerical bin pairs. The bins close to the diagonals were not sampled, as the difference between the averages is small (making the task too easy). b The difference between the linear and the geometric average depends on a single variable, the relative difference, RD = Delta(bins)/Sum(bins). The Spearman correlation between the RD and the delta of the averages is high (r_s = .96, p < .001). (Color figure online)

Method

Participants

Fifteen undergraduates from Tel-Aviv University (M_age = 22.4 years, SD = 1.2) participated in the experiment. Participants had normal or corrected-to-normal vision. Participants were awarded with course credit for their participation. All procedures and experimental protocols were approved by the ethics committee of the Psychology department of Tel Aviv University (Application 1-0000317). All experiments were carried out in accordance with the approved guidelines.

Apparatus and stimuli

Stimuli consisted of dots randomly scattered on the screen. The dots diameter varied from 25 to 45 pixels. Minimum distance between dots was 25 pixels. The color of the dots was light grey for the sequence arrays (RGB: 201, 201, 201) and red (RGB: 255, 0, 0) for the scale arrays. The dots appeared on a black background.

Training procedure and design

The experiment was built in OpenSesame. Before running the experiment, the participants received training with responding to a single numerosity stimulus using a continuous response scale. In order to assist them in doing so, the location of the mouse on the scale dynamically generated numerosity stimuli (in a different color from the one they estimated), which the subject could match to their mental representation of the stimulus (see Fig. 4a). In the training procedure, participants practiced the nonsymbolic number scale. Each trial began with a green fixation cross presented at the center of the screen for 1,000 ms. Next, the target, a cloud of white dots, was presented for 500 ms at the center of the screen. The numerosity of the target was between 5 and 90, in jumps of 5 (i.e., 5, 10, 15, 20, 25, . . . 90), 18 target numerosities in all. After the target, a blank black screen appeared for 500 ms. Next, a response screen appeared, in which the target was presented at the top part of the screen, and at the center the nonsymbolic number scale. When participants pointed to the scale, beneath it, a red dot cloud appeared, with the numerosity of that location on the scale. The scale ranged from 5 (left edge) to 90 (right edge) for 10 participants, and 5 (left edge) to 100 (right edge) for 5 participants.¹ In half of the trials, the starting point of the mouse was on the left edge, and in the other half, on the right edge. Participants were instructed to move the mouse until they find a red dot cloud that had the same (or as similar as possible) numerosity as the white dot cloud (participants were allowed and encouraged to move the mouse until they were satisfied of the match). Once participants clicked with the mouse, the trial ended and a new trial began. Each target numerosity appeared four times, 72 trials in all (see Fig. 4a).

Fig. 4

Examples of a trial in the training procedure (a) and in the averaging experiment (b)

Averaging experiment procedure and design

As illustrated in Fig. 4b, each trial began with a white fixation cross presented at the center of the screen for 1,000 ms. After the fixation, two white dot clouds appeared, one after the other, each for 500 ms, with a blank interstimulus interval screen for 500 ms between them. After the stimuli, the response screen appeared. The response screen included a nonsymbolic number scale, which was the same as in the training procedure. Participants were instructed to move the mouse on the response scale until the red dot cloud matched the average numerosity of the stimuli. The numerosities of the stimuli were sampled from eight bins of 10 between 6 and 85 (i.e., Bin 1 = 6–15; Bin 2 = 16–25, . . . ,Bin 8 = 76–85; see Fig. 3a). In each trial, two bins with a distance (∆) of at least two were sampled, corresponding to the area that is inside the encircled perimeter in Fig. 3a. For example, stimuli could include bins (1, 3), (1, 4), (2, 4); 21 combinations of bins in all. The experiment started with a practice block of 10 trials. Then, there were five experimental blocks with two repetitions of each bin combination, 210 trials in all, 42 trials per block.

Results

Training data analysis

For each participant, we plotted the response (averaging across trials with the same stimulus) as a function of the stimulus numerosity. In Fig. 5 we show the response of each participant (averaged over trials) as a function of the stimulus numerosity. As one can see, the participants are able to use the continuous scale to indicate their impression of the stimulus numerosity (Pearson correlations for each participant between the presented numerosity and the participant’s response was high. r = .97 SD = .02). The fitted linear slope was on average b = .71 (SD = .1).

Fig. 5

Correlation between presented numerosity and participant’s response for all participants (participants are ordered based on their sensitivity to the difference between the numerosity; see Fig. 7)

The purpose of the training task was twofold. First, we wanted participants to become familiar with the nonsymbolic number scale. Second, it enabled us to calibrate participants’ responses. Accordingly, we performed a regression analysis with the presented numerosity as the dependent variable, and participant’s response as the independent variable. We examined which fit was better: linear (y = b × x + a) or power (y = b × x^α) fit. Both AIC and BIC parameters were lower for the power fit: AIC, t(14) = −5.55, p < .001; BIC t(14) = −5.55, p < .001; see Table S1 in the Supplementary Materials), with a compression exponent (average α = .82, SD = .09. The lowest α was .68, and four participants had an α larger than .9). This indicates that despite the presence of the red stimulus, there was a small tendency to underestimate the numerosities.² Based on this calibration, we can transform each response, y, into the experienced stimuli (x) by inverting the y(x) function. The analysis in the main averaging experiment were carried out both with and without this calibration.

Averaging experiment data analysis

Analyses were performed both with participants’ raw responses and with their responses scaled according to the fit found in the training procedure. Results were similar for both, so here we report the results with the raw responses.

To see how the estimates vary along the x1–x2 continuum, we carried out a regression, in which we predicted the response based on three predictors: (i) the arithmetic average (x1 + x2) / 2, (ii) the difference |x1 –x2| (this corresponds to 10 × the ∆ of the bins), and (iii) a subject-dependent intercept. The second predictor allows us to test the presence of a compression in the representation of the numerosities. As illustrated in Fig. 3, the linear average is not affected by the ∆ of the bins. For example, in Fig. 3a, the ∆ of pairs of bins 8–1, 7–2, 6–3 , are 7, 5, and 3, respectively. While the ∆ for these cells varies, their linear averages are all equal (46). An average based on compressed representations predicts that the estimate decreases with the ∆ of the bins. For all participants, the linear average was a significant predictor (average b = .57, ps < .001), as illustrated in Fig. 6.

Fig. 6

Participants’ response as a function of the linear average of the stimuli presented. The blue line is the regression line, the red lines are the confidence interval, and the dashed black line is the identity line. Values in each panel correspond to the regression coefficient of the linear average. *p < .05. **p < .01. ***p < .001; participants are ordered as in Figs. 5 and 7. (Color figure online)

The delta variable, on the other hand, was only significant for seven participants (average b = −.14, all ps < .05). For the other eight participants, the delta coefficient was not significant (average b = −.01, all ps = ns; see Fig. 7).

Fig. 7

Participants’ response by the delta of bins; vertical lines are within-subject standard error. Participants are ordered by delta coefficient. Values in each panel correspond to the regression coefficient of delta(x). *p < .05. **p < .01. ***p < .001

Next, we contrasted the linear and the logarithmic representations regarding their expected response biases. If a participant relies on linear (noncompressed) numerosity representations, the deviation between the estimate and the arithmetic average should not correlate with the relative difference; however, the deviation between the estimate and the geometric average should correlate with the relative difference. The converse should happen if a participant relies on logarithmically compressed representations. For each participant, we compared two correlations: (i) The correlation between the relative difference and the linear average minus the subject’s estimate, and (ii) the correlation between the relative difference and subject’s estimate minus the geometric average.

For all participants except one, we found a stronger positive correlation between RD and their response minus the geometric average (mean r = .52, SD = .12, all ps < .001), compared with the correlation between their response minus the linear average (mean r = −.19, SD = .13), suggesting that their responses are more linear than geometric. Only one participant displayed a geometric-average pattern (Subject 2 in Fig. 7, top row, second panel from the left), a more positive correlation with the linear average minus the response (r = .22, p < .001, compared with r = .09), suggesting this participant is more geometric than linear. This participant also displayed a compressed pattern in the previous analysis. The rest of the participants that displayed a compressed pattern in the previous analysis were more linear than geometric in this analysis, suggesting that their compression is not as strong as a logarithmic compression.

Discussion

We examined the ability of participants to estimate the average of two numerosity stimuli by moving a mouse on a continuous response line. To facilitate the participants with the use of the scale, they first received training with single stimuli. In addition, the location of the mouse on the scale dynamically created a numerosity stimuli (in a different color; see Fig. 4), which the participant can compare with their mental estimate. For all the participants, the average estimates increase with the average of the stimuli pair; however, we also observe a (lower than 1) slope indicating the presence of regression to the mean (see Fig. 6). Since the task is not easy, the presence of regression to the mean is a normative way to deal with uncertainty (Anobile et al., 2012; Jazayeri & Shadlen, 2010). The results demonstrate that averaging is an operation that participants are able to carry out with a pair of numerosity stimuli.

The central question of this study was whether there are systematic deviations from the linear average, which are induced by the compression of the ANS representation. To examine this, we examined the dependency of the estimate on the difference between the two numerosities. For about half of the participants, such a dependency was found: The estimate decreased with the difference when the average was controlled for (akin to the phenomenon of risk aversion that would make a person prefer a lottery of 40 with p = .5, 60 with p = .5, to one of 10 with p = .5, 90 with p = .5. For the other half of the participants, the estimates were quite flat (with the difference) supporting noncompressed numerosity representations (those results were obtained using the raw data, but the results are similar if we use transformed values based on the training calibrations). When contrasting between the linear and logarithmic compression, in particular, we found that only one participant for which the estimates were closer to the geometric (than linear) average. This indicates that the compression that we have in the other subjects is milder than logarithmic. While we focused here on a binary contrast between the log-Gaussian and the linear (scalar variability) representation of numerosities, this binary (compression/no-compression) contrast is a simplification. As we have shown in Fig. 2c (blue lines), a milder compression can be obtained if, as previously suggested by Anobile et al. (2012), for the case of the number-line estimation of single numerosity stimuli, the participants (in our case with two stimuli) weight up the values of the two samples and the prior, based on their relative representational uncertainty. As the uncertainty is larger for the higher numerosity, it results in a milder compression effect (see Fig. 2c, blue lines) whose magnitude depends on the prior-variance parameter. Thus, differences in how the representational uncertainty increases with numerosity can account for the compression variability in our task.

Experiment 2

The aim of the next two experiments is twofold. First, we wanted to expand the task from pairs of stimuli to longer sequences: two, four, or eight. Second, we aimed to test the ANS population-coding prediction that the precision should improve with sequence length. In these experiments, we did not manipulate the variance of the sequences, so our focus is not on compression biases, but rather on how the precision of the estimate varies with the length of the sequence. We do examine, however, another type of bias: temporal biases (do people give more weight to recent or earlier stimuli?).

Method

Participants

Twenty undergraduates from Tel-Aviv University (M_age = 23.15, SD = 2.35) participated in the experiment. Participants had normal or corrected-to-normal vision. Participants were awarded with course credit for their participation. All procedures and experimental protocols were approved by the ethics committee of the Psychology department of Tel Aviv University (Application 1-0000317). All experiments were carried out in accordance with the approved guidelines.

Apparatus and stimuli

Stimuli consisted of dots randomly scattered on the screen. The dots diameter varied from 25 to 45 pixels. Minimum distance between dots was 25 pixels. The color of the dots was light grey for the sequence arrays (RGB: 201, 201, 201) and red for the scale (RGB: 255, 0, 0) for the probes. The dots appeared on a black background.

Training procedure and design

The experiment was built in MATLAB R2015. This procedure was similar to the training procedure in Experiment 1, except that the starting point of the mouse was the middle of the scale.

Averaging experiment procedure and design

Each trial began with a white fixation cross presented at the center of the screen for 250 ms. After the fixation, a sequence of two, four, or eight dot clouds appeared one after the other, each for 500 ms. Once the sequence terminated, the participants were instructed to estimate the sequence’s mean value by choosing a red dot cloud on the nonsymbolic number scale that represents the mean (see Fig. 8). Sequence length was randomized. The sequences were randomly drawn from three uniform distributions with a range of 30 and means 35, 50, and 65. Participants underwent 306 experimental trials divided into six blocks. Accordingly, there were 102 trials for each sequence length (two, four, eight), and within each sequence length 34 trials for each average (35, 50, 65).

Fig. 8

An example of a trial in Experiment 2

Results

Training procedure

To verify that participants were correctly performing the task, we calculated Pearson correlations for each participant between the presented numerosity and the participant’s response. The average correlation was very high (r = .97, SD = .03). Like Experiment 1, we performed a regression analysis, with the presented numerosity as the dependent variable and participant’s response as the independent variable. We examined which fit was better: linear (y = b × x + a) or power (y = b × x^ α). Both AIC and BIC parameters were lower for the power fit: AIC, t(19) = −3.37, p < .01; BIC, t(19) = −3.37, p < .01; see Table S3 in the Supplementary Materials). The average α was 0.96 (SD = .11).

Averaging experiment

All analyses were performed both with participants’ raw responses, and with their responses scaled according to the fit found in the training procedure. Results were similar for both, so here we report the results with the raw responses.

Averaging precision

We quantified participants averaging precision using two measures. First, we calculated the Pearson correlation between the real and estimated averages of the sequences. The average Pearson correlation was high (r = .66, SD = 0.12) and was significantly higher than zero (all ps < .001; see Fig. 9a for an individual participant). Second, we computed the root mean square deviation (RMSD) between the real averages and the participants’ responses (note that higher values of RMSD imply lower accuracy). The RMSD was significantly lower than the simulated RMSD generated by randomly shuffling participant’s responses across trials (RMSD = 11.92; shuffled RMSD = 22.18), t(19) = −21.78, p < .001.

Fig. 9

a A typical individual participant’s scatter plot of evaluated mean versus sequence average, r = .67; see Supplementary Materials for the data of all participants. b RMSD as a function of sequence length. The grey lines mark individual participants; the black line is the average

A repeated-measures ANOVA, with RMSD as the dependent variable and sequence length as the independent variable, was carried out. As illustrated in Fig. 9b, the main effect of sequence length was significant, F(2, 38) = 48.28, p < .001, η_p²=.71. Further analysis revealed a significant linear trend, t(38) = −9.83, p < .001. A repeated-measures ANOVA, with RTs as the dependent variable and sequence length as the independent variable, was also carried out. The main effect of sequence length was not significant, F(2, 38) < 1, p = ns), indicating that this improvement is not the result of a speed–accuracy trade-off.

Regression to the mean and temporal biases

To estimate these biases, we predicted the estimates based on two models. We compared a model without a temporal bias and a model with a temporal bias. In both models, we included the possibility of regression to the mean (corresponding to a slope parameter, b) and a subject dependent intercept, a. In the nontemporal bias model, we carried out a linear regression, with participant’s response as the dependent variable and the real average of the sequence as the independent variable:

$$ \hat{y}=a+b\ \left( sequence\ average\right). $$

(1)

For the temporal bias model, we regressed the participant’s response on the leaky integrated value with a leak parameter (λ > 1 indicates a primacy effect, λ < 1 indicates a recency effect, and λ = 1 means no temporal bias):

$$ \hat{y}=a+b\ {\sum}_{i=1}^n{x}_i\ast {\lambda}^{n-i}. $$

(2)

As shown in Table 1, the participants varied in their temporal bias. For five participants, a model without a temporal bias is better in both AIC and BIC measures. Indeed, the average lambda of these participants in the temporal bias model is 1.03. For six participants, a temporal bias model is better in both AIC and BIC measures, and their average lambda is 0.73. The rest of the participants (10 out of 15) have an average lambda of 0.83. In all these participants, the leak improves the log-likelihood of the fit. In nine of them, the complexity costs given by the AIC and BIC are inconsistent regarding the model selection, while in the last six, both the AIC and the BIC select the leaky integration as the best model.

Table 1 Parameters for linear and temporal bias fit

Discussion

We have shown that the ability to estimate the average of numerosity sequences extends to longer sequences in the range of two to eight. While this estimation is not perfect (and subject to a regression to the mean bias), one needs to keep in mind that the estimation of numerosity stimuli is noisy even with single stimuli. The important result is that the precision of the estimates improves with the length of the sequence. This could not happen if the participants form the estimates on the basis of few samples, say subject to WM capacity limitations (2-4). Instead, the results are consistent with a population code model, in which the responses to each stimuli is aggregated on the numerosity representation, and the estimate is obtained via a population code that estimates the center of mass (Brezis et al., 2018). In some of the participants, we also found small temporal biases. These subjects gave slightly more weight to more recent stimuli in the sequence.

Experiment 3

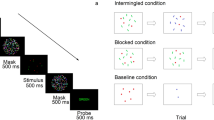
The aim of our final experiment is to replicate the results of Experiment 2, under two important modifications. First the most relevant variable, sequence length, is now blocked rather than randomized. This allows the participants to select the most optimal strategy for each sequence length and reduces task uncertainty. Second, we set out to use here a more conventional method of estimation. Instead of indicating the estimate on a continuous scale, here, the sequence is followed by a probe (in a different color), and the task is to decide whether this probe has a higher (lower) numerosity than the average of the sequence. Another difference (which was not planned) was imposed on us by the COVID-19 restrictions. Due to these restrictions, this experiment was conducted online and not in a laboratory setting.

Method

Participants

Twenty three undergraduates from Tel-Aviv University (M_age = 23.65, SD = 1.85) participated in the experiment. The experiment was carried out online. Importantly, the participants were from the same pool as the participants in the two previous experiments—psychology students from Tel Aviv University. Participants had normal or corrected-to-normal vision. Participants were awarded course credit for their participation. All procedures and experimental protocols were approved by the ethics committee of the Psychology department of Tel Aviv University (Application 1-0000317). All experiments were carried out in accordance with the approved guidelines.

Apparatus and stimuli

The stimuli consisted of dots randomly scattered on the screen. The dots diameter varied from 25 to 45 pixels. Minimum distance between dots was 25 pixels. The color of the dots was either light grey for the sequence array (RGB: 201, 201, 201) and yellow for target arrays (RGB: 255, 255, 0). The dots appeared on a black background.

Procedure and design

Due to COVID-19 limitations, the experiment was conducted online and not in a laboratory setting. The experiment was built on PsychoPy Builder v3 and ran via Pavlovia. Each trial began with a white fixation cross presented on a black screen for 1,000 ms. The fixation was followed by a sequence of dot clouds. Each presented in the middle of the screen for 500 ms. At the end of the sequence, there was a black screen for 500 ms, followed by the target stimulus. Participants were instructed to decide whether the target stimulus, a yellow dot cloud, was bigger or smaller than the average of the sequence using the keyboard (f key for smaller, j key for bigger). After each response, participants received feedback, a green v for correct answers and red x for wrong answers (see Fig. 10). As in Experiment 2, sequences were randomly drawn from three uniform distributions with a range of 30 and means of 35, 50, and 65. Unlike Experiment 2, sequence length was blocked, resulting in six blocks, two for each sequence length. The order of the blocks was fixed: 2, 4, 8, 2, 4, 8. Participants were informed about the sequence length before each block. The proportions of the target stimuli to the average of the sequence were 0.71, 0.77, 0.83, 0.91, 1.1, 1.2, 1.3, 1.4 (first four values are the reciprocal of the last four). Each proportion appeared seven times for each average and sequence length, 504 trials in all. The experiment began with a short practice block with 12 trials with a sequence length of two.

Fig. 10

Example of a trial in Experiment 3

Results

Participants’ overall accuracy was 74%, SD = .06 (one participant’s performance, while higher than chance, appeared as a low performance outlier, accuracy = .58. Removing this participant from the analysis does not affect any of the results). We computed a psychometric curve for each participant. The slope of the psychometric curve is another indication of accuracy; a steeper slope represents more accurate responses (see Fig. 11a, for example). We compared the slope of the three sequence lengths: n = 2 (mean = 5.12, SD = 2.14), n = 4 (mean = 5.6, SD = 1.5), and n = 8 (mean = 6.16, SD = 1.54) with a repeated-measures ANOVA. We found a significant main effect, F(2, 44) = 6.21, p < .005, η_p² = .22. Further analysis revealed a significant linear trend. t(44) = 3.52, p < .005 (see Fig. 11b). In a similar analysis of RT’s of sequence lengths, we did not find a significant effect (F(2,44)<1).

Fig. 11

a Psychometric curve of an individual participant, for each sequence length. b Slope of psychometric curve per sequence length. The grey lines mark individual participants. The black line is the average

Temporal bias

We compared between a model without a temporal bias and a model with a temporal bias of averaging. For the non-temporal bias model we computed a logistic regression with accuracy as the dependent variable and the delta between the target and the average of the sequence as the independent (predicting) variable.

$$ logit\Big(\hat{y\Big)}=a+b\left( target-\overline{x}\right). $$

(3)

For the temporal bias model we computed a logistic regression based on Eq. 4 where: λ > 1 indicates a primacy effect, λ < 1 indicates a recency effect, and λ = 1 means no temporal bias, and n is the sequence length.

$$ logit\Big(\hat{y\Big)}=a+b\left(\left( target-{x}_1\right)\ast {\lambda}^{n-1}+\left( target-{x}_2\right)\ast {\lambda}^{n-2}+\dots \left( target-{x}_n\right)\ast {\lambda}^{n-n}\right). $$

(4)

For 10 participants the model without a temporal bias was better (based on both AIC/BIC measures). The average λ in the temporal bias for these participants was 0.89 (SD=.13). For 10 participants the model with temporal bias was better (based on both AIC/BIC measures), their average λ was 0.75 (SD=.04). For 3 participants, the model selection is AIC/BIC ambiguous their average λ was 0.84 (SD=.04; see Table 2).

Table 2 Parameters for a model with and without a temporal bias

General discussion

In three experiments we examined the ability of human participants in a task of averaging of numerosity stimuli (sets of dots). This extends the range of operations on which numerosity representations were used from comparisons, addition or subtractions on pairs of stimuli, to the averaging of multiple stimuli – an operation that is of key importance to decision-making (Brusovansky et al., 2017; Vanunu et al., 2018; Weber, 2010). This task also extends the domain of stimuli on which the extraction of summary statistics was established, from domains such as size, orientation, emotional expression or object category (Ariely, 2001; Chong & Treisman, 2005; Dakin, 2001; Habrman et al., 2009; Haberman & Whitney, 2011; Khayat & Hochstein, 2018, 2019; Parkes et al., 2001; Robitaille & Harris, 2011) to the domain of nonsymbolic numerosities across temporal sequences.

Before discussing our results, we wish to mention a methodological dilemma that we have faced. There is an extensive debate in the numerical cognition literature, on distinguishing between the processing of number information (in dot stimuli sets) from other visual features, such as dot density, dot-size, dots-area (e.g., Gevers, Kadosh, & Gebuis, 2016; Leibovich & Henik, 2013; Leibovich, Katzin, Harel, & Henik, 2016). As this is a geometrically unsolvable problem, it is not possible to vary numerosity alone without co-varying some of the other variables. While we randomized the magnitude of the dots and their locations, in average, in our design the number was (negatively) correlated with dot-density. The problem of correlated features is thought to be more serious for comparison tasks (which of two arrays has more dots) than for estimation tasks (mapping onto a number line), as in the latter, the subject responds to numbers. While we did use a number-line type of response, we also set this up so that the participants could see, for each position of the mouse along the response line, a numerosity display corresponding to this specific location on the scale³. It may thus be possible to suggest that what the participants were doing is to move the mouse and, at each location on the scale, compare the display from memory with the one on the scale, based not on the number of dots, but rather on their density.

We believe this is unlikely for two reasons. First, unlike in the typical number line tasks, here the participants’ main challenge was to average across multiple numerosity displays and our main focus was the averaging process (rather than its mapping to the response scale). As each display varies on multiple visual features, the task of generating an average based on visual features is not any easier than that of generating an average numerosity (especially, as this is what the participants were instructed to pay attention to). Based on the idea that numerosity displays automatically activate ANS representations (Nieder et al., 2002; Nieder & Miller, 2003; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004), we reasoned that following the presentation of multiple displays, the ANS representation will contain the composite of each numerosity presented, from which a population code should generate an estimate of the average (as a center of mass; Brezis et al., 2018; see Fig. 1a–c). We believe it is less likely, that one could automatically generate a similar averaging response for a visual feature such as dot-density (unless it is derived from numerosity). If for example, the dot-density (say, the average distance between the dots) was the direct visual feature that a subject monitored, the compression curves should have been inversed. Since there is more precision at small compared to long distances, one may expect (based on a Bayesian model; Anobile et al., 2012), contrary to our results, that large numbers (small distances) will be less affected by the prior (and thus more linear) compared with the small numbers (large distances). Furthermore, the results we obtained here, mimic those obtained in tasks of numerical averaging of symbolic numbers (Brezis et al., 2018). Nevertheless, future studies should exclude the possibilities that subjects could track dot-densities (instead of numerosity in our tasks) by including trials in which the density is kept constant when the numerosity changes.

We started (Experiment 1) with short sequences of two stimuli and we used responses on a continuous scale (after participants received training with the use of the scale). We find that all the participants show responses that are highly correlated with the sequence-mean (Fig. 6), but we also see some biases. First, all subjects show a regression to the mean effect, which is normative for the case in which the subject faces uncertainty (due to, for example, encoding or attentional variability) and the stimuli are distributed on a specified range (Anobile et al., 2012; Hollingworth, 1910; Jazayeri & Shadlen, 2010). Second, we find that about half of the participants show a compressive bias, which makes them underestimate the averages of pairs as a function of their distance (i.e., they estimate the pair (10, 80) less than the pair (30, 60)), although the instruction was to estimate the "average number of dots". This compressive bias was subject to clear individual differences, with some of the subjects showing no compressive tendency whatsoever, while others showing a mild compression.

From a binary perspective, this variability (logarithmic vs. linear) in the architecture of the mental number line may seem surprising. The mental number line is considered to be a deeply rooted cognitive construct shared across species (Cantlon & Brannon, 2006). Accordingly, one might expect little individual differences. However, a close look at the literature might suggest otherwise. First, there are conflicting results, some found that the mental number line is linear (e.g., Ebersbach, Luwel, Frick, Onghena, & Verschaffel, 2008), while others reported a geometric mental number line (e.g., Dehaene, 2003) and the amount of compression appears to vary with age (Booth & Siegler, 2006; Siegler & Booth, 2004; Siegler & Opfer, 2003) or with attentional load (Anobile et al., 2012). One promising idea that can account for this variability is that it is based on the extension of the Bayesian central tendency model (Anobile et al., 2012) that is combined with the scalar-variability model with multiple samples. As we have shown in Fig. 2c, such a model can produce a range of compression effects. One attractive idea, which will require future research is that these individual differences would correlate with the risk-aversion tendencies (see Patalano et al., 2020; Peters, Slovic, Västfjäll, & Mertz, 2008; Peters et al., 2006, for similar ideas), since the task of averaging 10 and 90 dots shares much with the one of evaluating the attractiveness of a lottery that offers $10 or $90, each with probability .5.

In Experiment 2 and 3 we extended the length of the sequences from two to eight. Here we focused on how the precision of the estimate changes with the sequence-length. In Experiment 2 (using estimates on a continuous scale) we found that the estimates were highly correlated with the presented sequence average (average Pearson-r = .66; see Fig 9a, and Supplement) and in Experiment 3 (using a more traditional choice procedure), we found that accuracy increases as a sigmoidal function of the difference between the sequence-average and the target (Fig. 11a). Importantly, however, in both experiments we found that the precision increases with the length of the sequence. This is remarkable, for two reasons. First, one would naively expect that computing an average is easier for two compared with eight items. Second, this improvement indicates a pooling operation across multiple stimuli in the sequence, which exceeds the capacity of the VWM. If for example, the participants can only average over 3-4 stimuli, the precision for n=8 would be lower than that for n=4 (see red line in Fig. 1), which is opposite to what the data shows (Fig. 9b, 11b). Future, research, however, will be needed to obtain an estimate of the bounds (or inefficiency; Solomon, May & Tyler, 2016) that operate in the averaging of such numerosity sequences.

The results are consistent, however, with a mechanism in which the estimate is generated by population averaging of the response each stimuli generates on the numerosity representation. Similar results were previously obtained for the presentation of rapid sequences (rate of 2Hz) of two digit numbers (Brezis et al., 2015). In that study, however, the precision was not monotonic with sequence length (it decreased from 4 to 8, and then increased again from 8 to 16; Brezis et al., 2015, Experiment 1). Interestingly, however, the precision became monotonically decreasing (like in our present study) when the items were presented at a faster rate (10 instead of 2 Hz), or when a response deadline was introduced (for the 2Hz rate). Together with our present results this leads to a simple explanation. The mechanism of numerical-averaging with rapid sequences relies on population pooling over an ANS numerosity representation, for both numerosity and symbolic sequences, unless we present a sequence of 4 symbolic numbers and we do not impose a response deadline, which allows participants the opportunity to symbolically compute the average. The difference between numerosity and symbolic sequences, seems to be that with the former an analytic computation strategy is not available even for n=2 stimuli and thus precision improves monotonically with sequence-length.

Much research in the domain of numerosity research has looked into the brain mechanisms, indicating a parietal network of numerosity detectors (Cohen Kadosh, Cohen Kadosh, Kaas, Henik, & Goebel, 2007; Eger et al., 2009; Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003; Harvey, Klein, Petridou, & Dumoulin, 2013; Nieder & Miller, 2003; Piazza et al., 2004; Piazza et al., 2007). Most of this research has focused on comparison tasks. In one study, the brain mechanism of numerical averaging was examined via tDCS (Brezis et al., 2016), showing that anodal stimulation in the parietal brain area enhances averaging precision compared with frontal or sham-stimulation. In two more recent studies, it was shown the while processing symbolic numbers, the neural (dis)similarity in patterns of electroencephalogram activity reflected numerical distance (Luyckx, Nili, Spitzer, & Summerfield, 2019; Spitzer et al., 2017). Future research with numerosity stimuli, which de-correlate between numerosity and density is needed to further examine the brain mechanism of numerical averaging. Such research could also examine whether one can decode the response to a sequence-average from the brain response when the subject carries out an averaging task and explore the role of the ANS network in decision-making under risk.

Appendix

Bayesian version of the scalar-variability model simulation

We simulated the Bayesian version of the scalar-variability model (see Fig. 2c) using the following equation:

$$ EstimatedAverage=\frac{w_1\ast {x}_1+{w}_2\ast {x}_2+{w}_p\ast 50}{w_1+{w}_2+{w}_p}, $$

(5)

where x₁ and x₂ are the two samples. w₁, w₂ are their decision weights, which are inversely proportional to their standard deviation in the scalar variability model (here, we assumed SD(x) = .8 × x), and w_p is weight given to the prior, chosen here as the middle of the range value (50). For Fig. 2c, we assumed that x₁ = 50 − x, x₂ = 50 + x, and we varied w_p, via the a parameter (see Fig. 2c legend).