1 Introduction

Slab-coupled microstrips (Hammer et al. 2019), when considered in a context of photonic microresonators (Chremmos et al. 2010), can exhibit rather remarkable filtering properties. In the most basic configuration, a simple dielectric strip, positioned at some distance above a slab waveguide, is evanescently excited, at oblique angles of incidence, by the semi-guided waves supported by the slab. Narrow transmission resonances can be observed; the essentially lossless system is characterized by a Q-factor factor that grows exponentially with the gap between slab and strip, accompanied by a strong enhancement of the field in the cavity strip. Similar effects have been predicted for filter configurations that involve two bus waveguides, and one or two potentially coupled microstrip cavities (Ebers et al. 2019).

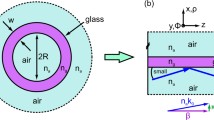
The rectangular microstrips considered previously by the authors support resonances of standing-wave type (Manolatou et al. 1999), as opposed to the traveling-wave resonances of ring- or disk-shaped optical microresonators (Hiremath and Hammer 2010). One might thus be interested in what happens if one replaces the former rectangular strip cavity by a hollow-core optical fiber, a dielectric “tube”, with circular cross section. Figure 1 shows a respective configuration.

Fig. 1
figure 1

Oblique evanescent excitation of a dielectric tube, schematic (a), and cross section view (b). Cartesian coordinates x, y, z are oriented such that x is normal to the slab plane, while y is parallel to the tube axis; polar coordinates r, \(\phi\) are positioned at the tube center. The incoming TE-polarized semi-guided wave propagates in the y-z-plane at an angle \(\theta\) with respect to the tube axis normal. Outgoing waves with reflectance R and transmittance T are observed under potentially different angles. Parameters: refractive indices \(n_{{g}} = 1.5\) (guiding regions), \(n_{{b}} = 1.0\) (background), slab and tube wall thicknesses \(d=0.4\,\upmu \hbox {m}\), tube radius \(\rho =5\,\upmu \hbox {m}\) (outer rim), variable gap g. TE excitation around a vacuum wavelength \(\lambda = 1.55\,\upmu \hbox {m}\) is considered

Full size image

On the one hand, a system as in Fig. 1 can be simulated readily by numerical means, solving a scattering problem in the frequency domain, on a 2-D cross-sectional (x-z-) computational window, equipped with transparent-influx-boundary conditions, and assuming a uniform harmonic dependence of all fields on the tube-axis-coordinate (Çivitci et al. 2014; Hammer et al. 2010). Respective simulations based on the rigorous finite-element solvers of the COMSOL-Multiphysics suite (http://www.comsol.com) will serve as our reference.

On the other hand, a composite structure like the present one is typically discussed in terms of interactions between the eigenstates of its constituents. Respective approaches are mostly termed coupled mode theory (CMT) (Hall and Thompson 1993; Huang 1994). In our case the constituents are the slab modes guided by the film layer, and the guided modes supported by the dielectric tube. We apply a model based on a specific, hybrid-analytical/numerical variant of coupled mode theory (HCMT, Hammer M 2017). Our emphasis is on the theoretical background of the technique and its adaptation to the present configuration, and on the validation of the HCMT model.

Section 2 introduces briefly the specifics of this 2.5-D setting (Hammer et al. 2010) with oblique propagation of semi-guided waves. Section 3 then outlines the HCMT ansatz, and comments on implementational details as required for the present structures. Details on the basis fields and their embedding into the formalism are discussed in Sects. 3.1, 3.2. Section 4 summarizes our results for the evanescently excited dielectric tube of Fig. 1.

Evanescent excitation of the 2-D whispering gallery modes in an optical fiber via a crossed second fiber at right angle (Birks et al. 2000), and excitation of the spiral resonances in a circular fiber via an external focused beam (Poon et al. 1998), has been observed experimentally. Already for some time there is interest in light waves that carry orbital angular momentum (Allen et al. 1992; Yao and Padgett 2011; Willner et al. 2015), and thus exhibit optical vortices (Wang 2016), either as free-space beams or as modes in circular optical fibers. Among the methods to generate these are spiral phase plates (Oemrawsingh et al. 2004), specific lens arrangements (Beijersbergen et al. 1993), spatial light modulators (Zhu and Wang 2015), further a series of grating/metasurface-based devices, but also specially designed and steered fiber couplers (Yan et al. 2011). As we shall see in this paper, also the present scheme with resonant oblique evanescent excitation should, in principle, be applicable to the generation of high-intensity waves with large orbital angular momentum, directly in the fiber tube, respectively.

2 Oblique propagation of semi-guided waves

The present work is to be seen in a context of high-contrast 2.5-D integrated optics (Hammer et al. 2010), where the specific features related to the oblique excitation of infinite structures, with two-dimensional cross sections, are exploited. Apart from the former microstrip-resonators, the list of proposals includes step- and corner-folds in slab waveguides (Hammer et al. 2015, 2016; Ebers et al. 2018), an anti-reflection-coating of a slab waveguide transition (Hammer et al. 2019), and configurations that realize filter functions related to bound states in the continuum (BIC states) in a waveguide photonics setting (Bezus et al. 2018a, b; Bykov et al. 2020).

We discuss the slab-coupled tube of Fig. 1 along a line of arguments from references Hammer et al. (2010, (2016), Hammer (2015). The central domain of interest, including the tube and the region of the slab waveguide underneath, connects to half-infinite slab regions that carry incoming and potentially reflected waves (\(z<0\)), and transmitted waves (\(z>0\)), in the form of both TE- and TM-polarized guided slab modes.

Time harmonic fields \(\sim \exp (\mathrm {i}\,\omega t)\) are considered, with angular frequency \(\omega = k{\mathrm{c}}= 2\pi {\mathrm{c}}/\lambda\), for vacuum wavelength \(\lambda\), wavenumber k and speed of light \({\mathrm{c}}\). Restricting the input to TE polarization, the incoming field can be assumed to be a TE polarized guided mode with vectorial profile \(\varvec{\displaystyle {\Psi }}_{{TE}}(k_y; x)\) and effective mode index \(N_{{TE}}\) [cf. references Biehlig and Langbein (1990), Hammer (2015)], propagating at angle \(\theta\) in the y-z-plane (cf. Fig. 1a). The input wave is thus of the form

$$\begin{aligned} \sim \varvec{\displaystyle {\Psi }}_{{TE}}(k_y; x)\, \exp (-\mathrm {i}\, (k_y y + k_z z)), \qquad \text{ with }\qquad k_y = k N_{{TE}} \sin \theta , \end{aligned}$$
(1)

\(k_z = k N_{{TE}} \cos \theta\), and \(k_y^2 + k_z^2 = k^2N_{{TE}}^2\). Since the entire problem is constant along the y-axis, the total solution can be restricted to the single spatial Fourier component \(k_y\) of the incident wave, where the angle of incidence \(\theta\) determines the wavenumber \(k_y\) according to Eq. (1).

Next we select some outgoing wave in modal form with profile \(\varvec{\displaystyle {\Psi }}_{{out}}\) and effective index \(N_{{out}}\). This can be a guided TE- or TM-mode of the slab, propagating either in the positive (\(\zeta = z\)) or negative (\(\zeta = -z\)) direction z, or some non-guided, radiated wave leaving the region of interest in some direction \(\zeta\) in the x–z-plane. Analogously to Eq. (1), one can assume a functional dependence

$$\begin{aligned} \sim \varvec{\displaystyle {\Psi }}_{{out}}(k_y; \xi )\, \exp (-\mathrm {i}\, (k_y y + k_{\zeta } \zeta )), \end{aligned}$$
(2)

for that particular outgoing wave, where the wave equation (Hammer 2015) requires that the relation

$$\begin{aligned} k^2 N_{{out}}^2 = k_y^2 + k_{\zeta }^2 \end{aligned}$$
(3)

holds for the cross-sectional wavenumber \(k_{\zeta }\). Here \(\xi\) is the cross-sectional coordinate of the 1-D mode profile in the direction perpendicular to the propagation \(\zeta\). The angle of incidence \(\theta\) determines, through Eq. (3), the propagation character of that particular outgoing mode. One needs to distinguish two cases:

For a sufficiently large effective mode index \(N_{{out}}\) with \(k^2N_{{out}}^2 > k_y^2\) and real \(k_{\zeta }\), the outgoing field propagates at an angle \(\theta _{{out}}\) with wavenumber \(k_\zeta = kN_{{out}} \cos \theta _{{out}}\). The effective indices of the incoming and outgoing waves, and the angles of incidence and refraction, satisfy a form of Snell’s law:

$$\begin{aligned} N_{{out}}\sin \theta _{{out}} = N_{{in}}\sin \theta . \end{aligned}$$
(4)

Different outgoing waves are thus observed at potentially different angles \(\theta _{{out}}\).

In case of modes with smaller effective index \(N_{{out}}\), however, with \(k^2N_{{out}}^2 < k_y^2\), the outgoing modes become evanescent with an imaginary wavenumber \(k_\zeta = -\mathrm {i}\, \sqrt{k_y^2 - k^2N_{{out}}^2}\). The waves decay with growing distance \(\zeta\). While they may well contribute significantly to the overall field in the central region of interest, these evanescent outgoing fields do not carry any optical power (Lohmeyer and Stoffer 2001).

Consequently, for an outgoing mode with effective index \(N_{{out}} < N_{{in}}\), one can define a characteristic angle

$$\begin{aligned} \sin \theta _{{cr}} = N_{{out}}/N_{{TE}} \end{aligned}$$
(5)

at which the type of the outgoing mode changes from \(\zeta\)-propagating (\(\theta < \theta _{{cr}}\)) to \(\zeta\)-evanescent (\(\theta > \theta _{{cr}}\)).

Specifically for the device of Fig. 1 one can draw the following conclusions. The effective indices of all outgoing radiative modes, with oscillatory behavior in the cladding regions (“cladding modes”), are below the upper limit \(n_{{b}}\) of the radiation continuum. The respective characteristic angles (5) are smaller than the critical angle \(\theta _{{b}}\), defined by \(\sin \theta _{{b}} = n_{{b}}/N_{{TE}}\), associated with the background refractive index. Consequently, all radiation losses vanish for incidence at angles \(\theta > \theta _{{b}}\).

Further, any outgoing TM polarized waves have effective indices below the level \(N_{{TM}}\) of the fundamental TM mode of the slab. Their characteristic angles (5) are thus smaller than the critical angle \(\theta _{{TM}}\), defined by \(\sin \theta _{{TM}} = N_{{TM}}/N_{{TE}}\), associated with the fundamental TM wave. Hence, for incidence at angles \(\theta > \theta _{{TM}}\), all incident optical power is carried away by outgoing guided TE modes.

3 Hybrid analytical/numerical coupled mode theory

As a step beyond the former fundamental considerations, we now discuss a coupled-mode model for the structure of Fig. 1. An overview of this hybrid variant (HCMT) of coupled mode theory can be found in Hammer M (2017). Using methods from finite-element numerics, the optical properties of a circuit are approximated by superpositions of—here analytic—eigen-solutions for its constituents, leading to quantitative, low-dimensional, and interpretable models in the frequency domain. The next section gives an outline of the theory; for further implementational details we refer to Hammer (2007). The approach has been applied successfully to a series of microresonator circuits, in a conventional scalar 2-D setting (Hammer 2010; Franchimon et al. 2013), as well as to a few configurations in 3-D (Hammer et al. 2017), then as a fully vectorial formulation. Adjustments as required for the present 2.5-D setting are detailed in this section.

We start with the Maxwell curl equations in the frequency domain, for the time harmonic optical electric field \(\varvec{\displaystyle \mathcal {E}}\) and magnetic field \(\varvec{\displaystyle \mathcal {H}}\), with vacuum permittivity \(\epsilon _0\) and permeability \(\mu _0\):

$$\begin{aligned} \varvec{\displaystyle {\nabla }}\times \varvec{\displaystyle \mathcal {H}} - \mathrm {i}\, \omega \epsilon _0 \epsilon \varvec{\displaystyle \mathcal {E}} = 0, \quad -\varvec{\displaystyle {\nabla }}\times \varvec{\displaystyle \mathcal {E}} - \mathrm {i}\, \omega \mu _0 \varvec{\displaystyle \mathcal {H}} = 0. \end{aligned}$$
(6)

For linear, isotropic, and nonmagnetic dielectric media, the optical properties are given by the spatially dependent relative permittivity \(\epsilon = n^2\), or refractive index n, respectively.

We seek solutions of Eq. (6) for the given incoming field (1). As detailed in Sect. 2, the entire optical electromagnetic field shares the y-dependence \(\sim \exp (-\mathrm {i}\, k_y y)\). \(\varvec{\displaystyle \mathcal {E}}\) and \(\varvec{\displaystyle \mathcal {H}}\) are thus of the form

$$\begin{aligned} \varvec{\displaystyle \mathcal {E}}(x, y, z) = \varvec{\displaystyle {E}}(x, z)\,\exp (-\mathrm {i}\, k_y y), \quad \varvec{\displaystyle \mathcal {H}}(x, y, z) = \varvec{\displaystyle {H}}(x, z)\,\exp (-\mathrm {i}\, k_y y). \end{aligned}$$
(7)

Equation (6) can be reformulated for the 2-D cross-sectional fields \(\varvec{\displaystyle {E}}\), \(\varvec{\displaystyle {H}}\) as

$$\begin{aligned} \mathsf{{C}}\varvec{\displaystyle {H}} - \mathrm {i}\, \omega \epsilon _0 \epsilon \varvec{\displaystyle {E}} = 0, \quad -\mathsf{{C}}\varvec{\displaystyle {E}} - \mathrm {i}\, \omega \mu _0 \varvec{\displaystyle {H}} = 0, \quad \text{ with } \quad \mathsf{{C}} = \left( \begin{array}{ccc} 0 &{} -\partial _z &{} -\mathrm {i}\, k_y \\ \partial _z &{} 0 &{} -\partial _x \\ \mathrm {i}\, k_y &{} \partial _x &{} 0 \end{array} \right) . \end{aligned}$$
(8)

Next our HCMT model requires a physically plausible ansatz, a “template”, for the (approximate) optical electromagnetic field. Separate contributions are specified for the slab waveguide and for the dielectric tube, respectively.

3.1 TE and TM slab modes at oblique angles

Without the tube, the structure of Fig. 1 is distinguished by a y- and z-constant permittivity. Solutions of Eq. (6) (or, more specifically, of Eq. 17) that depend on y as \(\sim \exp (-\mathrm {i}\, k_y y)\) are given by pairs \(\psi\), \(\beta\) of eigenfunctions and -values, which solve the TE- and TM mode equations associated with the permittivity profile \({\bar{\epsilon }}(x)\) of the slab. The corresponding vectorial cross-sectional fields can be stated in the form Hammer (2015)

$$\begin{aligned}&\text{(TE) }\qquad \partial _x^2 \psi + \left( k^2{\bar{\epsilon }} - \beta ^2\right) \psi = 0, \end{aligned}$$
(9)
$$\begin{aligned}&\bar{\varvec{\displaystyle {E}}}(x, z) = \left( \!\!\begin{array}{c} 0 \\ k_z \psi (x) / \beta ^2 \\ -k_y \psi (x) / \beta ^2 \end{array}\!\!\right) \!\!\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, k_z z}},\qquad \bar{\varvec{\displaystyle {H}}}(x, z) = \frac{1}{\omega \mu _0}\!\left( \!\!\begin{array}{c} -\psi (x) \\ \mathrm {i}\, k_y\partial _x\psi (x)/\beta ^2 \\ \mathrm {i}\, k_z\partial _x\psi (x)/\beta ^2 \end{array}\!\!\right) \!\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, k_z z}}, \end{aligned}$$
(10)

and

$$\begin{aligned}&\text{(TM) }\qquad {\bar{\epsilon }} \partial _x \frac{1}{{\bar{\epsilon }}} \partial _x \psi + \left( k^2{\bar{\epsilon }} - \beta ^2\right) \psi = 0, \end{aligned}$$
(11)
$$\begin{aligned}&\bar{\varvec{\displaystyle {E}}}(x, z) = \frac{1}{\omega \epsilon _0{\bar{\epsilon }}}\!\!\left( \!\!\begin{array}{c} \psi (x) \\ -\mathrm {i}\, k_y\partial _x\psi (x)/\beta ^2 \\ -\mathrm {i}\, k_z\partial _x\psi (x)/\beta ^2 \end{array}\!\!\right) \!\!\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, k_z z}},\qquad \bar{\varvec{\displaystyle {H}}}(x, z) = \left( \!\!\begin{array}{c} 0 \\ k_z \psi (x) / \beta ^2 \\ -k_y \psi (x) / \beta ^2 \end{array}\!\!\right) \!\!\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, k_z z}}. \end{aligned}$$
(12)

In both cases the slab mode propagation constant \(\beta\) is related to the directional wavenumbers \(k_y\), \(k_z\) by \(\beta ^2 = k_y^2 + k_z^2\). Once \(k_y\) is fixed by the choice of the input field and angle of incidence according to Eq. (1), the z-wavenumbers for all contributing slab modes are determined by the relation

$$\begin{aligned} k_z = \pm \sqrt{\beta ^2 - k_y^2}, \end{aligned}$$
(13)

where \(\beta\) results from the respective modal eigenvalue problems (9), (11) and the sign distinguishes propagation directions. Consequently, when looking at variations of the angle of incidence, the propagation characteristics of the individual modes can change between z-propagating (\(\beta ^2 - k_y^2>0\), real \(k_z\)) and z-evanescent.

Each mode with specific polarization and propagation direction thus corresponds to a field (10) or (12), here abbreviated as \(\varvec{\displaystyle {\Psi }}(x)\,\exp (-\mathrm {i}\, k_z z)\), with vectorial mode profile \(\varvec{\displaystyle {\Psi }}\) and cross-sectional propagation constant \(k_z\). The interaction with other waves must be expected to change this expression. We assume that the original, unperturbed mode profile remains a good approximation for part of the field in the composite structure, but that the mode contributes with a varying amplitude a to the overall field:

$$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}\\ \varvec{\displaystyle {H}} \end{array}\!\!\right) \!(x, z) = a(z) \left( \!\!\begin{array}{c} \bar{\varvec{\displaystyle {E}}}\\ \bar{\varvec{\displaystyle {H}}} \end{array}\!\!\right) \!(x, z) = a(z)\,\varvec{\displaystyle {\Psi }}(x)\,\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, k_z z}}. \end{aligned}$$
(14)

Here \(\varvec{\displaystyle {\Psi }}\) and \(k_z\) are known quantities, while a is an unknown function of the propagation coordinate z of the mode.

At this stage we switch to numerics. One can expect that the interaction remains restricted to a finite z-interval. Inside, a varies potentially with z, while a is assumed to be constant outside. We thus express a as a superposition

$$\begin{aligned} a(z) = \sum _j a_j\,\alpha _j(z) \end{aligned}$$
(15)

of standard 1-D linear finite elements \(\alpha _j\) on a regular mesh, with expansion coefficients \(a_j\), and with formally half-infinite first and last elements that are 1 outside the discretization interval. Explicit expressions for these “triangle functions” \(\alpha _j\) can be found in Hammer (2007). Then the contribution of this particular mode reads

$$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}\\ \varvec{\displaystyle {H}} \end{array}\!\!\right) \!(x, z) = \sum _j a_j \left( \alpha _j(z)\,\varvec{\displaystyle {\Psi }}(x)\,\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, k_z z}} \right) =: \sum _j a_j \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}_j\\ \varvec{\displaystyle {H}}_j \end{array}\!\!\right) \!(x, z). \end{aligned}$$
(16)

The second equality defines the “modal elements” \((\varvec{\displaystyle {E}}_j, \varvec{\displaystyle {H}}_j)\) as products of element functions \(\alpha _j\), mode profile \(\varvec{\displaystyle {\Psi }}\), and modal exponential. Depending on the propagation direction of the mode, one of the two coefficients \(a_0\), \(a_N\) at the ends of the discretization interval represents the input amplitude of that mode, i.e. is a given quantity, while all other coefficients are unknowns.

Two more issues need to be discussed concerning use of the basis fields (16) with the procedures of Sect. 3.4:

  • The formalism requires the fields \(\varvec{\displaystyle {E}}\), \(\varvec{\displaystyle {H}}\) of modal elements, but also the curls \(\mathsf{{C}}\varvec{\displaystyle {E}}\), \(\mathsf{{C}}\varvec{\displaystyle {H}}\). Here we observe that the original, unperturbed oblique slab mode fields (10), (12) satisfy the restricted curl equations

    $$\begin{aligned} \mathsf{{C}}\bar{\varvec{\displaystyle {H}}} - \mathrm {i}\, \omega \epsilon _0 {\bar{\epsilon }}\bar{\varvec{\displaystyle {E}}} = 0, \quad -\mathsf{{C}}\bar{\varvec{\displaystyle {E}}} - \mathrm {i}\, \omega \mu _0 \bar{\varvec{\displaystyle {H}}} = 0 \end{aligned}$$
    (17)

    with the permittivity \({\bar{\epsilon }}\) of the slab only. For fields \(\varvec{\displaystyle {A}}\), \(\bar{\varvec{\displaystyle {A}}}\) with \(\varvec{\displaystyle {A}}(x, z) = a(z) \bar{\varvec{\displaystyle {A}}}(x, z)\) one calculates \(\mathsf{{C}}\varvec{\displaystyle {A}} = (\partial _z a) \left( -{\bar{A}}_y, {\bar{A}}_x, 0 \right) ^\mathsf{{T}}+ a\,\mathsf{{C}}\bar{\varvec{\displaystyle {A}}}\). By combining this with Eq. (17), the curls of the modal elements can be expressed in terms of the oblique slab mode fields only:

    $$\begin{aligned} \mathsf{{C}}\varvec{\displaystyle {E}} = -\mathrm {i}\, \omega \mu _0\,a\,\bar{\varvec{\displaystyle {H}}} + (\partial _z a) \left( \!\!\begin{array}{c} -{\bar{E}}_y\\ {\bar{E}}_x\\ 0 \end{array}\!\!\right) , \quad \mathsf{{C}}\varvec{\displaystyle {H}} = \mathrm {i}\, \omega \epsilon _0 {\bar{\epsilon }}\,a\,\bar{\varvec{\displaystyle {E}}} + (\partial _z a) \left( \!\!\begin{array}{c} -{\bar{H}}_y\\ {\bar{H}}_x\\ 0 \end{array}\!\!\right) .\end{aligned}$$
    (18)

  • Depending on excitation conditions, a slab mode can become evanescent, then with an imaginary z-wavenumber \(k_z =: -\mathrm {i}\, \kappa _z\), with real \(\kappa\), according to Eq. (13). While that mode then does not carry any output power, it can well contribute significantly to the overall field in the region of interaction between slab and tube. Respective terms could thus well be included in the template for the total field. Here, for larger \(\kappa\) and/or a longer interaction interval, the exponential growth/decay can become unfavorable for the numerical stability of the overall scheme. A way out is found in rewriting Eq. (14) as

    $$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}\\ \varvec{\displaystyle {H}} \end{array}\!\!\right) \!(x, z) = a(z) \left( \!\!\begin{array}{c} \bar{\varvec{\displaystyle {E}}}\\ \bar{\varvec{\displaystyle {H}}} \end{array}\!\!\right) \!(x, z)\,\,{\mathrm{e}}^{\displaystyle {\kappa _z z}} = a(z)\,\varvec{\displaystyle {\Psi }}(x), \end{aligned}$$
    (19)

    i.e. in letting the anyway varying amplitude a cover the exponential dependence of the mode on z. Accordingly, Eq. (16) needs to be adapted,

    $$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}\\ \varvec{\displaystyle {H}} \end{array}\!\!\right) \!(x, z) = \sum _j a_j \left( \alpha _j(z)\,\varvec{\displaystyle {\Psi }}(x) \right) =: \sum _j a_j \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}_j\\ \varvec{\displaystyle {H}}_j \end{array}\!\!\right) \!(x, z), \end{aligned}$$
    (20)

    and, analogously to (18), the curls of the modal elements

    $$\begin{aligned} \mathsf{{C}}\varvec{\displaystyle {E}}= & {} -\mathrm {i}\, \omega \mu _0\,a\,\bar{\varvec{\displaystyle {H}}} + (\partial _z a+a\,\kappa _z) \left( \!\!\begin{array}{c} -{\bar{E}}_y\\ {\bar{E}}_x\\ 0 \end{array}\!\!\right) ,\nonumber \\ \mathsf{{C}}\varvec{\displaystyle {H}}= & {} \mathrm {i}\, \omega \epsilon _0 {\bar{\epsilon }}\,a\,\bar{\varvec{\displaystyle {E}}} + (\partial _z a+a\,\kappa _z) \left( \!\!\begin{array}{c} -{\bar{H}}_y\\ {\bar{H}}_x\\ 0 \end{array}\!\!\right) \end{aligned}$$
    (21)

    can be expressed through the original mode fields in case of an evanescent slab mode. Note that, for a propagating mode, the template (14) with the modal exponential appears to be favorable, since the discretization of a does not need to capture the rapid oscillations of the mode with z.

3.2 Guided modes of a circular dielectric tube-shaped fiber

For absent slab, the structure of Fig. 1 is defined by the permittivity function \({\tilde{\epsilon }}\) of the dielectric tube. Referring to the cylindrical coordinate system \(r, \phi , y\) of the tube with its polar origin at the tube axis, \({\tilde{\epsilon }}(r)\) is constant along the angular and axis coordinates \(\phi\), y, and piecewise constant along the radial coordinate r. Standard analysis procedures for the modes of cylindrical step-index optical fibers (Yeh 1987; Snyder and Love 1983; Brunet et al. 2014; Ebers et al. 2017; Hammer: http://www.computational-photonics.eu/fims.html) can be applied to find the guided modes of the dielectric tube as solutions of Eq. (6) for permittivity \({\tilde{\epsilon }}\). These are electromagnetic fields of the form

$$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle \mathcal {E}}\\ \varvec{\displaystyle \mathcal {H}} \end{array}\!\!\right) \!(r, \phi , y) = \left( \!\!\begin{array}{c} \tilde{\varvec{\displaystyle {E}}}\\ \tilde{\varvec{\displaystyle {H}}} \end{array}\!\!\right) \!(r, \phi )\,\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, \beta y}} = \left( \varvec{\displaystyle {\Psi }}(r)\,\,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, l \phi }}\right) \,{\mathrm{e}}^{\displaystyle {-\mathrm {i}\, \beta y}}, \end{aligned}$$
(22)

with integer angular mode order l, and real propagation constant \(\beta = k N_{{m}}\), where \(N_{{m}}\) is the effective index of the tube mode. Its profile \((\tilde{\varvec{\displaystyle {E}}}, \tilde{\varvec{\displaystyle {H}}})\) is given by the radial shape \(\varvec{\displaystyle {\Psi }}\) and the angular exponential \(\exp (-\mathrm {i}\, l \phi )\).

For nonzero angular order \(|l| \ge 1\) these are hybrid vectorial modes; in this case, all six electromagnetic components of the radial mode shape \(\varvec{\displaystyle {\Psi }}\) are nonzero. These orbital-angular-momentum (OAM)-modes (Bozinovic et al. 2013; Wang et al. 2016) correspond to vortex fields with a topological charge l. OAM modes of angular orders l and \(-l\) are degenerate. Plots of the physical field components of \(\varvec{\displaystyle {\Psi }}\) on the cross sectional plane show profiles that rotate clockwise (\(l \ge 1\)) or anticlockwise (\(l \le -1\)) for progressing time. Superpositions of the directional variants of an OAM mode with angular order \(\pm l\) constitute further valid eigensolutions for the same effective index. Relative amplitudes of unit absolute value lead to the well-known hybrid modal solutions of HE- or EH-type (Kapoor and Singh 2000), where the relative phase determines the orientation of the symmetry plane(s) and the polarization of the HE/EH modes.

Solutions for zero angular mode order \(l=0\) are independent of the coordinate \(\phi\). Two classes of modes with different polarization are distinguished. The radial shapes of TE modes are of the form \(\varvec{\displaystyle {\Psi }} = (0, E'_{\phi }, 0; \, H'_r, 0, H'_y)\), i.e. are characterized by a purely transverse electric field, with zero axial electric component. Likewise, the radial profiles of TM modes can be written as \(\varvec{\displaystyle {\Psi }} = (E'_r, 0, E'_y;\,0, \, H'_{\phi }, 0)\) with a purely transverse magnetic field and zero axial magnetic component. Note that it depends on the refractive index layering whether a TE/TM or an OAM mode is the fundamental mode of the structure.

Depending on the excitation conditions, any particular tube mode will play more or less of a role in our sought-after global solution. Even if the y-wavenumber \(\beta\) of the mode does not match the global wavenumber \(k_y\), one can still assume that the mode profile constitutes an adequate approximation to a part of the true cross sectional optical field. We thus write a contribution to the overall field in the form of the vectorial electromagnetic profile \((\tilde{\varvec{\displaystyle {E}}}, \tilde{\varvec{\displaystyle {H}}})\) of the tube mode, transformed to the global Cartesian coordinates, multiplied by some coefficient a:

$$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}\\ \varvec{\displaystyle {H}} \end{array}\!\!\right) \!(x, z) = a \left( \!\!\begin{array}{c} \tilde{\varvec{\displaystyle {E}}}\\ \tilde{\varvec{\displaystyle {H}}} \end{array}\!\!\right) \!(x, z). \end{aligned}$$
(23)

The amplitude a is not known at this stage. As in case of the slab modes, separate expressions (23), here with only one unknown each, need to be written for each tube mode that is to be included in the model. That concerns modes that differ with respect to angular order l (sign), and modes of different radial orders.

For the procedures of Sect. 3.4, the restricted curls of the modal elements, here the tube mode profiles, are required. The original modes (22) satisfy the curl equations (6) for the permittivity \({\tilde{\epsilon }}\) of the tube only. For some field \(\varvec{\displaystyle \mathcal {A}}(x,y,z) = \tilde{\varvec{\displaystyle {A}}}(x, z)\exp (-\mathrm {i}\,\beta y)\) one calculates \(\varvec{\displaystyle {\nabla }}\times \varvec{\displaystyle \mathcal {A}} = \left( \mathsf{{C}}\tilde{\varvec{\displaystyle {A}}} + \mathrm {i}\,(k_y - \beta ) ({\tilde{A}}_z, 0, -{\tilde{A}}_x)^\mathsf{{T}}\right) \exp (-\mathrm {i}\,\beta y)\). These observations can be combined to express the curls through the field components of the profile as

$$\begin{aligned} \mathsf{{C}}\tilde{\varvec{\displaystyle {E}}} = -\mathrm {i}\, \omega \mu _0\,\tilde{\varvec{\displaystyle {H}}} - \mathrm {i}\, (k_y-\beta ) \left( \!\!\begin{array}{c} {\tilde{E}}_z\\ 0 \\ -{\tilde{E}}_x \end{array}\!\!\right) , \quad \mathsf{{C}}\tilde{\varvec{\displaystyle {H}}} = \mathrm {i}\, \omega \epsilon _0 {\tilde{\epsilon }}\,\tilde{\varvec{\displaystyle {E}}} - \mathrm {i}\,(k_y-\beta ) \left( \!\!\begin{array}{c} {\tilde{H}}_y\\ 0\\ -{\tilde{H}}_x \end{array}\!\!\right) . \end{aligned}$$
(24)

Obviously, when using merely the guided modes of the tube as ingredients for the representation of the electromagnetic field in the cavity region, the model won’t be able to capture any radiative losses that are attributable to wave propagation along the curved interfaces. Hence, the present choice of basis elements for the tube region appears to be reasonable only for the angular region \(\theta > \theta _{{b}}\), where radiative losses are strictly suppressed anyway, as discussed in Sect. 2.

Alternative choices of basis elements for the cavity tube are possible. In the case of a standard 2-D setting, coupled-mode-models of microresonators with circular cavities can be based either on series of whispering gallery resonances (Franchimon et al. 2013), that cover the circular cavity, or on bend modes (Hammer 2010), which are valid solutions for angular cavity segments only. In both cases, adequate approximations can be obtained (Franchimon et al. 2013; Hammer 2016). For our 2.5-D configurations with oblique incidence, the 2-D bend modes would have to be replaced by the spiral-modes of Ebers et al. (2017). These are potentially lossy waves that propagate along spiral-shaped paths along the fiber surface; they are valid solutions for angular segments of the tube only. Respective coupled-mode models should be viable as well, then applicable to the full angular range \(0 \le \theta < \pi /2\), but lacking the direct access to the amplitudes of the TE-, TM-, and OAM-modes of the tube, as with the present model.

3.3 Coupled mode template

For our single-mode slab and z-bidirectional propagation, the field for the total, composite structure of Fig. 1 needs to include four terms of the form (16) for the forward and backward TE- and TM-modes, if we assume that all modes are potentially relevant. Likewise, separate terms (23) are required for every tube mode that is taken into account. Depending on the positioning of the tube and slab, the individual contributions are transformed to the global coordinates of the circuit, and are summed up, after suitable re-indexing. We thus obtain the following general field template in the form of a sum over all modal elements:

$$\begin{aligned} \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}\\ \varvec{\displaystyle {H}} \end{array}\!\!\right) \!(x, z) = \sum _k a_k\, \left( \!\!\begin{array}{c} \varvec{\displaystyle {E}}_k\\ \varvec{\displaystyle {H}}_k \end{array}\!\!\right) \!(x, z). \end{aligned}$$
(25)

Here the index k runs over the individual finite element indices for the directional TE and TM slab modes, and over all tube modes. In case of the slab channel, the modal elements \((\varvec{\displaystyle {E}}_k, \varvec{\displaystyle {H}}_k)\), combine the vectorial 1-D mode profiles, the related exponential dependences on the propagation coordinate z, and one of the finite element functions. The 2-D profiles of the tube modes serve directly as modal elements.

3.4 Projection and algebraic procedure

The unknown coefficients in the general expansion (25) remain to be determined. We apply a procedure of Galerkin type (Hammer 2007; Franchimon et al. 2013), borrowed from the realm of finite-element numerics. The restricted curl equations (8) are multiplied by trial fields \(\varvec{\displaystyle {F}}\), \(\varvec{\displaystyle {G}}\), and integrated over a suitable computational domain in the cross sectional x–z-plane. This leads to a weak form of Eq. (8):

$$\begin{aligned} \int \!\!\!\int \mathcal{{K}}( \varvec{\displaystyle {F}}, \varvec{\displaystyle {G}}; \, \varvec{\displaystyle {E}}, \varvec{\displaystyle {H}})\, \text{ d }x\,\text{ d }z = 0 \quad \text{ for } \text{ all } \varvec{\displaystyle {F}}, \varvec{\displaystyle {G}}, \end{aligned}$$
(26)

where

$$\begin{aligned} \mathcal{{K}}( \varvec{\displaystyle {F}}, \varvec{\displaystyle {G}}; \,\varvec{\displaystyle {E}}, \, \varvec{\displaystyle {H}}) = \varvec{\displaystyle {F}}^*\cdot \mathsf{{C}}\varvec{\displaystyle {H}} -\varvec{\displaystyle {G}}^*\cdot \mathsf{{C}}\varvec{\displaystyle {E}} - \mathrm {i}\, \omega \epsilon _0 \epsilon \varvec{\displaystyle {F}}^*\cdot \varvec{\displaystyle {E}} - \mathrm {i}\, \omega \mu _0 \varvec{\displaystyle {G}}^*\cdot \varvec{\displaystyle {H}} \,. \end{aligned}$$
(27)

Next we insert the generalized template (25) for \(\varvec{\displaystyle {E}}\), \(\varvec{\displaystyle {H}}\), and restrict Eq. (26) to the set of modal elements \((\varvec{\displaystyle {F}}, \varvec{\displaystyle {G}}) \in \left\{ (\varvec{\displaystyle {E}}_k, \varvec{\displaystyle {H}}_k)\right\}\). This leads to a system of linear equations of the form

$$\begin{aligned} \sum _{k} \left( K_{lk}\right) a_k = 0\,, \text{ for } \text{ all } \text{ l } \qquad \text{ with } \qquad K_{lk} = \int \!\!\!\int \mathcal{{K}}( \varvec{\displaystyle {E}}_l, \varvec{\displaystyle {H}}_l; \, \varvec{\displaystyle {E}}_k, \varvec{\displaystyle {H}}_k) \,\text{ d }x\,\text{ d }z\,. \end{aligned}$$
(28)

In matrix form, with the coefficients \(a_k\) collected into a vector \(\varvec{\displaystyle {a}} = (\varvec{\displaystyle {u}}, \varvec{\displaystyle {g}})\), and ordered such that \(\varvec{\displaystyle {u}}\) represents the actual unknowns, while \(\varvec{\displaystyle {g}}\) corresponds to the given excitation, and with the matrix elements arranged accordingly, the system (28) can be written

$$\begin{aligned} \left( \! \begin{array}{cc} \mathsf{{K}}_{{uu}} &{} \mathsf{{K}}_{{ug}} \\ \mathsf{{K}}_{{gu}} &{} \mathsf{{K}}_{{gg}} \end{array} \!\right) \left( \!\begin{array}{c} \varvec{\displaystyle {u}}\\ \varvec{\displaystyle {g}} \end{array}\!\right) = 0\,, \quad \text{ or } \quad \mathsf{{K}}_{{u}} \varvec{\displaystyle {u}} = -\mathsf{{K}}_{{g}}\varvec{\displaystyle {g}}\,, \quad \text{ with } \quad \mathsf{{K}}_{{u}} = \left( \! \begin{array}{c} \mathsf{{K}}_{{uu}} \\ \mathsf{{K}}_{{gu}} \end{array} \!\right) , \quad \mathsf{{K}}_{{g}} = \left( \! \begin{array}{c} \mathsf{{K}}_{{ug}} \\ \mathsf{{K}}_{{gg}} \end{array} \!\right) . \end{aligned}$$
(29)

The first matrix in Eq. (29) is square, thus the second system is overdetermined. Hence we solve it in a least squares sense. One obtains the response \(\varvec{\displaystyle {u}}\) for given input \(\varvec{\displaystyle {g}}\) as the solution of

$$\begin{aligned} \mathsf{{K}}_{{u}}^{\dagger } \mathsf{{K}}_{{u}} \varvec{\displaystyle {u}} = -\mathsf{{K}}_{{u}}^{\dagger } \mathsf{{K}}_{{g}} \varvec{\displaystyle {g}}\,. \end{aligned}$$
(30)

Here the symbol \(^\dagger\) denotes the adjoint. In case of the tube mode elements, the corresponding amplitudes \(u_k\) give directly the strengths of the modes’ contributions. For the slab modes, inspecting the respective amplitude functions (15) can give an impression of the local interaction. Assuming power normalized basis modes, the end-levels of the amplitude functions represent the guided output power, available individually per mode. The HCMT approximation to the full field can be assembled by substituting the values of \(\varvec{\displaystyle {u}}\) and \(\varvec{\displaystyle {g}}\), or \(\varvec{\displaystyle {a}}\), for the coefficients in Eqs. (25), or (16), (23), respectively.

3.5 Implementation

The former procedures have been implemented as part of a C++ subroutine collection (Hammer: http://metric.computational-photonics.eu/); the solvers for standard multilayer slab waveguides and for the modes of circular step-index fibers and the present dielectric tubes are also available online (Hammer: http://www.computational-photonics.eu/fims.html, http://www.computational-photonics.eu/oms.html). The finite element solvers of the COMSOL-Multiphysics suite (b) serve for purposes of verification (cf. the respective curves in Figs. 2, 3, 4) and for certain additional computations.

The implementation relies on analytic solutions for the vectorial slab modes and the guided modes of the dielectric tubes. The integrals of Eq. (29) are evaluated numerically by 10-point Gaussian quadrature (Press et al. 1992), applied piecewise over suitably small intervals, respecting the piecewise definition of the (linear) element functions \(\alpha _j\), and such that field discontinuities at dielectric interfaces are taken into account as far as possible. By applying the relations (18), (24), also the derivatives in Eq. (27) can be evaluated analytically, such that numerical finite-difference expressions are avoided. As far as can be expected from the numerical procedures, we observed the HCMT model to be strictly power conservative.

What concerns the computational effort, the actual solution of the final system (30) is comparably cheap. The evaluation of the modal element “overlaps” \(K_{lk}\) in Eq. (29) constitutes the largest computational burden, in particular in case of the tube mode elements with their large domain. Fortunately, depending on the structure under study, only a modest number of tube modes are supported or relevant.

4 Excitation of a dielectric tube by semi-guided waves at oblique angles

We consider specifically the configuration of Fig. 1, with a dielectric tube of outer-rim radius \(\rho = 5\,\upmu \hbox {m}\). The refractive indices \(n_{{g}} = 1.5\) (guiding regions), \(n_{{b}} = 1.0\) (background) resemble values for silica cores in air. The tube wall and the slab waveguide are of a thickness \(d = 0.4\,\upmu \hbox {m}\). Semi-guided TE waves excite the structure at vacuum wavelength \(\lambda = 1.55\,\upmu \hbox {m}\).

For these parameters, the slab waveguide supports fundamental modes with effective indices \(N_{{TE}} = 1.23026\) (TE) and \(N_{{TM}} = 1.10914\) (TM). Critical angles of incidence \(\theta _{{b}}\) and \(\theta _{{TM}}\) can be defined on the basis of these values, as discussed at the end of Sect. 2. Radiative losses are suppressed for wave incidence at angles \(\theta > \theta _{{b}} = 54.37^\circ\). Scattering to guided TM modes is forbidden for \(\theta > \theta _{{TM}} = 64.36^\circ\).

Modes of the tube-shaped fiber are designated by an identifier TE, TM, or OAM for the polarization state (c.f. the discussion in Sect. 3.2), with a first index that states the angular order l of the mode, and a second index that counts modes with that angular order, sorted by effective index \(N_{{m}}\), starting with the number 1 for the mode with highest \(N_{{m}}\). All OAM modes are strictly hybrid with six nonzero electromagnetic components. Considering the electric components of the mode profiles, for the present parameters we observed strong axial & azimuthal and weaker radial components for OAM(l, 1) modes (second index 1), and strong radial but weaker axial & azimuthal components for OAM(l, 2) modes. If one imagines the tube shell to be flattened, this relates the OAM(l, 1) fields to the oblique TE modes, the OAM(l, 2) fields to the TM modes of a respective slab. Our tube-shaped fiber supports the azimuthally constant TE(0, 1) and TM(0, 1)-modes, TE-like modes OAM(\(\pm l\), 1), for \(l = 1, 2, \ldots , 14\), and TM-like modes OAM(\(\pm l\), 2), for \(l = 1, 2, \ldots , 9\), i.e. a total of 48 orthogonal fields.

The results as shown have been computed with a template that covers all tube modes, for all angles of incidence. The amplitude functions Eq. (15) of slab modes are discretized on an interval \(z \in \{-8, 8\}\,\upmu \hbox {m}\) with a regular mesh of stepsize \(0.2\upmu m\). For the examples in this section, the number of contributions to the template (25), i.e. the dimension of the system (29), is 372, with four given coefficients (exception: for the computation leading to the plots of Fig. 8a, b we used a larger interval for the discretization of the slab mode amplitudes, leading to a larger dimension).

Figures 2, 3, 4, 5, 6, 7, 8 summarize the results of our simulations. Beyond the characteristics of the power transmission (Figs. 2, 3, 4, bottom panels) and the full optical electromagnetic field (Figs. 6, 8a, c, cross sectional fields; in principle the 3-D field is available through Eq. 7), the present formalism allows to inspect directly the contributions of individual tube modes (Figs. 2, 3, 4, upper panels; 5), and to assess the strength of the interaction between slab and tube in terms of the slab mode amplitude functions (Figs. 7, 8b, d).

With a view to the potential excitation of guided tube modes, we restrict the angular range to the region \(\theta > \theta _{{b}}\) where radiation losses are suppressed. Resonant features occur for configurations with phase matching of axial y-wavenumbers (1), hence we choose the angle of incidence \(\theta\) as a primary parameter. Analogously to Hammer et al. (2019), Ebers et al. (2019), the features can be expected to translate to wavelength or frequency spectra (not explicitly investigated here). Also according to Hammer et al. (2019), Ebers et al. (2019), the gap distance g plays a significant role. Therefore results for different values of g are compared.

Fig. 2
figure 2

Power transmission and tube mode excitation strength versus the angle of incidence \(\theta\), for a gap distance \(g = 1.0\,\upmu \hbox {m}\). Lower panels: reflectance \(R_{{TE}}\), \(R_{{TM}}\) and transmittance \(T_{{TE}}\), \(T_{{TM}}\) of the TE- (blue) and TM-polarized slab modes (black). Continuous lines show the results of the HCMT model; lighter dashed curves (almost completely superimposed) correspond to COMSOL simulations. Upper plots: amplitudes a of specific tube modes in the HCMT solution. Curves for TE- and TM- modes, and OAM modes with the same mode index (1, 2) and angular propagation direction (sign of l), of varying angular order |l| share the same axes; the curves largely overlap close to the zero-level. Thin vertical lines: mode angles (31) assigned to individual tube modes (modes OAM(l, m) and OAM(\(-l\), m) are strictly degenerate). Curves assigned to OAM modes with different angular order can be identified (with exceptions) by peaks in the vicinity of the respective mode angle. (Color figure online)

Full size image
Fig. 3
figure 3

Polarized reflectance \(R_{{TE}}\), \(R_{{TM}}\) and transmittance \(T_{{TE}}\), \(T_{{TM}}\), and tube mode amplitudes a, as a function of the angle of incidence \(\theta\), for a gap \(g = 1.4\,\upmu \hbox {m}\). See the caption of Fig. 2 for further comments on the interpretation of curves

Full size image
Fig. 4
figure 4

Polarized reflectance \(R_{{TE}}\), \(R_{{TM}}\) and transmittance \(T_{{TE}}\), \(T_{{TM}}\), and tube mode amplitudes a, as a function of the angle of incidence \(\theta\), for a gap \(g = 1.8\,\upmu \hbox {m}\). See the caption of Fig. 2 for further comments on the interpretation of curves

Full size image

4.1 Angular spectra

One expects that a pronounced interaction of the incident wave with a particular tube mode requires that the participating waves are reasonably phase matched with respect to propagation in the axial y-direction. To that end, separately for each tube mode, a critical angle \(\theta _{{m}}\) can be defined as

$$\begin{aligned} k N_{{TE}} \sin \theta _{{m}} = k N_{{m}} \quad \text{ or } \quad \sin \theta _{{m}} = N_{{m}}/N_{{TE}}, \end{aligned}$$
(31)

such that the associated wavenumber (cf. Eq. 1) coincides with the propagation constant \(k N_{{m}}\) of the mode. Since the effective indices \(N_{{m}} > n_{{b}}\) of guided tube modes are limited by the the background refractive index \(n_{{b}}\), the range \(\theta > \theta _{{b}}\), with \(\sin \theta _{{b}} = n_{{b}}/N_{{TE}}\) covers the characteristic mode angles \(\theta _{{m}}\) for all guided modes supported by the tube.

Axial phase matching is then realized if the actual angle of incidence \(\theta\) happens to be close to the critical angle \(\theta _{{m}}\) assigned to a particular tube mode. Respective mode angles are indicated in the angular spectra of Figs. 2, 3, 4 and in Fig. 5. The following general trends can be observed.

Resonances appear mostly as more or less well separated peaks in the reflectance curves, or as transmittance dips, respectively (lower panels). These are accompanied by corresponding peaks in the tube mode amplitude spectra (upper axes), and can thus be associated with particular modes, in most cases pairs of degenerate OAM(\(-l\), m) and OAM(l, m) fields. There are, however, instances (intermediate angles, \(\theta > \theta _{{TM}}\) where a strong excitation of specific tube modes does not (or does hardly) show up in the power transmission.

If one imagines moving along with the incoming slab mode, the distance where the slab and tube cores are close grows with increasing excitation angle \(\theta\). Hence, towards grazing incidence, one can expect a stronger interaction. Correspondingly, the transmission and reflectance spectra show more pronounced and wider peaks for incidence angles nearing \(90^\circ\) (the HCMT curves stop at \(\theta = 88^\circ\)).

An increasingly stronger interaction between slab and tube modes can also be expected for decreasing distance g. While there is rather a decrease in tube mode amplitudes, the features in the power transmission curves overlap more and more. Tube modes contribute at angles further away from their own angle of resonance; in general the features are more irregular. This trend becomes apparent in particular for small gaps, much below \(g = 1.0\,\upmu \hbox {m}\) (not shown). In contrast, for enlarged distance g, the tube modes appear with growing amplitudes at resonance. The resonance peaks become narrower, are better defined, and move closer to the native mode angles.

In order to further assess the role of the tube modes in the formation of resonance features, for comparison we carried out simulations with templates (25) that were restricted, for each angle of incidence \(\theta\), to those tube modes with mode angles (31) in an interval \([\theta -\Delta \theta , \theta +\Delta \theta ]\). Specifically, for the scan of Fig. 2, reduced templates with \(\Delta \theta =5^\circ\) lead to results with only minor deviations from the plots as shown, on the scale of the figures. One expects that further tube modes in a larger angular range will be relevant for modelling the wider resonances with more pronounced overlap at smaller gaps g, while templates with fewer tube modes should be sufficient for the narrower peaks at larger g (exception: the states discussed in Sect. 4.3).

Fig. 5
figure 5

Tube mode amplitudes \(|a|^2\) (logarithmic scale) versus angle of incidence \(\theta\), for different gap values g. Each panel focuses on one or two specific tube modes; curves can be assigned to the mode labels at the top of the panels by the maximum levels (shorter horizontal lines) for specific gaps. Continuous lines correspond to the mode label on the left of the mode angle(s) \(\theta _{{m}}\); dashed lines relate to the mode label on the right

Full size image

Figure 5 permits a closer look at some of the features in Figs. 2, 3, 4. The figure combines amplitude levels, now on a logarithmic scale, for selected tube modes and for different gaps, in an angular range around a related resonance. Levels \(|a|^2 < 1\) are omitted. As a general trend, for increasing gap g, the narrowing, growth in height, and positioning close to the mode angle, of resonance peaks can be confirmed.

The first panel Fig. 5a shows amplitudes for OAM(\(-14\), 1) and OAM(\(-9\), 2) with close-by mode angles \(\theta _{{m1}}\), \(\theta _{{m2}}\). For the smaller gaps, a combined resonance forms; this is less so for the narrowest resonance at the largest gap \(g=1.8\,\upmu \hbox {m}\) considered. Note that curves for OAM(14, 1) and OAM(9, 2) are at levels \(a < 1\), lower than the present range. Similarly, according to the two last panels Fig. 5g, h (these cover the same \(\theta\)-interval), the modes OAM(\(\pm 1\), 1) play a role in the formation of the resonance close to the mode angle for TE(0, 1) for smaller gap \(g=1.0\,\upmu \hbox {m}\) and below (not shown), with lesser contributions for larger gaps.

Otherwise, the resonances in Fig. 5 can all be attributed to a pair of degenerate modes OAM(\(\pm l\), 1). In Fig. 5d–g one observes roughly regular distances between the maximum levels of curves for g growing by steps of \(0.4\,\upmu \hbox {m}\), which hints at an exponential growth of mode amplitudes with g, with constant relative amplitudes of modes OAM(\(-l\), 1) and OAM(l, 1). This is consistent with Hammer et al. (2019), Ebers et al. (2019); here, however, each resonance is formed by the two strictly degenerate modes, and the excitation conditions decide on the relative amplitude.

In principle, for each of these states, OAM modes with both positive and negative angular momentum are excited. At higher angles \(\theta\), towards grazing incidence, one finds only moderate differences between the contributions of modes OAM(\(\pm l\), 1). However, at lower angles, for modes with higher absolute angular momentum |l|, there is a more pronounced difference between contributions. Here the phase matching condition in azimuthal \(\phi\) direction, or z-direction, respectively, appears to be more relevant. This leads to a strong predominant orbital angular momentum of the excited resonance: For examples (b, c), modes OAM(\(-12\), 1) and OAM(12, 1), or OAM(\(-9\), 1) and OAM(9, 1), contribute with amplitudes that differ by about four orders of magnitude.

This concerns tube modes that are normalized to unit axial power, and unit power input via the TE slab mode. Large amplitudes of the tube modes in the HCMT template can thus be translated to respective ratios of absolute field squares in the tube core and in the slab core. Just as for the configurations with standing wave resonances (Hammer et al. 2019; Ebers et al. 2019), the present simulations predict a strong resonant field enhancement, here for fields with large angular momentum.

4.2 Resonances

Fig. 6
figure 6

Cross sectional fields \(|\varvec{\displaystyle {E}}(x, z)|\) for excitation of the tube at angles \(\theta\) that correspond to the maximum levels indicated in Fig. 5(a–h), for the gap \(g=1.0\,\upmu \hbox {m}\). Color scales are adapted to the respective maxima, separately for each panel. (Color figure online)

Full size image
Fig. 7
figure 7

Amplitude functions a(z) as introduced in Eq. (16) for the slab mode contributions to the HCMT template, for a gap \(g=1.0\,\upmu \hbox {m}\) and excitation of the tube at angles \(\theta\) that correspond to the maximum levels indicated in Fig. 5a–h. Curves correspond to the amplitudes of TE fields (blue) and TM fields (black), for propagation in positive z-direction (|a|: bold, solid; \(\hbox {Re}\,a\): thin, solid; \(\hbox {Im}\,a\): thin, dash-dotted) and propagation in negative z-direction (|a|: bold, dashed; \(\hbox {Re}\,a\): thin, dashed; \(\hbox {Im}\,a\): thin, dotted). (Color figure online)

Full size image

Figure 6 gives an impression of the fields associated with the former extremal states. According to Fig. 5a, the field in panel (a) is constituted mostly by the TE-like mode OAM(\(-14\), 1) and the TM-like field and OAM(\(-9\), 2); there is hardly any interference visible due to the difference in polarization character. The resonances in panels b–g are attributable to degenerate modes OAM(\(-l\), 1) and OAM(l, 1) for \(l= 12, 9, 7, 4, 2, 1\), with a strong difference in amplitudes and thus predominantly anticlockwise propagation in (b), leading to the azimuthally constant field strength. From (b) to (g), with more and more equal amplitudes of OAM(\(\pm l\), 1), the interference pattern becomes more and more pronounced. The field in (h) consists of a mixture of modes TE(0, 1) and OAM(\(\pm 1\), 1) for \(g=1.0\,\upmu \hbox {m}\). According to Fig. 5(g, h), a nearly azimuthally constant field as expected for the TE(0, 1) mode only (not shown) is realized only for larger gaps, then closer to the TE(0, 1) mode angle.

Next we consider the contributions of the slab modes to the overall field. Figure 7 shows the evolution of the functions (15) for the resonances of 6a–h. The discretization allows variations in a for \(-8\,\upmu \hbox {m}<z <8\,\upmu \hbox {m}\); one observes constant levels at the edges of that interval. Thus the formalism identifies a coupling region where slab modes interact with the modes of the tube. Note that the full field (25) is expressed as a superposition of non-orthogonal basis elements; there is no reason why the amplitude functions should be restricted to \(|a| < 1\).

Panels (a) and (b) are for angles of incidence \(\theta <\theta _{{TM}}\). There is strong scattering to forward TM output; at these resonances the structure shows a pronounced polarization conversion. For the examples of Fig. 7c–h, the TM slab mode becomes z-evanescent. While the TM power output is suppressed, one still observes contributions of forward and backward TM modes in the interaction region, of decreasing magnitude from (c) onwards. For the series of examples from (a) to (h), resonances are built from more and more equal contributions of tube modes with opposite angular momentum. This leads to increasingly stronger TE-reflections at the resonances, consistent with the full reflectance observed for pure standing-wave resonances in Hammer et al. (2019). Panels (c, d) relate to states with close to full transmission; these resonances hardly show up in a plot of transmittance versus \(\theta\) (cf. Fig. 2). Still, variations of the amplitude functions hint at a strong interaction between slab- and tube-modes; at resonance the TE slab mode experiences a \(\pi\)-phase shift when traversing the tube.

4.3 Composite states

Further, at specific gap levels, we observed resonant states where multiple tube modes contribute to the HCMT approximation, even at angles of incidence that are comparably far away from their critical angles. Figure 8 shows cross sectional fields and slab mode amplitudes for two such states. The features include a mostly definite parity with respect to the x-axis, and full/pronounced reflection at resonance, with field pattern that are concentrated around the region of closest approach between slab and tube (a, b), or are distributed around the full tube, with some further localized strong field in the slab (c, d).

Fig. 8
figure 8

Excitation of the tube structure at angles \(\theta = 65.34^\circ\), for \(g=1.0\,\upmu \hbox {m}\) (a, b), and at \(\theta = 73.85^\circ\), for \(g=0.4\,\upmu \hbox {m}\) (c, d); cross sectional fields \(|\varvec{\displaystyle {E}}(x, z)|\) (a, c), and amplitudes a(z) of the slab modes involved in the formation of the resonances (b, d), interpretation of curves as in Fig. 7

Full size image

The X-shaped resonance of Fig. 8a, b is built with contributions \(|a|^2 > 10\) from TM(0, 1) (strongest), further from TM-like modes OAM(\(\pm l\), 2) for \(l = 1, 2, \ldots , 6\), and from TE-like OAM(\(\pm 10\), 1). Direct mode analysis of the composite system including slab and tube with COMSOL finds a guided mode with a profile similar to Fig. 8a and effective index \(N_{{m}} = 1.1177\). The latter can be translated to a mode angle \(\theta _{{m}} = 65.30^\circ\), close to the angle of incidence at which the resonance can be observed.

At smaller gap distance \(g=0.4\,\upmu \hbox {m}\), the tube-slab structure supports the resonance of Fig. 8c, d. Tube modes TE(0, 1), and OAM(\(\pm l\), 1) for \(l = 1, 2, \ldots , 9\) contribute with amplitudes \(|a|^2 > 10\). The interference pattern visible on the tube core is related to the large contributions of the OAM(\(\pm 7\), 1) modes. Here the COMSOL mode analysis of the composite tube-slab-system predicts a leaky mode with a profile that matches Fig. 8c, with complex effective index \(1.1816-5\cdot 10^{-5}\). The phase part of the latter corresponds to a mode angle of \(73.83^\circ\), which is again close to the angle of incidence at which the HCMT simulation places the resonance.

For both states, panels (b, d) show large localized slab mode amplitudes in the region of strongest interaction beneath the tube, and pronounced, close to unit reflectance, indicating a resonance of standing wave type. Respective resonances are absent from the scans of Figs. 3, 4, i.e. appear to be supported only at smaller distance between slab and tube.

One can conclude that these states correspond to guided modes, or low-loss leaky modes, that are supported by the composite slab-tube-system, at specific gap levels. Somewhat surprisingly, the present HCMT formalism works as well for these configurations. However, this concerns approximations where the tube modes attain large amplitudes at angular positions far away from their native mode angles, i.e. where the quality of the field representation in terms of the tube modes must be suspected to deteriorate. We thus do not pursue the issue any further here.

5 Concluding remarks

Our hybrid CMT method can work adequately in the present 2.5-D framework. Excellent quantitative approximations are obtained for the examples under test. Beyond transmittance and reflectance levels and access to the full vectorial optical electromagnetic field, the method permits to directly examine the contributions of the separate basis elements, here the local strengths of the directional TE- and TM-polarized slab modes, and the amplitudes assigned to the individual modes of the fiber tube, to the overall solution.

With the silica capillary suspended over a thin slica membrane, we have considered an elementary sample configuration, mainly for purposes of validating the HCMT model. The theory predicts that selective resonant excitation of only one of a pair of degenerate OAM modes with positive or negative angular order is possible under specific conditions. Potentially this could be an explicitly simple technique for generating strong fields with large orbital angular momentum in-fiber. We plan to further develop that concept, then for a perhaps more realistic structure where a substrate-deposited thin-film waveguide excites a solid circular, possibly coated dielectric rod.

So far the discussion has been restricted to 2.5-D solutions with infinite extent along the tube axis. Realistic 3-D fields, however, can be constructed by superimposing the present solutions for a range of angles of incidence, such that the incoming field is e.g. of the form of a semi-guided Gaussian beam of finite width (Hammer et al. 2016, 2019). Implementing that technique, on the basis of either the HCMT or the COMSOL-FEM -solutions, should be straightforward and will be followed up elsewhere.