Large-scale control on the frequency of tropical cyclones and seeds: a consistent relationship across a hierarchy of global atmospheric models

Abstract

A diagnostic framework is developed to explain the response of tropical cyclones (TCs) to climate in high-resolution global atmospheric models having different complexity of boundary conditions. The framework uses vortex dynamics to identify the large-scale control on the evolution of TC precursors—first non-rotating convective clusters and then weakly rotating seeds. In experiments with perturbed sea surface temperature (SST) and $\hbox {CO}_2$ concentration from the historical values, the response of TCs follows the response of seeds. The distribution of seeds is explained by the distribution of the non-rotating convective clusters multiplied by a probability that they transition to seeds. The distribution of convective clusters is constrained by the large-scale vertical velocity and is verified in aquaplanet experiments with shifting Inter tropical Convergence Zones. The probability of transition to seeds is constrained by the large-scale vorticity via an analytical function, representing the relative importance between vortex stretching and vorticity advection, and is verified in aquaplanet experiments with uniform SST. The consistency between seed and TC responses breaks down substantially when the realistic SST is perturbed such that the spatial gradient is significantly enhanced or reduced. In such cases, the difference between the responses is explained by a change in the ventilation index, which influences the fraction of seeds that develop into TCs. The proposed TC-climate relationship serves as a framework to explain the diversity of TC projection across models and forcing scenarios.

1 Introduction

High-resolution global models ($\varDelta x \le 50$ km in the atmosphere) are indispensable tools to project the frequency of tropical cyclones (TCs) in future climates. The explicitly resolved vortices are often used as proxies for real-world TCs because of the realistic geographic distribution, seasonal cycles and interannual variability (see Walsh et al. 2016 for a review). However, large uncertainties remain in the projections of TC frequency (Walsh et al. 2016; Knutson et al. 2019), due to inconsistency across models in the projected mean climate as well as the TC-climate relationship (Vecchi et al. 2019; Camargo et al. 2020).

The inconsistency of modeled TC-climate relationships arises in part from the fact that the TCs are not well-resolved, so they are much more sensitive to subgrid parameterization than the mean climate (e.g., Murakami et al. 2011; Zhao et al. 2012; Reed et al. 2015). Another complication is the under-estimation of the surface wind speed in intense storms, despite a somewhat realistic shape of modeled intensity distribution (Zhao and Held 2010). Therefore, typical GCM studies define TCs using a lower threshold on wind speeds than in the observations, but how to choose this threshold is ambiguous (Walsh et al. 2007).

Because of the uncertainty in explicit counting of TCs, the empirical genesis potential indices (e.g. Gray 1975; Emanuel and Nolan 2004; Tippett et al. 2010) are commonly used to explain the frequency of modeled TCs given the mean climate. Despite some success in capturing the geographical and seasonal variability in historical records, the proposed indices are poorly constrained when extrapolating to future warmer climates (Camargo et al. 2014; Lee et al. 2020). The indices have both dynamic and thermodynamic components, respectively predicting the supply of angular momentum and moist entropy that are essential for TC genesis. While the dynamic component is usually the large-scale low-level vorticity, the thermodynamic component is more ambiguous, in terms of the mathematical formulation (e.g. Emanuel 2010; Tippett et al. 2010) and which variables to use (e.g. Murakami and Wang 2010). The ambiguity highlights the need to constrain the regression-based indices with process-based understanding.

The ventilation index is a non-dimensional parameter that has been derived based on mesoscale dynamics (Rappin et al. 2010; Tang and Emanuel 2010) and used as a predictor on the weather (Tang and Emanuel 2012; Hoogewind et al. 2020) and climate (Vecchi et al. 2019) time scales. Following Vecchi et al. (2019), we posit that the ventilation index controls the probability that TC precursors (hereafter “seeds”) develop into mature TCs. The novelty of this paper is the suggestion that the frequency of seeds is controlled by the product of large-scale vertical velocity, which has been used to explain TC frequency in Held and Zhao (2011); Ballinger et al. (2015); Zhou et al. (2019); Walsh et al. (2019), and a non-dimensional parameter developed by Chavas and Reed (2019) describing a vortex-wave interaction. We hypothesize that this combination captures the geographical distribution and the climatological response to warming.

The importance of seeds in modulating TC frequency has been emphasized in Li et al. (2010); Vecchi et al. (2019); Sugi et al. (2020). Phenomenologically, they have been related to tropical variability such as the ITCZ breakdown (Ferreira and Schubert 1997) and African easterly waves (AEWs) (Thorncroft and Hodges 2001). However, it is not well understood what controls the climatology and variation of seeds at the global scale. Furthermore, it is unclear how to establish a useful definition of seeds. For instance, in a model of the North Atlantic, Patricola et al. (2018) showed that other types of precursors emerge to replace the seeding role of AEWs; the AEW by itself does not constrain TC frequency.

To address the problems above, we develop a novel diagnostic framework to analyze modeled storms across the entire intensity spectrum, including seeds and TCs. Our novel tracker does not require an arbitrary choice of surface wind speed threshold, and the framework offers a practical definition of seeds that connects the simulated dynamics with the statistical relationship between the TCs and climate.

Because the TC-climate relationship is derived based on hypotheses regarding TC dynamics rather than regression against the large-scale climate, we hypothesize that it holds over a range of climates. In this paper, the TC-climate relationship is systematically tested against prescribed-SST aquaplanet models with horizontally uniform SSTs as well as with zonally symmetric but meridionally varying SSTs. These aquaplanet models are important testbeds of TC response to surface warming (Merlis et al. 2016), planetary rotation (Chavas and Reed 2019), radiative forcing (Merlis et al. 2013; Viale and Merlis 2017), and ITCZ shift (Ballinger et al. 2015). Because of the simplified surface boundary conditions, the TC-climate relationships are often statistically robust and qualitatively consistent across models (Merlis and Held 2019). Building on the success in idealized global modeling of TCs, our analysis framework quantitatively connects the TC-climate relationship across a hierarchy of models with different complexity in the surface boundary conditions.

The paper is organized as follows: a theoretical framework is proposed in Sect. 2, which is tested in different idealized experiments described in Sect. 3. Results from the experiments are given in Sects. 4, 5 and 6 with increasing model complexity, including how they agree or disagree with the theory. Our experimental design mainly follows the existing literature, as we aim to further explain the results rather than to introduce many more scenarios. We will not report all aspects of the simulations but focus only on what is relevant to our theory.

2 Theoretical framework

In this section, we describe a strategy to derive a dynamics-based TC-climate relationship. The key is to connect TC-scale theories of intensification with global-scale statistics of TC frequency. Our ansatz is

$$\begin{aligned} n_\text {TC} = n_s P_2 = n_c P_1 P_2, \end{aligned}$$

(1)

where $n_\text {TC}$, $n_s$ and $n_c$ are frequency of TCs, seeds and tropical convective clusters respectively. The probabilities $P_1$ and $P_2$ are non-dimensional and bounded between 0 and 1.

Equation (1) describes three steps of TC development, each predominantly controlled by a different physical process (Fig. 1). Starting with $n_c$ convective clusters, $n_c P_1$ of them develop into weakly rotating seeds, and $n_c P_1 P_2$ of them eventually strengthen into TCs. In principal, all variables in Eq. (1) are functions of space and time. The exact space and time scales in which they are evaluated depend on the variability of environmental conditions and TC trajectories and are discussed in more detail in the results sections.

Fig. 1

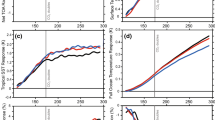
a The Venn diagram for the three categories, along with the two transitions and three large-scale predictors in our framework. The probability that convective clusters develop into seeds is $P_1$, and the probability that seeds develop into TCs is $P_2$. The concrete definitions are given in Sect. 2. b An example track in the uniform SST experiment, showing where it first occurs as a convective cluster, where it first exceeds the seed threshold, and where it first exceeds the TC threshold

The large-scale predictors for $n_c$, $P_1$ and $P_2$ that we use, and that will be described in more detail in the following sections, are:

$$\begin{aligned} n_c&= c_0 \cdot (-{\overline{\omega }}) \end{aligned}$$

(2)

$$\begin{aligned} P_1&= \frac{1}{1 + Z^{-1/\sigma }} \approx c_1 Z \end{aligned}$$

(3)

$$\begin{aligned} P_2&= \frac{1}{1 + (\varLambda _0/\varLambda )^{-1/\sigma '}}, \end{aligned}$$

(4)

where ${\overline{\omega }}$ and Z are functions of the large-scale climate as is $\varLambda$, the ventilation index of Tang and Emanuel (2012); while $c_0$, $c_1$, $\varLambda _0$, $\sigma$ and $\sigma '$ are fitting parameters determined as described in the results sections. The parameters Z and $\varLambda$ are non-dimensional; while $c_0$ is dimensional, indicating that we are not proposing a theory for the total absolute number of TCs. However, if $c_0$ can be assumed to be unchanged between two different climates, then the expression (1) can potentially provide a hypothesis for the change in the total number of TCs.

The proportionality in Eq. (2) is explained in Sect. 2.1. The non-dimensional variables, Z and $\varLambda$, are derived based on TC-scale dynamics in Sects. 2.2 and 2.3 . The analytical function relating Z with $P_1$ is obtained by fitting to aquaplanet simulations in Sects. 4 and 5 , where the approximation in Eq. (3) is justified. The analytical function of $P_2$ follows Tang and Emanuel (2012) using reanalysis data, and it is also motivated by its ability to predict the sensitivity in high-resolution GCMs (Vecchi et al. 2019).

The expressions (3) and (4) are both sigmoid functions of the respective non-dimensional parameter. This function interpolates smoothly between two limits: one where the non-dimensional parameter is much larger than unity and the other much smaller. The physical interpretations of the limits are given in Sects. 2.2 and 2.3 .

2.1 The initiation of a cluster

In our framework, the starting point of an eventual TC is the initiation of a non-rotating convective cluster. These are identified from the 3-h-mean precipitation rate maps, and the detailed procedure is described in Sect 3.2. The typical radius of convective clusters is 50–150 km, quantized by the grid in global models. An observational analogue of this phenomenon is the tropical cloud cluster, which has been regarded as TC precursors in Hennon et al. (2011). We posit, and later assess, that the expected frequency of convective clusters is proportional to the large-scale vertical velocity.

2.2 The first transition to a seed

The first transition is from a non-rotating convective cluster to a weakly rotating seed. This transition describes the evolution of a weak vortex before its low-level vorticity becomes substantially larger than the large-scale vorticity. To estimate the vorticity tendency using large-scale variables, consider the low-level vorticity equation

$$\begin{aligned} \frac{\text {d} \zeta }{\text {d} t} + (\beta + \partial _y {\overline{\zeta }})v = (f + {\overline{\zeta }}) (-\delta ) + \epsilon , \end{aligned}$$

(5)

where $\text {d}/\text {d}t$ is the Lagrangian tendency following a vortex, ${\overline{\zeta }}$ is the large-scale vorticity and $\zeta$ is the vorticity deviation, $\delta$ is horizontal divergence, and $\epsilon$ is the collection of small-scale terms, including $-\zeta \delta$ and other vorticity forcings. The low-level vorticity equation has been used to analyze TC intensification in e.g. Raymond and López Carrillo (2011); Smith et al. (2014).

A typical cyclonic vortex is convergent in low levels, due to some combination of convection and surface-driven convergence, so $\delta < 0$ and the right-hand side is positive if $\epsilon$ is negligible, representing a vorticity source due to vortex stretching. The second term on the left-hand side is the advection of large-scale vorticity and may act as a vorticity sink due to Rossby wave radiation (Theiss 2004; Chavas and Reed 2019).

To estimate the sign of $\text {d}\zeta /\text {d}t$, a scale analysis is performed. The velocity and length scales of the disturbance are denoted by V and L; while the scales of large-scale variables are denoted by their original expression to simplify the notation. For the weak vortices and waves of interest, the scales of $\text {d}/\text {d} t$, $\zeta$ and $\delta$ are all estimated by V/L. Some limitations of these estimations are discussed at the end of this section.

Consider two limits of the equation. In the first limit where the third term in Eq. (5) is negligible, scale analysis shows that,

$$\begin{aligned} L \sim \sqrt{V/(\beta + \partial _y {\overline{\zeta }})} \equiv L_\beta , \end{aligned}$$

(6)

which is the local Rhines scale. In the second limit where the second term in Eq. (5) is negligible,

$$\begin{aligned} L \sim V/(f + {\overline{\zeta }}) \equiv L_f, \end{aligned}$$

(7)

which is the scale of a wave or a cyclonic vortex with Rossby number of order unity. We note that this is also the scaling of TC radius if V is the potential intensity (Chavas and Emanuel 2014).

The ratio between the scales of the third and second terms in Eq. (5) may be estimated by

$$\begin{aligned} \frac{f + {\overline{\zeta }}}{(\beta + \partial _y {\overline{\zeta }})L} = \frac{f + {\overline{\zeta }}}{\sqrt{(\beta + \partial _y {\overline{\zeta }})V}} = \frac{L_\beta }{L_f}, \end{aligned}$$

(8)

where the first equality uses $L = L_\beta$. When the ratio is small, the dominant balance is between the two terms on the left-hand side of Eq. (5), whose typical solution is Rossby waves. In other words, the disturbance with velocity V in an environment with small $L_\beta /L_f$ is strongly influenced by $\beta$, and hence readily produces Rossby waves.

This interpretation is consistent with the uniform SST aquaplanet simulations of Chavas and Reed (2019): the equatorial flow is dominated by Rossby waves as $L_\beta /L_f$ is small; while the higher latitudes are conducive to nonlinear vortices as $L_\beta /L_f$ is large. The difference between Chavas and Reed (2019) and the present theory is in the velocity scales in $L_\beta$ and $L_f$. In Chavas and Reed (2019), the velocity scales have different dependence on the potential intensity. Here, the velocity scales are equal as they both scale with the root-mean-square velocity of the weak disturbance. We have adapted the Chavas and Reed (2019) theory to describe specifically the development of weak vortices.

Every variable in Eq. (8) is on the large scale except V, which varies across vortices. To make Eq. (8) a predictor based solely on large-scale variables, V is replaced by a constant representing a collective velocity scale over vortices weaker than $\zeta _\text {seed}$, the vorticity threshold representing the weakest seed. The constant is measured empirically in Sects. 4 and 5 and is independent of climate, denoted by $U = 20 \text { m s}^{-1}$. Note that the scale analysis is evaluated at 850 hPa; while the 10-m wind of the weakest seed has a smaller value around $12 \text { m s}^{-1}$.

While independent of climate, the value of U changes with the choice of vorticity threshold, $\zeta _\text {seed}$. This is because the collection of vortices that U represents would include stronger vortices if $\zeta _\text {seed}$ were increased. Plugging an increased U into Eq. (8) decreases the ratio $L_\beta /L_f$. By construction, the probability of transition ($P_1$) also decreases if $\zeta _\text {seed}$ were increased. The consistency of how $L_\beta /L_f$ and $P_1$ change with $\zeta _\text {seed}$ further supports $L_\beta /L_f$ as a predictor for $P_1$.

In practice, we measure the ratio (8) by

$$\begin{aligned} Z \equiv \frac{|f + {\overline{\zeta }}|}{\sqrt{|\beta + {\overline{\zeta }}_y| U}}, \end{aligned}$$

(9)

so that the square root in the denominator is taken over strictly positive values. In the numerator, any anticyclonic large-scale vorticity is replaced by zero. The inclusion of mean relative vorticity is a generalization from Chavas and Reed (2019). In addition, the ratio is defined as the inverse of Chavas and Reed (2019), such that it increases with the probability of vortex spinup, and that it is well-defined where $(f + {\overline{\zeta }}) = 0$.

In summary, a non-dimensional parameter characterizing the large-scale environment (Z) is derived by analyzing the scale of the low-level vorticity equation. An environment with $Z \gg 1$ is conducive to vortex spinup; while an environment with $Z \ll 1$ is dominated by waves. The probability $P_1$ is expressed as a function of Z in Eq. (3).

Some assumptions in the derivation do not extend to a well-developed vortex. First, the divergence scaling, $\delta \sim U/L$, is more accurate for a developing vortex, which is the case here, than a geostrophically or cyclostrophically balanced vortex having closed surface pressure contour. Second, as the low-level convergence and vorticity become well-correlated in space, such as in a pouch-like precursor (Wang 2012), the $-\zeta \delta$ term in $\epsilon$ may become more important than the large-scale terms in the vorticity Eq. (5). Thus, the probability of evolution for stronger vortices needs to be estimated differently as described in the following.

2.3 The second transition to a tropical cyclone

During the second transition, a weakly rotating seed intensifies into a strongly rotating TC. Theories of axisymmetric TCs become relevant in this stage. Similar to the previous section, a non-dimensional parameter is used to characterize the environment, which is the ventilation index:

$$\begin{aligned} \varLambda = \frac{v_s \cdot \chi }{v_p}, \end{aligned}$$

(10)

where $v_s$ is vertical wind shear, $v_p$ is potential intensity, and $\chi = (s - s_\text {mid})/(s_\text {sfc}^* - s)$ is the normalized deficit of moist entropy (s).

The ventilation index has been derived from scale analysis of the moist entropy budget (Tang and Emanuel 2010) and the power budget (Chavas 2017) over a TC. In addition, it has been used to predict the probability of TC development in Tang and Emanuel (2012); Vecchi et al. (2019); Hoogewind et al. (2020). Here we adopt the analytical function of Tang and Emanuel (2012) to express the probability of second transition ($P_2$) in terms of $\varLambda$ in Eq. (4).

3 Methods

3.1 Model setup

A number of experiments (Fig. 2) are conducted to test the validity and limitation of the theory. The experiments are designed to systematically vary the mean climate. In cases where the boundary conditions are zonally symmetric, TC statistics and the mean climate are averaged over longitude and time to collect robust statistics. With increasing complexity in the boundary conditions, we explore three categories of experiments: homogeneous aquaplanets with uniform SST, aquaplanets with zonally symmetric and time invariant but meridionally varying SST, and realistic geometry experiment with repeating seasonal cycles. The configurations generally follow the existing literature, where some basic TC-climate relationships have been documented. The relationships will be further explained using the new theoretical framework. This section explains the key model differences from the literature and among our experiments.

Fig. 2

List of experiments conducted in this paper. Experiments labeled by the same symbols (^∗ or^∧) are identical

The aquaplanet experiments are performed using the Atmospheric Model version 4 (AM4) developed at the Geophysical Fluid Dynamics Laboratory (GFDL) with 50-km horizontal resolution in the atmosphere. The explicit TCs in the 100-km version of this model have realistic geographical distribution and seasonal cycles (Zhao et al. 2018a), and those in the 50-km version have similar distributions with a more realistic intensity spectrum. Our model parameters follow Zhao (2020); Zhang et al. (2020) except that the land module is bypassed, such that the surface boundary condition is a prescribed SST constant in time.

For the “uniform” SST experiments, the SST is constant between 70°S and 70°N but drops by 7 K poleward of this range (Fig. 3a) based on the formula

$$\begin{aligned} \text {SST} = \text {SST}_0 + \frac{7}{2} \cdot \left[ \tanh \left( \frac{\phi + \pi /2.5}{\pi /50} \right) + \tanh \left( -\frac{\phi - \pi /2.5}{\pi /50} \right) \right] , \end{aligned}$$

(11)

where $\phi$ is latitude in radians and $\text {SST}_0$ is the constant value of SST in low latitudes. This modification, as opposed to similar experiments with globally uniform SST in Shi and Bretherton (2014); Merlis et al. (2016); Chavas and Reed (2019), is made to prevent the accumulation of TCs near the poles. The strong vertical wind shear around $70^\circ$ N/S provides a physical mechanism to destroy TCs as they migrate across those latitudes. Compared with the globally uniform SST test cases, this SST modification has little influence on the low and mid latitudes as the meridional overturning circulation remains weak.

Fig. 3

SST distributions for a the “uniform” SST aquaplanet experiments discussed in Sect. 4, where the SST gradients near the poles are prescribed to destroy TCs, b the zonally symmetric, meridionally varying aquaplanet experiments discussed in Sect. 5, and c the 1990s control experiment discussed in Sect. 6, averaged from July to October. The SST is constant in time and longitude in the aquaplanet experiments, and changes continuously with time and space in the realistic-boundary experiments

Two sets of experiments are performed using the “uniform” SST profile. In the first set, the SST is increased uniformly from 295, 297.5, 300, 302.5 to 305 K, similar to the experimental design in Merlis et al. (2016). The temperature drop around $70^\circ$ is kept at 7 K in all experiments. In the second set, the planetary rotation rate ($\varOmega$) is varied using the $\hbox {SST}_0$ = 302.5 K profile, similar to the design of Chavas and Reed (2019). The range of $\varOmega$, relative to the earth-like value, is $0.25\times$, $0.5\times$, $1\times$ and $2\times$.

In order to modify $\beta$ and f independently, an additional experiment is performed with the planetary radius reduced by half, which has also been done in Chavas and Reed (2019). The $\hbox {SST}_0$ is 302.5 K and $\varOmega$ is the earth-like value. The number of grid points is reduced by half, such that the horizontal grid spacing remains 50 km for consistency with other experiments.

In the zonally symmetric, meridionally varying aquaplanet experiments, the prescribed SST profiles (Fig. 3b) are analytical functions identical to the “+1.5C tropics” profiles in Ballinger et al. (2015). The use of SST profile with enhanced 1.5-K warming over the warmest ocean rather than their control profile increases the sample size of TCs. The experiments are conducted with the latitude of SST peak shifted from 8$^\circ$N to 17$^\circ$N with a 3-degree interval, and the latitude of simulated precipitation peaks are consistently located at 6 degrees to the south of the SST peaks, from 2$^\circ$N to 11$^\circ$N.

In experiments with land surfaces, the prescribed SST and sea ice have seasonal cycles but no interannual variability. The SST time series is constructed using the monthly climatology over 1986 to 2005 (Durack and Taylor 2018) and linearly interpolated to each time step, following the method of Vecchi et al. (2019). All radiative gases are fixed at the level of year 1990 from the CMIP5 historical forcings. We refer to this experiment as the 1990s control (Fig. 3c), based on which three sets of experiments are conducted. The first set changes the SST uniformly from the control, from $-4$ K, $-2$ K, $+2$ K to $+4$ K. The second set varies the $\hbox {CO}_2$ concentration, including $0.5 \times$ and $2 \times$ of the control value. An additional experiment is conducted with both $+2$ K uniform warming and $\hbox {CO}_2$ doubling, referred to as the mixed forcing experiment.

The third set of experiments is referred to as the patterned warming experiments, where the SST is altered non-uniformly from the 1990s control while the $\hbox {CO}_2$ concentration is fixed at the control value. Two experiments have increased warming over the warmest ocean, where the SST is raised by 1 K where it is larger than a threshold, chosen to be 26$^\circ$C and 28$^\circ$C respectively. The SST is not perturbed where it is smaller than the threshold, except that near the threshold the perturbation is interpolated smoothly using a logistic function:

$$\begin{aligned} \text {SST'} = (1 + \exp [2(\text {SST}_\text {thresh} - \text {SST})])^{-1}. \end{aligned}$$

(12)

Two additional experiments are performed with SST increase over the cooler ocean. The SST is increased by 1 K where it is smaller than a threshold, similarly chosen to be 26$^\circ$C and 28$^\circ$C respectively, using an inverse logistic function:

$$\begin{aligned} \text {SST'} = (1 + \exp [2(\text {SST} - \text {SST}_\text {thresh})])^{-1}. \end{aligned}$$

(13)

That is, the first pair of experiments warms the warmest ocean, and the other pair warms the coolest ocean.

The above procedure yields 12 experiments with different forcings. The simulations are performed for 30 years of repeating seasonal cycles, and the Northern-Hemisphere hurricane seasons (July to October) in the last 20 years are analyzed.

The realistic experiments are conducted using the GFDL HiRAM model with 50-km resolution (Zhao et al. 2009), which is a predecessor model to AM4 used for the aquaplanet experiments. We use HiRAM rather than AM4 for these realistic configurations because the performance of 50-km version of the AM4 has not yet been documented in the literature. The two models have similar globally averaged TC counts and similar TC response to realistic forcing, and their simulations of the large-scale tropical climate are more similar to each other than to other GFDL models, such as AM2 and AM3 (Zhao et al. 2018b). The main difference is in the convection scheme, where HiRAM has a single plume and AM4 has two plumes reflecting the difference between deep and shallow convection (Zhao et al. 2018b). As will be discussed in the following, the probability of transition from convective clusters to seeds and the percentage changes of seeds and TCs are insensitive to convective parameterization.

3.2 Tracking algorithm

Conventional TC trackers cannot test our theory because the criteria they use to define localized clusters often imply non-negligible vorticity. In this study, a new tracking algorithm is developed to track convective clusters regardless of their vorticity. A cluster is defined as contiguous grid cells whose three-hour-mean precipitation rates are larger than the 99.5th percentile, which is about $8 \times 10^{-4} \text { kg m}^{-2}\text { s}^{-1}$ on the uniform SST aquaplanet. The choice of this critical precipitation intensity is arbitrary, but modifying it does not change results appreciably. Properties associated with each cluster are recorded, including the 850-hPa vorticity, wind speed and the location of the centroid. This procedure is performed for every 6-hourly output. A track is defined to connect clusters in consecutive snapshots whose centroids are less than 300 km apart. Clusters smaller than 4 grid points and tracks shorter than 1 day are omitted to avoid grid-scale instability. Tracks initiated poleward of 30 degrees latitude are neglected to avoid counting extratropical storms.

Figure 4 compares our new tracker with a standard TC tracker documented in Harris et al. (2016). The tracker of Harris et al. (2016) identifies clusters based on closed surface pressure contours, and then apply thresholds on surface wind speed, core-to-environment temperature difference and so on to filter out non-TC clusters. The seeds in the Harris et al. (2016) tracker are defined as all tracks of closed-contour features before the thresholds are applied. The seeds and TCs in our tracker are defined as tracks whose vorticity exceed $\zeta _\text {seed} = 4 \times 10^{-4} \text { s}^{-1}$ and $\zeta _\text {TC} = 1 \times 10^{-3} \text { s}^{-1}$ at any instant. Note that this is different from the vorticity criterion in Harris et al. (2016), which requires the vortices to have sustained vorticity above the threshold.

Fig. 4

Latitudes of initial occurrence for each category detected by our tracker (blue curves) compared with those detected by the Harris et al. (2016) tracker (green and orange markers). The solid blue curve and orange circles represent tracks exceeding TC strength. The dashed blue curve and green squares represent tracks exceeding seed strength. The dotted blue curve represents all tracks detected by our tracker, which has no counterpart in Harris et al. (2016). The probability $P_1$ is the ratio between seeds and convective clusters, which can be measured by our tracker but not by the Harris et al. (2016) tracker. The probability $P_2$ is the ratio between TCs and seeds and can be measured by both trackers. The example shows the 1990s control experiment with realistic boundary conditions

Figure 4 shows the first detected latitudes of seeds and TCs given by the Harris et al. (2016) tracker, and those given by our new tracker. We emphasize that each track is labeled by the latitude in which the cluster is first detected, not the latitude in which it intensifies into a seed or a TC. In this example, the trackers are applied to the 1990s control experiment with realistic boundary conditions, averaged over all 20 Northern-hemisphere hurricane seasons (July to October). The two trackers give roughly the same latitudinal distributions of seeds and TCs, confirming the consistency of our TC statistics with the literature based on more conventional trackers.

The distribution of non-rotating convective clusters given by our new tracker is shown as the blue dotted curve in Fig. 4. This information is not given by conventional TC trackers. By definition, this distribution is greater than the distribution of seeds at every latitude. The ratio between those distributions is the measured probability of the first transition ($P_1$). In this example, roughly 40% of convective clusters become seeds, and roughly 30% of seeds become TCs. When measuring $P_2$, using a conventional tracker such as Harris et al. (2016) is sufficient, but our tracker gives additional information about $P_1$ and non-rotating convective clusters.

We clarify that the formation of a seed does not necessarily require a preceding non-rotating cloud cluster. For instance, a dry vortex generated by barotropic instability over land may reach the vorticity threshold ($\zeta _\text {seed}$) before precipitating. This part of the system lifetime would not be included in our track. Once it travels over moist surfaces, the low-level convergence will induce convection and it will be identified by our tracker as a seed, having a 100% probability of first transition. Consistently, a necessary condition for barotropic instability requires the potential vorticity gradient to change sign horizontally, so it must cross zero somewhere in the domain. If the regional circulation is persistent in the climatology, $(\beta + {\overline{\zeta }}_y)$ would have a small value close to zero, corresponding to a large Z, which predicts a large $P_1$.

4 Uniform SST aquaplanets

In this section, the development of weak vortices is analyzed in uniform SST aquaplanet experiments. The vorticity tendency along each track is measured and compared with Z. It will be shown that the vorticity is more often increasing in an environment with $Z > 1$ and vice versa. The fraction of convective clusters that eventually become seeds ($P_1$) is also measured and compared with Z. A universal relationship between $P_1$ and Z is found across a range of planetary rotation rates, planetary radii, and SSTs.

4.1 Vortex-scale vorticity tendency

Fig. 5

Two-dimensional histogram in the coordinates of Lagrangian vorticity tendency and non-dimensionalized background vorticity. The quantities are measured along each track and are constrained to $2.3 \times 10^{-4}< \zeta < 4 \times 10^{-4} \text { s}^{-1}$ in the 302.5-K uniform SST experiment. The frequency is normalized for each bin on the horizontal axis, such that every column in the plot sums up to 1. The sample size for each column is shown above the two-dimensional histogram. The top-right quadrant is where the background vorticity is large and the vortex spins up; while in the bottom-left quadrant the background vorticity is small and the vortex spins down

The information given by the tracker allows one to estimate the Lagrangian vorticity tendency following a vortex. Figure 5 shows the correlation between the vorticity tendency and Z, as a two-dimensional histogram. The vorticity tendency, denoted by $\text {d} \zeta /\text {d} t$, is measured by the following procedure. For each identified vortex, the vorticity is represented by the maximum vorticity over its area at 850 hPa. The vorticity difference between two consecutive snapshots divided by the time difference (6 h) is the approximated $\text {d} \zeta /\text {d} t$. We acknowledge that this simple representation using the maximum vorticity may not capture the tendency of mean vorticity or other more complicated change in the vorticity distribution over a vortex.

Similarly, a time series of latitudes is measured along each track and converted to a time series of Z. The ${\overline{\zeta }}$ and ${\overline{\zeta }}_y$ terms in Z are zonally averaged, and the constant U is the same as defined in Sect. 2.2. The two-dimensional histogram is constructed using those two time series for all tracks in the last five years of simulation. To focus on the development of weak vortices, Fig. 5 includes only data points whose instantaneous vorticity is less than $\zeta _\text {seed} = 4 \times 10^{-4} \text { s}^{-1}$. In addition, since the lifetime and area thresholds in the tracking algorithm create a bias towards a positive vorticity tendency in the first few steps, data points with instantaneous vorticity less than $2.3 \times 10^{-4} \text { s}^{-1}$ are excluded. With those restrictions applied, there are $O(10^4)$ data points in Fig. 5.

Since vortices are more likely to survive when $Z > 1$, there are more data points on the right half of Fig. 5 than the left half. For better visualization, the 2d histogram has been normalized for each bin on the horizontal axis, such that every column in the plot sums up to unity. The number of data points in each bin on the horizontal axis is shown above the 2d histogram.

Figure 5 is divided into four quadrants by the dashed lines representing $\text {d} \zeta /\text {d} t = 0$ and $Z = 1$ respectively. The distribution of data points are approximately diagonal, concentrated in the top-right and bottom-left quadrants. The top-right quadrant corresponds to vortex growth and a large Z; while the bottom-left quadrant corresponds to vortex decay and a small Z. The existence of data points on the top-left and bottom-right quadrants reflects the small-scale variability not captured in the zonal and temporal mean. The strong correlation between $\text {d} \zeta /\text {d} t$ and Z suggests that the former, which is a vortex-scale measurement, can be predicted by the latter, which is a large-scale average.

The vertical dashed line represents the environment having $Z = 1$, where the source and sink terms in the vorticity equation (5) have equal magnitudes. Note that the horizontal axis in the figure is expressed on the logarithmic scale for consistency with Figs. 6, 7 and 9 . For these values, the proportions of vortices intensifying or decaying are roughly equal, indicating that it is in between the regimes favorable and unfavorable to vortex development. Neither the vorticity source or sink dominates, and the sign of vorticity tendency is unpredictable by Z in this transitional regime.

Fig. 6

Fraction of convective clusters developing into seeds as a function of a latitude and b the large-scale predictor. The curves represent experiments with varying planetary rotation rates and radii indicated in the legend. The black dashed curve in b is the analytical function given by Eq. (3) with the width parameter $\sigma = 0.15$

Fig. 7

As in Fig. 6 except the SST is varied, showing the fraction of convective clusters developing into seeds. The probabilities are non-monotonic with SST increase, but the spread is slightly reduced from a to b. The experiment colored in green and the black dashed curve in b are the same as those in Fig. 6b

4.2 Large-scale statistics of transition probability

In addition to being a good indicator for the sign of the vorticity tendency (Sect. 4.1), the non-dimensional parameter Z also predicts the probability of first transition $P_1$. Figure 6a shows the measured $P_1$ for experiments with varying planetary rotation rates ($\varOmega$) and planetary radii (a). $P_1$ is the ratio between the latitudinal distributions of seeds and convective clusters, and it is bounded between 0 and 1 at every latitude. The probability is strongly suppressed near the equator and increases with latitude.

Comparing across experiments, the probability increases with $\varOmega$ and a at the same latitude. Among those experiments, the variation of planetary vorticity is more significant than the variation of zonal-mean relative vorticity. The non-dimensional parameter can thus be approximated as

$$\begin{aligned} Z \approx \frac{f}{\sqrt{\beta U}} = \frac{\sin \phi }{\sqrt{\cos \phi }} \sqrt{\frac{2a \varOmega }{U}}, \end{aligned}$$

(14)

which is consistent with the measured increase of $P_1$ with $\varOmega$ and a.

Figure 6b examines the correlation between $P_1$ and Z. The data is the same as in Fig. 6a except that the horizontal axis is converted Z. The spread of the curves is greatly reduced in Fig. 6b, suggesting a strong control of Z on $P_1$.

The shape of the universal function mapping $\log _{10} Z$ to the probability is approximated by a smooth step function centered at 0 on the horizontal axis (black dashed curve in Fig. 6b). The interpretation of a smooth step function is straightforward. The limit at the bottom left corner is where $L_\beta$ is smaller than $L_f$. That is, the flow is strongly influenced by $\beta$ and dominated by Rossby waves without much nonlinearity. In the other limit at the upper right corner, nonlinear vortices are not influenced by the relatively weak $\beta$, so spin-up mechanisms such as vortex stretching bring the probability of transition close to unity.

A critical value of $U = 20 \text { m s}^{-1}$ is chosen such that the probability is 0.5 at $Z = 1$. At this velocity, $L_\beta = L_f$ and the vorticity dissipation is comparable to vorticity generation. This is the intermediate regime between the two competing mechanisms.

The smooth transition between the two limits reflects the small-scale variability not captured by the zonal-mean variables. The analytical formula of the black dashed curve in Fig. 6b is Eq. (3), where $\sigma$ is a fitting parameter characterizing the width of transition zone. More than one analytical function can be used to represent a smooth step function, but the exact choice is not important for our purpose. The variability of environmental variables, latitudinal migration of weak vortices, imperfect estimation of scales using environmental variables, and other small-scale processes all contribute to increasing the width of transition.

We perform multiple experiments with different $\varOmega$ but only one with different a because the large-scale influence of changing a is equivalent to changing $\varOmega$ according to the hypohydrostatic rescaling theory (Kuang et al. 2005; Pauluis et al. 2006). In our example, the (0.5a, $\varOmega$) and (a, $0.5 \varOmega$) solutions are mathematically similar except a rescaling of diabatic forcing, which is not critical for a moist vortex as the surface forcing is much faster than the rotation. Therefore, the data collapse between these two solutions is likely a consequence of similarity and cannot serve as an evidence for the dynamical importance of Z. On the other hand, changing $\varOmega$ while fixing a creates a fundamentally different solution, in which case the data collapse between $P_1$ and Z is not trivial. Note that dimensional quantities need to rescaled based on Pauluis et al. (2006) to satisfy similarity, including halving the lifetime threshold in the tracking algorithm for the 0.5a experiment. In addition, the equivalence between reducing a and reducing $\varOmega$ applies only to hydrostatic solutions, which is the case here. Because nonhydrostatic convection follows a different scaling from hydrostatic flows (Pauluis et al. 2006; Hsieh et al. 2020), changing a would create fundamentally different solutions in higher-resolution, nonhydrostatic models.

Figure 7 shows the sensitivity of $P_1$ to SST increase. Similar to Fig. 6, the probability increases from 0 close to the equator and approaches 1 around 20$^\circ$N. There is some spread among the curves in Fig. 7a which is non-monotonic with SST. The spread is somewhat reduced when plotting against Z in Fig. 7b. Because U is a constant, the SST dependence in Fig. 7a can be attributed to the change in ${\overline{\zeta }}$. The change in ${\overline{\zeta }}$ is associated with the weak meridional overturning circulation that organizes spontaneously in uniform SST aquaplanet experiments and has complicated dependence on parameterized convection (e.g. Kirtman and Schneider 2000; Chao and Chen 2004).

The universal dependence in Fig. 7b supports the use of a constant U across a range of SSTs. In comparison, the potential intensity (computed using the Fortran code accompanying Bister and Emanuel 2002), which is another potentially relevant velocity scale, increases by 17% from the 295-K to 305-K experiments over the range of latitudes in Fig. 7. The intensities of the strongest TCs are found to increase with the potential intensity, but the potential intensity does not emerge as relevant to the development of weak vortices into seeds.

5 Zonally symmetric, meridionally varying SST aquaplanets

In this section, aquaplanet experiments with meridionally varying SST are performed to investigate the spatial distributions of $n_c$ and $P_1$. The SST profile is shifted poleward while maintaining the peak SST value and meridional gradient. The zonal symmetry is preserved to facilitate robust statistics in the zonal mean.

As opposed to the uniform SST experiments in Sect. 4, $n_c$ here has a strong latitudinal dependence as does $P_1$. It will be shown that $n_c$ follows the ascending portion of the overturning circulation, which is better organized in the experiments here, and that $P_1$ follows Z in the same way as the uniform SST experiments. The spatial overlap between $n_c$ and $P_1$ will be shown to increase the number of seeds with poleward shift of the ITCZ, which in turn explains the increasing number of TCs.

Figure 8a shows the distribution of convective clusters ($n_c$). There is a preferred latitude in each experiment that is equatorward of the SST peak. Figure 8b shows the zonal-mean large-scale vertical velocity at 500 hPa ($-{\overline{\omega }}_{500}$), which has roughly the same shape and peak latitude as the distributions in Fig. 8a. The poleward shift with SST is also captured. This variable is found to correlate with $n_c$ better than other common large-scale predictors, including the relative humidity, moist entropy deficit, vertical wind shear, background vorticity and potential intensity.

Fig. 8

a Distribution of convective clusters for the meridionally varying aquaplanet experiments. b Zonal-mean vertical velocity at 500 hPa for the corresponding experiments

The zonal-mean precipitation rate or precipitable water are other reasonable predictors for $n_c$ as they have similar latitudinal distributions to $-{\overline{\omega }}_{500}$. The correlation between $n_c$ and the zonal-mean precipitation rate is not a trivial result, because the convective clusters are identified using the extreme precipitation and have no direct information about the mean. In this set of experiments, the tracked clusters contribute less than 30% of the total precipitation. Nevertheless, we choose to use $-{\overline{\omega }}_{500}$ instead of zonal-mean precipitation as the predictor for $n_c$ because it is less sensitive to microphysics parameterization. In addition, $\omega$ has direct connections with the vortex stretching term in the vorticity equation, as well as the gross moist stability in the energy balance analysis discussed in Sect. 6.

Figure 9a shows the probability of first transition ($P_1$), which is from convective clusters to seeds. The vorticity threshold and the constant U are the same as defined before. The curves are plotted only over latitudes having large enough sample sizes. Far away from the peaks of the convective cluster distributions, the sample sizes are too small to robustly measure the probability.

Fig. 9

As in Fig. 6 except for the ITCZ-shift experiments, showing the fraction of convective clusters developing into seeds. The black dashed curve shows the analytical function given by Eq. (3) with the width parameter $\sigma = 0.3$

The probabilities in Fig. 9a increase with latitude, similar to the uniform SST results. Across experiments, the probability distribution shifts poleward with the SST peak and ITCZ. This shift can be explained by the large-scale predictor, Z. Here the zonal-mean relative vorticity terms in Z due to the horizontal circulation associated with the ITCZ is more important than the planetary vorticity terms to explain the poleward shift. Figure 9b shows $P_1$ as functions of Z, which gives a similar collapse of data to in the uniform SST experiments. The universal curve is still a sigmoid function centered at zero on the horizontal axis, suggesting that the velocity scale U is not strongly sensitive to the circulation.

Comparing the collapsed curves for meridionally varying SST (Fig. 9b) and for uniform SST (Figs. 6b and 7b), the width of the transition zone is twice as wide in the former as the latter. Presumably, this is because the more complicated large-scale flows and the stronger vertical wind shear increase the stochasticity of the vortex development process. Similar reasons may explain why the probability plateaus at 80% and does not reach 100%.

To explain the percentage change of seed frequency, it suffices to simplify the predictor of $P_1$ to be proportional to Z as expressed in Eq. (3). This is because when plotting Fig. 9b on a linear-linear scale, the sigmoid function near the origin may be approximated as a straight line. The error is less than 10% for $P_1 < 0.6$, beyond which the approximation breaks down as the probability increases more slowly in higher latitudes. The breakdown of the linear approximation is not important in practice because the peaks of $n_c$ occur in latitudes where $P_1$ is well below 0.6. The slope of the linear approximation (c) depends on the width of the sigmoid function ($\sigma$) but drops out when calculating the percentage change. That is,

$$\begin{aligned} \frac{\varDelta n_s}{n_s} = \frac{\varDelta \langle n_c P_1 \rangle }{\langle n_c P_1 \rangle }&\approx \frac{\varDelta \langle -{\overline{\omega }}_{500} \, Z \rangle }{\langle -{\overline{\omega }}_{500} \, Z \rangle }, \end{aligned}$$

(15)

where the angular bracket denotes a tropical mean. Note the absence of proportionality constants $c_0$ and $c_1$. Combined with the ventilation-index-based predictor, the percentage change of TC frequency is predicted by

$$\begin{aligned} \frac{\varDelta n_\text {TC}}{n_\text {TC}} = \frac{\varDelta (n_s P_2)}{n_s P_2}&\approx \frac{\varDelta (\langle -{\overline{\omega }}_{500} \, Z \rangle \langle W \rangle )}{\langle -{\overline{\omega }}_{500} \, Z \rangle \langle W \rangle }, \end{aligned}$$

(16)

where $W = 1/(1 + (\varLambda _0/\varLambda )^{-1/\sigma '})$ is the predictor for $P_2$ in Eq. (4) following Tang and Emanuel (2012).

Note the order in which the tropical mean and multiplication operators are taken. Because vortices during the first transition are weak and have little meridional migration, $P_1$ is measured as a function of latitude. In contrast, vortices during the second transition are more intense and drift more significantly over latitudes, so $P_2$ is defined as the ratio between the mean TC number and the mean seed number, and the predictor W is averaged over the tropics before multiplying by $\langle -{\overline{\omega }}_{500} \, Z \rangle$. This procedure accounts for the aggregated environmental influence on vortices during the second transition. More sophisticated spatial averaging, such as over latitudes poleward of the predicted seed distribution, also make sense. Nevertheless, in the present experiments the variability in seeds is more important than the variability in $P_2$, so it is sufficient to adopt the simplest spatial mean.

Figure 10a shows that the percentage change of tropical-mean seed frequency is well-captured by the large-scale predictor, Eq. (15). The four data points correspond to the four ITCZ shift experiments, and they line up along the one-to-one line which would represent a perfect prediction. The seed frequency increases with the poleward shift of the ITCZ, which is caused by the increasing overlap between $n_c$ and $P_1$.

Fig. 10

Percentage changes for the measured frequency of a seeds and b TCs, compared with the large-scale predictors given in Eqs. (15) and (16) respectively. The black dashed line is the one-to-one line representing a perfect prediction

Figure 10b shows that the percentage change of TCs is also captured by the large-scale predictor, Eq. (16). The TC frequency increases monotonically with the poleward shift of the ITCZ, which is primarily caused by the increase of seeds. The probability of second transition increases slightly with the poleward shift of the ITCZ. This is because the vertical wind shear is reduced due to thermal wind balance, when the meridional temperature gradient is constrained by the fixed SST gradient but the corresponding Coriolis parameter increases substantially. This effect is captured by the ventilation index, so that the measured and predicted changes of TCs are strongly correlated along the one-to-one line.

In our configuration, the TC frequency increases by 10% per degree latitude shift of the ITCZ. This value is consistent with Ballinger et al. (2015) using the same prescribed SST but is smaller than Merlis et al. (2013) when coupled to a slab ocean. We expect the same predictors to hold across model configurations, but the exact percentage of increase depends on the spatial patterns of the large-scale predictors.

6 Realistic boundary condition

In this section, increased complexity and more realistic boundary conditions, including land and seasonally-varying SST, are introduced to investigate seeds originated from mechanisms not necessarily related to the ITCZ. The linearized predictor, Eq. (15), is used to explain how seeds respond in different climates. The change of ${\overline{\omega }}$ is further analyzed using the gross moist stability.

6.1 Geographical distribution of seeds in the control climate

Figure 11a shows the distribution of seeds in the 1990s control climate averaged over July to October for 20 years, a total of 80 months. To effectively visualize the scatter of locations where the tracks initiate, the following procedure is performed to generate the map. For each grid point, the number of tracks initiated inside a $10^\circ$-longitude-by-$3^\circ$-latitude box centered at the grid point is measured. The value is then normalized such that the sum over all grid points is the global frequency of tracks per month. If the scatter points were on the model grid, this procedure is essentially a rolling mean along the aforementioned latitude and longitude ranges. This is not the case for the track location as it is defined as the centroid of the convective cluster.

Fig. 11

a Distribution of seeds from July to October in the 1990s control simulation smoothed by $10^\circ$ in longitude and $3^\circ$ in latitude. The values represent the number of tracks per month per $50 \times 50$ km$^2$. b The predictor of seeds (denominator of Eq. (15)) averaged over the same temporal and spatial scales as in a

Figure 11a concerns tracks whose vorticity at 850 hPa exceeds $\zeta _\text {seed}$, using the same value described in Sect. 3.2. As in the aquaplanet experiments, the tracks are labeled by the first coordinates where they are detected. The seeds are concentrated in regions over the West Pacific warm pool and the Bay of Bengal, and in the ITCZ bands in the East Pacific and North Atlantic. Even though the spatial distribution of seeds is similar to that of TCs, they are not equivalent as will be discussed in Sect. 6.3.

Figure 11b shows the predictor for seeds ($-{\overline{\omega }}_{500} Z$) averaged over the same 80 months in which the seeds are tracked. To preserve the zonal structure, the spatial average is taken over the scale of the box defined for the seed measurement instead of over all longitudes as in aquaplanet experiments. The color scale is chosen to emphasize positive-valued predictors (corresponding to large-scale ascent), which encompasses regions where seeds concentrate. However, the proportionality between the measured and predicted seed frequency varies across basins. For instance, the seeds are more sensitive to the predictor in the East Pacific than the West Pacific. This difference may reflect the dependence of the proportionality constants in Eqs. (2) and (3) on the large-scale circulation, such as ITCZ versus monsoon flows. We posit that the proportionality constant in each basin is approximately unchanged with the climate, so the percentage change across basins can be compared in a consistent manner.

Note that over the mountain ranges in North America and the Arabian Peninsula, the predictor overestimates the seeds because the pressure level of 850 hPa is not above the boundary layer. Those regions with elevated terrain are not directly relevant to seeds or TCs and are excluded when predicting the global frequency in Sect. 6.3.

A detailed breakdown of the seed predictor shows that most of the spatial variation is contributed by $-{\overline{\omega }} f$. The $(\beta + {\overline{\zeta }}_y)$ factor is dominated by $\beta$ and is approximately constant in the tropics. An exception is the East Pacific, where ${\overline{\zeta }}_y$ is negative and cancels out a large portion of $\beta$. Therefore, Z is enhanced in this region. Physically, the horizontal vorticity gradient likely changes sign temporarily, satisfying a necessary condition for barotropic instability. This mechanism is consistent with the observed TC genesis due to ITCZ instability (Ferreira and Schubert 1997).

6.2 Response of seed distribution to climate change

Figure 12 compares the measured and predicted response of seeds to a uniform 2-K surface warming. The quantities are measured in the same way as in Fig. 11 except a difference is taken from the control experiment. Locations with large-scale descent in the control climate that are unfavorable for TC genesis are masked out.

Fig. 12

As in Fig. 11 except showing the difference between the uniform-2K warming and the control experiments. Regions having insufficient samples in a and regions having large-scale subsidence in b are irrelevant and are masked out

The measured seed frequency shows a reduction in most area in Fig. 12a. The response pattern is consistent with the change of the large-scale predictor in Fig. 12b, including a significant reduction in the West Pacific, a southwestward shift in the East Pacific, and a weaker reduction in the North Atlantic off the coast of Africa.

Similar to the climatology, the change of the predictor is well-approximated by $-f\varDelta {\overline{\omega }}_{500}$. Therefore, the zonal variation is mostly caused by the time-mean $-\varDelta {\overline{\omega }}_{500}$, shown in Fig. 13a. No spatial averaging is performed to show the quantities in the primitive forms. The large-scale ascent is reduced in the West Pacific warm pool and North Indian Ocean. In the North Atlantic, the change is better described as an equatorward shift of the ITCZ, and the weighting by f leads to a reduction of seeds. The large-scale predictor captures those unfavorable changes of the environment.

Fig. 13

Differences between the uniform-2K warming and control experiments of a time-mean vertical velocity at 500 hPa, b vertical velocity predicted by the energy influx (F) divided by GMS (M), and c the negative of outgoing long wave radiation, which is a dominant term in the total F. Note that the color scale in c is not centered at 0 to emphasize the spatial pattern; while the other terms in F contribute to a nearly uniform increase. No spatial averaging is performed to show the complete spatial structure, unlike in Fig. 12

To help explain the spatial pattern of $-\varDelta {\overline{\omega }}_{500}$, we perform the gross moist stability (GMS) analysis (Neelin and Held 1987), which is based on the moist static energy balance in an atmospheric column. Figure 13 compares the measured $-\varDelta {\overline{\omega }}_{500}$ with the prediction based on the column energy input and the GMS. The column energy input includes the short wave and long wave radiation, as well as surface latent and sensible heat fluxes. The GMS is approximated as the moist static energy difference between the upper (350–150 hPa) and lower (900–750 hPa) levels following Zhou et al. (2019). That is,

$$\begin{aligned} F&\approx -\omega _\text {mid} (h_\text {upper} - h_\text {lower})/g \end{aligned}$$

(17)

$$\begin{aligned}\quad&= -\omega _\text {mid} M, \end{aligned}$$

(18)

$$\begin{aligned} \Rightarrow -{\overline{\omega }}_{500}&\approx F/M, \end{aligned}$$

(19)

where F is the influx of energy into the column, h is moist static energy, and M is GMS. The equation indicates that the ascending portion (${\overline{\omega }} < 0$) of the large-scale circulation corresponds to a net import of moist static energy ($F > 0$) given the generally positive GMS ($M > 0$). We believe that this rough two-level approximation to the GMS is adequate for the purposes of providing a physical picture of the change in the pattern of mean vertical motion, and providing evidence that this change is determined in large part by the large-scale energy balance and not by changes in the seeds or TCs themselves.

The spatial pattern and magnitude of $-\varDelta {\overline{\omega }}_{500}$ (Fig. 13a) are consistent with $-\varDelta (F/M)$ (Fig. 13b), which supports the approximations used when deriving the predictor. The small discrepancy reflects some imperfect assumptions, such as the neglect of horizontal moisture advection. The change in (F/M) captures the decreased large-scale ascent over the West Pacific and North Indian Ocean and the ITCZ shift.

The most important terms contributing to the change with warming are diagnosed in the model and summarized as follows:

$$\begin{aligned} f \varDelta (-{\overline{\omega }}_{500})&\approx f \varDelta \left( F/M \right) \\ &\approx f \varDelta F/M_\text {ctl} \\ &\approx f \varDelta (F_\text {lw,toa} + F_\text {latent})/M_\text {ctl}, \end{aligned}$$

(20)

where $M_\text {ctl}$ is the GMS averaged over July to October in the 1990s control experiment; $F_\text {lw,toa}$ and $F_\text {latent}$ are the influxes of top-of-atmosphere long wave radiation and surface latent heat, two dominant terms in the total F. The change in surface latent heat flux has little spatial structure in the tropics. It is the negative of outgoing long wave radiation that gives rise to the spatial structure (Fig. 13c). The importance of the long wave feedback is consistent with the mechanism proposed by Zhou et al. (2019) to explain the ITCZ shift with warming.

The same reasoning explains the response to a doubling of $\hbox {CO}_2$ despite a different spatial pattern. The large-scale ascent is reduced in every basin except the Central Pacific, and there is no significant ITCZ shift. The spatial pattern of seed response is captured by the same large-scale predictor (Fig. 14a, b). Similar to the uniform +2K scenario, the large-scale predictor is dominated by $-\varDelta {\overline{\omega }}_{500}$, which can be explained by the long wave radiative feedback through a GMS analysis (Fig. 14c–e).

Fig. 14

a, b As in Fig. 12 and (c–e) as in Fig. 13 except for the response to $\hbox {CO}_2$ doubling. The same large-scale predictor and GMS analysis explain the pattern of seed response

6.3 Spatial-mean response of seed and TC frequency

Figure 15a shows the seed frequency in the Northern Hemisphere across all 12 experiments, a plot analogous to Fig. 10a for the ITCZ shift experiments. The measured frequency and the large-scale predictor are compared in terms of the non-dimensional percentage change relative to the 1990s control climate. The frequency of seeds decreases with the increase of SST as well as $\hbox {CO}_2$ concentration. The experiments are scattered along the one-to-one line, suggesting that the change in seed frequency is captured by the predictor despite the different response patterns.

Fig. 15

The measured and predicted response to forcing for a seeds and b TCs over the Northern Hemisphere from July to October. The predictors are given in Eqs. (15) and (16), respectively. The black dashed line is the one-to-one line representing a perfect prediction

Over the entire Northern Hemisphere, removing ${\overline{\zeta }}$ from the predictor and using the approximated form, $-f \varDelta {\overline{\omega }}_{500}$, still captures the change of seeds with a strong correlation along the one-to-one line. The $r^2$ value of linear regression in Fig. 15a is 0.79 and reduces slightly to 0.73 without ${\overline{\zeta }}$. The insignificance of ${\overline{\zeta }}$ is due to the dominance of response in the West Pacific, which has little latitudinal shift. If the focus is on the East Pacific or the North Atlantic, it is important to include ${\overline{\zeta }}$ to capture the effect ITCZ migration analogous to section 5.

Figure 15b compares the predicted and measured changes of TC frequency. The variation across experiments is generally captured by the predictor, Eq. (16). As in the aquaplanet experiments, the ventilation index is averaged over the tropics before multiplying by the seed predictor to account for the meridional migration of strong vortices. The decrease of TCs with uniform SST increase or $\hbox {CO}_2$ increase is similar to that of seeds. While for the strongly patterned warming experiments, the response of seeds does not explain the response of TCs.

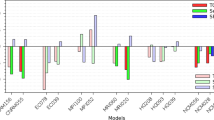
To examine the extent to which the variation of seeds explain the variation of TCs, Fig. 16 compares their frequency across the experiments. The correlation is linear for the uniform SST and $\hbox {CO}_2$ perturbation experiments, suggesting a strong influence of seed frequency on TC frequency in those scenarios.

Experiments with patterned surface warming do not follow the one-to-one line in Fig. 16. These four experiments have opposite trends in the responses of seeds and TCs. The seed response overestimates the TC response when the warmest ocean is warmed (the two larger crosses), which is compensated by an increase of ventilation index in most basins and thus a decrease in $P_2$. The opposite situation happens when the coolest ocean is warmed (the two smaller crosses). The seed response underestimates the TC response but is compensated by a decrease of ventilation index and thus an increase in $P_2$.

Fig. 16

Comparison of the TC and seed frequency in response to different forcings. The seed response explains most of the TC response in uniform surface warming and changing $\hbox {CO}_2$ experiments, but not in the patterned warming experiments. The discrepancy is explained by the second transition and entropy ventilation in Fig. 15

The inverse correlation between the ventilation index and $P_2$ is qualitatively consistent with Tang and Emanuel (2012); Vecchi et al. (2019); Hoogewind et al. (2020). The formulas to translate the ventilation index into probability are different in those three studies. While we adopt the formula of Tang and Emanuel (2012) for its physical interpretability and observational basis, our experiments do not rule out the plausibility of formulas in the other studies.

The combination of seed and ventilation responses brings the four patterned warming experiments closer to the one-to-one line in Fig. 15b. These experiments indicate that the seeds and TCs are not equivalent, and that it is important to consider both the seeds and the second transition to explain the TC response to climate change.

7 Discussion

The TC-climate relationship established in this paper and the physical interpretation bear strong similarity to observational studies and high-resolution modeling of a single TC, which supports the relevance of explicit TCs in 50-km global models to realistic TCs. In the simplest form, our predictor for TC frequency is positively correlated with the large-scale vertical velocity, low-level vorticity, and the potential intensity; and is negatively correlated with vertical wind shear and moist entropy deficit. Those five large-scale variables are precisely what comprise the genesis potential index of Murakami and Wang (2010).

In other indices of TC genesis without explicit dependence on ${\overline{\omega }}$, this information may be represented by the combination of other large-scale variables, such as the coincidence of low vertical wind shear, high relative humidity, and high potential intensity. Unlike regression-based techniques, this inter-dependence of variables does not affect the uniqueness of our formulation because of the physical separation of stages. The dependence on ${\overline{\omega }}$ in our formulation concerns the initiation of convective clusters, which is separate from the subsequent transitions to stronger vortices.

Our analysis provides a justification for a common practice to recalibrate GPI for a different model when performing statistical downscaling (e.g. Emanuel 2013). The proportionality constants between $-{\overline{\omega }}$ and $n_c$, as well as between Z and $P_1$ in the simplified form, may be sensitive to model details such as convective parameterization and divergence damping. The constants, if not sensitive to climate change, drops out when comparing the percentage changes of the predictor and the measurement (Eqs. (15), (16)).

Because the first transition is controlled more strongly by the dynamics than the thermodynamics, it is expected to be less sensitive to model physics and tracker parameters than the initiation or the second transition. The initiation of convective clusters may depend on the ability to resolve convective organization (Wing et al. 2016; Muller and Romps 2018) or the breakdown of large-scale flows such as the ITCZ (Narenpitak et al. 2020). The second transition may depend on the parameterized detrainment in the free troposphere. Those processes have complicated dependence on the model design.

The tropical clusters in our models are identified by applying a threshold on the three-hour-mean rain rate. The same procedure may be performed on any vertically integrated moisture fields that has a sharp boundary, such as the precipitable water or instantaneous rain rate. Sensitivity tests have been conducted and verified that the statistics of tracks are not influenced appreciably by the choices of moisture fields or threshold values. Therefore, we expect the same tracking algorithm to apply for satellite measurements after filtering out features much smaller than 50 km.

In our 50-km models, vorticity thresholds of $4 \times 10^{-4}$ and $1 \times 10^{-3} \text { s}^{-1}$ at 850 hPa are chosen to define the first and second transitions. Those values are chosen for consistency with the Harris et al. (2016) tracker and may need to be adjusted for a different model or a different grid spacing as like any TC tracker. The precise values are not critical for the theory, but the results suggest that the early and late stages of TC development are qualitatively different. The first transition has strong dependence on Z and weak dependence on SST; while the second transition is the opposite. Presumably, the regime shift is characterized by the formation of closed surface pressure contour and axisymmetrization. Cyclostrophic balance in the vortex reduces the relevance of f, and the axisymmetry makes the potential intensity theory more relevant.

Some differences between models and observations are noted. The correlation between $n_c$ and $-{\overline{\omega }}$ may reflect a pre-conditioning due to environmental moistening in observations; while in models it is influenced by the activation of grid-scale convection. The vortical hot towers in observations are not resolved in global models, and in the models the spinup is caused by vertical stretching on the vortex scale.

8 Summary and implications

In this paper, a theoretical framework is developed to connect the dynamics of TC evolution with statistics of TC genesis in 50-km global models. The result is a robust TC-climate relationship, Eqs. (1)–(4), that holds across a range of climates, created using different SST patterns or radiative forcings.

The importance of establishing a physical basis for the modeled TC-climate relationship is twofold. Since the modeled mean climate is less sensitive to the numerics, the relationship justifies that explicit TCs in the global model are controlled largely by physics rather than the numerical implementation. In addition, the physics behind the modeled TC-climate relationship is consistent with observational and mesoscale modeling studies of TCs, suggesting that TCs in global models are useful proxies for realistic TCs. Our analysis framework may further inform a theory for the realistic TC-climate relationship.

The key insight is that the probability of intensification can be simplified by conditioning on the vorticity. In particular, we separate the development of a TC into three stages, from a non-rotating convective cluster, to a weakly rotating seed, and then to a strongly rotating TC. The formation of a seed is characterized by closed surface pressure contour. The formation of a TC is defined based on a vorticity threshold chosen such that the TC frequency in the historical simulation matches the observation.

This paper focuses on the large-scale control on seeds rather than on their transition to TCs, as the latter has been studied more extensively in the literature (Tang and Emanuel 2012; Vecchi et al. 2019). A fundamental dynamics behind the transition from a convective cluster to a seed is a competition between vortex stretching and Rossby wave radiation at low levels. This process has been emphasized more in single-TC studies but less in global-scale studies until recently (Chavas and Reed 2019). Quantitatively, this competition is characterized by a non-dimensional parameter, Z. Aquaplanet experiments with varying planetary rotation rates, planetary radii, surface temperature and ITCZ latitudes all show a data collapse of the measured probability with respect to this parameter. The product of this parameter and the zonal-mean vertical velocity explains the increase of seeds with poleward shift of the ITCZ.

In the realistic experiments with uniform surface warming or $\hbox {CO}_2$ doubling, much of the TC response can be attributed to the seed response, which is well constrained by the same large-scale predictor that is verified in aquaplanet experiments. These results echo those of Vecchi et al. (2019); Sugi et al. (2020), who found that changes in seeds were dominant in the response to $\hbox {CO}_2$ warming. To explain the geographical distribution of TCs and the response to climate change, the leading order effect is the variation of large-scale vertical velocity multiplied by the Coriolis parameter. By analyzing the gross moist stability, the change in large-scale vertical velocity is dominated by the long wave radiation. The sensitivity of gross moist stability and other factors in the seed predictor to climate is not as significant for the experiments explored here, but could be for perturbations with direct heating in the atmospheric column. This framework suggests a pathway by which the long wave radiative feedback influences TC frequency.

The TC response does not always follow the seed response, as shown in the patterned warming experiments. The discrepancy is attributed to the different degree of entropy ventilation. When the warmest ocean is warmed, ventilation increases and the fraction of seeds becoming TCs decreases; and vice versa when the cooler ocean is warmed. In general, the fraction of seeds becoming TCs is between 20% and 50%, depending on the ventilation index. Therefore, the sensitivity of ventilation index on climate change is important for TC projection.

Our interpretation of TC genesis is an attempt to connect two explanations for the reduction of TC frequency with global warming, including increasing moist entropy deficit (e.g. Emanuel 2013) and decreasing convective mass flux (e.g. Satoh et al. 2015). The moist entropy deficit is more relevant when describing the growth of a developed vortex, and in our framework this term regulates the second transition. On the other hand, the mass flux is more relevant to explain the occurrence of the incipient convective cluster. With everything else being equal, both processes change in the direction to reduce TC frequency with global warming.

In practice, the spatial distributions of mass flux and entropy deficit may change with global warming. When weighted by other terms in the predictor, in particular the large-scale vorticity, it is possible that the warmed climate becomes more conducive to TCs. The aquaplanet simulation of Merlis et al. (2013) with a slab ocean is such an example. They decomposed the percentage change of TCs into a product of two terms: an increase with poleward shift of the ITCZ, and a decrease with uniform warming. This decomposition is consistent with our framework, where the ITCZ shift is reflected in the product of $n_c$ and $P_1$, and the increase of entropy deficit due to uniform warming is encoded in $P_2$.

This work illustrates an example to decompose a complex probability like the TC frequency into a series of probabilities that can be interpreted more easily and potentially be constrained by observations. The framework may be generalized, for instance to include the probability of rapid intensification (Bhatia et al. 2019; Ng and Vecchi 2020) or the probability of developing into major TCs (Kossin et al. 2020). We suggest that this is a useful framework to analyze the probabilistic forecast of TCs.