Abstract
We analyze a finite-difference approximation of a functional of Ambrosio–Tortorelli type in brittle fracture, in the discrete-to-continuum limit. In a suitable regime between the competing scales, namely if the discretization step \(\delta \) is smaller than the ellipticity parameter \(\varepsilon \), we show the \(\varGamma \)-convergence of the model to the Griffith functional, containing only a term enforcing Dirichlet boundary conditions and no \(L^p\) fidelity term. Restricting to two dimensions, we also address the case in which a (linearized) constraint of non-interpenetration of matter is added in the limit functional, in the spirit of a recent work by Chambolle, Conti and Francfort.
Similar content being viewed by others
1 Introduction
In this paper we provide a variational approximation by discrete finite-difference energies of functionals of the form
where \(\varOmega \) is a bounded subset of \(\mathbb {R}^d\), \(K\subseteq \varOmega \) is closed, \(u\in C^1(\varOmega \backslash K;\mathbb {R}^d)\), \(\mathcal {E}u\) denotes the symmetric part of the gradient of u, \(\mathrm{div}\,u\) is the divergence of u and \(\mathcal {H}^{d-1}\) is the \((d-1)\)-dimensional Hausdorff measure. Functionals as in (1.1) are widely used in the variational modeling of fracture mechanics for linearly elastic materials, in the framework of Griffith’s theory of brittle fracture (see, e.g. [29]). Here \(\varOmega \) stands for the reference configuration and u represents the displacement field of the body. The total energy (1.1) is composed by a bulk energy in \(\varOmega \backslash K\), where the material is supposed to be linearly elastic, and a surface term accounting for the energy necessary to produce the fracture, proportional to the area of the crack surface K. A rigorous weak formulation of the problem (1.1), which is usually complemented by the assignment of boundary Dirichlet datum, has been provided only in very recent years [21, 27]. In the appropriate functional setting, u is a (vector-valued) generalized special function of bounded deformation, for which the symmetrized gradient \(\mathcal {E}u\) and the divergence \(\mathrm{div}\,u\) are defined almost everywhere in an approximate sense (see [27]), and the set K is replaced by the \((d-1)\)-rectifiable set \(J_u\), the jump set of u.
However, the numerical treatment of functionals (1.1) presents relevant difficulties mainly connected to the presence of the surface term \(\mathcal {H}^{d-1}(J_u)\). Such difficulties already appear in the case of antiplane shear (see, e.g., [12]) where the energy (1.1) reduces to the Mumford–Shah-type functional
for a scalar-valued displacement \(u\in SBV(\varOmega )\), the space of special functions of bounded variation. In view of the aforementioned numerical issues, a particular attention has been devoted over the last three decades to provide suitable discrete approximations, by means of both finite-difference and finite-elements, of the functional (1.2).
A first approach, based on earlier models in Image Segmentation, has been proposed by Chambolle [16] in dimension \(d=1,2\); there, the discrete model depends on finite differences through a truncated quadratic potential. In the case \(d=2\), the surface term of the variational limit is described by an anisotropic function \(\varphi (\nu _u)\) of the normal \(\nu _u\) to \(J_u\) depending on the geometry of the underlying lattice. As a matter of fact, this anisotropy can be avoided by considering alternate finite-elements of different local approximations of the Mumford–Shah functional, as showed, still in dimension two, by Chambolle and Dal Maso [22]. We refer to [8] (cf. also [11]) and to [28] for some other approximations using finite-elements and continuous finite-difference approximations of (1.2), respectively.
A different strategy consists in replacing the Mumford–Shah functional by an elliptic approximation (with parameter \(\varepsilon >0\)) in the spirit of Ambrosio–Tortorelli [4, 5], and then by discretizing these elliptic functionals by means of either finite-difference or finite-elements with mesh-size \(\delta \), independent of \(\varepsilon \). For a suitable fine mesh, with size \(\delta =\delta (\varepsilon )\) small enough, these numerical approximations \(\varGamma \)-converge, as \(\varepsilon \rightarrow 0\), to the Mumford–Shah functional.
This suggests that a remarkable problem to be addressed is the so called “quantitative analysis”: i.e., the study of the limit behavior of these approximations as \(\delta \) and \(\varepsilon \) simultaneously tend to 0. Following on the footsteps of the approximation of the Modica–Mortola functional proposed by Braides and Yip [14], this analysis has been recently developed by Bach, Braides and Zeppieri in [6] for (1.2). They characterize the limit behavior of the energies
showing the variational convergence to the functional (1.2) in the regime \(\delta \!<\!<\varepsilon \). Other scalings of the parameters are also studied: in the regime \(\delta \sim \varepsilon \), the surface energy is described by a function \(\varphi (\nu _u)\) solution to a discrete optimal-profile problem, while if \(\delta \!>\!>\varepsilon \), the limit energy is the Dirichlet functional. Recently, approximations of (1.2) (thus without anisotropy in the limit) have been obtained even when \(\delta \sim \varepsilon \), by employing discretizations on random lattices. In particular, [7] analyzes the random version of the discrete energies in [6], basing on [31] (cf. also [15]).
Coming back to the problem of providing discrete approximations of the Griffith functional, we mention the finite-elements approximation in [30] and focus on the discrete-to-continuum analysis performed by Alicando et al. [1]. They considered, in the spirit of [16] and in the planar setting \(d=2\), discrete energies of the form
defined on a portion \(R_\delta ^\xi \) of \(\varOmega \cap \delta \mathbb {Z}^d\), where \(\rho \) is a positive kernel, \(\theta \) is a positive constant, \(f(t):=\min \{t,1\}\), \(D_\delta ^\xi u(x)\) denotes the difference quotient \(\frac{1}{\delta }(u(x+\delta \xi )-u(x))\) and \(\mathrm{div}_\delta ^\xi \, u\) is a suitable discretization of the divergence which takes into account three-point-interactions in the directions \(\xi \) and \(\xi ^\perp \) (the vector orthogonal to \(\xi \)). In order to obtain compactness of sequences of competitors with equibounded energy, they require that \(\rho (\xi )>0\) for \(\xi \in \{\pm e_1, \pm e_2, \pm (e_1\pm e_2)\}\), which amounts to consider nearest-neighbors (NN) and next-to-nearest neighbors (NNN) interactions in the energies. Furthermore, an \(L^\infty \) bound has to be imposed, which is quite unnatural in Fracture Mechanics. Differently from [6], the characterization of the limit energy cannot be achieved with the reduction to a 1-dimensional case by means of slicing techniques (see, e.g., [13, 17, 28]), due to the presence of the divergence term. Hence, a different strategy has to be used, involving the construction of suitable interpolants (see [1, Proposition 4.1]). As it happened in [16], the surface term in the limit energy is still reminiscent of the underlying lattice, and only a continuous version of (1.3) allows to obtain \(\mathcal {H}^{d-1}(J_u)\) as surface energy. Furthermore, a possible extension of the model to dimension \(d=3\), still involving NN and NNN interactions is proposed, but no compactness result is provided.
Our results This leads us to the motivation of our paper, which complements the results of both [1, 6]. On the one hand, we provide a discrete Ambrosio–Tortorelli approximation to the Griffith functional both in dimension \(d=2\) and \(d=3\), of the form
where \(S_d\) is a set of lattice directions (depending on the dimension d), \(D_{\delta ,\xi }u\) and \(\mathrm{Div}_{\delta }\,u\) are suitable discretizations of the symmetrized gradient and of the divergence of the vector-valued u, and the latter term is a discrete Modica–Mortola functional. Notice that \(\mathrm{Div}_{\delta }\,u\) takes into account \((d+1)\)-point-interactions on a complete set of orthogonal directions (see (3.4)). Then we prove, as main result (Theorem 3), that (1.4) \(\varGamma \)-converges as \(\varepsilon \rightarrow 0\) to the Griffith’s functional under the assumption that \(\delta \!<\!<\varepsilon \).
On the other hand, we conclude the analysis started in [1] for the finite-difference approximation of (1.1) in dimension \(d=3\), although with a different approach, by both rigorously proving a compactness result under more general assumptions, and recovering an isotropic surface energy in the limit. We also stress the fact that the extension of the two-dimensional model to the case \(d=3\) is not just a minor modification but requires the introduction of additional interactions in the elastic term of the energies by specifying the set of directions \(S_3\) (see (2.24)); namely, we need to take into account also next-to-next-nearest neighbors (NNNN) interactions, corresponding to lattice vectors \(\xi \in \{\pm (e_1\pm e_2\pm e_3)\}\).
The aforementioned compactness result, which is the content of Proposition 1, determines the functional space domain of the limit: we benefit from the recent results [21, 25] and prove that sequences \((u_\varepsilon ,v_\varepsilon )\) with equibounded energies (1.4) converge (up to subsequences) to a limit pair \((u,v)\in GSBD^2_\infty (\varOmega )\times \{1\}\). We refer the reader to Sect. 2 for a precise definition of this function space, where also the value \(\infty \) is allowed. We underline that our compactness result, valid under the weaker assumption that \(\frac{\delta }{\varepsilon }\) be bounded, cannot be obtained in our view through any slicing procedure (as it happened, on the contrary, in [6]) and also refines the compactness lemma [17, Lemma 1] to deal with the vector-valued case. Indeed, while in the scalar-valued case controlling the total variation along d independent slices of \(u_\varepsilon \) is enough to provide BV-compactness, no analogue procedure is at the moment known in GSBD (whose definition [27, Definition 4.1] in principle requires a uniform control of the symmetrized slices on a dense set of directions in the unit sphere, cf. also [27, Remark 4.15]). Such issue prevents us to get a uniform bound in GSBD from a control on the slices corresponding to the directions of the lattice vectors, that could be easily obtained from the discrete functional as in [6, 17]. We notice that the situation is different with respect to the BD case, where it is enough to control the slices on a finite set of directions, see [2, Proposition 3.2].
In fact, we are able to prove that a continuous Ambrosio–Tortorelli functional, defined on the standard piecewise affine interpolations \({\bar{u}}_\varepsilon \) of the \(u_\varepsilon \) and on suitable piecewise constant interpolations \({{\tilde{v}}}_{min, \varepsilon }\) of the \(v_\varepsilon \) (different than the standard ones), bounds from below the discrete energies (1.4). To this aim, taking the additional (NNNN) interactions is crucial in dimension \(d=3\) . In addition, we do not need to add any \(L^p\) fidelity term to the discrete energies, since compactness in \(GSBD^2_\infty \) does not require such limitations and is also able to handle the fact that u may take value \(\infty \).
The proof of the \(\varGamma \)-liminf inequality is subdivided into two steps. The lower semicontinuity of the elastic part of the limit energies (see Lemma 5 and Proposition 2) can be obtained by combining slicing arguments on suitable interpolations of \(u_\varepsilon \) and \(v_\varepsilon \) with a splitting into sublattices of \(\delta \mathbb {Z}^d\), which are frequently used techniques to work with discrete energies with both short and long-range interactions (see, e.g., [1, 13]). It must be noticed, at this point, that both the first two summands in (1.4) give a contribution to the second term in (1.1). As, within the proof technique described above, both are assumed to be nonnegative, the constants \(\mu \) and \(\lambda \) appearing there are related by \(2\mu =\lambda +2\theta \) with \(\theta \ge 0\), as it also happened, for instance, in the statement of [1, Theorem 7.1]. Hence, our main result is stated in terms of the two indendent parameters \(\lambda \) and \(\theta \) and is valid for materials whose Poisson ratio (due to the inequality \(2\mu \ge \lambda \)) does not exceed the value \(\frac{1}{3}\).
The lower bound for the surface term, instead, requires a more refined blow-up procedure (Proposition 3) and this is the very first technical point where we need to assume that \(\frac{\delta }{\varepsilon }\rightarrow 0\), in order to recover the optimal constant. Indeed a slicing argument under the weaker assumption that \(\delta /\varepsilon \) be bounded would provide a lower bound with a wrong constant. We remark that, also in this proof, similar arguments as in Proposition 1 have to be used, in order to get compactness of a rescaled version of the \(u_\varepsilon \). Moreover, additional care is needed in order to deal with the fact that our limit displacements may assume the value infinity (see e.g. Step 2 in Proposition 2).
The construction of a recovery sequence (Proposition 4) relies on the density result for \(GSBD^2\) functions [19, Theorem 1.1], recalled here with Theorem 1. The upper bound for the elastic term is obtained by first reducing the discrete energies to continuous ones by means of a classical translation argument (see, e.g. [1, Proposition 4.4]) and then by exploiting the upper estimates coming from the approximations of \(\int |\langle (\mathcal {E}u)\xi ,\xi \rangle |^2\,\mathrm {d}x\) and \(\int (\mathrm{div}\,u)^2\,\mathrm {d}x\) outside an infinitesimal neighborhood of the jump set of the target function u. The limsup inequality for the surface term is developed as in [6, Proposition 4.2], by also employing the one-dimensional solution to the Ambrosio–Tortorelli optimal profile problem.
We conclude our analysis by investigating the compatibility of our two-dimensional model with the constraint of non-interpenetration. The answer is positive under the assumptions of [18] but, in order to obtain the desired upper bound, we need to require the stronger scaling \(\frac{\delta }{\varepsilon ^2}\rightarrow 0\) between the parameters.
As a final remark, we mention that our results also give a partial insight on the case \(\delta \sim \varepsilon \). Indeed, the constructions in Sects. 5 and 6 can also be used to show that, whenever the ratio \(\delta /\varepsilon \) stays bounded, the \(\varGamma \)-limit of the energy (1.4) can be controlled from above and from below by functionals of the kind (1.1), with different constants appearing in the surface term. However, a precise characterization of the limit energy in this case has to face additional issues. The analysis performed in [6] for the scalar-valued case, indeed, relies on two major ingredients. First of all, the limit energy is characterized as an abstract integral surface energy by means of the global method for relaxation introduced in [10]. This could be also done in our setting, by exploiting a recent integral representation result for energies on spaces of functions of bounded deformation [26] (see also [23] in the planar setting). However, a crucial step in this procedure consists in proving that a separation of bulk and surface contributions takes place in the limit. In [6] this is done by means of an explicit construction which, however, is confined to 2 dimensions and strongly exploits the SBV-setting. A more general point of view, also suitable for higher dimensions, is for instance used in [7, Proposition 4.11] with the help of a weighted coarea formula. This is unfortunately also a tool which is not available when dealing with (G)SBD functions. The investigation of these issues has therefore to be deferred to further contributions.
Outline of the paper The paper is organized as follows. In Sect. 2 we fix the basic notation and collect some definitions and results on the function spaces we will deal with. In Sect. 3 we introduce our discrete model and state the main results of the paper. Section 4 contains the compactness result of Proposition 1. Section 5 is devoted to the liminf inequality, proved with Proposition 3, while Sect. 6 deals with the upper inequality (Proposition 4). Eventually, in Sect. 7 we analyze the compatibility of the two-dimensional model with a non-interpenetration constraint.
2 Preliminaries
2.1 Notation
The symbol \(\langle \cdot ,\cdot \rangle \) denotes the scalar product in \(\mathbb {R}^d\), while \(|\cdot |\) stands for the Euclidean norm in any dimension. For any \(x,y\in \mathbb {R}^d\), [x, y] is the segment with endpoints x and y. The symbol \(\varOmega \) will always denote an open, bounded subset of \(\mathbb {R}^d\). The Lebesgue measure in \(\mathbb {R}^d\) and the s-dimensional Hausdorff measure are written as \(\mathcal {L}^d\) and \(\mathcal {H}^s\), respectively. We will often use the notation |A| for the Lebesgue measure of a Borel set A. The symbols \(\lesssim \) and \(\gtrsim \) denote the boundedness modulo a constant.
For any locally compact subset \(B \subset \mathbb {R}^d\) (i.e. any point in B has a neighborhood contained in a compact subset of B), the space of bounded \(\mathbb {R}^m\)-valued Radon measures on B [respectively, the space of \(\mathbb {R}^m\)-valued Radon measures on B] is denoted by \(\mathcal {M}_b(B;\mathbb {R}^m)\) [resp., by \(\mathcal {M}(B;\mathbb {R}^m)\)]. If \(m=1\), we write \(\mathcal {M}_b(B)\) for \(\mathcal {M}_b(B;\mathbb {R})\), \(\mathcal {M}(B)\) for \(\mathcal {M}(B;\mathbb {R})\), and \(\mathcal {M}^+_b(B)\) for the subspace of positive measures of \(\mathcal {M}_b(B)\). For every \(\mu \in \mathcal {M}_b(B;\mathbb {R}^m)\), its total variation is denoted by \(|\mu |(B)\). We write \(\{e_1,\dots ,e_d\}\) for the canonical basis of \(\mathbb {R}^d\).
2.2 GBD, GSBD, and \(GSBD^2_\infty \) functions
We recall here some basic definitions and results on generalized functions with bounded deformation, as introduced in [27]. Throughout the paper we will use standard notations for the spaces SBV and SBD, referring the reader to [3] and [2, 9, 32], respectively, for a detailed treatment on the topics.
Let \(\xi \in \mathbb {R}^d\backslash \{0\}\) and \(\varPi ^\xi =\{y\in \mathbb {R}^d:\, \langle \xi ,y\rangle =0\}\). If \(y\in \varPi ^\xi \) and \(\varOmega \subset \mathbb {R}^d\) we set \(\varOmega _{\xi ,y}:=\{t\in \mathbb {R}:\, y+t\xi \in \varOmega \}\) and \(\varOmega _\xi :=\{y\in \varPi ^\xi :\, \varOmega _{\xi ,y}\ne \emptyset \}\). Given \(u:\varOmega \rightarrow \mathbb {R}^d\), \(d\ge 2\), we define \(u^{\xi ,y}: \varOmega _{\xi ,y}\rightarrow \mathbb {R}\) by
while if \(h: \varOmega \rightarrow \mathbb {R}\), the symbol \(h^{\xi ,y}\) will denote the restriction of h to the set \(\varOmega _{\xi ,y}\); namely,
Definition 1
An \({\mathcal {L}}^{d}\)-measurable function \(u:\varOmega \rightarrow \mathbb {R}^{d}\) belongs to \(GBD(\varOmega )\) if there exists a positive bounded Radon measure \(\lambda _u\) such that, for all \(\tau \in C^{1}(\mathbb {R}^{d})\) with \(-\frac{1}{2} \le \tau \le \frac{1}{2}\) and \(0\le \tau '\le 1\), and all \(\xi \in S^{d-1}\), the distributional derivative \(D_\xi (\tau (\langle u,\xi \rangle ))\) is a bounded Radon measure on \(\varOmega \) whose total variation satisfies
for every Borel subset B of \(\varOmega \).
If \(u\in GBD(\varOmega )\) and \(\xi \in \mathbb {R}^d\backslash \{0\}\) then, in view of [27, Theorem 9.1, Theorem 8.1], the following properties hold:
-
(a)
\({\dot{u}}^{\xi ,y}(t)=\langle \mathcal {E}u(y+t\xi )\xi ,\xi \rangle \) for a.e. \(t\in \varOmega _y^\xi \);
-
(b)
\(J_{u^{\xi ,y}}=(J_u^\xi )_y^\xi \) for \(\mathcal {H}^{n-1}\)-a.e. \(y\in \varPi ^\xi \), where
$$\begin{aligned} J_u^\xi :=\{x\in J_u:\, \langle u^+(x)-u^-(x),\xi \rangle \ne 0\}\,; \end{aligned}$$(2.3)
Definition 2
A function \(u \in GBD(\varOmega )\) belongs to the subset \(GSBD(\varOmega )\) of special functions of bounded deformation if in addition for every \(\xi \in S^{d-1}\) and \({\mathcal {H}}^{d-1}\)-a.e. \(y \in \varPi ^\xi \), the function \(u^{\xi ,y}\) belongs to \(SBV_{\mathrm {loc}}(\varOmega ^\xi _y)\).
By [27, Remark 4.5] one has the inclusions \(BD(\varOmega )\subset GBD(\varOmega )\) and \(SBD(\varOmega )\subset GSBD(\varOmega )\), which are in general strict. Some relevant properties of functions with bounded deformation can be generalized to this weak setting: in particular, in [27, Theorem 6.2 and Theorem 9.1] it is shown that the jump set \(J_u\) of a GBD-function is \({\mathcal {H}}^{d-1}\)-rectifiable and that GBD-functions have an approximate symmetric differential \(\mathcal {E}u(x)\) at \(\mathcal {L}^{d}\)-a.e. \(x\in \varOmega \), respectively. The space \(GSBD^2(\varOmega )\) is defined through:
Every function in \(GSBD^2(\varOmega )\) is approximated by bounded SBV functions with more regular jump set, as stated by the following result ( [19, Theorem 1.1]). In order to deal with the Dirichlet boundary value problem (in fact we will impose a Dirichlet boundary datum \(u_0 \in H^1(\mathbb {R}^d;\mathbb {R}^d)\) on a subset \(\partial _D \varOmega \subset \partial \varOmega \)), we report a version adapted for boundary data (cf. [19, Section 5]). For technical reasons, we suppose that \({\partial \varOmega }={\partial _D \varOmega }\cup {\partial _N \varOmega }\cup N\) with \({\partial _D \varOmega }\) and \({\partial _N \varOmega }\) relatively open, \({\partial _D \varOmega }\cap {\partial _N \varOmega }=\emptyset \), \(\mathcal {H}^{d-1}(N)=0\), \({\partial _D \varOmega }\ne \emptyset \), \(\partial ({\partial _D \varOmega })=\partial ({\partial _N \varOmega })\), and that there exist a small \({\overline{\delta }}\) and \(x_0\in \mathbb {R}^d\) such that for every \(\delta \in (0,{\overline{\delta }})\)
where \(O_{\delta ,x_0}(x):=x_0+(1-\delta )(x-x_0)\).
In the following, we denote by \(\mathrm{tr}(u)\) the trace of u on \(\partial \varOmega \) which is well defined for functions in \(GSBD^2(\varOmega )\) if \(\varOmega \) is Lipschitz (see [27, Section 5]).
Theorem 1
Let \(\varOmega \subset \mathbb {R}^d\) be a bounded open Lipschitz set, and \(u\in GSBD^2(\varOmega ;\mathbb {R}^d)\). Then there exists a sequence \(u_n\) such that
(i) \(u_n\in SBV^2(\varOmega ;\mathbb {R}^d)\cap L^\infty (\varOmega ;\mathbb {R}^d)\);
(ii) each \(J_{u_n}\) is closed and included in a finite union of closed connected pieces of \(C^1\)-hypersurfaces;
(iii) \(u_n\in W^{1,\infty }({\varOmega }\backslash J_{u_n};\mathbb {R}^d)\), and
Moreover, if \(\partial _D \varOmega \subset \partial \varOmega \) satisfies (2.4) and \(u_0 \in H^1(\mathbb {R}^d;\mathbb {R}^d)\), then one can ensure that each \(u_n\) satisfies \(u_n=u_0\) in a neighborhood \(U_n \subset \varOmega \) of \(\partial _D \varOmega \), provided that (2.7) is replaced by
A further approximation result, by Cortesani and Toader [24, Theorem 3.9], allows us to approximate \(GSBD^2(\varOmega )\) functions with the so-called “piecewise smooth” SBV-functions, denoted \(\mathcal {W}(\varOmega ;\mathbb {R}^d)\), characterized by the three properties
As observed in [20, Remark 4.3], we may even approximate through functions u such that, besides (2.9), also \({\overline{J}}_u \subset \varOmega \) holds and the \((d{-}1)\)-dimensional simplexes in the decomposition of \({\overline{J}}_u\) may be taken pairwise disjoint with \(J_u \cap \varPi _i \cap \varPi _j=\emptyset \) for any two different hyperplanes \(\varPi _i\), \(\varPi _j\). Furthermore, in the assumption under which (2.8) holds true, we may also ensure that \(u=u_0\) in a neighborhood of \({\partial \varOmega }\). We will employ these properties in Sect. 6.
We recall the following general \(GSBD^2\) compactness result from [21]. In the following, when we deal with sets of finite perimeter, such as \(A^\infty _u\), we identify the set with its subset of points with density 1, with respect to d-dimensional Lebesgue measure (cf. [3, Definition 3.60]), while we denote explicitly their essential boundary with the symbol \(\partial ^*\).
Theorem 2
(\(GSBD^2\) compactness) Let \(\varOmega \subset \mathbb {R}\) be an open, bounded set, and let \((u_n)_n \subset GSBD^2(\varOmega )\) be a sequence satisfying
Then there exists a subsequence, still denoted by \(u_n\), such that the set \(A^\infty _u := \lbrace x\in \varOmega : \, |u_n(x)| \rightarrow +\infty \rbrace \) has finite perimeter, and there exists \(u \in GSBD^2(\varOmega )\) such that
\(GSBD^2_\infty \) functions.
Inspired by the previous compactness result, in [25] a space of \(GSBD^2\) functions which may also attain a limit value \(\infty \) has been introduced, as we recall. The space \(\bar{\mathbb {R}}^d := \mathbb {R}^d \cup \lbrace \infty \rbrace \) (with its sum given by \(a + \infty = \infty \) for any \(a \in \bar{\mathbb {R}}^d\)) is in a natural bijection with \( \mathbb {S}^d =\lbrace \xi \in \mathbb {R}^{d+1}:\,|\xi | =1 \rbrace \) through the stereographic projection of \(\mathbb {S}^{d}\) to \(\bar{\mathbb {R}}^d\): for \(\xi \ne e_{d+1}\), \(\phi (\xi ) = \frac{1}{1-\xi _{d+1}}(\xi _1,\ldots ,\xi _d),\) \(\phi (e_{d+1}) = \infty \). Let \(\psi :\bar{\mathbb {R}}^d\rightarrow \mathbb {S}^{d}\) denote the inverse. Note that
induces a bounded metric on \(\bar{\mathbb {R}}^d\). Then
Symbolically, we will also write \(u = u \chi _{\varOmega \setminus A^\infty _u} + \infty \chi _{A^\infty _u}.\) Moreover, for any \(u \in GSBD^2_\infty (\varOmega )\)
In particular,
where \(\widetilde{u}_t\) is the function from (2.12). Hereby, we also get a natural definition of a normal \(\nu _u\) to the jump set \(J_u\), and the slicing properties described for \(GSBD^2\) still hold in \(\varOmega \setminus A^\infty _u\). Finally, we point out that all definitions are consistent with the usual ones if \(u \in GSBD^2(\varOmega )\); i.e., if \(A^\infty _u= \emptyset \). Since \(GSBD^2(\varOmega )\) is a vector space, we observe that the sum of two functions in \(GSBD^2_\infty (\varOmega )\) lies again in this space. A metric on \(GSBD^2_\infty (\varOmega )\) is given by
where \(d_{\bar{\mathbb {R}}^d}\) is the distance in (2.11). In Sects. 4 and 5, when we work in an extended domain \(\widetilde{\varOmega }\), we will still write d(u, v) for \(\int _{\widetilde{\varOmega }} d_{\bar{\mathbb {R}}^d}(u(x),v(x)) \, \,\mathrm {d}x\). We say that a sequence \((u_n)_n \subset GSBD^2_\infty (\varOmega )\) converges weakly to \(u \in GSBD^2_\infty (\varOmega )\) if
2.3 Some lemmas
For \(a<b\), we introduce the space \(PC_\delta (a,b)\) of piecewise-constant functions on partitions of \((a,b)\subset \mathbb {R}\) with size \(\delta \); namely,
For every \(v\in PC_\delta (a,b)\), we denote by \(\hat{v}\) the corresponding piecewise-affine interpolation on the nodes of the same partition, defined as
Lemma 1
Let \((v_\varepsilon )_\varepsilon \) be a sequence such that \(v_\varepsilon \in PC_\delta (a,b)\), \(v_\varepsilon \ge 0\), and let \((\hat{v}_\varepsilon )_\varepsilon \) be the sequence of the corresponding piecewise-affine interpolations defined as in (2.17). Assume that there exists \(C>0\) such that
Then, setting
we have:
(a) for every fixed constant \(N_C>0\) depending only on C, it holds that
(b) for every A open such that \(A\subset \!\subset \!(a,b)\backslash I\), there exists \(\eta _A>0\) such that
Proof
The assertion (b) immediately follows from (a). As for the proof of (a), let us fix \(N_C:=\lfloor 4C\rfloor \) and, arguing by contradiction, we assume that \(\#I=N_C+1\) and \(I=\{s^1,s^2,\dots , s^{N_C+1}\}\). For every such index i, we denote by \((s_\varepsilon ^i)_\varepsilon \) the sequence defined by (2.19) such that \(s_\varepsilon ^i\rightarrow s^i\) and
Since by (2.18) \(v_\varepsilon \rightarrow 1\) a.e. in (a, b), we can find a sequence \((t_\varepsilon ^i)_\varepsilon \) such that
-
(i)
\(s_\varepsilon ^i<t_\varepsilon ^i<s_\varepsilon ^{i+1}\) ;
-
(ii)
\(t_\varepsilon ^i\rightarrow s^i\) ;
-
(iii)
\(\displaystyle \mathop {\lim \inf }_{\varepsilon \rightarrow 0}v_\varepsilon (t_\varepsilon ^i)=1\).
Moreover, we may assume that the subsequences of \(s_\varepsilon ^i\) and \(t_\varepsilon ^i\) realizing the liminf in (2.20) and (iii), respectively, have infinite terms of the sequences of the indices in common. Now, let \(\hat{s}^i_\varepsilon \) and \(\hat{t}^i_\varepsilon \) be the greatest nodes of the partition that are less or equal than \(s^i_\varepsilon \) and \(t^i_\varepsilon \), respectively. Since \(\delta \rightarrow 0\) as \(\varepsilon \rightarrow 0\), we have that \(|s^i_\varepsilon -\hat{s}^i_\varepsilon |\rightarrow 0\) and \(|t^i_\varepsilon -\hat{t}^i_\varepsilon |\rightarrow 0\), which, combined with the fact that \(\hat{v}_\varepsilon (\hat{s}^i_\varepsilon )={v}_\varepsilon (\hat{s}^i_\varepsilon )\), \(\hat{v}_\varepsilon (\hat{t}^i_\varepsilon )={v}_\varepsilon (\hat{t}^i_\varepsilon )\), with (2.20) and (iii) give
Now, for every i and \(\varepsilon \), let \({\tilde{t}}_\varepsilon ^i\) be the first node of the partition such that \({\tilde{t}}_\varepsilon ^i\ge \hat{s}_\varepsilon ^i\) and \(v_\varepsilon ({\tilde{t}}_\varepsilon ^i)\ge \frac{1}{2}\), and let \(\tau _\varepsilon ^i\) be the first point in \((\hat{s}_\varepsilon ^i,{\tilde{t}}_\varepsilon ^i)\) such that \(\hat{v}_\varepsilon (\tau _\varepsilon ^i)=\frac{1}{2}\), whose existence is ensured by the Mean Value Theorem. We then have
whence
Now, by Young’s inequality and (2.18),
which gives a contradiction. \(\square \)
Lemma 2
Let \(\varOmega '\subset \!\subset \!\varOmega \) and \((f_\varepsilon )_\varepsilon \), \((g_\varepsilon )_\varepsilon \) be sequences of real-valued measurable functions such that
-
(i)
\(f_\varepsilon \rightarrow f\) a.e. in \(\varOmega \), \(0\le f_\varepsilon (x)\le M\);
-
(ii)
\(g_\varepsilon \rightharpoonup g\) in \(L^2(\varOmega ')\),
for some measurable f and g. Then,
In particular,
For \(\delta >0\), and for any measurable function \(u:\varOmega \subset \mathbb {R}^d\rightarrow \mathbb {R}^d\) and \(y\in \mathbb {R}^d\backslash \{0\}\) we define the translations
where \(\lfloor z \rfloor :=\sum _{i=1}^d\left\lfloor {\langle z,e_i\rangle }\right\rfloor e_i\) and, for every \(t\in \mathbb {R}\), \(\lfloor t \rfloor \) denotes the integer part of t. We have that \(T_y^{\delta }u\) is constant on each d-cube \(\alpha +\delta (0,1]^d\), \(\alpha \in \delta \mathbb {Z}^d\). Moreover, the following result holds (see, e.g., [1, Lemma 2.11]).
Lemma 3
Let \(u_\delta \rightarrow u\) in \(L^1(\varOmega ;\mathbb {R}^d)\) as \(\delta \rightarrow 0\). Then for every \(\varOmega '\!\subset \!\subset \varOmega \) it holds
-
(i)
$$\begin{aligned} \lim _{\delta \rightarrow 0}\int _{[0,1]^d}\Vert T_y^{\delta } u_\delta - u\Vert _{L^1(\varOmega ',\mathbb {R}^d)}\,\mathrm {d}y=0; \end{aligned}$$(2.23)
-
(ii)
if \(C_\delta \subset [0,1]^d\) is a family of sets such that \(\displaystyle \mathop {\lim \inf }_{\delta \rightarrow 0}|C_\delta |>0\), then there exists a sequence \(y_\delta \in C_\delta \) such that \(T_{y_\delta }^{\delta }u_\delta \rightarrow u\) in \(L^1(\varOmega ';\mathbb {R}^d)\).
Let \(d\in \{2,3\}\). We set
and consider a kernel function \(\sigma :\mathbb {Z}^d\rightarrow [0,+\infty )\) such that
and \(\sigma (\xi )\ne 0\) for every \(\xi \in S_d\); we will often use the shortcut
Lemma 4
Let \(d\in \{2,3\}\) and M be a \(d\times d\) symmetric matrix. Then, defining \(S_d\) and \(\sigma \) as before, it holds that
where
Proof
We can rewrite the sum on left hand side of (2.25c) as (recall that \(\{e_1, \dots , e_d\}\) denote the canonical basis of \(\mathbb {R}^d\))
which coincides with the right hand side of (2.25c). \(\square \)
Remark 1
Notice that setting \({\tilde{c}}_{\sigma ,d}:=\min \{c_{1,\sigma ,d},c_{2,\sigma ,d}\}\), from (2.25c) we may deduce the bound
Moreover, choosing in (2.25c)
we obtain the identity
3 Discrete models and approximation results
Let \(d\in \{2,3\}\), \(\varOmega \subset \mathbb {R}^d\) an open, bounded, Lipschitz set, with \({\partial \varOmega }\) satisfying (2.4) and the related assumptions, and let \(u_0\in H^1(\mathbb {R}^d;\mathbb {R}^d)\). For any \(\delta >0\), we consider the scaled lattice \(\delta \mathbb {Z}^d\) and set \(\varOmega _\delta :=\varOmega \cap \delta \mathbb {Z}^d\). We introduce suitable discretizations for both the symmetrized gradient and the divergence. For \(\xi \in \mathbb {R}^d\backslash \{0\}\), \(\delta >0\), and \(u:\varOmega \rightarrow \mathbb {R}^d\) measurable we define
For a scalar function \(v:\varOmega \rightarrow \mathbb {R}\), we will often adopt the notation
Moreover, for any \(\{\psi _1,\dots ,\psi _d\}\) orthogonal basis of \(\mathbb {R}^d\), we set
Then we define
In order to impose a non-interpenetration constraint in the limit fracture energy, we treat differently in the approximation the positive and negative part of the discrete divergence. We set, for \(u:\varOmega \rightarrow \mathbb {R}^d\) measurable,
For \(u:\varOmega \rightarrow \mathbb {R}^d\), \(v:\varOmega \rightarrow \mathbb {R}\) measurable, \(\xi \in \mathbb {Z}^d\backslash \{0\}\), \(\sigma _{|\xi |}\) fixed from (2.25), we consider the functionals \(F_\varepsilon ^\xi \), \(F_\varepsilon \), \({F}^\mathrm{div}_\varepsilon \) defined as
where
and \({F}^{\mathrm{div}^+}_\varepsilon \), \({F}^{\mathrm{div}^-}_\varepsilon \), \(F_\varepsilon ^{\mathrm {div},\mathrm {NI}}\) given by
Notice that \({F}^{\mathrm{div}^-}_\varepsilon \) does not include any contribution in v. Moreover, we introduce the discrete Modica–Mortola-type functional
It will be useful to introduce also a localized version of the functionals defined above. For every \(A\subset \varOmega \) open bounded set, the symbols \(F_\varepsilon ^\xi (u,v,A)\), \({F}^\mathrm{div}_\varepsilon (u,v,A)\) and \(G_\varepsilon (v,A)\) denote the energies as in (3.6a), (3.6b) and (3.9), respectively, where the sums are restricted to \(\alpha \in R_\delta ^\xi (A)\) defined as in (3.7) with A in place of \(\varOmega \).
For \(\lambda \), \(\theta >0\), let \(E_\varepsilon ^{\lambda , \theta }\) and \((E_{\lambda , \theta }^{\mathrm {NI}})_\varepsilon \) be defined on \( L^1(\varOmega ;\mathbb {R}^d)\times L^1(\varOmega ;\mathbb {R})\) by
and
Let us define the class of vector-valued piecewise constant functions on \(\varOmega \)
and, analogously, the class of real-valued piecewise constant functions \(\mathcal {A}_\delta (\varOmega ;\mathbb {R})\); in order to deal with the Dirichlet boundary value problem, we set
and \(\mathcal {A}_\delta ^{\mathrm {Dir}}(\varOmega ;\mathbb {R})\) for real-valued functions, with \(u_0\) replaced by the constant function 1.
We introduce the energy functionals \((E_{\lambda ,\theta }^{\mathrm {Dir}})_\varepsilon \) and, for every \(M>0\), \((E_{\lambda , \theta }^{\mathrm {NI},M})_\varepsilon \) defined for u and v measurable by
and
For fixed \(\lambda \), \(\theta >0\) we consider the Griffith functional \(\mathcal {G}_{\lambda , \theta }\) defined on \(GSBD^2_\infty (\varOmega )\) (recall (2.13)) by
and its Dirichlet version
Notice that a more compact expression of the jump part is obtained by considering a set \(\widetilde{\varOmega } \supset \varOmega \) with
and by extending u to a function \(u' \in GSBD^2_\infty (\widetilde{\varOmega })\) defined as
then
We also set
and, for every \(M>0\),
Notice that \({\mathcal {G}}_{\lambda , \theta }^\mathrm {Dir}(u)={\widetilde{\mathcal {G}}} _{\lambda , \theta }^\mathrm {Dir}(\widetilde{u}_t,1)\) for \(\mathcal {L}^d\)-a.e. \(t\in \mathbb {R}^d\), by (2.14). Moreover, \({\mathcal {G}}_{\lambda ,\theta }^{\mathrm {NI},M}\) displays a non-interpenetration constraint, not present in \({{\mathcal {G}}}_{\lambda , \theta }^\mathrm {Dir}\). We define it directly accounting for an \(L^\infty \) bound for |u| at level M, for technical reasons. Finally, we do not take into account the role of boundary conditions for the functional with non-interpenetration constraint, since we employ results from [18] (cf. Lemma 7), where the boundary value problem was not explicitly addressed.
We are now ready to state the main results of the paper. In the following we assume that \(u_0\), \(\lambda \), \(\theta \) are fixed and that \(\lim _{\varepsilon \rightarrow 0} \frac{\delta }{\varepsilon }=0\).
Theorem 3
Under the assumptions above, it holds that:
-
(i)
as \(\varepsilon \rightarrow 0\), \((E_{\lambda ,\theta }^{\mathrm {Dir}})_\varepsilon \) \(\varGamma \)-converges with respect to the topology of the convergence in measure to \({\widetilde{\mathcal {G}}}_{\lambda , \theta }^\mathrm {Dir}\);
-
(ii)
for \(((u_\varepsilon , v_\varepsilon ))_\varepsilon \) such that \(\sup _\varepsilon (E_{\lambda ,\theta }^{\mathrm {Dir}})_\varepsilon (u_\varepsilon , v_\varepsilon ) <+\infty \), there exists \(u \in GSBD^2_\infty (\varOmega )\) such that \(d(u_\varepsilon ,u)\rightarrow 0\), \(v_\varepsilon \rightarrow 1\), and
$$\begin{aligned} {\mathcal {G}}_{\lambda , \theta }^\mathrm {Dir}(u,v) \le \liminf _{\varepsilon \rightarrow 0}(E_{\lambda ,\theta }^{\mathrm {Dir}})_\varepsilon (u_\varepsilon , v_\varepsilon ). \end{aligned}$$(3.14)
We remark that any sequence of minimizers \((u_\varepsilon , v_\varepsilon )_\varepsilon \) for \((E_{\lambda ,\theta }^{\mathrm {Dir}})_\varepsilon \) satisfies, up to a subsequence, \(d(u_\varepsilon , u)\rightarrow 0\), for \(u \in GSBD^2_\infty (\varOmega )\) such that any \((\widetilde{u}_t,1)\) minimizes \(\widetilde{\mathcal {G}}_{\lambda , \theta }^\mathrm {Dir}\) (recall \(\widetilde{u}_t=u \chi _{\varOmega \setminus A^\infty _u} + t \chi _{A^\infty _u}\)). In particular, \(u_\varepsilon \) converges to u a.e. in \(\varOmega \setminus A^\infty _u\) and the bulk energies of \(u_\varepsilon \) vanish in \(A^\infty _u\) (cf. [19, Theorem 5.8]).
Theorem 4
Under the assumptions above, for every \(M >0\) it holds that:
-
(i)
\({\mathcal {G}}_{\lambda ,\theta }^{\mathrm {NI},M}\le \varGamma \text {-}\liminf _{\varepsilon \rightarrow 0} (E_{\lambda , \theta }^{\mathrm {NI},M})_\varepsilon \);
-
(ii)
every \(((u_\varepsilon , v_\varepsilon ))_\varepsilon \) such that \(\sup _{\varepsilon }(E_{\lambda , \theta }^{\mathrm {NI},M})_\varepsilon (u_\varepsilon , v_\varepsilon )<+\infty \) converges, up to a subsequence, in \(L^1(\varOmega ;\mathbb {R}^d) \times L^1(\varOmega )\) to (u, 1) for \(u \in SBD^2(\varOmega )\);
-
(iii)
if \(d=2\) and \(\lim _{\varepsilon \rightarrow 0}\frac{\delta }{\varepsilon ^2}=0\), then \({\mathcal {G}}_{\lambda ,\theta }^{\mathrm {NI},M}\ge \varGamma \text {-}\limsup _{\varepsilon \rightarrow 0} (E_{\lambda , \theta }^{\mathrm {NI},M})_\varepsilon \),
where the \(\varGamma \)-\(\liminf \) and \(\varGamma \)-\(\limsup \) above are with respect to the strong \(L^1(\varOmega ;\mathbb {R}^d) \times L^1(\varOmega )\) topology.
In Sects. 4 and 5 we actually work in the enlarged configuration \(\widetilde{\varOmega } \subset \mathbb {R}^d\) satisfying (3.11) and with functions \(u_\varepsilon \), \(v_\varepsilon \) in \(\mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R}^d)\), \(\mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R})\), where
and \(\mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R})\) is defined similarly, for 1 in place of \(u_0\) in \(\widetilde{\varOmega }\setminus \varOmega \). In particular, if \(u_\varepsilon \rightarrow \bar{u}\) in \(GSBD^2_\infty (\widetilde{\varOmega })\) for some \(\bar{u}\), then \(\bar{u}=u_0\) in \(\widetilde{\varOmega }\setminus \varOmega \). Let us also fix once and for all \(\lambda \), \(\theta >0\).
4 Compactness
In this section we prove a compactness result (Proposition 1) for the discrete approximations of the Griffith energy, that holds under the assumption that \(\frac{\delta }{\varepsilon }\) be bounded. We show that sequences \((u_\varepsilon ,v_\varepsilon )_\varepsilon \) with equibounded energy \(E_\varepsilon ^{\lambda , \theta }\) are approximated, in the sense of the convergence in measure, by sequences with bounded continuous Griffith energy (for which compactness is known from Theorem 2).
Proposition 1
Let \(\frac{\delta }{\varepsilon }\) be bounded as \(\varepsilon \rightarrow 0\). Let \((u_\varepsilon ,v_\varepsilon )_\varepsilon \subset L^1(\widetilde{\varOmega };\mathbb {R}^d)\times L^1(\widetilde{\varOmega };\mathbb {R})\) be such that \(u_\varepsilon \in \mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R}^d)\), \(v_\varepsilon \in \mathcal {A}_\delta ^{\mathrm {Dir}}(\varOmega ;\mathbb {R})\) with
Then there exist functions \(\overline{u}_\varepsilon \in SBD^2(\widetilde{\varOmega };\mathbb {R}^d)\) such that
and
Moreover, if \(\Vert u_\varepsilon \Vert _{L^\infty }\le M\), then \(\Vert \bar{u}_\varepsilon \Vert _{L^\infty }\le M\).
Proof
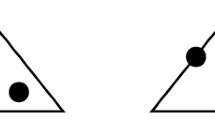
We introduce a suitable triangulation \(\mathcal {T}^d_\varepsilon \) of \(\widetilde{\varOmega }\), based on the Freudenthal partition \(\varSigma _d\) of the d-cube (see Fig. 1).
It is defined as the set of all d-simplexes T obtained through minimal chains of ordered vertices connecting the origin to the vertex \((1,1,\dots ,1)\). They are d! congruent simplexes and each has volume 1/d!. In the case \(d=2\), we choose
while if \(d=3\), the decomposition is given by
where
For every simplex \(T\in \varSigma _d\), we denote by \(D_{T}\) the set of the edges directions for T, which contains \(d(d+1)/2\) linearly independent vectors of \(S_d\). For any vector \(\xi \in \mathbb {R}^d\), we denote by \(\ell _j^{\xi ,T}\) the coordinates of \(\xi \otimes \xi \) in the basis \(\{\tilde{\nu }_j\otimes \tilde{\nu }_j:\, \tilde{\xi }_j\in D_T\}\) of \(\mathbb {R}^{d\times d}_{sym}\), where \(\tilde{\nu }_j:= \tilde{\xi }_j/|\tilde{\xi }_j|\).
Finally, we define the triangulation of \(\widetilde{\varOmega }\) induced by the partition \(\varSigma _d\) as
We then denote by \(\hat{u}_\varepsilon =(\hat{u}_\varepsilon ^1,\dots ,\hat{u}_\varepsilon ^d)\) and \(\hat{v}_\varepsilon \) the piecewise-affine interpolations of \(u_\varepsilon \) and \(v_\varepsilon \) on \(\mathcal {T}^d_\varepsilon \), respectively. We also consider the piecewise constant functions
The result will be an immediate consequence of the following crucial claim and of [1, Proposition A.1, Remark A.2], which hold true for any distance inducing the convergence in measure on bounded sets (in particular, for the metric d(u, v) defined in (2.15)).
Claim: There exists a set \(K_\varepsilon \subset \widetilde{\varOmega }\), with
such that, setting \(\bar{u}_\varepsilon := \hat{u}_\varepsilon (1-\chi _{K_\varepsilon })\), we have that \(\overline{u}_\varepsilon \) satisfy (4.3). We subdivide the proof of this fact into two steps.
Step 1: The preliminary remark is that from the equi-boundedness of the energies (4.1) we can get
Let \(\eta >0\) be fixed, and consider \(\widetilde{\varOmega }^\eta :=\{x\in \widetilde{\varOmega }:\, \mathrm{dist}(x,\mathbb {R}^d \setminus \widetilde{\varOmega })>\eta \}\). Since \(\hat{u}_\varepsilon \) is the affine interpolation of \(u_\varepsilon \) on each simplex of partition \(\varSigma _d\), we have that
for every pair \(s_i,s_j\) of vertices of \([0,1]^d\), with \(\nu =\frac{s_i-s_j}{|s_i-s_j|}\).
In order to prove (4.6), a simple computation based on (2.25d), (4.4) and (4.8) shows that
where \(s_j, s_j+\tilde{\xi }_j\) represent the only two vertices of T whose difference is \(\tilde{\xi }_j\). Thus, by simple inequalities we infer that
whence the assertion easily follows from (4.1) and by the arbitrariness of \(\eta \). For what concerns (4.7), we notice that \(\hat{v}_\varepsilon (x)\) can be rewritten on each simplex \(\alpha +\delta T\), with vertices \(\alpha +\delta \tilde{\xi }_i\), \(i=0,1,\dots ,d\) (we use here the convention \(\alpha +\delta \tilde{\xi }_0:=\alpha \)), as
for some affine functions \(p_i(x),\, i=0,1,\dots ,d\) such that \(\displaystyle \sum _{i=0}^dp_i(x)=1\).
We first prove that
for \(\delta \) small. Indeed, on the one hand, since \(\hat{v}_\varepsilon \) is the piecewise affine interpolation of \(v_\varepsilon \) on each simplex of the decomposition, we deduce that
so that, by means of elementary inequalities, for \(\delta \) sufficiently small we have that
On the other hand, rewriting \(\hat{v}_\varepsilon (x)\) as in (4.9) on each symplex \(\alpha +\delta T\) for every \(\alpha \in \delta \mathbb {Z}^d\cap \widetilde{\varOmega }\), with the convexity of \(z\rightarrow (z-1)^2\) we obtain
Hence, summing up on all simplices \(\alpha +\delta T\in \mathcal {T}^d_\varepsilon \) we finally get, for \(\delta \) small enough,
Now, as a consequence of (4.10), (4.1) and the Cauchy–Schwarz inequality we deduce that
whence (4.7) follows by the arbitrariness of \(\eta \).
Step 2: We can start with the construction of the set \(K_\varepsilon \). As a consequence of the coarea formula and (4.7), we then have
whence, by the mean-value theorem, there exists \(\bar{s}\in (0,1)\), say \(\bar{s}=\frac{1}{4}\), such that
where we have set
Thus, with (4.12) and (4.13) we deduce that
Furthermore, again by the equi-boundedness of the energies and (4.11), we have
Now, with \(\kappa >0\) fixed, we consider the set
and, denoting by \(Q_\alpha \) the cube \(\alpha +[0,\delta )^d\), we correspondingly define
Notice that, if \(\alpha \in \mathcal {I}_{\varepsilon ,\delta }^\kappa \), then by the triangle inequality there exists \(\beta \in \alpha +\delta ([-1,1]^d\cap \mathbb {Z}^d)\) such that
Since different \(\alpha ',\alpha ''\in \mathcal {I}_{\varepsilon ,\delta }^\sigma \) may share the same \(\beta \) complying with (4.16) if and only if \(\alpha '-\alpha ''\in \delta ([-2,2]^d\cap \mathbb {Z}^d)\), then
From (4.1), the definition of \(\mathcal {I}_{\varepsilon ,\delta }^\kappa \), and (4.17) we then infer that
whence
Consequently, taking into account the boundedness of the ratio \(\frac{\delta }{\varepsilon }\), we have
Hence, setting
with (4.14), (4.15) and (4.19) we find that
It will be sufficient to show that, for every fixed \(\kappa >0\),
Indeed, choosing, e.g., \(\kappa =\frac{1}{16}\) and setting \(K_\varepsilon :=K_{\varepsilon ,\frac{1}{16}}\), (4.20) and (4.6) allow us to deduce a uniform bound for \(\Vert \mathcal {E}\hat{u}_\varepsilon \Vert _{L^2}\) outside the set \(K_\varepsilon \); namely,
In order to prove (4.20), let \(x\in \widetilde{\varOmega }\backslash K_{\varepsilon ,\kappa }\) and \(\alpha \in \delta \mathbb {Z}^d\cap \widetilde{\varOmega }\) be such that \(x\in Q_\alpha \). Since \(\hat{v}_\varepsilon (x)\ge \frac{1}{4}\), it must be
Now, \(\alpha \not \in \mathcal {I}_{\varepsilon ,\delta }^\kappa \), so that \(v_\varepsilon (\alpha )\ge \frac{1}{4}-\kappa \) and, by triangle inequality, \({\tilde{v}}_{min,\varepsilon }(x)\ge \frac{1}{4}-2\kappa \) as desired.
Finally, setting \(\bar{u}_\varepsilon := \hat{u}_\varepsilon (1-\chi _{K_\varepsilon })\), we notice that \(J_{\bar{u}_\varepsilon }=\partial ^*K_\varepsilon \) so that, taking into account (4.21) and \(\mathcal {H}^{d-1}(\partial ^* K_\varepsilon )<+\infty \) we obtain (4.3). By the way, it is immediate to see that \(\Vert \bar{u}_\varepsilon \Vert _{L^\infty } \le \Vert u_\varepsilon \Vert _{L^\infty }\). This concludes the proof of Claim and then of the theorem. \(\square \)
5 Semicontinuity properties for the Griffith energy
This section is devoted to prove the semicontinuity inequality (3.14) in Theorem 3, assuming the convergence of \(u_\varepsilon \) to u guaranteed in Sect. 4 on sequences with bounded approximating energies. In particular, we deduce the lower limit inequality for the \(\varGamma \)-convergence approximation of the classic Griffith energy, with Dirichlet boundary conditions.
As in Sect. 4, we work with the extended set \(\widetilde{\varOmega }\subset \mathbb {R}^d\), \(d\in \{2,3\}\), and functions in \(\mathcal {A}^\mathrm {Dir}_\delta (\widetilde{\varOmega };\mathbb {R}^d)\), \(\mathcal {A}^\mathrm {Dir}_\delta (\widetilde{\varOmega };\mathbb {R})\). As observed in Sect. 3, if \(u_\varepsilon \in \mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R}^d)\) are such that \(u_\varepsilon \rightarrow \bar{u}\) a.e. in \(\widetilde{\varOmega }\), then \(\bar{u}=u_0\) in \(\widetilde{\varOmega }\setminus \varOmega \). Then (recall the definition of \(u'\) (3.12) and (3.13)), prove the lower limit inequality for \((E_{\lambda , \theta }^{\mathrm {Dir}})_\varepsilon \) is equivalent to prove the lower inequality for the energies \((\widetilde{E}_{\lambda , \theta }^{\mathrm {Dir}})_\varepsilon \) defined in the very same way of \((E_{\lambda , \theta }^{\mathrm {Dir}})_\varepsilon \), but with all the integrals and corresponding notation considered in \(\widetilde{\varOmega }\) in place of \(\varOmega \). To ease the reading, in the following we keep the same notation of Sect. 3 for the functionals, just referring to the set \(\widetilde{\varOmega }\) in place of \(\varOmega \) in integrals, in sets of nodes, and in \(\mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R}^d)\), \(\mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R})\).
We estimate separately from below the terms \(F_\varepsilon \) and \(F_\varepsilon ^{\mathrm {div}}\) (Lemma 5, Lemma 6, and Proposition 2), and then address in Proposition 3 the lower bound for the Modica–Mortola part \(G_\varepsilon \), by a blow-up argument. We remark that the results concerning \(F_\varepsilon \) and \(F_\varepsilon ^{\mathrm {div}}\) hold under the only assumption that \(\delta =\delta (\varepsilon )\) vanishes as \(\varepsilon \rightarrow 0\). In contrast, we use the assumption \(\lim _{\varepsilon \rightarrow 0}\frac{\delta }{\varepsilon }=0\) to estimate the Modica–Mortola terms from below in Step 3 of Proposition 3.
Lemma 5
Let \(u_\varepsilon \in \mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R}^d)\), \(v_\varepsilon \in \mathcal {A}_\delta ^{\mathrm {Dir}}(\widetilde{\varOmega };\mathbb {R})\) be such that
\(d(u_\varepsilon , u) \rightarrow 0\), with \(u \in GSBD^2_\infty (\widetilde{\varOmega })\), and \(v_\varepsilon \rightarrow 1\) in \(L^2(\widetilde{\varOmega })\). Then, for every \(\xi \in S_d\),
Proof
For simplicity, we develop the proof in dimension \(d=3\), although the following slicing argument would hold in any dimension \(d\ge 2\). Let \(\xi \in S_3\) be fixed, and \(\{\xi _1,\xi _2,\xi _3\}\) be an orthogonal basis of \(\mathbb {R}^3\) such that \(\xi _i\in \mathbb {Z}^3\) for every \(i=1,2,3\) and \(\xi _1=\xi \). Setting \(Q_\xi :=\sum _{i=1}^3[0,1)\xi _i\), we note that \(M_\xi :=|Q_\xi |=\mathrm{det}(\xi _1,\xi _2,\xi _3)\) and \(M_\xi \in \mathbb {Z}\). If we denote by \(z_l\) the points of \(\varPi ^\xi \) such that
we can split \(\mathbb {Z}^3\) into the union of disjoint copies of \(Z^\xi :=\bigoplus _{i=1}^3\mathbb {Z}\xi _i\) as
(see the proof of [13, Theorem 4.1] and Fig. 2, in the sample case of \(\xi =e_1+e_2+e_3\)).
We claim that
for \(\zeta =\pm \xi \) and for every \(l=1,\dots ,M_\xi \), where \(Z_{\delta }^{l}(\widetilde{\varOmega }):=R_\delta ^{\xi }(\widetilde{\varOmega })\cap \delta Z^{\xi ,l}\). The conclusion (5.2) will follow up to multiplying by \(\frac{1}{|\xi |^4}\) both the sides of (5.3) and summing up over the sublattices.
In order to prove (5.3), we introduce two other piecewise constant interpolations \({\tilde{u}}_\varepsilon \) and \({\tilde{v}}_\varepsilon \) of \(u_\varepsilon \) and \(v_\varepsilon \), respectively. For \(\alpha \in Z_{\delta }^l(\widetilde{\varOmega })\) and \(Q_\xi \) as before, we set
The triangular inequality implies that \({{\tilde{v}}}_\varepsilon \rightarrow 1\) in \(L^1(\widetilde{\varOmega })\). We also have that \(d({{\tilde{u}}}_\varepsilon , u)\rightarrow 0\). This follows from the fact that \(u_\varepsilon - {\tilde{u}}_\varepsilon \rightarrow 0\) in measure. To see this, set \({\tilde{g}}^\zeta _\varepsilon =\arctan (\langle {\tilde{u}}_\varepsilon , \zeta \rangle )\), \(g^\zeta _\varepsilon =\arctan (\langle u_\varepsilon , \zeta \rangle )\), \(\zeta \in \{e_1,e_2,e_3\}\). We have by definition of the interpolants that
where \(N_\xi \) is finite depending on \(\xi \) and \(\psi _i\) are the vectors connecting \(\alpha \) with the \(N_\xi \) remaining integer vertices in \(Q_\xi \). We now observe two facts: (1) from Proposition 1 we have that there exist \(\overline{u}_\varepsilon \) with \(\overline{u}_\varepsilon -u_\varepsilon \rightarrow 0\) in measure and \(\overline{u}_\varepsilon \rightarrow u\) weakly in \(GSBD^2_\infty (\widetilde{\varOmega })\); (2) arguing for any fixed \(\zeta =e_i\) as in [21, proof of Theorem 1.1, Compactness] we have that \(\arctan (\langle \overline{u}_\varepsilon ,\zeta \rangle )\) is compact in \(L^1(\widetilde{\varOmega })\) (in fact, in \(\widetilde{\varOmega } \setminus A^\infty _u\), \(\arctan (\langle \overline{u}_\varepsilon ,\zeta \rangle )\rightarrow \arctan (\langle u , \zeta \rangle )\) for any \(\zeta \in \mathbb {S}^2\), and, in \(A^\infty _u\), \(|\arctan (\langle \overline{u}_\varepsilon , \zeta \rangle )|\rightarrow \frac{\pi }{2}\) for \(\mathcal {H}^2\)-a.e. \(\zeta \in \mathbb {S}^{2}\), but the limit exists for any \(\zeta \)). Then \(g^\zeta _\varepsilon \) is compact in \(L^1(\widetilde{\varOmega })\) so that, summing up on all \(\alpha \)’s in \(Z_{\delta }(\widetilde{\varOmega })\) and using the Fréchet–Kolomogorov criterion, we get \({\tilde{g}}^\zeta _\varepsilon - g^\zeta _\varepsilon \rightarrow 0\) in \(L^1(\widetilde{\varOmega })\). Hence, the claim is proved.
We define \(\widetilde{\varOmega }^\eta \) as the set of \(x \in {\tilde{\varOmega }}\) whose distance from \(\partial \widetilde{\varOmega }\) is at least \(\eta \). Setting \(\widetilde{\varOmega }^l_\delta :=\bigcup _{\alpha \in Z_{\delta }^l}(\alpha +\delta Q_\xi )\), we clearly have that \(\widetilde{\varOmega }^\eta \subseteq \widetilde{\varOmega }^l_\delta \) for \(\delta \) small enough. Furthermore (we argue for \(\zeta =\xi \) in (5.3), the case \(\zeta =-\xi \) is analogous)
Observe that \({\tilde{u}}_\varepsilon ^{\xi ,y} \in PC_\delta ((\widetilde{\varOmega }^l_\delta )_{\xi ,y})\), where \(PC_\delta \) here denotes the space of piecewise constant functions on intervals of size \(\delta \). We now define \({\hat{u}}_{\varepsilon ,\xi ,y}\) as the piecewise linear interpolation of \({\tilde{u}}_\varepsilon ^{\xi ,y}\) on \((\widetilde{\varOmega }^l_\delta )_{\xi ,y}\). We remark that \({\hat{u}}_{\varepsilon ,\xi ,y}\) has nothing to do with the slices \(\hat{u}_\varepsilon ^{\xi , y}\) of the affine function \({\hat{u}}_\varepsilon \) used in Proposition 1, hence the different notation. Now, (5.5) can be rewritten as
and we are left to prove that, for \(\mathcal {H}^{2}\)-a.e. \(y\in \varPi ^\xi \),
Indeed, if the above holds, (5.2) will follow as a consequence of Fatou’s lemma by integrating the above estimate over \(\varPi ^\xi \) and observing that, since \(u\in GSBD^2_\infty ({\widetilde{\varOmega }})\), then \({\dot{u}}^{\xi ,y}(t)=\langle \mathcal {E}u(y+t\xi )\xi ,\xi \rangle \) for a.e. \(t\in {(\widetilde{\varOmega }\setminus A^\infty _u)}_{\xi ,y}\) and \({\mathcal {E}} u=0\) in \(A^\infty _u\). (Notice that we have also to use the arbitrariness of \(\eta >0\).)
In the following we argue for \(\widetilde{\varOmega }\) in place of \(\widetilde{\varOmega }_\eta \), in order to simplify the notation, since we know that \(d({\tilde{u}}_\varepsilon ,u)\rightarrow 0\). Nevertheless, all the inequalities may be localized on \(\widetilde{\varOmega }_\eta \). Since \(\tilde{u}_\varepsilon \rightarrow u\) in measure in \(\widetilde{\varOmega } \setminus A^\infty _u\), by Fubini’s Theorem (see [19, (5.5)]) we have that \({\tilde{u}}_\varepsilon ^{\xi ,y}\rightarrow u^{\xi ,y}\) in measure in \({(\widetilde{\varOmega } \setminus A^\infty _u)}_{\xi ,y}\) for \(\mathcal {H}^2\)-a.e. \(y\in \varPi ^\xi \). The same holds then for the piecewise affine functions \({\hat{u}}_{\varepsilon ,\xi ,y}\). Summarizing, we have for \(\mathcal {H}^2\)-a.e. \(y\in \varPi ^\xi \):
where the second one follows by Fubini’s Theorem. For fixed \(y \in \varPi ^\xi \) such that (5.7) holds and the \(\liminf \) in (5.6) is finite, denoting by \(\hat{v}_{\varepsilon , \xi ,y}\) the piecewise affine interpolations of \(\tilde{v}^{\xi ,y}_\varepsilon \), from (5.1) and the triangular inequality we deduce that
In view of Lemma 1, there exists a finite set \(I^{\xi ,y}\subset {\widetilde{\varOmega }}_{\xi ,y}\) such that for every \(A^{\xi ,y}\) open, with \(A^{\xi ,y}\subset \!\subset \!{\widetilde{\varOmega }}_{\xi ,y}\setminus I^{\xi ,y}\), there exists \(\kappa >0\) such that
In particular, we may assume that there exists \(\kappa '>0\) such that, for \(\varepsilon \) small enough,
so that
Up to considering separately its connected components, we may assume that \(A^{\xi ,y}\) be connected and contained in one of the finitely many connected components of \(\widetilde{\varOmega }_{\xi ,y}\setminus I^{\xi ,y}\) (it is not restrictive to assume \(\widetilde{\varOmega }\) connected). Arguing as in [21, part below (3.21)], we have that by the regularity of \(\hat{u}_{\varepsilon , \xi ,y}\), (5.7), and (5.8) one of the following two alternative possibilities hold:
-
1.
either \(|\hat{u}_{\varepsilon , \xi ,y}(x)|\) converge to \(+\infty \) for some \(x \in A^{\xi ,y}\) and then \(|\hat{u}_{\varepsilon , \xi ,y}| \rightarrow +\infty \) on \(A^{\xi ,y}\) and \(A^{\xi ,y} \subset (A^\infty _u)_{\xi ,y}\);
-
2.
or \((\hat{u}_{\varepsilon , \xi ,y})_\varepsilon \) is bounded in \(H^1(A^{\xi ,y})\) and then
$$\begin{aligned} u^{\xi ,y}\in H^1(A^{\xi ,y}) \text { and } \hat{u}_{\varepsilon , \xi ,y}\rightharpoonup u^{\xi ,y} \text { in }H^1(A^{\xi ,y}) . \end{aligned}$$
In particular, \({\widetilde{\varOmega }}_{\xi ,y} \setminus I^{\xi ,y}\) is made up of a finite union of intervals, where either \(\hat{u}_{\varepsilon , \xi ,y}\) converge in \(H^1_{\mathrm{loc}}\) or \(\hat{u}_{\varepsilon , \xi ,y}\rightarrow +\infty \). Therefore we may partition \(\widetilde{\varOmega }_{\xi ,y}\) as \(\widetilde{\varOmega }_{\xi ,y}^1 \cup \widetilde{\varOmega }_{\xi ,y}^2 \cup I^{\xi ,y}\), where \(\widetilde{\varOmega }_{\xi ,y}^1\), \(\widetilde{\varOmega }_{\xi ,y}^2\) are finite unions of open intervals with boundary contained in \(I^{\xi ,y}\), such that \(\hat{u}_{\varepsilon , \xi ,y} \rightarrow +\infty \) in \(\widetilde{\varOmega }_{\xi ,y}^2\) and \(\hat{u}_{\varepsilon , \xi ,y} \rightarrow u^{\xi ,y}\) in \(H^1(A^{\xi ,y})\) for every \(A^{\xi ,y} \subset \subset \widetilde{\varOmega }_{\xi ,y}^1\).
With (5.7) and Lemma 2 we obtain that for every \(A^{\xi ,y}\subset \subset {\widetilde{\varOmega }}_{\xi ,y}^1\)
Notice that (5.9) holds for any arbitrary open set \(A^{\xi ,y}\subset \widetilde{\varOmega }_{\xi ,y}^1\), so that (since \(\widetilde{\varOmega }_{\xi ,y}^2 \subset (A^\infty _u)_{\xi ,y}\))
As observed before, the above estimate may be localized in \(\widetilde{\varOmega }_\eta \), obtaining (5.6) and thus concluding the proof. \(\square \)
For every \(\xi \in \mathbb {R}^d\backslash \{0\}\), \(u\in L^1(\widetilde{\varOmega };\mathbb {R}^d)\), \(v\in L^1(\widetilde{\varOmega })\), we define
Setting \(Z_{\delta }(\widetilde{\varOmega }):=R^\mathrm{div}_\delta (\widetilde{\varOmega })\cap \delta Z\), where \(R^\mathrm{div}_\delta (\widetilde{\varOmega })\) was defined in (3.7) (for the domain \(\varOmega \), here we consider as always the analogous one for \(\widetilde{\varOmega }\)), and \(Z:=2\mathbb {Z}^d\), and
(see Fig. 3), we introduce the class of real-valued piecewise constant functions on the cells \(\alpha +\delta Q_{2m}\) defined as
Lemma 6
Let \(u\in GSBD^2_\infty (\widetilde{\varOmega })\) and \((w_\varepsilon )_\varepsilon \), \((v_\varepsilon )_\varepsilon \) be sequences such that \(v_\varepsilon \in \mathcal {A}_{2\delta }(\widetilde{\varOmega };\mathbb {R})\), \(d(w_\varepsilon , u)\rightarrow 0\),
Then
Proof
Notice that, under the assumption (5.13), from the identity
we infer that \(\sup _{\varepsilon >0}\int _{\widetilde{\varOmega }} (v_\varepsilon (x))^2 (\mathrm {div}\, w_\varepsilon (x))^2 \,\mathrm {d}x< +\infty \). We then show that
from which (5.16) immediately follows, recalling that \({\mathcal {E}} u=0\) in \(A^\infty _u\). Note that by Egorov’s Theorem, with fixed \(\eta >0\) there exists \({\widetilde{\varOmega }}_\eta \subset {{\widetilde{\varOmega }}\setminus A^\infty _u}\) such that \(|{({\widetilde{\varOmega }}\setminus A^\infty _u)}\setminus {\widetilde{\varOmega }}_\eta |<\eta \) and \(v_\varepsilon >1-\eta \) on \({\widetilde{\varOmega }}_\eta \) for \(\varepsilon \) small enough.
Now, under assumptions (5.13)–(5.15), an analogous slicing argument as for the proof of Lemma 5 applied to \(w_\varepsilon ^{e_i,y}\) shows that
for every \(g\in L^2(\widetilde{\varOmega } \setminus A_u^\infty )\) and every \(i=1,\dots ,d\). The proof of (5.19) can be developed in the case \(g=0\), the general case following by approximation of \(g\in L^2(\widetilde{\varOmega }\setminus A_u^\infty )\) with piecewise constant functions on a Lipschitz partition of \(\widetilde{\varOmega }\).
From (5.19) we then get
whence, by the identity (5.17) we obtain
Finally, since \(|{(\widetilde{\varOmega }\setminus A^\infty _u)} \setminus \widetilde{\varOmega }_\eta |<\eta \), letting \(\eta \rightarrow 0\) and by the absolute continuity of the integral we obtain
The assertion (5.18) now follows from (5.21) and Lemma 2 since \(v_\varepsilon \le 1\) and \(v_\varepsilon \rightarrow 1\) a.e. in \({\widetilde{\varOmega }}\). \(\square \)
As a consequence of Lemma 6, we deduce now the optimal lower bound for the functionals \(F_\varepsilon ^\mathrm{div}(u,v)\) as defined in Sect. 3.
Proposition 2
Let \(u_\varepsilon \in \mathcal {A}_\delta ({\widetilde{\varOmega }};\mathbb {R}^d)\), \(v_\varepsilon \in \mathcal {A}_\delta ({\widetilde{\varOmega }};\mathbb {R})\) be such that
\(d(u_\varepsilon , u) \rightarrow 0\), with \(u \in GSBD^2_\infty (\widetilde{\varOmega })\), and \(v_\varepsilon \rightarrow 1\) in \(L^2(\widetilde{\varOmega })\). Then
Proof
We prove (5.23) for \(d=3\), the case \(d=2\) being analogous. Notice that \(\mathbb {Z}^3\) admits the following decomposition:
Correspondingly, recalling that \(Z_{\delta }^{l}(\widetilde{\varOmega })=R_\delta ^\mathrm{div}(\widetilde{\varOmega })\cap \delta Z^{l}\) and setting
we can rewrite the energies as \({F}_\varepsilon ^{\mathrm{div}}(u,v)=\sum _{l=1}^8{F}_\varepsilon ^{\mathrm{div},l}(u,v)\), so that
With fixed \(\eta >0\) and \(\widetilde{\varOmega }_\eta \) defined as in the proof of Lemma 6 we argue for \(l=1\) and claim that
For this, we start by defining two other piecewise constant interpolations \({\tilde{u}}_\varepsilon \) and \({\tilde{v}}_\varepsilon \) of \(u_\varepsilon \) and \(v_\varepsilon \), respectively. For \(\alpha \in Z_{\delta }(\widetilde{\varOmega })\) and \(Q_2\) as in (5.11), we set
It is immediate to check that \({{\tilde{v}}}_\varepsilon \rightarrow 1\) in \(L^1(\widetilde{\varOmega })\), and, more in general, that (5.15) are satisfied. Indeed, for every \(\alpha \in \delta \mathbb {Z}^3\) and \(i=1,2,3\), by triangle inequality we have
We also have that \(d({\tilde{u}}_\varepsilon , u)\rightarrow 0\). This follows arguing as in Lemma 5.
We introduce further interpolations of \(u_\varepsilon \), whose components \(z_\varepsilon ^i\), \(i=1,2,3\) are piecewise affine, defined as
where \(Q_{2,i,\pm }\) are as in (5.12).
Notice that, by the definition (5.27), the first component of \(z_\varepsilon \) is continuous across interfaces which are orthogonal to \(e_1\). Indeed, clearly no discontinuity of \(z^1_\varepsilon (x)\) can appear at points x on the interface between \(\alpha +\delta Q_{2,1,+}\) and \(\alpha +\delta Q_{2,1,-}\); the only points to be checked are those \({\bar{x}}\) on the boundary between \(\alpha +\delta Q_{2}\) and \((\alpha +2\delta e_1)+\delta Q_{2}\). A direct computation shows that, since \({\bar{x}}\in \partial (\alpha +\delta Q_{2,1,+})\cap \partial ((\alpha +2\delta e_1)+\delta Q_{2,1,-})\), one has
which proves the claim.
It follows that \(z_\varepsilon ^{e_1,y} \in H^1(\widetilde{\varOmega }_{e_1, y})\) for \(\mathcal {H}^2\)-almost every \(y\in \varPi ^{e_1}\). A similar argument shows that \(z_\varepsilon ^{e_i,y} \in H^1(\widetilde{\varOmega }_{e_i, y})\) for \(\mathcal {H}^2\)-almost every \(y\in \varPi ^{e_i}\) for every \(i=2,3\). We now prove that \(z_\varepsilon \rightarrow u\) in measure on \(\widetilde{\varOmega }\). It will be enough to show that
To see this, again we may argue componentwise and observe that, since \(|\delta Q_2|=8\delta ^3\),
By the Cauchy–Schwarz inequality, and using equiboundedness of the energies, we get
which entails the convergence of \(z_\varepsilon \rightarrow u\) in measure on \(\widetilde{\varOmega }\).
For all \(\psi \in S^2\) it holds \(\langle \mathcal {E}z(x)\psi , \psi \rangle = \partial _\psi \langle z(x),\psi \rangle \), where \(\partial _\psi w\) stands for the directional derivative of w with respect to \(\psi \). Applying this to the unitary vectors \(e_i\), by (5.27) we have that
Then, by using the identity (5.17), we have that
for every \((k_1,k_2,k_3)\in \{-1,1\}^3\), where we have set
(see Fig. 4). Since \(|\delta \mathcal {Q}^{k_1e_1,k_2e_2,k_3e_3}|=\delta ^3\), it holds
Now, from the equi-boundedness of the energies (5.22), we infer that
where \(H^\zeta \) is defined as in (5.10). Thus, the conclusion (5.16) of Lemma 6 holds with \(z_\varepsilon \) and \({\tilde{v}}_\varepsilon \) in place of \(w_\varepsilon \) and \(v_\varepsilon \), respectively. Therefore, with (5.31), it follows that
which proves the claim (5.25).
We now observe that we have also, for every l and \(\eta \) small,
In fact, (5.28)–(5.31) continue to hold, since the lattices \(Z^{l}\) are just suitable translations of \(Z^1\equiv Z\), while the compact subset \(\widetilde{\varOmega }_\eta \) of \(\widetilde{\varOmega }\) appears on the right-hand side. We deduce that (5.25) follows also for general \({F}_\varepsilon ^{\mathrm{div},l}\) in place of \({F}_\varepsilon ^{\mathrm{div},1}\).
By (5.24) we eventually obtain that
whence (5.23) follows by the arbitrariness of \(\eta >0\). \(\square \)
With the results proven before in this section, we are in position to prove the liminf inequality for \((E^\mathrm {Div}_{\lambda , \theta })_\varepsilon \).
Proposition 3
Assume that \(\lim _{\varepsilon \rightarrow 0} \frac{\delta }{\varepsilon }=0\). Let \((u_\varepsilon ,v_\varepsilon )_\varepsilon \subset L^1(\widetilde{\varOmega };\mathbb {R}^d)\times L^2(\widetilde{\varOmega };\mathbb {R})\) be such that \(u_\varepsilon \in \mathcal {A}_\delta (\widetilde{\varOmega };\mathbb {R}^d)\), \(v_\varepsilon \in \mathcal {A}_\delta (\widetilde{\varOmega };\mathbb {R})\),
\(d(u_\varepsilon , u)\rightarrow 0\) for \(u\in GSBD^2_\infty (\widetilde{\varOmega })\), \(v_\varepsilon \rightarrow 1\) in \(L^2(\widetilde{\varOmega })\). Then
Proof
Let us fix a small \(\zeta \in (0,1)\). For every \(\varepsilon >0\), we define the discrete measures
where \(\mathbb {1}_\alpha \) denotes the Dirac delta in \(\alpha \). We observe that
In view of Lemma 5 (recall Remark 1) and Proposition 2, the general proof will be a consequence of
by the arbitrariness of \(\zeta \in (0,1)\). Therefore we prove (5.35) in the following. We divide the proof into three steps: in Step 1 we see that (5.35) is guaranteed from (5.37); in Step 2 we show that, after a blow up procedure around a fixed \(x_0\) in a set of full \(\mathcal {H}^{d-1}\)-measure of \(J_u\), (5.37) would follow from (5.46); in Step 3 we prove (5.46).
Step 1. Since by (5.33) it holds that
we have that there exists a positive bounded Radon measure \(\mu ^\zeta \) such that, up to subsequences, \(\mu _\varepsilon ^\zeta {\mathop {\rightharpoonup }\limits ^{*}}\mu ^\zeta \) weakly\(^*\) in \(\mathcal {M}_b^+(\widetilde{\varOmega })\). Since \(J_u\) is countably rectifiable, so that  is \(\sigma \)-finite, and \(\mu ^\zeta \in \mathcal {M}_b^+(\widetilde{\varOmega })\), then the Radon-Nikodym derivative of \(\mu ^\zeta \) with respect to
is \(\sigma \)-finite, and \(\mu ^\zeta \in \mathcal {M}_b^+(\widetilde{\varOmega })\), then the Radon-Nikodym derivative of \(\mu ^\zeta \) with respect to  exists (cf. e.g. [20, Theorem 2.9]). Denoting its density by \(\mu ^\zeta _J \in L^1(J_u;\mathbb {R}^+)\), we have that \(\mu ^\zeta _J\) may be explicitly computed by (see e.g. [3, Theorems 1.28 and 2.83])
exists (cf. e.g. [20, Theorem 2.9]). Denoting its density by \(\mu ^\zeta _J \in L^1(J_u;\mathbb {R}^+)\), we have that \(\mu ^\zeta _J\) may be explicitly computed by (see e.g. [3, Theorems 1.28 and 2.83])
where \(\nu :=\nu _u(x_0)\) and \(Q^\nu _\rho (x_0)=x_0+ \rho \, Q^\nu \), \(Q^\nu \) being the unitary cube centered in \(x_0\) with two faces in planes orthogonal to \(\nu \). Let us set \((Q_\rho ^\nu (x_0))^\pm :=x_0+\rho \, Q^{\nu ,\pm }=\{x\in Q_\rho ^\nu (x_0):\, \pm \langle x-x_0,\nu \rangle >0\}\) for the following discussion.
We now claim that
Once (5.37) has been proved, the conclusion (5.35) follows by a standard argument. Indeed, by choosing an increasing sequence of cut-off functions \((\varphi _k)\subset C_c^\infty (\widetilde{\varOmega })\) such that \(0\le \varphi _k\le 1\) and \(\sup _k\varphi _k=1\), we get
whence (5.35) follows letting \(k\rightarrow +\infty \) by the Monotone Convergence Theorem.
Step 2. Since \(u \in GSBD^2_\infty ({\widetilde{\varOmega }})\), we may subdivide \(J_u\) into \(J_u \cap ({\widetilde{\varOmega }} \setminus A^\infty _u)\) and \(\partial ^* A^\infty _u\). Moreover, \(\widetilde{u}_t:=u\chi _{{\widetilde{\varOmega }}\setminus A^\infty _u} + t \chi _{A^\infty _u} \in GSBD^2({\widetilde{\varOmega }})\) and \(J_u=J_{\widetilde{u}_t}\) (up to a \(\mathcal {H}^{d-1}\)-negligible set) for \(\mathcal {L}^d\)-a.e. \(t \in \mathbb {R}^d\). Therefore, for \(\mathcal {H}^{d-1}\)-a.e. \(x_0 \in J_u \cap ({\widetilde{\varOmega }} \setminus A^\infty _u)\) there exist two values \(u^\pm (x_0) \in \mathbb {R}^d\) such that
moreover, for \(\mathcal {H}^{d-1}\)-a.e. \(x_0 \in \partial ^* A^\infty _u\), assuming that \(\nu \) is the outer normal to \({\widetilde{\varOmega }}\setminus A^\infty _u\), it holds that there exists \(u^-(x_0)\in \mathbb {R}^d\) such that
In fact, the latter identity may be seen by considering the \(GSBD^2\) function \(\widetilde{u}_t\) for a t for which \(J_u=J_{\widetilde{u}_t}\), so that \(x_0 \in J_{\widetilde{u}_t}\). Thus the approximate limit of \(\widetilde{u}_t\) as \(x\rightarrow x_0\) in \((Q_\rho ^\nu (x_0))^+\) is t; on the other hand, we have that \(\widetilde{u}_t(x)=t\) if and only if \(|u(x)|=+\infty \), so we deduce the latter identity in (5.39).
Let us fix \(x_0 \in J_u\) such that (5.36) and either (5.38) (if \(x_0 \in \widetilde{\varOmega }\setminus A^\infty _u\)) or (5.39) (if \(x_0 \in \partial ^* A^\infty _u\)) hold. Notice that this corresponds to fix \(x_0\) in a subset of \(J_u\) of full \(\mathcal {H}^{d-1}\)-measure. Since \(\mu ^\zeta \in \mathcal {M}_b^+({\widetilde{\varOmega }})\), we have that \(\mu ^\zeta (Q_\rho ^\nu (x_0))=\mu ^\zeta (\overline{Q_\rho ^\nu (x_0)})\) except for a countable family of \(\rho \)’s. Moreover, for \(\rho \) small the upper semicontinuous function \(\chi _{\bar{Q}_\rho }\) has compact support in \({\widetilde{\varOmega }}\). Thus, in view of [3, Proposition 1.62(a)] and the Besicovich Derivation Theorem (see, e.g., [3, Theorem 2.22]) we infer that for every \(\rho _m\rightarrow 0\) and every \(\varepsilon _j\rightarrow 0\) it holds that
so that we need an estimate from below of \(\frac{\mu ^\zeta _{\varepsilon _j}(Q_{\rho _m}^\nu (x_0))}{\rho _m^{d-1}}\). For this, we first note that for every j and for every m we can find \(x_0^j\in \delta _j\mathbb {Z}^d\) and \(\rho _{m,j}>0\) such that \(x_0^j\rightarrow x_0\), \(\rho _{m,j}\rightarrow \rho _m\) as \(j\rightarrow +\infty \) and \(\delta _j\mathbb {Z}^d\cap Q_{\rho _{m,j}}^\nu (x_0^j)=\delta _j\mathbb {Z}^d\cap Q_{\rho _{m}}^\nu (x_0)\). Now, setting in correspondence to \(\delta _j=\delta (\varepsilon _j)\)
we introduce the functions \(u_{j,m} \in \mathcal {A}_{\tau _{m,j}}(Q^\nu ;\mathbb {R}^d)\), \(v_{j,m} \in \mathcal {A}_{\tau _{m,j}}(Q^\nu ;\mathbb {R})\) characterized by the following “change of variables in the nodes”
Let \(G_{\sigma _{m,j}}\) and \(F_{\sigma _{m,j}}\) be defined by replacing, in (3.9) for \(G_{\sigma _{m,j}}\), both \(\delta _{m,j}\) with \(\tau _{m,j}\) and \(\varepsilon _{m,j}\) with \(\sigma _{m,j}\), and, in (3.6a) for \(F_{\sigma _{m,j}}\), \(\delta _{m,j}\) with \(\tau _{m,j}\). We find that
In particular we have that
Notice that we used above that \(\zeta >0\) is fixed, and it holds indeed that \(\lim _{m,j} F_{\sigma _{m,j}}(u_{j,m}, v_{j,m})=0\).
By (5.41), (5.42), Proposition 1, and Theorem 2, we obtain that \((u_{j,m}, v_{j,m})_{j,m}\) converges, up to a subsequence, towards a suitable couple in \(GSBD^2_\infty ({\widetilde{\varOmega }}) \times L^2({\widetilde{\varOmega }})\).
Moreover, setting \(u_m(y):=u(x_0+\rho _m y)\) for \(y \in Q^\nu \), it holds that \((u_m)_m\) converges in \(L^0(Q^\nu ;\mathbb {R}^d)\) to
while, if \(x_0 \in \partial ^* A^\infty _u\), we have that \(u_m|_{Q^{\nu ,-}}\) converges in \(L^0({Q^{\nu ,-}};\mathbb {R}^d)\) to \(u_0^-(x):= u^-(x_0)\) in \({Q^{\nu ,-}}\) and that \(\tanh (|u_m|)|_{{Q^{\nu ,+}}}\) converges in \(L^1({Q^{\nu ,+}};\mathbb {R}^d)\) to the constant function 1. Since, for fixed m, \(u_{j,m}\), \(v_{j,m}\) converge in measure to \(u_m\), \(v_m\) as \(j\rightarrow +\infty \), by a diagonal argument we may find a sequence \(m_j\rightarrow +\infty \) such that the above properties hold for \(u_j:=u_{j,m_j}\) as \(j\rightarrow +\infty \) in place of \(u_m\) as \(m\rightarrow +\infty \) and \(v_j:=v_{j,m_j}\rightarrow 1\) in \(L^2(Q^\nu )\), \(\sigma _j:=\sigma _{m_j,j}\rightarrow 0\), \(\tau _j:=\tau _{m_j,j}\rightarrow 0\), and
We now collect these informations and the fact that \((u_j, v_j)_j\) converges \(\mathcal {L}^d\)-a.e., up to a subsequence (see discussion below (5.42)). Therefore
and \(v_j \rightarrow 1\) in \(L^2(Q^\nu )\), where \(u_0\) is given by (5.43) if \(x_0 \in J_u \cap ({\widetilde{\varOmega }}\setminus A^\infty _u)\) and by
Thus, (5.37) (and then the result) would follow from
that we show in the remaining part of the present proof.
Step 3. Up to passing to a subsequence, we may assume that the liminf in (5.46) is actually a limit. Now, we consider a suitable triangulation \(\mathcal {T}_j^d\) of \(Q^\nu \), as introduced in Proposition 1. Namely, we set
We then denote by \(\hat{u}_j=(\hat{u}_j^1,\hat{u}_j^2,\dots , \hat{u}_j^d)\) and \(\hat{v}_j\) the piecewise-affine interpolations of \(u_j\) and \(v_j\) on \(\mathcal {T}^d_j\), respectively. We have that \(\hat{u}_j\rightarrow u_0\) in measure on \(Q^\nu \), and \(\hat{v}_j\rightarrow 1\) in \(L^2(Q^\nu )\).
With fixed \(\eta >0\), by arguing as for the proof of (4.10) we can prove that for j large
Now, we introduce the piecewise constant functions \({\tilde{v}}_{min,j}\) as in (4.4) and, along the lines of the proof of (4.6), with (5.33) (here we use again that \(\zeta >0\) is fixed in the definition of \(\mu _\varepsilon ^\zeta \), as done for (5.42)) we have that
whence we can assume, by taking a further (not relabeled) subsequence, that
Recalling the notation for slicing in Section 2, for any fixed \(\eta >0\) there exists \(\gamma =\gamma (\eta )\) such that, setting \(I_\eta :=(\frac{-1+\eta }{2},\frac{1-\eta }{2})\), it holds
Therefore, recalling also (5.44), (5.45), we infer that for \(\mathcal {H}^{d-1}\)-a.e. \(y\in Q^\nu _{1-\eta }\cap \varPi ^\nu \) and \(\vartheta \in \nu ^\perp \), \(|\vartheta |<\gamma \) (with the notation for slicing from (2.1), (2.2))
We now have that for \(\mathcal {H}^{d-1}\)-a.e. \(\vartheta \in \nu ^\perp \), \(0\ne |\vartheta |<\gamma \)
for \(\mathcal {H}^1\)-a.e. \(y\in Q^\nu _{1-\eta } \cap \varPi ^\nu \). In the case where \(x_0 \in J_u\cap ({\widetilde{\varOmega }}\setminus A^\infty _u)\), (5.49) are readily obtained and the second expression holds true for every \(\vartheta \). In the case \(x_0 \in \partial ^* A^\infty _u\), we regard the points where \(u_0^{{(\nu {+}\vartheta )},y}\) (here possibly \(\theta =0\)) passes from a finite to an infinite value as jump points, that is we adopt the same convention as for \(GSBD^2_\infty \) functions, and we work with the usual product between two numbers in \(\widetilde{\mathbb {R}}\) and \(\mathbb {R}\), setting \(0\cdot (\pm \infty )=0\). By standard arguments (in the spirit of e.g. [21, Lemma 2.7]), we can see that for \(\mathcal {H}^{d-1}\)-a.e. \(\xi \), \(\lim _{t \rightarrow 0^+}|u_0^{\xi ,y}(t)|=+\infty \) for \(\mathcal {H}^{d-1}\)-a.e. y.
From now on we assume that \(\langle u^+(x_0){-}u^-(x_0) , \nu \rangle \ne 0\), so that we may take \(\vartheta =0\) to ease the reading. In the opposite case, we may argue in the very same way, just replacing the slices along the direction \(\nu \) through the slices along a direction \(\nu {+} \vartheta \), for some \(\vartheta \in \nu ^\perp \), \(0\ne |\vartheta | < \gamma \), and considering, below (5.53), \(\pi ^{\nu {+}\vartheta } :\mathbb {R}^d\rightarrow \varPi ^\nu \) given by \(\pi ^{\nu {+}\vartheta }(x)=\{x+t(\nu {+}\vartheta ) :t \in \mathbb {R}\} \cap \varPi ^\nu \), in place of \(\pi ^\nu \).
Then, with (5.48) and Fubini’s Theorem, we have
whence we deduce the existence of a set \(N\subset \varPi ^\nu \) with \(\mathcal {H}^{d-1}(N)=0\) such that
for every \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash N\). It is not restrictive to assume that \(\hat{u}_j^{\nu ,y}\in H^1(I_\eta )\) for every \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash N\). Now, let \(I'_\eta \) be any open interval such that \(0\in \overline{I'_\eta }\subset I_\eta \). If it were
from (5.50) we would infer that \(\hat{u}_j^{\nu ,y}\rightharpoonup u_0^{\nu ,y}\) in \(H^1(I'_\eta )\) and \(J_{u_0^{\nu ,y}}\cap I'_\eta =\emptyset \), which clearly would contradict (5.49). Thus, the liminf in (5.51) is 0, so that for every \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash N\) there exists a sequence \((s_j^y)_j\subset I_\eta \) complying with
Now, with fixed \(\kappa >0\), we claim that there exists a set \(N_j^\kappa \subset \varPi ^\nu \), with \(\mathcal {H}^{d-1}(N_j^\kappa )\rightarrow 0\) as \(j\rightarrow +\infty \), such that for every \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash (N\cup N_j^\kappa )\) there exists \(j_0:=j_0(y,\kappa )\) satisfying
For this, for every \(\alpha \in \tau _j\mathbb {Z}^d\cap Q^\nu \) we set
and
From the equiboundedness of the energies (5.33) and an analogous argument as for the proof of (4.18), we deduce that there exists a constant \(C>0\) such that
for every j, whence
Let \(\pi ^\nu :\mathbb {R}^d\rightarrow \varPi ^\nu \) be the orthogonal projection onto the hyperplane \(\varPi ^\nu \) and set
then, with (5.53) we infer that
Now let \(j\in \mathbb {N}\) be large, \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash (N\cup N_j^\kappa )\), and consider the corresponding sequence \((s_j^y)\) as defined in (5.52). By the definition of \({\tilde{v}}_{min,j}\) we deduce the existence of \(\alpha _0:=\alpha _0(y)\in (\tau _j\mathbb {Z}^d\cap Q^\nu )\backslash \mathcal {I}_j^\kappa \) such that \(y+s_j^y\nu \in \alpha _0+\tau _j[0,1)^d\) and \({\tilde{v}}_{min,j}(\alpha _0)=\min \{v_j(\alpha _0), \{v_j(\alpha _0\pm \tau _j\xi )\}_{\xi \in S_d}\}\rightarrow 0\) as \(j\rightarrow +\infty \).
Therefore, for every \(\kappa >0\) and every \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash (N\cup N_j^\kappa )\) there exists \(j_0:=j_0(\kappa ,y)\in \mathbb {N}\) such that \({\tilde{v}}_{min,j}(\alpha _0)<\frac{\kappa }{4}\) for every \(j\ge j_0\). Moreover, since \(\alpha _0\in (\tau _j\mathbb {Z}^d\cap Q^\nu )\backslash \mathcal {I}_j^\kappa \) we also have \(v_j(\alpha _0)<\frac{3}{4}\kappa \), \(v_j(\alpha _0\pm \tau _j\xi )<\frac{5}{4}\kappa \) for every \(j\ge j_0\) and every \(\xi \in S_d\). This implies, by convexity, that
Since in the previous argument \(\kappa >0\) was chosen arbitrarily, from now on we may assume that \(0<\kappa <\frac{4}{9}\). As we already know, up to a possible subsequence, \(\hat{v}_j^{\nu ,y}\rightarrow 1\) a.e., so that we can find \(r_j^y,t_j^y\in I_\eta \) such that \(r_j^y<s_j^y<t_j^y\) and
Now, for every fixed \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\backslash (N\cup N_j^\kappa )\), by using the Cauchy Inequality and taking into account (5.55)–(5.56) we obtain
for every \(j\ge j_0\).
From (5.54) we deduce that, up to subsequences,
so that
for \(\mathcal {H}^{d-1}\)-a.e. \(y\in (Q^\nu _{1-\eta }\cap \varPi ^\nu )\). Finally, from (4.10), the Fatou’s Lemma with (5.57) we obtain
whence (5.46) follows letting \(\kappa \rightarrow 0\) and then \(\eta \rightarrow 0\). \(\square \)
6 The upper limit for the Griffith energy
In this section we prove the \(\varGamma \)-limsup inequality for the convergence stated in Theorem 3. Differently to what done in the previous sections, here we argue for the reference configuration \(\varOmega \). The constraint \(u_\varepsilon \in \mathcal {A}_\delta ^\mathrm {Dir}(\varOmega ; \mathbb {R}^d)\), \(v_\varepsilon \in \mathcal {A}_\delta ^\mathrm {Dir}(\varOmega ; \mathbb {R})\) for the recovery sequence will follow from the part of the density result Theorem 1 concerning the treatment of Dirichlet boundary conditions.
Proposition 4
Assume that \(\lim _{\varepsilon \rightarrow 0} \frac{\delta }{\varepsilon }=0\), and let \(u\in GSBD^2({\varOmega })\). Then there exists a sequence \((u_\varepsilon ,v_\varepsilon )\in \mathcal {A}_\delta ^\mathrm {Dir}(\varOmega ; \mathbb {R}^d)\times \mathcal {A}^\mathrm {Dir}_\delta (\varOmega ; \mathbb {R})\) such that \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in measure on \({\varOmega }\times {\varOmega }\) and
Proof
In view of Theorem 1 and remarks below, by a diagonal argument it is not restrictive to assume that \(u\in \mathcal {W}(\varOmega ;\mathbb {R}^d)\) and that \(J_u\) is a closed subset of the hyperplane \(\varPi ^{e_d}=\{x_d=0\}\), that we denote by K. To fix the notation we argue for \(d=3\), the case \(d=2\) being analogous.
We recall from [6, (4.23)-(4.24)] the following fact about the optimal profile problem for the Ambrosio–Tortorelli functional: for fixed \(\eta >0\), there exist \(T_\eta >0\) and \(f_\eta \in C^2([0,+\infty ))\) such that \(f_\eta (0)=0\), \(f_\eta (t)=1\) for \(t\ge T_\eta \), \(f_\eta '(T_\eta )=f_\eta ''(T_\eta )=0\), and
Let \(x=(x',x_d)\) for each \(x \in \mathbb {R}^d\), and \(K_h:=\{x\in \varPi ^{e_d}:\, \mathrm{dist}(x,K)< h\}\) for every \(h>0\).
Let \(T>T_\eta \) and \(\gamma _\varepsilon >0\) be a sequence such that \(\gamma _\varepsilon /\varepsilon \rightarrow 0\) as \(\varepsilon \rightarrow 0\). We set
and \(A_{\varepsilon ,\delta }:=A_\varepsilon \cap \delta \mathbb {Z}^3\), \(A'_{\varepsilon ,\delta }:=A'_\varepsilon \cap \delta \mathbb {Z}^3\). Notice that, for \(\varepsilon \) small,
recalling that \(K \subset \varOmega \). Let \(\phi _\varepsilon \) be a smooth cut-off function between \(B_\varepsilon \) and \(B'_\varepsilon \), and set
Since \(u\in W^{1,\infty }({\varOmega }\backslash J_u;\mathbb {R}^3)\) we have \(u_\varepsilon \in W^{1,\infty }({\varOmega };\mathbb {R}^3)\). Moreover, since \(A'_\varepsilon \) is a compact set in \(\varOmega \) and \(u=u_0\) in a neighborhood of \({\partial _D \varOmega }\), also \(u_\varepsilon =u_0\) in a neighborhood of \({\partial _D \varOmega }\). Note also that, by the Lebesgue Dominated Convergence Theorem, \(u_\varepsilon \rightarrow u\) in \(L^1(\varOmega ;\mathbb {R}^3)\). If \(\psi _\varepsilon \) is a cut-off function between \(K_{\varepsilon +\sqrt{3}\delta }\) and \(K_{2\varepsilon +\sqrt{3}\delta }\), we define
where the function \(h_\varepsilon :[0,+\infty )\rightarrow \mathbb {R}\) is given by
By construction, \(v_\varepsilon \in W^{1,\infty }(\varOmega )\cap C^0(\varOmega )\cap C^2(\varOmega \backslash A_\varepsilon )\) and \(v_\varepsilon \rightarrow 1\) in \(L^1(\varOmega )\).
We start proving that there exists a sequence \((\bar{u}_\varepsilon ,\bar{v}_\varepsilon )\in \mathcal {A}^{\mathrm {Dir}}_\delta (\varOmega ;\mathbb {R}^3)\times \mathcal {A}^{\mathrm {Dir}}_\delta (\varOmega ; \mathbb {R})\) converging in measure to (u, 1) on \(\varOmega \times \varOmega \) such that
and
Setting
since \(F_\varepsilon (\cdot , \bar{v}_\varepsilon )\le F_\varepsilon (\cdot ,1)\) and \(F_\varepsilon ^\mathrm{div}(\cdot , \bar{v}_\varepsilon )\le F_\varepsilon ^\mathrm{div}(\cdot ,1)\), it will be sufficient to prove both (6.3) and (6.4) for the pair of admissible functions \((\bar{u}_\varepsilon ,1)\). Notice that \(\bar{v}_\varepsilon \in \mathcal {A}^\mathrm {Dir}_\delta (\varOmega ;\mathbb {R})\) by (6.2) and since \(A'_\varepsilon \) is a compact subset of \(\varOmega \).
Let \(\xi \in S_3\) be fixed. Define
Since \(v_\varepsilon (\alpha )=0\) for all \(\alpha \in A_{\varepsilon ,\delta }\), let \(x\in \varOmega _\delta ^\xi \backslash A_\varepsilon \): by construction, \(x\pm \delta \xi \in \varOmega _\delta ^\xi \backslash B'_\varepsilon \) and \(u_\varepsilon =u\) on \(\varOmega \backslash B'_\varepsilon \). Thus, by using the Fundamental Theorem of Calculus and Jensen’s inequality we deduce that
for every \(\zeta \in \{\pm \xi \}\). Moreover, setting \(\varOmega _\delta ^\mathrm{div}:=\varOmega _\delta ^{e_1}\cap \varOmega _\delta ^{e_2}\cap \varOmega _\delta ^{e_3}\), by arguing as for [1, (4.9)], we have that
for every \((k_1,k_2,k_3)\in \{-1,1\}^3\).
For simplicity, we prove (6.7) in the case \((k_1, k_2, k_3)=(1,1,1)\). We first notice that
Now, since \(|\varOmega \backslash (\varOmega _\delta ^\mathrm{div}\backslash B_\varepsilon ')|\rightarrow 0\) as \(\varepsilon \rightarrow 0\), with the absolute continuity of the integral, Jensen’s inequality and the Cauchy–Schwarz inequality we deduce that
as \(\varepsilon \rightarrow 0\). Finally, as a consequence of Fubini’s theorem we have
as \(\varepsilon \rightarrow 0\), whence (6.7) follows from the continuity of translations in \(L^2\).
With the estimates (6.6), by summing over \(\xi \in S_3\) and taking into account Remark 1 we infer that
From (6.7), we deduce that
Now, we adapt to our case the argument of the proof of [1, Proposition 4.4], which combined with (6.8)–(6.9) will give (6.3)–(6.4).
For every \(y\in (0,1]^3\), we introduce the sequence \(T_y^\delta u_\varepsilon \) as defined in (2.22) for \(d=3\), which satisfies \(T_y^\delta u_\varepsilon (x)=u_\varepsilon (\delta y +\alpha )\) for every \(x\in \alpha +(0,\delta ]^3\), \(\alpha \in \delta \mathbb {Z}^3\).
Now, since for \(\alpha \in \delta \mathbb {Z}^3\) and \(\xi \in \mathbb {Z}^3\) we have \(\delta \lfloor \frac{\alpha }{\delta }\rfloor =\alpha \) and \(\delta \lfloor \frac{\alpha +\delta \xi }{\delta }\rfloor =\alpha +\delta \xi \), we get
whence, with (6.8)–(6.9), we infer that
Moreover, with fixed \(\eta >0\), (6.11) implies that the set
has strictly positive Lebesgue measure for \(\varepsilon \) small enough. Indeed, for \(\varepsilon \) small enough and with (6.11) we deduce that
so that \(|C_\eta ^\varepsilon |\ge 1-\frac{M}{M+\eta }>0\). Now, as a consequence of Lemma 3(ii) we deduce that, for every \(\varepsilon >0\), there exists \(z_\varepsilon \in C_\eta ^\varepsilon \) such that \(T_{z_\varepsilon }^\delta u_\varepsilon \rightarrow u\) in \(L^1\) and
Finally, setting \(\bar{u}_\varepsilon :=T_{z_\varepsilon }^\delta u_\varepsilon \), with (6.11)–(6.12) we obtain
whence the assertion follows letting \(\eta \rightarrow 0\). We observe that \(\bar{u}_\varepsilon \in \mathcal {A}^\mathrm {Dir}_\delta (\varOmega ;\mathbb {R}^d)\), since \(u_\varepsilon =u_0\) in a neighborhood of \({\partial _D \varOmega }\).
We provide now an estimate for \(G_\varepsilon (\bar{v}_\varepsilon )\). Setting, for \(\alpha \in \varOmega _\delta \) such that \(\alpha +\delta e_k\in \varOmega \),
we have (below we have to restrict the sums over \(\alpha \in \varOmega _\delta \) such that \(\alpha +\delta e_k\in \varOmega \), we omit it to ease the notation)
The argument now follows the proof of [6, Proposition 4.2], so that we will only recall briefly the main steps.
First, we note that
since for any \(\alpha \in \varOmega _\delta \backslash A'_\varepsilon \) we have that \(v_\varepsilon (\alpha +\delta e_k)=v_\varepsilon (\alpha )=1\) for every \(k=1,2,3\) from the definition of \(h_\varepsilon \). Then, by exploiting also the regularity of \(v_\varepsilon \), it can be proved that (for \(B_\delta :=B\cap \delta \mathbb {Z}^3\) for every \(B\subset \mathbb {R}^3\) Borel)
Indeed, we have that \(v_\varepsilon (\alpha )=v_\varepsilon (\alpha +\delta e_k)=0\), \(k=1,2,3\) for every \(\alpha \in (A_{\varepsilon })_{\delta }\) such that \(\alpha +\delta e_k\in (A_{\varepsilon })_{\delta }\) for every \(k=1,2,3\). This implies that
On the other hand,
Finally, taking into account the fact that \(f_\eta \) is a Lipschitz function, we obtain
Now, collecting the estimates (6.14), (6.15), (6.16), (6.17) we deduce that
whence the desired bound follows by the arbitrariness of \(\eta >0\).
In addition, (6.18) implies that
then \(\bar{v}_\varepsilon \rightarrow 1\) in \(L^1(\varOmega )\). \(\square \)
Remark 2
The argument for the proof of Proposition 4 shows that an analogous (local version) of the upper bound inequality (6.18) can be obtained also under the assumption that \(l:=\displaystyle \lim _{\varepsilon \rightarrow 0}\frac{\delta }{\varepsilon }\in (0,+\infty )\). In this case, there exists a constant \(C_l>0\) such that
In particular, this permits to control from above the \(\varGamma \)-\(\limsup \) of \(E^{\mathrm {Dir}}_{\lambda , \theta }\) through a Griffith-type functional.
7 The non-interpenetration constraint
This section contains the proof of the \(\varGamma \)-convergence approximation in Theorem 4. The lower inequality relies on the results proven in Section 4. For the upper inequality we employ a density result for couples (u, v), here recalled in Lemma 7, which has been shown in dimension 2 in [18] to prove the upper bound in a continuum approximation for the Griffith energy with a linearized non-interpenetration constraint. We give first the proof of Theorem 4, keeping in the last part of the section the auxiliary results.
Proof of Theorem 4
As a preparation for (i) and (ii) we notice that, since \(v \le 1\), then \(F_\varepsilon ^{\mathrm {div}}\le F_\varepsilon ^{\mathrm {div},\mathrm {NI}}\) (see (3.6b) and (3.8b)), and \(E^{\lambda , \theta }_\varepsilon \le (E^{\mathrm {NI}}_{\lambda , \theta })_\varepsilon \).
Proof of (ii). Consider \((u_\varepsilon , v_\varepsilon )_\varepsilon \) with \(\sup _{\varepsilon }(E^{\mathrm {NI}}_{\lambda , \theta })_\varepsilon (u_\varepsilon , v_\varepsilon )<+\infty \). In particular, from the previous observations, (4.1) holds true. Then by Proposition 1 we have that \(u_\varepsilon \) has the same pointwise limit of a suitable function \(\bar{u}_\varepsilon \), that satisfies (4.3) and \(\Vert \bar{u}_\varepsilon \Vert _{L^\infty } \le M\). Therefore (cf. [9]) \((u_\varepsilon )_\varepsilon \) converges in every \(L^p(\varOmega ;\mathbb {R}^d)\), \(p \in [1, \infty )\), to some \(u \in SBD^2(\varOmega )\) with \(\Vert u\Vert _{L^\infty } \le M\).
Proof of (i). We argue for \(d=3\), the case \(d=2\) being analogous. Fix \((u_\varepsilon , v_\varepsilon )_\varepsilon \) such that \(\sup _{\varepsilon }(E^{\mathrm {NI}}_{\lambda , \theta })_\varepsilon (u_\varepsilon , v_\varepsilon )<+\infty \) and \(u_\varepsilon \rightarrow u\), \(u \in SBD^2(\varOmega )\). By (ii), \(\Vert u\Vert _{L^\infty } \le M\) and \(u_\varepsilon \rightarrow u\) in every \(L^p(\varOmega ;\mathbb {R}^d)\). In particular, \(\mathrm {E} u\) is a measure, with

Let us show that u satisfies \(\mathrm {Div}^-u=\mathrm {Tr}^-(\mathrm {E}u)\in L^2(\varOmega )\). In fact, let us examine the proof of Proposition 2, with now the control on \(F_\varepsilon ^{\mathrm {div},\mathrm {NI}}(u_\varepsilon , v_\varepsilon )\) at hand, which improves that on \(F_\varepsilon ^{\mathrm {div}}(u_\varepsilon , v_\varepsilon )\). (The only difference is that in Section 4 we worked with \(\widetilde{\varOmega }\), now with \(\varOmega \); anyway, one could as well in this case obtain the lower limit inequality imposing a Dirichlet datum). Arguing as in that proof, we introduce the functions \(z_\varepsilon \) as in (5.27). Then \(z_\varepsilon \rightarrow u\) in every \(L^p(\varOmega ;\mathbb {R}^d)\), since they converge in measure to u and \(\Vert z_\varepsilon \Vert _{L^\infty }\le M\). Moreover, taking the negative part of the scalar functions in (5.28), we obtain that
for every \((k_1,k_2,k_3)\in \{-1,1\}^3\), where we recall the definition of \( \delta \mathcal {Q}^{k_1e_1,k_2e_2,k_3e_3}(\alpha )\) in (5.30). Then, arguing as for (5.31), we get that
Summing over \(\alpha \) and recalling the control on \(F_\varepsilon ^{\mathrm {div},\mathrm {NI}}(u_\varepsilon , v_\varepsilon )\), (3.8b), and (3.7), we infer that if \(\varepsilon >0\) is small enough then
for \(C>0\) depending on M and \(\theta \). In view of the \(L^1\) convergence of \(z_\varepsilon \) to u, we have that \(\mathrm {div}\,z_\varepsilon \) converges in the sense of distributions on \(\varOmega \) to \(\mathrm {Div}\, u=\mathrm {Tr}(\mathrm {E} u)\). Then, arguing as in e.g. [3, Proposition 1.62], we can see that \(\mathrm {div}^- z_\varepsilon \) converges weakly in \(L^2(\varOmega _\eta )\) to a suitable non negative function f, with \(f \ge \mathrm {Div}^- u\). Then the positive measure \(\mathrm {Div}^- u=\mathrm {Tr}^-(\mathrm {E}u)\) is indeed in \(L^2(\varOmega )\).
Now, computing the negative part of the trace of the identity (7.1), we obtain the non-interpenetration condition \([u]\cdot \nu \ge 0\) \(\mathcal {H}^{d-1}\)-a.e. on \(J_u\), since \(\mathrm {Div}^- u\) has no singular part. We deduce that \({\mathcal {G}}_{\lambda ,\theta }^{\mathrm {NI},M}(u,1)={\mathcal {G}}_{\lambda ,\theta }(u,1; \varOmega ) < +\infty \). Then, by Theorem 3 and \(E^{\lambda , \theta }_\varepsilon \le (E^{\mathrm {NI}}_{\lambda , \theta })_\varepsilon \) we conclude (i).
Proof of (iii). Let \(u_\varepsilon ^{\beta , l}\), \(v_\varepsilon ^{\beta , l}\) the functions provided by Lemma 7, in correspondence to families of \(\varepsilon \), \(\beta \), \(l \in (0,1)\). First we show that for every l, \(\beta \)
Indeed, in view of the assumption \(\lim _{\varepsilon \rightarrow 0} \frac{\delta }{\varepsilon ^2}=0\) and of Remark 3, we have that
uniformly with respect to \(\xi \in \mathbb {R}^2 \setminus \{0\}\), \(\beta \), l, and x with \({{\,\mathrm{dist}\,}}(x,\partial \varOmega )> \delta |\xi |\). Therefore
for every \(\zeta \in \{\pm \xi \}\). Similarly, one estimates
and then obtains (7.4).
From (7.4) we pass to an estimate on \(\lambda \sum _{\xi \in S_2}\sigma _{|\xi |}F_\varepsilon ^\xi (u_\varepsilon ^{\beta , l},v_\varepsilon ^{\beta , l})+\theta {F}^{\mathrm {div}, \mathrm {NI}}_\varepsilon (u_\varepsilon ^{\beta , l},v_\varepsilon ^{\beta , l})\) by arguing as in the proof of Proposition 4. We thus consider for every \(y\in (0,1]^2\) the functions \(T_y^\delta u_\varepsilon ^{\beta , l}\), \(T_y^\delta v_\varepsilon ^{\beta , l}\) as defined in (2.22) for \(d=2\) and \(u= u_\varepsilon ^{\beta , l}\), \(v_\varepsilon ^{\beta , l}\). By the definition of the operator \(T_y^\delta \), arguing similarly to (6.10) we deduce
Following the very same argument as that to get (6.13), applied to \((T_y^\delta u_\varepsilon ^{\beta , l},T_y^\delta v_\varepsilon ^{\beta , l})\) in place of \(T_y^\delta u_\varepsilon \), for \(\eta >0\) fixed we infer that for every l, \(\beta \), \(\varepsilon \) there exists \(z_\varepsilon ^{\beta , l}\in (0,1)^2\) such that, setting \(\bar{u}_\varepsilon ^{\beta , l}:= T_{z_\varepsilon ^{\beta , l}}^\delta u_\varepsilon ^{\beta , l}\), \(\bar{v}_\varepsilon ^{\beta , l}:= T_{z_\varepsilon ^{\beta , l}}^\delta v_\varepsilon ^{\beta , l}\), it holds that
and
As for the Modica–Mortola term, we first introduce a variant of \(G_\varepsilon \) obtained by replacing \(\alpha \) by \(\alpha +\delta y\) in the expression of \(G_\varepsilon \) (3.9), namely for every \(v:\varOmega \rightarrow \mathbb {R}\) measurable we set
Now we may argue exactly as done in [6, Proposition 4.2, Step 2] and in the last part of the proof of Proposition 4, with \(\alpha + \delta y\) in place of \(\alpha \) (that is, the functions are evaluated in \(\alpha +\delta y\) instead of \(\alpha \), inside each cube \(\alpha +\delta [0,1)^2\)) and the role of K, \(h_\varepsilon \) played now by \(\varGamma ^\beta \), \(\gamma (\frac{\cdot }{\varepsilon })\) from (i) in Lemma 7 (notice that we use the regularity of \(\varGamma ^\beta \) to control its discretized neighborhoods). We then obtain that for every \(y \in [0,1)^2\)
Moreover, notice that for every \(y \in [0,1)^2\)
Let us choose l, \(\beta \), \(\eta \) in dependence on \(\varepsilon \), vanishing as \(\varepsilon \rightarrow 0\), and denote by \(\bar{u}_\varepsilon \), \(\bar{v}_\varepsilon \) the corresponding \(\bar{u}_\varepsilon ^{\beta , l}\), \(\bar{v}_\varepsilon ^{\beta , l}\) (before we omit the further dependence on \(\eta \)). By collecting (7.5), (7.7), (7.8), (7.9) and (iv) in Lemma 7, we eventually deduce that
and (7.6) with (ii) in Lemma 7 give that \(\bar{u}_\varepsilon \), \(\bar{v}_\varepsilon \) converge to u and 1. This concludes the proof of (iii). \(\square \)
We recall the following result, which is a direct outcome of [18].
Lemma 7
Let \(d=2\) and \(u\in SBD^2(\varOmega ) \cap L^\infty (\varOmega ;\mathbb {R}^d)\) with \(\mathrm {Div}^-u=\mathrm {Tr}^-(\mathrm {E}u) \in L^2(\varOmega )\). Then, for every families of parameters \(\varepsilon \), \(\beta \), \(l \in (0,1)\) there exist functions \(v_\varepsilon ^{\beta , l}\in C^\infty (\varOmega ; [0,1])\), \(u_\varepsilon ^{\beta , l}\in C^\infty (\varOmega ;\mathbb {R}^d)\) such that
-
(i)
for every \(\beta >0\) there exists a set \(\varGamma ^\beta \), which is a finite union of \(C^1\) hypersurfaces and of at most \(C\beta /(\varepsilon l)\) isolated points (for \(C>0\) a universal constant), such that \(\mathcal {H}^1(J_u \triangle \varGamma ^\beta ) < \beta ^2\) and \(v_\varepsilon ^{\beta , l}\) has the form
$$\begin{aligned} v_\varepsilon ^{\beta , l}=\gamma \Bigg ( \frac{({{\,\mathrm{dist}\,}}(x, \varGamma ) - 16 \sqrt{2} \varepsilon l )^+ }{\varepsilon } \Bigg ) \end{aligned}$$where \(\gamma \) is a smooth scalar function with \(\gamma (t)\in [0,1]\), \(\gamma (0)=0\), \(\lim _{t\rightarrow +\infty }\gamma (t)=1\). In particular, for every \(\beta \), l, it holds \(v_\varepsilon ^{\beta , l}\rightarrow 1\) in \(L^2(\varOmega )\) as \(\varepsilon \rightarrow 0\);
-
(ii)
for every l, it holds \(\limsup _{\beta \rightarrow 0} \limsup _{\varepsilon \rightarrow 0}\Vert u_\varepsilon ^{\beta , l}- u\Vert _{L^2}=0\);
-
(iii)
\(u_\varepsilon ^{\beta , l}=\varphi _{\varepsilon l} *\widetilde{u} _\varepsilon ^{\beta , l}\), for a suitable \(\widetilde{u}_\varepsilon ^{\beta , l}\) in \(L^\infty (\varOmega ;\mathbb {R}^d)\) with \(\Vert \widetilde{u}_\varepsilon ^{\beta , l}\Vert _{L^\infty } \le \Vert u\Vert _{L^\infty }\) and \(\varphi _{\varepsilon l}=(\varepsilon l)^{-2} \varphi (\frac{\cdot }{\varepsilon l})\) for \(\varphi \in C_c^\infty (B_{1/2})\) with \(\int \varphi \,\mathrm {d}x=1\) a given radially symmetric mollifier;
-
(iv)
it holds that
$$\begin{aligned} \begin{aligned} \limsup _{l\rightarrow 0}&\limsup _{\theta \rightarrow 0} \limsup _{\varepsilon \rightarrow 0} \Bigg [ \int _{\varOmega }(v_\varepsilon ^{\beta , l})^2 \bigg (\lambda |\mathcal {E}(u_\varepsilon ^{\beta , l})|^2 + \Big (\frac{\lambda }{2} + \beta \Big ) |\mathrm {div}^+\,u_\varepsilon ^{\beta , l}|^2 \bigg ) \,\mathrm {d}x\\&+ \Big (\frac{\lambda }{2} + \beta \Big ) \int _\varOmega |\mathrm {div}^-\,u_\varepsilon ^{\beta , l}|^2 \,\mathrm {d}x+ \frac{1}{2} \int _\varOmega \Big ( \frac{(v_\varepsilon ^{\beta , l}-1)^2}{\varepsilon } + \varepsilon |\nabla v_\varepsilon ^{\beta , l}|^2 \Big ) \,\mathrm {d}x\Bigg ] \\&\le {\mathcal {G}}^{\lambda ,\theta }(u)\,. \end{aligned} \end{aligned}$$
Proof
Properties (i), (ii), (iii) are clear from the construction for the \(\limsup \) inequality for [18, Theorem 1], in [18, Subsections 3.1 and 3.2]. In particular, for (i) see (with the numeration in [18]) the definition of \(v_\varepsilon ^l\) at the beginning of Subsection 3.1 and (17), for (ii) the very last sentence of Section 3, and for (iii) the definition of \(u_\varepsilon \) below (24), where u has to be replaced by \(u_I\), as explained below (34).
As for (iv), this is a consequence of (18) for the Modica–Mortola part in v (with a minor modification since the Modica–Mortola term here is slightly different), of (27), that states that \(\mathcal {E}u_\varepsilon ^{\beta , l}\) is a good approximation of \(\mathcal {E}u\) where \(v_\varepsilon ^{\beta , l}\ne 0\) (then one can treat separately \(\mathcal {E}u_\varepsilon ^{\beta , l}\) and \(\mathrm {div}^+u_\varepsilon ^{\beta , l}\), as we did), and of (36)–(37) for the treatment of \(\mathrm {div}^-u_\varepsilon ^{\beta , l}\). \(\square \)
Remark 3
From (iii) it follows that
for every fixed \(\beta \), l, \(\varepsilon \), C depending only on \(\Vert u\Vert _{L^\infty }\) and \(\varphi \), and \(\varOmega _{\varepsilon l}:=\{x \in \varOmega :{{\,\mathrm{dist}\,}}(x, {\partial \varOmega })>\varepsilon l\}\). In fact, for x, \(y \in \varOmega _{\varepsilon l}\)
We deduce the claim by noticing that \(\Vert \nabla \varphi _{\varepsilon l}\Vert _{W^{1,\infty }}\le (\varepsilon l)^{-4}\Vert \nabla \varphi \Vert _{W^{1,\infty }}\) and that the above integral is indeed computed on the set \(B_{\varepsilon l /2}(x+y) \cup B_{\varepsilon l/2}(x)\), with area \(C(\varepsilon l)^2\).
References
Alicandro, R., Focardi, M., Gelli, M.S.: Finite-difference approximation of energies in fracture mechanics. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze 29, 671–709 (2000)
Ambrosio, L., Coscia, A., Dal Maso, G.: Fine properties of functions with bounded deformation. Arch. Ration. Mech. Anal. 139, 201–238 (1997)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Clarendon Press, Oxford (2000)
Ambrosio, L., Tortorelli, V.M.: Approximation of functionals depending on jumps by elliptic functionals via \(\Gamma \)-convergence. Commun. Pure Appl. Math. 43, 999–1036 (1990)
Ambrosio, L., Tortorelli, V.M.: On the approximation of free-discontinuity problems. Boll. Un. Mat. Ital. 6, 105–123 (1992)
Bach, A., Braides, A., Zeppieri, C.I.: Quantitative analysis of finite-difference approximations of free-discontinuity problems. Interfaces Free Bound. 22, 317–381 (2020)
Bach, A., Cicalese, M., Ruf, M.: Random finite-difference discretizations of the Ambrosio-Tortorelli functional with optimal mesh size, arXiv:1902.08437 (2019)
Bellettini, G., Coscia, A.: Discrete approximation of a free discontinuity problem. Numer. Funct. Anal. Optim. 15, 201–224 (1994)
Bellettini, G., Coscia, A., Dal Maso, G.: Compactness and lower semicontinuity properties in \({SBD}(\Omega )\). Mathematische Zeitschrift 228, 337–351 (1998)
Bouchitté, G., Fonseca, I., Mascarenhas, L.: A global method for relaxation. Arch. Ration. Mech. Anal. 145, 51–98 (1998)
Bourdin, B.: Image segmentation with a finite element method, M2AN Math. Model. Numer. Anal. 33, 229–244 (1999)
Bourdin, B., Francfort, G., Marigo, J.-J.: The variational approach to fracture. J. Elasticity 91, 5–148 (2008)
Braides, A., Gelli, M.S.: Limits of discrete systems with long-range interactions, vol. 9, 2002, pp. 363–399. Special issue on optimization (Montpellier, 2000)
Braides, A., Yip, A.: A quantitative description of mesh dependence for the discretization of singularly perturbed nonconvex problems. SIAM J. Numer. Anal. 50, 1883–1898 (2012)
Cagnetti, F., Dal Maso, G., Scardia, L., Zeppieri, C.I.: Stochastic homogenisation of free-discontinuity problems. Arch. Ration. Mech. Anal. 233, 935–974 (2019)
Chambolle, A.: Image segmentation by variational methods: Mumford and Shah functional and the discrete approximations. SIAM J. Appl. Math. 55, 827–863 (1995)
Chambolle, A.: Finite-differences discretizations of the Mumford-Shah functional. ESAIM: Math. Model. Numer. Anal. 33, 261–288 (1999)
Chambolle, A., Conti, S., Francfort, G.A.: Approximation of a brittle fracture energy with a constraint of non-interpenetration. Arch. Ration. Mech. Anal. 228, 867–889 (2018)
Chambolle, A., Crismale, V.: A density result in \({GSBD}^p\) with applications to the approximation of brittle fracture energies. Arch. Rational Mech. Anal. 232, 1329–1378 (2019)
Chambolle, A., Crismale, V.: Phase-field approximation for a class of cohesive fracture energies with an activation threshold. Adv. Calc. Var. https://doi.org/10.1515/acv-2019-0018 (in press)
Chambolle, A., Crismale, V.: Compactness and lower semicontinuity in \(GSBD\). J. Eur. Math. Soc. (JEMS). Preprint arXiv:1802.03302 (2018) (to appear)
Chambolle, A., Dal Maso, G.: Discrete approximation of the Mumford-Shah functional in dimension two. Math. Model. Numer. Anal. 33, 651–672 (1999)
Conti, S., Focardi, M., Iurlano, F.: Integral representation for functionals defined on \({SBD}^p\) in dimension two. Arch. Ration. Mech. Anal. 223, 1337–1374 (2017)
Cortesani, G., Toader, R.: A density result in SBV with respect to non-isotropic energies. Nonlinear Anal. 38, 585–604 (1999)
Crismale, V., Friedrich, M.: Equilibrium configurations for epitaxially strained films and material voids in three-dimensional linear elasticity. Arch. Ration. Mech. Anal. 237, 1041–1098 (2020)
Crismale, V., Friedrich, M., Solombrino, F.: Integral representation for energies in linear elasticity with surface discontinuities. Preprint arXiv:2005.06866 (2020)
Dal Maso, G.: Generalised functions of bounded deformation. J. Eur. Math. Soc. 15, 1943–1997 (2013)
Gobbino, M.: Finite difference approximation of the Mumford-Shah functional. Commun. Pure Appl. Math. 51, 197–228 (1998)
Griffith, A.A.: The phenomenon of rupture and flow in solids. Philos. Trans. R. Soc. Lond. A 221, 163–198 (1920)
Negri, M.: A finite element approximation of the Griffith’s model in fracture mechanics. Numer. Math. 95, 653–687 (2003)
Ruf, M.: Discrete stochastic approximations of the Mumford-Shah functional. Ann. Inst. H. Poincaré Anal. Non Linéaire 36, 887–937 (2019)
Temam, R.: Mathematical Problems in Plasticity. Gauthier-Villars (1985)
Acknowledgements
For this project V. Crismale has received funding from the European Union’s Horizon 2020 research and innovation programme under the the Marie Skłodowska-Curie grant agreement No. 793018. He also acknowledges the support of the CMAP.
G. Scilla and F. Solombrino have been supported by the Italian Ministry of Education, University and Research through the Project “Variational methods for stationary and evolution problems with singularities and interfaces” (PRIN 2017).
Funding
Open access funding provided by Universitá degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J.Ball.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Crismale, V., Scilla, G. & Solombrino, F. A derivation of Griffith functionals from discrete finite-difference models. Calc. Var. 59, 193 (2020). https://doi.org/10.1007/s00526-020-01858-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-020-01858-7