Analysis of robust control method for the flexible manipulator in reliable operation of medical robots during COVID-19 pandemic

Abstract

A novel coronavirus disease (COVID-19) is transmitting throughout the globe. During this Pandemic situation, medical robots are playing an important role in protecting front line medical staff from this disease. The flexible robotic manipulator has mechanical flexibility, due to that fluctuation or oscillations can be seen either during or after the movement of a manipulator and can create uncertainty in medical operations. During this pandemic situation, reliable operations of these robots are necessary that depend upon the stability of flexible manipulators. In this article, Linear Quadratic Regulator (LQR), Pole Placement, and Proportional-Integral-Derivatives (PID) control methods have been used to investigate the robust control method for controlling the position of manipulator with flexible link in medical robots. To carry out this research, an effective variant of the flexible Link robotic manipulator has been used as a framework to analyze the robust control method. The Matlab®/Simulink result shows that the LQR control method provides better control response compared to PID and pole placement method and thus provides reliable operation to Medical Robots.

1 Introduction

A novel coronavirus infection disease named ‘COVID-19′ is a vast community of viruses which are extending from the normal cold to destructive diseases just like the ‘Severe Acute Respiratory Syndrome’ (SARS-CoV) and ‘Middle East respiratory syndrome’ (MERS-CoV) (Romanov 2020). Thousands of physicians and nurses have fallen ill in the COVID-19 epidemic, and hundreds have died. Globally, according to ‘Situation report-159’ by world health organization (WHO) total of 96, 53,048 confirmed cases and 4, 91,128 deaths have been reported till 27 June 2020 (WHO 2020).

During the COVID-19 pandemic, medical robots are playing a very important role by decreasing workmanship. In healthcare, the need for these robots is rising day by day to reduce the chances of community transmission. This technology can assist with social distancing (implemented by the various governments across the globe) that reduces the risk of infections for patients and health workers acquired by healthcare (Wee et al. 2020; WHO 2020). Hospitals are using intelligent robots to assist in various applications like; surgeries, delivering food and medicines to patients, hospital sanitization, and provide information to patients. One can say that the Tele-nursing paradigm also playing a crucial role. Tele-Nursing is the process in which a person can monitor a robot remotely to perform many of the tasks involved in patient care. Figure 1 shows the robots engaged in surgical operations. Reporting has been made about ‘industry 4.0 technologies’ where various applications of these technologies have been described in fighting COVID-19 pandemic (Javaid et al. 2020).

Fig. 1

Role of medical robots in Surgical operations

Due to the growing requirement for low weight medical robots in this COVID-19 pandemic, the reliable operation of these robots is essential. Reliable operation means efficient operation with precision, high accuracy and increased stability of any robot without any fluctuation or oscillation whether assisting surgeries, delivering food, etc. Several types of robotics systems and special-purpose surgical tools have been identified that were designed to perform a variety of operating procedures (Yousef 2012).

Flexible-link manipulators play an important role in the overall stable operation of medical robots. The meaning of flexible-link manipulator has been reported as the robot whose flexibility of link (majorly torsion and bending) affects the position of the tip or joint parameters considerably (Sayahkarajy et al. 2016). A large weight manipulator poses disadvantages in terms of size, energy usage, and versatility. To mitigate these drawbacks researchers are working towards manufacturing flexible robotic manipulators. Flexible robotic manipulators offer benefits, like low energy consumption, reduced cost of production (Spong et al. 1989; Tzes et al. 1988). Such type of manipulators has a flexible arm that is of infinite order system of distributed parameters and incorporates the flexible additives. Owing to elastic properties of manipulators, system modeling and the associated model-based regulation is a complex task. A wide range of control strategies have been reported to form a controller that precisely control the flexible link’s vibrations and position within a short period so for deriving the equation for motion and for expressing the deflection of a point along the arm, the Euler-beam theory has been used (Geniele et al. 1997). Various control schemes, study, and construction of serial robotic manipulators have been addressed (Wolovich 1993; Gopal et al. 1976). Further ‘Timoshenko beam theory’ has been reported to flourish a mathematical model of flexible link manipulators (Loudini et al. 2007). The flexible robotic manipulator has mechanical flexibility, due to that fluctuation or oscillations can be seen either during or after the movement of a manipulator and can create uncertainty in medical operations especially in surgeries as well as in healthcare management. So it is important to investigate a robust control method for reducing the fluctuations or oscillations i.e. controlling the position of manipulator. To carry out this research, an effective variant of the flexible Link robotic manipulator has been used as a framework to analyze the robust control method.

In this work, the attention has been given to make the system more stable by maintaining the link’s angle of rotation at an appropriate position and to reduce end effectors’ fluctuations. This work aims to investigate an optimal control method for flexible link manipulators in medical robots where control of the position & oscillations is very important. For this purpose, three control methods like; Linear Quadratic Regulator (LQR), Pole Placement, and Proportional-Integral-Derivatives (PID) have been used to investigate the robust control method among them for controlling the position of a robotic manipulator with the flexible link for reliable operation of medical robots. Matlab® / Simulink platform has been used to analyze the result with real-time data of the physical manipulator system.

2 Dynamic modeling

The robotic manipulator has mechanical flexibility in their joints, due to vibration or oscillations that can be seen either during or after the movement of a manipulator. This behaviour reduces the precision of the position, but on the other hand, due to lower inertia and mass the flexibility can appear due to higher acceleration in the manipulator’s motion or long slender ties. Flexibility plays an essential role in a modern robotic system since it meets the requirement of automation industries (Javaid et al. 2020). In various applications, flexible mechanisms and flexible-link manipulators are playing an important role.

In robotics, flexibility causes vibrations and static deflections (Roshin and Shihabudheen 2013). Further non-linear dynamics also the reason for causing various control problems (Pratt and Williamson 1995). Because of such problems settling period ‘t_s’ is affected as non-linear vibrations, the accuracy of the endpoint is reduced (Roshin and Shihabudheen 2013; Pawar et al. 2018). They offer other advantages such as lower energy usage; maximize weight ratio, and reduced production costs. Figure 2 represents the elementary circuit and prototype of a manipulator with flexible link. The manipulator maintains the dynamics to attain the optimal performance that depends directly on the precision of the dynamic model and control algorithm’s efficiency.

Fig. 2

Elementary circuit & prototype of flexible link manipulator driven by DC motor

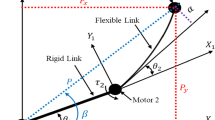
This dynamic model of ‘SLFM’ incorporates modeling of flexible link and rotational base with the help of Euler’s-Lagrange method. Langrangian of the system assessed by the estimation of the kinetic energy and potential energy. The Schematic diagram of an ‘SLFM’ with an angle of oscillation (β) and angle of rotation (θ) is illustrated in Fig. 3. The system input is voltage (${v}_{i}$) and output is obtained as a deflection angle or angle of oscillation (β) and gear angle (θ). Table 1 depicts the symbols used in modeling. This framework comprises a single low weight flexible arm with an appendage and powered by a base mounted DC motor. A servo amplifier controls the DC motor. This amplifier gets control signal within the range from − 5 to + 5v from the device through the ‘DAS20’ digital to analog converter. At each sampling period, the deviation of the shaft is assessed using an encoding device that is linked to the DC motor shaft. Figure 3 shows the end effector angle of rotation (θ) and angle of oscillation (β). The Lagrangian function (L) of the system

Fig. 3

Diagram of SLFM: single link flexible manipulator with oscillation angle (β) and rotation angle (θ)

Table 1 Robot manipulator’s parameters with flexible Link

$$L=Kinetic energy \left(KE\right)-Potential \, energy (PE)$$

(1)

According to Euler Lagrange equation

$$\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{p}}_{i}}\right)-\left(\frac{\partial L}{\partial {p}_{i}}\right)= {\tau }_{i}$$

(2)

here, ${p}_{i}$ is ${i}^{th}$ variable of the manipulator, ${\tau }_{i}$ is force or torque applied to ${i}^{th}$ link. So the total PE and KE with flexible link system is shown as follows-

$$\mathrm{PE }=\left(\frac{1}{2}{C}_{s}.{\beta }^{2}\right)$$

(3)

$$\mathrm{KE }=\left\{\left( \frac{1}{2}{J}_{eq}{\dot{\theta }}^{2}\right)+\frac{1}{2}{J}_{arm}\left(\dot{\theta } +\dot{\beta }\right)\right\}$$

(4)

Now let, that β and θ are two generalized coordinates. So

$$\frac{\partial }{\partial t}\left(\frac{\partial L}{\partial {\dot{\theta }}}\right)-\left(\frac{\partial L}{\partial \theta }\right) ={\tau }_{op} -\dot{\theta }\gamma$$

(5)

$$\frac{\partial }{\partial t}\left(\frac{\partial L}{\partial {\dot{\theta }}}\right)-\left(\frac{\partial L}{\partial \theta }\right)=0$$

(6)

From Eq. (3), (4) and (5) we get,

$$L=\left(\frac{1}{2}{J}_{eq}{\dot{\theta }}^{2}\right)+\left\{ \frac{1}{2}{J}_{arm}\left(\dot{\theta } +\dot{\beta }\right)\right\}-\left\{\frac{1}{2}{C}_{s}.{\beta }^{2}\right\}$$

(7)

After solving Eq. (5), (6) and (7) we get

$${{\tau }_{op} =({J}_{eq}\ddot{\theta } +C}_{s}.\beta )=0$$

(8)

Here, ${\tau }_{op}=\left(\frac{{C}_{m}^{2}\eta+{\mathrm{N}}^{2}{\mathrm{R}}_{\mathrm{a}}\upgamma }{{R}_{a}}\right)$ is the output torque.

From Eqs. (7) and (8) we obtain

$${\ddot{\theta}}=\beta .\frac{{C}_{s}}{{J}_{eq}}-\frac{{\eta}{C}_{m}^{2}{\text{N}}+{\text{R}}_{\text{a}}\upgamma }{{R}_{a}}\dot{\theta }+{v}_{i} \eta \frac{{\text{N}C}_{m}}{{J}_{eq}{R}_{a}}$$

(9)

$$\ddot{\alpha }=\left\{\upbeta \frac{\left({J}_{eq}+{J}_{arm}\right){K}_{stiff}}{{J}_{arm}{J}_{eq}}\right\}+\left\{{\eta}\dot{\theta }\frac{{C}_{m}^{2}{\mathrm{N}}^{2}+ {R}_{a}\upgamma }{{J}_{eq}{J}_{arm}}\right\}- \left\{\frac{{\eta{C}}_{m}\mathrm{N}}{{{J}_{arm}J}_{eq}}{v}_{i}\right\}$$

(10)

By choosing state variable x(t) a state-space model has been obtained for flexible link manipulator as

$X\left(t\right)=\left[\theta\, \beta\, \dot{\theta }\, \dot{\beta\, }\right]$

$$X\left( t \right) = Ax\left( t \right) + Bu\left( t \right)$$

(11)

$$y\left(t\right)= x(t)C$$

(12)

A state-space model is obtained by writing the equations in matrix form as given below-

$$\left[\begin{array}{c}\dot{\theta }\\ \dot{\beta }\\ \ddot{\theta }\\ \ddot{\beta }\end{array}\right]=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& \frac{{C}_{S}}{{J}_{eq}}& -\frac{{\eta}_{g}{C}_{t}{C}_{m}{\eta}_{m}{\mathrm{N}}^{2}+{R}_{m}\gamma }{{R}_{m}{J}_{eq}}& 0\\ 0& -\frac{{C}_{s}\left({J}_{link}+{J}_{eq}\right)}{{J}_{link}{J}_{eq}}& \frac{{\eta}_{g}{C}_{t}{C}_{m}{\eta}_{m}{\mathrm{N}}^{2}+{R}_{m}\gamma }{{R}_{m}{J}_{eq}}& 0\end{array}\right]\left[\begin{array}{c}\theta \\ \beta \\ \dot{\theta }\\ \dot{\beta }\end{array}\right]$$

$$+\left[\begin{array}{c}0\\ 0\\ \frac{{\eta}_{g}{\eta}_{m}N{C}_{t}}{{R}_{m}{J}_{eq}}\\ \frac{-{\eta}_{g}{\eta}_{m}N{C}_{t}}{{R}_{m}}\end{array}\right]{v}_{i}$$

(13)

$$\mathrm{Y }(\mathrm{t}) = [1 \,0 \,0 \,0] \left[\begin{array}{c}\theta \\ \beta \\ \dot{\theta }\\ \dot{\beta }\end{array}\right]$$

(14)

For this work, the values for different real-time parameters of the manipulator with flexible link are listed in Table 1. These values are utilized to evaluate the matrices of the manipulator. Putting the parameters in Eq. (13) and (14) with numerical values shown in Table 1, Eqs. (15), and (16) are obtained.

$$\left[\begin{array}{c}\dot{\theta }\\ \dot{\beta }\\ \ddot{\theta }\\ \ddot{\beta }\end{array}\right]=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 663.070& -30.16& 0\\ 0& -1003.07& 30.16& 0\end{array}\right]\left[\begin{array}{c}\theta \\ \beta \\ \dot{\theta }\\ \dot{\beta }\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 60.63\\ -60.63\end{array}\right]{v}_{i}$$

(15)

$$\mathrm{Y }(\mathrm{t}) = [1 \,0 \,0 \,0] \left[\begin{array}{c}\theta \\ \beta \\ \dot{\theta }\\ \dot{\beta }\end{array}\right]$$

(16)

3 Control methods utilized for manipulator with flexible link

Several methods of control are designed to hold the measured output to the target value to improve the result or to reduce the error (Federlein 1989). Here, the following methods of control like; ‘Pole placement’, ‘LQR’, and ‘PID’ have been utilized to investigate the optimal method for the control of position and fluctuations of the manipulator with the flexible link.

3.1 Proportional-integral-derivatives (PID) method of control

‘PID’ is the control method or a controller used in a variety of disciplines. Due to their robustness, they are easy to incorporate in design, so they are widely used in various areas like industrial processes, medical applications, etc. (Moudgal et al. 1994). PID controller evaluates the mismatch among the measured output and the setting of the reference, and attempt to reduce the gap that is called ‘error’. PID control method optimizes the system’s transient performance by mitigating the peak over-shoot & settling period that has the potential to alleviate the error by using integral action (Pawar et al. 2018; Pan et al. 2019). The diagram of the PID control method is depicted in Fig. 4, where the input signal is set to point u(t), and the controller output is

Fig. 4

Structure of Parallel Proportional-integral-derivatives (PID) Controller

$$F\left(t\right)=\left\{{K}_{P}e\left(t\right)\right\}+ \left\{{K}_{I }\int e\left(t\right)dt\right\}+\left\{{K}_{d}\frac{d}{dt}e(t)\right\}$$

(17)

Here,${K}_{p}$- proportional gain; delivers an overall control operation through the all-pass gain factor which is proportional to the error signal, and ${K}_{d}$- derivative gain; enhance the transient output by providing high-frequency differentiator compensation. The consequences of the above parameters on the effectiveness of closed-loop system are listed in Table 2.

Table 2 Consequence of Independent tuning for Parameters of PID (‘ ’: increasing, ‘ ’: decreasing)

3.2 Tuning process for PID controller

‘Tuning’ is a method that is used to achieve the system’s optimized response by analyzing the parameters of the PID model. This is an essential process for systems (closed-loop). ‘N’ numbers approaches are available to tune the parameters of this controller. They are splitting as closed & open loop methods.

• Open-loop Method

In its manual state, this system tunes the controller and the plant continues to run in open-loop mode. Many strategies fall under this group.

These techniques are:

• ‘Cohen-Coon’ Technique

• Minimum error criteria(IAE,ISE,ITE)

• Ziegler- Nichols Technique (Open-loop)

• ‘C-H-R’ Technique

• ‘IMC’ Technique

• Closed-loop Method

This method refers to those where controller tuning is performed during the auto condition wherein the plant is executing in a closed loop. Several techniques come under this category:

• Damped oscillation Technique

• Ziegler-Nichols Technique

• Tyreus-Luyben Technique

3.3 Pole-placement method

Full State Feedback or Pole Placement method is a vital segment of the advanced control system, assisted by effective state feedback in which the system can be established with reduced deflections and improved stability (Zahidi et al. 2012). This method allows poles to be placed by the specifications. Let

$$\dot{x}(t)=\left\{A x\left(t\right)+B u(t)\right\}$$

(18)

$$y(t)=\left\{C x\left(t\right)+D u(t)\right\}$$

(19)

Here, A: system matrix of (n x n), B: input matrix of (n × 1), and C: output matrix of (1 × n). The input signal provided as

$$u\left(t\right)=[-K]x\left(t\right)$$

(20)

Here, K is given as a matrix of gain. Figure 5, depicts the basic process of controlling the feedback system. Putting, Eq. 20 in 18, expression of closed-loop system’s state variables given as:

Fig. 5

Schematic of State feedback process

$$\dot{x}\left(t\right)=x\left(t\right)\left[A-KB\right]=x(t){A}_{f}$$

(21)

The system must be controllable for the implementation of it. This method is employed at the feedback system for positioning of a plant’s closed-loop poles at the required s-plan position. The main aim of this control method is the positioning of dominant poles as well as all poles at required places. As per pole placement method, the ‘K’ is given in a fashion so that

$$\left|sI-\left(A-BK\right)\right|=\left(S-{a}_{1}\right)\left(s-{a}_{2}\right)\dots \dots .(s-{a}_{n})$$

(22)

where the required location of poles are ${a}_{1}{a}_{2}\dots ..{a}_{n}$. for obtaining the ‘K’ matrix, the following strategies are used

• First, acquire the model.

• Test the controllability

• Then Find the required characteristics equation

• Finally, solve matrix ‘K’

3.4 LQR method

The quadratic method plays a significant role in the controller in control systems. The control framework can be measured and interpreted in the form of state variables. Figure 6 illustrates the schematic of ‘LQR’. The control signal for the LQR method is provided as –

Fig. 6

Schematic of Linear quadratic regulator

$$u=-xK$$

(23)

So

$$J= \left\{\frac{1}{2}{\int }_{0}^{\infty }({Qx}^{T}x+{Ru}^{T}u)dt\right\}$$

(24)

here, ‘R' as a definite and ‘Q’ denotes semi-definite matrix. So putting the value of ‘u’ in Eq. 24, resultant is given as

$$J= \left\{\frac{1}{2}{\int }_{0}^{\infty }{x}^{T}x(Q+{KK}^{T}R)dt\right\}$$

(25)

The ‘J’ can be full-filled with energy function. Here in ‘J’ the control input ‘u(t)’ and state ‘x(t)’ is weighted, so they can’t be substantial. If the PI is reduced, then finite reveal the- closed-loop structure where it needs to be balanced or stable. Let’s take a constant square matrix ‘P’ to get robust feedback ‘K’ as

$$\frac{d}{dt}({x}^{T}{Px)=-x}^{T}\left(Q+{RKK}^{T}\right)x$$

Substituting in Eq. (24) yield: (26)

$$J=- \frac{1}{2}{\int }_{0}^{\infty }\frac{d}{dt}\left({x}^{T}Px\right)dt=\frac{1}{2}{x}^{T}\left(0\right)Px(0)$$

(26)

In a linear quadratic regulation problem ‘K’ is quadratic and ascertain for reducing the ‘J’. To check the feedback variables ‘K’, it begins with searching the model of the system. By using error & trial process design parameters of ‘R’ and ‘Q’ are selected. Further Eq. 27 has been solved for getting the matrix ‘P’. By choosing the gain ‘PI’ as Eq. (27), ‘J’ can be minimized as:

$$K={R}^{-1}{PB}^{T}$$

(27)

The P (n x n) matrix is determined from Eq. (28), called “Algebraic Riccati Equation” (ARE).

$$\left(Q+AP+{PA}^{T}-{B}^{T}PB{R}^{-1}P\right)=0$$

(28)

4 Results and discussions

4.1 Open-loop behavior

A flexible link manipulator has been simulated with step input references using MATLAB® / Simulation platform. As a result Fig. 7 shows the instability of the system without a controller.

Fig. 7

open loop behaviour of system

4.2 PID control method results

For controlling the position, the Ziegler Nichols method has been utilized to design the PID controller (Yucelen et al. 2006; Copeland 2008). The resultant gains for this controller obtained from the Ziegler Nichols method have been listed in Table 3.

Table 3 Gain of PID controller with the help of Ziegler Nichols Method

Figure 8, illustrates the PID controller’s position i.e. step response of theta using PID. From the results, the system has been found stabilized and achieved the steady-state error zero within a second. Here, the rise time meets the requirement but the overshoot and settling period must be minimized. Figure 9, shows the result for tracking error using PID.

Fig. 8

Step response of theta using PID control method

Fig. 9

Tracking error using PID control method

4.3 Pole placement method

The main aim of this control method is the positioning of dominant poles as well as all poles at required places. To enforce this method system needs to be controllable. Here, new poles have been inserted in such a fashion that they must be placed on the left side for a stability point of view. The required pole locations are as follow:

P = [− 15, − 012, − 010, − 014, 016]

Using the command ‘K = place (A B, p)’, K matrix is

K = [6.14180, − 1.98290, 0.3240, 0.16930, 16.2687]

Figure 10 indicates the simulation result of theta by using the value of the ‘K’ in series with state variables. From the result, the response has been found better in comparison to the PID control method but one thing that is important to check is larger the settling time. Further Fig. 11, illustrates the theta dot response that is faster with no oscillation than PID. Figure 12 indicates the simulation result for the deflection angle, and Fig. 13 depicts the result for beta dot. Figure 14 depicts the performance for tracking error through the pole-placement method.

Fig. 10

Theta response via step signal

Fig. 11

Response of theta dot

Fig. 12

Response of Beta

Fig. 13

Behaviour of Beta dot

Fig. 14

Tracking error

4.4 Linear quadratic regulator method

Matrix ‘Q’ (selecting weights) is given as

Q = diag (80, 10, 1, 50)

The feedback gains are

K = [6.1480, − 1.9829, 0.3239, 0.1693]

Figure 15 reveals the LQR simulation response for the manipulator with a flexible link. From the gain ‘K’, it is evident from the response that the LQR control method yields faster response in comparison to PID as well as pole placement methods. Figure 16, 17, 18, 19 illustrate the results of theta dot, the beta response, beta dot response, tracking error using LQR respectively. Figure 20 and 21 depicts a comparison graph of theta, and 2norm error for the flexible link manipulator respectively. It explicitly showcases that the LQR method of control performs better in comparison to PID and Pole-Placement methods of control.

Fig. 15

Response of theta under reference input

Fig. 16

Response of theta dot

Fig. 17

Response of Beta

Fig. 18

Beta dot response

Fig. 19

Tracking error using Linear quadratic regulator method

Fig. 20

Comparison of theta for LQR, PID and Pole-Placement methods

Fig. 21

2norm error for flexible link manipulator

5 Conclusions

As the whole world is suffering from COVID-19 pandemic, many of the front line staff like; doctors, nurses, and supporting staff are getting affected by this virus due to community transmission and lack of social distancing. During such a situation where social distancing is the key factor for reducing community transmission of this coronavirus, medical robots come into the picture as helping hands. The medical robots are comprised of manipulator arms with rigid or flexible links. Due to the increasing demand of these medical robots in various applications reliable operations, wherein control of fluctuation as well as the position becomes highly essential. The flexible robotic manipulator has mechanical flexibility, due to that vibration or oscillations can be seen either during or after the movement of a manipulator and can create uncertainty in medical operations. So it is important to investigate a robust control method for controlling the position of manipulator. In this paper, dynamic modeling has been done by utilizing the Euler–Lagrange’s approach through state-space modeling for a flexible link manipulator extensively used in medical robots. The behavior of open-loop reveals the instability of the system. To investigate the robust control method for the reliable operation of medical robots, three control-methods have been utilized. For the PID control method, Matlab® / Simulation has been performed and ultimately the system found stabilized. During this time, the position attains zero steady-state error. Furthermore, the rise time has been observed fulfilled as per requirement, but both overshoots as well as settling time need to be improved. For this purpose pole placement method of control is utilized. From the results, it is clear that the pole placement method is improved in comparison to the PID method of control but the obtained response is unsatisfactory for vibration as well as position control of the manipulator's arm with flexible link thus provide an unreliable operation to medical robots. So to achieve better response the linear quadratic regulator method of control has been incorporated. From linear quadratic regulator method, it has been found that the manipulator achieves quicker response using LQR controller feedback gain in comparison to the PID and Pole Placement methods that consequently offers improved control in term of position and stability and thus reduce the chances of accidents and provides the overall reliable operation to medical robots.